基于Fractal模型的复电阻率法2.5D有限元数值模拟

doi:10.11720/wtyht.2022.1377

基于Fractal模型的复电阻率法2.5D有限元数值模拟

龙秀洁^,¹, 陈汉波^,², 莫亚军¹, 区小毅¹, 卢胜辉¹

1.广西壮族自治区地球物理勘察院,广西柳州 545005

2.桂林理工大学地球科学学院,广西桂林 541006

Fractal model-based 2.5 D finite element modeling of complex resistivity method

Long Xiu-Jie^,¹, Chen Han-Bo^,², Mo Ya-Jun¹, Ou Xiao-Yi¹, Lu Sheng-Hui¹

1. Guangxi Geophysical Investigation Institute,Liuzhou 545005,China

2. College of Earth Sciences, Guilin University of Technology,Guilin 541006,China

通讯作者: 陈汉波,(1990-),男,博士后,主要从事电磁场数值模拟与反演研究工作。Email:chenhanbo@glut.edu.cn

责任编辑: 王萌

收稿日期: 2021-07-9 修回日期: 2021-10-11

基金资助:

桂林理工大学科研启动基金(RD2100002165)
中国博士后科学面上基金(2021MD703820)

Received: 2021-07-9 Revised: 2021-10-11

作者简介 About authors

龙秀洁,(1989-),男,工程师,从事地球物理勘查及相关研究工作。Email: 496178747@qq.com

摘要

复电阻率法在油气资源、矿产勘查中发挥了重要的作用,为了深刻认识复电阻率法异常特征变化规律,本文对复电阻率2.5D正演问题展开研究。首先直接给出复电阻率法2.5D有限元正演所满足的变分问题,并详细地推导相应的刚度矩阵的计算过程。引入Fractal模型作为等效模型研究频谱激电异常特征。对单元内的复电导率及复电位均进行线性插值,而后,采用不完全LU分解的稳定双共轭梯度算法求解有限元线性方程组,获得异常复电位值。设计3个典型的地电模型验证了本文算法的正确性及精确性,并分析了不同装置下,不同频率的2.5D复电阻率异常响应特征。数值模拟结果表明,采用Fractal模型研究激发极化异常特征是可行、有效的;不同装置、不同频率下的复电阻率法异常特征有着显著的差异。

关键词： 有限元; 复电导率; Fractal模型; 异常复电位

Abstract

This study proposed the variational problem of 2.5D finite element forward modeling of the complex resistivity method and detailed the process of solving stiff matrix of finite equations. The Fractal model was introduced as a research model for studying the equivalent induced polarization anomalies of spectra. Furthermore, the complex conductivity and complex potential of a grid unit were linearly interpolated. Then, to obtain anomalous complex potential, finite element linear equations were solved using the biconjugate gradient stabilized method with incomplete LU decomposition. The results of three typical geoelectric models validated the correctness and accuracy of the algorithm proposed in this study. Furthermore, this study analyzed the abnormal response characteristics of 2.5D complex resistivity under different frequencies.

Keywords： finite element method; complex resistivity; Fractal model; anomalous complex potential

PDF (7643KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

龙秀洁, 陈汉波, 莫亚军, 区小毅, 卢胜辉. 基于Fractal模型的复电阻率法2.5D有限元数值模拟[J]. 物探与化探, 2022, 46(4): 887-896 doi:10.11720/wtyht.2022.1377

Long Xiu-Jie, Chen Han-Bo, Mo Ya-Jun, Ou Xiao-Yi, Lu Sheng-Hui. Fractal model-based 2.5 D finite element modeling of complex resistivity method[J]. Geophysical and Geochemical Exploration, 2022, 46(4): 887-896 doi:10.11720/wtyht.2022.1377

0 引言

复电阻率法是一种重要的地球物理勘探方法,具有电性参数多的特点,在金属矿勘探领域起着重要的作用,较其他物探方法具有抗干扰能力强,多参数对比解释可提供更丰富的异常信息的优点。近年来,该方法被广泛应用于石油地震勘探、水文地质调查等领域^[1]。

国内外学者对于复电阻率法数值模拟做了大量的研究,取得众多成果。如国内的罗延钟等^[2-3]、张桂清等^[4]、刘菘等^[5]。国外的研究者,如G.W. Hohmann等^[6]、A. Weller等^[7]、D.W. Oldenburg等^[8]等。然而,大多对于频谱激电法的研究均基于Core-Core模型,且没有考虑复电导率呈线性变化的情况。因此,本文在前人的基础上,基于异常复电位法,采用Fractal模型^[9]研究复电导率呈线性变化的复电阻率法2.5D有限元数值模拟,并对其相应的异常响应特征进行分析,以期能为复电阻率法野外实际工作提供理论依据。

1 复电阻率法边值问题

1.1 Fractal 模型

Fractal 模型是由B.R.P. Rocha提出用来描述岩、矿石激发极化现象的数学模型,B.R.P. Rocha等^[9]对大量岩、矿石标本及露头进行测量,结果表明,岩、矿石的激发极化响应所引起的复电阻率可用以下公式进行表述:

(1)ρ(ω)=ρ₀

[1 - m (1 - \frac{1}{1 + \frac{1 + u}{δ_{r} (1 + v)}})]

r_h,

其中:ρ₀为岩、矿石未极化的直流电阻率;m为介质的极化率(无量纲);δ_r为矿物颗粒电阻率百分比;r_h=1/(1+iωτ₀);u=iωτ(1+v); v=(iωτ_f)^-^η; τ为双层振荡相关的松弛时间常数;τ₀为采样松弛时间常数;τ_f为分形松弛时间;η为介质的分形几何直接相关的参数(无量纲)。

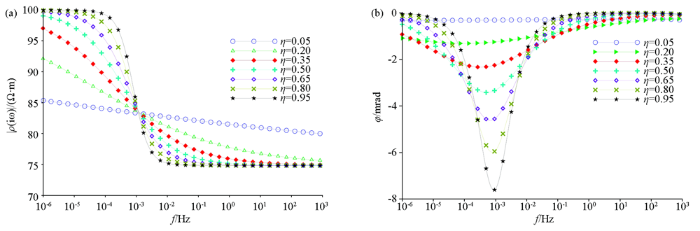
式(1)对于定量描述岩矿石的激发极化现象提供了一种新的手段,相对于常用的core-core模型来说,其提供了更多的岩石物性参数,从而可以更详细地解释岩矿石激发极化效应所产生的原因及影响因素。图1展示了不同η的复电阻率的振幅和相位随着频率的变化规律。计算参数为:ρ₀=100 Ω·m、m=0.5、δ_r=1.0、τ=10^-6 s、τ₀=10^-12 s、τ_f=100、η分别取0.05、0.20、0.35、0.5、0.65、0.80、0.95。由图1可以看得到复电祖率ρ(ω)幅值随着频率的增大而递减,在低频时,且η取较小值时,复电祖率幅值趋向于ρ₀。而相位φ的绝对值与η成正比,在低频及高频时趋向于0。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 不同η时的复电阻率振幅(a)及相位频谱(b)

Fig.1 The amplitude (a) and phase (b) of complex resistivity for different frequency exponent

1.2 基于Fractal模型的复电阻率变分问题

点源条件下,复电阻率法2.5D变分问题如下所示:

(2)

\begin{matrix} \begin{array}{l} F (\bar{u}) = \int_{Ω} [\frac{1}{2} σ {(\nabla \bar{u})}^{2} + \frac{1}{2} σ k^{2} {\bar{u}}^{2} + σ' \nabla {\bar{u}}_{0} \nabla \bar{u} + σ' k^{2} {\bar{u}}_{0} \bar{u}] d Ω + \\ \int_{Γ_{\infty}} \frac{k [K_{1} (k r_{A}) c o s (r_{A}, n) - K_{1} (k r_{B}) c o s (r_{B}, n)]}{K_{0} (k r_{A}) - K_{0} (k r_{B})} (\frac{1}{2} σ {\bar{u}}^{2} + σ' {\bar{u}}_{0} \bar{u}) d Γ \\ δ F (\bar{u}) = 0 \end{array} \end{matrix}

其中:Ω为研究区域; $Γ_{\infty}$ 为无穷远边界;σ为介质的复电导率;σ₀为均匀介质的复电导率(电源点处的电导率);σ'=σ-σ₀ 为介质的异常复电导率,k为波数;K₀ 、 K₁分别为零阶和1阶贝塞尔函数;r_A、r_B分别为观测点距源点的距离; ${\bar{u}}_{0}$ 为正常复电位。可通过以下公式进行计算:

(3)

{\bar{u}}_{0} = \frac{I K_{0} (k r_{A}) - I K_{0} (k r_{B})}{2 π σ_{0}},

式中:I为电流大小。

2 有限单元法分析

2.1 有限单元剖分

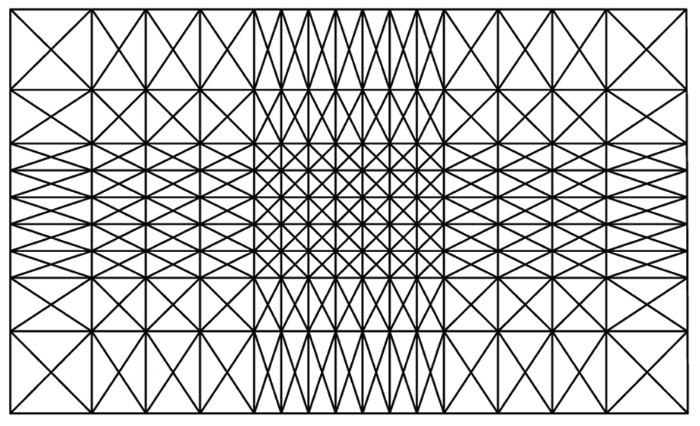
采用矩形网格进一步细分为4个三角形网格剖分方式对研究区域进行剖分,如图2所示:将方程(2)对研究区域Ω和无穷边界 $Γ_{\infty}$ 的积分分为各个单元的积分之和:

(4)

\begin{array}{l} F (\bar{u}) = \sum_{Ω} \int_{Ω} [\frac{1}{2} σ {(\nabla \bar{u})}^{2} + \frac{1}{2} σ k^{2} {\bar{u}}^{2}] d Ω + \sum_{Ω} \int_{Ω} [σ' \nabla {\bar{u}}_{0} \nabla \bar{u} + σ' k^{2} {\bar{u}}_{0} \bar{u}] d Ω + \\ \sum_{Ω} \int_{Γ_{\infty}} (\frac{k [K_{1} (k r_{A}) c o s (r_{A}, n) - K_{1} (k r_{B}) c o s (r_{B}, n)]}{K_{0} (k r_{A}) - K_{0} (k r_{B})}) \frac{1}{2} σ {\bar{u}}^{2} d Γ + \\ \begin{array}{l} \sum_{Ω} \int_{Γ_{\infty}} (\frac{k [K_{1} (k r_{A}) c o s (r_{A}, n) - K_{1} (k r_{B}) c o s (r_{B}, n)]}{K_{0} (k r_{A}) - K_{0} (k r_{B})}) σ' {\bar{u}}_{0} \bar{u} d Γ \\ δ F (\bar{u}) = 0 \end{array} \end{array}

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 有限单元网格剖分示意

Fig.2 Sketch of finite element mesh

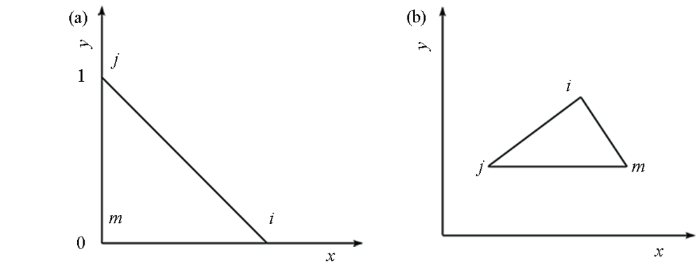
在单元内对复电位及复电导率进行线性插值。线性插值的母单元与子单元如图3所示。则单元内的复电位及复电导率则可表示为

(5)

\bar{u} = N_{1} {\bar{u}}_{1} + N_{2} {\bar{u}}_{2} + N_{3} {\bar{u}}_{3},

(6)

σ=N₁σ₁+N₂σ₂+N₃σ₃,

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 线性插值的母单元(a)及子单元(b)

Fig.3 Parent element (a) and sub-element(b) of linear interpolation

其中:N₁、N₂、N₃为插值形函数; ${\bar{u}}_{1}$ 、 ${\bar{u}}_{2}$ 、 ${\bar{u}}_{3}$ 为三角单元节点复电位;σ₁、σ₂、σ₃为单元节点复电导率。形函数的具体形式如下所示:

(7)N₁=

\frac{1}{2 Δ}

(a₁x+b₁y+c₁);N₂=

\frac{1}{2 Δ}

(a₂x+b₂y+c₂);N3₌

\frac{1}{2 Δ}

a3_x+b3_y+c3₎,

其中:a₁=y₂-y₃ ;a₂=y₃-y₁ ;a₃=y₁-y₂ ;b₁=x₃-x₂ ;b₂=x₁-x₃ ;b₃=x₂-x₁ ;c₁=x₂y₃-x₃y₂ ;c₂=x₃y₁-x₁y₃ ;c₃=x₁y₂-x₂y₁ ;Δ= $\frac{1}{2}$ (a₁b₂-a₂b₁) 为三角单元面积。

2.2 单元分析

方程(4)中的第1项

(8)

\begin{matrix} \int_{Ω}^{} [\frac{1}{2} σ {(\nabla \bar{u})}^{2}] d Ω = \int_{Ω} \frac{1}{2} σ [{(\frac{\partial \bar{u}}{\partial x})}^{2} + {(\frac{\partial \bar{u}}{\partial y})}^{2}] d x d y = \frac{1}{2} {\bar{u}}_{e}^{T} K_{1 e} {\bar{u}}_{e}, \end{matrix}

其中:

(9)

\begin{matrix} K_{1 e} = \frac{(σ_{i} + σ_{j} + σ_{m})}{12 Δ} [\begin{array}{l} a_{i} a_{i} + b_{i} b_{i} & a_{i} a_{j} + b_{i} b_{j} & a_{i} a_{m} + b_{i} b_{m} \\ a_{i} a_{j} + b_{i} b_{j} & a_{j} a_{j} + b_{j} b_{j} & a_{j} a_{m} + b_{j} b_{m} \\ a_{i} a_{m} + b_{i} b_{m} & a_{j} a_{m} + b_{j} b_{m} & a_{m} a_{m} + b_{m} b_{m} \end{array}], \end{matrix}

方程(4)积分第2项

(10)

\begin{matrix} \int_{Ω}^{} \frac{1}{2} σ k^{2} {\bar{u}}^{2} d Ω = \frac{1}{2} σ k^{2} {\bar{u}}_{e}^{T} \int_{Ω}^{} N N^{T} d Ω {\bar{u}}_{e} = \frac{1}{2} {\bar{u}}_{e}^{T} K_{2 e} {\bar{u}}_{e}, \end{matrix}

其中

(11)

\begin{matrix} K_{2 e} = \frac{k^{2}}{60 Δ} [\begin{array}{l} 6 σ_{i} + 2 σ_{j} + 2 σ_{m} & 2 σ_{i} + 2 σ_{j} + σ_{m} & 2 σ_{i} + σ_{j} + 2 σ_{m} \\ 2 σ_{i} + 2 σ_{j} + σ_{m} & 2 σ_{i} + 6 σ_{j} + 2 σ_{m} & σ_{i} + 2 σ_{j} + 2 σ_{m} \\ 2 σ_{i} + σ_{j} + 2 σ_{m} & σ_{i} + 2 σ_{j} + 2 σ_{m} & 2 σ_{i} + 2 σ_{j} + 6 σ_{m} \end{array}], \end{matrix}

方程(4)积分第3项

(12)

\begin{matrix} \int_{Γ_{\infty}} (\frac{k [K_{1} (k r_{A}) c o s (r_{A}, n) - K_{1} (k r_{B}) c o s (r_{B}, n)]}{K_{0} (k r_{A}) - K_{0} (k r_{B})}) \frac{1}{2} σ {\bar{u}}^{2} d Γ = \frac{1}{2} {\bar{u}}_{e}^{T} K_{3 e} {\bar{u}}_{e}, \end{matrix}

其中:

(13)

\begin{matrix} K_{3 e} = \frac{k [K_{1} (k r_{A}) c o s (r_{A}, n) - K_{1} (k r_{B}) c o s (r_{B}, n)]}{K_{0} (k r_{A}) - K_{0} (k r_{B})} [\begin{array}{l} 3 σ_{i} + σ_{j} & σ_{i} + σ_{j} & 0 \\ σ_{i} + σ_{j} & σ_{i} + 3 σ_{j} & 0 \\ 0 & 0 & 0 \end{array}], \end{matrix}

方程(4)积分第4项

(14)

\begin{matrix} \int_{Ω}^{} σ' \nabla {\bar{u}}_{0} \nabla \bar{u} d Ω = {\bar{u}}_{e}^{T} K_{1 e}^{'} {\bar{u}}_{e 0}, \end{matrix}

其中:

(15)

\begin{matrix} K'_{1 e} = \frac{(σ'_{i} + σ'_{j} + σ'_{m})}{12 Δ} [\begin{array}{l} a_{i} a_{i} + b_{i} b_{i} & a_{i} a_{j} + b_{i} b_{j} & a_{i} a_{m} + b_{i} b_{m} \\ a_{i} a_{j} + b_{i} b_{j} & a_{j} a_{j} + b_{j} b_{j} & a_{j} a_{m} + b_{j} b_{m} \\ a_{i} a_{m} + b_{i} b_{m} & a_{j} a_{m} + b_{j} b_{m} & a_{m} a_{m} + b_{m} b_{m} \end{array}], \end{matrix}

方程(4)积分第5项

(16)

\begin{matrix} \int_{Ω} σ' k^{2} {\bar{u}}_{0} \bar{u} d Ω = {\bar{u}}_{e}^{T} K'_{2 e} {\bar{u}}_{e 0}, \end{matrix}

其中:

(17)

\begin{matrix} K'_{2 e} = \frac{k^{2}}{60 Δ} [\begin{array}{l} 6 σ'_{i} + 2 σ'_{j} + 2 σ'_{m} & 2 σ'_{i} + 2 σ'_{j} + σ'_{m} & 2 σ'_{i} + σ'_{j} + 2 σ'_{m} \\ 2 σ'_{i} + 2 σ'_{j} + 2 & 2 σ'_{i} + 6 σ'_{j} + 2 σ'_{m} & σ'_{i} + 2 σ'_{j} + 2 σ'_{m} \\ 2 σ'_{i} + σ'_{j} + 2 σ'_{m} & σ'_{i} + 2 σ'_{j} + 2 σ'_{m} & 2 σ'_{i} + 2 σ'_{j} + 6 σ'_{m} \end{array}], \end{matrix}

方程(4)积分第6项

(18)

\begin{matrix} \int_{Γ_{\infty}} (\frac{k [K_{1} (k r_{A}) c o s (r_{A}, n) - K_{1} (k r_{B}) c o s (r_{B}, n)]}{K_{0} (k r_{A}) - K_{0} (k r_{B})}) σ' {\bar{u}}_{0} \bar{u} d Γ = {\bar{u}}_{e}^{T} K'_{3 e} {\bar{u}}_{e 0}, \end{matrix}

式中:

(19)

\begin{matrix} K'_{3 e} = \frac{k [K_{1} (k r_{A}) c o s (r_{A}, n) - K_{1} (k r_{B}) c o s (r_{B}, n)]}{K_{0} (k r_{A}) - K_{0} (k r_{B})} [\begin{array}{l} 3 σ'_{i} + σ'_{j} & σ'_{i} + σ'_{j} & 0 \\ σ'_{i} + σ'_{j} & σ'_{i} + 3 σ'_{j} & 0 \\ 0 & 0 & 0 \end{array}], \end{matrix}

2.3 总体合成

在单元内,将式(9)、式(11)、式(13)、式(15)、式(17)、式(19)的积分结果进行相加后,再扩展成由全体节点组成的矩阵或列阵:

(20)F(

\bar{u}

\frac{1}{2} {\bar{u}}^{T}

(K₁_e+K₂_e+K₃_e)

\bar{u}

{\bar{u}}^{T}

(

K_{1 e}^{'}

K_{2 e}^{'}

K_{3 e}^{'}

)

{\bar{u}}_{0}

\frac{1}{2} {\bar{u}}^{T}

K_e

\bar{u}

{\bar{u}}^{T} K_{e}^{'} {\bar{u}}_{0}

式中: ${\bar{u}}^{T}$ 、 ${\bar{u}}_{0}$ 为所有场值的列向量;K_e、K'_e为扩展矩阵。

2.4 求解线性方程组

对方程(20) 进行求变分:

(21)δF(

\bar{u}

)=δ

{\bar{u}}^{T}

K_e

\bar{u}

+δ

{\bar{u}}^{T}

K'_e

{\bar{u}}_{0}

令δF( $\bar{u}$ )=0,有

(22)δ

{\bar{u}}^{T}

K_e

\bar{u}

=-δ

{\bar{u}}^{T} K_{e}^{'} {\bar{u}}_{0}

又因δ ${\bar{u}}^{T}$ ≠0,有

(23)K_e

\bar{u}

=K'_e

{\bar{u}}_{0}

。

求解方程(22)便可得波数域中的异常复电位值。本文采用不完全LU分解的稳定双共轭梯度算法来求解线性方程组,具体求解过程请详见文献[10],在此不再赘述。求解出异常复电位后,再通过傅里叶反变换便可得到三维空间中的异常复电位。

2.5 复电阻率的计算

求解出三维空间中的异常复电位,便可按照以下公式计算复电阻率及相位值:

(24)ρ_s=k

\frac{\bar{u} (M) - \bar{u} (N)}{I}

+ρ₀,

(25)φ_s=arctan

[\frac{R e (ρ_{s})}{I m (ρ_{s})}]

\frac{180}{π}

其中:k为装置系数; $\bar{u} (M)$ 、 $\bar{u} (N)$ 为接收电极M、N处异常复电位;ρ₀为按式(1)计算出来的均匀介质的复电阻率值。

3 模型计算

3.1 模型1

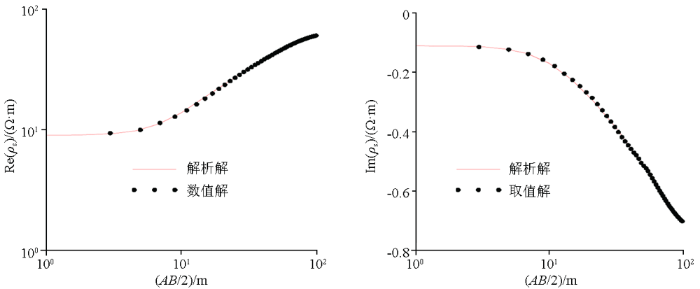
为了检验文中算法及所编制的程序的正确性,设置一个两层水平层状极化介质模型,厚度为6 m,电阻率为100 Ω。Fractal模型参数如表1所示。供电频率f=0.125 Hz,将2.5D有限元数值解与一维数字滤波算法所计算出来的解析解进行对比,如图4所示。由图4可知,复电阻率的实分量和虚分量数值解与解析解基本一致,从而验证了本文所述算法及所编制的程序的正确性。

表1 模型1参数

Table 1 parameters of the first model

n	h/m	ρ₀/(Ω·m)	m	δ_r	τ/μs	τ_f/ms	η	τ₀/ps
1 2	5 ∞	100 10	0.906 0.885	4.959 4.877	23.43 18.72	10 100	0.20 0.44	1.0 1.0

新窗口打开| 下载CSV

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 2.5维有限元数值解与一维数字滤波解析解对比

Fig.4 Comparison of 2.5D FEM result with numerical filter wave numerical solution

3.2 模型2

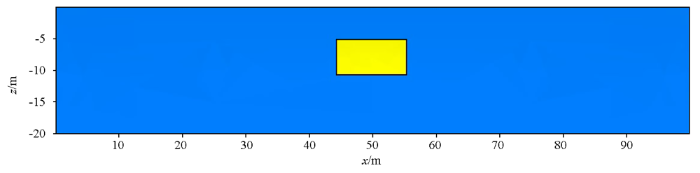
模型2 为极化半空间中有一异常体。具体几何参数如图5所示,Fractal模型参数如表2所示。图6、图7为频率为0.125、0.25、0.5、1.0 Hz的复电阻率法2.5D有限元数值模拟结果。由图6、图7可看到,复电阻率的各分量都很好地反映出异常体的存在,且异常响应范围与异常体的埋藏位置基本吻合。在计算的频率范围内,复电阻率的相位及虚分量均为负值,偶极装置下的复电阻率振幅和相位均呈“八”字型异常特征,特别值得注意的是复电阻率的虚分量,其幅值随着频率的增大而减小,且远小于实分量。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 模型2断面示意

Fig.5 Cross section of second model

表2 模型2的Fractal 模型参数

Table 2 Fractal parameters of the second model

Kind	ρ₀/(Ω·m)	m	δ_r	τ/μs	τ_f/ms	η	τ₀/ps
半空间异常体	5200 1470	0.906 0.885	4.959 4.877	23.43 18.72	10 100	0.20 0.44	1.0 1.0

新窗口打开| 下载CSV

图6

新窗口打开| 下载原图ZIP| 生成PPT

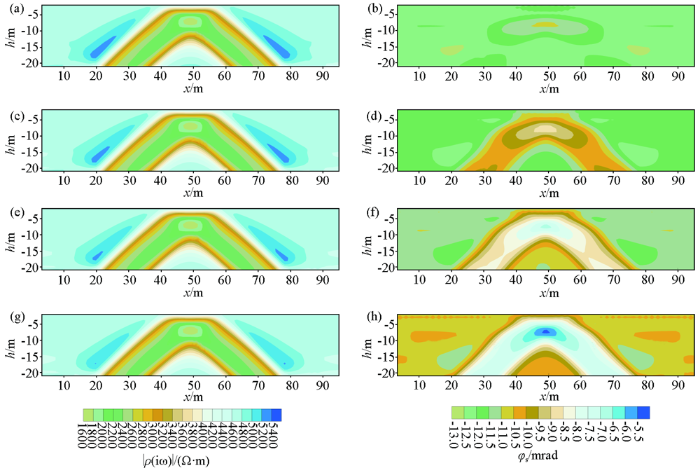
图6 给定频率的偶极—偶极测量方式复电阻率振幅(左列)和相位(右列)拟断面

a、b—0.125 Hz;c、d—0.25 Hz;e、f—0.5 Hz;g、h—1.0 Hz

Fig.6 The pseudo section of amplitude and phase of apparent complex resistivity in dipole-dipole array for giving the frequencies

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 给定频率的对称四极测量方式复电阻率实部(左列)和虚部(右列)拟断面

a、b—0.125 Hz;c、d—0.25 Hz;e、f—0.5 Hz;g、h—1.0 Hz

Fig.7 The pseudo section of real and imaginary component of apparent complex resistivity in four-pole array for giving the frequencies

3.3 模型3

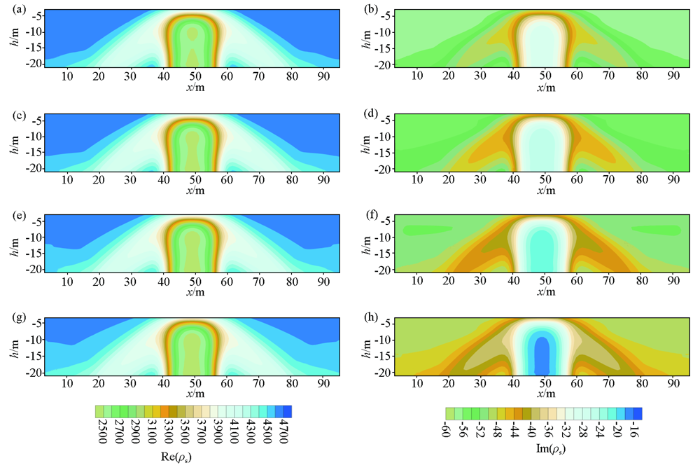
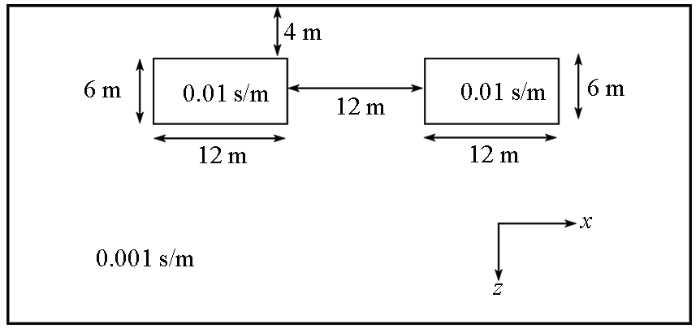
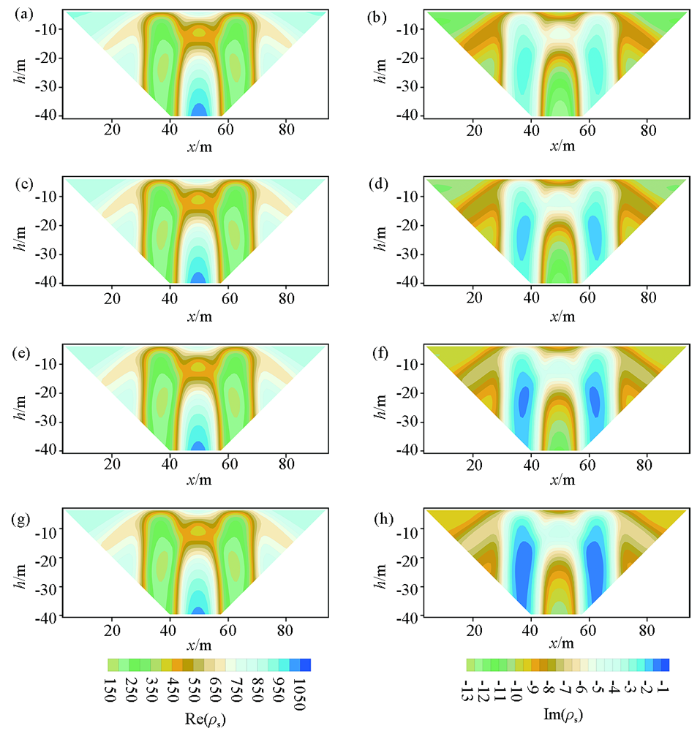
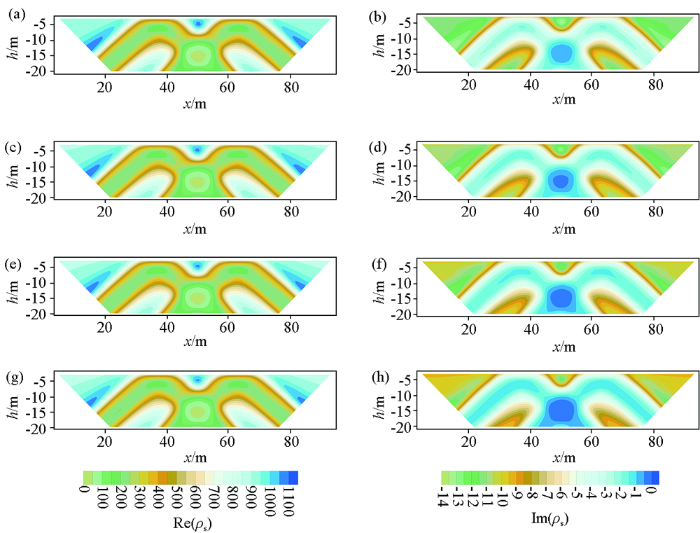
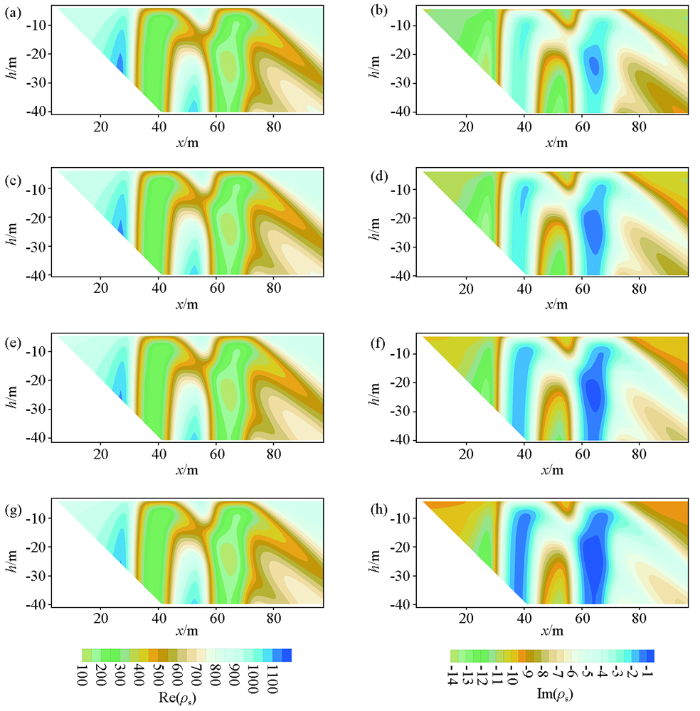
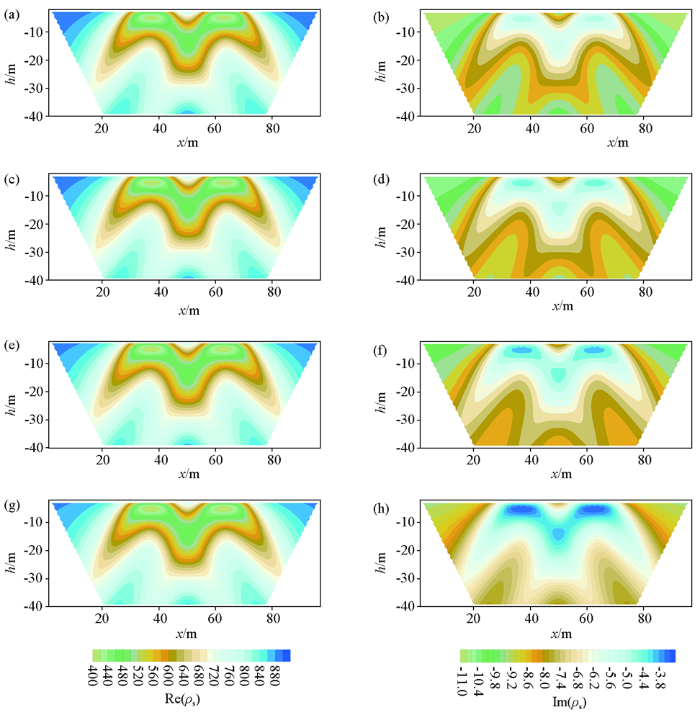
为了进一步验证本文算法的有效性,设计一个极化半空间中有双异常体模型。异常体大小均为12 m×6 m,埋深维4 m,两者相距12 m。异常体电导率为0.01 s/m,背景介质的电导率为0.001 s/m。具体几何参数如图8所示,Fractal模型参数如表3所示。图9~12为频率为0.125、0.25、0.5、1.0 Hz的不同测量装置下的复电阻率法2.5D有限元数值模拟结果。由图9~12可看到,复电阻率的各分量都很好地反映出异常体的存在,且异常响应范围与异常体的埋藏位置基本吻合。在计算的频率范围内,4种测量装置下的视复电阻率的虚分量均为负值;对称四极装置下,复电阻率的实部和虚部呈现双“柱体”型异常特征,如图9所示;如图10所示,偶极装置下的复电阻率实部和虚部均呈双“八”字型异常特征;从图11可知,三极测量装置,复电阻率的实部和虚部的异常特征与对称四极类似,不过虚部的右侧部分的值大于左侧;如图12可知,二极装置下,可以看到复电阻率的异常位置与模型非常吻合,其纵向分辨率较于三极和对称四极测量装置高。同样,我们可以观察到,在4种测量装置下,复电阻率的实部随着频率的增大,产生的变化不大;不同于实部分量,复电阻率的虚分量,其幅值随着频率的增大而减小,且远小于实分量。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 模型3断面示意

Fig.8 Cross section of second model

表3 模型3的Fractal 模型参数

Table 3 Fractal parameters of the second model

Kind	ρ₀/ (Ω·m)	m	δ_r	τ/μs	τ_f/ms	η	τ₀/ps
半空间	1000	0.906	4.959	23.43	10	0.20	1.0
异常体 (左)	100	0.885	4.877	18.72	100	0.44	1.0
异常体 (右)	100	0.885	4.877	18.72	100	0.44	1.0

新窗口打开| 下载CSV

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 给定频率的对称四极测量方式复电阻率实部(左列)和虚部(右列)拟断面

a、b—0.125 Hz;c、d—0.25 Hz;e、f—0.5 Hz;g、h—1.0 Hz

Fig.9 The pseudo section of real and imaginary component of apparent complex resistivity in four-pole array for giving the frequencies

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 给定频率的偶极—偶极测量方式复电阻率实部(左列)和虚部(右列)拟断面

a、b—0.125 Hz;c、d—0.25 Hz;e、f—0.5 Hz;g、h—1.0 Hz

Fig.10 The pseudo section of real and imaginary component of apparent complex resistivity in dipole-dipole array for giving the frequencies

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 给定频率的三极剖面测量方式复电阻率实部(左列)和虚部(右列)拟断面

a、b—0.125 Hz;c、d—0.25 Hz;e、f—0.5 Hz;g、h—1.0 Hz

Fig.11 The pseudo section of real and imaginary component of apparent complex resistivity in pole-dipole array for giving the frequencies

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 给定频率的二极测量方式复电阻率实部(左列)和虚部(右列)拟断面

a、b—0.125 Hz;c、d—0.25 Hz;e、f—0.5 Hz;g、h—1.0 Hz

Fig.12 The pseudo section of real and imaginary component of apparent complex resistivity in pole-pole array for giving the frequencies

4 结论

本文实现了复电阻率法2.5D有限元数值模拟,采用异常复电法,避免了源的奇异性的影响,提高了数值解的精度;引入Fractal 模型对频率域激发极化响应进行研究,可以为更好解释激发极化效应提供一种新的手段;对复电导率及复电位进行线性插值,可以模拟更为真实的野外地质情况;分析了所设计的地电模型的复电祖率异常响应特征,可为野外实际勘探提供理论依据。数值模拟结果验证了本文基于Fractal 模型的CR2.5D有限元数值模拟算法的正确性和精确性,表明引入Fractal 模型研究复电导率呈线性变化的CR响应特征是可行的、有效的。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

杨振威, 郑伟, 李晓斌, 等.

频谱激电法的发展与展望

[J]. 物探与化探, 2015, 39(1):22-28.

[本文引用: 1]

Yang

Z W

, Zhen

, Li

X B

, et al.

The development and prospect of the spectral induced polarization method

[J]. Geophysical and Geochemical Exploration, 2015, 39(1):22-28.

[本文引用: 1]

[2]

罗延钟, 张桂青. 频率域激电法原理[M]. 北京: 地质出版社, 1988.

[本文引用: 1]

Luo

Y Z

, Zhang

G Q

. Principle of frequency domain IP method[M]. Beijing: Geological Publishing House, 1988.

[本文引用: 1]

[3]

罗延钟, 方胜.

视复电阻率频谱的一种近似反演方法

[J]. 地球科学, 1986, 11(1) : 9-102.

[本文引用: 1]

Luo

Y Z

, Fang

An approximate invrtsion of the apparent complex resistivity spectrum

[J]. Earth Science, 1986, 11(1) : 9-102.

[本文引用: 1]

[4]

张桂青, 崔先文, 罗延钟.

一种反演频谱激电法视频谱求取真参数的方法

[J]. 地质与勘探, 1987, 23(4) : 48-54.

[本文引用: 1]

Zhang

G Q

, Cui

X W

, Luo

Y Z

The Determination of intrinsic parameters by inversing IP apparent spectrum

[J]. Geology and Exploration, 1987, 23(4) : 48-54.

[本文引用: 1]

[5]

刘崧, 官善友, 高鹏飞.

求极化椭球体真 Cole-Cole 参数的联合谱激电反演

[J]. 地球物理学报, 1994, 37(S1) : 542-551.

[本文引用: 1]

Liu

, Guan

S Y

, Gao

P F

Joint sip inversion for estimation of intrinsiccole-cole parameters of apolarizable ellipsoid

[J]. Chinese Journal of Geophysice, 1994, 37(S1) : 542-551.

[本文引用: 1]

[6]

Hohmann

G W

Three-dimensional induced polarization and electromagnetic modelling

[J]. Geophysics, 1975, 40 (2) :309-324.

DOI:10.1190/1.1440527 URL [本文引用: 1]

[7]

Weller

, Seichter

, Kampke

Induced-polarization modelling using complex electrical conductivities

[J]. Geophys. J. Int., 1996, 127(1):387-398.

DOI:10.1111/j.1365-246X.1996.tb04728.x URL [本文引用: 1]

[8]

Oldenburg

D W

, Li

Inversion of induced polarization data

[J]. Geophysics, 1994, 59 (9) :1327-1341.

DOI:10.1190/1.1443692 URL [本文引用: 1]

[9]

Rocha

B R P

, Habashy

T M

. Fractal geometry, porosity and complex resistivity. I: From rough pore interfaces to hand specimens, in: Developments in Petrophysics[M], London: Geological Society Publishing House, London, 1995.

[本文引用: 2]

[10]

柳建新, 蒋鹏飞, 童孝忠, 等.

不完全LU分解预处理的BICGSTAB算法在大地电磁二维正演模拟中的应用

[J]. 中南大学学报:自然科学版, 2009, 40(2):484 -491.

[本文引用: 1]

Liu

J X

, Jiang

P F

, Tong

X Z

, et al.

Application of BICGSTAB algorithm with incomplete LU decomposition preconditioning to two-dimensional magnetotelluric forward modeling

[J]. Journal of Central South University: Science and Technology, 2009, 40(2):484 -491.

[本文引用: 1]

频谱激电法的发展与展望

2015

... 复电阻率法是一种重要的地球物理勘探方法,具有电性参数多的特点,在金属矿勘探领域起着重要的作用,较其他物探方法具有抗干扰能力强,多参数对比解释可提供更丰富的异常信息的优点.近年来,该方法被广泛应用于石油地震勘探、水文地质调查等领域^[1]. ...

频谱激电法的发展与展望

2015

1988

... 国内外学者对于复电阻率法数值模拟做了大量的研究,取得众多成果.如国内的罗延钟等^[2-3]、张桂清等^[4]、刘菘等^[5].国外的研究者,如G.W. Hohmann等^[6]、A. Weller等^[7]、D.W. Oldenburg等^[8]等.然而,大多对于频谱激电法的研究均基于Core-Core模型,且没有考虑复电导率呈线性变化的情况.因此,本文在前人的基础上,基于异常复电位法,采用Fractal模型^[9]研究复电导率呈线性变化的复电阻率法2.5D有限元数值模拟,并对其相应的异常响应特征进行分析,以期能为复电阻率法野外实际工作提供理论依据. ...

1988

视复电阻率频谱的一种近似反演方法

1986

视复电阻率频谱的一种近似反演方法

1986

一种反演频谱激电法视频谱求取真参数的方法

1987

一种反演频谱激电法视频谱求取真参数的方法

1987

求极化椭球体真 Cole-Cole 参数的联合谱激电反演

1994

求极化椭球体真 Cole-Cole 参数的联合谱激电反演

1994

Three-dimensional induced polarization and electromagnetic modelling

1975

Induced-polarization modelling using complex electrical conductivities

1996

Inversion of induced polarization data

1994

1995

... Fractal 模型是由B.R.P. Rocha提出用来描述岩、矿石激发极化现象的数学模型,B.R.P. Rocha等^[9]对大量岩、矿石标本及露头进行测量,结果表明,岩、矿石的激发极化响应所引起的复电阻率可用以下公式进行表述: ...

不完全LU分解预处理的BICGSTAB算法在大地电磁二维正演模拟中的应用

2009

... 求解方程(22)便可得波数域中的异常复电位值.本文采用不完全LU分解的稳定双共轭梯度算法来求解线性方程组,具体求解过程请详见文献[10],在此不再赘述.求解出异常复电位后,再通过傅里叶反变换便可得到三维空间中的异常复电位. ...

不完全LU分解预处理的BICGSTAB算法在大地电磁二维正演模拟中的应用

2009

〈

〉