E-mail Alert Rss
 

物探与化探, 2022, 46(3): 729-736 doi: 10.11720/wtyht.2022.1216

方法研究·信息处理·仪器研制

基于组合震源编码的多尺度全波形反演方法

国运东,

中国石化集团中原油田分公司 物探研究院,河南 濮阳 457001

Multi-scale full waveform inversion method using combined source encoding

GUO Yun-Dong,

Geophysical Exploration Research Institute,Zhongyuan Oilfield Company of Sinopec,Puyang 457001,China

责任编辑: 叶佩

收稿日期: 2021-04-12   修回日期: 2022-01-14  

基金资助: 中原油田分公司科研项目(JC21-12)
中石化集团公司项目(P21003)

Received: 2021-04-12   Revised: 2022-01-14  

作者简介 About authors

国运东(1991-),男,博士后,2020年毕业于中国石油大学(华东),研究方向为全波形反演。Email: gyd_upc@edu.cn

摘要

全波形反演(full waveform inversion,FWI)是目前精度最高的一种速度反演工具,通过迭代反演得到高精度的地下构造,为叠前成像技术提供更准确的速度场,满足目前勘探开发日益复杂的需求。但FWI需要估计精确的震源子波,而从野外采集的地震数据提取子波是非常困难的,此外,反演过程中,模型参数与观测数据存在强的非线性关系,容易产生周波跳跃现象。针对中低波数反演过程中存在周波跳跃现象与地震子波难提取的问题,本文构建了一种基于组合震源的多尺度波形反演方法。首先对子波和地震数据进行时移组合叠加,再进行互相关梯度求取,只需要一次逆时偏移的计算量,就可以完成梯度的求取,实现多尺度反演的目标。通过模型试算,基于组合震源的FWI方法,可以达到多尺度反演的目的,使得反演结果更稳定;与不依赖子波的方法相结合,反演结果相对准确。

关键词： 全波形反演; 组合震源编码; 多尺度; 不依赖子波

Abstract

Full waveform inversion (FWI) is one of the most accurate velocity inversion tools.It can be used to obtain high-precision subsurface structures through iterative inversion and provide a more accurate velocity field for prestack imaging technology,thus satisfying the increasingly complex demand for petroleum exploration and development.However,FWI requires accurately estimated source wavelets,which are very difficult to extract from the seismic data collected in the field.Furthermore,in the inversion process,there is a strong nonlinear relationship between model parameters and observed data,which is liable to induce cycle skipping.To overcome the cycle skipping and the difficulty in extracting seismic wavelets in the inversion process of medium-low wavenumber,this paper developed a multi-scale waveform inversion method using combined source encoding.Specifically,the wavelets and seismic data were combined by applying time-shift stacking,and gradients can be determined through only one calculation of reverse time migration.According to the calculation results using a model,the FWI method using combined source encoding can be used to achieve multi-scale inversion and obtain more stable inversion results.Meanwhile,relatively accurate inversion results can be obtained by combining this method with a source-independent method.

Keywords： full waveform inversion; combined source encoding; multi-scale inversion; source-independent inversion

PDF (3548KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

国运东. 基于组合震源编码的多尺度全波形反演方法[J]. 物探与化探, 2022, 46(3): 729-736 doi:10.11720/wtyht.2022.1216

GUO Yun-Dong. Multi-scale full waveform inversion method using combined source encoding[J]. Geophysical and Geochemical Exploration, 2022, 46(3): 729-736 doi:10.11720/wtyht.2022.1216

0 引言

全波形反演方法(FWI)综合利用地震数据的走时、相位、振幅等全波场信息,通过地震数据与模拟数据的差值建立目标泛函,不断更新地下参数模型,使得模拟地震数据越来接近观测数据,从而达到建立不同参数场的目标,是一种高精度、高分辨率的物性参数建模方法。20世纪80年代,Tarantola[1-2]首先建立了FWI基于L2范数的观测数据和模拟数据差值泛函,奠定了波形反演的理论框架,FWI逐步成为地球物理工作者的研究热点。但是由于波形反演是一种迭代的计算过程,计算量巨大并受当时计算硬件的限制,导致FWI方法发展甚是缓慢。20世纪90年代,Song等和Pratt等将全波形反演方法从时间域推广到到频率域,建立了一套完整的频域FWI理论[3-4]。近年来随着计算机的迅速发展,特别是大型CPU集群以及GPU显卡的发展,全波形反演方法得到更多学者的广泛关注与发展,介质从简单到复杂,从声介质到弹性介质[5-6],再到各向异性[7]以及各向异性弹性介质[8⇓-10];反演参数逐步增多,从单一速度参数反演到速度、密度、各向异性、黏滞系数等多参数联合反演[11];反演过程在不同反演域中进行,从时间域发展到频率域,再到Laplace域[12]以及Laplace-Fourier域[13]等;近年来针对FWI不同问题的解决方法也相继被提出[14⇓⇓-17]。

全波形反演中参数模型与地震观测数据存在强的非线性关系,当地震数据主频较高时,其对初始模型的依赖性高,当初始模型与真实模型差异过大时,则会产生周波跳跃的现象。20世纪80年代Claerbout等指出地震数据中的低频成分对于背景速度场中的反演较为敏感[18],Jannane等分析得到数据中的高频成分对于速度扰动(反射系数)较为敏感[19]。Bunks等提出分频多尺度反演方法与网格多尺度反演方法,指出在大网格、低频尺度下反演的背景速度场,可以有效地解决全波形反演的周波跳跃问题[20];Sirgue等给出了频域多尺度FWI的频率选取策略[21];Boonyasiriwat等构建了地震数据的维纳滤波器[22],在获取准确地震子波的基础上,实现了时域FWI的多尺度方法。

波形反演过程中,需要多次迭代进行参数更新,每次除了进行求取梯度的波场正演与残差反传外,还需要多次正演模拟求取步长等额外的计算量,因此计算量巨大的问题也一直是限制FWI实用化的重要因素。早在1992年Rietveld等人指出应用控制照明的方法将单炮地震记录合成平面波编码的地震波记录,然后应用传统偏移方法处理,面炮成像在目标区域取得较好的效果,同时比传统逐炮偏移方法计算效率大大提高[23⇓-25]。Romero等通过相位编码的方法来压制不同炮间的串扰噪声,通过应用几种不同的编码方法,获得了较好的偏移剖面[26-27]。Vigh和Starr将多震源技术引入到三维全波形反演中来提高反演效率,但会引入很多串扰噪声[28]。Krebs 等在全波形反演过程中使用了动态极性编码方法[29],在得到与传统方法相近反演结果的同时,减小了一个数量级的计算量。随后,Tang等通过相位编码的多震源最小二乘方法,大大提高了反演成像的效率[30]。Schuster等通过详细分析多震源编码的各种影响因素,根据编码函数和相干项强度的关系,建立了多震源反演中编码函数与信噪比的定量关系[31-32]。Huang等和黄建平等实现了分频编码的多震源LSM,加快了反演成像的收敛速度[33⇓-35],并且其适用于移动观测系统。

通过分频方法可以有效地实现速度场的多尺度反演方法,克服反演过程中存在周波跳跃现象,提高全波形反演计算的稳定性,并且基于维纳滤波方法反演效果较好[34],但是维纳滤波需要准确的地震子波。为避免在数据域滤波,胡春辉和曲英铭等学者提出了时移多尺度反演方法[36⇓-38],其避免了对数据进行低通滤波的预处理步骤,通过计算梯度时使用多次时移成像,并应用加权求和获取低波数的更新梯度,这种时间域反演方法更加自然和巧妙,但是这种方法再求取更新梯度时需要多次时移成像。本节进一步发展了一种组合震源的方法,首先对子波和地震数据进行时移组合叠加,再进行互相关梯度求取,只需要一次逆时偏移的计算量,就可以完成梯度的求取,实现多尺度反演。

1 方法原理

基于L2范数全波形反演理论的目标函数为:

E(v)=∑n=1Ns‖p(v,sn)-dn‖2,

其中E(v)为目标函数,p(v,sn)为用震源sn对速度模型v正演模拟的炮记录,dn为野外观测的地震记录,Ns为炮记录的总数量。

为提高反演的计算效率将编码技术引入到反演过程,并对震源和炮记录进行编码,并且本文将所有炮都编成一个超级炮,得到基于编码的多震源波形反演的目标函数[29]:

E(v)=‖p(v,∑n=1Nsen⊗sn)-∑n=1Nsen⊗dn‖2,

式中:en为编码矩阵序列,⊗表示时间域褶积。需要指出的是,对于正交极性编码序列en来源于正交矩阵e满足或近似满足以下条件:eeT=I,其中T表示矩阵转置运算,I为对角单位阵。

对子波和地震数据进行时移组合叠加,得到新的目标函数:

E(v)=‖p[v,∑iCmax∑n=1Nsen⊗sn(t-τi)]-∑iCmax∑n=1Nsen⊗dn(t-τi)‖2,

其中,τi为第i次的时移量,Cmax为组合叠加的个数,本文发现一般选取3就可以达到理想的反演效果。

梯度求取公式不变,只是换成组合震源的伴随源即可:

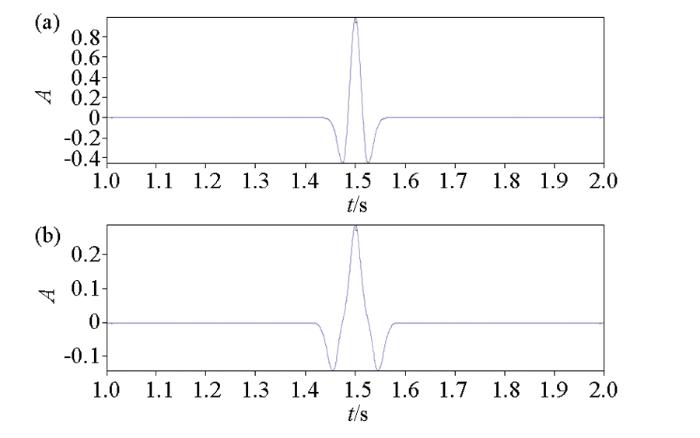
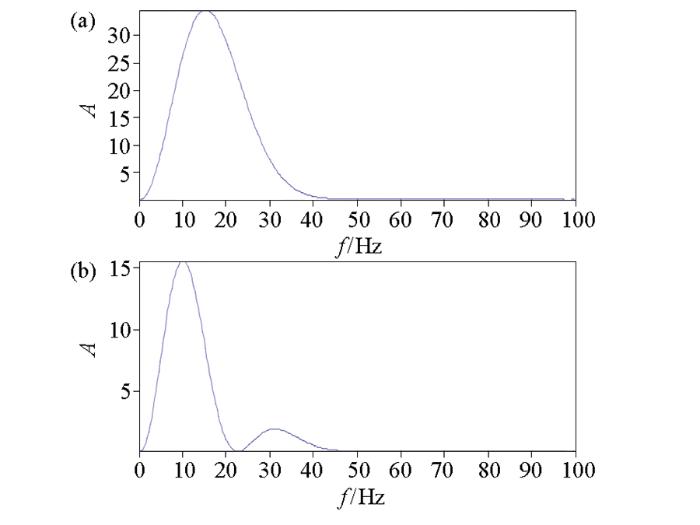
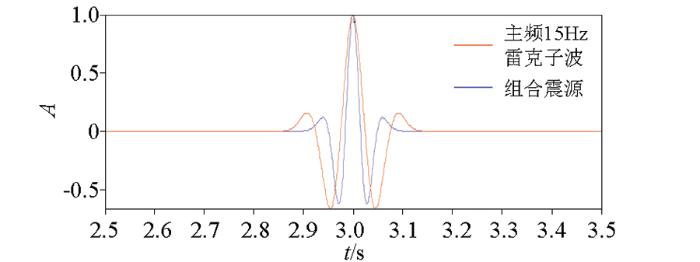
gk=δE(v)δv=2v3∑t∂2p[v,∑iCmax∑n=1Nsen⊗sn(t-τi)]∂t2,L†E(v)∑tp[v,∑iCmax∑n=1Nsen⊗sn(t-τi)],p[v,∑iCmax∑n=1Nsen⊗sn(t-τi)]。

本文对地震子波的组合震源进行了时域和频域的分析,说明组合震源方法在多尺度反演的有效性。假设震源子波是主频为15 Hz的雷克子波,其波形如图1a所示,对震源子波进行时移组合,其中时移参数的选取至关重要,本文后面会进行讨论,发现半波长的时移组合可以达到理想的效果。在这先做出半波长的时移波形图(图1b)和频谱图(图2b),一般记波峰到波谷选取半波长(在组合时移中一般选取半波长减去几个点为最佳选取组合)。通过组合时移的波形图可以看出通过组合时移,子波波形明显变宽。本文中仅需两次时移组合,权值矩阵为[0.25,0.5,0.25],通过频谱分析,发现组合震源子波的频带明显往低频端移动,从15 Hz的主频位置移动到10 Hz主频位置。通过分析一维目标泛函的形态曲线(图3),得出组合震源子波的目标泛函互相关函数,出现局部极值的宽度明显增加。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   不同子波时间域波形示意

a—主频15 Hz的雷克子波波形;b—半波长的组合震源波形

Fig.1   Waveform diagram in time domain of different wavelet

a—Rake wavelet waveform with dominant frequency of 15 Hz;b—half wavelength combined source waveform


图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   不同子波频谱示意

a—主频15 Hz的雷克子波频谱;b—时移半波长的组合震源频谱

Fig.2   Spectrogram of different wavelet spectrum

a—Rake wavelet spectrum with dominant frequency of 15 Hz;b—half wavelength combined source spectrum


图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   不同子波互相关示意

Fig.3   Cross correlation of different wavelets


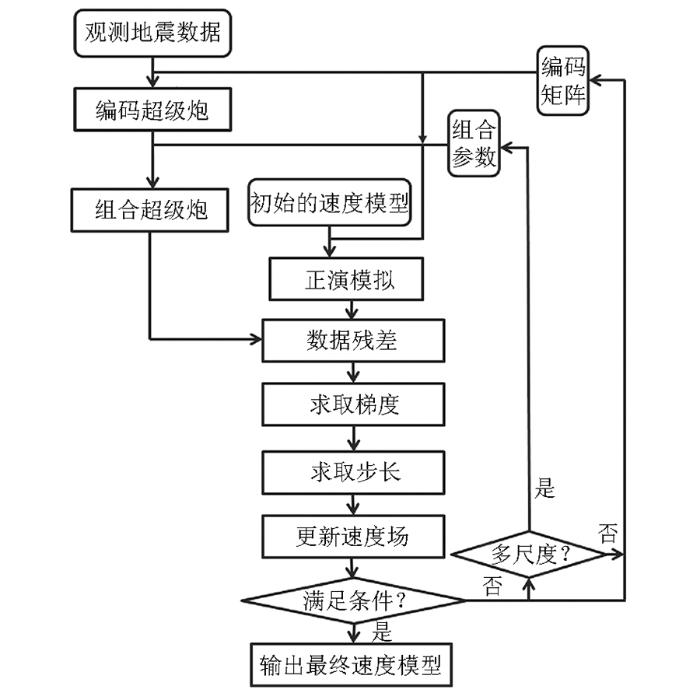
从组合震源编码的全波形反演方法流程图4可知:相比于传统的全波形反演方法,其每次反演都需要选取不同的组合参数,对炮记录先进行编码形成超级炮,然后对超级炮进行时移组合,可以有效地减少计算量;对震源子波先进行组合得到组合震源,再用组合震源进行编码,形成超级炮正演,并且在不同的迭代过程中选择动态编码方法,压制部分串扰。并且相对于传统的时移全波形反演,再进行互相关梯度求取,只需要一次逆时偏移的计算量移的计算量,就可以完成梯度的求取,大大减少了计算量,实现多尺度反演。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   组合震源编码的全波形反演流程

Fig.4   The flow of combine coding FWI


2 模型测试

使用Marmousi模型(图5a)进行测试,来验证本文方法的有效性。速度模型大小为4.6 km×1.5 km,横纵向网格间距均为10 m,速度从1.5~5.5 km/s变化。放炮数量为46,炮间隔100 m,为避免反演假像和检波点分布在表面每个网格点上。采用一个线性梯度速度模型,从1.5 km/s增加到4 km/s(平均速度略低于真实模型),作为反演的初始模型(图5b)。反演过程中水层速度为1.5km/s,并设为恒定。采用交错网格一阶有限差分方程进行正演模拟和伴随波场的计算,时间精度为2阶,空间精度为8阶。

图5

新窗口打开| 下载原图ZIP| 生成PPT

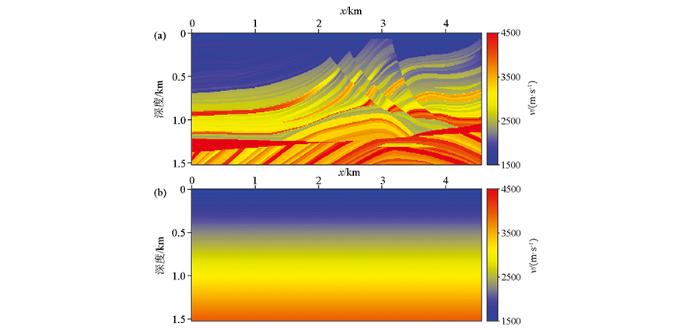
图5   反演用的真实速度模型(a)和初始速度模型(b)

Fig.5   The waveform inversions velocity model with the real model(a) and the initial model(b)


为说明所提出的组合震源FWI方法的特征,将组合震源的震源项与传统方法产生的震源炮记录进行比较,其中权值矩阵为[0.25,0.50,0.25],组合时移参数选取为半波长。图6a展示了单炮地震观测记录,图6b显示了组合震源单炮地震记录;图6c显示了基于极性编码的记录超级炮,图6d显示了组合震源FWI的观测记录超级炮。通过传统炮记录和组合震源炮记录可以看出不管是单炮记录或者编码超级炮记录组,组合震源炮记录的地震同相轴明显变宽,说明其数据更加凸显低波数成分,对大尺度构造的反演能力相对增强。

图6

新窗口打开| 下载原图ZIP| 生成PPT

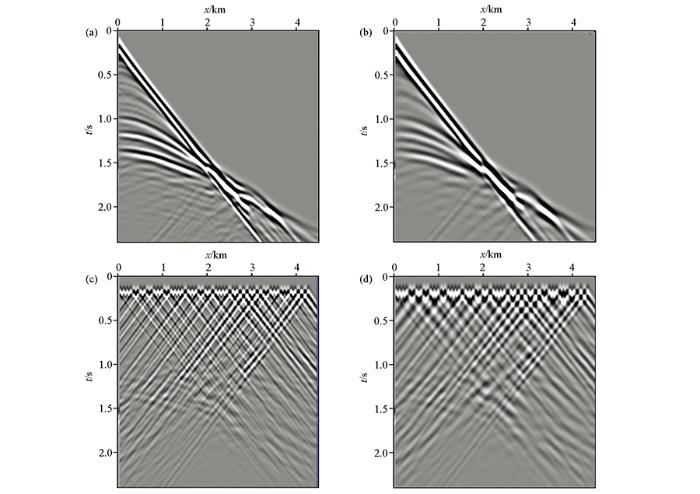
图6   不同观测地震记录以及对应的组合震源炮记录

a—Marmousi模型雷克子单炮地震记录;b—组合震源单炮记录;c—极性编码超级炮记录;d—组合震源超级炮记录

Fig.6   Different shot gathers generated by the Marmousi model using the Rake wavelet and the combine gather of different shot gathers

a—single shot gather generated by the Marmousi model using the Rake wavelet;b—single shot gather with the combined source;c—super shot gather with polarity coding;d—super shot gather with the combined source


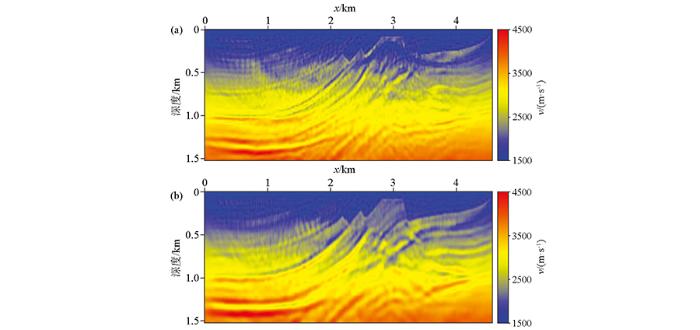
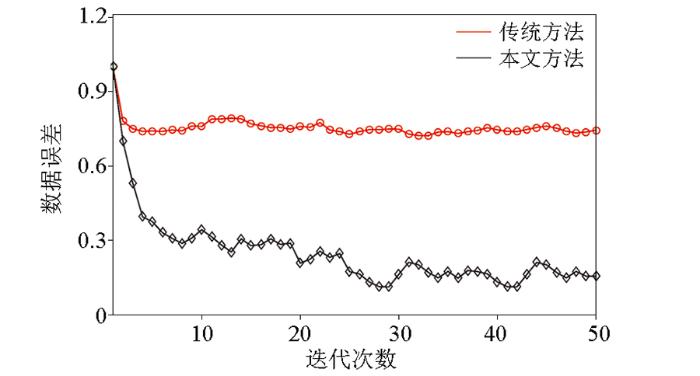
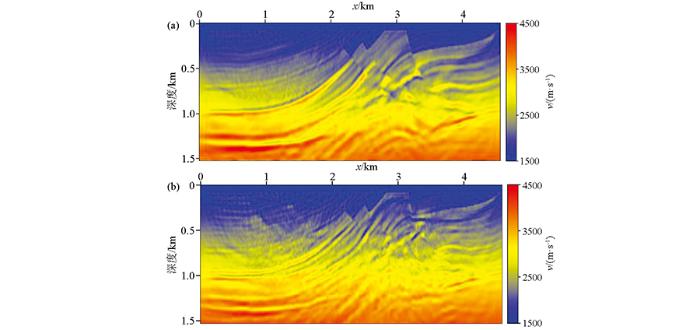
使用主频15 Hz的Ricker子波作为震源项的常规FWI的反演结果如图7a所示。由于地震数据的主频较高,在反演过程中存在周波跳跃问题,在较浅的区域中含有一些较强的反演噪声。对于较深的区域,反演的速度模型中仅看出少部分结构背景以及含有较强的背景噪声,这是因为伴随源中高频组分能量要强得多。为验证本文方法的多尺度反演效果,利用上面提出的反演策略进行速度场构建,组合参数从半波长到0变化,采用相同的迭代次数,反演结果如图7b所示。由于初始速度场采用的是线性梯度模型,其与真实模型存在显著差异,因此组合震源FWI反演结果其深部结构的反演效果也不够好。但是,与常规FWI的反演结果相比,可以看出在很大程度上克服了周波跳跃问题,较浅部分(深度小于0.5 km,水平位置:2~4 km)的反演结果与真实的速度模型非常接近。通过收敛的误差曲线(图8)可以看出本文方法可以收敛到更低的水平。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   常规FWI反演(a)和使用组合震源的FWI(b)反演结果对比

Fig.7   The inversion results for with conventional FWI(a) and FWI using combine source inversion strategy(b)


图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   不同反演方法的数据误差曲线

Fig.8   Convergence curves of different multi-source FWIs


在测试中发现,组合震源反演对于组合时移参数的选取十分关键,发现时移参数选取过小,不能改善的反演效果有限,当时移参数τi=0时,组合震源的反演与常规方法一致,但是当时移参数选取过大时,反演不仅不能取得好的效果,而且有可能会变差。本文建议时移参数选取半波长,并且越接近反演效果越好。为对比反演参数对结果的影响,选取与2中维纳滤波结合组合震源反演方法一致,权值系数矩阵[c1,c2,c3]=[0.25,0.50,0.25],测试结果如图9所示。通过对比发现当时移组合参数选取0.25半波长时,反演的结果(图9a)比常规的维纳滤波方法具有改善,但是不如半波长的反演效果(图7b);当组合时移参数选取一个波长的时间长度,反演结果甚至不如常规的维纳滤波方法,出现了周波跳跃问题,复杂构造的反演变得不清晰,断层的反演也不准确(图9b)。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   不同组合时移参数反演

a—组合时移参数τ=0.25λ;b—组合时移参数τ=1.0λ

Fig.9   The inversion results with different combined time shift parameter

a—combined time shift parameters τ=0.25λ;b—combined time shift parameters τ=1.0λ


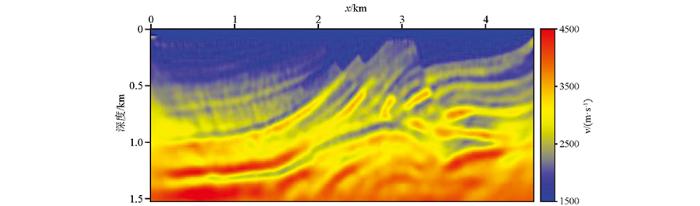
通过分频方法可以有效地实现速度场的多尺度反演,提高全波形反演计算的稳定性,且基于维纳滤波方法反演效果较好[34],但是维纳滤波需要准确的地震子波。而组合震源方法可以与不依赖子波的方法相结合达到多尺度反演的目的。首先,假设原始子波是主频率为15 Hz的Ricker子波,采用组合震源方法对数据进行处理,处理完的数据直接采用不依赖子波的反演方法,不依赖子波的方法选取基于卷积的方法,可以通过将收集的数据与来自正演波场的参考道和来自观测波场的参考道卷积从而达到消除震源子波的影响[39],其中参考道的选取采用极性编码加权的参考道的方法[40]。图10展示了不依赖子波的组合震源FWI的反演结果,可以看出反演的速度模型可以平稳地收敛到正确的位置。利用组合震源的多尺度反演方法,尽管分辨率相对于准确子波有所降低,但是成功避免了因为周波跳跃问题产生的反演假象。多尺度反演策略通过恢复速度模型中更多的波数分量,可以更好地应用所有数据成分,反演更加复杂的构造。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   不依赖子波的组合震源反演结果

Fig.10   The inversion results using combine-source multi-scale source independent FWI


3 结论及讨论

本文针对FWI在中低波数反演中,由于强非线性导致反演过程中存在周波跳跃问题,提出了新的多尺度反演策略,通过利用对子波和地震数据进行时移组合叠加,发展了一种组合震源的方法,通过模型试算对比分析,得出如下几点认识:

1)通过组合震源反演方法,可以实现从中低波数到高波数多尺度的反演策略,其可以有效地克服周波跳跃现象。基于组合震源的FWI方法与传统的维纳滤波相结合,突出低波数的成分,使得反演结果更加稳定;与不依赖子波的方法相结合实现多尺度的反演,反演结果相对准确。

2)基于组合震源的方法与多震源相结合,在进行互相关梯度求取时,只需要一次逆时偏移的计算量,就可以完成梯度的求取,与在梯度场的互相关叠加的方法相比,可以有效减少计算量。

3)组合震源的方法对于组合时移参数的选取比较关键,一般要小于波长并接近半波长,当地震数据的频率成分较高时,可以采用多次组合迭代策略,其可以进一步突出低频的成分,反演的结果更稳定。

虽然本文的组合震源方法可以特定地突出中低波数分量,但是如果地震数据中不存在低频成分也无能为力。因此如果地震数据缺少低频成分,可以采用包络、反射波反演等其他方法先进行背景速度更新。此外,本文采用极性编码多震源方法,在减少计算量的同时也存在串扰噪声影响,如果受观测系统的限制,比较难合成多震源数据,下一步可以发展不同观测系统下与组合震源相结合的方法,提高反演的稳定性。

参考文献

Tarantola A.

Inversion of seismic reflection data in the acoustic approximation

[J]. Geophysics, 1984, 49(8):1259-1266.

DOI:10.1190/1.1441754      URL     [本文引用: 1]

Tarantola A.

Inverse problem theory:Methods for data fitting and model parameter estimation

[J]. Physics of the Earth & Planetary Interiors, 1987, 57(3):350-351.

[本文引用: 1]

Song Z M, Williamson P R, Pratt R G.

Frequency-domain acoustic-wave modeling and inversion of crosshole data:Part II—Inversion method,synthetic experiments and real-data results

[J]. Geophysics, 1995, 60(3):796-809.

DOI:10.1190/1.1443818      URL     [本文引用: 1]

Pratt R G.

Seismic waveform inversion in the frequency domain,Part 1:Theory and verification in a physical scale model

[J]. Geophysics, 1999, 64(3):888-901.

DOI:10.1190/1.1444597      URL     [本文引用: 1]

Mora P.

Nonlinear two-dimensional elastic inversion of multi-offset seismic data

[J]. Geophysics, 1987, 52(9):1211-1228.

DOI:10.1190/1.1442384      URL     [本文引用: 1]

Wang G C, Du Q Z.

Elastic full waveform inversion based on envelope objective function

[J]. Geophysical Prospecting for Petroleum, 2016, 55(1):133-141.

[本文引用: 1]

Plessix R E, Rynja H.

VTI full waveform inversion:A parameterization study with a narrow azimuth streamer data example

[C]// SEG Technical Program Expanded Abstracts 2010,Society of Exploration Geophysicists, 2010:962-966.

[本文引用: 1]

刘玉柱, 黄鑫泉, 万先武, 等.

各向异性介质弹性波多参数全波形反演

[J]. 地球物理学报, 2019, 62(5):1809-1823.

[本文引用: 1]

Liu Y Z, Huang X Q, Wan X W, et al.

Elastic multi-parameter full-waveform inversion for anisotropic media

[J]. Chinese Journal of Geophysics, 2019, 62(5):1809-1823.

[本文引用: 1]

Kamath N, Tsvankin I.

Elastic full-waveform inversion for VTI media:Methodology and sensitivity analysis

[J]. Geophysics, 2016, 81(2):C53-C68.

DOI:10.1190/geo2014-0586.1      URL     [本文引用: 1]

Brossier R, Operto S, Virieux J.

Seismic imaging of complex onshore structures by 2D elastic frequency-domain full-waveform inversion

[J]. Geophysics, 2009, 74(6):WCC105-WCC118.

DOI:10.1190/1.3215771      URL     [本文引用: 1]

杨积忠, 刘玉柱, 董良国.

变密度声波方程多参数全波形反演策略

[J]. 地球物理学报, 2014, 57(2):628-643.

[本文引用: 1]

Yang J Z, Liu Y Z, Dong L G.

A multi-parameter full waveform inversion strategy for acoustic media with variable density

[J]. Chinese Journal of Geophysics, 2014, 57(2):628-643.

[本文引用: 1]

Shin C, Cha Y H.

Waveform inversion in the Laplace domain

[J]. Geophysical Journal International, 2008, 173(3):922-931.

DOI:10.1111/j.1365-246X.2008.03768.x      URL     [本文引用: 1]

Shin C, Young H C.

Waveform inversion in the Laplace—Fourier domain

[J]. Geophys. J. Int., 2009, 177(3):1067-1079.

DOI:10.1111/j.1365-246X.2009.04102.x      URL     [本文引用: 1]

戴前伟, 陈威, 张彬.

改进型粒子群算法及其在GPR全波形反演中的应用

[J]. 物探与化探, 2019, 43(1):90-99.

[本文引用: 1]

Dai Q W, Chen W, Zhang B.

Improved particle swarm optimization and its application to full-waveform inversion of GPR

[J]. Geophysical and Geochemical Exploration, 2019, 43(1):90-99.

[本文引用: 1]

胡光辉, 王立歆, 王杰, 等.

基于早至波的特征波波形反演建模方法

[J]. 石油物探, 2015, 54(1):71-76.

[本文引用: 1]

Hu G H, Wang L X, Wang J, et al.

Characteristics waveform inversion based on early arrival wave

[J]. Geophysical Prospecting for Petroleum, 2015, 54(1):71-76.

[本文引用: 1]

周斯琛, 李振春, 张敏, 等.

基于截断牛顿法的频率域全波形反演方法

[J]. 物探与化探, 2017, 41(1):147-152.

[本文引用: 1]

Zhou S C, Li Z C, Zhang M, et al.

Full waveform inversion in frequency domain using the truncated Newton method

[J]. Geophysical and Geochemical Exploration, 2017, 41(1):147-152.

[本文引用: 1]

Yong P, Liao W, Huang J, et al.

Misfit function for full waveform inversion based on the Wasserstein metric with dynamic formulation

[J]. Journal of Computational Physics, 2019, 399:108911.

DOI:10.1016/j.jcp.2019.108911      URL     [本文引用: 1]

Claerbout J F.

Fundamentals of geophysical data processing

[J]. Geophysical Journal International, 1986, 86(1):217-219.

[本文引用: 1]

Jannane M, Beydoun W, Crase E, et al.

Wavelengths of earth structures that can be resolved from seismic reflection data

[J]. Geophysics, 1989, 54(7):906-910.

DOI:10.1190/1.1442719      URL     [本文引用: 1]

Bunks C, Saleck F M, Zaleski S, et al.

Multiscale seismic waveform inversion

[J]. Geophysics, 1995, 60(5):1457-1473.

DOI:10.1190/1.1443880      URL     [本文引用: 1]

Sirgue L, Pratt R G.

Efficient waveform inversion and imaging:A strategy for selecting temporal frequencies

[J]. Geophysics, 2004, 69(1):231-248.

DOI:10.1190/1.1649391      URL     [本文引用: 1]

Boonyasiriwat C, Valasek P, Routh P, et al.

An efficient multiscale method for time-domain waveform tomography

[J]. Geophysics, 2009, 74(6):WCC59-WCC68.

DOI:10.1190/1.3151869      URL     [本文引用: 1]

Rietveld W E A, Berkhout A J.

Depth migration combined with controlled illumination

[J]. SEG Technical Program Expanded Abstracts, 1999, 11(1):931-934.

[本文引用: 1]

Rietveld W E A, Berkhout A J, Wapenaar C P A.

Optimum seismic illumination of hydrocarbon reservoirs

[J]. Geophysics, 1992, 57(10):1334-1345.

DOI:10.1190/1.1443200      URL     [本文引用: 1]

Rietveld W E A, Berkhout A J.

Prestack depth migration by means of controlled illumination

[J]. Geophysics, 1994, 59(5):801-809.

DOI:10.1190/1.1443638      URL     [本文引用: 1]

Romero L A, Ghiglia D C, Ober C C, et al.

Phase encoding of shot records in prestack migration

[J]. Geophysics, 2000, 65(2):426-436.

DOI:10.1190/1.1444737      URL     [本文引用: 1]

Jing X, Finn C J, Dickens T A, et al.

Encoding multiple shot gathers in prestack migration

[M]. Society of Exploration Geophysicists, 2000:786-789.

[本文引用: 1]

Vigh D, Starr E W.

3D prestack plane-wave,full-waveform inversion

[J]. Geophysics, 2008, 73(5):VE135-VE144.

DOI:10.1190/1.2952623      URL     [本文引用: 1]

Krebs J R, Anderson J E, Hinkley D, et al.

Fast full-wavefield seismic inversion using encoded sources

[J]. Geophysics, 2009, 74(6):WCC177-WCC188.

DOI:10.1190/1.3230502      URL     [本文引用: 2]

Tang Y.

Target-oriented wave-equation least-squares migration/inversion with phase-encoded hessian

[J]. Geophysics, 2009, 74(6):WCA95-WCA107.

DOI:10.1190/1.3204768      URL     [本文引用: 1]

Schuster G T, Wang X, Huang Y, et al.

Theory of multisource crosstalk reduction by phase-encoded statics

[J]. Geophysical Journal International, 2011, 184(3):1289-1303.

DOI:10.1111/j.1365-246X.2010.04906.x      URL     [本文引用: 1]

Guitton A, Díaz E.

Attenuating crosstalk noise with simultaneous source full waveform inversion

[J]. Geophysical Prospecting, 2012, 60:759-768.

DOI:10.1111/j.1365-2478.2011.01023.x      URL     [本文引用: 1]

Huang Y, Schuster G T.

Multisource least-squares migration of marine streamer and land data with frequency-division encoding

[J]. Geophysical Prospecting, 2012, 60(4):663-680.

DOI:10.1111/j.1365-2478.2012.01086.x      URL     [本文引用: 1]

黄建平, 孙陨松, 李振春, 等.

一种基于分频编码的最小二乘裂步偏移方法

[J]. 石油地球物理勘探, 2014, 49(4):702-707.

[本文引用: 3]

Huang J P, Sun Y S, Li Z C, et al.

Least-squares split-step migration based on frequency-division encoding

[J]. Oil Geophysical Prospecting, 2014, 49(4):702-707.

[本文引用: 3]

Dai W, Huang Y, Schuster G T.

Least-squares reverse time migration of marine data with frequency-selection encoding

[J]. Geophysics, 2013, 78(4):S233-S242.

DOI:10.1190/geo2013-0003.1      URL     [本文引用: 1]

胡春辉. 时间域时移多尺度全波形反演[D]. 合肥: 中国科学技术大学, 2017.

[本文引用: 1]

Hu C H. A time-shift method for time domain multiscale full waveform inversion[D]. Hefei: University of Science and Technology of China, 2017.

[本文引用: 1]

曲英铭, 李振春, 黄建平, 等.

基于多尺度双变网格的时间域全波形反演

[J]. 石油物探, 2016, 55(2):241-250.

[本文引用: 1]

Qu Y M, Li Z C, Huang J P, et al.

Full waveform inversion based on multi-scale dual-variable grid in time domain

[J]. Geophysical Prospecting for Petroleum, 2016, 55(2):241-250.

[本文引用: 1]

Qu Y, Li Z, Huang J, et al.

Multi-scale full waveform inversion for areas with irregular surface topography in an auxiliary coordinate system

[J]. Exploration Geophysics, 2016, 49(1):68-80.

DOI:10.1071/EG16037      URL     [本文引用: 1]

Choi Y, Alkhalifah T.

Source-independent time-domain waveform inversion using convolved wavefields:Application to the encoded multisource waveform inversion

[J]. Geophysics, 2011, 76(5):R125-R134.

DOI:10.1190/geo2010-0210.1      URL     [本文引用: 1]

Guo Y, Huang J, Cui C, et al.

Multi-source multi-scale source-independent full waveform inversion

[J]. Journal of Geophysics and Engineering, 2019, 16(3):479-492.

DOI:10.1093/jge/gxz013      URL     [本文引用: 1]

/

〈 〉

京ICP备05055290号-3
版权所有 © 2021《物探与化探》编辑部
通讯地址：北京市学院路29号航遥中心 邮编：100083
电话：010-62060192；62060193 E-mail：whtbjb@sina.com , whtbjb@163.com