多源并发下Mur二阶吸收边界和非分裂递归卷积完全匹配层对比研究

doi:10.11720/wtyht.2022.1180

多源并发下Mur二阶吸收边界和非分裂递归卷积完全匹配层对比研究

崔凡^,¹^,², 陈毅^,¹, 薛晗鹏¹, 彭苏萍¹^,², 杜云飞¹

1.中国矿业大学(北京) 地球科学与测绘工程学院,北京 100083

2.中国矿业大学(北京) 煤炭资源与安全开采国家重点实验室,北京 100083

A comparative study of Mur second-order absorbing boundary condition and unsplit recursive convolutional perfectly matched layer method under multi-source concurrency

CUI Fan^,¹^,², CHEN Yi^,¹, XUE Han-Peng¹, PENG Su-Ping¹^,², DU Yun-Fei¹

1. School of Geosciences and Surveying Engineering,China University of Mining and Technology(Beijing),Beijing 100083,China

2. State Key Laboratory of Coal Resources and Safe Mining,China University of Mining and Technology(Beijing),Beijing 100083,China

通讯作者: 陈毅(1997-),男,苗族,贵州瓮安人,硕士,研究方向为探地雷达数值模拟研究工作。Email:cy18729242764@163.com

责任编辑: 叶佩

收稿日期: 2021-04-12 修回日期: 2022-01-14

基金资助:

国家自然科学基金项目(52074306)
国家能源投资集团科技创新项目(GJNY2030XDXM-19-03.2)
陕煤化集团重大项目(2018SMHKJ-A-J-03)

Received: 2021-04-12 Revised: 2022-01-14

作者简介 About authors

崔凡(1984-),男,汉族,安徽淮南人,博士,副教授,从事探地雷达理论与方法研究工作。Email:cuifan_cumtb@126.com

摘要

多个激励源无延时发射(多源并发)相同中心频率脉冲会形成平面波束信号,增强数据记录质量。本文通过数值模拟对比分析在多源并发情况下,非分裂递归卷积完全匹配层作为吸收边界条件和Mur二阶吸收边界条件对电磁波的吸收效果。其研究结果表明,传统的Mur二阶吸收边界条件对多源并发、多角度掠射情况下电磁波的吸收效果不佳,在大偏移距下会造成波形畸变和形成虚假反射。而在多源并发情况下采用非分裂递归卷积完全匹配层作为吸收边界条件,将坐标伸缩因子引进时域有限差分算法中。通过傅里叶逆变换将频率域坐标伸缩变换PML方程转换到时域,对电场和磁场值在离散状态下进行递归卷积运算求解。从而避免了直接对卷积进行数值求解的复杂计算,在保证计算准确性的同时,节约了内存空间,提高了计算效率。在不分裂波场情况下,改善了网格截断位置对电磁波的吸收效果。

关键词： 多源并发; 坐标伸缩因子; 递归卷积; 完全匹配层; 时域有限差分; 傅里叶逆变换

Abstract

Plane beam signals form when multiple excitation sources simultaneously emit pulses with the same center frequency (multiple-source concurrency),thus enhancing the quality of data records.This paper compares and analyzes the electromagnetic wave absorption effects of unsplit recursive convolutional perfectly matched layer (PML) as the absorbing boundary condition and Mur second-order absorbing boundary condition under multi-source concurrency through numerical simulation.According to study results,the traditional Mur second-order absorbing boundary condition did not perform well in absorbing electromagnetic waves under the conditions of multi-source concurrency and multi-angle grazing,and it will cause waveform distortion and spurious reflections in the case of large offsets.For the unsplit recursive convolutional perfectly matched layer as the absorbing boundary condition under multi-source concurrency,coordinate scale factors were introduced into the finite-difference time-domain (FDTD) algorithm.Then,the PML equation for coordinate stretching was transformed from frequency domain into time domain through the inverse Fourier transform.Finally,the electric and magnetic field values were solved using the recursive convolution method in the discrete state,thus avoiding the complicated calculation involved in directly determining the numerical solution of convolution.This allows less memory space and high calculation efficiency while ensuring accuracy.Therefore,the unsplit recursive convolutional perfectly matched layer method improves the electromagnetic wave absorption effect at the positions where the grid terminate without inducing wave-field splitting.

Keywords： multi-source concurrency; coordinate stretch factor; recursive convolution; perfect matched layer(PML); finite difference time-domain; inverse Fourier transform

PDF (6493KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

崔凡, 陈毅, 薛晗鹏, 彭苏萍, 杜云飞. 多源并发下Mur二阶吸收边界和非分裂递归卷积完全匹配层对比研究[J]. 物探与化探, 2022, 46(3): 693-703 doi:10.11720/wtyht.2022.1180

CUI Fan, CHEN Yi, XUE Han-Peng, PENG Su-Ping, DU Yun-Fei. A comparative study of Mur second-order absorbing boundary condition and unsplit recursive convolutional perfectly matched layer method under multi-source concurrency[J]. Geophysical and Geochemical Exploration, 2022, 46(3): 693-703 doi:10.11720/wtyht.2022.1180

0 引言

目前,在时域有限差分方法中运用边界条件来截断网格存在很多方法。Bayliss和Turkel^[1] 采用外行波的模拟法作为吸收边界条件,实现了对电磁波的简单吸收;Engquist和Majda ^[2]提出了基于单向波动方程的Engquist-Majda吸收边界条件;Mur^[3] 给出了波动方程的各阶近似及差分形式,表明了在高阶近似时,对电磁波的吸收效果较好,然而对于各向异性介质和色散介质,以二阶近似Mur作为吸收边界条件会在网格截断处发生强反射。之后,Berenger^[4]提出了完全匹配层吸收边界条件,他将电磁波在吸收边界区域进行波场分裂,并对各个分裂场赋予不同的损耗值,这相当于在FDTD网格外加入一层吸收媒介,它具有不依赖于外向传播的电磁波入射角及频率的波阻抗,因此,进入完全匹配层内的电磁波快速地衰减,实现了对不同频率、不同角度的入射波较好的吸收效果。有很多研究发现^[5⇓-7],Berenger完全匹配层作为吸收边界条件比旁轴近似吸收边界条件、Higdon吸收边界条件^[8]、廖氏吸收边界条件^[9]和指数衰减吸收边界条件^[10]具有更好地吸收效果。但是,Berenger的PML理论违背了波的折射原理,在Maxwell方程中是不能实现的,同时,电磁场的分裂增加了数值计算的难度,计算效率低,而且只对行波具有吸收效果,对空域中衰减的隐失波、低频波以及入射角度较小的掠射波吸收效果差^[11]。为了改善边界条件的吸收效果,Sacks等^[12],Gedney等^[13]提出了单轴各向异性完全匹配层作为吸收边界条件,该方法在数学上与Berenger提出的经典完全匹配层等价,它是基于Maxwell方程的,不分裂波场,而是在吸收系数中引入线性吸收因子,实现了对隐失波、低频波以及在PML层内凋落波等干扰波的吸收,该方法作为良好的吸收边界条件在差分算法中被广泛使用。如肖明顺等^[14]、詹应林等^[15]将各向异性完全匹配层应用于二维探地雷达的正演中;中南大学冯德山等^[16⇓-18]实现了在二维和三维空间中将各向异性完全匹配层引入交替方向隐式时域有限差分算法中(ADI-FDTD);吉林大学的李静等^[19] 人开展了三维各向异性完全匹配层作为吸收边界条件的高阶时域有限差分正演。同一时间段内,Chew等^[20] 提出了拉伸坐标完全匹配层理论;Kuzuoglu等^[21] 在复频域内的完全匹配层变量S_k中引进低频分量吸收参数,将复平面的极点从实轴移动到虚轴,加强了对低频波和隐失波的吸收。然而到现研究阶段,所有的吸收边界条件都是在单个激励源的条件下对电磁波进行数值模拟。

本文基于Maxwell方程推导了一种在时域有限差分算法中运用递推卷积求解电磁场的方法,该方法在离散网格条件下通过递推形式计算卷积,不分裂变量,直接计算卷积,避免了对卷积求解的复杂计算。并将该方法运用到多源并发下对电磁波的吸收,为阵列探地雷达数值仿真做了铺垫。

1 基本原理

1.1 坐标伸缩变化下Maxwell卷积方程

非递归卷积完全匹配层主要求解是在麦克斯韦方程的频率域进行,对连续和时谐场,麦克斯韦旋度支配方程可写为:

(1)

\nabla \times H = j ω ε E + σ E = j ω (ε - j \frac{σ}{ω}) E = j ω \bar{ε} E,

(2)$\begin{aligned}\nabla \times \boldsymbol{E} &=-j \omega \mu \boldsymbol{H}+\sigma_{m} \boldsymbol{H} \\&=-j \omega\left(\mu-j \frac{\sigma_{m}}{\omega}\right) \boldsymbol{H}=-j \omega \bar\mu{-} \boldsymbol{H}\end{aligned}$

在PML中电导率不是由物理空间模型的基本参数决定的,而是设置电导率参数使网格截断的反射最小。在此意义上,电导率σ具有任意性,将一个从属于特定位置的相对介电常数来规范电导率,在分裂场PML条件下定义:

(3)

S_{w} = 1 + \frac{σ}{j ω ε_{0}},

当频率趋于0时,S_w没有意义。这将导致低频引发数值异常,为修正这个问题,增加额外的参数来保证频率趋于0时S_w值的有限性。引入更一般化的坐标伸缩因子S_i:

(4)

S_{i} = K_{i} + \frac{σ_{i}}{α_{i} + j ω ε_{0}},

式中:K_i是改善PML对表面波吸收的参数;σ_i为PML层内k方向电导率参数;α_i为改善PML对低频分量的吸收参数;σ_i和α_i都为大于零的正实数;K_i≥1。在三维空间下,i∈{x,y,z},每一个S_i项总是与i∈{x,y,z}方向的道数是成对的。有耗介质中,在TM极化模式下(H_x,H_y,E_z),三维空间下电场频域方程表达式为:

(5)

j ω ε E_{z} + σ E_{z} = \frac{1}{S_{x}} \frac{\partial H_{y}}{\partial x} - \frac{1}{S_{y}} \frac{\partial H_{x}}{\partial y} 。

将方程(5)通过傅里叶逆变换转化到时域,由于坐标伸缩因子与频率无关,所以在时域内方程右边存在卷积,即:

(6)

ε \frac{\partial}{\partial t} E_{z} + σ E_{z} = {\bar{s}}_{x} (t) * \frac{\partial}{\partial x} H_{y} - {\bar{s}}_{y} (t) * \frac{\partial}{\partial y} H_{x},

式中:*表示卷积运算; ${\bar{S}}_{x}$ 和 ${\bar{S}}_{y}$ 分别为 $\frac{1}{S_{x}}$ 和 $\frac{1}{S_{y}}$ 的逆傅里叶变换,即 ${\bar{S}}_{i}$ =F^-1 $[\frac{1}{S_{i}}]$ 。坐标伸缩因子S_i的倒数为:

(7)

\frac{1}{S_{i}} = \frac{1}{K_{i} + \frac{σ_{i}}{α_{i} + j ω ε_{0}}} = \frac{α_{i} + j ω ε_{0}}{α_{i} K_{i} + σ_{i} + j ω ε_{0}},

对坐标伸缩因子的倒数求傅里叶逆变换有:

(8)

\begin{array}{l} F^{- 1} [\frac{b}{d} + \frac{\frac{a}{c} - \frac{b}{d}}{1 + j ω \frac{d}{c}}] = F^{- 1} [\frac{ε_{0}}{K_{i} ε_{0}} + \frac{\frac{α_{i}}{α_{i} K_{i} + σ_{i}} - \frac{ε_{0}}{K_{i} ε_{0}}}{1 + j ω \frac{K_{i} ε_{0}}{α_{i} K_{i} + σ}}] \\ = \frac{1}{K_{i}} δ (t) - \frac{σ_{i}}{K_{i}^{2} ε_{0}} e x p [- t (\frac{α_{i}}{ε_{0}} + \frac{σ_{i}}{K_{i} ε_{0}})] u (t), \end{array}

其中δ(t)是Dirac冲击函数,u(t)是单位阶跃函数。定义:

(9)

\begin{array}{l} ζ_{i} (t) = - \frac{σ_{i}}{K_{i}^{2} ε_{0}} e x p [- t (\frac{α_{i}}{ε_{0}} + \frac{σ_{i}}{K_{i} ε_{0}})] u (t), \\ i = (x, y, z) 。 \end{array}

根据傅里叶逆变换, ${\bar{S}}_{i}$ 的脉冲响应为:

(10)

{\bar{S}}_{i} = \frac{δ (t)}{K_{i}} - \frac{σ_{i}}{ε_{0} K_{i}^{2}} e^{- t (\frac{α_{i}}{ε_{0}} + \frac{σ_{i}}{K_{i} ε_{0}}) u (t)} = \frac{δ (t)}{K_{i}} + ζ_{i} (t) 。

因为Dirac冲击函数和其他函数的卷积仍为原函数,即δ(t)*f(t)=f(t),将式(10)代入式(6)有:

(11)

\begin{array}{l} ε_{r} ε_{0} \frac{\partial E_{z}}{\partial t} + σ E_{z} = \frac{1}{K_{x}} \frac{\partial}{\partial x} H_{y} - \frac{1}{K_{y}} \frac{\partial}{\partial y} H_{x} \\ + ζ_{x} (t) * \frac{\partial}{\partial x} H_{y} - ζ_{y} (t) * \frac{\partial}{\partial y} H_{x} 。 \end{array}

式(11)为电场z分量的时域递推卷积方程,直接在递推方程(14)中计算时域卷积效率是很低的,为有效计算卷积,下面给出递归卷积求解原理和在时域有限差分方法中的实现步骤。

1.2 基于递归卷积的非分裂场PML的FDTD实现

时域有限差分方法是对时间和空间进行离散化,在时间相差半个步长上迭代求解电场和磁场值。对式(11)的卷积求解,定义函数 $ψ_{E_{u} i}^{q}$ 为:

(12)$\begin{aligned} \psi_{E_{u} i}^{q} &=\left.\zeta_{i}(t) * \frac{\partial H_{v}}{\partial i}\right|_{t=q \Delta t} \\ &=\int_{0}^{q \Delta t} \zeta_{i}(\tau) \frac{\partial H_{v}(q \Delta t-\tau)}{\partial i} \mathrm{~d} \tau, \end{aligned}$

式中:E_ui表明这个函数将会在电场E_u分量上更新,并与i(i=x,y,z)方向的空间导数有关。假设积分变量τ在式(12)中是连续变化的,由于时域有限差分方法的离散性,所以H_v场是离散变化的。用连续变量t表示H_v时,只取离散值,即

(13)

\frac{\partial H_{v} (t)}{\partial i} = \overset{I_{m a x}}{\sum_{i = 0}} \frac{\partial H_{v} (k Δ t)}{\partial i} p_{k} (t) 。

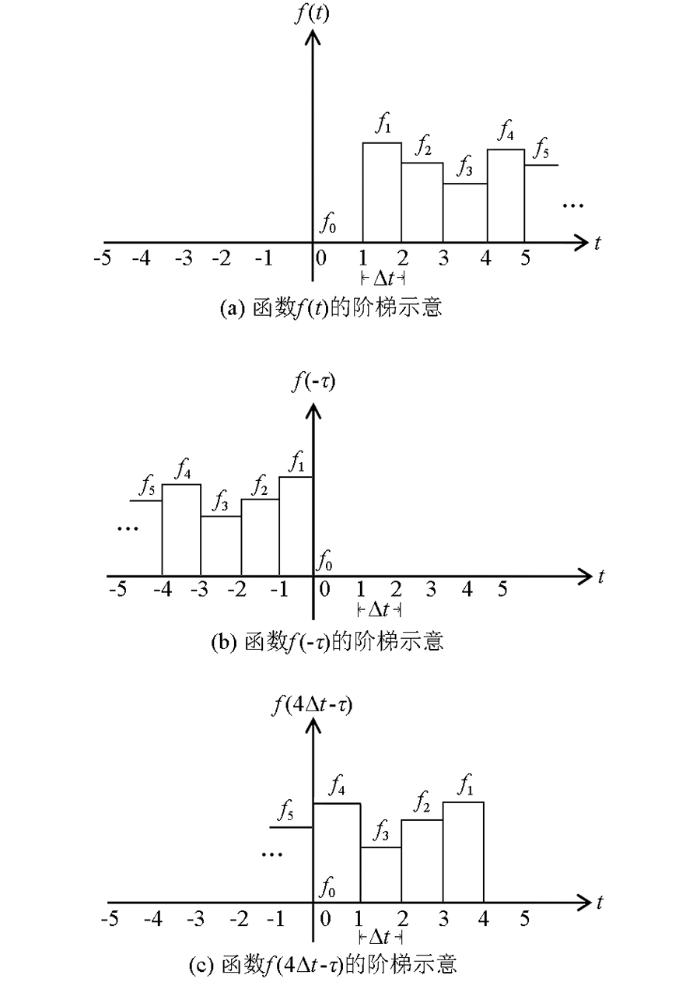
令f(t)= $\frac{\partial H_{v}}{\partial i}$ ,此函数的阶梯表示如图1a所示。假设函数在第一个时间步时为0,在t=Δt时刻函数值为f₁并保持不变,直到t=2Δt时函数值变为f₂,当t=3Δt时函数值为f₃,以此类推得到在任意时刻的磁场随空间i分量上的变化值。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 函数f(t)阶梯表示法

Fig.1 Stepped representation of function f(t)

卷积包含f(qΔt-τ)函数。在时间步为q=0时,函数值为f(-τ),如图1b所示。在所有采样点f_n都关于原点反转对称,在-Δt≤τ<0上函数值为f₁,在-2Δt≤τ<-Δt上函数值为f₂,在-3Δt≤τ<-2Δt上函数值为f₃,其余各时刻的函数值以此类推。

图1c展示了在特定时刻q=4时f(qΔt-τ)的函数值。如图所示,扩展到τ=0右侧右边的第一个脉冲具有f_q的值,扩展到τ=Δt右边的值为f_q_-1,扩展到τ=2Δt右边的值为f_q_-2,以此类推。此时移动函数可表示为:

(14)

f (q Δ t - τ) = \overset{q - 1}{\sum_{k = 0}} f_{q - k} p_{k} (τ),

对磁场求导数有:

(15)

\frac{\partial H_{v} (q Δ t - τ)}{\partial i} = \overset{q - 1}{\sum_{k = 0}} \frac{\partial H_{v}^{q - k}}{\partial i} p_{k} (τ),

其中: $H_{v}^{q - k}$ 表示磁场在时间步q-k时刻的值,空间导数用空间有限差分来实现。在时间步q时刻, $ψ_{E_{u} i}^{q}$ 变换积分和求和顺序可得到:

(16)$\begin{aligned}\psi_{E_{u} i}^{q} &=\sum_{k=0}^{q-1} \frac{\partial H_{v}^{q-k}}{\partial i} \int_{0}^{q \Delta t} \zeta_{i}(\tau) p_{k}(\tau) \mathrm{d} \tau \\&=\sum_{k=0}^{q-1} \frac{\partial H_{v}^{q-k}}{\partial i} \int_{k \Delta t}^{(k+1) \Delta t} \zeta_{i}(\tau) \mathrm{d} \tau\end{aligned}$

式(16)中,脉冲函数p_k(t)用来确定积分上下限。考虑如下特殊积分:

(17)

\begin{array}{l} - \int_{k Δ t}^{(k + 1) Δ t} e^{- a t} d t = \frac{1}{a} e^{- a t} |_{k Δ t}^{(k + 1) Δ t} = \frac{1}{a} [e^{- a (k + 1) Δ t} - e^{- a k Δ t}] \\ = \frac{1}{a} (e^{- a Δ t} - 1) (e^{- a Δ t})^{k}, \end{array}

把式(16)中的ζ_i(t)离散冲击响应定义为:

(18) $\begin{aligned}Z_{0 i}(k) &=\int_{k \Delta t}^{(k+1) \Delta t} \zeta_{i}(\tau) \mathrm{d} \tau \\&=-\frac{\sigma_{i}}{\varepsilon_{0} K_{i}^{2}} \int_{k \Delta t}^{(k+1) \Delta t} \mathrm{e}^{-\left(\frac{\sigma_{i}}{\varepsilon_{0} K_{i}}+\frac{\alpha}{\varepsilon_{0}}\right) \tau} \mathrm{d} \tau \\&=a_{i} \mathrm{e}^{-\left(\frac{\sigma_{i}}{K_{i}}+\alpha_{i}\right) \frac{k \Delta t}{\varepsilon_{0}}}=a_{i}\left(b_{i}\right)^{k},\end{aligned}$

式中:

(19)

\begin{array}{l} a_{i} = \frac{σ_{i}}{(σ_{i} K_{i} + K_{i}^{2} α_{i})} (e^{- (\frac{σ_{i}}{K_{i}} + α_{i}) \frac{Δ t}{ε_{0}}} - 1.0) \\ i = (x, y, z), \end{array}

(20)

b_{i} = e x p [- (\frac{σ_{i}}{ε_{0} K_{i}} + \frac{α}{ε_{0}}) Δ t] i = (x, y, z),

将式(17)、(18)、(19)、(20)代入式(16)中有:

(21)

ψ_{E_{u} i}^{q} = \overset{q - 1}{\sum_{k = 0}} \frac{\partial H_{v}^{q - k}}{\partial i} a_{i} (b_{i})^{k},

将k=0项和其他项分离有:

(22)

ψ_{E_{u} i}^{q} = a_{i} \frac{\partial H_{v}^{q}}{\partial i} + \overset{q - 1}{\sum_{k = 1}} \frac{\partial H_{v}^{q - k}}{\partial i} a_{i} (b_{i})^{k},

令n=k-1代替指数项,即k=n+1:

(23)

ψ_{E_{u} i}^{q} = a_{i} \frac{\partial H_{v}^{q}}{\partial i} + \overset{q - 2}{\sum_{n = 0}} \frac{\partial H_{v}^{q - n - 1}}{\partial i} a_{i} (b_{i})^{n + 1},

用k来表示指数项n有:

(24)

ψ_{E_{u} i}^{q} = a_{i} \frac{\partial H_{v}^{q}}{\partial i} + \overset{[q - 1] - 1}{\sum_{k = 0}} \frac{\partial H_{v}^{q - 1 - k}}{\partial i} a_{i} (b_{i})^{k},

对比式(24)和式(21)有:

(25)

ψ_{E_{u} i}^{q} = a_{i} \frac{\partial H_{v}^{q}}{\partial i} + b_{i} ψ_{E_{u} i}^{q - 1},

根据式(25), $ψ_{E_{u} i}^{q}$ 在时间步q是q-1时刻的函数,因此 $ψ_{E_{u} i}^{q}$ 求解可以通过递推求解。

空间离散下的电场递推式,按照Yee氏网格将式(25)进行时间和空间上的离散,可得:

(26)

\begin{array}{l} ε_{r} ε_{0} \frac{E_{z}^{n + 1} (i, j, k) - E_{z}^{n} (i, j, k)}{Δ t} + σ \frac{E_{z}^{n + 1} (i, j, k) - E_{z}^{n} (i, j, k)}{2} \\ = \frac{H_{y}^{n + 1 / 2} (i, j, k) - H_{y}^{n + 1 / 2} (i - 1, j, k)}{K_{x} Δ x} \\ - \frac{H_{x}^{n + 1 / 2} (i, j, k) - H_{x}^{n + 1 / 2} (i - 1, j, k)}{K_{y} Δ y} \\ + \overset{N - 1}{\sum_{m = 0}} Z_{0 x} (m) \frac{H_{y}^{n - m + 1 / 2} (i, j, k) - H_{y}^{n - m + 1 / 2} (i - 1, j, k)}{Δ x} \\ + \overset{N - 1}{\sum_{m = 0}} Z_{0 y} (m) \frac{H_{x}^{n - m + 1 / 2} (i, j, k) - H_{x}^{n - m + 1 / 2} (i, j - 1, k)}{Δ y} \end{array}

上式中Z₀_i(k)项含有卷积的计算,离散卷积计算十分复杂,但是同时Z₀_i(k)项是简单的指数形式,从而它们的和可以通过递归卷积来得到,引入一组新的辅助表达式φ_i:

(27)

\begin{array}{l} φ_{e_{z i}}^{n + 1 / 2} (i, j, k) = b_{i} φ_{e_{z i}}^{n - 1 / 2} (i, j, k) \\ + a_{i} [H_{i}^{n + 1 / 2} (i, j, k) - H_{i}^{n + 1 / 2} (i - 1, j, k)] / Δ i \\ (i = x, y) \end{array}

将φ_i代入式(26)经整理后得到电场E_z分量的递推表达式:

(28)

\begin{array}{l} E_{z}^{n + 1} (i, j, k) = \frac{1 - \frac{σ (m) Δ t}{2 ε (m)}}{1 + \frac{σ (m) Δ t}{2 ε (m)}} E_{z}^{n} (i, j, k) \\ + \frac{\frac{Δ t}{ε (m)}}{1 + \frac{σ (m) Δ t}{2 ε (m)}} [φ_{e_{z x}}^{n + 1 / 2} (i, j, k) - φ_{e_{z y}}^{n + 1 / 2} (i, j, k)] \\ + \frac{\frac{Δ t}{ε (m)}}{1 + \frac{σ (m) Δ t}{2 ε (m)}} [\frac{H_{y}^{n + 1 / 2} (i, j, k) - H_{y}^{n + 1 / 2} (i - 1, j, k)}{K_{x} Δ x} \\ - \frac{H_{x}^{n + 1 / 2} (i, j, k) - H_{x}^{n + 1 / 2} (i, j - 1, k)}{K_{y} Δ y}], \end{array}

式(28)中:σ为电导率,ε为介质的介电常数,m=(i,j,k),在仿真时令模拟区域的K值为1,在PML层内使K值渐进变化,PML层为有限的厚度单元,σ、K和α在PML层中单调变化:

(29)

σ_{z} (z) = \frac{σ_{m a x} | z - z_{0} |^{m}}{d^{m}},

(30)

K_{z} (z) = 1 + (K_{m a x} - 1) \frac{| z - z_{0} |^{m}}{d^{m}},

(31)

α_{z} (z) = \frac{α_{m a x} | z - z_{0} |}{d},

式中:d为PML层的厚度,z₀为PML层靠近FDTD区域的界面位置,在仿真时取m=4。σ_max的最佳值可取为σ_max= $\frac{m + 1}{\sqrt{ε_{r}} 150 π δ}$ ,其中δ为元胞尺寸。K_max=5~11,α_max=0~0.05。根据探地雷达的频率段,K_max取5左右,α_max取0.008为适当值。

1.3 Mur二阶吸收边界条件的FDTD实现

在二维直角坐标系下,行波的平面波解为:

(32)

f (x, y, t) = A e x p [j (ω t - α_{x} x - α_{y} y)],

假设在x=0的位置设置截断边界,则在x≥0的区域会同时存在入射波和反射波。因此式(32)可写为:

(33)

\begin{array}{l} f (x, y, t) = A^{-} e x p [j (ω t + \sqrt{α^{2} - α_{y}^{2}} x + α_{y} y)] \\ + A^{+} e x p [j (ω t + \sqrt{α^{2} - α_{y}^{2}} x + α_{y} y)], \end{array}

可将上式分解为左行波f^-(入射波)和右行波f⁺(反射波)之和:

(34)

f^{-} = A^{-} e x p [j (ω t + \sqrt{α^{2} - α_{y}^{2}} x + α_{y} y)],

(35)

f^{+} = A^{+} e x p [j (ω t + \sqrt{α^{2} - α_{y}^{2}} x + α_{y} y)] 。

令微分算子L使得L^±f^±=0,其中:

(36)

L^{\pm} = \frac{\partial}{\partial x} \pm \sqrt{\frac{1}{v^{2}} \frac{\partial^{2}}{\partial t^{2}} - \frac{\partial^{2}}{\partial y^{2}}},

对左行波使得L^-f^-|_x₌₀中并令f=E_z,化简后得到:

(37)

(\frac{1}{v} \frac{\partial^{2}}{\partial x \partial t} - \frac{1}{v^{2}} \frac{\partial^{2}}{\partial t^{2}} + \frac{1}{2} \frac{\partial^{2}}{\partial y^{2}}) E_{z} = 0

根据 $\frac{\partial E_{z}}{\partial y}$ =-μ $\frac{\partial H_{x}}{\partial t}$ ,对二维电磁场问题,Mur指出二阶吸收边界条件可降低为只含电场(E)和磁场(H)分量的一阶导数:

(38)

\frac{\partial E_{z}}{\partial x} - \frac{1}{v} \frac{\partial E_{z}}{\partial t} - \frac{v μ}{2} \frac{\partial H_{x}}{\partial y} = 0,

在(i+1/2,j)点和t=(n+1/2)Δt时刻对式(62)进行差分离散并进行线性插值可得到左截断边界处Mur的二阶吸收边界条件递推式:

(39)

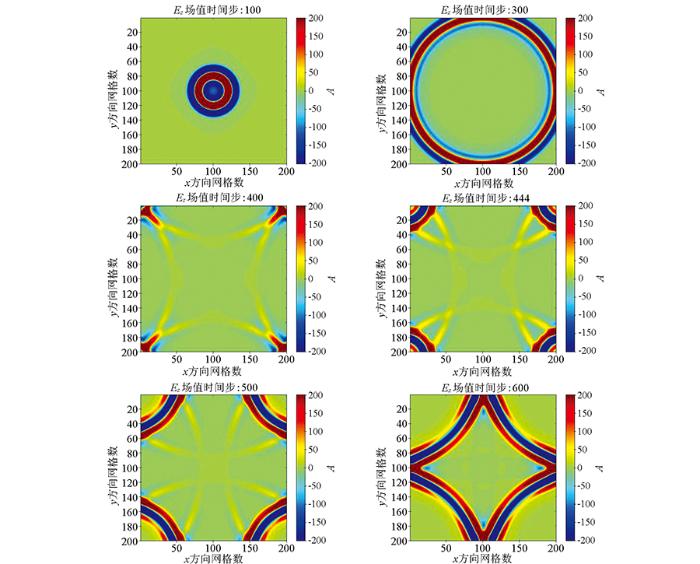
\begin{array}{l} E_{z}^{n + 1} (i, j) = E_{z}^{n} (i + 1, j) + \\ \frac{v Δ t - Δ x}{v Δ t + Δ x} [E_{z}^{n + 1} (i + 1, j) - E_{z}^{n} (i, j)] - \\ \frac{v^{2} μ Δ t}{2 (v Δ t + Δ x)} \cdot (\frac{Δ x}{Δ y}) \times [H_{x}^{n + 1 / 2} (i, j + \frac{1}{2}) - \\ H_{x}^{n + 1 / 2} (i, j - \frac{1}{2})] + H_{x}^{n + 1 / 2} (i + 1, j + \frac{1}{2}) - \\ H_{x}^{n + 1 / 2} (i + 1, j - \frac{1}{2}), \end{array}

式(39)中,v为电磁波传播速度,μ为磁导率,Δx、Δy、Δt分别为x、y方向的空间步长和时间步长。式(39)给出的Mur二阶吸收边界条件递推公式没有在边角点处对电场值进行修正,因此,在4个边角位置处发生明显的波反射,如图2所示,给出了激励源位于模型区域中心位置处,E_z波场在600个时间步的变化,在第400个时间步时,由于没有对边角进行修正,此时4个角点位置处都发生了明显的反射,在500和600时间步时刻的研究区域内存在4个角点反射的波场。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 未修正角点不同时间步的E_z波场

Fig.2 E_z wave field at different time steps of uncorrected corners

1.4 Mur二阶吸收边界条件的角点修正

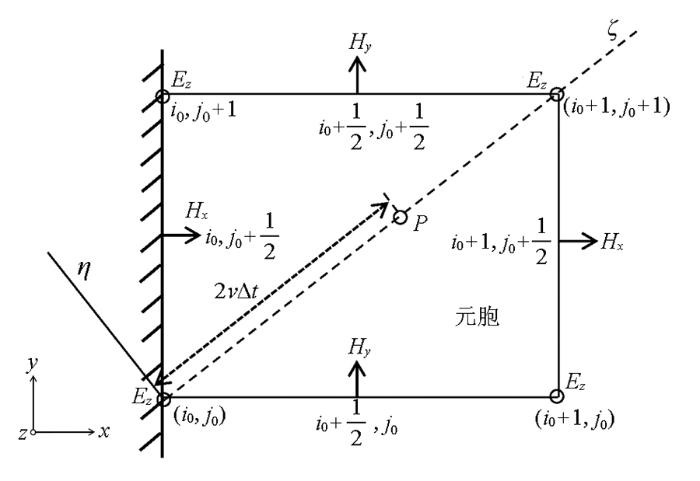
二维仿真时,研究区域是矩形,此时在4个边角点位置处出现场重合的情况,因此需要对角点进行处理,以TM波为例,假设角点处存在沿元胞对角线传播的行波。如图3所示,在距离坐标(i₀,j₀)为2vΔt处的对角线上取一点P,根据FDTD的离散稳定条件,有2vΔt≤ $\sqrt{2}$ δ,其中δ=Δx=Δy,沿对角线传播的行波:

(40)

E_{z}^{n} (i_{0}, j_{0}) = E_{z}^{n - 2} (P),

创建新坐标系ηoξ,新坐标系于原始坐标系逆时针旋转45°,在新坐标系下Mur一阶近似公式可表示为:

(41)

\frac{\partial E_{z}}{\partial ξ} - \frac{1}{v} \frac{\partial E_{z}}{\partial t} = 0 。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 TM波左下角点修正示意

Fig.3 Schematic diagram of TM wave lower left corner correction

由于P点与原点在同一离散网格内,忽略波振幅衰减,利用线性插值可得到:

(42)

\frac{E_{z}^{n - 2} (i_{0}, j_{0}) - E_{z}^{n - 2} (P)}{2 v Δ t} = \frac{E_{z}^{n - 2} (i_{0}, j_{0}) - E_{z}^{n - 2} (i_{0} + 1, j_{0} + 1)}{\sqrt{2} δ} 。

根据式(40)结合式(42),当Δx≠Δy时,有:

(43)

\begin{array}{l} E_{z}^{n + 1} (i_{0}, j_{0}) = E_{z}^{n} (i_{0} + 1, j_{0} + 1) + \\ \frac{v Δ t - \sqrt{{(Δ x)}^{2} + {(Δ y)}^{2}}}{v Δ t + \sqrt{{(Δ x)}^{2} + {(Δ y)}^{2}}} \cdot \\ [E_{z}^{n + 1} (i_{0} + 1, j_{0} + 1) - E_{z}^{n} (i_{0}, j_{0})], \end{array}

根据式(43),修正角点位置处的电场值取决于该角点相邻一个时间步位置处前一时刻的电场值和该点的速度值。

2 模型验证

2.1 均匀介质

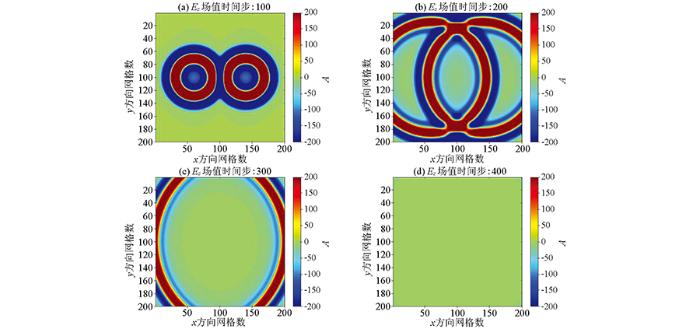
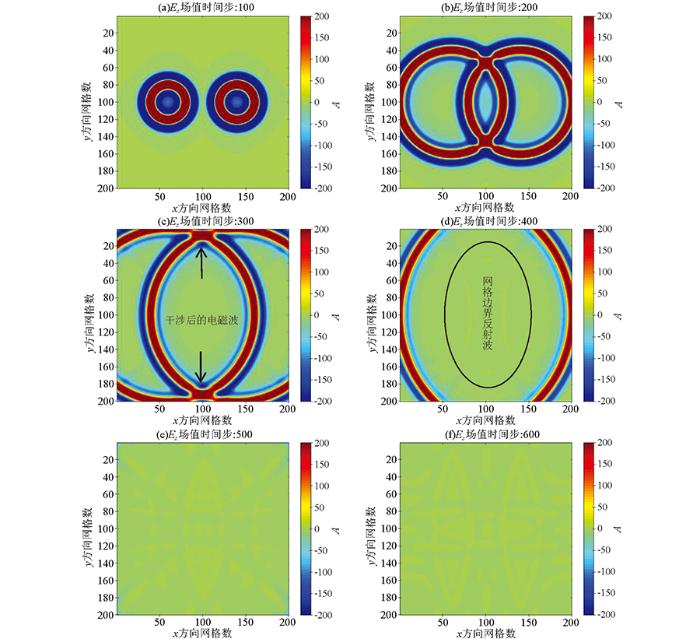
为验证在均匀介质下Mur二阶近似吸收边界条件和基于递归卷积完全匹配层作为吸收边界条件在多源并发下对电磁波的吸收效果,设置模拟区域网格大小为200×200,四周PML层厚度为10个网格。模拟区域的物性参数为:ε_r=3.5,u_r=1,σ=2.5 mS/m。两个激励源采用主频为900 MHz的布莱克曼—哈里斯脉冲,两个激励源的位置沿x轴相距80个空间步长,空间步长为0.006 m,时间步长为 0.015 ns。不同时间步的E_z波场如图4所示。图4为应用递归卷积完全匹配层作为吸收边界条件的E_z波场快照,仿真时间持续400个时间步长。在第100时间步时(图4a),两个并发激励源电磁波相遇,经相互干涉作用后继续扩散;在时间步200时(图4b),部分电磁波进入PML层被吸收掉; 时间步300时(图4c)两个激励源产生的扩散电磁波到达彼此对面PML层,此时部分波到达边界进入PML层无任何反射发生;时间步400时(图4d),波扩散离开研究区域,在整个仿真持续时间段内,无任何明显反射发生,电磁场在网格截断位置处被PML层有效吸收掉了。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 均匀介质递归卷积完全匹配层不同时间步E_z波场快照

Fig.4 Snapshots of E_z wave field at different time steps of the homogeneous medium recursive convolution perfectly matched layer

图5给出了Mur二阶吸收边界条件不同时间步E_z波场快照,二阶Mur吸收边界条件是运用微分二阶近似来求解单向行波方程,它是将微分方程进行泰勒级数展开后去掉高阶项的近似算法,此时反射系数不为零,因此不能实现对波的良好吸收。在两个激励源并发的条件下,电磁波相互干涉,重构后的波场形成小方形包络,如图5c箭头所示位置,随着时间推移,小方形包络在水平方向上扩展开来,以平面波束形式达到网格边界位置。这时,Mur二阶吸收边界对电磁波吸收效果较差,会在边界处发生反射。在前300个时间步内(图5a,5b,5c),由单个激励源产生的电磁波在均匀介质中扩散,以球面的形式到达网格边界处, 在第400个时间步时(图5d),经过干涉后的波到达边界,此时部分波返回研究区域;在时间步500时,波已经扩散离开研究区,然而因吸收不完全导致部分反射波返回研究区域,如图5e、5f所示,此时波在边界位置发生多次反射,形成谐振,对下一时间段内的有效波场造成二次干扰。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 均匀介质Mur二阶吸收边界不同时间步E_z波场快照

Fig.5 Snapshots of E_z wave field at different time steps of Mur second-order absorbing boundary in homogeneous medium

2.2 低洼模型

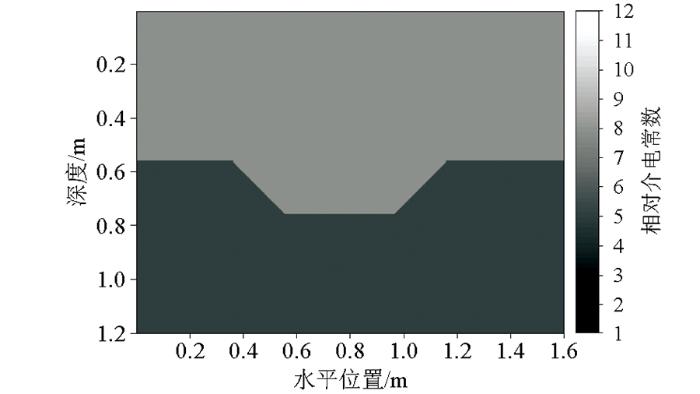
在复杂地质构造条件下,在地下介质空间中扩散的电磁波会产生反射、绕射现象。绕射波会以不同的角度入射到匹配层中,为体现两种不同的吸收边界对波的吸收效果,构造了复杂低洼地质模型,模拟现实地质环境中的正、逆断层。设置模型区域网格大小为300×400,模拟区域的物性参数为:上层介质相对介电常数ε₁=8,电导率σ₁=0.003 S/m,下层介质相对介电常数ε₂=5,电导率σ₂=0.001 S/m。所有激励源采用主频为900 MHz的布莱克曼—哈里斯脉冲,空间步长为0.006 m,时间步长为 0.015 ns,26个激励源的位置沿x轴分布,每个激励源相距5个空间步长,其模型的空间分布如图6所示。对于递归卷积完全匹配层在四周设置10个网格大小的PML层厚度。为方便更加清晰显示波场信息,下面将使用灰度图显示不同时间步E_z波场的信息。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 低洼模型结构示意

Fig.6 Schematic diagram of low-lying model structure

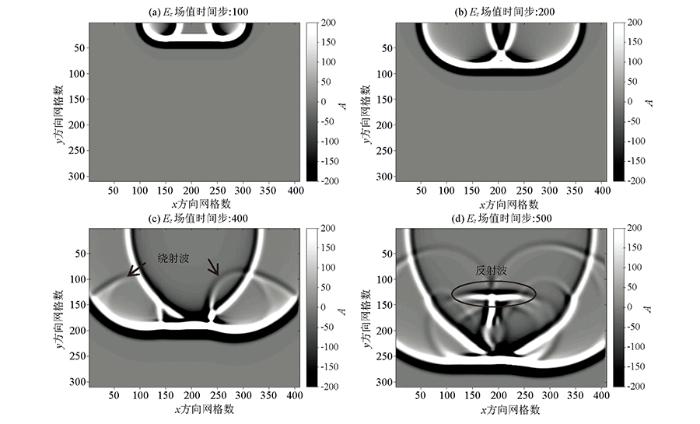
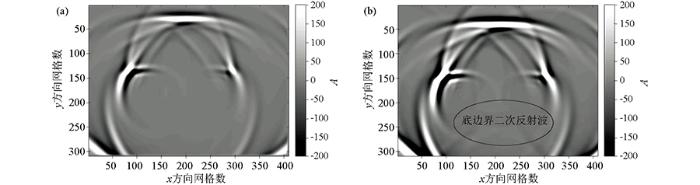
在多个激励源并发的情况下,采用相同主频的脉冲电磁波,此时在近地表区域,由单个激励源产生的球面波在空间上进行波场重构,子波波前形成平面电磁波束,如图7a,7b所示。平面电磁波束在地下空间扩散,在第400个时间步时遇到第二层介质产生绕射波,如图7c箭头指示位置;第500个时间步时,低洼模型底部产生的反射波如图7d标记所示,此时反射波的能量明显高于绕射波能量;两种吸收边界条件下,电磁波在介质区域内传播规律相同,有相同的波场快照;在第700个时间步时,平面电磁波束到达底部边界,基于递归卷积完全匹配层作为吸收边界条件的波场快照如图8a所示,此时平面电磁波束进入完全匹配层被有效地吸收掉,而以二阶Mur作为吸收边界条件在底部网格截断处发生了反射,部分波返回介质区域,如图8b圆圈位置,这将对能量相对较弱的绕射波造成了二次干扰,影响有效波场。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 低洼模型不同时间步E_z波场快照

Fig.7 Snapshots of the E_z wave field of the low-lying model at different time steps

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 低洼模型700时间步E_z波场快照

a—递归卷积完全匹配层波场快照;b—Mur二阶吸收边界波场快照

Fig.8 Snapshot of the low-lying model at 700 time step E_z wave field

a—recursive convolution complete matching layer wave field snapshot;b—snapshot of Mur second-order absorbing boundary wave field

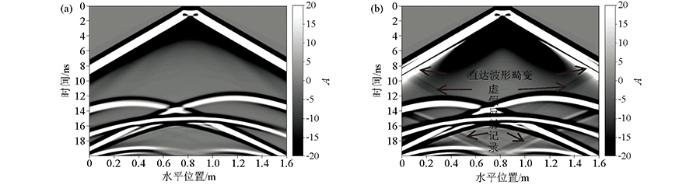
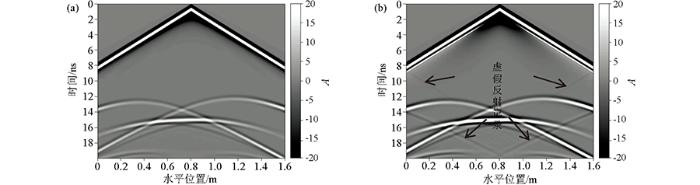
为了对比在不同偏移距下,两种吸收边界条件对多源并发电磁波的吸收效果,设置了宽角法观测低洼模型,将26个发射天线(激励源)置于低洼位置正上方,每个发射天线间隔两个空间步长,接收天线沿x轴移动,采集200道雷达数据。天线参数依然采用900 MHz主频的布莱克曼—哈里斯脉冲,多个发射天线无延时同时发射相同信号脉冲电磁波,得到在多源并发下,以递归卷积完全匹配层作为吸收边界条件的数据记录如图9a所示。此时,由于采用的是相同极化方向的激励信号,直达波、反射波与单个激励源雷达数据记录(如图10a所示)相比加大了子波时宽,增强了来自地下界面的反射信号,此时在直达波左、右两翼无明显畸变,无虚假反射。而Mur二阶吸收边界条件在大偏移距处有强烈的虚假反射记录;这是由于偏移距越大,波入射到匹配层的入射角度越大,掠射情况越严重。而在多个激励源的情况下,在大偏移距下,虚假反射会更加明显;这是由于加大了子波的时宽和介质的不均一性导致的色散造成的。如图9b箭头所指示的位置,在直达波的左右翼都发生了明显的波形畸变和虚假反射记录。虽然在单个天线时的雷达数据记录上,直达波左右两翼畸变不明显,但是也产生了明显的虚假反射信号,如图10b箭头所指示的位置。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 多源并发雷达数据记录

a—递归卷积完全匹配层数据记录;b—Mur二阶吸收边界数据记录

Fig.9 Multi-source concurrent radar data recording

a—recursive convolution complete matching layer data record;b—Mur second-order absorbing boundary data record

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 单个激励源雷达数据记录

a—递归卷积完全匹配层数据记录;b—Mur二阶吸收边界数据记录

Fig.10 Single excitation source radar data record

a—recursive convolution complete matching layer data record;b—Mur second-order absorbing boundary data record

3 结论与展望

1)在均匀介质下,Mur二阶吸收边界条件对多源并发下电磁波的吸收不完全,会在网格截断处产生反射回波返回波场模拟区域。而基于非分裂的递推卷积完全匹配层能很好地吸收多源并发下的电磁波,有效改善边界位置处对干涉后的电磁波吸收效果。

2)在复杂地质构造下,电磁波在地下介质中发生反射、绕射后以不同的入射角度到达网格截断处,传统的Mur二阶吸收边界条件在网格截断位置直接对微分方程进行近似求解,不能很好地消除强电磁反射,在边界网格截断位置处会有部分反射波返回研究区域对有效波造成二次干扰,特别是在大偏移距下,会造成直达波波形畸变,形成虚假反射记录;而基于非分裂递归卷积的完全匹配层作为吸收边界条件能很好地抑制直达波波形畸变现象,消除虚假反射记录。

3)基于非分裂递归卷积的完全匹配层作为吸收边界条件在不分裂波场的情况下,又避免了直接对卷积的求解的复杂运算,提升了计算的效率,改善了吸收的效果。

本文详细介绍了非分裂递归卷积完全匹配层和Mur二阶吸收边界结合时域有限差分的实现方法,并将它们运用到多个激励源并发下探地雷达正演模拟,基于C语言和matlab平台开发了相应的数值计算程序,为阵列探地雷达的数值模拟研究提供了帮助。

致谢

感谢煤炭资源与安全开采国家重点实验室提供的计算设备,感谢评审的专家提出的宝贵意见。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Bayliss

, Turkel

Radiation boundary conditions for wave-like equations

[J]. Communications on Pure and Applied Mathematics, 1980, 33(6):707-725.