0 引言
近年来,随着地面重磁勘探工作的广泛应用,多数大比例重磁面积测量使用规则测网采样,且通常都是线距、点距相等或线距是点距的2倍。以1∶5万重力测量为例,线距和点距一般为500 m×250 m或500 m×500 m[8]。因此,研究规则分布重力数据的最优插值参数具有实际意义。
本文模拟1∶5万野外实测规则分布采样点,以模型理论异常提取的重力数据为基础,采用Surfer软件的径向基函数法进行插值参数优选;依据检查点法获取的残差统计标准偏差指标对比结果,优选出精度较高的插值参数。通过定量比较克服了软件选择参数的随机性和人为选取的不确定性,在探讨各种参数变化引起插值结果精度变化的基础上,提出插值精度较优的参数组合。本文研究结果可为规则分布重力数据的插值工作提供定量依据和参考借鉴。
1 插值参数与精度评价
1.1 主要插值参数
插值参数是构成插值算法的基本元素[16],包括搜索规则和插值核函数(或称基函数)。Surfer软件中径向基函数插值法使用5种核函数[16,17],分别是:反多重二次曲面函数(inverse multiquadric function,IMQF)、多重对数函数(multilog function,MLF)、多重二次曲面函数(multiquadric function,MQF)、自然三次样条函数(natural cubic spline function,NCSF)、薄板样条函数(thin plate spline function,TPSF),其他主要涉及的参数还有:插值间距、插值范围、R2参数(平滑因子)、搜索邻域的形状,搜索半径、搜索角度、搜索扇区、搜索点数等。
1.2 插值精度评价
数据插值效果是否符合实际,需要采用一定的方法评价数据插值方法的合理性和有效性。本文采用检查点法进行插值效果对比,采用Surfer软件中的残差功能,以标准偏差(standard deviation, SD)指标的统计结果来定量分析插值精度并优选插值参数,见式(1)。
式中:Gi为第i个数据点(即测点)的实测重力值;gi为第i个数据点(即测点)插值后的重力值;i:1,2,3,…,n;n为数据点的个数。
2 数据来源与插值准备
2.1 数据来源及说明
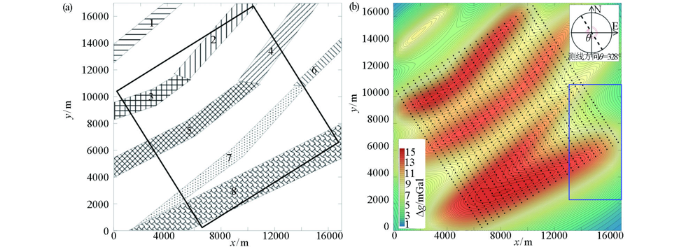
本次采用RGIS软件设计了由8个异常体组成的地质模型(表1,图1,模型范围17 km×17 km),以该模型的正演重力异常为基础,在异常区内,根据 1∶5万野外工作点线布设原则,模拟部署了点距250 m和线距500 m的工作区(工区范围12 km×12 km),设计测线方向为328°(总体测线方向与异常走向垂直),部署测线25条,每条测线49个测点,合计测点1225个(图1)。采用这1 225个测点为模拟“实测点”,从理论异常中提取出各个“实测点”的重力值作为“实测值”,以此“实测值”为基础进行插值,待插值完成后,使用这1 225个“实测点”作为检查点进行残差分析,统计残差结果获得的标准偏差指标,根据标准偏差值定量比较不同参数对应结果的插值精度。
表1 理论模型参数
Table 1
| 模型 编号 | (x,y)角点坐标/m | 顶面埋 深/m | 底面埋 深/m | 密度差 /(g·cm-3) | |
|---|---|---|---|---|---|
| 1 | (5104,16963);(3736,16963);(17,13939);(17,12520) | 500 | 1500 | 0.6 | |
| 2 | (10691,16927);(9092,16927);(4514,11690);(5642,11300) | 600 | 2600 | 0.6 | |
| 3 | (5750,11259);(4669,11631);(2889,10576);(41,9582);(41,8278);(3152,9324) | 600 | 2600 | 0.6 | |
| 4 | (15271,16969);(13632,16969);(9272,11182);(10803,10968) | 800 | 3000 | 0.5 | |
| 5 | (10951,10934);(9419,11152);(5412,8185);(39,5461);(39,3982);(6094,7051) | 800 | 3000 | 0.5 | |
| 6 | (16972,13434);(16972,14379);(13395,10836);(14274,10796) | 600 | 2100 | 0.5 | |
| 7 | (14326,10770);(13576,10811);(8905,6189);(1616,307);(4525,1783);(9646,5535) | 600 | 2100 | 0.5 | |
| 8 | (16954,5371);(16954,7963);(1155,36);(5574,36) | 900 | 3400 | 0.4 | |
图1
图1
地质模型(a)及其理论重力异常(b)
Fig.1
The model (a) and its theoretical gravity anomaly (b)
2.2 插值间距与插值范围
3 插值核函数与R2参数
3.1 五种核函数对比
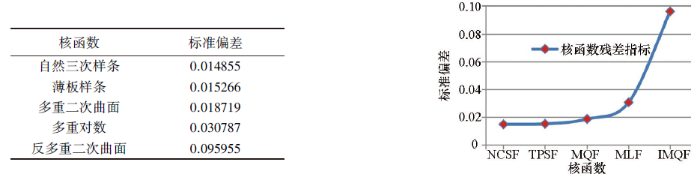
分别采用径向基函数所属的5种核函数(IMQF、MLF、MQF、NCSF、TPSF)为变量进行插值,其余插值参数统一设置为系统默认值,其中,R2参数为0.018;各向异性中:比率为1,角度为0°;搜索的扇区数为4,从所有扇区使用的最大的数据个数为64,从每个扇区使用的最大的数据个数为16,所有扇区的最小数据个数(更少则白化节点)为8,如果空白扇区多于3个则白化节点;搜索椭圆中,半径R1为11.7,半径R2为11.7,角度为0°。插值结束后采用残差统计结果的标准偏差指标来分析不同核函数的插值效果。
根据检查点法残差指标统计结果可见(图2),自然三次样条函数、薄板样条函数、多重二次曲面函数这3种核函数的插值精度均较高,而多重对数函数插值精度相对较低,反多重二次曲面函数的插值精度最低。因此,对5种核函数插值精度的评级顺序为:自然三次样条函数>薄板样条函数>多重二次曲面函数>多重对数函数>反多重二次曲面函数。通过标准偏差结果的定量对比,认为自然三次样条函数插值精度最高,因而本次优选的核函数为自然三次样条函数。
图2
3.2 R2参数对比
表2 R2参数残差结果
Table 2
| R2 | 标准偏差 | R2 | 标准偏差 | R2 | 标准偏差 | R2 | 标准偏差 |
|---|---|---|---|---|---|---|---|
| 0 | 0.014886 | 2 | 0.014985 | 20 | 0.033150 | 200 | 0.187007 |
| 0.018 | 0.014855 | 3 | 0.014956 | 30 | 0.040566 | 300 | 0.200942 |
| 0.1 | 0.014847 | 4 | 0.014869 | 40 | 0.043862 | 400 | 0.208563 |
| 0.2 | 0.014857 | 5 | 0.014919 | 50 | 0.046008 | 500 | 0.217865 |
| 0.3 | 0.014870 | 6 | 0.015109 | 60 | 0.046918 | 600 | 0.220763 |
| 0.4 | 0.014882 | 7 | 0.015389 | 70 | 0.050115 | 700 | 0.223089 |
| 0.5 | 0.014893 | 8 | 0.015562 | 80 | 0.051539 | 800 | 0.223366 |
| 0.6 | 0.014903 | 9 | 0.015653 | 90 | 0.054638 | 900 | 0.225889 |
| 0.7 | 0.014912 | 10 | 0.015804 | 100 | 0.057953 | 1000 | 0.227657 |
| 0.8 | 0.014920 | ||||||
| 0.9 | 0.014928 | ||||||
| 1 | 0.014935 |
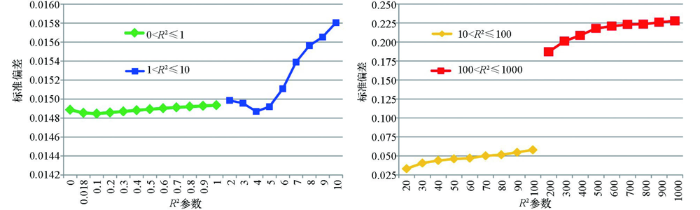
图3
由R2参数标准偏差值的结果可见,当R2参数较大时(10<R2<1 000,第三和第四区间),残差分析对应的标准偏差较大,表明插值误差的累计效应大,因此R2参数不宜过大。当R2参数较小时,位于第一区间或第二区间时,标准偏差的变化趋势均为先减小后增大,但是,第二区间内标准偏差值的变化较大、波动范围大,相比而言,第一区间内标准偏差值的变化较小、插值精度更趋稳定。根据白世彪等[17]的研究,R2参数的一个合理试验值是在平均样本间隔和平均样本间隔的一半之间,本次数据相邻样本(实测点)间隔为0.25 km或0.5 km(图1),平均样本间隔约为0.375 km,据此,R2参数在0.1875~0.375之间(位于本次讨论的第一区间)较为合适。综合考量R2参数的选取原则,结合本次试验标准偏差指标的变化情况,研究认为R2参数不能太大也不宜太小,当R2位于第一区间时插值结果较稳定,根据定量对比结果,本次插值选择R2参数为0.1。
4 搜索邻域及搜索点数
在利用已知点对一个未知点的预测值进行插值计算的过程中,需要指定一个搜索邻域来限制参与计算的已知点的数量和结构。对同一个未知点来说,随着搜索邻域的形状或方向不同,搜索区域内包含的参与计算的已知点的数量和位置也会不同[17]。为了讨论邻域形状及相关参数对插值结果的影响情况,本次设置搜索邻域的形状为圆形和椭圆形分别进行研究,在此基础上对搜索半径,搜索扇区的个数,搜索角度,从所有扇区使用的最大数据个数等参数进行插值讨论并优选。
4.1 搜索邻域为圆形
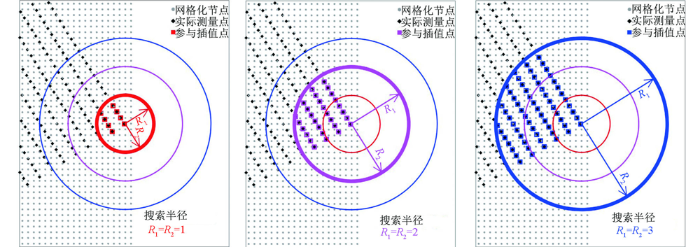
4.1.1 圆形邻域的搜索半径通过设置搜索半径R1和R2的大小来调整搜索邻域的形状,搜索半径不能太大也不能太小[11],当搜索邻域为圆形时,设置搜索半径R1=R2,本次参考系统默认值(11.7 km),分别取搜索半径为6、8、10、14、16 km这5种大小进行对比,插值过程中,插值核函数为自然三次样条函数,R2参数为0.1,其余插值参数设置为系统默认值(与3.1系统默认值相同)。由残差指标统计结果表3可见,当搜索半径R1=R2且介于6~16 km之间时,其标准偏差值未发生变化,可见搜索半径选择6~16 km之间均可,根据王玉敏等的研究可知,在搜索规则不变的条件下,任意改变搜索半径的大小,对数值点区域的等值线不产生影响[11],本次考虑到搜索半径不能太小,因而初步设置搜索半径为6 km进行插值参数优选。
表3 圆形邻域搜索半径残差结果
Table 3
| 半径R1=R2 | 标准偏差 |
|---|---|
| 6、8、10、11.7、14、16 | 0.014847 |
4.1.2 圆形邻域的搜索扇区与搜索角度
表4 搜索扇区及对应搜索点数
Table 4
| 搜索选项 | 对应参数 | ||
|---|---|---|---|
| ①搜索扇区个数/个 | 1 | 4 | 8 |
| ②从所有扇区使用的最大的数据个数/个 | 64 | 64 | 64 |
| ③从每个扇区使用的最大的数据个数/个 | 64 | 16 | 8 |
| ④所有扇区的最小数据个数(更少则白化节点)/个 | 8 | 8 | 8 |
| ⑤如果空白扇区多于此数则白化节点/个 | 1 | 3 | 7 |
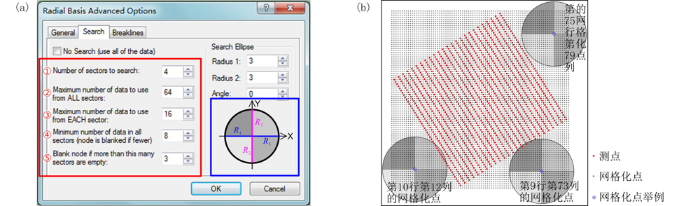
由表4可见,搜索扇区设置主要涉及5个参数(图4a中红色线框内):第①个参数为搜索扇区个数,即指将搜索区域划分为几个扇区;此处以4个扇区为例(图4a中蓝色线框内)对表4中相关参数进行说明,同时,设置搜索邻域为圆形(Radius1=Radius2),搜索半径R1=R2=3 km,搜索角度(Angle)为0°。第②个参数为从所有扇区使用的最大的数据个数,即指在所有扇区内参与插值的最大数据个数。第③个参数为从每个扇区使用的最大的数据个数,即指在每个扇区内参与插值的最大数据个数。第④个参数为所有扇区的最小数据个数(更少则白化节点),由图4(b)可见,对于第10行第12列的网格化点而言,在所有搜索扇区内共有9个测点(大于8个),因此该网格化点插值后可以得到一个网格值,但是对于第9行第73列的网格化点而言,在所有搜索扇区内共有4个测点(小于8个),因此该网格化点被白化,插值后没有网格值(意指更少则白化节点)。第⑤个参数为如果空白扇区多于此数则白化节点,由图4(b)可见,对于第75行第79列的网格化点而言,所有扇区内没有测点,4个扇区均为空白扇区(空白扇区大于3个),此时该网格化点被白化,插值后没有网格值。
图4
图4
搜索界面选项(a)与搜索点分布图示(b)
Fig.4
Search interface options (a) and search points distribution (b)
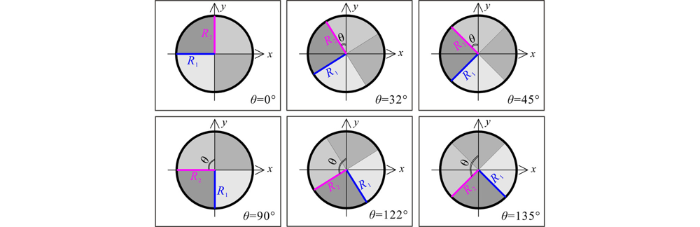
为了同时比较搜索角度(本文设置搜索角度Angle为搜索半径R2与Y轴的夹角)对插值精度的影响,本次设置搜索角度为0°、32°(搜索半径R2平行测线)、45°、90°、122°(搜索半径R2垂直测线),135°这6个方向(图5)。
图5
表5 圆形邻域不同搜索扇区对应残差结果
Table 5
| 搜索扇区1个 | 搜索扇区4个 | 搜索扇区8个 | |||
|---|---|---|---|---|---|
| 搜索角度=各向异性角度 | 标准偏差 | 搜索角度=各向异性角度 | 标准偏差 | 搜索角度=各向异性角度 | 标准偏差 |
| 0° | 0.014645 | 0° | 0.014847 | 0° | 0.014833 |
| 32° | 0.014645 | 32° | 0.014311 | 32° | 0.014827 |
| 45° | 0.014645 | 45° | 0.014776 | 45° | 0.014833 |
| 90° | 0.014645 | 90° | 0.014847 | 90° | 0.014833 |
| 122° | 0.014645 | 122° | 0.014311 | 122° | 0.014827 |
| 135° | 0.014645 | 135° | 0.014776 | 135° | 0.014833 |
图6
图6
圆形邻域不同搜索扇区残差曲线
Fig.6
Residual curves of different search sectors in circular neighborhood
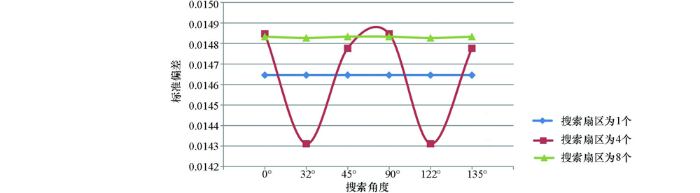
由表5、图6可见,采用不同搜索扇区插值时,获得的插值精度有所不同:搜索扇区为1个时,标准偏差值无变化;搜索扇区为4个时,标准偏差值变化较大,与搜索扇区为1个时的残差结果相比插值精度有高有低;搜索扇区为8个时,标准偏差值变化较小,且总体比搜索扇区为1个时的残差结果大。进一步分析发现,不同搜索扇区中,搜索角度的变化对插值结果也有不同的影响:当搜索扇区为1个时,插值精度不会随着搜索角度的变化而变化;当搜索扇区为4个时,不同搜索角度的插值结果精度大小为:32°=122°>45°=135°>0°=90°;当搜索扇区为8个时,不同搜索角度的插值结果精度大小为:32°=122°>0°=45°=90°=135°。
综合考虑搜索扇区与搜索角度对插值结果的影响可见,搜索扇区为4个时,搜索半径R2与测线平行(或垂直)时,残差分析获得的标准偏差值最小、插值精度最高,因此,搜索扇区选为4个,搜索角度选为搜索半径R2与测线平行(或垂直)时的角度插值效果最好。
4.1.3 圆形邻域时从所有扇区使用的最大的数据个数
表6 圆形邻域扇区为4个时最大数据个数
Table 6
| 参数设置条目 | A组 | B组 | C组 | D组 | E组 | F组 | G组 |
|---|---|---|---|---|---|---|---|
| 从所有扇区使用的最大的数据个数 | 16 | 32 | 48 | 64 | 80 | 96 | 112 |
| 从每个扇区使用的最大的数据个数 | 4 | 8 | 12 | 16 | 20 | 24 | 28 |
| 所有扇区的最小数据个数(更少则白化节点) | 8 | 8 | 8 | 8 | 8 | 8 | 8 |
| 如果空白扇区多于此数则白化节点 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
图7
图7
圆形邻域扇区为4个时最大数据个数残差结果与曲线
Fig.7
Residual results and curve of maximum number data of 4 search sectors in circular neighborhood
4.2 搜索邻域为椭圆形
4.2.1 椭圆形邻域的搜索半径与扇区和角度
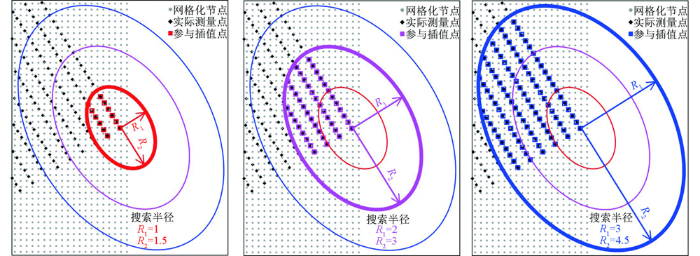
当搜索邻域的形状为椭圆形时,综合考虑搜索半径、搜索扇区和搜索角度的影响,同时设置相关参数进行对比。参考圆形邻域搜索半径试验情况,设置椭圆形邻域的搜索半径R1和R2为4类组合进行插值比较,其中,A类:R1=6,R2=12;B类:R1=6,R2=9;C类:R1=9,R2=6;D类:R1=12,R2=6。设置搜索扇区分别为1个、4个、8个,各扇区对应的搜索点数设置与表4中参数相同。设置搜索角度为0°、32°、45°、90°、122°、135°这6个方向,其余参数设置:插值核函数为自然三次样条函数,R2参数为0.1,各向异性比率=搜索半径R1与R2之比,各向异性角度=搜索角度,插值残差统计结果见表7~表9。
表7 椭圆形邻域扇区为1个时不同参数对应的残差结果
Table 7
| 分 类 | 搜索半径 R1~R2 | 各向异性比 率=R1/R2 | 各向异性角度=搜索角度 | |||||
|---|---|---|---|---|---|---|---|---|
| 0° | 32° | 45° | 90° | 122° | 135° | |||
| A类 | 6~12 | 0.5 | 0.015916 | 0.018210 | 0.016184 | 0.014729 | 0.014776 | 0.014756 |
| B类 | 6~9 | 0.667 | 0.014668 | 0.015528 | 0.015483 | 0.014895 | 0.014786 | 0.014899 |
| C类 | 9~6 | 1.5 | 0.014873 | 0.014765 | 0.014852 | 0.014689 | 0.015694 | 0.015587 |
| D类 | 12~6 | 2 | 0.014672 | 0.014756 | 0.014723 | 0.015882 | 0.019098 | 0.016929 |
表8 椭圆形邻域扇区为4个时不同参数对应的残差结果
Table 8
| 分 类 | 搜索半径 R1~R2 | 各向异性比 率=R1/R2 | 各向异性角度=搜索角度 | |||||
|---|---|---|---|---|---|---|---|---|
| 0° | 32° | 45° | 90° | 122° | 135° | |||
| A类 | 6~12 | 0.5 | 0.015553 | 0.020861 | 0.015845 | 0.014718 | 0.014723 | 0.014730 |
| B类 | 6~9 | 0.667 | 0.014799 | 0.014106 | 0.015380 | 0.014883 | 0.014755 | 0.014870 |
| C类 | 9~6 | 1.5 | 0.014850 | 0.014735 | 0.014825 | 0.014822 | 0.014330 | 0.015475 |
| D类 | 12~6 | 2 | 0.014660 | 0.014698 | 0.014702 | 0.015532 | 0.021106 | 0.016584 |
表9 椭圆形邻域扇区为8个时不同参数对应的残差结果
Table 9
| 分 类 | 搜索半径 R1~R2 | 各向异性比 率=R1/R2 | 各向异性角度=搜索角度 | |||||
|---|---|---|---|---|---|---|---|---|
| 0° | 32° | 45° | 90° | 122° | 135° | |||
| A类 | 6~12 | 0.5 | 0.015604 | 0.016997 | 0.017085 | 0.014793 | 0.014747 | 0.014735 |
| B类 | 6~9 | 0.667 | 0.014908 | 0.014409 | 0.015404 | 0.014794 | 0.014797 | 0.014857 |
| C类 | 9~6 | 1.5 | 0.014764 | 0.014758 | 0.014822 | 0.014924 | 0.014575 | 0.015488 |
| D类 | 12~6 | 2 | 0.014721 | 0.014718 | 0.014715 | 0.015600 | 0.017782 | 0.017769 |
图8
图8
椭圆形邻域扇区为1个时残差曲线
Fig.8
Residual curves of different parameters of 1 search sector in elliptical neighborhood
图9
图9
椭圆形邻域扇区为4个时残差指标曲线
Fig.9
Residual curves of different parameters of 4 search sectors in elliptical neighborhood
图10
图10
椭圆形邻域扇区为8个时残差指标曲线
Fig.10
Residual curves of different parameters of 8 search sectors in elliptical neighborhood
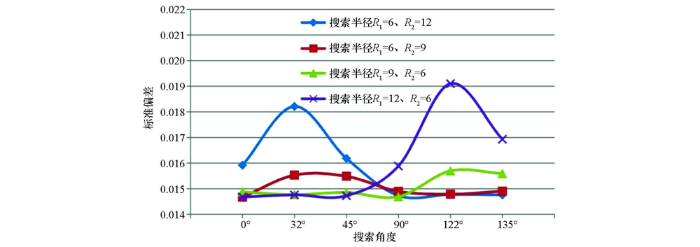
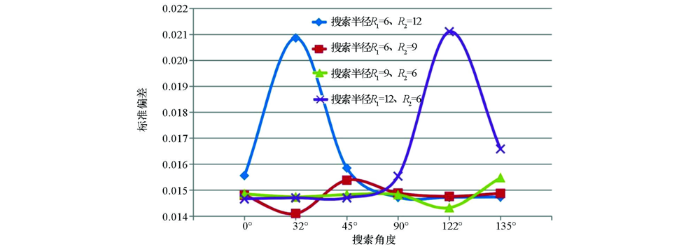
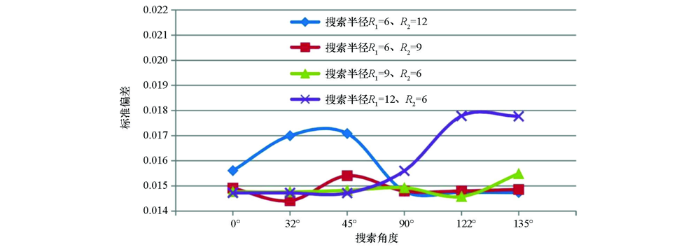
当搜索扇区固定时,不同搜索半径对应的插值结果变化趋势较为相似:① 当搜索半径R1/R2=6/12时,较大的搜索角度(90°~135°)插值得到的标准偏差值相对较小,而较小的搜索角度(0°~45°)插值得到的标准偏差值相对较大;② 当搜索半径R1/R2=12/6时,较小的搜索角度(0°~45°)插值得到的标准偏差值相对较小,而较大的搜索角度(90°~135°)插值得到的标准偏差值相对较大;③ 当搜索半径R1/R2=6/9时,较大的搜索角度(90°~135°)插值得到的标准偏差值相对集中,而较小的搜索角度(0°~45°)插值得到的标准偏差值同时出现了最小和最大值;④ 当搜索半径R1/R2=9/6时,较小的搜索角度(0°~45°)插值得到的标准偏差值相对集中,而较大的搜索角度(90°~135°)插值得到的标准偏差值同时出现了最小和最大值。
4.2.2 椭圆形邻域时从所有扇区使用的最大的数据个数
图11
图11
椭圆形邻域扇区为4个时最大数据个数残差指标结果与曲线
Fig.11
Residual results and curve of maximum number data of 4 search sectors in elliptical neighborhood
5 搜索半径的优化
根据不同形状搜索邻域初步设置的搜索半径为基础,通过对搜索扇区、搜索角度、搜索点数的比较,优选了各个插值参数相应的最佳取值范围;反之,当这些搜索参数均有明确的定量化取值与条件限制时,搜索半径的大小能否更加优化进一步提高插值效率?下面针对搜索半径相等与不等两种情况进行讨论。
5.1 搜索半径R1与R2相等
当搜索邻域为圆形时,搜索半径R1与R2相等,设置搜索半径R1=R2并分别为1、2、3、4、5 km等5种情况进行对比,插值核函数为自然三次样条函数,R2参数为0.1,其他参数依据圆形邻域比较的最优指标设置为:搜索扇区个数为4个,搜索角度为32°,各向异性比率为1,各向异性角度为32°,从所有扇区使用的最大的数据个数为64,从每个扇区使用的最大的数据个数为16,所有扇区的最小数据个数(更少则白化节点)为8,如果空白扇区多于3个则白化节点。
图12
图12
搜索半径R1与R2相等时残差结果与曲线
Fig.12
Residual results and curve of same search radius in circular neighborhood
另外,对于周围“实测点”数量较少的边界点而言,以边界测线的拐角“预测点”(网格化节点)为例(见图1中蓝色线框),当搜索半径变化时,其半径内包含的“在所有扇区的最大数据个数”也随之变化(图13),搜索半径为1 km时最大数据约8个、搜索半径为2 km时最大数据约29个、搜索半径为 3 km时最大数据约63个、搜索半径为4 km时最大数据约109个(远大于4.1.3中优选的64个点)。由此可见,搜索半径小于3 km时其搜索范围内的数据点个数太少,不能满足插值需求;当搜索半径大于3 km时,搜索数据点个数能够满足插值需求,但是由于距离较大,一定距离范围之外实测点对预测点的影响比较小,对插值结果的贡献不大。综合对比认为,当搜索半径R1与R2相等时,搜索半径设置为3 km即能够得到较高的插值精度、获得较好的插值结果。
图13
图13
搜索半径R1与R2相等时插值点分布图示(网格化节点范围见
Fig.13
Map of the interpolation points distribution with the same search radius
5.2 搜索半径R1与R2不等
当搜索邻域为椭圆形时,搜索半径R1与R2不等,根据椭圆形邻域不同半径对比结果,当搜索半径R1/R2=6/9=0.667,且搜索扇区为4个,搜索角度为32°,获得的插值精度更高。因此,分别设置搜索半径R1=1 km、R2=1.5 km,R1=2 km、R2=3 km,R1=3 km、R2=4.5 km,R1=4 km、R2=6 km,R1=5 km、R2=7.5 km,R1=6 km、R2=9 km等6组情况进行比较,插值核函数为自然三次样条函数,R2参数为0.1,其他参数依据椭圆形邻域研究的最优指标设置为:搜索扇区个数为4个,搜索角度为32°,各向异性比率为0.667,各向异性角度为32°,从所有扇区使用的最大的数据个数为80,从每个扇区使用的最大的数据个数为20,所有扇区的最小数据个数(更少则白化节点)为8,如果空白扇区多于3个则白化节点。
由残差统计结果(图14)可见,随着搜索半径的增加,残差指标值先减小后增大,这与半径R1、R2相等时的特征相似,即:对同一个预测点来说,在一定距离之外,实测点对预测点的影响很小,随着搜索半径的增大,插值精度基本不变。
图14
图14
搜索半径R1与R2不等时残差结果与曲线
Fig.14
Residual results and curve of different search radius in elliptical neighborhood
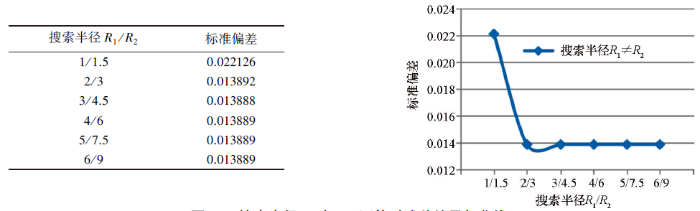
同样,当搜索半径变化时,其半径内包含的“在所有扇区的最大数据个数”也随之变化,以边界测线的拐角预测点为例(见图1中蓝色线框),搜索半径R1/R2为1/1.5时最大数据约12个(图15)、搜索半径R1/R2为2/3时最大数据约43个、搜索半径R1/R2为3/4.5时最大数据约93个(大于4.2.2中优选的80个点)。对比图14残差统计结果可见,当搜索半径R1/R2为1/1.5或2/3时,个别边界测点对应的最大搜索点个数较少(远小于80个),因此其插值结果精度较低,当搜索半径R1/R2为4/6或5/7.5和6/9时,搜索点数均能够满足插值需求,插值精度较高且较稳定,综合对比而言,当搜索半径R1/R2为3/4.5时标准偏差值最小,插值精度最高,因而选择搜索半径R1/R2为3/4.5进行插值可获得较优的插值结果。
图15
图15
搜索半径R1与R2不等时插值点分布图示(网格化节点范围见
Fig.15
Map of the interpolation points distribution with the different search radius
6 结论
本文采用理论模型的正演重力异常,模拟部署1∶5万野外实测点并进行插值参数优选,采用检查点法根据残差分析的标准偏差指标大小定量比较插值精度,综合分析插值效果选定了最优插值参数,研究结果对于选取插值参数的大小和范围具有定量化的参考和指导意义,通过本次研究取得以下几点认识:
2) 5种核函数插值精度高低排序为:自然三次样条函数>薄板样条函数>多重二次曲面函数>多重对数函数>反多重二次曲面函数,其中自然三次样条函数的插值精度最高。
3) R2(平滑因子)参数对应的4个区间插值精度大小为:第一区间>第二区间>第三区间>第四区间,其中第一区间标准偏差指标变化较小、插值精度更趋稳定,本次优选R2参数为0.1。
4) 搜索邻域为圆形时,最优插值参数分别为:搜索半径R1=R2=3 km,搜索扇区为4个,搜索角度为32°(或122°,即搜索半径R2与测线平行或垂直时的角度),各向异性比率为1(等于搜索半径R1与R2之比),各向异性角度为32°(或122°与搜索角度一致),从所有扇区使用的最大的数据个数为64个,从每个扇区使用的最大的数据个数为16个,所有扇区的最小数据个数(更少则白化节点)为8个,如果空白扇区多于3个则白化节点。
5) 搜索邻域为椭圆形时,最优插值参数分别为:搜索半径R1=3 km、R2=4.5 km,搜索扇区为4个,搜索角度为32°(即搜索半径R2与测线平行时的角度),各向异性比率为0.667(等于搜索半径R1与R2之比),各向异性角度为32°(与搜索角度一致),从所有扇区使用的最大的数据个数为80个,从每个扇区使用的最大的数据个数为20个,所有扇区的最小数据个数(更少则白化节点)为8个,如果空白扇区多于3个则白化节点。
6) 重力异常为各向异性异常,建议选用椭圆形邻域进行插值,且主半轴R1小于次半轴R2;在插值过程中应考虑特定方向上的权重值,主半轴R1垂直测线,次半轴R2与测线平行。
参考文献
自然邻点插值算法及其在二维不规则数据网格化中的应用
[J].
Natural neighbour interpolation and its application to 2D grid of irregular data
[J].
重力插值方法研究
[J].
Research on interpolation methods in gravity field
[J].
地球物理不规则分布数据的空间网格化法
[J].
Gridding methods of geophysical irregular data in space domain
[J].
一种稳定的位场数据最小曲率网格化方法研究
[J].
The research to a stable minimum curvature gridding method in potential data processing
[J].
大面积物探数据的网格化处理方法
[J].
Grid processing method of large area geophysical data
[J].
一种实用的等值线型数据网格化方法
[J].
A practical contour type data gridding technique
[J].
重力数据网格化方法比较
[J].
Comparison among methods for gravity data gridding
[J].
DZ/T 0004—2015重力调查技术规范(1∶50000)
[S].
DZ/T 0004—2015 The technical specification for gravity survey (1∶50000)
[S].
地球物理勘探中几种二维插值方法的误差分析
[J].
Error analysis of several two-dimensional interpolation methods in the geophysical exploration
[J].
基于Surfer的1∶50000规则测网重力数据网格化方法选取——以银额盆地赛汉陶来区块重力资料为例
[J].
Selection of gridding methods for 1∶50000 regular-grid gravity data based on surfer—A case from gravity data in Saihantaolai block of Yin’e basin
[J].
地球物理数据网格化参数的确定及模型的选择
[J].
The Determination about the grid parameters of geophysical data and the selection about the grid model
[J].
基于Surfer软件的数据网格化方法探析
[J].
The discussion on the geophysical data gridding based on the surfer software
[J].
交叉验证在离散数据网格化时的应用
[J].
Using cross validation in gridding
[J].
DEM产品数据质量分析研究与系统实现
[J].
Research of DEM quality-precision analysis and system implementation
[J].
径向基函数算法中插值参数对DEM精度的影响
[J].
Effects of interpolation parameters in multi-log radial basis function on DEM accuracy
[J].
DEM插值参数优选的试验研究
[J].
Experimental research on optimization of DEM interpolation parameters
[J].
离散数据网格化参数的确定和数学模型的选择——以Surfer7.0、Mapgis6.0为例
[J].
Specifying the parameters of gridding and choosing gridding algorithm
[J].
位场向下延拓的迭代法的扩边方法
[J].
Study of extending methods of iteration of downward continuation in potential field
[J].
高精度海洋重力异常格网插值技术研究
[J].
The study of high precision interpolation technology in marine gravity anomaly
[J].