回线源瞬变电磁法的一维Occam反演

doi:10.11720/wtyht.2021.0103

回线源瞬变电磁法的一维Occam反演

邢涛^,¹, 袁伟², 李建慧^,³

1.北京探创资源科技有限公司,北京 100071

2.内蒙古地质工程有限责任公司,内蒙古呼和浩特 010010

3.中国地质大学(武汉) 地球物理与空间信息学院,湖北武汉 430074

One-dimensional Occam's inversion for transient electromagnetic data excited by a loop source

XING Tao^,¹, YUAN Wei², LI Jian-Hui^,³

1. Beijing Exploration Resources Technology Co., Ltd., Beijing 100071, China

2. Inner Mongolia Geological Engineering Co., Ltd., Hohhot 010010, China

3. Institute of Geophysics and Geomatics, China University of Geosciences(Wuhan), Wuhan 430074, China

通讯作者: 李建慧(1982-), 男,副教授, 博士生导师, 主要研究方向为电磁法数值计算与资料处理研究。 Email:ljhiiicumt@126.com

责任编辑: 沈效群

收稿日期: 2021-02-26 修回日期: 2021-05-18

基金资助:

国家重点研发计划项目. 2020YFE0201300-06
国家自然科学基金. 42022030

Received: 2021-02-26 Revised: 2021-05-18

作者简介 About authors

邢涛(1983-),男,硕士,高级工程师,长期从事地球物理勘探方面的研究工作。Email: 156663062@qq.com

摘要

基于Dipole 1D一维正演程序和Occam算法开发了回线源瞬变电磁法一维反演程序,并以四层介质模型验证了其正确性。对于倾斜界面模型,待反演数据由时域矢量有限单元法三维正演计算,通过对比实际模型和等效模型的反演结果,说明了一维反演可直接应用于此类情形。最后,开展了那仁宝力格煤田玄武岩深部探测案例研究。在反演电阻率断面图中,玄武岩整体形态呈“锅底状”,与多个钻孔资料吻合良好,进一步验证了该反演程序的正确性。

关键词： 回线源 ; 瞬变电磁法 ; Occam算法 ; 一维反演

Abstract

A 1D inversion code is developed for the loop-source transient electromagnetic method (TEM) based on the open-source code Dipole1D and Occam's algorithm. This code is tested by a four-layer stratified model. Then, the model with a tilted earth-air interface is considered, for which the synthetic data are calculated by 3D finite-element method. The inversion results show that 1D inversion can be directly used for the scenario with tilted interface. Finally, this 1D inversion code is used for a field case, in which TEM is employed to delineate the 3D distributed domains of a basalt which intruded into shale and sandstone. The inversion result shows that the thickness of the basalt coincides with the drilling data, and the shape of the basalt like a pot bottom.

Keywords： loop source ; TEM ; Occam's method ; 1D inversion

PDF (5104KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

邢涛, 袁伟, 李建慧. 回线源瞬变电磁法的一维Occam反演. 物探与化探[J], 2021, 45(5): 1320-1328 doi:10.11720/wtyht.2021.0103

XING Tao, YUAN Wei, LI Jian-Hui. One-dimensional Occam's inversion for transient electromagnetic data excited by a loop source. Geophysical and Geochemical Exploration[J], 2021, 45(5): 1320-1328 doi:10.11720/wtyht.2021.0103

0 引言

目前,回线源瞬变电磁法已广泛应用于金属矿产勘探^[1,2,3]、环境水文地质调查^[4,5,6]等领域。随着三维正演算法的逐渐成熟和计算机软硬件性能的不断提升,瞬变电磁法三维反演的报道陆续出现^[3,7],但实用化的资料处理解释手段仍以一维反演为主^[8]。

瞬变电磁法一维反演始于20世纪80年代。如:Raiche等基于阻尼最小二乘法对瞬变电磁法重叠回线和电阻率法施伦贝谢装置采集的数据开展了联合反演^[9],黄皓平、王维中采用阻尼最小二乘法实现了时间域航空电磁数据的一维反演^[10];上述反演算法均采用了层状介质参数化反演,即同时反演层厚度和电阻率,反演结果依赖于模型层数和初始模型^[11]。Farquharson和Oldenburg在目标函数中加入待求模型与某个参考模型之间的偏离程度表征项,并设定反演模型层数多于观测数据个数,且各层介质层厚固定,只反演电阻率^[11]。随后,丹麦奥胡斯大学Auken课题组采用阻尼最小二乘法也开展了瞬变电磁法一维反演^[12],并引入横向约束项用于解决反演断面图中电阻率和层厚横向连续性差、薄层分辨率低等问题^[13,14],引入空间约束项用于解决反演深度切片中层界面不光滑等问题^[15]。德国科隆大学Tezkan课题组采用基于阻尼最小二乘法和Occam算法^[16]的反演程序,开展回线源瞬变电磁法、长偏移距瞬变电磁法、射频大地电磁法等方法的单一反演或联合反演^[17]。

国内课题组也开展了类似研究。如:毛立峰等采用自适应正则化方法开展了直升机航空瞬变电磁法数据一维反演^[18],齐彦福等采用Occam算法对m序列发射波形多道瞬变电磁法数据开展了反演研究^[19],类似工作也见于李海等^[20]。除了上述线性化优化方法外,模拟退火法^[6]、粒子群优化——阻尼最小二乘混合算法^[21]等智能优化算法也被成功用于瞬变电磁法一维反演。

综上所述,瞬变电磁法一维反演发展比较完善成熟。本研究基于Constable等开发的Occam反演算法^[16]和Key课题组开发的Dipole1D一维正演程序^[22],开展了回线源瞬变电磁法一维反演研究。

1 一维正演框架

Dipole1D适用于水平电偶源和垂直电偶源,并能通过方位角和倾角控制电偶源形态,且发射源和接收点可放置于层状介质任意层位。本节中只叙述电磁法勘探的一维正演框架,不再给出公式,具体公式详见上述文献。

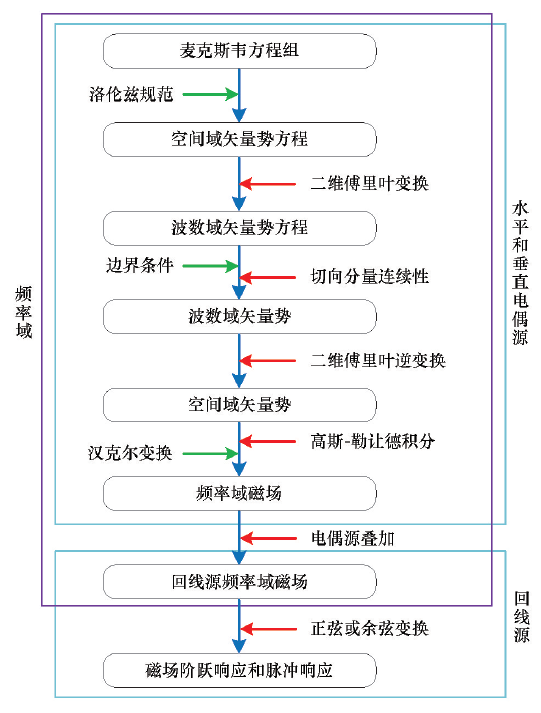
图1为回线源瞬变电磁法一维正演框架,该框架从水平电偶源和垂直电偶源激发的电磁场空间域、频率域麦克斯韦方程组出发。需要说明的是,此处的电偶源并非点源,而是具有一定长度的接地线源,当收发距远大于线源尺度时,其可视为电偶源。一个方形回线可简单视为由4个首尾相连的接地线源组成,当回线尺寸比较小时,每个接地线源还可进一步细分。一个复杂形态发射回线可视为一系列首尾相连的接地线源,这些电偶源的方位角和倾角不尽相同。Dipole1D程序处理这种复杂形态场源时,如果该场源方位角与x和y轴斜交,需采用x和y两个方向布设的电偶源组合求解;如果该场源倾角不为零,还需引入z方向布设的电偶源来共同求解。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 回线源瞬变电磁法一维正演框架

Fig.1 The framework of 1D forward modeling for loop-source transient electromagnetic methods

借助势表示电场E和磁场H是求解麦克斯韦方程组的有效途径之一。引入矢量势和标量势后,由麦克斯韦方程组推导出关于矢量势的双旋度方程,再结合一些限定条件,比如洛伦兹规范,可得到关于矢量势在空间域的亥姆霍兹方程。对于一维介质,介质分界面在水平坐标x和y无限延伸,并与垂直坐标面(等z平面)重合,可利用二维傅里叶变换将亥姆霍兹方程从空间域转换至波数域;伴随着这种转换,将关于x、y和z的偏微分方程转变为易于求解、关于z的常微分方程。结合电磁场衰减的边界条件和在界面处电磁场切向分量的连续性,可以唯一求解上述关于矢量势的微分方程,获得波数域矢量势;再利用二维傅里叶逆变换得到空间域矢量势,并根据势与场的转换关系,获得频率域电磁场。这一转换过程中,需数值求解多个关于发射源长度和波数的二重积分。对关于发射源长度的积分,通常采用高斯—勒让德积分求解,该方法可通过增大积分点数来提高求解精度。关于波数的积分含有零阶或一阶形式的第一类贝塞尔函数,该类积分通常采用汉克尔变换求解。关于汉克尔变换及常用的变换系数,可参考Guptasarma和Singh^[23]等已发表的文献。

逐个计算并累加每个接地线源激发的频率域磁场,即可获得回线源激发的磁场,再采用正弦变换或余弦变换求得磁场阶跃响应或脉冲响应,进而得到感应电动势。本研究采用Anderson研发的787个系数的正弦变换和余弦变换^[24]。

2 Occam反演方法

采用经典的Occam算法^[16]开展一维反演计算。该算法的基本思想是:通过在目标函数中引入模型粗糙度的正则化项,来获得能够拟合数据的最光滑模型。设定反演的目标函数为

(1)

\begin{array}{l} U = || \partial m {||}^{2} + || P (m - m_{*}) {||}^{2} + \\ μ^{- 1} [|| W (d - F (m)) {||}^{2} - χ_{*}^{2}], \end{array}

等式右边第一项为模型粗糙度,第二项表征反演待求模型与某个参考模型m_*之间的偏离程度,第三项为实测数据与正演模型响应的拟合差函数。式中:m为模型参数向量,本研究中定义为各层介质电导率的对数,即[lg σ₁,lg σ₂,…,lg σ_N];d为数据向量,定义为[d₁,d₂,…,d_M],这些数据既可以为磁感应强度脉冲响应,也可以为磁感应强度;F(m)为模型m对应的瞬变电磁法正演模型响应;∂为由一阶差分算子组成的矩阵,因此对于一维层状介质模型,∂m为lg σ的空间垂向导数;P为参考模型权重矩阵,当某层介质电导率确定参考值后,其相应的权重设置为1;W为数据协方差加权函数,此处为一个对角矩阵,每个对角元素为相应采集数据标准差的倒数,这使得那些观测精度较低的数据对反演结果的影响较小;μ为正则化因子; $χ_{*}^{2}$ 为人为设定的目标拟合差,用于平衡数据拟合项与模型粗糙度和参考模型偏离度。

为了使得目标函数最小化,通常求取它关于模型参数m的一阶导数,并令其为零。由于正演函数F(m)是模型参数m的非线性函数,对其在某个模型m_k处进行泰勒展开,有:

(2)

F (m_{k} + Δ m) \approx F (m_{k}) + J_{k} Δ m,

式中J_k为正演函数对模型参数的一阶导数(称为雅可比矩阵):

(3)$J_k=▽_m F(m_k);$

矩阵元素为

(4)

J_{mn} = \frac{\partial F_{m} (m_{k})}{\partial \lg σ_{n}} 。

Dipole 1D程序在正演时,可采用解析法一并计算灵敏度矩阵。

Occam反演的模型更新公式与传统的高斯牛顿法(Gauss-Newton,GN)相同,即:

(5)

\begin{array}{l} m_{k + 1} = m_{k + 1} - H_{k}^{- 1} g_{k} = [μ (\partial^{T} \partial + PP) + \\ (W J_{k})^{T} W J_{k}]^{- 1} \cdot [(W J_{k})^{T} W \dot{d} + μP m_{*}] 。 \end{array}

式中:g_k和H_k分别为目标函数在m_k处对模型参数的一阶和二阶导数; $\dot{d}$ =d-F(m_k)+J_km_k。然而,Occam与传统GN法最大的不同之处在于正则化因子μ的选取,GN法的μ在反演迭代过程中通常固定不变或者通过一些非常简单的算法选取,而Occam则通过一元函数优化来选取正则化因子,这使得其反演算法非常稳定,不仅对μ初始值依赖程度不高,而且往往只需要很少的迭代次数便能收敛。当然,由于一元函数优化需要大量的正演计算,Occam法的每一次迭代计算量也比GN法要大得多。

在本研究中,使用均方根拟合差(RMS misfit)来衡量数据的拟合程度,其表达式为:

(6)

x_{rms} = \sqrt[]{\frac{χ^{2}}{M}} = \sqrt[]{\frac{1}{M} \overset{M}{\sum_{m = 1}} {\{\frac{d_{m} - F_{m} [m_{k + 1} (μ)]}{s_{m}}\}}^{2}},

式中:M为数据数目,s_m为第m个数据对应的标准差,[d_m-F_m(m_k₊₁(μ))]/s_m为单个数据的拟合差。

3 理论模型

3.1 层状介质模型

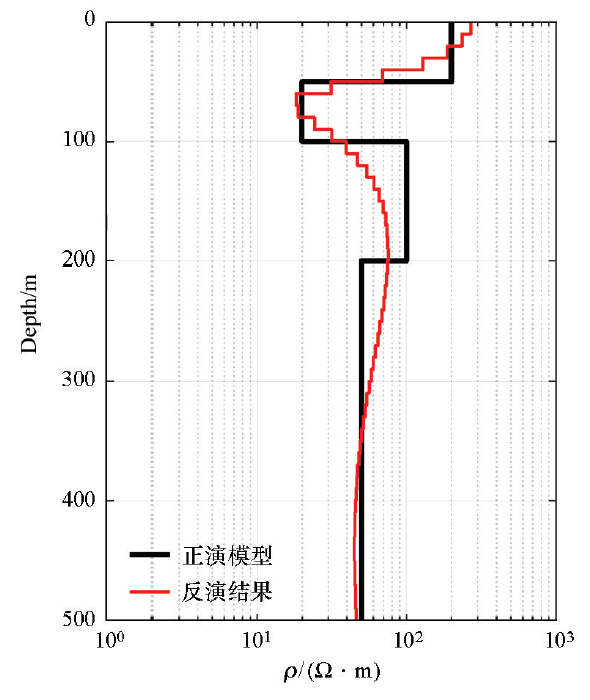
采用中心回线装置,发射源为边长50 m的方形回线。该层状介质共含4层,第一至第四层介质厚度依次为50、50、100 m和∞,电阻率ρ依次为200、20、100 Ω·m和50 Ω·m。观测时间序列共含31个时刻,其范围在10^-5~10^-2 s。待反演感应电动势由Dipole 1D计算,并添加了5%的随机噪音。Occam反演中,地电模型(含空气层)共含52层,其中地下51层介质电阻率待反演,层厚度均为10 m。反演时电阻率范围为10⁰~10³ Ω·m,初始模型为均匀半空间(10^1.5 Ω·m),无参考模型。反演中,最大迭代次数为40,目标拟合差为3。对于该模型,迭代7次后,均方根拟合差小于3,迭代终止。

如图2所示,对于该模型,反演结果能够较好地反映真实地电结构。图3中,由反演结果计算的感应电动势与待反演数据吻合良好,二者拟合差绝对值多数在3以内,只有个别大于3。通过这一模型,验证了程序的正确性。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 对于四层模型,回线中心点反演地电模型

Fig.2 The inversion geo-electric model for the loop-center point and for 4-layer model

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 四层模型的反演结果

Fig.3 The data computed from the inversion model

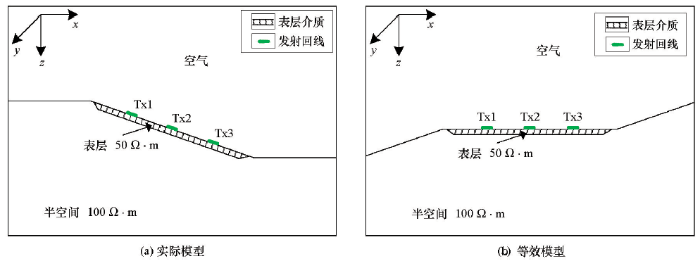
3.2 倾斜界面模型

如图4a所示,发射回线铺设在倾角为20°的斜坡之上。该模型表层介质厚度为30 m,电阻率为50 Ω·m,沿走向方向长度为200 m;表层下伏介质为100 Ω·m的半空间。发射回线为10 m×10 m的正方形。图4a中,发射回线Tx1、Tx2和Tx3的中心位置分别为(-93.969, 0.0,-34.302)、(0.0, 0.0,0.0)和(93.969, 0.0, 34.302)。采用中心回线装置,观测量为倾斜界面法向方向的感应电动势。采用课题组开发的时域矢量有限单元法^[25]计算磁感应强度脉冲响应三分量,并将其合成观测量。观测时间序列范围为0.025~1.995 ms,共20个时刻。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 倾斜界面模型示意

Fig.4 The sketch map for the tilted-surface model

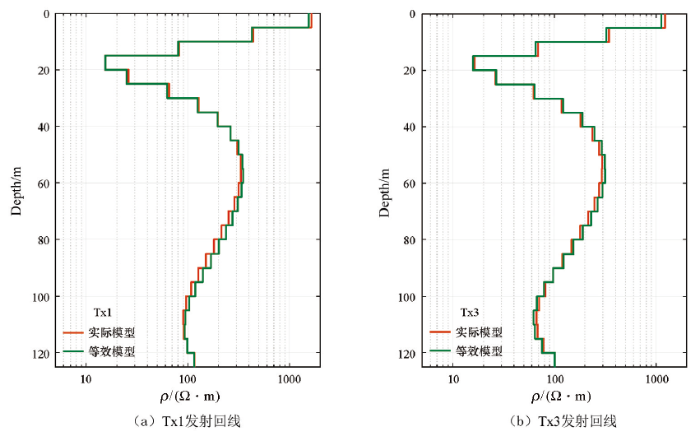
将该倾斜界面模型逆时针旋转20°可得到其等效模型(图4b)。该模型中,发射回线Tx1、Tx2和Tx3均铺设于水平界面之上,其中心位置分别为(-100,0.0,0.0) m、(0.0,0.0,0.0) m和(100,0.0,0.0) m,观测量为感应电动势垂直分量。接下来对实际模型和等效模型开展一维反演。Occam反演中,地电模型(含空气层)共含26层,其中地下25层介质电阻率待反演,层厚度均为5 m。反演时电阻率范围为10⁰~10⁴ Ω·m,初始模型为均匀半空间(10^1.5 Ω·m),无参考模型,这种设置我们称之为反演方案1。反演中,最大迭代次数为40,目标拟合差为3。考虑到此处反演主要用于验证上述两种模型反演结果的等价性,我们对待反演的感应电动势只添加了1%的随机噪音。

在发射回线Tx1和Tx3激发情况下,反演结果如图5所示。图中可见实际模型和等效模型的反演结果具有良好的一致性,这说明了对于铺设于倾斜界面的发射回线模型,如果观测量是界面法向方向的感应电动势,那么可按水平界面情形开展一维反演。值得注意的是,尽管反演结果中深部结果与真实模型吻合较好,但浅层结果与真实模型存在较大差异,如反演结果中低阻层主要集中于地下15~25 m,其电阻率远小于50 Ω·m,低阻层的上下介质均为高阻层,地表电阻率甚至超过1 000 Ω·m。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 回线中心测点数据反演获取的地电模型(反演方案1)

Fig.5 Geoelectric model obtained by inversion of data at the center of the loop( inversion schemes 1)

为了使反演结果与真实模型一致,反演算法中考虑了参考模型以及结构约束,即反演方案2和反演方案3。方案2中,将模型中地下第一、第二层介质电阻率设置为50 Ω·m;方案3在方案2的基础上,允许电阻率结构在地下30 m处不连续。如图6a所示,以发射回线Tx2激发时情形为例,采用3种反演方案获取的地电模型结构基本一致,即使考虑参考模型和结构约束也未能改变低阻层上下介质均为高阻层的这一现象。再次对相应的一维模型(即表层低阻层在水平方向足够延伸)开展反演计算(图6b),结果显示,真实模型为一维情形时反演获取的地电模型结构与三维情形的结果基本一致。

图6

新窗口打开| 下载原图ZIP| 生成PPT

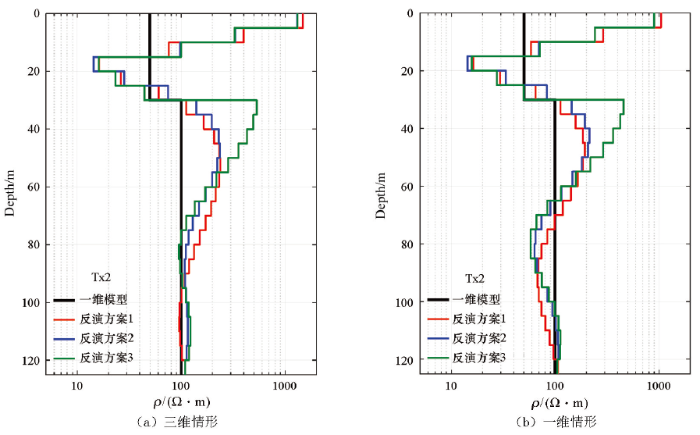
图6 采用不同反演方案时,实际模型(Tx2发射回线)和一维情形的反演地电模型

Fig.6 The inversion geo-electric models obtained from different inversion schemes

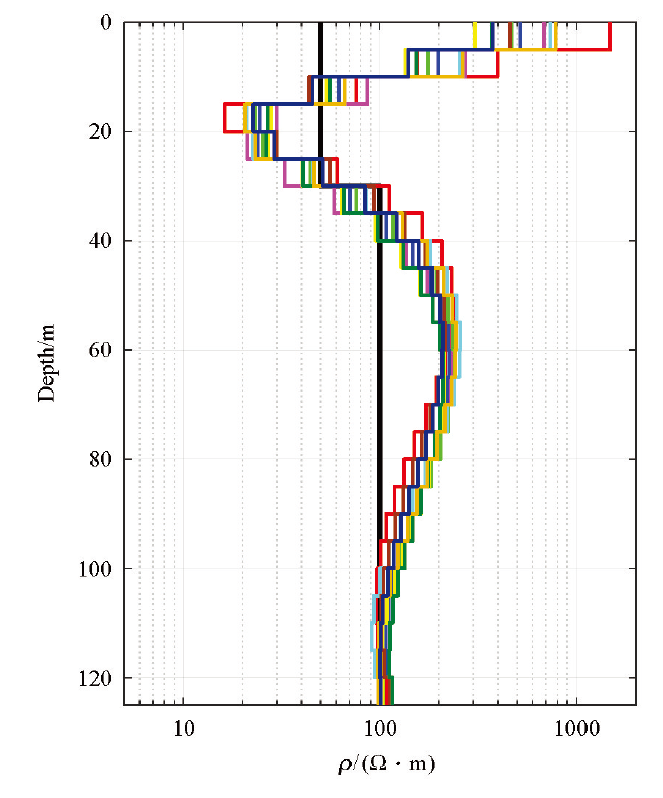
图7是在反演数据中添加5%的随机误差并经过10次反演计算的结果。由于每一次反演添加的误差并不一样,反演结果也略有差异,但地电模型结构基本一致,这也验证了反演算法的稳定性。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 随机噪声影响下,实际模型(Tx2发射回线)的反演地电模型

黑色曲线为一维模型,彩色曲线为反演结果

Fig.7 Under the influence of random noise, the inversion geoelectric model of the actual model (Tx2 loop)

The black line denotes the realistic model, the color lines denote the inversion models

4 实例

内蒙古自治区那仁宝力格煤田分布区内地势平坦,新近系喷出岩发育。从火山口和火山锥的存在和分布形态看,以中心式喷发为主,裂隙式喷发次之;岩性组合主要有橄榄拉斑玄武岩和玄武岩。勘探区内,玄武岩体电阻率可达上千欧姆米,而砂岩和泥岩地层电阻率仅为几十欧姆米。这种明显的电性差异也是采用瞬变电磁法圈定玄武岩在沉积岩中分布范围的物性基础。本次野外工作布设了11条测线,线距100 m,点距40 m。仪器采用加拿大Phoenix公司的V8多功能电法仪,观测时间序列为5 Hz的30个时间窗口。发射回线边长为600 m×300 m,其中600 m边长沿测线方向布置。

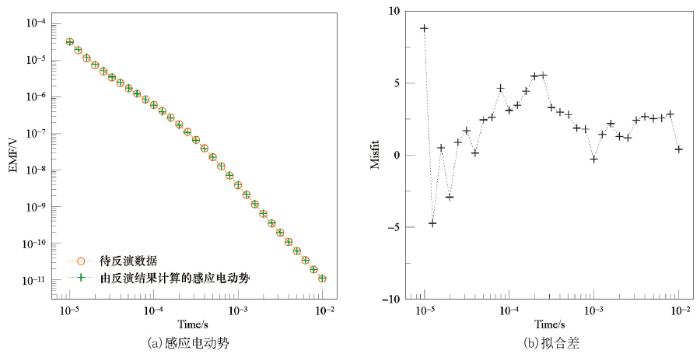
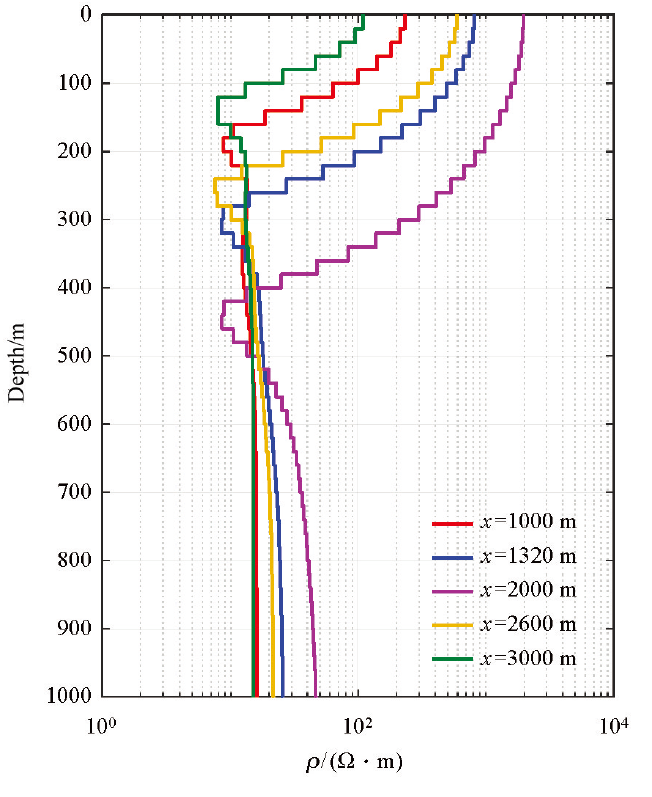
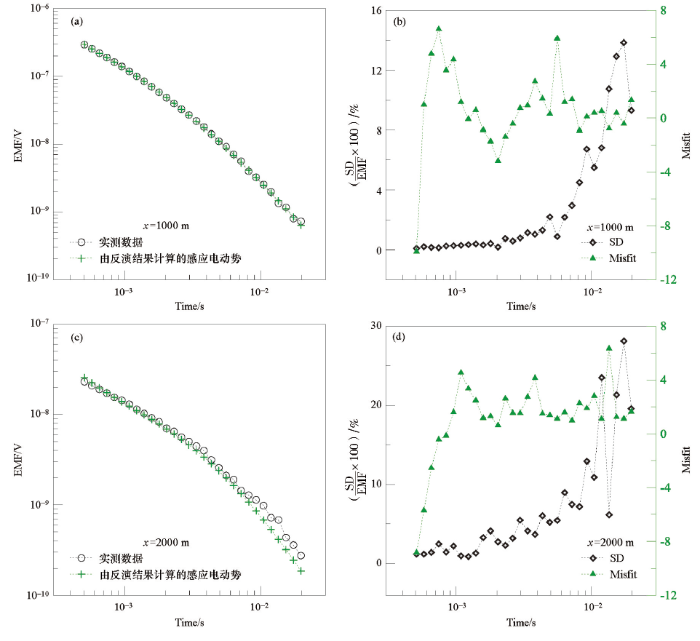
选取测线1作为本次研究的实例。该测线横穿喷出于地表的玄武岩露头,其长度为2 600 m,共66个测点,测点x坐标范围为680~3 280 m。Occam反演中,地电模型(含空气层)共含52层,其中地下51层介质电阻率待反演,层厚度均为20 m。反演时电阻率范围为10^0.5~10⁴ Ω·m,反演数据为感应电动势,初始模型为均匀半空间(10^1.5 Ω·m),无参考模型。图8为该工区5个测点的一维反演电阻率曲线,其曲线形态大致为电阻率随深度的增加而先减小再增大。测点x坐标由1 000 m增大至3 000 m时,反演结果中电阻率变化趋势是先增大后减小,其中浅层幅值变化最为明显。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 5个测点数据分别反演获取的地电模型

Fig.8 The inversion geo-electric models for five survey points

图9a、c中,由反演结果计算的感应电动势与实测数据曲线形态基本一致。当x=1 000 m时,由反演结果计算的感应电动势与实测数据吻合程度良好(图9a);x=2 000 m时,两类数据在8 ms之后吻合程度较低(图9c)。这一现象与其晚期时刻实测数据的标准差(standard deviation,SD)偏大有关。如图9d所示,该测点标准差与实测数据比值在8 ms之后快速上升,最大值接近28%。另外,如图9b、d所示,由反演结果计算的感应电动势与实测数据之间的拟合差绝对值在大多数时刻都小于3,仅在少数时刻偏大。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 x=1 000 m和2 000 m时的一维反演结果

a、c—不同测点的感应电动势;b、d—拟合差与实测数据标准差

Fig.9 The data computed from the inversion model for x=1 000 m and 2 000 m

a、c—EMF curves at different measuring points; b、d—Misfit curver and the standard deviation curves of measured data

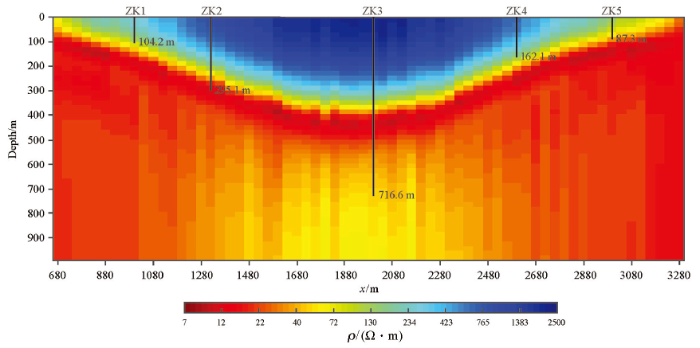
图10是由单点反演结果拼接的测线1地电模型断面。该测线共经过5个钻孔,图中数字为钻孔揭露的玄武岩厚度。断面图中,上部高阻区域(蓝色和绿色)为玄武岩分布范围,下部低阻区域(红色)为沉积岩分布范围,二者分界面连续、清晰,并呈现出喷出岩典型的“锅底状”分布形态,但未见火山通道。对比反演结果与钻孔资料,发现两种方法获取的玄武岩厚度在钻孔ZK1、ZK2、ZK4和ZK5处基本一致,但在钻孔ZK3处差异明显。由此推断,钻孔ZK3可能位于火山通道分布范围之内。进一步推断,由于火山通道随着深度增加,分布范围逐渐缩小,导致一维反演结果与真实情况偏差较大。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 由单点反演结果拼接的测线1地电模型断面

Fig.10 The section view stitched from the single-point 1D inversion models for survey line 1

5 结论

本研究实现了基于Occam算法的回线源瞬变电磁法一维反演,并采用理论模型和野外实例验证了程序的正确性,为瞬变电磁法资料处理解释提供了有力工具,也为后续反演研究考虑更多影响因素奠定了基础。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Flores

, Peralta-Ortega

S A

Induced polarization with in-loop transient electromagnetic soundings: A case study of mineral discrimination at El Arco porphyry copper, Mexico

[J]. Journal of Applied Geophysics, 2009, 68(3):423-436.

DOI:10.1016/j.jappgeo.2009.03.009 URL [本文引用: 1]

[2]

Xue

G Q

, Qin

K Z

, Li

, et al.

Discovery of a large-scale porphyry molybdenum deposit in Tibet through a modified TEM exploration method

[J]. Journal of Environmental and Engineering Geophysics, 2012, 17(1):19-25.

DOI:10.2113/JEEG17.1.19 URL [本文引用: 1]

[3]

Yang

, Oldenburg

D W

Three-dimensional inversion of airborne time-domain electromagnetic data with applications to a porphyry deposit

[J]. Geophysics, 2012, 77(2):B23-B34.

DOI:10.1190/geo2011-0194.1 URL [本文引用: 2]

[4]

Scholl

, Helwig

S L

, Tezkan

, et al.

1-D multimodel joint inversion of TEM-data over multidimensional structures

[J]. Geophysical Journal International, 2009, 176(1):81-94.

DOI:10.1111/gji.2008.176.issue-1 URL [本文引用: 1]

[5]

Kirkegaard

, Auken

A parallel, scalable and memory efficient inversion code for very large-scale airborne electromagnetics surveys

[J]. Geophysical Prospecting, 2015, 63(2):495-507.

DOI:10.1111/gpr.2015.63.issue-2 URL [本文引用: 1]

[6]

孙怀凤, 张诺亚, 柳尚斌, 等.

基于L1范数的瞬变电磁非线性反演

[J]. 地球物理学报, 2019, 62(12):4860-4873.

[本文引用: 2]

Sun

H F

, Zhang

N Y

, Liu

S B

, et al.

L1-norm based nonlinear inversion of transient electromagnetic data

[J]. Chinese J. Geophys., 2019, 62(12):4860-4873.

[本文引用: 2]

[7]

Liu

, Yin

, Qiu

, et al.

3-D inversion of transient EM data with topography using unstructured tetrahedral grids

[J]. Geophysical Journal International, 2019, 217(1):301-318.

DOI:10.1093/gji/ggz014 URL [本文引用: 1]

[8]

Auken

, Christiansen

A V

, Kirkegaard

, et al.

An overview of a highly versatile forward and stable inverse algorithm for airborne, ground-based and borehole electromagnetic and electric data

[J]. Exploration Geophysics, 2015, 46(3):223-235.

DOI:10.1071/EG13097 URL [本文引用: 1]

[9]

Raiche

A P

, Jupp

D L B

, Ruter

, et al.

The joint use of coincident loop transient electromagnetic and Schlumberger sounding to resolve layered structures

[J]. Geophysics, 1985, 50(10):1618-1627.

DOI:10.1190/1.1441851 URL [本文引用: 1]

[10]

黄皓平, 王维中.

时间域航空电磁数据的反演

[J]. 地球物理学报, 1990, 33(1):87-97.

[本文引用: 1]

Huang

H P

, Wang

W Z

Inversion of time-domain airborne electromagnetic data

[J]. Chinese J. Geophys., 1990, 33(1):87-97.

[本文引用: 1]

[11]

Farquharson

C G

, Oldenburg

D W

Inversion of time-domain electromagnetic data for a horizontally layered earth

[J]. Geophysical Journal International, 1993, 114(3):433-442.

DOI:10.1111/gji.1993.114.issue-3 URL [本文引用: 2]

[12]

Effersø

, Auken

, Sørensen

K I

Inversion of band-limited TEM responses

[J]. Geophysical Prospecting, 1999, 47(4):551-564.

DOI:10.1046/j.1365-2478.1999.00135.x URL [本文引用: 1]

[13]

Auken

, Christiansen

A V

Layered and laterally constrained 2D inversion of resistivity data

[J]. Geophysics, 2004, 69(3):752-761.

DOI:10.1190/1.1759461 URL [本文引用: 1]

[14]

Auken

, Christiansen

A V

, Jacobsen

L H

, et al.

A resolution study of buried valleys using laterally constrained inversion of TEM data

[J]. Journal of Applied Geophysics, 2008, 65(1):10-20.

DOI:10.1016/j.jappgeo.2008.03.003 URL [本文引用: 1]

[15]

Viezzoli

, Christiansen

A V

, Auken

, et al.

Quasi-3D modeling of airborne TEM data by spatially constrained inversion

[J]. Geophysics, 2008, 73(3):F105-F113.

DOI:10.1190/1.2895521 URL [本文引用: 1]

[16]

Constable

S C

, Parker

R L

, Constable

C G

Occam’s inversion: A practical algorithm for generating smooth models from electromagnetic sounding data

[J]. Geophysics, 1987, 52(3):289-300.

DOI:10.1190/1.1442303 URL [本文引用: 3]

[17]

Sudha

, Tezkan

, Siemon

Appraisal of a new 1D weighted joint inversion of ground based and helicopter-borne electromagnetic data

[J]. Geophysical Prospecting, 2014, 62(3):597-614.

DOI:10.1111/gpr.2014.62.issue-3 URL [本文引用: 1]

[18]

毛立峰, 王绪本, 陈斌.

直升机航空瞬变电磁自适应正则化一维反演方法研究

[J]. 地球物理学进展, 2011, 26(1):300-305.

[本文引用: 1]

Mao

L F

, Wang

X B

, Chen

Study on an adaptive regularized 1D inversion method of helicopter TEM data

[J]. Progress in Geophysics, 2011, 26(1):300-305.

[本文引用: 1]

[19]

齐彦福, 殷长春, 王若, 等.

多通道瞬变电磁m序列全时正演模拟与反演

[J]. 地球物理学报, 2015, 58(7):2566-2577.

[本文引用: 1]

Y F

, Yin

C C

, Wang

, et al.

Multi-transient EM full-time forward modeling and inversion of m-sequences

[J]. Chinese J. Geophys., 2015, 58(7):2566-2577.

[本文引用: 1]

[20]

李海, 薛国强, 钟华森, 等.

多道瞬变电磁法共中心点道集数据联合反演

[J]. 地球物理学报, 2016, 59(12):4439-4447.

[本文引用: 1]

, Xue

G Q

, Zhong

H S

, et al.

Joint inversion of CMP gathers of multi-channel transient electromagnetic data

[J]. Chinese J. Geophys., 2016, 59(12):4439-4447.

[本文引用: 1]

[21]

, Cheng

, Wang

, et al.

Transient electromagnetic inversion based on the PSO-DLS combination algorithm

[J]. Exploration Geophysics, 2019, 50(5):472-480.

DOI:10.1080/08123985.2019.1627172 URL [本文引用: 1]

[22]

Key

1D inversion of multicomponent, multifrequency marine CSEM data: Methodology and synthetic studies for resolving thin resistive layers

[J]. Geophysics, 2009, 74(2):F9-F20.

DOI:10.1190/1.3058434 URL [本文引用: 1]

[23]

Guptasarma

, Singh

New digital linear filters for Hankel J0 and J1 transforms

[J]. Geophysical Prospecting, 1997, 45(5):745-762.

DOI:10.1046/j.1365-2478.1997.500292.x URL [本文引用: 1]

[24]

Anderson

W L

Fourier cosine and sine transforms using lagged convolutions in double-precision (subprograms DLAGF0/DLAGF1)

[R]. U.S. Geological Survey, 1983.

[本文引用: 1]

[25]

, Lu

, Farquharson

C G

, et al.

A finite-element time-domain forward solver for electromagnetic methods with complex-shaped loop sources

[J]. Geophysics, 2018, 83(3):E117-E132.

DOI:10.1190/geo2017-0216.1 URL [本文引用: 1]

Induced polarization with in-loop transient electromagnetic soundings: A case study of mineral discrimination at El Arco porphyry copper, Mexico

2009

... 目前,回线源瞬变电磁法已广泛应用于金属矿产勘探^[1,2,3]、环境水文地质调查^[4,5,6]等领域.随着三维正演算法的逐渐成熟和计算机软硬件性能的不断提升,瞬变电磁法三维反演的报道陆续出现^[3,7],但实用化的资料处理解释手段仍以一维反演为主^[8]. ...

Discovery of a large-scale porphyry molybdenum deposit in Tibet through a modified TEM exploration method

2012

Three-dimensional inversion of airborne time-domain electromagnetic data with applications to a porphyry deposit

2012

... [3,7],但实用化的资料处理解释手段仍以一维反演为主^[8]. ...

1-D multimodel joint inversion of TEM-data over multidimensional structures

2009

A parallel, scalable and memory efficient inversion code for very large-scale airborne electromagnetics surveys

2015

基于L1范数的瞬变电磁非线性反演

2019

... 国内课题组也开展了类似研究.如:毛立峰等采用自适应正则化方法开展了直升机航空瞬变电磁法数据一维反演^[18],齐彦福等采用Occam算法对m序列发射波形多道瞬变电磁法数据开展了反演研究^[19],类似工作也见于李海等^[20].除了上述线性化优化方法外,模拟退火法^[6]、粒子群优化——阻尼最小二乘混合算法^[21]等智能优化算法也被成功用于瞬变电磁法一维反演. ...

基于L1范数的瞬变电磁非线性反演

2019

3-D inversion of transient EM data with topography using unstructured tetrahedral grids

2019

An overview of a highly versatile forward and stable inverse algorithm for airborne, ground-based and borehole electromagnetic and electric data

2015

The joint use of coincident loop transient electromagnetic and Schlumberger sounding to resolve layered structures

1985

... 瞬变电磁法一维反演始于20世纪80年代.如:Raiche等基于阻尼最小二乘法对瞬变电磁法重叠回线和电阻率法施伦贝谢装置采集的数据开展了联合反演^[9],黄皓平、王维中采用阻尼最小二乘法实现了时间域航空电磁数据的一维反演^[10];上述反演算法均采用了层状介质参数化反演,即同时反演层厚度和电阻率,反演结果依赖于模型层数和初始模型^[11].Farquharson和Oldenburg在目标函数中加入待求模型与某个参考模型之间的偏离程度表征项,并设定反演模型层数多于观测数据个数,且各层介质层厚固定,只反演电阻率^[11].随后,丹麦奥胡斯大学Auken课题组采用阻尼最小二乘法也开展了瞬变电磁法一维反演^[12],并引入横向约束项用于解决反演断面图中电阻率和层厚横向连续性差、薄层分辨率低等问题^[13,14],引入空间约束项用于解决反演深度切片中层界面不光滑等问题^[15].德国科隆大学Tezkan课题组采用基于阻尼最小二乘法和Occam算法^[16]的反演程序,开展回线源瞬变电磁法、长偏移距瞬变电磁法、射频大地电磁法等方法的单一反演或联合反演^[17]. ...

时间域航空电磁数据的反演

1990

时间域航空电磁数据的反演

1990

Inversion of time-domain electromagnetic data for a horizontally layered earth

1993

... [11].随后,丹麦奥胡斯大学Auken课题组采用阻尼最小二乘法也开展了瞬变电磁法一维反演^[12],并引入横向约束项用于解决反演断面图中电阻率和层厚横向连续性差、薄层分辨率低等问题^[13,14],引入空间约束项用于解决反演深度切片中层界面不光滑等问题^[15].德国科隆大学Tezkan课题组采用基于阻尼最小二乘法和Occam算法^[16]的反演程序,开展回线源瞬变电磁法、长偏移距瞬变电磁法、射频大地电磁法等方法的单一反演或联合反演^[17]. ...

Inversion of band-limited TEM responses

1999

Layered and laterally constrained 2D inversion of resistivity data

2004

A resolution study of buried valleys using laterally constrained inversion of TEM data

2008

Quasi-3D modeling of airborne TEM data by spatially constrained inversion

2008

Occam’s inversion: A practical algorithm for generating smooth models from electromagnetic sounding data

1987

... 综上所述,瞬变电磁法一维反演发展比较完善成熟.本研究基于Constable等开发的Occam反演算法^[16]和Key课题组开发的Dipole1D一维正演程序^[22],开展了回线源瞬变电磁法一维反演研究. ...

... 采用经典的Occam算法^[16]开展一维反演计算.该算法的基本思想是:通过在目标函数中引入模型粗糙度的正则化项,来获得能够拟合数据的最光滑模型.设定反演的目标函数为 ...

Appraisal of a new 1D weighted joint inversion of ground based and helicopter-borne electromagnetic data

2014

直升机航空瞬变电磁自适应正则化一维反演方法研究

2011

直升机航空瞬变电磁自适应正则化一维反演方法研究

2011

多通道瞬变电磁m序列全时正演模拟与反演

2015

多通道瞬变电磁m序列全时正演模拟与反演

2015

多道瞬变电磁法共中心点道集数据联合反演

2016

多道瞬变电磁法共中心点道集数据联合反演

2016

Transient electromagnetic inversion based on the PSO-DLS combination algorithm

2019

1D inversion of multicomponent, multifrequency marine CSEM data: Methodology and synthetic studies for resolving thin resistive layers

2009

New digital linear filters for Hankel J0 and J1 transforms

1997

... 借助势表示电场E和磁场H是求解麦克斯韦方程组的有效途径之一.引入矢量势和标量势后,由麦克斯韦方程组推导出关于矢量势的双旋度方程,再结合一些限定条件,比如洛伦兹规范,可得到关于矢量势在空间域的亥姆霍兹方程.对于一维介质,介质分界面在水平坐标x和y无限延伸,并与垂直坐标面(等z平面)重合,可利用二维傅里叶变换将亥姆霍兹方程从空间域转换至波数域;伴随着这种转换,将关于x、y和z的偏微分方程转变为易于求解、关于z的常微分方程.结合电磁场衰减的边界条件和在界面处电磁场切向分量的连续性,可以唯一求解上述关于矢量势的微分方程,获得波数域矢量势;再利用二维傅里叶逆变换得到空间域矢量势,并根据势与场的转换关系,获得频率域电磁场.这一转换过程中,需数值求解多个关于发射源长度和波数的二重积分.对关于发射源长度的积分,通常采用高斯—勒让德积分求解,该方法可通过增大积分点数来提高求解精度.关于波数的积分含有零阶或一阶形式的第一类贝塞尔函数,该类积分通常采用汉克尔变换求解.关于汉克尔变换及常用的变换系数,可参考Guptasarma和Singh^[23]等已发表的文献. ...

Fourier cosine and sine transforms using lagged convolutions in double-precision (subprograms DLAGF0/DLAGF1)

1983

... 逐个计算并累加每个接地线源激发的频率域磁场,即可获得回线源激发的磁场,再采用正弦变换或余弦变换求得磁场阶跃响应或脉冲响应,进而得到感应电动势.本研究采用Anderson研发的787个系数的正弦变换和余弦变换^[24]. ...

A finite-element time-domain forward solver for electromagnetic methods with complex-shaped loop sources

2018

... 如图4a所示,发射回线铺设在倾角为20°的斜坡之上.该模型表层介质厚度为30 m,电阻率为50 Ω·m,沿走向方向长度为200 m;表层下伏介质为100 Ω·m的半空间.发射回线为10 m×10 m的正方形.图4a中,发射回线Tx1、Tx2和Tx3的中心位置分别为(-93.969, 0.0,-34.302)、(0.0, 0.0,0.0)和(93.969, 0.0, 34.302).采用中心回线装置,观测量为倾斜界面法向方向的感应电动势.采用课题组开发的时域矢量有限单元法^[25]计算磁感应强度脉冲响应三分量,并将其合成观测量.观测时间序列范围为0.025~1.995 ms,共20个时刻. ...

〈

〉