超参数对GRU-CNN混合深度学习弹性阻抗反演影响研究

doi:10.11720/wtyht.2021.1001

超参数对GRU-CNN混合深度学习弹性阻抗反演影响研究

梁立锋^,¹, 刘秀娟^,¹, 张宏兵², 陈程浩¹, 陈锦华¹

1.岭南师范学院地理系,广东湛江 524057

2.河海大学地球科学与工程学院,江苏南京 210098

A study of the effect of hyperparameters GRU-CNN hybrid deep learning EI inversion

LIANG Li-Feng^,¹, LIU Xiu-Juan^,¹, ZHANG Hong-Bing², CHEN Cheng-Hao¹, CHEN Jin-Hua¹

1. Department of Geography,Lingnan Normal University,Zhanjiang 524057,China

2. School of Earth Science and Engineering,Hohai University,Nanjing 210098,China

通讯作者: 刘秀娟(1980-),女,工程师,硕士,主要研究方向为地震反演与深度学习。Email:544022065@qq.com

责任编辑: 叶佩

收稿日期: 2020-01-2 修回日期: 2020-11-12 网络出版日期: 2021-02-20

基金资助:

广东省教育厅基金项目.  2019KTSCX089
岭南师范学院人才专项.  ZL1936
岭南师范学院科研项目.  LY1912,LP2036

Received: 2020-01-2 Revised: 2020-11-12 Online: 2021-02-20

作者简介 About authors

梁立锋(1978-),男,博士,讲师,工程师,主要研究方向为地震反演与深度学习。Email:121436068@qq.com

摘要

CNN-GRU混合深度学习反演弹性阻抗取得了较好的反演效果。但是,基于深度学习的叠前反演参数众多,包括内部深度学习网络可学习参数和外部超参数等,目前超参数选取对网络性能及计算速度影响尚缺乏系统性研究,这直接影响到了该方法的进一步推广应用。因此,本文在混合深度学习反演弹性阻抗基础上,探讨学习率、Epoch、batch_size、正则化参数及参与网络训练的测井个数等5个超参数对网络性能及计算速度的影响,为深度学习地震反演超参数选取提供依据。研究结果可为三维大面积深度学习反演提供一个可行的质控手段,对于推动深度学习方法在石油物探中广泛应用具有一定意义。

关键词： 超参数 ; 门控循环单元 ; 卷积神经网络 ; 混合深度学习 ; 弹性阻抗

Abstract

Previous studies have shown that CNN-GRU hybrid deep learning inversion EI has the advantages of strong applicability and strong generalization capability.However,there are many pre-stack inversion parameters based on deep learning,such as internal deep learning network learnable parameters and external hyperparameters.At present,there is still no systematic research on the impact of hyperparameter selection on network performance and computing speed,which will directly affect the further promotion and application of the method.Therefore,based on the hybrid deep learning inversion elastic impedance,this paper discusses the impact of five hyperparameters,i.e.,learning rate,Epoch,batch_size,regularization parameter,and the number of wells participating in network training on network performance and calculation speed,thus providing a basis for studying the selection of seismic inversion hyperparameters.The research results can provide a feasible quality control method for three-dimensional large-area deep learning inversion,which is of certain significance for promoting the wide application of deep learning methods in petroleum geophysical prospecting.

Keywords： super-parameter ; gate recurrent unit ; convolutional neural network ; mixed deep learning ; elastic impedance

PDF (2494KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

梁立锋, 刘秀娟, 张宏兵, 陈程浩, 陈锦华. 超参数对GRU-CNN混合深度学习弹性阻抗反演影响研究. 物探与化探[J], 2021, 45(1): 133-139 doi:10.11720/wtyht.2021.1001

LIANG Li-Feng, LIU Xiu-Juan, ZHANG Hong-Bing, CHEN Cheng-Hao, CHEN Jin-Hua. A study of the effect of hyperparameters GRU-CNN hybrid deep learning EI inversion. Geophysical and Geochemical Exploration[J], 2021, 45(1): 133-139 doi:10.11720/wtyht.2021.1001

0 引言

卷积神经网络(convolutional neural network,CNN)是一种被广泛使用的深度学习方法^[1],包括图像分类、图像定位和图像分割^[2]。近年来,CNN已被应用于各种地震问题,包括随机地震道编辑^[3]、噪声衰减^[4]、地震岩相反演^[5]和储层预测^[6]和断层解释方面^[7,8]。

递归神经网络(recurrent neural network,RNN)是解决序列数据问题的一种神经网络。与卷积神经网络结构不同,RNN考虑了前一个样本对下一个样本的影响^[9]。在RNN网络基础上,LSTM能更准确地学习时间序列的长期依赖性,解决了需要人工提取时间序列特征的问题。但该方法存在收敛速度慢等问题。门控递归单元神经网络(GRU)是在LSTM的基础上进行改进和优化的神经网络。它具有更快的收敛速度和保持与LSTM相似的精度。RNN及优化的网络广泛应用于测井曲线重建^[10],并在自然语言处理^[11]、医疗^[12]等领域也得到了广泛的应用。

CNN网络能够提取地震图像的局部特征,GRU网络能够提取地震数据的低频趋势,两者构成混合深度学习网络,可以完整地反演地震EI全频信息。CNN-GRU混合深度学习反演弹性阻抗(EI)取得了较好的反演效果^[13]。CNN模型无法对所有数据集进行最佳泛化^[14],混合深度学习模型也面临同样的问题,所以在对新的数据集进行混合深度学习方法时,必须选取合适的超参数。而混合深度学习中,超参数可以分为网络内部参数和网络外部参数,内部参数包含网络层数、每一层的激活函数、每个网络层卷积核尺寸、偏置项的尺寸,网络的不同链接方式、群组归一化尺寸、反卷积尺寸等,外部参数包括学习率、训练轮次(Epoch)、批尺寸(batch_size)、正则化参数及参与网络训练的测井个数等。这些参数即使对于小型的深度学习网络,总体参数个数也可能达到上千个,对于特定的数据集,我们可以采用穷举的方式,获得一套能够充分发挥深度学习网络性能的超参数,但这样无疑会耗费大量人工和机器运行时间。从文献调研结果来看,国外学者对学习率这个超参数进行了研究,并利用线性循环迭代可变学习率在图像处理领域取得了较好的应用效果^[15]。Breuel探讨了MNIST手写数字识别问题中超参数对CNN神经网络训练的影响,主要研究了批尺寸、学习率与训练误差、测试误差的关系^[16]。在混合深度学习地震反演领域,不同类型的超参数对网络性能及计算速度影响尚缺乏系统性研究,直接影响了反演精度和推广应用。

因此,本文在混合深度学习反演弹性阻抗基础上^[13],重点探讨 Epoch、batch_size、正则化参数、参与网络训练的测井个数、学习率等5个超参数对网络性能及计算速度的影响,为深度学习地震反演超参数选取提供依据。

1 数据集及深度学习网络框架

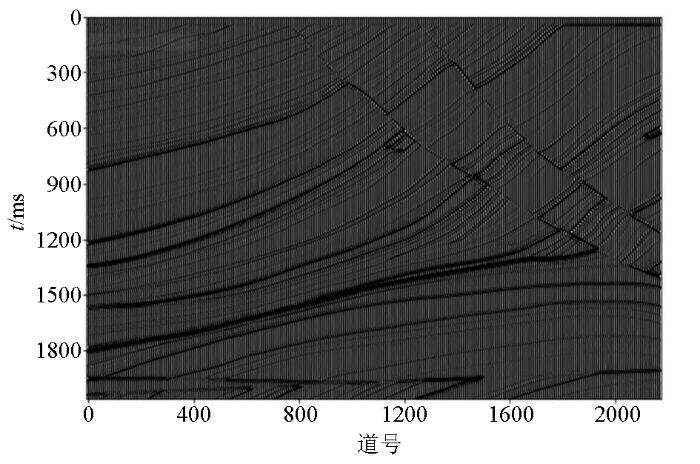
为了研究超参数对反演结果的影响,选取Marmousi 2模型^[17]作为深度学习的数据集。Marmousi 2模型是Marmousi合成模型的弹性扩展,整个模型宽度为17 km,深度为3.5 km,垂直分辨率为1.25 m。根据研究需要,我们选取了整个二维地震剖面的中间部分,共计2 720道,其时间域地震剖面如图1所示。对选取的地震道集重新进行数据集划分,即把数据集重新划分为训练集、测试集和验证集,这样划分的好处是可以验证混合深度学习网络的泛化性能。GRU-CNN混合深度学习采用Motaz在2019年提出的网络框架^[13]。由于该网络总体参数达到上千个,难以对其全部进行研究,因此本文在内部网络参数保持不变情况下,重点研究5个外部超参数。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 Marmorsi2模型时间域地震剖面(局部)

Fig.1 Time domain seismic profile of marmorsi2 model(local)

2 不同网络模型反演效果及效率对比

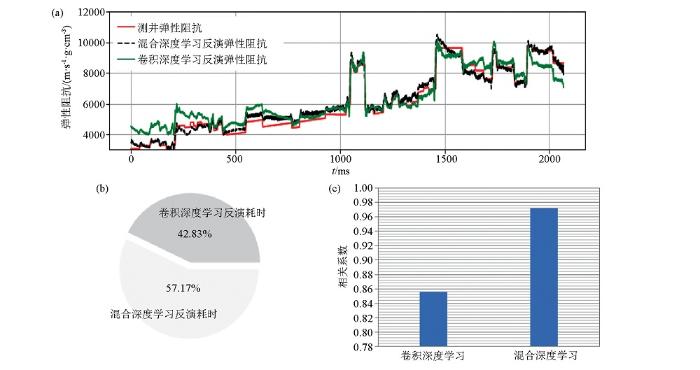
图2a对比了混合深度学习与卷积深度学习两种弹性阻抗反演方法,反演时长为2 070 ms,从生产上看,长时窗地震反演会增加反演的难度。整体上看,混合深度学习反演结果与测井弹性阻抗拟合较好,低频趋势合理,局部地层反演达到预设要求,探究其原因,主要是混合深度学习反演方法在算法中有机结合了卷积神经网络(CNN)及门控循环单元(GRU)两种深度学习方法,而卷积神经网络能够对小套地层进行特征提取,门控循环单元(GRU)深度学习则可以对地震长时间序列进行低频信息的提取。从图2a中可以看出,在0~400ms和1 800~2 100 ms两个时窗范围内,绿线较大程度地偏离了测井弹性阻抗结果,说明反演误差较大,主要原因是卷积深度学习对低频信息提取能力较差。图2b对比了两种反演方法计算时间,CNN用时197.64 ms,CNN+GRU混合反演用时263.8 ms,混合反演用时略高,其原因是在混合深度学习反演中,当地震数据流向CNN网络时,同时地震数据也流向了GRU网络,而每一部分的数据流均会耗费GPU计算时间。这造成两种反演方法的耗时差异。图2c对比了两种反演方法的相关系数,统计时窗是图2a中的整条曲线时窗,统计方法采用R²相关方法,这种相关方法的优点是考虑了两条曲线的均方误差。卷积深度学习的相关系数代表图2a中卷积深度学习反演结果(绿线)与测井弹性阻抗(红线)的相关系数,混合深度学习的相关系数代表图2a中黑线与红线的相关系数,图2c表明,混合深度学习的相关系数明显高于卷积深度学习反演方法。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 卷积深度学习与混合深度学习反演效率效果对比

a—反演结果对比;b—耗时对比;c—相关系数对比

Fig.2 Comparison of inversion efficiency and result between convolution deep learning and hybrid deep learning

a—inversion results comparison;b—time consmption comparison;c—correlation coefficient comparison

3 超参数对反演影响

3.1 batch-size对反演影响

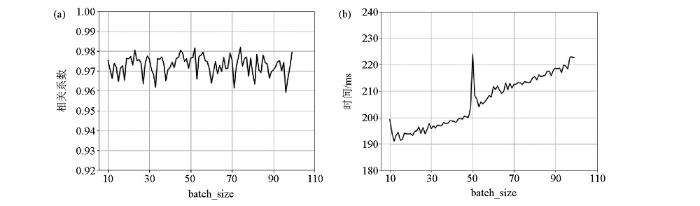
图3为不同batch-size对相关系数及计算时间的影响。图3a为batch_size测试图,纵轴表示整个地震剖面上反演的EI道与实测EI的总相关系数,从图中可以看出,整体上相关系数在0.96 ~0.98之间,随着batch_size逐渐变大而呈现出非规律性的相关系数变化,这也说明如果想取得最佳的反演效果,需要进行多次的batch_size参数测试。图3b为不同batch_size情况下反演耗时分布,为保证具有可对比性,每次batch_size测试,反演均包含模型训练与模型测试两部分,深度学习程序在GPU上运算,除了batch_size参数不同,其余实验参数均相同,除了batch_size=50时运行时间有突变,随着batch_size的增加,实验耗时逐渐递增。因此结合图3,综合时间成本及相关系数,选取batch_size参数为33次为适宜参数。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 Batch-size对相关系数(a)及计算时间(b)的影响

Fig.3 Batch-size effect on correlation coefficient(a) and calculation time(b)

3.2 测井个数(标签数量)对反演影响

图4为参与模型训练的井的个数对相关系数及计算时间的影响。图4a纵轴表示整个地震剖面上反演的EI道与实测EI的总相关系数,从图中可以看出,当井的个数从1口到45口井递增变化时,相关系数整体上呈现非周期性的波动。当只有1口井时,相关系数较小;当大于2口井时,整体上相关系数处于0.96~0.98之间。这表明了深度学习网络受参与训练的井数的影响较小,也说明了混合深度学习网络的稳健性。图4b表明随着参与训练的井数递增,深度学习网络耗时整体上近似线性递增,因此,综合图4选取参与训练的井数为13时,相关系数较高,同时时间成本较低。

图4

新窗口打开| 下载原图ZIP| 生成PPT

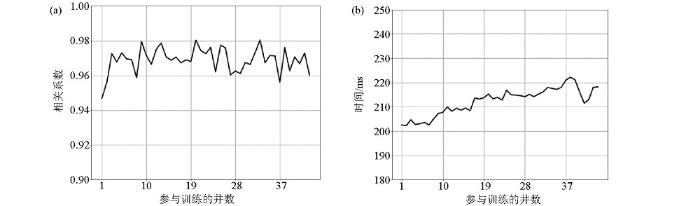
图4 参与训练的井数对相关系数(a)、计算时间(b)的影响

Fig.4 Influence of number of wells participating in the training on correlation coefficient(a) and calculation time(b)

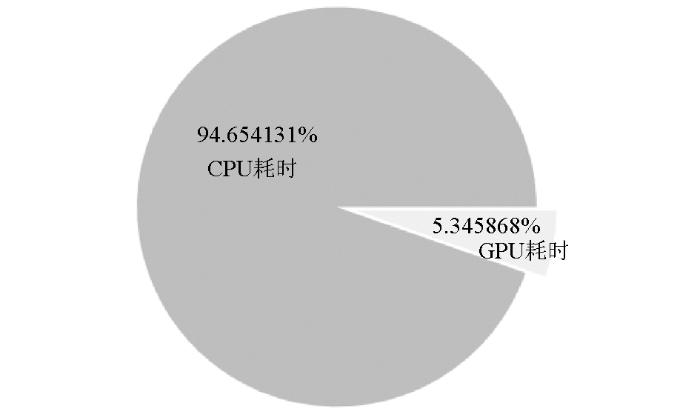
在相同超参数情况下,将深度学习网络分别运行在CPU和GPU上,其CPU型号是intel i7-8550U,主频是1.8 GHz,GPU显卡型号是NVIDIA GeForce GTX1050独立显卡,参与反演的地震道是2 720道,深度学习网络在CPU运行时间是6 746 ms,在GPU上运行时间是381 ms,CPU耗时将近是GPU耗时的18倍。其饼状图如图5所示。可见,对于深度学习反演算法,利用GPU运算更加具有实用性。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 相同超参数情况下GPU运算与CPU运算耗时比较

Fig.5 Comparison of operation time between GPU and CPU with the same hyper-parameters

3.3 训练轮次对反演影响

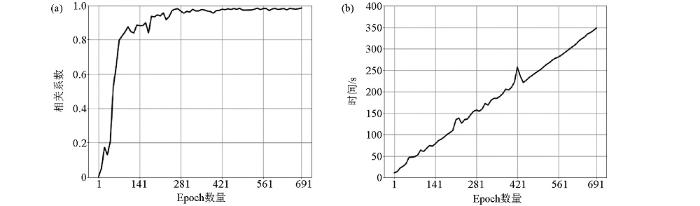
在深度学习中,由于数据集一般都很庞大,而每个数据单元都可能需要计算梯度,在这种情况下,一次性将全部数据加入计算机内存是不可能的,笔者尝试开辟虚拟内存空间,依然会存在内存爆满(内存利用率100%)的情况,影响深度学习效率。图6a表示不同Epoch数量与相关系数关系,纵轴表示整个地震剖面上反演的EI道与实测EI的总相关系数;图6b表示反演耗时与Epoch数量选择的变化关系。可以看出,Epoch数量增加导致计算耗时近似线性增加。当Epoch<70时,相关系数变化剧烈,对照图6b,此时虽然计算耗时较少,但可以认为反演结果不稳定;当Epoch数量为280~700时,相关系数趋于稳定;随着Epoch数量增加,耗时呈现近似线性增加;综上,可以优选Epoch=280作为较好的超参数选择。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 轮次(Epoch)与相关系数(a)、计算耗时(b)的关系

Fig.6 Relation diagram of Epoch vs the correlation coefficient(a) and time consumption(b)

3.4 正则化参数对反演的影响

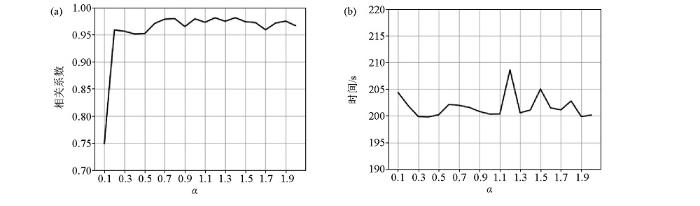
图7是α参数与相关系数、计算耗时关系图,反映了两个正则化参数α、β之间的比例关系,其中,α代表了弹性阻抗EI在整个损失函数中所占的权重,β代表了地震在整个损失函数中所占的权重。α,β两个正则化参数的内涵是,相当于在地震反演中更加认同地震数据还是更加相信测井数据。为了完备讨论这个问题,一般α、β都需要给定各自的范围,之后两两组合,再进行反演试算。本文为了达到上述效果,简化了表征方式,即取α∈[0.1,2.0],步长为0.1,同时针对每一个α取值,β取值均为1,相当于α∶β∈[0.1,2.0],步长为0.1,特别说明,这里面也包含了α∶β=1∶1情况,即地震与测井所占权重相等(两者同等重要)。从图7a可以看出当α∶β≤0.5∶1,相关系数变化剧烈,最小相关系数仅为0.75;当α∶β≥0.6∶1时,相关系数大于 0.95。图7a整条曲线表明,地震非监督与测井监督部分的比例关系对于最终的反演结果是有影响的,这说明,深度学习虽然可以通过网络的正向传播及反向梯度自动求导,从而寻求得到最佳的网络参数,但是,超参数的选取依然是值得关注的问题,尤其对于实际的生产项目,应该有必要做好这部分的测试工作,从而全面发挥深度学习网络的超强性能。从图7b可以看出,当α∈[0.1,2.0],整个耗时在200 s和205 s之间,当α∶β=1.2∶1时耗时出现突变。这说明,对于三维大工区,要结合图7的相关系数及时间消耗图综合选取正则化参数。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 正则化参数α与相关系数(a)、计算耗时(b)关系

Fig.7 Relation diagram of regularization parameter α vs correlation coefficient(a) and time consumption(b)

3.5 学习率对反演的影响

在最原始的梯度更新算法^[13]中:

(1)$\omega_{t+1} \leftarrow \omega_{t}-\alpha \frac{\partial E}{\partial \omega_{t}}$

式中:ω_t为当前权值参数; $\frac{\partial E}{\partial ω_{t}}$ 为目标函数对于ω_t的梯度;α为学习率,是一个取值区间为(0,1)的超参数。根据公式可以看出,学习率是控制权值变化的一个关键参数,同时决定了深度学习网络收敛的速度。当学习率设置过大,深度学习的损失函数(也是目标函数)就会震荡,难于收敛;当学习率设置过小,损失函数虽然可以收敛,但收敛速度慢,这对于大型的深度学习网络则会浪费大量的计算时间,同时易于陷入局部极小值。为此,采用余弦曲线学习率^[15]。如图8a所示,当模型训练的Epoch从0增加到300时,学习率在[0.001,0.05]闭区间取值,学习率散点呈现余弦曲线形态变化。这样设置学习率的好处是,可以使学习率在大步长和小步长之间周期变化,大步长可以使目标函数跳出局部最优解,在全局范围内找到优化解,在此基础上,利用小步长精细微调局部优化解,如此反复达到全局最优解的目的。图8b实验了学习率等于 0.001 常数的损失曲线和学习率按照余弦曲线变化的损失曲线,从图中可以看出,余弦学习率曲线在Epoch∈(1,20)范围内极其快速收敛,当Epoch=50左右,损失曲线基本已经稳定,而采用常数学习率,损失曲线收敛速度较慢,这说明对于大型的深度学习网络,即使依赖云计算,通过改进学习率的方式,仍可以明显地提高计算速度。

图8

新窗口打开| 下载原图ZIP| 生成PPT

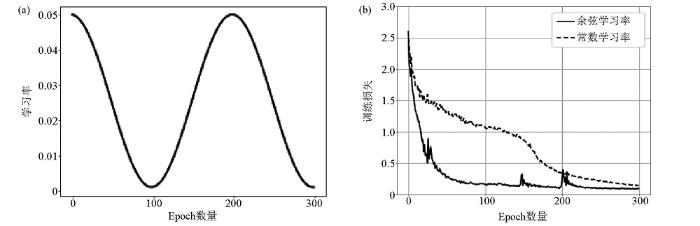
图8 学习率曲线及改进方法

a—余弦学习率曲线;b—常数学习率与余弦学习率损失曲线对比

Fig.8 Learning rate curve and improvement method

a—cosinc learning rate curve;b—loss curve comparison between constant learning rate and cosinc learning rate

4 结论

1)对于深度学习反演,超参数选取是值得探讨的内容。在生产项目中一般依靠经验进行参数选择,难以对反演精度进行准确量化。本文的模拟结果表明,选取不同的超参数,虽然深度学习算法都能使深度学习网络收敛,但最终的反演结果及反演耗时是有优劣之分的。

2)本文为深度学习反演提供了一个可行的超参数选取思路,即通过挑选典型的二维测线,利用深度学习算法在GPU上的快速运算技术,快速提取正则化参数α、Epoch、batch_size、参与网络训练的井数等参数与相关系数、时间关系图,从而为深度学习超参数选取提供科学依据。

3)关于超参数的完全自动化选取及深度学习的自我进化机制研究是未来进一步研究方向。

致谢：

感谢审稿专家和编辑老师对本文提出的宝贵意见和建议,感谢成都理工大学陈学华教授对论文初稿提出的宝贵意见。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

王逸宸, 柳林涛, 许厚泽.

基于卷积神经网络识别重力异常体

[J]. 物探与化探, 2020,44(2):394-400.