海底电缆电磁场分布模拟与分析

doi:10.11720/wtyht.2020.1410

海底电缆电磁场分布模拟与分析

甘团杰¹, 陈剑平^,¹, 杨玺¹, 周庆东¹, 曾亮²

1. 广东电网有限责任公司江门供电局,广东江门 510630

2. 中国能源建设集团广东省电力设计研究院有限公司,广东广州 510663

Modelling and analysis study of electromagnetic field distribution around submarine cable

GAN Tuan-Jie¹, CHEN Jian-Ping^,¹, YANG Xi¹, ZHOU Qing-Dong¹, ZENG Liang²

1. Jiangmen Power Supply Bureau, Guangdong Electrifc Network Liability Co., Ltd., Jiangmen 510630, China

2. Guangdong Electric Power Design Institute Liability Co., Ltd., China Energy Resource Construction Group, Guangzhou 510663, China

通讯作者: 陈剑平(1973-),男,三峡大学毕业,高级工程师,主要从事输电设备设计、施工及运行管理工作。Email:jmchenjianping@126.com

责任编辑: 沈效群

收稿日期: 2019-08-26 修回日期: 2019-12-17 网络出版日期: 2020-06-20

基金资助:

南方电网集团科研发展项目“海底电缆监测技术研究及应用科技项目”. GDKJXM20172879

Received: 2019-08-26 Revised: 2019-12-17 Online: 2020-06-20

作者简介 About authors

甘团杰(1970-),男,西安交通大学毕业,高级工程师,主要研究方向为高压电技术、电气设备检修及运行管理。Email:13702207210@139.com 。

摘要

海底电缆的探测和识别技术是海底电缆维护与建设中非常重要的研究内容。海底电缆布设于海底,在通电情况下产生电场和磁场,符合可控源电磁法探测理论。本文采用频率域可控源电磁法2.5维高精度有限元数值模拟算法对海底电缆模型进行模拟与分析研究,以水平地形和起伏地形海底电缆模型为基础,重点对海水层厚度和海底界面两种参数变化前后电磁场分布特征进行了模拟与分析。数值算例表明:磁场分量H_y对于海水层厚度非常敏感,厚度变化0.2 m时,变化前后H_y偏差可达5%,从而论证了采用可控源电磁法理论对于海底电缆的探测和识别可行。

关键词： 海洋探测 ; 电磁场 ; 海底电缆 ; 数值模拟 ; 可控源电磁法

Abstract

The detection and identification technology in the maintenance and construction of submarine cables has become a very important research content. In this paper, a 2.5-dimensional high-precision finite element numerical simulation algorithm of the frequency domain CSEM method was used to simulate and analyze the submarine cable model. Based on the horizontal terrain and undulating terrain submarine cable models, this study focused on the simulation and analysis of the characteristics of the electromagnetic field distribution with the changing of seawater layer thickness and the submarine interface. Numerical examples show that the magnetic field component H_y is very sensitive to the thickness of the seawater layer. When the thickness is changed by 0.2m, the H_y error anomaly amplitude can reach 5%, thus demonstrating that the CSEM theory is feasible for detection and identification of submarine cables.

Keywords： ocean exploration ; electromagnetic field ; submarine cable ; numerical simulation ; controlled source electromagnetic method ; finite element numerical simulation

PDF (6274KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

甘团杰, 陈剑平, 杨玺, 周庆东, 曾亮. 海底电缆电磁场分布模拟与分析. 物探与化探[J], 2020, 44(3): 550-558 doi:10.11720/wtyht.2020.1410

GAN Tuan-Jie, CHEN Jian-Ping, YANG Xi, ZHOU Qing-Dong, ZENG Liang. Modelling and analysis study of electromagnetic field distribution around submarine cable. Geophysical and Geochemical Exploration[J], 2020, 44(3): 550-558 doi:10.11720/wtyht.2020.1410

0 引言

海底电缆是用绝缘材料包裹的导线,铺设于海底,用于输送电力和传输数据,在安装完成后需要对电缆进行挖沟埋设,以避免落锚、拖网等行为对电缆造成损伤。近年来,我国跨海电力电缆的建设越来越多,水下电缆已遍布各处海域。因此,海底电缆的探测和识别技术成为海底电缆维护与建设中非常重要的研究内容。目前,海底电缆探测的方法主要包括:侧扫声纳^[1]、多波束测量^[2]、海洋磁力仪^[3]、浅地层剖面仪^[4,5]、瞬变电磁法^[6]、高分辨率地震等技术^{[7,8,9,10,11]}。

海底电缆通电后会在周围产生电磁场,从基本原理上讲,该研究问题等效于可控源电磁法中长导线场源的计算问题。可控源电磁法(CSEM)数值模拟^{[12,13,14,15,16,17]}包括2.5维和三维。海底电缆通常近似呈直线铺设于浅海域海底淤泥层(或基岩层)中,由于海水层电阻率较低(约0.3 Ω·m),电磁场衰减较快,海底电缆模型在垂直于电缆铺设方向电性结构具有较好的二维性,适合采用CSEM2.5D数值模拟算法进行研究,该方法相比3D计算量和耗费计算机资源大大减少,计算效率高。

本文将通电海底电缆看成长导线场源,建立海底电缆模型,然后采用频率域可控源电磁法进行数值模拟,获得海底电缆周围电磁场分布情况。文中首先对可控源电磁法2.5D有限元数值模拟算法的计算精度进行了验证,以水平地形和起伏地形海底电缆模型为基础,重点对海水层厚度和海底界面两种参数变化前后电磁场分布特征进行了模拟,最后通过对数值模拟结果进行总结,分析出该方法在海底电缆测深中的应用前景。

1 数值模拟算法理论

1.1 CSEM长导线源2.5维数值模拟算法

考虑具有一定走向的二维构造地电模型,y轴为其走向方向,x轴垂直y轴并保持水平,z轴垂直向上。取谐变时间因子为(与后文三维数值模拟保持一致),则有源区电场(E)和磁场(H)频率域Maxwell方程组为^[18]:

(1)$\begin{cases} \nabla \times E = \text{i}\omega\mu H ,\\ \nabla \times H = J_{s} + \sigma E - \text{i}\omega \varepsilon E ,\end{cases} $

式中:ε为介电常数;i为虚数单位;ω为角频率(ω=2πf_p,f_p为电磁波频率);μ为磁导率;σ为电导率,为电阻率的倒数;J_s为外加电性源的电流密度。在真空中,ε₀=8.85×10^-12 F/m,μ₀=4π×10^-7 H/m。

引入导纳率 $\hat{y}$ =σ-iωε和阻抗率 $\hat{z}$ =iωμ,则式(1)可以重写为:

(2)$\begin{cases} \nabla \times E = \hat{z} H ,\\ \nabla \times H = J_{s} + \hat{y}E \text{ 。}\end{cases} $

将方程组(2)展开为分量形式:

(3)

\{\begin{array}{l} \frac{\partial H_{z}}{\partial y} - \frac{\partial H_{y}}{\partial z} = \hat{y} E_{x} + J_{sx}, \\ \frac{\partial H_{x}}{\partial z} - \frac{\partial H_{z}}{\partial x} = \hat{y} E_{y} + J_{sy}, \\ \frac{\partial H_{y}}{\partial x} - \frac{\partial H_{x}}{\partial y} = \hat{y} E_{z} + J_{sz}, \\ \frac{\partial E_{z}}{\partial y} - \frac{\partial E_{y}}{\partial z} = \hat{z} H_{x}, \\ \frac{\partial E_{x}}{\partial z} - \frac{\partial E_{z}}{\partial x} = \hat{z} H_{y}, \\ \frac{\partial E_{y}}{\partial x} - \frac{\partial E_{x}}{\partial y} = \hat{z} H_{z} 。 \end{array}

J_sx、J_sy、J_sz分别表示沿x方向、走向y方向和垂直z方向布设的电性场源(井中电磁法)。

方程组(2)为三维问题,沿构造走向方向(y)做一维傅里叶变换得到二维问题:

(4)

\hat{F} (x, k_{y}, z, w) = \int_{-}^{\infty} F (x, y, z, w) e^{- i k_{y} y} d y,

式中:k_y为波数, $\hat{F}$ 表示波数域值。消去方程组(3)中 ${\hat{E}}_{x}$ 、 ${\hat{E}}_{z}$ 、 ${\hat{H}}_{x}$ 和 ${\hat{H}}_{z}$ 分量,得到沿走向方向电场( ${\hat{E}}_{y}$ )和磁场( ${\hat{H}}_{y}$ )的耦合微分方程:

(5)

\{\begin{array}{l} \frac{\partial}{\partial x} (\frac{\hat{y}}{k_{e}^{2}} \frac{\partial {\hat{E}}_{y}}{\partial x}) + \frac{\partial}{\partial z} (\frac{\hat{y}}{k_{e}^{2}} \frac{\partial {\hat{E}}_{y}}{\partial z}) - \hat{y} {\hat{E}}_{y} - \\ i k_{y} [\frac{\partial}{\partial x} (\frac{1}{k_{e}^{2}}) \frac{\partial {\hat{H}}_{y}}{\partial z} - \frac{\partial}{\partial z} (\frac{1}{k_{e}^{2}}) \frac{\partial {\hat{H}}_{y}}{\partial x}] = \\ {\hat{J}}_{sy} - i k_{y} [\frac{\partial}{\partial x} (\frac{1}{k_{e}^{2}} {\hat{J}}_{sx}) + \frac{\partial}{\partial z} (\frac{1}{k_{e}^{2}} {\hat{J}}_{sz})], \\ \frac{\partial}{\partial x} (\frac{\hat{z}}{k_{e}^{2}} \frac{\partial {\hat{H}}_{y}}{\partial x}) + \frac{\partial}{\partial z} (\frac{\hat{z}}{k_{e}^{2}} \frac{\partial {\hat{H}}_{y}}{\partial z}) - \hat{z} {\hat{H}}_{y} + \\ i k_{y} [- \frac{\partial}{\partial x} (\frac{1}{k_{e}^{2}}) \frac{\partial {\hat{E}}_{y}}{\partial z} + \frac{\partial}{\partial z} (\frac{1}{k_{e}^{2}}) \frac{\partial {\hat{E}}_{y}}{\partial x}] = \\ - \frac{\partial}{\partial x} (\frac{\hat{z}}{k_{e}^{2}} {\hat{J}}_{sz}) + \frac{\partial}{\partial z} (\frac{\hat{z}}{k_{e}^{2}} {\hat{J}}_{sx}) 。 \end{array}

式中:k²=- $\hat{z} \hat{y}$ , $k_{e}^{2}$ = $k_{y}^{2}$ -k²。

求解得到 ${\hat{E}}_{y}$ 和 ${\hat{H}}_{y}$ 分量后,根据空间导数计算出其他分量:

(6)

\{\begin{array}{l} {\hat{E}}_{x} = \frac{1}{k_{e}^{2}} (- i k_{y} \frac{\partial {\hat{E}}_{y}}{\partial x} - \hat{z} \frac{\partial {\hat{H}}_{y}}{\partial z} + \hat{z} {\hat{J}}_{sx}), \\ {\hat{H}}_{z} = \frac{1}{k_{e}^{2}} (- i k_{y} \frac{\partial {\hat{H}}_{y}}{\partial z} + \hat{y} \frac{\partial {\hat{E}}_{y}}{\partial x} + i k_{y} {\hat{J}}_{sx}), \\ {\hat{E}}_{z} = \frac{1}{k_{e}^{2}} (- i k_{y} \frac{\partial {\hat{E}}_{y}}{\partial z} + \hat{z} \frac{\partial {\hat{H}}_{y}}{\partial x} + \hat{z} {\hat{J}}_{sz}), \\ {\hat{H}}_{x} = \frac{1}{k_{e}^{2}} (- i k_{y} \frac{\partial {\hat{H}}_{y}}{\partial x} - \hat{y} \frac{\partial {\hat{E}}_{y}}{\partial z} - i k_{y} {\hat{J}}_{sz}) 。 \end{array}

空间导数的计算精度直接影响辅助场的计算精度,因此,在CSEM 2.5维数值模拟中,这是一个非常重要的环节。空间导数的计算方法有很多种,包括差分算法、多次函数拟合法、有限单元形函数计算方法等,其中差分算法是最容易实现的方法,当网格剖分均匀可以采用中心差分算法(向前向后计算精度均不能满足要求),当网格剖分不均匀可以采用多次函数拟合的方法。本文中在水平方向采用二次函数拟合的方法,根据三点的坐标及场值计算出二次函数的三个系数,对二次函数求导,代入中间点的坐标即得到中间点的水平导数。在垂向方向采用中心差分的方法,以地下一层的差分结果代替地表界面。

1.2 算法验证

为了验证本项目数值算法有效性,选取具有数值滤波解的均匀半空间模型进行验证。

设计电阻率为100 Ω·m的均匀半空间模型(空气中电阻率为10¹² Ω·m),电偶极子场源沿x方向布设于地表中心点,偶极距为40 m,供电电流幅值为100 A,计算频率为100 Hz。模型网格剖分参数N_z×N_x为201×201,网格做均匀剖分,网格间距为10 m,地表所在的层数为101层,边界取10个节点做扩边处理,正演一次耗时18 s。

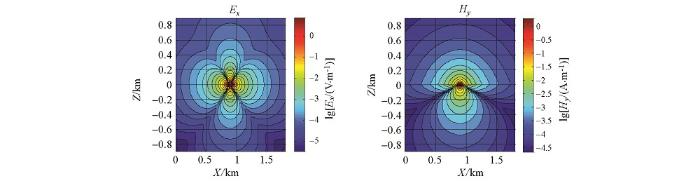
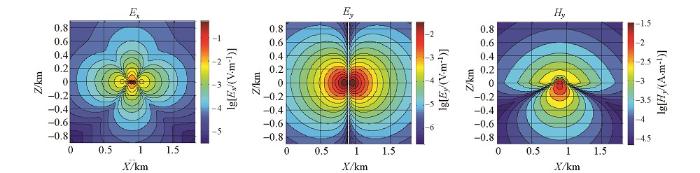
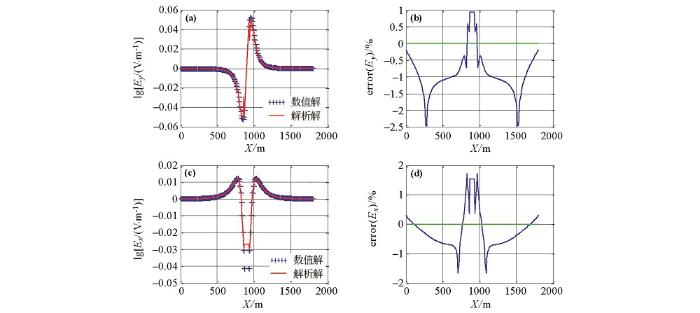
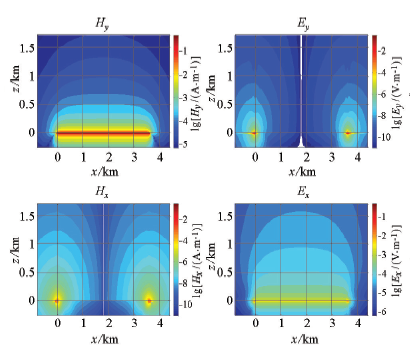
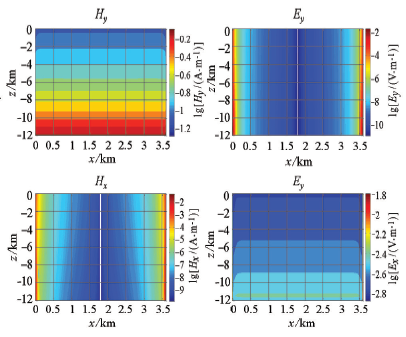
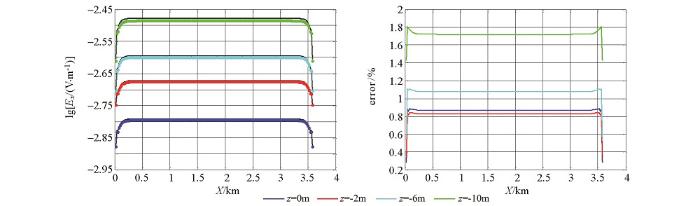
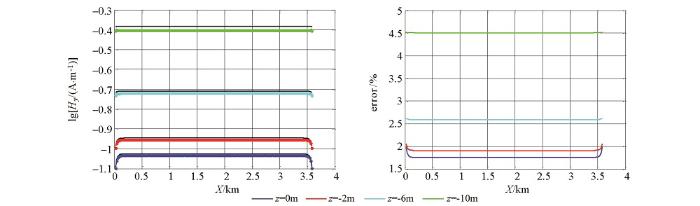
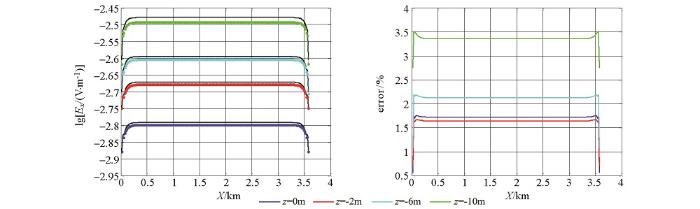
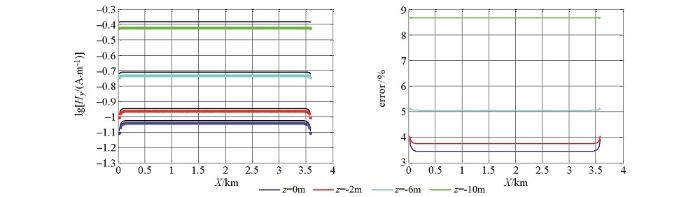
图1所示为主剖面(y=0 m)数值计算结果,图2所示为y=100 m剖面数值计算结果。图3所示为y=100 m剖面地表测线数值解与解析解对比,其中图3a为E_y分量,3b为E_y在对数区间上的偏差曲线,3c为E_x分量,3d为E_x在对数区间上的偏差曲线,偏差曲线中绿线为参考线,在参考线以下数值偏差低于1%。从图中可以看出,除了场源的附近测点外数值精度在1%以内(平均数值偏差为0.3%),E_y较E_x具有更好的数值精度,这是由于E_y为主场值,E_x的数值精度除了与主场值有关以外,还与空间导数的计算有关。数值算例表明本文采用的数值算法具有非常高的计算精度,从而为海底电缆监测数值模拟提供了支撑条件。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 y=0 m剖面电场、磁场数值解

Fig.1 Numerical solution of E_x and H_y for y=0 m section

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 y=100 m剖面电场、磁场数值解

Fig.2 Numerical solution of E_x、E_y and H_yfor y=100 m section

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 y=100 m剖面地表测线数值解与解析解对比

Fig.3 Comparison between numerical solution and analytical solution of y=100 m profile

2 水平地形海底电缆模型数值模拟

海底电缆监测(探测)模型中,变化的参数主要包括海平面高度和海底电缆埋深位置(沉积、海浪冲刷等活动均引起埋深位置发生变化)。水平地形海底电缆模型数值算例中,主要对海底电缆埋深位置变化引起的电磁场分布特征进行数值模拟研究。

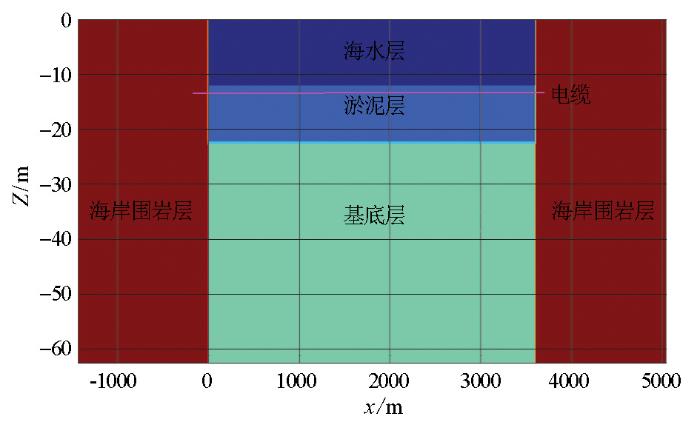
建立如图4所示模型,模型分为两个区域:计算区域和外围海岸围岩区域。计算区域为三层模型,第一层为海水层,厚度为12 m,电阻率为0.3 Ω·m;第二层为淤泥层,厚度为10 m,电阻率为2 Ω·m;第三层为基底层,电阻率为5 Ω·m。通电电缆位于淤泥层中,其长度贯穿于整个海底。数值模拟中,将通电电缆看成长导线场源,计算整个计算区域(海水层区域及观测区域)中电磁场分布。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 水平地形海底电缆模型示意

Fig.4 Schematic diagram of submarine cable model in horizontal terrain

2.1 水平地形算例一

模型计算参数为:通电电流幅值10 A,发射频率100 Hz,场源位于淤泥层1 m厚度之下。数值计算结果如图5所示。由于海底电缆探测中观测点通常位于海水层中,图6所示为观测区域电磁场分量剖面。从图5、图6中可以看出:磁场分量H_y与电场分量E_x沿着电缆方向表现为均匀场特征,且磁场分量H_y信号最强。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 水平地形算例一电磁场分量剖面

Fig.5 Section of electromagnetic field component

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 水平地形算例一海水层电磁场分量剖面

Fig.6 Section of electromagnetic field components in seawater layer

2.2 水平地形算例二

将模型算例一中电缆埋深位置下移0.2 m,按照相同的计算参数进行数值模拟,然后将计算结果与模型算例一中计算结果进行对比研究。图7和8所示分别为电场分量E_x和磁场分量H_y前后两次不同深度对比,可以看出:

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 水平地形算例一与算例二E_x分量对比

Fig.7 Comparison of different depths of E_x component

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 水平地形算例一与算例二H_y分量对比

Fig.8 Comparison of different depths of H_y component

1) E_x与H_y在横向呈现为均匀场,但是随着观测深度的增加(距离电缆越近)数值逐渐增加,其规律在对数上呈近似线性。

2) 电缆下移0.2 m,电场分量E_x和磁场分量H_y变化非常大,其变化趋势为随着深度的增加数值差异加大。

3) E_x在海平面前后两次计算差异基本相等(偏差仅为1%),在z=10 m处,偏差为1.8%;H_y在z=0 m偏差为1.8%,z=10 m处偏差为4.5%,说明磁场分量H_y对于海水层厚度的变化更为敏感。

2.3 水平地形算例三

将模型算例一中电缆下移0.4 m,按照相同的计算参数进行数值模拟,然后将计算结果与算例一的计算结果进行对比。图9、图10分别为电场分量E_x和磁场分量H_y前后两次不同深度对比,从图中可以看出:将模型中电缆下移0.4 m,E_x在海平面前后两次计算偏差1.7%,在z=10 m处,偏差为3.3%;H_y在z=0 m偏差为3.5%,z=10 m处偏差为8.6%。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 水平地形算例一与算例三E_x分量对比

Fig.9 Comparison of different depths of E_x component

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 水平地形算例一与算例三H_y分量对比

Fig.10 Comparison of different depths of H_y component

3 起伏地形海底电缆模型数值模拟

3.1 起伏地形算例一

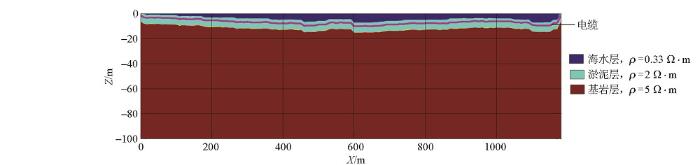
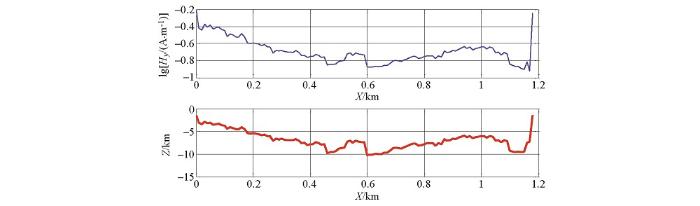
设计如图11所示起伏模型,第一层为海水层,电阻率为0.33 Ω·m;海水层下面为淤泥层,电阻率为2 Ω·m;第三层为基岩层,电阻率为5 Ω·m。其中,电缆位于淤泥层中(图中紫色线),数值模拟计算中,通电电流幅值10 A,发射频率100 Hz。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 起伏地形海底电缆模型

Fig.11 Submarine cable model in undulating terrain

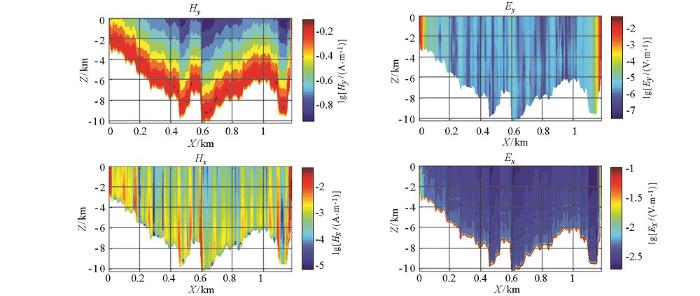
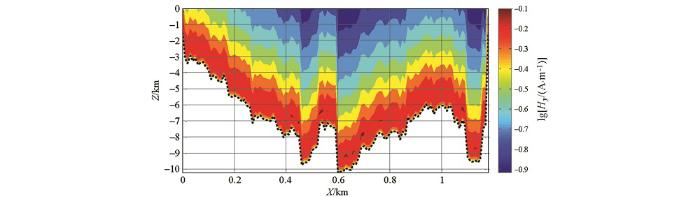
图12所示为海底电缆模型电磁场x分量和y分量剖面,图中截取了电缆至海平面区域,可以看出:①H_y幅值远大于E_x,因此建议实测中观测H_y分量;②当场源(电缆)不再水平时,磁场分布近似随电缆起伏而起伏,同一观测面H_y分量不再为均匀场。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 起伏地形算例一海底电缆模型电磁场在x、y方向的分量(计算区域)

Fig.12 Component diagram of electromagnetic field in x and y directions of submarine cable model (calculation area)

图13所示为z=0 m平面测线磁场分量H_y分布,下图为海底电缆布设示意。从图中可以看出该测线磁场分量不再为均匀磁场,其变化趋势与海底电缆在深度方向的埋设位置一致,这一特征对于海底电缆埋深的探测具有重要的指示意义。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 起伏地形算例一z=0 m测线H_y分布

Fig.13 H_y distribution of magnetic field component of z=0 m line

3.2 起伏地形算例二

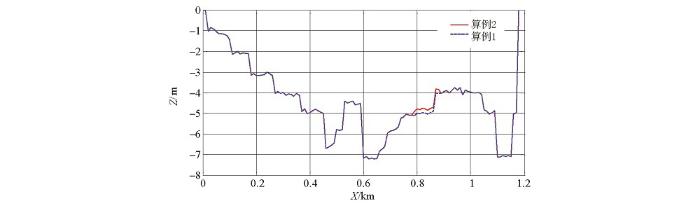
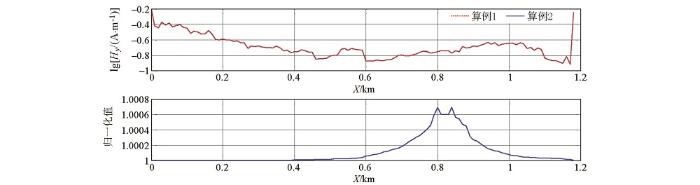
本算例中不考虑海平面高度的变化,对海底淤泥层顶界面高度变化引起的电磁场分布特征进行模拟研究。随着淤泥沉积或被海水冲刷,淤泥层到电缆之间的厚度会发生变化。本算例在起伏地形算例一基础上改变部分区域淤泥层顶界面高度,改变后的淤泥层顶界面高度随测线的变化关系如图14所示,数值模拟结果如图15所示。分别取出算例一和算例二中Z=0 m平面H_y分量进行归一化,结果见图16。

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 起伏地形算例二淤泥层顶界面

Fig.14 Mud layer top interface

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 起伏地形算例二磁场分量H_y剖面

Fig.15 H_y section of magnetic field component

图16

新窗口打开| 下载原图ZIP| 生成PPT

图16 起伏地形算例二H_y归一化结果

Fig.16 H_y normalization results

由图16所示,局部区域淤泥层顶界面上升0.2 m后,在z=0 m平面上,位于淤泥层顶界面变化的上部,前后两次数值计算结果具有异常,但由于异常太小,无法分辨出来。

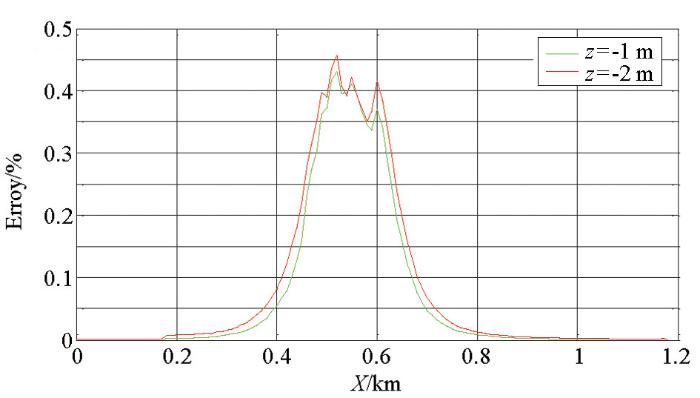
以0.5 m的变化量更改模型中淤泥层顶界面变化的位置段和厚度,分别进行两次数值模拟,然后将计算得到的H_y分量做归一化处理。图17所示为z=-1 m和z=-2 m磁场分量H_y归一化偏差分布,可以看出:当海平面高度不发生变化,淤泥层顶界面变化量为0.5 m时,前后偏差低于0.45%。

图17

新窗口打开| 下载原图ZIP| 生成PPT

图17 起伏地形算例二不同层位磁场分量H_y归一化偏差分布

Fig.17 Distribution of H_y normalized error deviation of magnetic field components in different horizons

3.3 起伏地形算例三

本算例中不考虑由于海水沉积或冲击海底造成的淤泥层顶界面变化,只考虑海平面高度变化。当海平面高度变化后,海水层厚度以及电缆距离海平面的高度相应发生变化。

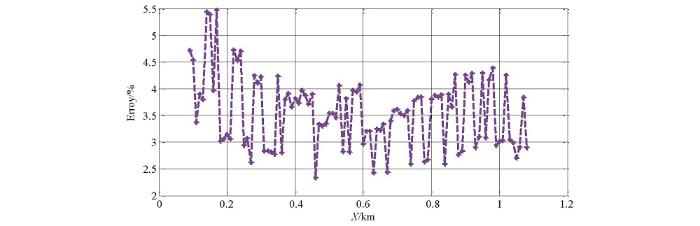
针对算例一中模型,海水层厚度增加0.2 m,将数值模拟计算得到的磁场分量H_y与算例一中对应数值进行归一化处理,从图18中可以看出,海水层厚度变化0.2 m后H_y偏差增加到了3.5%左右。对比算例二可知,海平面发生变化后相比海底淤泥层发生变化对于电磁场分布的影响更大。

图18

新窗口打开| 下载原图ZIP| 生成PPT

图18 起伏地形算例三z=-1 m平面磁场分量H_y归一化偏差分布

Fig.18 Distribution of H_y normalized error deviation of plane magnetic field component z=-1 m

4 结论

采用频率域CSEM长导线源2.5维数值算法对海底电缆模型进行了模拟研究:分别对水平地形和起伏地形海底电缆模型中海水层厚度和海底电缆埋深参数进行数值模拟,通过对数值结果进行分析得出以下结论:

1) 频率域CSEM长导线源探测方法在海底电缆被动源探测领域具有应用潜力,在海洋探测环境中,电磁噪音较少,观测信号强、信噪比质量高。

2) 磁场信号H_y分量最强,建议观测中对此分量进行观测;

3) 当地形水平时,磁场H_y分量分布特征与电缆埋深位置相关:电缆平行铺设于海底淤泥层中,则观测磁场分量呈均匀场特征;当地形起伏时,观测磁场H_y分量分布与海底地形及电缆铺设埋深一一对应,可以利用沿电缆方向观测线H_y分布特征判断电缆埋深起伏特征。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

罗深荣

侧扫声纳和多波束测深系统在海洋调查中的综合应用

[J]. 海洋测绘, 2003,23(1):22-24.