精密单点定位技术在青藏高原地区物探测量中的应用研究

doi:10.11720/wtyht.2019.0103

精密单点定位技术在青藏高原地区物探测量中的应用研究

杜辉¹^,²^,³, 耿涛¹^,²^,³, 段星星¹^,²^,³, 冀显坤¹^,²^,³, 白运¹^,²^,³

1. 自然资源部岩浆作用成矿与找矿重点实验室,陕西西安 710054

2. 中国地质调查局西安地质调查中心,陕西西安 710054

3. 西北地质科技创新中心,陕西西安 710054

The application of precise point positioning to local geophysical prospecting in the Tibetan Plateau

DU Hui¹^,²^,³, GENG Tao¹^,²^,³, DUAN Xing-Xing¹^,²^,³, JI Xian-Kun¹^,²^,³, BAI Yun¹^,²^,³

1. Key laboratory for the Study of Focused Magmatism and Giant Ore Deposits,MLR,Xi’an 710054, China

2. Xi’an Center of China Geological Survey,Xi’an 710054, China;

3. Northwest Geological Science and Technology Innovation Center,Xi’an 710054, China;

责任编辑: 王萌

收稿日期: 2019-03-1 修回日期: 2019-04-17 网络出版日期: 2019-10-20

基金资助:

国家重点研发计划“典型覆盖区航空地球物理技术示范处理解释软件平台开发”所属课题“北秦岭华阳川地区隐伏铀矿空—地—井协同勘查技术示范研究”项目. 2017YFC0602205

Received: 2019-03-1 Revised: 2019-04-17 Online: 2019-10-20

作者简介 About authors

杜辉(1987-),男,工程师,学士,从事物探测量工作。Email:296772098@qq.com 。

摘要

精密单点定位技术具有无需控制点、单台GPS接收机静态测量可获得高精度的坐标成果等优点,在青藏高原等困难地区的物探测量实践中具有广阔的应用前景。本文以利用精密单点定位技术处理青藏高原西部和东部的两个1:25万区域重力调查项目形成的控制点观测数据为基础,经过计算对比这些点的精密单点定位成果和传统测量平差方法所得的CGCS2000坐标成果之间的差值,分析误差来源,得出误差的主要来源是两者坐标值在历元和框架差异引起,进而通过历元和框架校正得出控制点的CGCS2000坐标,重新对比发现校正后的坐标值具有与传统测量平差坐标值相一致的精度,在此基础上提出了在实际物探测量中利用精密单点定位技术得到CGCS2000坐标成果的思路和注意事项,同时讨论了该方法的应用范围。

关键词： 精密单点定位 ; CGCS2000 ; 青藏高原 ; 物探测量

Abstract

The precise point positioning method has such advantages as no control point and the fact that single receiver can obtain high precision coordinate results by static measurement. It has wide application in geophysical exploration in the Tibetan Plateau and other difficult areas. This paper is based on the dealing with observation data of control points formed by two 1:250,000 regional gravity survey projects in the west and east of the Tibetan Plateau using the precise point positioning method; by calculating and comparing the difference between the precision single point positioning result of these points and the CGCS2000 coordinate result obtained by traditional measurement adjustment method, the error source is analyzed. It is concluded that the main source of the error of two coordinates is caused in the calendar and frame difference, and then through calendar and frame correction the CGCS2000 coordinates of control point are obtained. It is found that the corrected coordinates have the same precision as the traditional adjustment coordinate. On such a basis, the authors put forward an idea of using precise point positioning method to obtain CGCS2000 coordinates and pointed out the items deserving attention in using this method, and the application range of this method.

Keywords： PPP ; CGCS2000 ; Tibetan plateau ; geophysical prospecting

PDF (2070KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

杜辉, 耿涛, 段星星, 冀显坤, 白运. 精密单点定位技术在青藏高原地区物探测量中的应用研究. 物探与化探[J], 2019, 43(5): 1046-1053 doi:10.11720/wtyht.2019.0103

DU Hui, GENG Tao, DUAN Xing-Xing, JI Xian-Kun, BAI Yun. The application of precise point positioning to local geophysical prospecting in the Tibetan Plateau. Geophysical and Geochemical Exploration[J], 2019, 43(5): 1046-1053 doi:10.11720/wtyht.2019.0103

0 引言

精密单点定位(PPP,precise point positioning)是利用全球若干地面IGS(international GNSS service)跟踪站的GPS 观测数据计算出的精密卫星星历和轨道钟差, 对单台GPS 接收机所采集的载波相位观测值和伪距观测值进行高精度非差定位解算,得出高精度坐标成果的一种技术方法。该方法最初是由美国喷气推进实验室(JPL)的Zumberge等于1997年提出,并在他们开发的数据处理软件GIPSY上给予实现^[1,2]。

自精密单点定位技术提出以来,国内外大量学者研究的焦点集中于如何优化计算模型^[3,4]、开发精密单点定位处理软件^[5]、分析各种软件的计算精度^[6,7,8,9]、对比选择数据处理策略软件^{[10,11,12,13,14]}等,这些研究解决了精密单点定位技术应用的基本问题,主要不足之处是基于研究处理IGS参考站的观测数据得出的一些结论,因IGS站的观测条件好、数据质量高,导致这些结论在实际测量工作中的可参考性较低。

现阶段精密单点定位的技术方法已经成熟,可用于静态精密单点定位数据处理的软件很多,比较知名的有美国JPL的GIPSY软件、瑞士的Bernese软件以及我国武汉大学的PANDA(positioning and navigation data analyst)软件和Trip软件等,虽然这些软件采用的算法和策略都不尽相同,但试验验证表明解算的结果与真实数据能很好的吻合^[14]。PANDA软件是武汉大学卫星导航定位技术研究中心自主研发的卫星导航定位系统综合处理软件,采用非差处理模式,尽可能地探测与修复周跳并剔除异常值和考虑多种改正项,采用最小二乘估计器对接收机位置坐标参数、接收机钟差参数、对流层延迟参数和无电离层组合模糊度参数进行最有估计,采用IGS中心提供的精密轨道和精密星历等文件进行处理,进而得出可靠的定位解算结果^[12]。

应用方面的研究主要集中在各类具体测量实例中^[15,16],这些研究展示了精密单点定位技术在不同测量领域均取得良好的应用效果。物探测量的工作区域一般位于基础测绘程度低、人烟稀少、交通不便的联网困难地区,精密单点定位技术在这些地区的定位控制测量中体现出巨大的优越性。但仍存在一些不足之处,一是未分析精密单点定位与传统测量方法得出的坐标值之间产生差值的原因,笼统的认为这些差值是精密单点定位技术的定位误差引起;二是未将精密单点定位成果有效地同CGCS2000坐标联系起来,不符合自然资源部关于今后的地、物、化等成果只能采用CGCS2000坐标的要求。本文结合青藏高原地区的两个1:25万区域重力调查项目,利用PANDA软件进行静态精密单点定位计算,尝试解决上述问题,为精密单点定位技术在实际物探测量中的应用提供一些思路。

1 精密单点定位试验

1.1 试验方案

1:25万区域重力调查项目的测量工作目前遵循“先整体后局部、先控制后碎部”的基本测量原则。首先利用Trimble 5700接收机静态定位的方式建立控制网,联测国家B级GPS控制点作为控制网的起算点,观测完成后利用Gamit/Globk软件进行基线处理和平差计算,得到控制网点的高精度坐标;其次,以这些控制点为基准站,利用快速静态或动态测量的方式进行后续测点的坐标采集工作。本试验方案是将上述产生的控制网联测数据和每日参考站的观测数据利用PANDA软件进行精密单点定位计算,得到这些点的精密单点定位坐标值,然后与利用Gamit/Globk软件平差计算的控制点坐标值进行比较,得出这两套坐标值之间的差异并分析产生差异的原因。以下通过2 个试验实例进行分析说明。

1.2 试验实例一

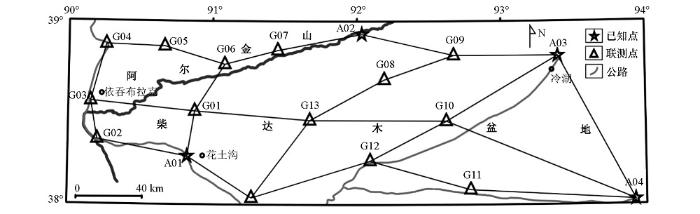
实例一的数据来源于“青海1:25万油墩子、库朗米其提、老茫崖、布伦台、茫崖镇幅区域重力调查”项目,该项目工作区地处青藏高原腹地,柴达木盆地西北缘,总体交通不便,是我国基础测绘程度相对较低的地区,基础控制点分布较少且不均匀。本区GPS控制网测量采用边连式的作业方式进行,总计联测17个GPS控制点,其中4个为国家B级GPS控制点,具体的GPS控制点分布如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 青海油墩子项目GPS控制网示意

Fig.1 GPS control net sketch alh map of Youdunzi project

该GPS控制网按照D级控制网的观测要求进行联测,考虑到网的平均边长较大,延长观测时间至单时段4 h并至少观测2个时段。观测完成后,利用Gamit/Globk软件进行基线解算,约束已知的B级GPS控制点成果平差计算,最终得出各点的平差坐标值。经统计,控制网平均边长73 km,平面位置中误差±0.58 cm,高程中误差±2.15 cm;精度最差点为G04,平面位置中误差±0.79 cm,高程中误差±3.27 cm。

GPS控制网联测完成后,控制点在作为快速静态作业的基准站进行观测,产生了大量的基准站数据。因精密单点定位的结果精度与数据观测时长有关^[11],那么怎样选择用于计算的数据的观测时长?考虑到观测条件和数据观测质量应与实际作业中一致,任意选择观测时长大于12 h的数据,将其截成12~2 h的每1 h间隔的11个数据,对这11个观测数据进行PPP计算,以12时数据的坐标值为准,求得其他10个坐标数据与该数据的坐标残差(图2)。

图2

新窗口打开| 下载原图ZIP| 生成PPT

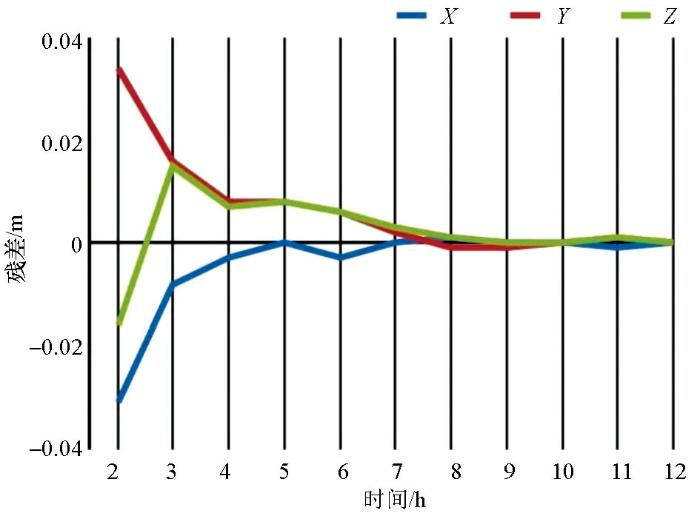
图2 坐标值收敛与观测时长的关系

Fig.2 The relation of coordinates converge with observation time

如图2所示,坐标值在3 h以后已全部收敛至 2 cm以内,4 h以后全部收敛至1 cm以内,考虑到控制网联测数据的观测时长为4 h,那么选取基准站和控制网联测数据中观测时长大于4 h的数据用于PPP计算。以此统计每个控制点可以进行精密单点定位计算的数据个数(表1)。

表1 油墩子项目各控制站参与计算的数据个数

Table 1 The number of data calculated by each control station in Youdunzi project

	A01	A02	A03	A04	G01	G02	G03	G04	G05	G06	G07	G08	G09	G10	G11	G12	G13
N	15	4	3	3	3	14	10	4	11	6	4	3	5	12	3	11	3

新窗口打开| 下载CSV

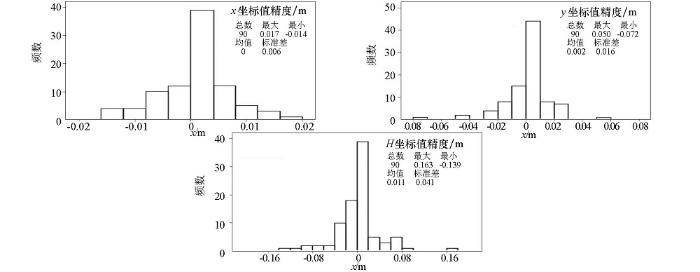
利用PANDA软件并采用一致的解算策略对上述数据进行精密单点定位计算,以各数据观测时长为权的加权平均坐标值作为该控制站的PPP计算坐标值,分别统计解算结果的内符合精度和外符合精度,进行评价。内符合精度利用各单次解算与该计算坐标值之差进行统计,外符合精度利用该控制站的平差坐标值与计算坐标值之差进行统计。为了便于直观的显示内、外符合精度在应用坐标系中的具体量值,将平差坐标值和计算坐标值都进行高斯正算,转换为高斯平面坐标值和大地高系统后进行比较。因不涉及椭球之间的变换,坐标系统变换不会引起的精度损失,且都采用统一的中央经线,可以认为投影变形的影响在坐标值求差之后可忽略不计。实例一PPP计算坐标值的内符合精度统计如图3所示,外符合精度统计如图4所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

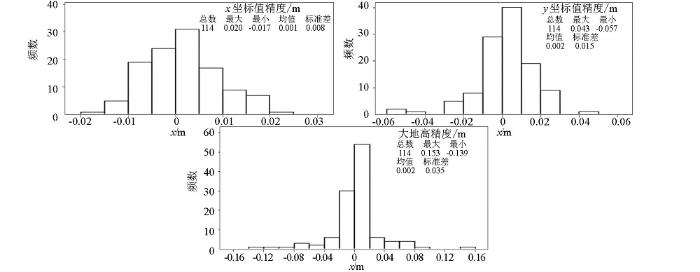
图3 实例-PPP计算坐标值内符合精度统计

Fig.3 Inner coincidence accuracy of PPP coordinate in first example

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 实例-PPP计算坐标值外符合精度统计

Fig.4 Outer coincidence accuracy of PPP coordinate in first example

1.3 试验实例二

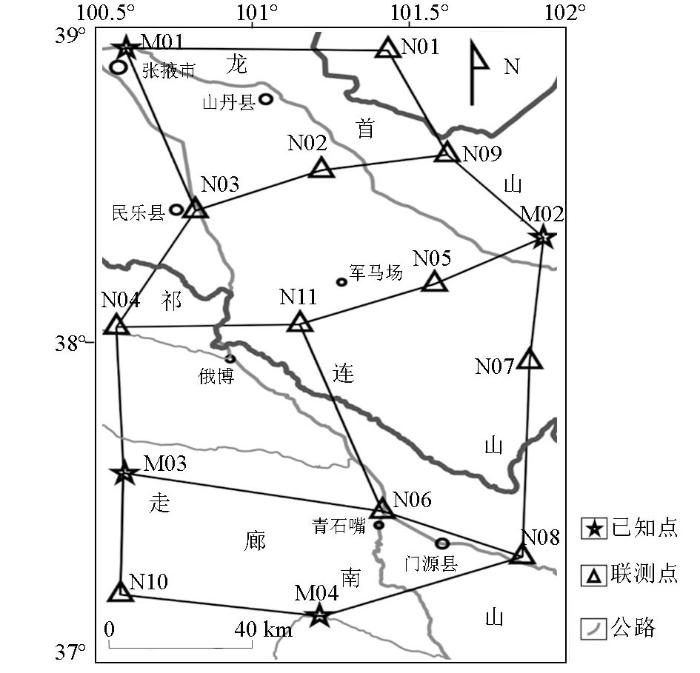
实例二的数据来源于“青海1:25万门源回族自治县幅、山丹县幅区域重力调查”项目,该项目工作区地处青藏高原东部,横跨祁连山中段两侧,总体交通便利,各类基础控制点数量较多且分布均匀。GPS控制网测量采用边连式的作业方式进行,总计联测15个GPS控制点,其中4个为国家B级GPS控制点,具体的GPS控制点分布如图5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 青海门源项目GPS控制网示意

Fig.5 GPS control net sketch alh map of Menyuan project

采用与实例一完全一致的控制网联测标准,相同的数据处理方法进行网平差处理。经统计,控制网平均边长79 km,平面位置中误差±0.69 cm,高程中误差±3.63 cm;精度最差点为N10,平面位置中误差±1.55 cm,高程中误差±5.03 cm。

同样选取控制网联测数据和基准站数据,利用PANDA采用同样的数据处理策略进行精密单点定位解算,解算完成后以同样的方法统计各坐标值的内符合精度和各控制站的外符合精度。各控制站进行精密单点定位计算的数据个数如表2所示,各坐标值的内符合精度统计如图6所示,各控制站的外符合精度如图7所示。

表2 门源项目各控制站参与计算的数据个数

Table 2 The number of data calculated by each control station in Menyuan project

	M01	M02	M03	M04	N01	N02	N03	N04	N05	N06	N07	N08	N09	N10	N11
N	4	4	4	11	3	7	15	12	7	3	3	8	3	3	3

新窗口打开| 下载CSV

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 实例二PPP计算坐标值内符合精度统计

Fig.6 Inner coincidence accuracy of PPP coordinate in second example

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 实例二PPP计算坐标值外符合精度统计

Fig.7 Outer coincidence accuracy of PPP coordinate in second example

2 试验结果分析及误差改正

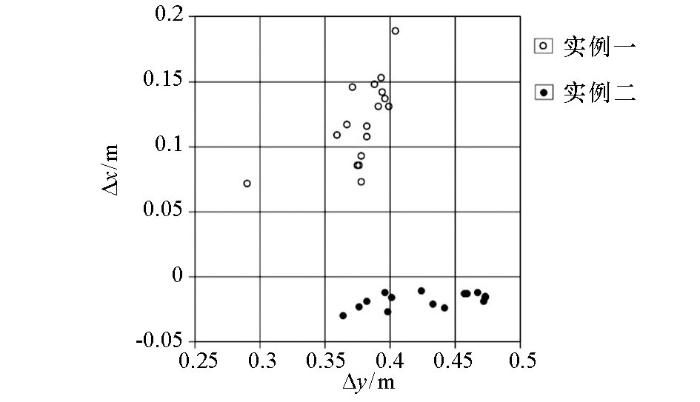
由实例一和实例二的内符合精度统计图(图3、图6)可以看出,PANDA软件计算的坐标值精度为:x误差大部分位于±0.01 m的区间内,y误差大部分位于±0.02 m的区间内,大地高大部分位于±0.08 m的区间内,说明PANDA软件的PPP计算精度高,结果可靠性好。而从实例一和实例二的外符合精度统计图(图4、图7)中可以看出,PPP计算值与平差值之间存在明显的差异。一般情况下,外符合精度的差值是由已知点误差、控制网联测误差、控制网平差误差、PPP计算误差等原因造成,但实例一的x坐标差值集中在0.1~0.2 m之间,实例二的x坐标差值集中在-0.1~0 m之间;实例一的y坐标差值集中在0.3~0.4 m之间,实例二的y坐标值集中在0.4~0.5 m之间;实例一的H坐标差值集中在-0.2~0 m区间,实例二的H坐标差值集中在-0.1~0.1 m之间;上述这些差值显示出明显的系统误差的特性。将实例一和实例二中各控制点外符合坐标差值Δx、Δy标绘至平面坐标系中,如图8,可见坐标差值分布有明显的分区现象,也具有系统误差的特性。而已知点误差等都是偶然误差,应呈现随机分布的特性,显然还有其他的原因造成上述外符合的坐标差值。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 外符合坐标差值分布

Fig.8 Distribution of outer-coincidence coordinate difference

考虑到外符合精度是PPP计算后的加权平均值与网平差值比较得出的,网平差值是B级GPS已知点约束平差的成果,已知点坐标属于CGCS2000坐标系,那么平差值均属于CGCS2000坐标系统,而PPP计算时采用IGS提供的与观测日期对应的精密星历,那么计算坐标值统属于ITRF(international terrestrial reference frame)框架下实时历元的坐标系统。CGCS2000坐标系统对准IRTF97框架、2000.0历元^[17],而PPP计算值的框架为ITRF08、历元为观测时间(实例一观测时间为2010年,实例二观测时间为2012年),这两者之间存在框架和历元的差异,由于板块运动的原因,历元不同的同一站点坐标也会有所不同,所以需要将两者的历元和框架进行统一后再进行外符合精度评价。

因ITRF公布的框架转换参数也涉及参考历元的问题,所以先进行历元归算,然后进行框架转换。空间直角坐标系下历元归算的公式如下:

$[\begin{array}{l} X_{t} \\ Y_{t} \\ Z_{t} \end{array}] = [\begin{array}{l} X_{t_{c}} \\ Y_{t_{c}} \\ Z_{t_{c}} \end{array}] + (t - t_{c}) [\begin{array}{l} V_{x} \\ V_{y} \\ V_{z} \end{array}]$

式中t_c为原始历元,t为目标历元,X_t、Y_t、Z_t为历元t时刻的坐标,X_tc、Y_tc、Z_tc为历元t_c时的坐标,V_x、V_y、V_z为站点速度。

CGCS2000坐标的参考历元为2000.0,实例一的观测时间中值为2010年10月,其观测历元约为2010.8,实例二的观测时间中值为2012年7月,其观测历元约为2012.6。站点速度值采用文献[18]给出的中国大陆3°×3°格网平均速度表中相应区域的速度值(表3)进行计算。

表3 历元校正时采用的平均速度值

Table 3 Mean velocities for Epoch correction in project

	V_x/(mm·a^-1)	V_y/(mm·a^-1)	V_z/(mm·a^-1)
实例一	-32.6	-5.8	4.7
实例二	-34.1	-3.6	-5.7

新窗口打开| 下载CSV

历元改正完成后,进行框架转换,空间直角坐标系下框架转换的公式如下:

$\begin{array}{l} {[\begin{array}{l} X \\ Y \\ Z \end{array}]}_{ITRF 97} = {[\begin{array}{l} X \\ Y \\ Z \end{array}]}_{ITRF 08} + [\begin{array}{l} T_{x} \\ T_{y} \\ T_{z} \end{array}] + \\ [\begin{array}{l} D & - R_{z} & R_{y} \\ R_{z} & D & - R_{x} - \\ R_{y} & R_{x} & D \end{array}] {[\begin{array}{l} x \\ y \\ z \end{array}]}_{ITRF 08} \end{array}$

其中:T_x、T_y、T_z、D、R_x、R_y、R_z为ITRF提供的框架转换参数。ITRF2008至ITRF97的转换参数如表4。

表4 ITRF2008至ITRF97的转换参数

Table 4 Conversion parameter of ITRF2008 to ITRF 97

T_x/mm	T_y/mm	T_z/mm	D/ppb	R_x/mas	R_y/mas	R_z/mas	Eopch
4.8	2.6	-33.2	2.92	0	0	0.06	2000.0

新窗口打开| 下载CSV

经历元和框架转换后,PPP的计算坐标值就转换为CGCS2000坐标,按照前述计算外符合精度的方法,重新统计两个实例的外符合精度如图9所示。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 校正后的外符合精度

Fig.9 Outer coincidence accuracy after correction

考虑到历元改正的速度值采用了格网平均值,可以认为图9显示的校正后的外符合精度基本呈现偶然误差的特性,其x坐标最大0.048 m,最小-0.039 m;y坐标最大0.043 m,最小0.074 m;H坐标最大0.086 m,最小-0.085 m。不考虑平差坐标本身的误差,实例一校正前的坐标精度:平面位置中误差±0.282 m,高程中误差±0.140 m,校正后的坐标精度:平面位置中误差±0.026 m,高程中误差±0.048 m;实例二校正前的坐标精度:平面位置中误差±0.304 m,高程中误差±0.038 m,校正后的坐标精度:平面位置中误差±0.033 m,高程中误差±0.040 m。可以看出,校正后实例一的平面位置和高程精度都有显著提高,平面位置提高一个数量级,高程位置提高3倍;校正后实例二的平面位置精度提高一个数量级,高程精度基本保持不变。经框架和历元改正后的PPP计算成果即为CGCS2000坐标系统下的成果,利用上述校正后的外符合坐标差值统计PPP计算的CGCS2000坐标精度为:平面位置中误差±0.029 m,高程中误差±0.045 m。

3 精密单点定位的应用技术

上述精密单点定位试验的两个实例表明,PPP计算的坐标成果经校正后的精度能够满足绝大部分物探测量的精度要求。现阶段实际物探测量中,主要的工作有控制网的联测和测点的放样及坐标采集两大类工作^[19],目的是获得满足精度要求的测点CGCS2000坐标。由《物化探工程测量规范 DZ/T0153-95》中各物探方法的测量精度要求得知,磁法和电法工作对测量的精度要求较低,一般只进行测点的放样和坐标采集工作,该工作使用标称精度为米级或亚米级的校正后的手持式GPS来完成;而地震和重力工作对测量的精度要求高,一般利用GPS静态测量的方法建立控制网,然后在此基础上采用RTK技术进行测点的放样和坐标采集。

PPP计算属于事后处理技术,在计算过程中需要使用IGS站公布的精密卫星数据,而这些数据的公布具有滞后性,虽然关于动态的历元级(观测时长为秒级)精密单点定位技术也有相关研究,但由于不具备测点放样功能,且在效率上等都和传统的RTK作业方式相比,不具备优势。根据上述各物探测量工作的具体要求及PPP计算的特点和计算精度,可以得出其应用领域有:磁法和电法工作中,提供高精度的控制点坐标以便校正手持式GPS;地震和重力工作中代替GPS控制网的联测工作,得到可作为RTK基准站的高精度坐标。

根据上述两个实例获得高精度的PPP坐标成果的过程,总结得出精密单点定位技术在实际应用中的测量方法等如下:

1) 野外测量方法:每个用于手持机校正的控制点或RTK基准站需要采用双频GPS接收机进行观测,根据传统GPS控制网联测的观测要求进行观测。同时参考图2中的观测时长与坐标值的收敛关系,要求每点观测时长应大于4 h(X、Y、Z精度优于1 cm),观测次数以3次及以上为宜,便于统计精度。

2) PPP计算技术要求:首先应采用TEQC等软件对观测数据进行预分析,了解观测值的观测质量。第二,应采用成熟的精密单点定位软件进行计算,默认解算策略即可。第三,计算完成后,应对各PPP坐标值进行误差分析,以3倍中误差为限剔除粗差后,再进行加权平均计算(以观测时长定权),作为该控制点的高精度坐标值。

3) PPP成果的精度评价:与实例一、二中统计内符合精度的方法一致,即根据基准站每个观测数据的PPP坐标值与该站最终的加权平均坐标值的误差,统计该站的坐标精度。

精密单点定位技术获得CGCS2000坐标的一般流程和注意事项如下:

1) 单台GPS进行野外静态测量,获得各控制点观测数据;

2) 进行PPP计算,求取各控制点的最终坐标值,并统计精度;

3) 根据文献[18]给出的中国大陆3°×3°的格网平均速度及上述历元改正公式对坐标值进行历元校正;

4) 根据上述框架校正公式及ITRF给出的各系列ITRF框架至ITRF97的框架转换参数坐标值进行框架校正,如果没有直接对应的转换参数,也可以通过中间框架二次转换进行,如ITRF2014-ITRF2008-ITRF97;

5) 获得控制点的高精度CGCS2000坐标(根据实例一、二的内符合精度显示,其平面坐标精度约为0.017 m,大地高精度0.041 m)。

4 结论

1) 对青藏高原西部和东部两个项目的测量数据进行精密单点定位计算,得出该技术的内符合精度约为平面x坐标最大0.008 m,y坐标最大0.016 m,大地高最大0.041 m;采用各控制点的PPP加权平均坐标值与该点传统控制网平差获得的坐标值进行求差比较的方法,获得实例一外符合精度:平面位置中误差±0.282 m,高程中误差±0.140 m,实例二外符合精度:平面位置中误差±0.304 m,高程中误差±0.038 m。

2) 根据精密单点定位的成果性质,得出造成外符合精度较差原因是精密单点定位计算得出的坐标值与传统网平差得出的坐标值在参考历元、坐标框架上不一致。根据CGCS2000坐标系定义的参考历元和坐标框架,将精密单点定位坐标成果进行参考历元和坐标框架校正,校正后得出精密单点定位的控制点CGCS2000坐标值与网平差的CGCS2000坐标值比较,显示实例一校正后的坐标精度:平面位置中误差±0.033 m,高程中误差±0.040 m,实例二校正后的坐标精度:平面位置中误差±0.026 m,高程中误差±0.048 m。

3) 在两个实例中,展示了参考历元校正、坐标框架校正的具体公式,以及通过参考文献给出的中国大陆地区速度场值和框架转换参数校正后,精密单点定位坐标值具有可与传统网平差方法相一致的坐标精度,这为精密单点定位技术在实际应用中获得CGCS2000坐标提供了一条可行的技术路线。

4) 在上述基础上,提出了通过精密单点定位计算、参考历元校正、坐标框架校正即可获得控制点高精度CGCS2000坐标的测量方法、技术要求、精度评价方式以及一般流程,也分析了精密单点定位技术在物探测量中的具体应用领域。

5) 精密单点定位技术能够在全球范围内利用单台接收机进行高精度静态定位,通过校正即可直接获得高精度的CGCS2000坐标成果这一技术在一些没有国家级控制点或联网困难地区的物探测量工作显示出巨大的优越性。

致谢:

感谢武汉大学卫星导航定位技术研究中心提供的PANDA软件,以及IGS分析中心提供的数据和相关产品;感谢各位审稿专家和《物探与化探》编辑部的辛勤付出。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Zumberge J

, Heflin M

, Jefferson D

, et al.

Precise point positioning for the efficient and robust analysis of GPS data from large networks

[J]. Journal of Geophysical Research, 1997,102(B3):5005-5017.