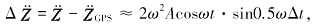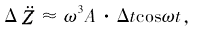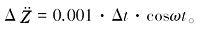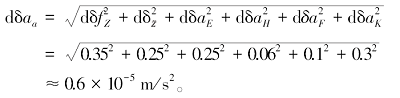E-mail Alert Rss
 

物探与化探, 2019, 43(2): 408-414 doi: 10.11720/wtyht.2019.1327

方法研究·信息处理·仪器研制

高精度航空重力测量系统分项指标设计分析

张虹1, 屈进红2,3, 姜作喜2,3, 王萌3, 李行素2,3

1. 北京信息科技大学 信息管理学院,北京 100192

2. 自然资源部 航空地球物理与遥感地质重点实验室,北京 100083

3. 中国自然资源航空物探遥感中心,北京 100083

Design and analysis of sub-index of high precision Airborne Gravity System

ZHANG Hong1, QU Jin-Hong2,3, JIANG Zuo-Xi2,3, WANG Meng3, LI Xing-Su2,3

1. Beijing information technology School of Information Management, Beijing 100092, China

2. Key laboratory of Airborne Geophysics and Remote Sensing Geology, Ministry of Natural Resources, Beijing 100083, China

3. China Aero Geophysical Survey and Remote Sensing Center for Natural Resources, Beijing 100083, China

责任编辑: 王萌

收稿日期: 2018-09-11   修回日期: 2019-01-14   网络出版日期: 2019-04-20

基金资助: 国家重点研发计划项目.  2017YFC0601706
国家重点研发计划项目.  2017YFC0601705

Received: 2018-09-11   Revised: 2019-01-14   Online: 2019-04-20

作者简介 About authors

张虹(1963-),女,辽宁锦县人,副教授,北京信息科技大学,现主要从事地球物理测量方法技术、数理统计应用技术等领域的研究工作。Email:Zhanghong921228@sohu.com 。

摘要

为研制高精度航空重力仪,开展了高精度航空重力仪分项指标设计与分析,为高精度航空重力测量系统设计提供依据。笔者基于航空重力测量的数学模型,归纳出影响航空重力测量的主要因素;结合航空重力测量的相关理论公式,使用理论模型,推导出各影响因素的误差模型;开展了各项误差的分析研究,并通过设定合理的分项指标精度来有效地控制分项误差,确保航空重力测量精度优于0.6×10 -5 m/s 2。

关键词： 高精度航空重力仪 ; 误差模型 ; 各项误差分析 ; 分项指标精度

Abstract

In order to meet the needs of development of high-precision airborne gravimeter , the sub-index design and analysis of high-precision airborne gravimeter were carried out, which provided the basis for the design of high-precision airborne gravimeter system. Based on the mathematical model of airborne gravimetry, this paper summarizes the main errors affecting airborne gravimetry, uses the theoretical model formula, deduces the error models of various influencing factors, and carries out the analysis and study of various errors, and sets reasonable sub-index by combining the relevant theoretical formula of airborne gravimetry. Accuracy can effectively control the sub item errors and ensure the accuracy of airborne gravity measurement is better than 0.6×10 -5 m/s 2.

Keywords： high precision Airborne Gravimeter ; error model ; error analysis ; sub item accuracy

PDF (426KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

张虹, 屈进红, 姜作喜, 王萌, 李行素. 高精度航空重力测量系统分项指标设计分析. 物探与化探[J], 2019, 43(2): 408-414 doi:10.11720/wtyht.2019.1327

ZHANG Hong, QU Jin-Hong, JIANG Zuo-Xi, WANG Meng, LI Xing-Su. Design and analysis of sub-index of high precision Airborne Gravity System. Geophysical and Geochemical Exploration[J], 2019, 43(2): 408-414 doi:10.11720/wtyht.2019.1327

0 引言

早期航空重力测量技术主要是发达国家来研究和应用。1958年,美国空军进行了第一次航空重力测量试验,直到20世纪90年代以来,随着GPS、INS技术及高灵敏度、高稳定度重力仪器的发展及应用,使航空重力测量的研究与应用取得了突破性进展[1,2]。21世纪初,相继研制出二轴惯性稳定平台型、三轴惯性稳定平台型和捷联式航空重力仪试验样机,便逐步形成实用化的航空重力仪。其中三轴惯性稳定平台型航空重力仪的测量精度最高,测量精度达到0.6×10-5 m/s2,开始了大规模的商业应用[3,4,5]。

我国从2006年开始进行航空重力测量技术研究和航空重力仪研制的工作。到目前为止,已经研制出三轴惯性稳定平台型和捷联式航空重力仪样机,测量精度达到1.0×10-5 m/s2,取得了突破性进展[6]。为了进一步提高我国自主研制航空重力勘查系统的测量精度,使其达到国际先进水平,“十三五”期间开始了新一轮航空重力测量系统的研制工作。

航空重力测量精度取决于传感器误差、传感器姿态误差、卫星导航误差等各方面[7],为了研制测量精度优于0.6×10-5 m/s2的航空重力测量系统,须控制好各分项指标的误差,从而保证航空重力测量精度满足要求。笔者通过建立航空重力(标量重力)测量的误差模型,分析各分项误差对航空重力测量精度的影响贡献,由此通过设定合理的分项指标有效控制分项误差,实现航空重力测量精度优于0.6×10-5 m/s2的研究目标。

1 航空重力标量测量的数学模型

航空重力的垂向重力传感器观测值主要包括:①航空重力仪自身所包含的载体垂向加速度、厄特渥斯效应、水平加速度耦合、零点漂移量;②观测点空间位置的不同而由地球重力场引起的重力值变化;③重力仪和差分GPS随机噪声[8,9]。

假设在重力传感器处于垂向时,航空重力标量测量数学模型[10]可表示为:

$g_{a}=g_{b}+(f_{z}-f^{0}_{z})-\ddot{Z}+\delta_{a_{E}}+\delta_{a_{H}}+\delta_{a_{F}}+\delta_{a_{K}}+\delta_{a_{1}}-\gamma_{0}$,

其中: ga是航空自由空间重力值,m/s2; gb是停机坪处的基点重力值,由陆地重力仪从重力基准点联测得到,m/s2;fZ是重力传感器测点观测值,m/s2; fz0是重力传感器在停机坪上基点上的观测值,m/s2;$ \ddot{Z}$是载体垂向加速度改正,m/s2;δaE是厄特渥斯改正,m/s2;δaH是水平加速度改正(因重力传感器非垂向而对观测值产生的重力影响),m/s2;δaF是高度改正,m/s2;δaK是零漂改正(因航空重力仪存在零点漂移),m/s2;δaI是重力仪和差分GPS随机噪声,m/s2;γ0是椭球面上的正常重力场改正值,m/s2。

为了获得航空自由空间重力值,须对垂向重力传感器观测值进行载体垂向加速度改正、厄特渥斯改正、水平加速度改正、零漂改正、正常重力场改正和高度改正。

航空重力测量误差可表示为各项改正误差传递[10],由式(1)可得:

$d\delta{a^{2}_{a}}=d\delta{g^{2}_{b}}+d\delta{f^{2}_{z}}+d\delta{^{2}_{\ddot{Z}}}+d\delta{a^{2}_{E}}+d\delta{a^{2}_{H}}+d\delta{a^{2}_{F}}+d\delta{a^{2}_{K}}+d\delta{a^{2}_{1}}+d\delta\gamma{^{2}_{0}},$

其中:dδgb为停机坪处重力基点误差;dδfz为重力传器观测误差;d$\delta_{\ddot{Z}}$为载体垂向加速度测量误差;dδaE为厄特渥斯改正误差;dδaH为水平加速度改正误差;dδaF为高度改正误差;dδaK为零漂改正误差;dδaI为重力仪和差分GPS的随机误差;dδγ0为椭球面上的正常重力场改正误差。

航空重力测量的误差主要由4部分组成[10,11]:①航空重力传感器的观测误差和重力传感器非垂向引起的误差;②由差分GPS解算得到的载体位置、运动速度和加速度的误差,造成重力正常场改正、高度改正、厄特渥斯改正和载体垂向加速度改正的误差;③航空重力仪和差分GPS之间的同步误差;④重力基点引点误差、重力仪和差分GPS的随机误差。

2 航空重力测量各项误差分析

2.1 载体垂向加速度测量误差

载体飞行高度、测量精度直接影响着航空重力的测量精度,可以说决定了航空重力的测量精度[9]。

当沿着某一测线进行航空重力测量飞行时,假设:飞行高度变化幅值为A,飞行高度变化周期(T)为60 s,且飞行高度按正弦规律变化,因此载体飞行高度(Z)变化可表示为[10]:

Z=Asin(2π/T·t)=Asinωt,

其中:ω=2π/T=2×3.14/60≈0.1 s-1。

从飞行高度的位移可得到载体垂向加速度为:

$\ddot{Z}=\omega^{2}Asin\omega t$(4)

当测得的飞行高度幅度A=1 mm时,由此可得载体最大垂向加速度为:

$\ddot{Z}_{max}=0.1^{2} · 0.001=1 \times 10^{-5}m/s^{2}$

由此可得,高程1 mm的误差可引起载体垂向加速度最大误差1×10-5 m/s2,同时载体垂向加速度误差与飞行起伏周期T2反比。因此,飞行起伏周期60 s时GPS高程测量误差须小于1 mm,而当飞行起伏周期100 s以上时GPS高程测量误差可放宽到2~3 mm,才能保证载体垂向加速度最大误差控制在1×10-5 m/s2之内。

由于被测航空重力异常位于低频段,在解算航空重力异常时,须通过低通滤波方法滤去观测数据中的高频噪声[12,13,14]。常用滤波器窗口为100 s[15],经低通滤波后载体的垂向加速度改正误差可优于(0.25~0.4)×10-5 m/s2。

2.2 同步精度引起的测量误差

仍采用2.1的飞行方法,假设GPS记录的载体加速度滞后或超前Δt s,因此由GPS解算得到的载体垂向加速度可表示为[7]:

$\ddot{Z}_{GPS}=\omega^{2}Asin\omega (t+\Delta t)$

由此可得到由于采样不同步造成载体垂向加速度与GPS解算垂向加速度之间的误差:

由于Δt≪t且Δt值很小,所以式(6)可简化为:

将A=1、ω=0.1代入式(7),可得:

当Δt=±1 ms时,Δ$\ddot{Z}$max=±0.1(10-5 m/s2);

当Δt=±10 ms 时,Δ$\ddot{Z}$max=±1.0(10-5 m/s2)。

由此可知:当航空重力仪与GPS时间同步误差在1 ms时,将产生0.1×10-5 m/s2的重力测量误差,因此设计的航空重力仪与GPS的同步精度应好于 1 ms。实际上,同步精度可达微秒级,其造成的误差可以忽略不计。

2.3 厄特渥斯改正误差

因载体的运动而使航空重力仪产生了附加离心力,这种影响称为厄特渥斯效应,消除该影响的方法即为厄特渥斯改正。载体飞行速度的测量精度直接影响了厄特渥斯的改正精度[16]。

厄特渥斯改正的严密数学表达式[7,8]为:

δaE=vE2RN+h+vN2RM+h+2vEωcosφ,

以RN+h=RM+h=R代入式(9),即近似情况下的厄特渥斯改正公式:

δaE=v2R+2vωsinAcosφ,

其中:vN、vE、v分别为载体速度的N向、E向分量和水平速度,单位m/s;φ、h分别为测点的地理纬度和载体的飞行高度,单位分别为rad、m; R、RM、RN分别为地球半径、参考椭球上各点的子午圈半径和卯酉圈半径,单位m; ω是地球自转角速度,单位rad/s; A是飞行航向角(或方位角),单位rad。

从式(10)可以看出,厄特渥斯改正的计算精度主要取决于载体速度、大地纬度以及方位角的确定精度。按误差传播定理可得厄特渥斯改正误差:

dδaE=2vR+2ωsinAcosφdv+2vωcosAcosφdA-2vωsinAsinφdφ,

取地球半径R为6 378 137 m,平均自转角速度ω为7.292 1×10-5 rad/s。

1) 位置误差引起的厄特渥斯改正误差[7]

由式(11)右端第三项先分析测点纬度误差对δaE的影响,令|sinA|=1,|sinφ|=1,计算测点纬度误差对厄特渥斯改正影响(如表1)。目前利用GPS测量纬度的精度远优于0.1’,不同航行速度下该改正项精度将优于0.07×10-5 m/s2,通常可以忽略不计。

表1   纬度误差对厄特渥斯改正的影响 (单位:10-5 m/s2)

Table 1  The influence of latitude error on the Eotvos correction

速度/(km/h)
纬度误差/(‘)		100200300400500600
0.050.00590.01180.01770.02360.02950.0354
0.10.01180.02360.03540.04710.05890.0707
0.20.02360.04710.07070.09430.11780.1414

新窗口打开| 下载CSV


2) 速度误差引起的厄特渥斯改正误差

由式(11)右端第一项分析速度误差对δaE的影响[14]。令|sinA|=1,|cosφ|=1,计算出速度误差对厄特渥斯改正的影响(如表2),目前GPS的测速精度一般优于±0.02 m/s,因此,该改正项精度将优于±0.35×10-5 m/s2。

表2   速度误差对厄特渥斯改正的影响 (单位:10-5 m/s2)

Table 2  The influence of velocity error on the Eotvos correction

速度误差/(m/s)
飞行速度/(m/s)		0.0050.010.0150.020.0250.03
500.08080.16150.24230.32300.40380.4846
600.08230.16470.24700.32930.41160.4940
700.08390.16780.25170.33560.41950.5034
800.08550.17090.25640.34190.42730.5128
900.08700.17410.26110.34810.43520.5222

新窗口打开| 下载CSV


3) 航向角误差引起的厄特渥斯改正误差

由式(11)右端第二项分析航向误差对δaE的影响。令|cosA|=1,|cosφ|=1,计算出航向误差对厄特渥斯改正的影响(如表3)。

表3   航向误差对厄特渥斯改正的影响 (单位:10-5 m/s2)

Table 3  The influence of course deviation on the Eotvos correction

飞行速度/(m/s)
航向误差/(‘)		200220300400500600
0.10.02360.02590.03540.04710.05890.0707
0.50.11780.12960.17680.23570.29460.3535
10.23570.25930.3535———

新窗口打开| 下载CSV


目前航向精度优于1’,航向误差将引起最大0.36×10-5 m/s2厄特渥斯的改正误差。同时由式(11)可以看出在EW向上航向误差对厄特渥斯改正影响最小,在SN航向上航向误差对其影响最大。

4) 航空重力厄特渥斯改正综合误差

测点纬度误差对厄特渥斯改正影响小,可以忽略不计。载体在赤道附近EW向飞行时,速度测量误差对厄特渥斯改正影响最大,但航向误差影响接近0,厄特渥斯改正的精度优于0.35×10-5 m/s2。载体在赤道附近SN向飞行时,航向误差对厄特渥斯改正影响最大,速度测量误差影响很小,厄特渥斯改正的精度优于0.36×10-5 m/s2。

因此,综合考虑到测点纬度误差、速度测量误差和航向误差对厄特渥斯改正的影响,厄特渥斯改正最大误差参考值取为(0.20~0.30)×10-5 m/s2,此时位置纬度精度应优于0.1’、速度精度应优于0.02 m/s和航向精度应优于1’。

2.4 水平改正误差

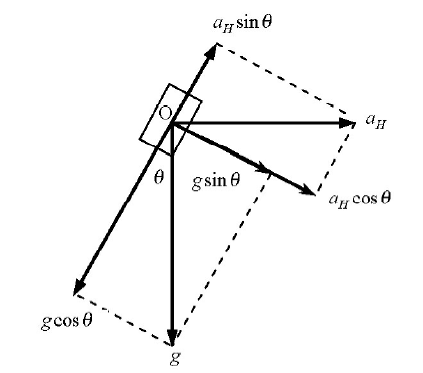
航空重力测量时,载体一直处于动态运动中,往往稳定平台不能完全保持自己处于水平状态,或解算的重力传感器姿态角存在误差[7]。假设稳定平台(或姿态角度)发生偏离(如图1),其偏离角为θ,那么此时重力传感器测到的重力值a为:

a=ag-aaH=gcosθ-aHsinθ,

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   平台非水平时重力传感器感知的重力值示意

Fig.1   The gravity value perceived by the gravity sensor when the platform is not horizontal


其中:g为当地重力值,单位m/s2;aH为水平加速度,单位m/s2;

通常情况下,稳定平台(或姿态)偏离角θ很小,于是水平加速度改正值可简化为:

δaH=g-a=g2θ2+aHθ,

由式(13)可得,平台偏离角(或姿态角)测量误差dθ引起水平加速度改正误差dδaH可表示为:

dδaH=(gθ+ax)dθ,

取g=9.8 m/s2,aH=0.1 m/s2,利用式(14)计算因平台姿态角测量误差引起的水平加速度改正误差(如表4)。

表4   平台测量误差对水平加速度改正的影响 (单位:10-5 m/s2)

Table 4  The influence of platform measurement Error on horizontal acceleration correction

θ
dθ		-30″-1’-2’-5’
1″-0.0235-0.0229-0.0215-0.0173
5″-0.1177-0.1143-0.1074-0.0867
10″-0.2355-0.2286-0.2148-0.1733
15″-0.3532-0.3429-0.3221-0.2600
20″-0.4710-0.4572-0.4295-0.3466

新窗口打开| 下载CSV


由表4可见,在外加水平加速度0.1 m/s2(测量时通常小于该值)时,平台测量角(或姿态角)误差为10″(角秒)所造成的水平加速度改正误差小于0.24×10-5 m/s2。

实际上平台角(或姿态角)测量误差可放宽到1’~2’(角分)[5,8],通过后处理可使其测量精度达到10″(角秒)的要求。因此,平台角(或姿态角)测量精度应好于1~2’(角分),此时水平加速度改正误差约为(0.20~0.25)×10-5 m/s2。

2.5 正常重力场改正改正误差

国际大地测量协会(IAG)1980年[9]大地测量参考系统中的正常重力场改正γ0(m/s2):

γ0=9.780327(1+5.3024×10-3sin2φ-5.9×10-6sin22φ),

其中:φ是观测点地理纬度,单位rad。

由式(15)可得到正常重力场值改正误差dγ0(m/s2):

dγ0=0.000814sin2φ̅×dd,

式中: φ̅是测区平均地理纬度,单位rad;dd是重力测点定位均方误差,单位m/s2。

目前差分GPS定位的水平定位精度好于1.0 m,由此引起的正常重力场测量误差小于0.001×10-5 m/s2,可以忽略不计。

2.6 高度改正误差

航空重力的空间(高度)改正δaF(m/s2)的计算公式为[14]:

δaF=0.3086·(1+0.0007cos2φ)(h-Δh-N)-0.72×10-7·(h-Δh-N)2,

其中:φ是观测点的地理纬度,单位rad;h是观测点的飞行高度,单位m;N是大地水准面高,单位m;Δh是大地高的偏心改正值,单位m。

由式(17)可得航空重力高度改正误差dδaF(m/s2)为:

dδaF=0.3086·(1+0.0007cos2φ̅)dh,

其中: φ̅是测区平均地理纬度,单位rad;dh是重力测点高程误差均方误差,单位m。 目前,差分GPS定位的高程定位精度远好于 0.2 m,由此引起的航空重力高度改正误差小于 0.06×10-5 m/s2。

2.7 零漂改正误差

零漂改正误差取决于重力仪零漂线性度[17],一般重力仪漂移非线性引起的改正误差约0.10×10-5 m/s2,因此,重力仪零漂改正误差约小于0.1×10-5 m/s2。

2.8 重力基点误差

停机坪处的基点重力值gb,由陆地重力仪从重力基准点联测得到[4],其测量精度一般优于0.05×10-5 m/s2,因此,航空重力测量误差可以不考虑基点引点误差的影响。

2.9 重力传感器观测误差

航空重力传感器观测值fZ来自于重力传感器的测量值。目前重力传感器有两种类型:通用的加速度计和弹簧类的重力传感器,其测量精度一般都优于0.3×10-5 m/s2,并可通过地面静态测量精度来衡量[5]。因此,航空重力传感器静态测量精度可优于0.3×10-5 m/s2。

3 航空重力仪各分项精度要求

忽略重力基点误差、正常重力场改正误差、重力仪和差分GPS的随机误差的影响[19],利用误差传递公式计算式(2)各项误差的总误差,并将前文分析的各项误差值代入计算,即获得航空重力测量精度为:

因此,要实现航空重力测量精度优于0.6×10-5 m/s2,分项技术设计指标应优于表5所示。在保证总精度指标的前提下,可以根据需要适当调配各分项精度指标。

表5   航空重力测量系统分项指标精度要求

Table 5  Precision requirements of sub-index of airborne gravity system

名称重力传感器
观测精度(静态)		载体高程
测量精度		载体位置
测量精度		载体速度
测量精度		稳定平台角(或姿
态角)测量精度		同步精度
指标优于0.3(10-5 m/s2)优于3 mm优于1 m优于0.02 m/s优于10″优于1 ms

新窗口打开| 下载CSV


4 总结

为满足新研制航空重力测量系统总体设计指标的要求,针对影响航空重力测量精度的分项指标,建立航空重力各分项误差模型,并开展了分析研究,总结归纳出航空重力测量系统所涉及的各分项指标的精度要求,为航空重力测量系统设计奠定了基础。主要成果为:

1) 建立了航空重力测量的数学模型,给出了影响航空重力测量精度的主要因素;

2) 逐一建立了航空重力各影响因素的数学模型,或使用理论模型公式,推导出各影响因素的误差计算公式。

3) 通过设定一定的分项指标,计算出各分项所产生的误差大小,分析各因素对测量结果的影响程度;

4) 总结出要实现航空重力测量精度优于0.6×10-5 m/s2各分项误差的控制范围,从而得出引起误差的各分项指标的精度要求。

总之,要想设计出高精度的航空重力测量系统,各分项指标的控制十分重要,论文研究成果一定程度上为读者开展航空重力测量系统设计提供了各项指标的分析方法和技术支撑数据,同时为十三五国家重点研发计划项目航空重力测量系统设计和研制打下坚实的理论基础。

The authors have declared that no competing interests exist.
作者已声明无竞争性利益关系。

参考文献

熊盛青 .

我国航空重磁技术现状与发展趋势

[J]. 地球物理学进展, 2009,24(1):113-117.

DOI:      URL     Magsci     [本文引用: 1]

<FONT face=Verdana>本文概要介绍了我国航空磁力测量方法技术现状,近年来测量技术与解释方法方面的最新进展.首次介绍了我国引进国外航空重力测量系统以来的最新测量技术成果.分析了我国航空物探技术与国际上先进国家的差距,并对我国航空物探的发展趋势进行了分析与预测.</FONT>

Xiong S Q .

The present situation and development of airborne gravity and magnetic survey techniques in China

[J]. Progress in Geophysics, 2009,24(1):113-117.

Magsci     [本文引用: 1]

王静波, 熊盛青, 周锡华 , 等.

航空重力测量系统研究进展

[J]. 物探与化探, 2009,33(4):368-373.

Magsci     [本文引用: 1]

<p>简要回顾了航空重力测量的发展过程，在介绍了航空重力测量基本原理的基础上，系统地叙述了航空标量重力测量系统的研发历程、研究现状及发展动态。最后，阐述了我国航空重力测量的研究现状和未来的发展方向。</p>

Wang J B, Xiong S Q, Zhou X H , et al.

The advances in the study of the airborne gravimetry system

[J]. Geophysical and Geochemical Exploration, 2009,33(4):368-373.

Magsci     [本文引用: 1]

Glennie C, Schwarz K P .

A comparison of stable platform and stapdown airborne gravity

[J]. Journal of Geodesy, 2000,( 74):383-389.

DOI:10.1007/s001900000082      URL     [本文引用: 1]

To date, operational airborne gravity results have been obtained using either a damped two-axis stable platform gravimeter system such as the LaCoste and Romberg (LCR) S-model marine gravimeter or a strapdown inertial navigation system (INS), showing comparable accuracies. In June 1998 three flight tests were undertaken which tested an LCR gravimeter and a strapdown INS gravity system side by side. To the authors' knowledge, this was the first time such a comparison flight was undertaken. The flights occurred in Disko Bay, off the west coast of Greenland. Several of the flight lines were partly flown along existing shipborne gravity profiles to allow for an independent source of comparison of the results. The results and analysis of these flight tests are presented. The measurement method and error models for both the stable platform and strapdown INS gravity systems are presented and contrasted. An intercomparison of gravity estimates from both systems is given, along with a comparison of the individual estimates with existing shipborne gravity profiles. The results of the flight tests show that the gravity estimates from the two systems agree at the 2 3 Gal level, after the removal of a linear bias. This is near the combined noise level of the two systems. It appears that a combination of both systems would provide an ideal airborne gravity survey system, combining the excellent bias stability of the LCR gravimeter with the higher dynamic range and increased spatial resolution of the strapdown INS.

Brozena J M, Peters M F .

State-of-the-art Airborne Gravimetry [A]. In Gravity and Geoid: Joint Symposium of the International Gravity Commission and the International Geoid Commission, Graz, Austria: Springer,

Berlin, 1994, ( 113):187-197.

[本文引用: 2]

Gabell A, Tuckett H, Olson D .

The GT-1A mobile gravimeter

[A]. In ASEG-PESA, Airborne Gravity 2004 Workshop, 2004: 55-61.

[本文引用: 3]

Yang N H, Arne V O, Mei P W .

SGA-WZ: A New Strapdown Airborne Gravimeter

[J]. Sensors 2012, 2012,12:9336-9348.

[本文引用: 1]

孙中苗 .

航空重力测量理论方法及应用研究

[D]. 郑州:解放军信息工程大学, 2004.

[本文引用: 5]

Sun Z M .

Theory, methods and applications of airborne gravimetry

[D]. Zhengzhou: Information Engineering University, 2004.

[本文引用: 5]

王丽红, 张传定, 王俊勤 , 等.

航空重力测量数学模型及其测量精度分析

[J]. 测绘科学技术学报, 2008,25(1):68-71.

[本文引用: 3]

Wang L H, Zhang C D, Wang J Q , et al.

Mathematical models and accuracy evaluation for the airborne gravimetry

[J]. Journal of Geomatics Science and Technology, 2008,25(1):68-71.

[本文引用: 3]

吴美平, 张开东 .

基于捷联惯导系统/差分全球定位系统的航空重力测量技术

[J]. 科技导报, 2007,25(17/239):74-80.

[本文引用: 3]

Wu M P, Zhang K D .

Technology of airborne gravimetry based on SINS/DGPS

[J]. Science & Technology Review, 2007,25(17/239):74-80.

[本文引用: 3]

熊盛青, 周锡华, 郭志宏 , 等. 航空重力勘探理论方法及应用[M]. 北京: 地质出版社, 2010.

[本文引用: 4]

Xiong S Q, Zhou X H, Guo Z H , et al.

Theory, method and application of the airborne gravity prospecting

[M]. Beijing: Geological publishing House, 2010.

[本文引用: 4]

邹欣蕾, 蔡劭琨, 吴美平 , 等.

基于经验模态分解的航空重力测量动态误差分离

[J]. 物探与化探, 2016,40(6):1217-1221.

[本文引用: 1]

Zou X L, Cai S K, Wu M P , et al.

Dynamic errors separation of airborne gravimetry based on empirical mode decomposition

[J]. Geophysical and Geochemical Exploration, 2016,40(6):1217-1221.

[本文引用: 1]

Bolotin Y V, Popelensky M Y .

Accuracy analysis of airborne gravity when gravimeter parameters are identified in flight

[J]. Journal of Mathematical Sciences, 2007,146(3):5911-5519.

[本文引用: 1]

罗锋, 郭志宏, 骆遥 , 等.

航空重力数据的等波纹FIR低通滤波试验

[J]. 物探与化探, 2012,36(5):856-860.

[本文引用: 1]

Luo F, Guo Z H, Luo Y , et al.

Experimental researches on FIR low pass filter based on equiripple

[J]. Geophysical and Geochemical Exploration, 2012,36(5):856-860.

[本文引用: 1]

郭志宏, 罗锋, 安战锋 .

航空重力数据窗函数法FIR低通数字滤波试验

[J]. 物探与化探, 2007,31(6):568-571, 576.

[本文引用: 3]

Guo Z H, Luo F, An Z F . Experimental researches on FIR low pass digital filters based on window functions of airborne gravity data, 2007,31(6):568-571, 576.

[本文引用: 3]

王静波, 熊盛青, 周锡华 , 等.

利用Kalman平滑技术估算航空重力测量中的载体垂直加速度

[J]. 地球物理学进展, 2010,25(3):968-974.

[本文引用: 1]

Wang J B, Xiong S Q, Guo Z H , et al.

Estimation of the vertical acceleration for the airborne gravimetry using Kalman smoothing

[J]. Progress in Geophysics, 2010,25(3):968-974.

[本文引用: 1]

王丽红, 张传定 .

航空矢量重力测量中科里奥利加速度对测速精度要求分析

[J]. 海洋测绘, 2008,28(2):1-4,8.

[本文引用: 1]

Wang L H, Zhang C D .

Analysing the accuracy of measuring velocity for the airborne vectror gravity survey according to coriolis acceleration

[J]. Hydrographic Surveying and Charting, 2008,28(2):1-4, 8.

[本文引用: 1]

屈进红, 郭素然, 周锡华 , 等.

相关性分析在GT航空重力仪零漂改正中的应用

[J]. 物探与化探, 2016,40(4):838-842.

[本文引用: 1]

Qu J H, Guo S R, Zhou X H , et al.

The correlation analytical method and its application to GT aerogravimeter drift correction

[J]. Geophysical and Geochemical Exploration, 2016,40(4):838-842.

[本文引用: 1]

Bar-Itzhack I Y, Berman N .

Control theoretic approach to inertial navigation systems

[J]. Journal of Guidance, 1988,11(3):237-245.

Berzhitsky V N, Iljin V N, Saveliev E B , et al.

GT-1A inertial gravimeter system design consideration and results of flight tests

[C]// In Proc.2002, 9th Saint-Petersburg Int. Conf. on Integrated Navigation Systems, Russia, St. Petersburg.

[本文引用: 1]

肖云, 夏哲仁 .

航空重力测量中载体运动加速度的确定

[J]. 地球物理学报, 2003,46(1):63-67.

Xiao Y, Xia Z R .

Determination of acceleration of carrier motion in aeronautical gravity measurement

[J]. Journal of Geophysics, 2003,46(1):63-67.

孙中苗 .

航空矢量重力测量误差模型的建立及初步分析

[J]. 测绘科技, 1998,98(4):1-7.

Sun Z M .

Establishment and preliminary analysis of error model of aeronautical vector gravity measurement

[J]. Surveying and Mapping Science and Technology, 1998,98(4):1-7.

孙中苗 .

航空重力测量精度估计

[J]. 测绘科技, 1999,46(1):29-34.

Sun Z M .

Accuracy estimation of airborne gravimetryJ]

Surveying and Mapping Science and Technology, 1999,46(1):29-34.

肖云 .

基于GPS双差相位率确定运动载体的速度和加速度

[J]. 解放军测绘研究所学报, 1999,19(1):61-64.

Xiao Y .

Determination of velocity and acceleration of moving carrier based on GPS double difference phase rate

[J]. Journal of PLA Institute of Surveying and Mapping, 1999,19(1):61-64.

/

〈 〉

京ICP备05055290号-3
版权所有 © 2021《物探与化探》编辑部
通讯地址：北京市学院路29号航遥中心 邮编：100083
电话：010-62060192；62060193 E-mail：whtbjb@sina.com