ZTEM二维非线性共轭梯度反演研究

doi:10.11720/wtyht.2019.1297

ZTEM二维非线性共轭梯度反演研究

许智博¹, 谭捍东²

1. 北华大学土木与交通学院,吉林吉林 132013

2. 中国地质大学(北京) 地球物理与信息技术学院,北京 100083

Two-dimensional nonlinear conjugate gradient inversion of ZTEM

XU Zhi-Bo¹, TAN Han-Dong²

1. Civil and Transportation College of Beihua University, Jilin 132013, China

2. School of Geophysics and Information Technology, China University of Geoscience (Beijing), Beijing 100083, China

责任编辑: 沈效群

收稿日期: 2018-08-10 修回日期: 2018-12-1 网络出版日期: 2019-04-20

基金资助:

国家重点研发计划课题“综合航空地球物理数据处理

解释和管理软件平台研发”. 2017YFC0602204

国家自然科学基金(41830429)联合资助

Received: 2018-08-10 Revised: 2018-12-1 Online: 2019-04-20

作者简介 About authors

许智博(1990-),男,硕士,助教,主要从事电法勘探、数值模拟算法研究。Email:283483358@qq.com; 。

摘要

ZTEM(Z轴倾子电磁法)是一种天然场源的频率域航空电磁法,其特点是磁场垂直分量在空中机载平台测量,磁场水平分量在地面的固定基站测量,具有勘探深度大、速度快、成本低、覆盖面积大等技术优势。本文实现了ZTEM二维有限差分正演和二维非线性共轭梯度(NLCG)反演算法。研究对象是倾子资料,反演过程中通过解“拟正演”问题来避开雅克比矩阵的直接计算。通过理论模型合成数据反演试算,验证了ZTEM倾子资料二维NLCG反演算法的稳定性与可靠性。与大地电磁(MT)TE模式阻抗资料反演结果进行对比,发现在异常体横向边界的约束方面,ZTEM倾子反演比MT阻抗反演更具优越性。

关键词： ZTEM ; 倾子 ; 航空电磁法 ; 二维反演 ; 非线性共轭梯度法

Abstract

The ZTEM (Z-Axis Tipper Electromagnetics) is a frequency-domain airborne electromagnetic method that results from natural sources. It has the feature that the vertical component of magnetic field is measured from a moving helicopter platform and the horizontal component of magnetic field is measured at a reference station on the ground. In addition, it has the advantages of deep exploration, fast speed, low cost and large coverage area. This paper realizes the 2D finite difference forward modeling and NLCG inversion of ZTEM. The object of the study is the tipper data. The direct calculation of Jacobian matrix is avoided by solving the "quasi-forward" problem in the inversion process. The stability and reliability of the 2D NLCG inversion of ZTEM tipper data are verified by the trial calculation of synthetic data inversion of theoretical model. A comparison with the inversion result of impedance data of magnetotelluric (MT) TE mode shows that the ZTEM tipper inversion is superior to the MT impedance inversion in the constraint of the lateral boundary of the anomalous body.

Keywords： Z-Axis Tipper Electromagnetics ; tipper ; airborne electromagnetic survey ; 2D inversion ; NLCG

PDF (1892KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

许智博, 谭捍东. ZTEM二维非线性共轭梯度反演研究. 物探与化探[J], 2019, 43(2): 393-400 doi:10.11720/wtyht.2019.1297

XU Zhi-Bo, TAN Han-Dong. Two-dimensional nonlinear conjugate gradient inversion of ZTEM. Geophysical and Geochemical Exploration[J], 2019, 43(2): 393-400 doi:10.11720/wtyht.2019.1297

0 引言

天然场源的大地电磁法(MT)具有较大的勘探深度,不容易受到高阻层屏蔽的影响,对低阻层反应比较灵敏,因此,MT的应用范围非常广泛,其在二维和三维资料处理和正反演研究中取得了巨大进展,其中共轭梯度法^[1,2,3]以其计算效率的突出表现而被广泛采用并取得不断发展。然而,由于采集MT数据需要很大的工作量,因此勘探的成本花费相对较大,耗时也比较长。如果能在飞机上采集MT数据是最好的,但是由于电场测量难度太大,所以这一目标还无法实现。因此,如何将天然场勘探深度大和航空测量工作效率高的特点有效地结合起来,成了人们所关注的焦点。在音频磁场(AFMAG)技术^[4,5]的基础上,国际上提出了一种新型航空电磁法—Z轴倾子电磁法(ZTEM)^[6],该方法只采集音频段(25~720 Hz)天然源磁场信号,磁场垂直分量在整个研究区域上空测量,磁场水平分量则在地面某一基站上观测。由于在空中测量磁场的垂直分量可以克服调查区域地形复杂、范围巨大的问题,而且大型调查区域的数据可以快速采集到,这样既提高了效率,也相对节省了成本。通过取两个磁场的比值,来消除未知源的影响,即使用倾子作为研究参数^[7]。另一点就是天然场源航空电磁法相比人工源航空电磁法,在勘探深度方面有着更大的优势。

目前对倾子的研究主要集中于MT方法中。吴頔^[8]对二维及三维倾子响应和异常体识别方法进行了讨论;余年^[9]基于二维Occam反演实现了二维 MT 视电阻率、相位资料与倾子资料的联合反演算法;林昌洪^[10]实现了MT倾子资料三维有限差分正演和NLCG反演算法。在过去的几年中,业内人士已经认识到ZTEM技术的潜力,但需要能够反演ZTEM倾子数据的算法。加拿大Geotech公司2009年在阿拉斯加南部的布里斯托湾地区将ZTEM应用到了实际生产工作中,并取得了很好的效果。Holtham和Oldenburg^[11,12]实现了ZTEM三维正演数值模拟和反演算法的研究;国内王涛等^[13]采用三维有限差分数值模拟算法进行了ZTEM 响应特征的研究,为 ZTEM 的反演研究奠定了较好的基础。

文中探讨了如何利用ZTEM倾子资料进行二维反演获得地下二维电阻率结构信息,建立了ZTEM倾子二维NLCG反演的目标函数,不直接计算雅克比矩阵,而是通过解多次的“拟正演”问题来实现ZTEM倾子二维NLCG反演;给出理论模型合成数据的二维反演试算结果,比较了ZTEM倾子反演相对MT阻抗反演对模型约束的效果,说明了ZTEM方法在一定背景电阻率条件下,具有对异常体恢复横向约束优于垂向的特点。

1 二维有限差分正演

1.1 ZTEM倾子响应计算公式

ZTEM倾子二维有限差分正演是基于MT二维有限差正演,唯一的区别就是磁场的垂直分量的采集位置不同。

在以z方向垂直向下的右手坐标系中,倾子矢量T的定义为^[6]

(1)

H_{z} = T_{zx} H_{x} + T_{zy} H_{y} 。

把整个地球模拟为地下半空间介质作为二维地质模型,其上方为绝缘空气层,电磁场源为在地表或地表上方z=-h处的平面电流层。在二维地下结构中,x轴正向是走向的方向,y轴与x轴是相互垂直的,保持水平,z轴垂直向下。根据麦克斯韦方程组:

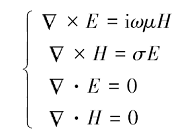
以x分量为准,将得到的两个独立方程组分为TE模式和TM模式。由于H_z只存在于TE模式中,所以式(1)可以简化为

$H_{z} = T_{zy} H_{y} 。$

其中,TE模式的数值模拟问题的基本公式为^[14]

(2)

\begin{array}{l} \frac{\partial H_{z}}{\partial y} - \frac{\partial H_{y}}{\partial z} = σ E_{x}, \end{array}

$\begin{array}{l} H_{y} = \frac{1}{i ωμ} \frac{\partial E_{x}}{\partial z}, \\ H_{z} = - \frac{1}{i ωμ} \frac{\partial E_{x}}{\partial y} 。 \end{array}$

所以,ZTEM倾子响应的计算表达式为

(3)

T_{zy} = \frac{H_{z}}{H_{y}} = - \frac{\partial E_{x}}{\partial y} / \frac{\partial E_{x}}{\partial z},

式中:H_z为空气层中的场值,H_y为地表固定一点的场值。

1.2 二维有限差分方程

文中的二维数值模拟采用有限差分法。电工学中的传输线方程为^[15]

(4)

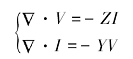
式中Z和Y分别是单位长度上的分布阻抗和分布导纳参数。

传输线方程对应的是一维问题,所以可以把这种概念推广到与二维问题相对应的情况,形成传输面的概念。对于传输面来说,方程(2)可以展成如下的形式:

$\begin{array}{l} \frac{\partial I_{y}}{\partial y} + \frac{\partial I_{z}}{\partial z} = - YV \\ \frac{\partial V}{\partial z} = - Z I_{z} \\ \frac{\partial V}{\partial y} = - Z I_{y} \end{array}$

利用能量保持守恒的条件,选择二维构造条件下大地电磁场方程式与传输面方程式进行对比,以此能够建立他们之间的对应关系。因此,TE极化模式和TM极化模式下的麦克斯韦方程组可以写成如下的统一形式:

$\begin{array}{l} \frac{\partial}{\partial y} (\frac{1}{Z} \frac{\partial V}{\partial y}) + \frac{\partial}{\partial z} (\frac{1}{Z} \frac{\partial V}{\partial z}) = YV \\ \frac{\partial V}{\partial z} = - Z I_{z} \\ \frac{\partial V}{\partial y} = - Z I_{y} \end{array}$

对于TE模式来说,V对应E_x,I_z对应H_y,I_y对应-H_z,Z对应-iωμ,Y对应σ。

由此可见,解偏微分方程其实就是二维有限差分数值模拟问题,需要给出正确的边界条件,进而得到偏微分方程的解。对于TE极化模式,文中将网格的上边界取在地表上方z=-h处,在其上H_y为常数,即电磁场源。

在确定边界条件和网格参数之后,根据麦克斯韦方程组就可以对每一个节点写出电流连续性方程:

(5)

\begin{array}{l} \sum \frac{V_{adjacent} - V_{ij}}{Z_{connecting}} + Y_{ij} V_{ij} = S_{ij}, \end{array}

$\begin{array}{l} i = 1, \dots, M; j = 1, \dots, N 。 \end{array}$

式中:i为水平网格数,j为竖直网格数,Z_connecting为相邻节点间的集总阻抗,Y_ij为所论节点对地的集总导纳,S_ij为仅在TE模式情况下在网格的顶部z=-h处存在的外加线电流源。按顺序排列每个节点上的电磁场分量,可将式(5)写成标准形式:

(6)

Kv = s 。

式中:K为对称的大型稀疏系数矩阵,v在TE模式下对应为E_x,s是与源及边界场值有关的列向量。

将求得的E_x代入式(3),就可以得到二维模型的倾子响应。因此ZTEM倾子可以表示为

(7)

T = \frac{a^{T} v}{b^{T} v},

式中:a和b为给定的向量。

1.3 正演精度的验证

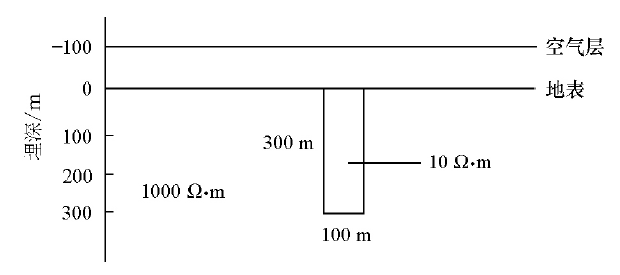
为验证ZTEM二维有限差分正演的准确性,选取一个二维地下目标体模型(图1)进行试算。目标体的几何尺寸为100 m×300 m,电阻率为10 Ω·m,上顶面位于地表,围岩电阻率为1 000 Ω·m。H_z在地表上方100 m处的空气层测量,H_y在地表固定一点测量。用ZTEM二维有限差分法计算出目标体的倾子响应,计算结果与王涛等的ZTEM三维有限差分法^[13]计算得到的数值解进行对比验证。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 二维目标体模型

Fig.1 A schematic diagram of two dimensional object model

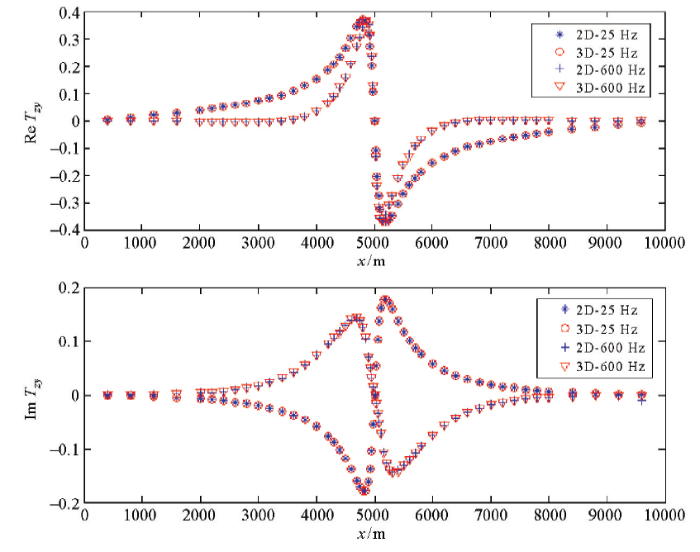
图2是两种有限差分算法在频率为25 Hz和600 Hz时计算结果的对比。由图可见,ZTEM倾子数据的实部和虚部都拟合得非常好,证明了ZTEM二维有限差分正演是准确可靠的。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 二维模型倾子响应的二维有限差分数值解与三维数值解的对比

Fig.2 The tipper response comparison between the 2D finite difference modeling results and the 3D finite difference modeling results generated from 2D model

2 二维NLCG反演

2.1 目标函数

ZTEM倾子二维NLCG反演算法的目标函数定义为

(8)

ψ (m) = [T - F {(m)]}^{T} V^{- 1} [T - F (m)] + λ m^{T} L^{T} Lm

式中:T是倾子数据的观测值;F(m)是用正演函数数值模拟得到的ZTEM倾子数据(倾子的实部或虚部);λ为正则化参数,一般是取正数;L表示二次差分拉普拉斯算子;V是误差向量e的方差。

目标函数的梯度相应可以表示为

(9)

g (m) = - 2 A {(m)}^{T} V^{- 1} [T - F (m)] + 2 λ L^{T} Lm 。

式中A表示雅可比矩阵,取e=d-F(m_ref)。

2.2 “拟正演”问题

反演问题中,最关键的部分在于求取雅可比矩阵。在计算出雅可比矩阵后,便可获得每次模型更新所需的模型修正量,实现模型的更新迭代。ZTEM倾子二维NLCG反演过程避开了实际计算和存储雅可比矩阵的每个元素,而以通过计算雅可比矩阵的转置与一个向量的乘积以及雅可比矩阵与另一个向量的乘积直接获得模型修正量,其算法流程与MT阻抗二维NLCG反演^[2]的算法流程类似。ZTEM倾子二维非线性共轭梯度反演最主要的计算量在于梯度g(m)和f=A(m_ref)p的计算。可见,想要计算出模型的修正量,迭代更新模型的参数,只需要计算出 $A (m_{ref})^{T}$ V^-¹e和A(m_ref)p的值就可以了。下面介绍ZTEM倾子二维NLCG反演如何求取这两个值。

令V^-1e=q,那么A(m_ref)^TV^-1e和eA(m_ref)p可以表示为A^Tq和Ap。方程(6)表示所有频率和TE极化模式下的麦克斯韦方程组的有限差分形式。对于向量m来说,ZTEM倾子响应的正演函数可以表示为

(10)

F (m) = \frac{a_{i} {(m)}^{T} v (m)}{b_{i} {(m)}^{T} v (m)} 。

用如下的公式表示A与正演函数的关系:

(11)

A^{ij} (m) = \partial_{j} F^{i} (m),

式中:i=1,2,…,N;代表数据的个数;j=1,2,…,M代表模型参数的个数。

把公式(10)代入公式(11),可得A的表达式:

(12)

\begin{array}{l} A^{ij} = A_{1}^{ij} + A_{2}^{ij}, \end{array}

(13)

\begin{array}{l} A^{ij} = \{{(\frac{1}{{a^{T}}_{i} v} \partial_{j} a_{i} - \frac{1}{{b^{T}}_{i} v} \partial_{j} b_{i})}^{T} v + \\ {(\frac{1}{{a^{T}}_{i} v} a_{i} - \frac{1}{{b^{T}}_{i} v} b_{i})}^{T} \partial_{j} v\} \frac{{a^{T}}_{i} v}{{b^{T}}_{i} v} 。 \end{array}

在本文中考虑到a和b的取值,方程(13)可进一步化简为

(14)

A^{ij} = \frac{{a^{T}}_{i} v}{{b^{T}}_{i} v} {(\frac{1}{{a^{T}}_{i} v} a_{i} - \frac{1}{{b^{T}}_{i} v} b_{i})}^{T} \partial_{j} v 。

取

(15)

c_{i} = \frac{{a^{T}}_{i} v}{{b^{T}}_{i} v} (\frac{1}{{a^{T}}_{i} v} a_{i} - \frac{1}{{b^{T}}_{i} v} b_{i}),

因为向量v可以使用解ZTEM倾子二维有限差分方程(6)的方法算出,本文已经确定选取TE极化模式,而且在向量v也已经算出的情况下,其中a_i和b_i也是已知给定的,那么$\partial$_ja_i和$\partial$_jb_i也就可以得出了,因此,就可以得出雅克比矩阵的表达式的第一部分 $A_{1}^{ij}$ 。但是,计算雅克比矩阵表达式的第二部分 $A_{2}^{ij}$ 相对来说是比较有难度的,下面主要讨论这一部分的计算方法。

通过ZTEM倾子正演的有限差分方程(6)能够得到:

(16)

K \partial_{j} v = \partial_{j} s - (\partial_{j} K) v, j = 1,2, \dots, M;

同样的,假设已经知道K,s和$\partial$_js,$\partial$_jK的值,如果把方程(16)中的$\partial$_jv看作方程的解向量,把$\partial$_js-($\partial$_jK)v当成是方程的右端向量,则可把方程(16)当成是一个正演模拟的有限差分方程,通过计算M次“拟正演”问题,就能够得到$\partial$_jv,然后把$\partial$_jv代入方程(14),这样就能够得到雅克比矩阵表达式的第二项 $A_{2}^{ij}$ 了。

第二种方法就是利用矩阵K的对称性还有正演问题的互换性,把方程(16)代入方程(14),能够得到:

(17)

A_{2}^{ij} = {c^{T}}_{i} K^{- 1} [\partial_{j} s - (\partial_{j} K) v],

取

(18)

K u_{i} = c_{i}, i = 1,2, \dots, N;

由于K具有对称的性质,可以将公式(17)变为

(19)

A_{2}^{ij} = {u^{T}}_{i} [\partial_{j} s - (\partial_{j} K) v] 。

在方程(18)中,假如向量u_i作为解向量,向量c_i作为方程的右端向量, 则方程(18)也可以看作是一个正演模拟的有限差分方程,通过计算N次“拟正演”问题,就能够计算出u_i,然后将u_i带回到方程(19)就能够计算出 $A_{2}^{ij}$ 。

由此可得出,计算雅可比矩阵所使用的两种传统方法会占据大量的内存空间,同时也需要大量的计算时间,这样会严重影响反演的计算效率;尤其是ZTEM倾子数据的反演往往都是要处理大量的航测数据,这就更需要计算效率的提高,否则反演计算将很难进行。

通过公式(12)可以得到:

$\begin{array}{l} Ap = A_{1} p + A_{2} p, \\ A^{T} q = {A^{T}}_{1} q + {A^{T}}_{2} q 。 \end{array}$

与之前的道理一样,假设方程的第一项基本都是已知的或者是可以计算得到的,还是主要研究方程的第二项。首先是计算Ap。从方程(14)可知:

(20)

\sum_{j} A_{2}^{ij} p^{j} = {c^{T}}_{i} t,

其中定义t为

$t = \sum_{j} p^{j} \partial_{j} v,$

通过方程(16)能够得到t:

(21)

Kt = \sum_{j} p^{j} [\partial_{j} s - (\partial_{j} K) v] 。

在方程(21)中,假如把t当成是是方程的解向量,然后把 $\sum_{j} p^{j} [\partial_{j} s - (\partial_{j} K) v]$ 当成是方程的右端向量,这样实际上方程(21)也是一个正演模拟的有限差分方程。在计算一次“拟正演”之后,就能够计算出t,然后把得到的t代入到方程(20)之中,这样 $A_{2}^{ij}$ p就能够计算得到了。

接着计算A^Tq。原理上是一样的,通过方程(19)得到:

(22)

\sum_{i} q^{i} A_{2}^{ij} = r^{T} [\partial_{j} s - (\partial_{j} K) v] 。

其中,定义r为:r= $\sum_{i}$ qⁱu_i ,通过方程(18)能够得到r:

(23)

Kr = \sum_{i} q^{i} c_{i} 。

在方程(23)中,假如把r当成是方程的解向量,然后把 $\sum_{i} q^{i} c_{i}$ 当成是方程的右端向量,这样方程(23)也是一个正演模拟的有限差分方程,在计算一次“拟正演”之后,就能够计算出r。把得到的r代入到方程(22)中,这样A^Tq就能够计算得到了。

综上所述,相比于传统的反演算法存在的计算效率低下的问题(尤其是在计算雅克比矩阵的时候),共轭梯度(NLCG)反演算法仅仅是计算2次或4次(单极化模式计算2次,双极化模式计算4次)“拟正演”问题。在TE极化模式的情况下,NLCG反演每迭代一次,正演模拟的次数为:3(3次正演)×频率的个数。如此,计算效率得到了很明显的提升,也有利于对大量的ZTEM倾子数据进行处理计算。

3 算例

基于以上的理论和公式,编程开发了ZTEM倾子数据二维NLCG反演算法。为了验证二维反演算法的正确性和稳定性,设计了两个二维地电模型。ZTEM倾子二维 NLCG反演比较依赖于初始模型的选取。当选取的初始模型的电阻率与背景电阻率相差较大时,反演的结果不是很好,只有当初始模型选取与背景电阻率值相接近的电阻率时,反演才能达到比较好的效果。所以需要预先知道背景电阻率才能得到更好的反演结果,比如通过MT阻抗的反演结果或者是钻孔资料等得到背景电阻率值,再进行反演。

3.1 模型一

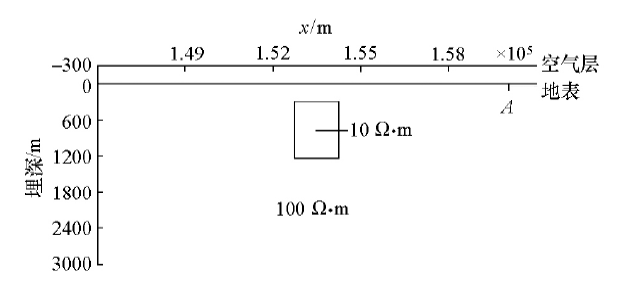
单个异常体模型如图3所示,异常体的长度为1 500 m,宽度为1 250 m,顶面距离地表350 m,异常体的电阻率为10 Ω·m,地下均匀半空间的背景电阻率为100 Ω·m。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 单个异常体模型示意

Fig.3 Schematic diagram of single abnormal body model

二维网格剖分为46×38,其中空气层的层数为10。选取5个计算频率,分别为:25 Hz、75 Hz、150 Hz、300 Hz和500 Hz。在地表上方300 m处的空气层中设置46个测点采集H_z数据,在地表的点A处固定采集H_y数据,对正演算出的ZTEM倾子数据中加入3%的高斯随机误差,对合成数据做ZTEM倾子数据的二维NLCG反演。图4是ZTEM倾子数据的拟合差收敛曲线(均方根数据拟合差,RMS misfit);图5是ZTEM倾子二维NLCG反演电阻率断面;图6是MT阻抗二维NLCG反演电阻率断面。

由图4可看出,ZTEM倾子反演迭代了9次,数据的拟合差从初始值3.2一直收敛至1.1左右趋于平稳。在将ZTEM倾子的反演结果(图5)与MT阻抗的反演结果(图6)相对比的过程中,可以发现ZTEM倾子的反演基本上能够恢复异常体的空间位置、大小和形状,但是对异常体电阻率的恢复结果要稍逊于MT阻抗反演,倾子反演的电阻率最低值在16 Ω·m左右,而阻抗反演的电阻率最低值可以达到10 Ω·m左右。然而,在异常体的横向边界的约束方面,从电阻率断面图来看,ZTEM倾子资料的反演效果都比MT阻抗的反演效果好。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 拟合差随迭代次数收敛曲线

Fig.4 Convergence Curve of RMS misfit versus iteration number

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 对单个异常体模型产生的ZTEM倾子数据进行反演的结果

Fig.5 The inversion results of ZTEM tipper data generated by a single abnormal body model

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 对单个异常体模型产生的MT阻抗数据进行反演的结果

Fig.6 The inversion results of ZTEM tipper data generated by a single abnormal body model

3.2 模型二

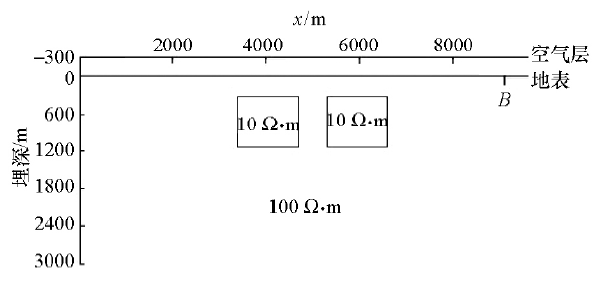
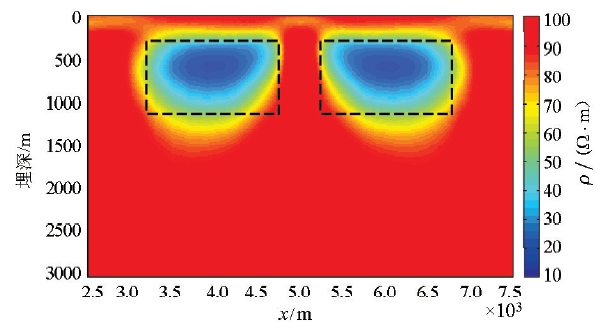
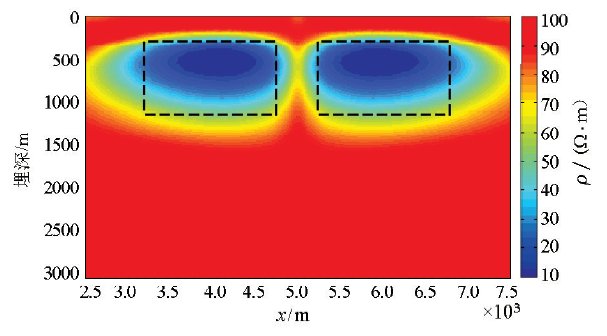
两个异常体模型如图7所示,两个异常体的长度均为1 200 m,宽度均为800 m,顶面距离地表均为300 m,异常体的电阻率均为10 Ω·m,地下均匀半空间的背景电阻率为100 Ω·m。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 两个异常体模型示意

Fig.7 Schematic diagram of two abnormal bodies model

二维网格剖分为58×51,其中空气层的层数为10。选取5个计算频率,分别为25、75、150、300、500 Hz。在地表上方300 m处的空气层中设置有58个测点采集H_z数据,在地表的点B处固定采集H_y数据,对正演算出的ZTEM倾子数据中加入3%的高斯随机误差,对合成数据做ZTEM倾子数据的二维NLCG反演。图8是ZTEM倾子数据的拟合差收敛曲线,图9是ZTEM倾子二维NLCG反演的电阻率断面,图10是MT阻抗二维NLCG反演的电阻率断面。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 拟合差随迭代次数收敛曲线

Fig.8 Convergence Curve of RMS misfit versus iteration number

图9

新窗口打开| 下载原图ZIP| 生成PPT

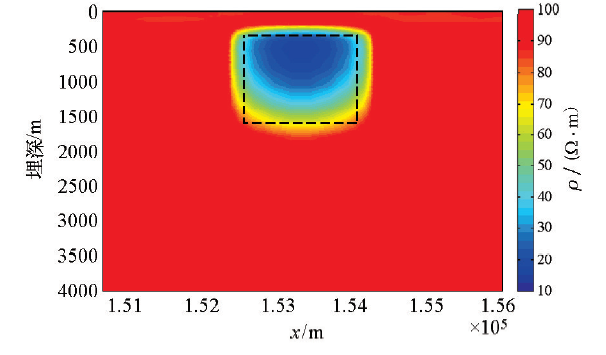
图9 对两个异常体模型产生的ZTEM倾子数据进行反演的结果

Fig.9 The inversion results of ZTEM tipper data generated by two abnormal bodies model

图10

新窗口打开| 下载原图ZIP| 生成PPT

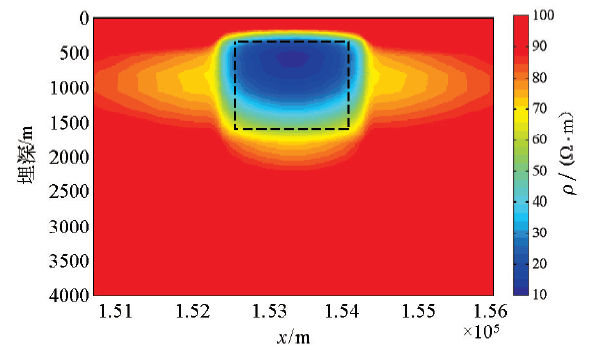
图10 对两个异常体模型产生的MT阻抗数据进行反演的结果

Fig.10 The inversion results of MT tipper data generated by two abnormal bodies model

由图8可以看出,ZTEM倾子反演迭代了14次,数据的拟合差从初始值2.8一直收敛至1.2左右趋于平稳。在将ZTEM倾子的反演结果(图9)与MT阻抗的反演结果(图10)相对比的过程中,可以发现ZTEM倾子的反演基本上能够恢复异常体的空间位置、大小和形状,但是对异常体电阻率的恢复结果要稍逊于MT阻抗反演,倾子反演的电阻率最低值在20 Ω·m左右;而阻抗反演的电阻率最低值可以达到10 Ω·m左右。然而,在异常体的横向边界的约束方面,从电阻率断面图来看,ZTEM倾子资料的反演效果都比MT阻抗的反演效果好。

4 结论

作为大地电磁测深法中的一个重要参数,倾子数据也可以进行定量解释,本文正是实现了ZTEM倾子资料的二维反演,从而获取了地下二维模型的电阻率结构。在将ZTEM倾子二维NLCG反演的结果与MT阻抗二维NLCG反演的结果进行对比时,可以发现ZTEM倾子二维NLCG反演基本上能够恢复异常体的空间位置、大小和形状,但是对异常体电阻率的恢复结果要稍逊于MT阻抗二维NLCG反演结果;在异常体横向边界的约束方面,ZTEM倾子反演比MT阻抗反演更具优越性。所以本文中的ZTEM倾子二维NLCG反演算法是可靠且稳定的。

ZTEM倾子二维 NLCG反演比较依赖于初始模型的选取。当选取的初始模型的电阻率与背景电阻率相差较大时,反演的结果不是很好;只有当初始模型选取与背景电阻率值相接近的电阻率时,反演才能达到比较好的效果。所以需要预先知道背景电阻率才能得到更好的反演结果。

The authors have declared that no competing interests exist.

作者已声明无竞争性利益关系。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Mackie R

, Madden T

Three-dimensional magnetotelluric inversion using conjugate gradients

[J]. Geophysics.J.Int., 1993,115:215-229.

DOI:10.1111/j.1365-246X.1993.tb05600.x URL [本文引用: 1]

We have developed an inversion procedure that uses conjugate gradient relaxation methods. Although one can generalize the method to all inverse problems, we demonstrate its use to invert magnetotelluric data for 3-D earth models. This procedure allows us to bypass the actual computation of the sensitivity matrix A or the inversion of the A T A term. In fact, with the relaxation approach, one only needs to compute the effect of the sensitivity matrix or its transpose multiplying an arbitrary vector. We show that each of these requires one forward problem with a distributed set of sources either in the volume (for A multiplying a vector) or on the surface (for A T multiplying a vector). This significantly reduces the computational requirements needed to do a 3-D inversion. For this paper, we have simplified the boundary conditions by assuming the model is repeated in the horizontal directions, but this is not a necessary constraint of the method. The algorithm reduces data errors to the 2 per cent level for noise-free synthetic 3-D magnetotelluric data.

[2]

Rodi

, Mackie R

Nonlinear conjugate gradients algorithm for 2-D magnetotelluric inversion

[J]. Geophysics, 2001,1(1):174-187.

[本文引用: 2]

[3]

Lin C

, Tan H

, Tong

Three-dimensional conjugate gradient inversion of magnetotelluric sounding data

[J]. Applied Geophysics (in Chinese), 2008,5(4):314-321.

DOI:10.1007/s11770-008-0043-1 URL [本文引用: 1]

基于 conjugate 坡度算法的分析，我们实现一三维(3D ) 与磁电机结合坡度倒置算法碲的阻抗数据。在倒置过程期间， 3D 结合坡度倒置算法 doesn' t 需要计算并且存储 Jacobian 矩阵但是直接从 Jacobian 矩阵的计算更新模型。每频率要求仅仅前面的和四伪 forward 建模应用在每次重复生产模型更改，这个算法高效地减少倒置的计算。从有 3D 的碲的数据，有效性和稳定性结合的合成磁电机的试用倒置，坡度倒置算法被验证。

[4]

Ward S

AFMAG—airborne and ground

[J]. Geophysics, 1959,24(4):761-787.

DOI:10.1190/1.1438657 URL [本文引用: 1]

Not Available

[5]

Ward S

, O’Donnell

, Rivera

,et al.

AFMAG-application and limitation

[J]. Geophysics, 1966,31(3):576-605.

DOI:10.1190/1.1439795 URL [本文引用: 1]

Not Available

[6]

, Zang

Numerical modeling of Z-TEM (airborne AFMAG) responses to guide exploration strategies

[C]// 78th International Exposition and Annual Meeting, SEG, Expanded Abstracts, 2008, 1098-1102.

[本文引用: 2]

[7]

Labson V

, Becker

, Morrison H

, et al.

Geophysical exploration with audiofrequency natural magnetic fields

[J]. Geophysics, 1985,50(4):656-664

DOI:10.1190/1.1441940 URL [本文引用: 1]

[8]

吴頔

二维及三维倾子响应和异常体识别

[D]. 长沙:中南大学, 2012.

[本文引用: 1]

2D and 3D tipper response and abnormal body recognition

[D]. Changsha: Central South University, 2012.

[本文引用: 1]

[9]

余年, 王绪本, 阚瑷珂 , 等.

倾子和视倾子的研究及在断裂解释中的应用

[J]. 工程地物学报, 2007,4(4):275-281.

DOI:10.3969/j.issn.1672-7940.2007.04.002 URL [本文引用: 1]

应用二维正演程序对倾斜断裂模型进行正演模拟,计算出了倾子资料,完善了视倾子的定义,由视电阻率和阻抗相位的资料直接计算求得视倾子资料特征,经对比得出了利用倾子和视倾子资料识别构造的判断依据。研究结果表明:倾子和视倾子资料对介质电阻率水平方向的不均匀性,特别是对断裂反映明显;应用质量较好的四分量观测数据计算出高频段(频率大于1Hz)的视倾子资料,可以用来判断断裂的位置、倾向和规模。并通过对一条野外四分量的观测数据进行视倾子资料的处理和解释,表明相对电阻率反演结果而言,视倾子资料对断裂构造的反映更细致、信息更丰富。

, Wang X

, Kan Y

, et al .

Research on tilter and apparent tilter and its application in fracture interpretation

[J]. Geophysical and Geochemical Exploration, 2007,4(4):275-281.

[本文引用: 1]

[10]

林昌洪, 谭捍东, 佟拓 .

倾子资料三维共轭梯度反演研究

[J]. 地球物理学报, 2011,54(4):1106-1113.

DOI:10.3969/j.issn.0001-5733.2011.04.026 URL Magsci [本文引用: 1]

在对倾子响应和共轭梯度算法深入分析的基础上,我们实现了倾子资料三维共轭梯度反演算法.基于倾子资料的三维共轭梯度反演研究,探讨了利用倾子资料进行三维反演定量解释的方法.通过对理论模型合成数据进行反演试算,验证了所实现的倾子资料三维共轭梯度反演算法的有效性和稳定性.该反演算法可用于对大地电磁测深和地磁测深(地震地磁台站进行的三分量地磁观测)所整理出的倾子资料进行三维定量反演,获得地下三维模型的电阻率结构.

Lin C

, Tan H

, Tong

3D conjugate gradient inversion of dipper data

[J]. Applied Geophysics, 2011,54(4):1106-1113.

Magsci [本文引用: 1]

[11]

Holtham

, Oldenburg D

Three-dimensional inversion of ZTEM data

[J]. Geophysical Journal International, 2010,182:168-182.

[本文引用: 1]

[12]

Holtham

, Oldenburg D

Three-dimensional inversion of MT and ZTEM data

[C]// 80th Ann Internet Mtg, SEG,Expanded Abstracts, 2010: 655-659.

[本文引用: 1]

[13]

Wang

, Tan H

, Li Z

, et al.

3D finite-difference modeling algorithm and anomaly features of ZTEM

[J]. Applied Geophysics (in Chinese), 2016,13(3):553-560.

DOI:10.1007/s11770-016-0566-9 URL [本文引用: 2]

The Z-Axis tipper electromagnetic (ZTEM) technique is based on a frequency-domain airborne electromagnetic system that measures the natural magnetic field. A survey area was divided into several blocks by using the Maxwell equations, and the magnetic components at the center of each edge of the grid cell are evaluated by applying the staggered-grid finite-difference method. The tipper and its divergence are derived to complete the 3D ZTEM forward modeling algorithm. A synthetic model is then used to compare the responses with those of 2D finite-element forward modeling to verify the accuracy of the algorithm. ZTEM offers high horizontal resolution to both simple and complex distributions of conductivity. This work is the theoretical foundation for the interpretation of ZTEM data and the study of 3D ZTEM inversion.

[14]

王绪本

二维大地电磁测深资料处理与反演解释方法研究

[D]. 成都:成都理工大学, 2002.

[本文引用: 1]

Wang X

Research on processing and inversion interpretation method of two-dimensional magnetotelluric sounding data

[D]. Chengdu:Chengdu University of Technology, 2002.

[本文引用: 1]

[15]

Madden T

Transmission systems and network analogies to geophysical forward and inverse problems

[M]. ONR Technical Report, 1972: 72-3.

[本文引用: 1]

[16]

胡文宝, 苏朱刘, 陈清礼 , 等.

倾子资料的特征及应用

[J]. 石油地球物理勘探, 1997,32(2):202-213.

URL Magsci

本文系统地研究了大地电磁测深(MT)资料中倾子多数的特征。研究结果表明:倾子异常主要反映了地电构造的水平非均匀性;倾子异常的幅值不仅与水平非均匀界面两边介质电导率的对比度有关。还与上覆层的电导率和厚度以及观测频率有关;利用倾于异常的频率特征。可以定量地解释出垂直断面的上覆层厚度。在倾子资料解释方法上,可采用图象处理中的模板相关匹配技术。以理想模型的响应为样板,对野外实测资料进行匹配。可以较准确地解释出垂直断面的位置和埋深以及电阻车的分布情况等。文中对一条测线的野外实测倾子资料进行了处理和解释,在没有参考任何其它地质信息的情况下,解释结果能很好地反映该测线的地质构造特征,分辨率和可信度均较常规解释方法要高。

Hu W

, Su Z

, Chen Q

, et al.

Characteristics and application of tilter data

[J]. Oil Geophysical Prospecting, 1997,32(2):202-213.

Magsci

[17]

陈小斌, 赵国泽, 詹艳 , 等.

磁倾子矢量的图示分析及其应用研究

[J]. 地学前缘, 2004,1(4):626-636.

DOI:10.3321/j.issn:1005-2321.2004.04.030 URL

对磁倾子矢量的图示方式进行了研究。根据平面上矢量与复数之间的关系，在原有Schmucker感应矢量定义的基础上，提出了虚感应矢量及其他图示矢量的新定义，并对其旋转特性进行了分析；根据感应矢量的旋转不变特性以及其在二维情况下的特点定义了倾子二维近似度，该参数可作为定性判别某点电性结构二维性的一种衡量标准。利用二维和三维模型对新提出的倾子图示方式进行了计算，并将其应用于海原大震区的实际资料的处理和解释当中，主要讨论了感应矢量尤其是虚感应矢量的响应特征。理论计算和实际应用结果表明本文所定义的感应矢量和倾子二维偏离度有着较为明确的物理意义，对于MT资料处理和解释有一定的指导作用。

Chen X

, Zhao G

, Zhan

, et al.

Analysis of tipper visual vectors and its application

[J]. Geoscience Frontiers, 2004,1(4):626-636.

[18]

陈清礼, 胡文宝, 李金铭 , 等.

埋藏球体的倾子响应特征分析

[J]. 石油天然气学报, 2007,29(3):75-78.

URL

倾子是大地电磁测深方法的一个重要资料,到现在为止,该资料在生产中基本上没有被使用,原因是因为垂直磁信号十分微弱。随着高温超导量子干涉磁力仪在大地电磁测深中的应用,倾子资料将发挥其应有的作用。推导出基于半空间中球体的电磁响应的解析式,计算了均匀半空间中低阻和高阻埋藏球体的倾子的平面、拟断面和频率响应,分析了其特征和规律。对认识倾子的特性和开发利用倾子具有重要的指导意义。

Chen Q

, Hu W

, Li J

, et al.

Analysis of tipper response characteristics of buried sphere

[J]. Journal of Oil and Gas Technology, 2007,29(3):75-78.

[19]

马为

MT 二维正演中辅助场计算新方法研究[R]

中国地震局地质研究所, 2007.

A new method for calculating auxiliary field in MT two-dimensional forward modeling[R].Institute of Geology,

China Earthquake Administration, 2007.

[20]

陈小斌

MT二维正演计算中地形影响的研究

[J]. 石油物探, 2000,39(3):112-120.

DOI:10.3969/j.issn.1000-1441.2000.03.015 URL

本文以有限元直接迭代算法为基础,首先给出了各种基本地表条件下的有限元迭代格式和复杂地表条件下视电阻率的定义.在此算法的基础上,通过2个简单的算例讨论了地形起伏对MT视电阻率和相位的影响,证实了复杂地表下2种极化模式的MT观测资料都有明显的异常,并且以TM模式尤为严重.文中总结了一些地形起伏对MT资料的影响情况,同时分析了MT视电阻率异常的成因,提出了一些自己的观点.

Chen X

Research on terrain effect in MT two-dimensional forward modeling

[J]. Oil Exploration, 2000,39(3):112-120.

Three-dimensional magnetotelluric inversion using conjugate gradients

1993

... 天然场源的大地电磁法(MT)具有较大的勘探深度,不容易受到高阻层屏蔽的影响,对低阻层反应比较灵敏,因此,MT的应用范围非常广泛,其在二维和三维资料处理和正反演研究中取得了巨大进展,其中共轭梯度法^[1,2,3]以其计算效率的突出表现而被广泛采用并取得不断发展.然而,由于采集MT数据需要很大的工作量,因此勘探的成本花费相对较大,耗时也比较长.如果能在飞机上采集MT数据是最好的,但是由于电场测量难度太大,所以这一目标还无法实现.因此,如何将天然场勘探深度大和航空测量工作效率高的特点有效地结合起来,成了人们所关注的焦点.在音频磁场(AFMAG)技术^[4,5]的基础上,国际上提出了一种新型航空电磁法—Z轴倾子电磁法(ZTEM)^[6],该方法只采集音频段(25~720 Hz)天然源磁场信号,磁场垂直分量在整个研究区域上空测量,磁场水平分量则在地面某一基站上观测.由于在空中测量磁场的垂直分量可以克服调查区域地形复杂、范围巨大的问题,而且大型调查区域的数据可以快速采集到,这样既提高了效率,也相对节省了成本.通过取两个磁场的比值,来消除未知源的影响,即使用倾子作为研究参数^[7].另一点就是天然场源航空电磁法相比人工源航空电磁法,在勘探深度方面有着更大的优势. ...

Nonlinear conjugate gradients algorithm for 2-D magnetotelluric inversion

2001

... 反演问题中,最关键的部分在于求取雅可比矩阵.在计算出雅可比矩阵后,便可获得每次模型更新所需的模型修正量,实现模型的更新迭代.ZTEM倾子二维NLCG反演过程避开了实际计算和存储雅可比矩阵的每个元素,而以通过计算雅可比矩阵的转置与一个向量的乘积以及雅可比矩阵与另一个向量的乘积直接获得模型修正量,其算法流程与MT阻抗二维NLCG反演^[2]的算法流程类似.ZTEM倾子二维非线性共轭梯度反演最主要的计算量在于梯度g(m)和f=A(m_ref)p的计算.可见,想要计算出模型的修正量,迭代更新模型的参数,只需要计算出

A (m_{ref})^{T}

V^-¹e和A(m_ref)p的值就可以了.下面介绍ZTEM倾子二维NLCG反演如何求取这两个值. ...

Three-dimensional conjugate gradient inversion of magnetotelluric sounding data

2008

AFMAG—airborne and ground

1959

AFMAG-application and limitation

1966

Numerical modeling of Z-TEM (airborne AFMAG) responses to guide exploration strategies

2008

... 在以z方向垂直向下的右手坐标系中,倾子矢量T的定义为^[6] ...

Geophysical exploration with audiofrequency natural magnetic fields

1985

二维及三维倾子响应和异常体识别

2012

... 目前对倾子的研究主要集中于MT方法中.吴頔^[8]对二维及三维倾子响应和异常体识别方法进行了讨论;余年^[9]基于二维Occam反演实现了二维 MT 视电阻率、相位资料与倾子资料的联合反演算法;林昌洪^[10]实现了MT倾子资料三维有限差分正演和NLCG反演算法.在过去的几年中,业内人士已经认识到ZTEM技术的潜力,但需要能够反演ZTEM倾子数据的算法.加拿大Geotech公司2009年在阿拉斯加南部的布里斯托湾地区将ZTEM应用到了实际生产工作中,并取得了很好的效果.Holtham和Oldenburg^[11,12]实现了ZTEM三维正演数值模拟和反演算法的研究;国内王涛等^[13]采用三维有限差分数值模拟算法进行了ZTEM 响应特征的研究,为 ZTEM 的反演研究奠定了较好的基础. ...

二维及三维倾子响应和异常体识别

2012

倾子和视倾子的研究及在断裂解释中的应用

2007

倾子和视倾子的研究及在断裂解释中的应用

2007

倾子资料三维共轭梯度反演研究

2011

倾子资料三维共轭梯度反演研究

2011

Three-dimensional inversion of ZTEM data

2010

Three-dimensional inversion of MT and ZTEM data

2010

3D finite-difference modeling algorithm and anomaly features of ZTEM

2016

... 为验证ZTEM二维有限差分正演的准确性,选取一个二维地下目标体模型(图1)进行试算.目标体的几何尺寸为100 m×300 m,电阻率为10 Ω·m,上顶面位于地表,围岩电阻率为1 000 Ω·m.H_z在地表上方100 m处的空气层测量,H_y在地表固定一点测量.用ZTEM二维有限差分法计算出目标体的倾子响应,计算结果与王涛等的ZTEM三维有限差分法^[13]计算得到的数值解进行对比验证. ...

二维大地电磁测深资料处理与反演解释方法研究

2002

... 其中,TE模式的数值模拟问题的基本公式为^[14] ...

二维大地电磁测深资料处理与反演解释方法研究

2002

... 其中,TE模式的数值模拟问题的基本公式为^[14] ...

Transmission systems and network analogies to geophysical forward and inverse problems

1972

... 文中的二维数值模拟采用有限差分法.电工学中的传输线方程为^[15] ...

倾子资料的特征及应用

1997

倾子资料的特征及应用

1997

磁倾子矢量的图示分析及其应用研究

2004

磁倾子矢量的图示分析及其应用研究

2004

埋藏球体的倾子响应特征分析

2007

埋藏球体的倾子响应特征分析

2007

MT 二维正演中辅助场计算新方法研究[R]

2007

MT 二维正演中辅助场计算新方法研究[R]

2007

MT二维正演计算中地形影响的研究

2000

MT二维正演计算中地形影响的研究

2000

〈

〉