|
|
|
| Estimation of pre-stack Q-values in the radial trace transform domain |
TANG Chuan-Zhang1( ), WANG Jin-Kuan1, WEI Tao1, HUANG Xin-Ya1, CHENG Wan-Li2,3,4, WANG Shou-Dong2,3, LI Ying2,3 ), WANG Jin-Kuan1, WEI Tao1, HUANG Xin-Ya1, CHENG Wan-Li2,3,4, WANG Shou-Dong2,3, LI Ying2,3 |
1. Huabei Oilfield Company, PetroChina, Renqiu 062552, China
2. College of Geophysics, China University of Petroleum(Beijing), Beijing 102249, China
3. State Key Laboratory of Petroleum Resources and Engineering, China University of Petroleum(Beijing), Beijing 102249, China
4. CNOOC(China) Limited Hainan Branch, Haikou 570100, China |
|
|
|
|
Abstract Accurate estimation of the quality factor(Q) is essential for enhancing seismic data resolution and reservoir characterization.Conventional Q estimation methods generally utilize post-stack data, which neglect the impacts of raypaths.Moreover,the average effect of stacking alters the attenuation of seismic data,reducing the accuracy of Q estimation.Compared to post-stack data,the pre-stack data more faithfully preserve the attenuation properties of subsurface media,enabling more accurate Q estimation.Therefore,this study converted pre-stack data into the apparent velocity and travel time(R-T) domain,using the radial trace(RT) transform.Combined with the logarithmic spectral area double difference(LSADD) method,a pre-stack Q estimation method named QVAV_LSADD was proposed.This method accounted for the impacts of raypaths under imprecise interval velocities.Its high accuracy and strong noise resistance were validated through the processing of both synthetic and real data.
|
|
Received: 15 June 2025
Published: 30 December 2025
|
|
|
|
|
|

|
The three-layer model with parameters
|

|
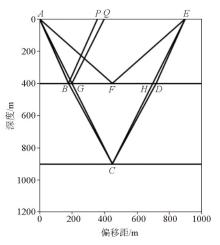
A synthetic CMP gather in the X-T domain(a) and transformed into the R-T domain(b)
Points A and B on the radial ray(red line) of the X-T domain are maps of points C and D on the same apparent velocity(1 000 m/s) of the R-T domain
|
|
Q-value estimation diagram in RT transform domain
|

|
The five-layer model with parameters
|

|
A synthetic CMP gather in the X-T domain(a) and transformed into the R-T domain(b)
|

|
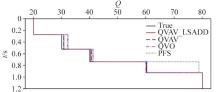
Variation curves of Q values with offset estimated by different methods(LSADD, LSR, and PFS) for different layers
|
|
Comparison of Q values estimated by different methods from the CMP gather
|

|
A field CMP gather in the (a) X-T domain and (b) transformed into the R-T domain
|

|
Estimated interval-Q and average-Q using the QVAV_LSADD method(a) and QVAV method(b)
|
| [1] |
Tonn R. The determination of the seismic quality factor Q from vsp data:A comparison of different computational methods[J]. Geophysical Prospecting, 1991, 39(1):1-27.
|
| [2] |
王本锋, 陈小宏, 李景叶, 等. 基于反演的稳定高效衰减补偿方法[J]. 地球物理学报, 2014, 57(4):1265-1274.
|
| [2] |
Wang B F, Chen X H, Li J Y, et al. A stable and efficient attenuation compensation method based on inversion[J]. Chinese Journal of Geophysics, 2014, 57(4):1265-1274.
|
| [3] |
刘国昌, 陈小宏, 杜婧, 等. 基于整形正则化和S变换的Q值估计方法[J]. 石油地球物理勘探, 2011, 46(3):417-422,500,327.
|
| [3] |
Liu G C, Chen X H, Du J, et al. Seismic Q estimation using S-transform with regularized inversion[J]. Oil Geophysical Prospecting, 2011, 46(3):417-422,500,327.
|
| [4] |
Luo C, Huang G T, Li X Y, et al. Q estimation by combining ISD with LSR method based on shaping-regularized inversion[J]. IEEE Geoscience and Remote Sensing Letters, 2019, 16(9):1457-1461.
|
| [5] |
Cheng W L, Wang S D, Zhou C, et al. Q estimation based on the logarithmic spectral area double difference[J]. Geophysics, 2022, 87(2):V155-V167.
|
| [6] |
Dasgupta R, Clark R A. Estimation of Q from surface seismic reflection data[J]. Geophysics, 1998, 63(6):2120-2128.
|
| [7] |
Reine C, Clark R, van der Baan M. Robust prestack Q-determination using surface seismic data:Part 1—Method and synthetic examples[J]. Geophysics, 2012, 77(1):R45-R56.
|
| [8] |
Reine C, Clark R, van der Baan M. Robust prestack Q-determination using surface seismic data:Part 2—3D case study[J]. Geophysics, 2012, 77(1):B1-B10.
|
| [9] |
Hackert C L, Parra J O. Improving Q estimates from seismic reflection data using well-log-based localized spectral correction[J]. Geophysics, 2004, 69(6):1521-1529.
|
| [10] |
Zheng J J, Wang Y G, Liu H J, et al. The stratum Q estimated by instantaneous seismic wavelets in prestack domain[C]//Houston: SEG Technical Program Expanded Abstracts 2017, Society of Exploration Geophysicists, 2017:3325-3329.
|
| [11] |
Wu Z W, Wu Y J, Xu M H, et al. Q estimation on CMP gather based on continuous spectral ratio slope method:A Case study in Ahdeb Oil Field,Iraq[C]// Anaheim:SEG Technical Program Expanded Abstracts 2018, Society of Exploration Geophysicists, 2018:1544-1548.
|
| [12] |
Zhang C J, Ulrych T J. Estimation of quality factors from CMP records[J]. Geophysics, 2002, 67(5):1542-1547.
|
| [13] |
Behura J, Tsvankin I. Estimation of interval anisotropic attenuation from reflection data[J]. Geophysics, 2009, 74(6):A69-A74.
|
| [14] |
Beckwith J, Clark R, Hodgson L. Estimating frequency-dependent attenuation quality factor values from prestack surface seismic data[J]. Geophysics, 2017, 82(1):O11-O22.
|
| [15] |
De S Oliveira F, de Figueiredo J J S, Oliveira A G, et al. Estimation of quality factor based on peak frequency-shift method and redatuming operator:Application in real data set[J]. Geophysics, 2017, 82(1):N1-N12.
|
| [16] |
Claerbout J F. Slant-stacks and radial traces[J]. Stanford Exploration Project, 1975:1-12.
|
| [17] |
Claerbout J F. Ground roll and radial traces[J]. Stanford Exploration Project, 1983:43-53.
|
| [18] |
Li F, Wang S D, Chen X H, et al. Prestack nonstationary deconvolution based on variable-step sampling in the radial trace domain[J]. Applied Geophysics, 2013, 10(4):423-432.
|
|
|
|

