|
|
|
| A method for identifying anomalous values of groundwater levels at candidate sites for the geological disposal of high-level radioactive waste |
JI Zi-Jian1,2( ), Zhou Zhi-Chao1,2, Zhao Jing-Bo1,2, JI Rui-Li1,2, ZHANG Ming1,2 ), Zhou Zhi-Chao1,2, Zhao Jing-Bo1,2, JI Rui-Li1,2, ZHANG Ming1,2 |
1. Division of Environmental Engineering, Beijing Research Institute of Uranium Geology, Beijing 100029, China
2. CAEA Innovation Center for Geological Disposal of High-Level Radioactive Waste, Beijing 100029, China |
|
|
|
|
Abstract Dynamic groundwater monitoring provides critical foundational data for the safety assessment of candidate sites for the geological disposal of high-level radioactive waste. However, research has revealed that actual monitoring data frequently contain numerous anomalous values, severely interfering with the accurate assessment of the dynamic monitoring process. Therefore, there is an urgent need to develop an efficient method to accurately identify these anomalous values. This study built a combined model for anomalous value detection of the groundwater level using local weighted regression-based time series decomposition and the minimum covariance determinant (MCD) method. This combined model allowed the MCD method to achieve anomaly detection in more independent residuals. Results indicate that the combined model exhibited higher sensitivity and detection accuracy for anomalous data than the single MCD model. Furthermore, this study established that the threshold of the combined model should be close to the actual proportion of anomalous values to achieve optimal detection results. Besides, this study validated the applicability of the combined model using groundwater level data from boreholes BSQ01, BSQ25, BS35, and BS26 at the new site. The validation results demonstrate that the combined model can accurately identify anomalous values amidst a large volume of data on the normal groundwater level and is applicable to the detection of different types of anomalous events.
|
|
Received: 21 December 2023
Published: 08 January 2025
|
|
|
|
|
|
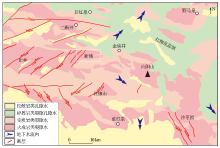
|
Hydrogeological map of the Xinchang site
|
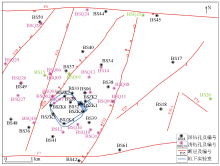
|
Location map of monitoring boreholes around the Xinchang site
|
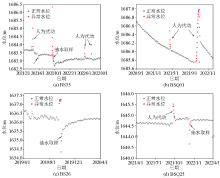
|
Distribution of groundwater level monitoring data and anomaly values in boreholes
|
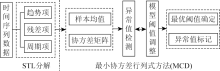
|
Anomaly detection process for the combined STL decomposition and minimum covariance determinant method
|
|
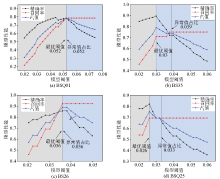
Map of model performance with model thresholds
|

|
Combined model and single model detection results in borehole BS35
|

|
Combined model and single model detection results in borehole BS26
|

|
Combined model and single model detection results in borehole BSQ01
|

|
Combined model and single model detection results in borehole BSQ25
|

| 钻孔号 | 单一模型 | 组合模型 | | 精确率 | 召回率 | F1值 | 精确率 | 召回率 | F1值 | | BS26 | 0.71 | 0.76 | 0.74 | 0.85 | 0.92 | 0.88 | | BS35 | 0.11 | 0.08 | 0.09 | 0.89 | 0.71 | 0.79 | | BSQ01 | 0.50 | 0.50 | 0.50 | 0.78 | 0.64 | 0.71 | | BSQ25 | 0.64 | 0.54 | 0.58 | 0.82 | 0.69 | 0.75 |
|
Evaluation index score for groundwater level anomaly detection in boreholes around the site
|
| [1] |
郭永海, 王驹, 金远新. 世界高放废物地质处置库选址研究概况及国内进展[J]. 地学前缘, 2001, 8(2):327-332.
|
| [1] |
Guo Y H, Wang J, Jin Y X. The general situation of geological disposal repository siting in the world and research progress in China[J]. Earth Science Frontiers, 2001, 8(2):327-332.
|
| [2] |
Wang J, Chen L, Su R, et al. The Beishan underground research laboratory for geological disposal of high-level radioactive waste in China:Planning,site selection,site characterization and in situ tests[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2018, 10(3):411-435.
|
| [3] |
Calderwood A J, Pauloo R A, Yoder A M, et al. Low-cost,open source wireless sensor network for real-time,scalable groundwater monitoring[J]. Water, 2020, 12(4):1066.
|
| [4] |
Drage J, Kennedy G. Building a low-cost,internet-of-things,real-time groundwater level monitoring network[J]. Groundwater Monitoring & Remediation, 2020, 40(4):67-73.
|
| [5] |
Muharemi F, Logofătu D, Leon F. Machine learning approaches for anomaly detection of water quality on a real-world data set[J]. Journal of Information and Telecommunication, 2019, 3(3):294-307.
|
| [6] |
Pang G S, Shen C H, Cao L B, et al. Deep learning for anomaly detection:A review[J]. ACM Computing Surveys, 2021, 54(2):1-38.
|
| [7] |
Schmidl S, Wenig P, Papenbrock T. Anomaly detection in time series:A comprehensive evaluation[J]. Proceedings of the VLDB Endowment, 2022, 15(9):1779-1797.
|
| [8] |
Rousseeuw P J, Hubert M. Anomaly detection by robust statistics[J]. WIREs Data Mining and Knowledge Discovery, 2018, 8(2):e1236.
|
| [9] |
Yu Y, Zhu Y L, Li S J, et al. Time series outlier detection based on sliding window prediction[J]. Mathematical Problems in Engineering, 2014:1-14.
|
| [10] |
Kulanuwat L, Chantrapornchai C, Maleewong M, et al. Anomaly detection using a sliding window technique and data imputation with machine learning for hydrological time series[J]. Water, 2021, 13(13):1862.
|
| [11] |
Cabana E, Lillo R E, Laniado H. Multivariate outlier detection based on a robust Mahalanobis distance with shrinkage estimators[J]. Statistical Papers, 2021, 62(4):1583-1609.
|
| [12] |
Sripriya T P, Srinivasan M R, Gallo M. Robust distance measure to detect outliers for categorical data[J]. Soft Computing, 2020, 24(18):13557-13564.
|
| [13] |
Li J B, Izakian H, Pedrycz W, et al. Clustering-based anomaly detection in multivariate time series data[J]. Applied Soft Computing, 2021, 100:106919.
|
| [14] |
Smiti A. A critical overview of outlier detection methods[J]. Computer Science Review, 2020, 38:100306.
|
| [15] |
何黎, 陈磊, 纪莎莎, 等. 基于K-shape聚类的连续液位监测数据异常检测方法[J]. 中国给水排水, 2023, 39(11):56-61.
|
| [15] |
He L, Chen L, Ji S S, et al. Abnormal detection of continuous water level monitoring data based on K-shape clustering[J]. China Water & Wastewater, 2023, 39(11):56-61.
|
| [16] |
Shi H X, Guo J, Deng Y D, et al. Machine learning-based anomaly detection of groundwater microdynamics:Case study of Chengdu,China[J]. Scientific Reports, 2023, 13(1):14718.
|
| [17] |
Ayadi A, Ghorbel O, Obeid A M, et al. Outlier detection approaches for wireless sensor networks:A survey[J]. Computer Networks, 2017, 129(1):319-333.
|
| [18] |
Sunderland K M, Beaton D, Fraser J, et al. The utility of multivariate outlier detection techniques for data quality evaluation in large studies:An application within the ONDRI project[J]. BMC Medical Research Methodology, 2019, 19:102.
|
| [19] |
Hardin J, Rocke D M. Outlier detection in the multiple cluster setting using the minimum covariance determinant estimator[J]. Computational Statistics & Data Analysis, 2004, 44(4):625-638.
|
| [20] |
Hubert M, Debruyne M, Rousseeuw P J. Minimum covariance determinant and extensions[J]. WIREs Computational Statistics, 2018, 10(3):e1421.
|
| [21] |
孙杰. 基于FAST-MCD算法的异常成绩检测研究[J]. 现代计算机, 2021, 27(29):59-62.
|
| [21] |
Sun J. Research on the abnormal grade detection based on the FAST-MCD algorithm[J]. Modern Computer, 2021, 27(29):59-62.
|
| [22] |
Zhou Y J, Ren H R, Li Z W, et al. Anomaly detection via a combination model in time series data[J]. Applied Intelligence, 2021, 51(7):4874-4887.
|
| [23] |
Lin S, Clark R, Birke R, et al. Anomaly detection for time series using VAE-LSTM hybrid model[C]// ICASSP 2020-2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP),2020:4322-4326.
|
| [24] |
Yokkampon U, Chumkamon S, Mowshowitz A, et al. Anomaly detection using variational autoencoder with spectrum analysis for time series data[C]// 2020 Joint 9th International Conference on Informatics,Electronics & Vision (ICIEV) and 2020 4th International Conference on Imaging,Vision & Pattern Recognition (icIVPR), 2020:1-6.
|
| [25] |
Lyu J M, Wang Y Q, Chen S J. Adaptive multivariate time-series anomaly detection[J]. Information Processing & Management, 2023, 60(4):103383.
|
| [26] |
Samariya D, Thakkar A. A comprehensive survey of anomaly detection algorithms[J]. Annals of Data Science, 2023, 10(3):829-850.
|
| [27] |
Cleveland R B, Cleveland W S. STL:A seasonal-trend decomposition procedure based on Loess[J]. Journal of official statistics, 1990, 6(1):3-73.
|
| [28] |
Rousseeuw P J, Driessen K V. A fast algorithm for the minimum covariance determinant estimator[J]. Technometrics, 1999, 41(3):212-223.
|
| [29] |
Li J B, Zhang Y K, Zhou Z C, et al. Using multiple isotopes to determine groundwater source,age,and renewal rate in the Beishan preselected area for geological disposal of high-level radioactive waste in China[J]. Journal of Hydrology, 2024, 629:130592.
|
| [30] |
Hubert M, Debruyne M. Minimum covariance determinant[J]. WIREs Computational Statistics, 2010, 2(1):36-43.
|
| [31] |
Rousseeuw P J, Hubert M. Robust statistics for outlier detection[J]. WIREs Data Mining and Knowledge Discovery, 2011, 1(1):73-79.
|
| [32] |
李航. 统计学习方法[M]. 北京: 清华大学出版社, 2012.
|
| [32] |
Li H. Statistical learning methodology[M]. Beijing: Tsinghua University Press, 2012.
|
| [1] |
WANG Ju, LUN Long. Definition, classification, and functions of underground research laboratories for the geological disposal of high-level radioactive waste and the scientific research plan of Beishan underground research laboratory[J]. Geophysical and Geochemical Exploration, 2024, 48(6): 1507-1518. |
| [2] |
YUN Long, CHEN Su, FU Lei, ZHUANG Hai-Yang, WANG Ju. Seismic response characteristics of the cavern group of the Beishan underground research laboratory for the geological disposal of high-level radioactive waste[J]. Geophysical and Geochemical Exploration, 2024, 48(6): 1519-1529. |
|
|
|
|

