|
|
|
| Forward modeling and wave field analysis of seismic surface waves and guided P-waves |
LIU Tong( ), SUN Cheng-Yu, CAI Rui-Qian ), SUN Cheng-Yu, CAI Rui-Qian |
| School of Geosciences,China University of Petroleum(East China),Qingdao 266580,China |
|
|
|
|
Abstract Surface waves and guided P-waves,as two boundary-related wave phenomena,are a crucial part of the near-surface seismic wave field.This study investigated their generation mechanism and propagation regularity using the high-order staggered-grid finite-difference algorithm.First,it solved the problems like numerical dispersion and boundary conditions in numerical simulation.Based on this,it designed medium models under different thicknesses and elastic parameters for forward modeling.Furthermore,it extracted dispersion profiles and amplitude versus offset curves for analysis.In the case of a low-velocity thin layer on the surface,guided P-waves can be generated when the phase velocities of P and SV waves from the same source exceed the S-wave velocity but are less than the P-wave velocity of the underlying high-velocity layer.In media with high Poisson's ratios(>0.4),the phase velocities of surface waves and guided P-waves are sensitive to the S- and P-wave velocities,respectively.Surface waves and guided P-waves usually contain near-surface information that is unavailable in refracted and reflected waves.The appropriate acquisition,analysis,and inversion of near-surface information enable the establishment of a high-resolution near-surface model.This study generalized the generation conditions and wave field characteristics of surface waves and guided P-waves under the same source and deepened the understanding of their propagation regularity,laying a foundation for inversion and denoising research.
|
|
Received: 23 October 2023
Published: 19 September 2024
|
|
|
|
|
|
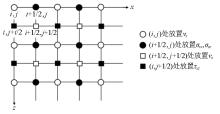
|
Diagram of stagger-grid difference
|
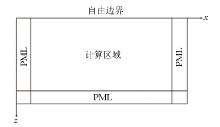
|
Diagram of model setting
|

|
Wave field snapshot
a—wave field snapshot with free boundary;b—wave field snapshot without free boundary
|
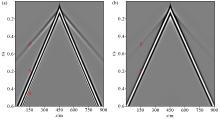
|
Seismic record
a—surface seismic records with free boundary;b—surface seismic records without free boundary
|
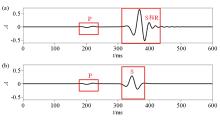
|
Comparison of single-channel seismic records
a—230th seismic record with free boundary;b—230th seismic record without free boundary
|

|
Elastic wave forward modeling record
a—seismic record(horizontal component);b—seismic record(vertical component);c—150 ms wave field snapshot
|

|
Analysis results of forward record
a—the particle motion trajectory of surface wave;b—curve of surface wave amplitude changing with offset;c—dispersion imaging
|

| 模型 | 层序 | 层厚/m | vp/
(m·s-1) | vs/
(m·s-1) | ρ/
(kg·m-3) | 泊松比 | | 1 | 1 | 10 | 1100 | 330 | 1600 | 0.45 | | 2 | ∞ | 1800 | 540 | 2000 | | 2 | 1 | 20 | 1100 | 330 | 1600 | 0.45 | | 2 | ∞ | 1800 | 540 | 2000 | | 3 | 1 | 40 | 1100 | 330 | 1600 | 0.45 | | 2 | ∞ | 1800 | 540 | 2000 | | 4 | 1 | 10 | 1100 | 450 | 1600 | 0.40 | | 2 | ∞ | 1800 | 730 | 2000 | | 5 | 1 | 10 | 1100 | 490 | 1600 | 0.30 | | 2 | ∞ | 1800 | 960 | 2000 |
|
Elastic parameters of model
|

|
Model 1 seismic record(a) and dispersion relation(b)
|

|
Model 2 seismic record(a) and dispersion relation(b)
|

|
Model 3 seismic record(a) and dispersion relation(b)
|

|
Model 4 seismic record(a) and dispersion relation(b)
|

|
Model 5 seismic record(a) and dispersion relation(b)
|
fig.8a;b—amplitude curves extracted from seismic records in fig.9a
">

|
Curve of amplitude changing with offset
a—amplitude curves extracted from seismic records in fig.8a;b—amplitude curves extracted from seismic records in fig.9a
|

| 2N | C0 | C1 | C2 | C3 | C4 | | 2 | 0 | 5.0000000×10-1 | | | | | 4 | 0 | 6.6666667×10-1 | -8.3333333×10-2 | | | | 6 | 0 | 7.5000000×10-1 | -1.5000000×10-1 | 1.6666667×10-2 | | | 8 | 0 | 8.0000000×10-1 | -2.0000000×10-1 | 3.8095238×10-2 | -3.5414286×10-3 |
|
The first derivative corresponds to the weight coefficient values of different order accuracies
|
| [1] |
Roth M, Holliger K, Green A G. Guided waves in near-surface seismic surveys[J]. Geophysical Research Letters, 1998, 25(7):1071-1074.
|
| [2] |
吴华, 李庆春, 邵广周. 瑞利波波形反演的发展现状及展望[J]. 物探与化探, 2018, 42(6):1103-1111.
|
| [2] |
Wu H, Li Q C, Shao G Z. Development status and prospect of Rayleigh waveform inversion[J]. Geophysical and Geochemical Exploration, 2018, 42(6):1103-1111.
|
| [3] |
Sun C Y, Wang Z N, Wu D S, et al. A unified description of surface waves and guided waves with relative amplitude dispersion maps[J]. Geophysical Journal International, 2021, 227(3):1480-1495.
|
| [4] |
Wang Z J, Xiao J Y, Li D, et al. Full waveform inversion guided wave tomography with a recurrent neural network[J]. Ultrasonics, 2023, 133:107043.
|
| [5] |
Rayleigh L. On waves propagated along the plane surface of an elastic solid[J]. Proceedings of the London Mathematical Society, 1885,s1- 17(1):4-11.
|
| [6] |
Leslie D M, Evans B. The cause and effects of multilayer-generated guided-waves[J]. Exploration Geophysics, 2000, 31(4):543-551.
|
| [7] |
Alterman Z S, Karal F C J. Propagation of elastic waves in layered media by finite difference methods[J]. The Bulletin of the Seismological Society of America, 1969, 59(1):471.
|
| [8] |
Boore D. Finite difference methods for seismic wave propagation in heterogeneous materials[M]// Methods in computational physics: Advances in Research and Applications. Amsterdam:Elsevier, 1972:1-37.
|
| [9] |
Madariaga R. Dynamics of an expanding circular fault[J]. The Bulletin of the Seismological Society of America, 1976, 66(3):639-666.
|
| [10] |
Jean V. SH-wave propagation in heterogeneous media:Velocity-stress finite-difference method[J]. Geophysics, 1984, 49(11):1933.
|
| [11] |
Jean V. P-SV wave propagation in heterogeneous media:Velocity-stress finite-difference method[J]. Geophysics, 1986, 51(4):889-901.
|
| [12] |
Levander A R. Fourth-order finite-difference P-SV seismograms[J]. Geophysics, 1988, 53(11):1425.
|
| [13] |
董良国, 马在田, 曹景忠, 等. 一阶弹性波方程交错网格高阶差分解法[J]. 地球物理学报, 2000, 43(3):411-419.
|
| [13] |
Dong L G, Ma Z T, Cao J Z, et al. A staggered-grid high-order difference method of one-order elastic wave equation[J]. Chinese Journal of Geophysics, 2000, 43(3):411-419.
|
| [14] |
Collino F, Tsogka C. Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media[J]. Geophysics, 2001, 66(1):294.
|
| [15] |
张伟, 甘伏平, 刘伟, 等. 双相介质瑞雷面波有限差分正演模拟[J]. 物探与化探, 2014, 38(6):1275-1283.
|
| [15] |
Zhang W, Gan F P, Liu W, et al. Rayleigh surface wave modeling by finite difference method in biphasic media[J]. Geophysical and Geochemical Exploration, 2014, 38(6):1275-1283.
|
| [16] |
廉西猛, 张睿璇. 基于GPU集群的大规模三维有限差分正演模拟并行策略[J]. 物探与化探, 2015, 39(3):615-620.
|
| [16] |
Lian X M, Zhang R X. Parallel strategy of large-scale 3D seismic forward by finite difference method on GPU cluster[J]. Geophysical and Geochemical Exploration, 2015, 39(3):615-620.
|
| [17] |
彭更新, 刘威, 郭念民, 等. 基于时空域交错网格有限差分法的应力速度声波方程数值模拟[J]. 石油物探, 2022, 61(1):156-165,173.
|
| [17] |
Peng G X, Liu W, Guo N M, et al. A time-space domain dispersion-relationship-based staggered-grid finite-difference scheme for modeling the stress-velocity acoustic wave equation[J]. Geophysical Prospecting for Petroleum, 2022, 61(1):156-165,173.
|
| [18] |
Pekeris C L. Theory of propagation of explosive sound in shallow water[J]. Geological Society of America Memoirs, 1948, 27(1):1-116.
|
| [19] |
Robertsson J O A, Holliger K, Green A G, et al. Effects of near-surface waveguides on shallow high-resolution seismic refraction and reflection data[J]. Geophysical Research Letters, 1996, 23(5):495-498.
|
| [20] |
Sheriff R E, Geldart L P. Exploration seismology(2nd ed)[M]. Cambridge: Cambridge University Press, 1995.
|
| [21] |
Roth M, Holliger K. Joint inversion of Rayleigh and guided waves in high-resolution seismic data using a genetic algorithm[C]// SEG Technical Program Expanded Abstracts 1998.Society of Exploration Geophysicists, 1998:1570-1573.
|
| [22] |
Herman G C, Milligan P A, Huggins R J, et al. Imaging shallow objects and heterogeneities with scattered guided waves[J]. Geophysics, 2000, 65(1):247.
|
| [23] |
Carcione J M, Helle H B. The physics and simulation of wave propagation at the ocean bottom[J]. Geophysics, 2004, 69(3):825-839.
|
| [24] |
Klein G, Bohlen T, Theilen F, et al. Acquisition and inversion of dispersive seismic waves in shallow marine environments[J]. Marine Geophysical Researches, 2005, 26(2):287-315.
|
| [25] |
Ernst F E. Long-wavelength statics estimation from guided waves[C]// London:69th EAGE Conference and Exhibition incorporating SPE EUROPEC 2007,European Association of Geoscientists & Engineers, 2007:1-5.
|
| [26] |
李正波. 频率贝塞尔变换法提取地震记录中的频散信息[D]. 合肥: 中国科学技术大学, 2020.
|
| [26] |
Li Z B. Frequency-Bessel transform method for extracting dispersion information from seismic records[D]. Hefei: University of Science and Technology of China, 2020.
|
| [27] |
刘辉, 李静, 曾昭发, 等. 基于贝叶斯理论面波频散曲线随机反演[J]. 物探与化探, 2021, 45(4):951-960.
|
| [27] |
Liu H, Li J, Zeng Z F, et al. Stochastic inversion of surface wave dispersion curves based on Bayesian theory[J]. Geophysical and Geochemical Exploration, 2021, 45(4):951-960.
|
| [28] |
Boerner D E, West G F. A generalized representation of the electromagnetic fields in a layered earth[J]. Geophysical Journal International, 1989, 97(3):529-547.
|
| [29] |
Collino F. Perfectly matched absorbing layers for the paraxial equations[J]. Journal of Computational Physics, 1997, 131(1):164-180.
|
| [30] |
Roth M, Holliger K. Inversion of source-generated noise in high-resolution seismic data[J]. The Leading Edge, 1999, 18(12):1402-1406.
|
| [31] |
Robertsson J O A. A numerical free-surface condition for elastic/viscoelastic finite-difference modeling in the presence of topography[J]. Geophysics, 1996, 61(6):1921-1934.
|
| [32] |
董良国, 马在田. 一阶弹性波方程交错网格高阶差分解法稳定性研究[J]. 地球物理学报, 2000, 43(6):856-864.
|
| [32] |
Dong L G, Ma Z T. A study on stability of the staggered-grid high-order difference method of first-order elastic wave equation[J]. Chinese Journal of Geophysics, 2000, 43(6):856-864.
|
| [33] |
伍敦仕, 孙成禹, 林美言. 基于互相关相移的主动源地震面波频散成像方法[J]. 地球物理学进展, 2017, 32(4):1693-1700.
|
| [33] |
Wu D S, Sun C Y, Lin M Y. Activeseismic surface wave dispersion imaging method based on cross-correlation and phase-shifting[J]. Progress in Geophysics, 2017, 32(4):1693-1700.
|
| [34] |
熊嫘, 孙成禹, 蔡瑞乾. 柱对称条件下地震面波波场正演研究[J]. 石油地球物理勘探, 2023, 58(1):133-144.
|
| [34] |
Xiong L, Sun C Y, Cai R Q. Forward wavefield modeling of seismic surface waves under cylindrical symmetry[J]. Oil Geophysical Prospecting, 2023, 58(1):133-144.
|
| [35] |
Buchen P W, Ben-Hador R. Free-mode surface-wave computations[J]. Geophysical Journal International, 1996, 124(3):869-887.
|
| [36] |
邱新明, 王赟, 韦永祥, 等. 多分量面波研究进展[J]. 石油物探, 2021, 60(1):46-56.
|
| [36] |
Qiu X M, Wang Y, Wei Y X, et al. Advancements in multi-component surface waves:A review[J]. Geophysical Prospecting for Petroleum, 2021, 60(1):46-56.
|
| [37] |
Shi C W, Ren H X, Chen X F. Dispersion inversion for P- and S-wave velocities based on guided P and Scholte waves[J]. Geophysics, 2023, 88(6):R721-R736.
|
| [1] |
LIU Hong-Hua, ZHANG Hui, WANG Ru-Jie, YU Peng, QIN Sheng-Qiang, LI Wen-Yu, CHE Rong-Qi. 3D simulations of geological structures in coastal cities using a electrical resistivity method[J]. Geophysical and Geochemical Exploration, 2024, 48(4): 1037-1044. |
| [2] |
SUN Hong-Lin, LIU Tie-Hua, LIU Tie, ZHANG Zhan-Rong, CHEN Zhi-Xing. Multi-source frequency-domain seismic exploration technique and its application[J]. Geophysical and Geochemical Exploration, 2024, 48(3): 618-628. |
|
|
|
|

