|
|
|
| An online magnetic compensation method for carriers based on vector measurement |
LING Jie-Ya1( ), JIN Huang-Huang2, ZHUANG Zhi-Hong1, WANG Hong-Bo1, DONG Sheng-Ya1 ), JIN Huang-Huang2, ZHUANG Zhi-Hong1, WANG Hong-Bo1, DONG Sheng-Ya1 |
1. School of Eloctronic Engineering and Optoelectronic Technology, Nanjing University of Science and Technology, Nanjing 210094, China
2. Huangshan University, Huangshan 245041, China |
|
|
|
|
Abstract Aiming at the ill-conditioned coefficients in the traditional carrier magnetic compensation, this study investigated the main source of magnetic interference, simplified the original model by ignoring the influence of the eddy current field, and established a three-component magnetic compensation model. Accordingly, it proposed an online carrier magnetic compensation method for the magnetic field components. Compared with the traditional method, the method proposed in this study effectively improved the compensation accuracy by about 1.14 nT. This study conducted embedded hardware simulations of this method using the high-level synthesis (HLS) tool of the field programmable gate array (FPGA), verifying the real-time performance and magnetic compensation accuracy of this method in a hardware system.
|
|
Received: 26 May 2022
Published: 27 April 2023
|
|
|
|
|
|
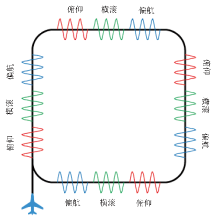
|
Schematic diagram of total field calibration flight
|

| 传统总场
方法考虑
地磁梯度 | 传统总场方
法不考虑地
磁梯度 | 本文方法
考虑地磁
梯度 | 本文方法
不考虑地
磁梯度 | | 标准差/nT | 2.3631 | 0.0105 | 0.0170 | 0.0107 |
|
Standard deviations with and without geomagnetic gradients
|
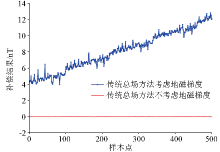
|
Influence of geomagnetic gradient on the compensation result of traditional total field method
|
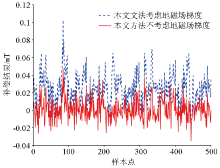
|
Influence of geomagnetic gradient on the compensation results of this method
|

| 条件数 | 标准差/nT | | 本文方法 | 59.8869 | 0.0108 | | 传统总场方法 | 1.76e+16 | 1.1589 |
|
Comparison of standard deviation and condition number
|
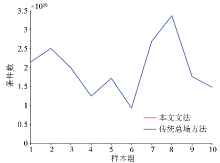
|
Comparison and simulation of the condition number between the method in this paper and the traditional model
|
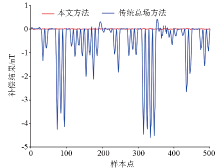
|
Comparison and simulation of the compensation results between the method in this paper and the traditional model
|

| 补偿系数真实值 | 传统总场方法 | | 10 | 25.57 | | 30 | 55.40 | | 50 | 81.44 | | 0.6 | -23.47 | | 0.6 | -4.22 | | 0.6 | -5.05 | | 0.6 | -28.12 | | 0.6 | -8.78 | | 0.6 | -32.34 | | 0.3 | -4.81 | | 0.3 | -3.01 | | 0.3 | -9.50 | | 0.3 | -2.54 | | 0.3 | -0.43 | | 0.3 | 2.09 | | 0.3 | 6.18 | | 0.3 | 2.84 | | 0.3 | 4.89 |
|
Compensation coefficients calculated by traditional total field method
|

| 补偿系数真实值 | 本文方法 | | 100 | 99.96 | | 39180 | 39180.00 | | -250 | -249.96 | | -950 | -949.98 |
|
The method of this paper to solve the compensation coefficient of x component
|
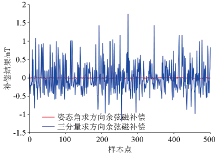
|
Simulation comparison of attitude angle and three-component solution direction cosine compensation effect
|

| 姿态角求方向
余弦磁补偿 | 三分量求方向
余弦磁补偿 | | 标准差/nT | 0.0109 | 0.4260 |
|
Standard deviation of compensation results for direction cosine of three components and attitude angle
|
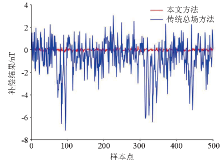
|
Comparison of the measured flight method and the compensation results of the traditional model
|
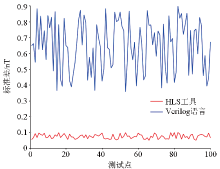
|
Comparison of standard deviation between HLS tool and Verilog language
|
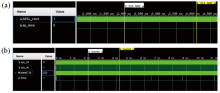
|
Time consumption comparison of the HLS tool (a) and the Verilog language (b)
|
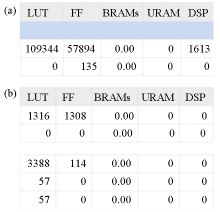
|
Resource consumption comparison of the HLS tool (a) and the Verilog language (b)
|

| 资源消
耗:LUT | 资源消
耗:FF | 资源消
耗:DSP | 时间消
耗/ns | 平均值/
nT | | HLS工具 | 109344 | 58029 | 1613 | 2090 | 0.0753 | | Verilog语言 | 4818 | 1422 | 0 | 2235 | 0.6047 |
|
FPGA comparison between HLS tools and traditional Verilog language
|
| [1] |
张昌达. 关于磁异常探测的若干问题[J]. 工程地球物理学报, 2007, 4(6),549-553.
|
| [1] |
Zhang C D. Several issues on the detection of magnetic anomalies[J]. Journal of Engineering Geophysics, 2007, 4(6),549-553.
|
| [2] |
Reeves C V. Aeromagnetic surveys principles,practices & interpretation[M]. Washington:GEOSOFT, 2005:31-32.
|
| [3] |
Xiong S Q, Tong J, Ding Y Y, et al. Aeromagnetic data and geological structure of continental China:A review[J]. Applied Geophysics, 2017, 13(2):227-237.

|
| [4] |
朱学军. 无人机航磁测量中载体干扰磁场补偿方法研究[D]. 长沙: 国防科学技术大学, 2014.
|
| [4] |
Zhu X J. Research on compensation method of carrier interference magnetic field in field in UAV aeromagnetic survey[D]. Changsha: National University of Defense Technology, 2014.
|
| [5] |
张光, 张英堂, 尹刚, 等. 一种磁张量探测系统载体的磁张量补偿方法[J]. 地球物理学报, 2016, 59(1):311-317.
|
| [5] |
Zhang G, Zhang Y T, Yi G, et al. Magnetic tensor compensation method for magnetic tensor detection system carrier[J]. Acta Geophysics, 2016, 59(1):311-317.
|
| [6] |
Tolles W E. Compensation of induced magnetic fields in MAD equipped aircraft[R]. Airborne Instruments Lab,OSRD, 1943.
|
| [7] |
Tolles W E, Lawson J D. Magnetic compensation of MAD equipped aircraft[R]. Airborne Instruments Lab.Inc., 1950.
|
| [8] |
韩磊. 航空磁异常探测关键技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2014.
|
| [8] |
Han L. Research on key technologies of aeromagnetic anomaly detection[D]. Harbin: Harbin Institute of Technology, 2014.
|
| [9] |
谭斌, 林春生, 张宁, 等. 地磁场梯度对飞机磁场求解精度的影响分析[J]. 武汉大学学报:信息科学版, 2011, 36(12):1482-1485.
|
| [9] |
Tan B, Lin C S, Zhang N, et al. Analysis of the influence of geomagnetic field gradient on the accuracy of aircraft magnetic field solution[J]. Journal of Wuhan University :Information Science Edition, 2011, 36(12):1482-1485.
|
| [10] |
何敬礼. 飞机磁场的自动补偿方法[J]. 物探与化探, 1985, 9(6):464-469.
|
| [10] |
He J L. Automatic compensation method of aircraft magnetic field[J]. Geophysical and Geochemical Exploration, 1985, 9(6):464-469.
|
| [11] |
Williams P M. Aeromagnetic compensation using neural networks[J]. Neural Computing & pplications, 1993 (1):207-214.
|
| [12] |
边刚, 刘雁春, 卞光浪, 等. 海洋磁力测量中多站地磁日变改正值计算方法研究[J]. 地球物理学报, 2009, 52(10):2613-2618.
|
| [12] |
Bian G, Liu Y C, Bian G L, et al. Research on calculation method of multi-station geomagnetic diurnal correction value in marine magnetometric survey[J]. Acta Geophysics, 2009, 52(10):2613-2618.
|
| [13] |
Hardwick C D. Techniques for achieving stableand aeromagnetic compensation coefficients[C]// 1986 SEG Annual Meeting. Houston,Texas: Society of Exploration Geophysicists, 1986:140-141.
|
| [14] |
Leach B W. Aeromagnetic compensation as a linear regression problem[J]. Information Linkage Between Applied Mathematics and Industry, 1980, 2(2):139-161.
|
| [15] |
伍东凌, 陈正想, 王秀. 基于遗传算法的磁干扰补偿方法[J]. 探测与控制学报, 2012, 34(6):16-20.
|
| [15] |
Wu D L, Cheng Z X, Wang X. Magnetic interference compensation method based on genetic algorithm[J]. Journal of Detection and Control, 2012, 34(6):16-20.
|
| [16] |
潘雪, 张琦, 潘孟春, 等. 一种考虑地磁梯度变化的航磁补偿方法[J]. 传感器与微系统, 2020, 39(10):5-7,10.
|
| [16] |
Pan X, Zhang Q, Pan M C, et al. An aeromagnetic compensation method considering geomagnetic gradient changes[J]. Sensors and Microsystems, 2020, 39(10):5-7,10.
|
| [17] |
赵塔. 海域环境下铁磁性载体地磁场矢量差分检测方法研究[D]. 长春: 吉林大学, 2016.
|
| [17] |
Zhao T. Research on vector difference detection method of ferromagnetic carrier geomagnetic field in marine environment[D]. Changchun: Jilin University, 2016.
|
| [18] |
高全明. 固定翼无人机航磁三分量系统误差校正与干扰补偿技术研究[D]. 长春: 吉林大学, 2020.
|
| [18] |
Gao Q M. Research on error correction and interference compensation technology of fixed-g UAV aeromagnetic three-component system[D]. Changchun: Jilin University, 2020.
|
| [19] |
冯彦, 蒋勇, 孙涵, 等. 地磁场水平梯度及高空地磁场的计算与分析[J]. 地球物理学进展, 2013, 28(2):735-746.
|
| [19] |
Fen Y, Jiang Y, Sun H, et al. Calculation and analysis of horizontal gradient of geomagnetic field and high-altitude geomagnetic field[J]. Advances in Geophysics, 2013, 28(2):735-746.
|
| [20] |
张永军, 吴磊, 林立文, 等. 摄影测量中病态问题的条数指标分析[J]. 武汉大学学报:信息科学版, 2010, 35(3):308-312.
|
| [20] |
Zhang Y J, Wu L, Lin L W, et al. Analysis of number index of pathological problems in photogrammetry[J]. Journal of Wuhan University:Information Science Edition, 2010, 35(3):308-312.
|
| [21] |
Moulin M, Goudon J C, Marsy J M, et al. Process for compensating the magnetic disturbances in the determination of a magnetic heading,and devices for carrying out this process:US, US4414753 A[P].
|
| [1] |
GUO Jian-Hong, DU Ting, ZHANG Zhan-Song, XIAO Hang, QIN Rui-Bao, YU Jie, WANG Can. The coal structure identification method based on support vector machine and geophysical logging data[J]. Geophysical and Geochemical Exploration, 2021, 45(3): 768-777. |
| [2] |
GU Guan-Wen, WU Ye, SHI Yan-Bin. Research on fast three-dimensional forward algorithm of magnetotelluric sounding based on vector finite element[J]. Geophysical and Geochemical Exploration, 2020, 44(6): 1387-1398. |
|
|
|
|

