|
|
|
| Detection of karst caves using the cross-hole resistivity method based on the squirrel search algorithm |
LIANG Sen1( ), CHEN Jian-Hua1, LI Hong-Tao1, LUO Wei-Li2( ), CHEN Jian-Hua1, LI Hong-Tao1, LUO Wei-Li2( ), LUO Ying-Zhou1, Ai Jiao-Jiao1, LIAO Wei1 ), LUO Ying-Zhou1, Ai Jiao-Jiao1, LIAO Wei1 |
1. The First Construction Engineering Co., Ltd. of China Construction Fourth Engineering Bureau, Guangzhou 510800, China
2. School of Civil Engineering, Guangzhou University, Guangzhou 510006, China |
|
|
|
|
Abstract Aiming at the low-detection precision of traditional geophysical prospecting inversion methods for unfavorable geological conditions such as karst caves in the early detection stage of infrastructure projects, this study proposed a cross-hole resistivity detection and inversion method of karst caves based on the squirrel search algorithm to improve the performance of the traditional Tikhonov regularization-based sensitivity iteration method, which is sensitive to initial values and noise and easy to fall into local optimization. The detection results obtained using different intelligent search algorithms and sensitivity iteration methods were compared and analyzed using three numerical examples of small, large, and beaded karst caves. Moreover, an indoor physical model was also built to validate the proposed method. The results show that the inversion method based on the squirrel search algorithm has a high convergence speed and precision and can significantly improve the detection precision of karst caves using the cross-hole resistivity method.
|
|
Received: 12 May 2021
Published: 03 January 2023
|
|
|
|
Corresponding Authors:
LUO Wei-Li
E-mail: 6976993@qq.com;wlluo@gzhu.edu.cn
|
|
|
|
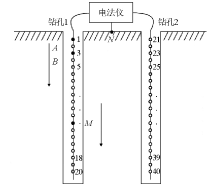
|
A sketch of observation mode
|
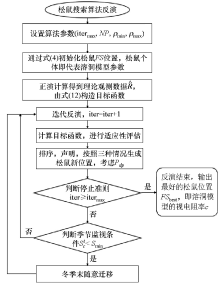
|
An inversion flowchart of the squirrel search algorithm
|
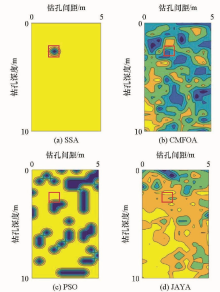
|
Inversion diagrams of different intelligent optimization algorithms
|
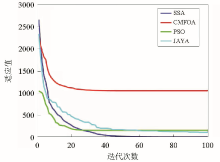
|
Inversion iterations of different intelligent optimization algorithms
|

|
The inversion results of the sensitivity iterative method
|

|
The inversion results of the squirrel search algorithm
|

|
Iterative graphs of the squirrel search algorithm
|

| 反演算法 | 溶洞定位 | 溶洞轮廓 | 多解性 | | 灵敏度迭代法 | 稍有偏差 | 基本对应 | 不能抑制 | | 松鼠搜索算法 | 精准 | 完全对应 | 有效抑制 |
|
Contrast of inversion results
|

|
High-density electric detector
|

|
Cave models
|

| 项目 | 原型尺寸/m | 模型尺寸/m | | 探测截面(深度×宽度) | 15×10 | 1.5×1 | | 溶洞尺寸(长度×宽度×高度) | 1×1 ×1 | 0.1×0.1×0.1 | | 电极套管(深度×测点间距) | 15×1 | 1.5×0.1 |
|
The comparison of the prototype dimensions of each geometric factor with the size of the model
|
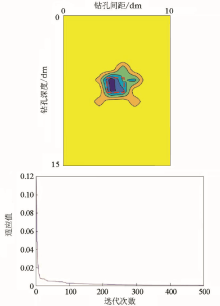
|
Inversion results of water-filled karst cave model (a) and iterative curve (b)
|
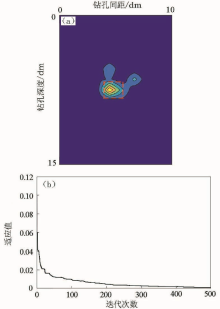
|
Inversion results of the gas-filled cave model (a) and iterative curve (b)
|

| 介质 | 视电阻率/(Ω·m) | 备注 | | 素填土 | 100~200 | 灰黑色;松散;湿;顶部10~20 cm含植物根系 | | 粉质黏土 | 10~100 | 灰白色;很湿;可塑;主要成分为粉黏粒,韧性低,干强度低,刀切面光滑,夹砂 | | 砾砂 | 10~300 | 黄色;松散—稍密;饱和;主要成分为石英颗粒,分选性差,级配较好,局部含黏土 | | 中风化石灰岩 | >400 | 灰色;隐晶质结构,层状结构,裂隙发育,局部含方解石脉,敲击声脆,岩心呈碎石状,见溶蚀发育 | | 溶洞 | 10~100 | 全填充,充填物为流塑状粉质黏土,溶洞呈串珠状发育 | | 微风化石灰岩 | >400 | 灰色;隐晶质结构,层状结构,裂隙发育,局部含方解石脉,敲击声脆,岩心呈短柱状,节长多为10~30 cm |
|
The visual resistivity distribution table of the measured area
|

| 钻孔1L16-4 | | 岩土名称 | 层底高程/m | 层底深度/m | 分层厚度/m | | 素填土 | 11.87 | 1.00 | 1.00 | | 砾砂 | 1.57 | 11.30 | 10.30 | | 中风化石灰岩 | 0.07 | 12.80 | 1.50 | | 微风化石灰岩 | -0.33 | 13.20 | 0.40 | | 溶洞 | -2.03 | 14.90 | 1.70 | | 微风化石灰岩 | -2.93 | 15.80 | 0.90 | | 溶洞 | -5.13 | 18.00 | 2.20 | | 中风化石灰岩 | -6.13 | 19.00 | 1.00 | | 微风化石灰岩 | -10.13 | 23.00 | 4.00 | | 钻孔1L16-5 | | 岩土名称 | 层底高程/m | 层底深度/m | 分层厚度/m | | 素填土 | 12.00 | 1.00 | 1.00 | | 砾砂 | 0.00 | 13.00 | 12.00 | | 中风化石灰岩 | -0.20 | 13.20 | 0.20 | | 溶洞 | -3.00 | 16.00 | 2.80 | | 微风化石灰岩 | -7.00 | 20.00 | 4.00 |
|
Summary of the results of the drilling bar chart section
|
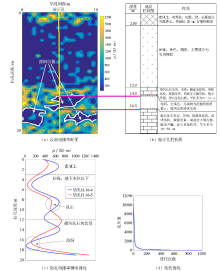
|
Inversion results of field experiment
|
| [1] |
周文龙, 吴荣新, 肖玉林. 充水溶洞特征的高密度电阻率法反演分析研究[J]. 中国岩溶, 2016, 35(6):699-705.
|
| [1] |
Zhou W L, Wu R X, Xiao Y L. Study on inversion analysis of water filled karst cave characteristics by high density resistivity method[J]. Carsologica Sinica, 2016, 35(6): 699-705.
|
| [2] |
欧元超, 胡雄武, 徐宝超, 等. 夹角和偏移距对岩溶区高密度电法响应特征的影响试验研究[J]. 水利水电技术, 2018, 49(6):156-162.
|
| [2] |
Ou Y C, Hu X W, Xu B C, et al. Experimental study on the influence of included angle and offset on the response characteristics of high-density electrical method in Karst Area[J]. Water Conservancy and Hydropower Technology, 2018, 49(6): 156-162.
|
| [3] |
薛国强, 宋建平, 马宇, 等. 用瞬变电磁法探测灰岩溶洞[J]. 地球科学与环境学报, 2003, 25(2):50-53.
|
| [3] |
Xue G Q, Song J P, Ma Y, et al. Detection of limestone cave by transient electromagnetic method[J]. Journal of Earth Science and Environment, 2003, 25(2): 50-53.
|
| [4] |
黎华清, 卢呈杰, 韦吉益, 等. 孔间电磁波探测揭示水库坝基岩溶形态特征:以广西靖西大龙潭水库帷幕灌浆为例[J]. 岩土力学, 2008, 29(S1):611-614.
|
| [4] |
Li H Q, Lu C J, Wei J Y, et al. Inter hole electromagnetic wave detection reveals the morphological characteristics of bedrock dissolution of reservoir dam: A case study of curtain grouting of Dalongtan reservoir in Jingxi, Guangxi[J]. Geotechnical Mechanics, 2008, 29(S1): 611-614.
|
| [5] |
高阳, 张庆松, 原小帅, 等. 地质雷达在岩溶隧道超前预报中的应用[J]. 山东大学学报:工学版, 2009, 9(4):82-86.
|
| [5] |
Gao Y, Zhang Q S, Yuan X S, et al. Application of geological radar in advance prediction of Karst Tunnel[J]. Journal of Shandong University: Engineering Edition, 2009, 9(4): 82-86.
|
| [6] |
漆立新, 顾汉明, 李宗杰, 等. 基于地震波振幅分辨塔河油田溶洞最小高度的理论探讨[J]. 地球物理学进展, 2008, 23(5):1499-1506.
|
| [6] |
Qi L X, Gu H M, Li Z J, et al. Theoretical discussion on resolving the minimum height of karst cave in Tahe oilfield based on seismic wave amplitude[J]. Advances in Geophysics, 2008, 23(5): 1499-1506.
|
| [7] |
席超强, 周文龙, 李建宁. 多道瞬态面波法在岩溶注浆质量检测中的应用[J]. 宿州学院学报, 2016, 31(10):123-126.
|
| [7] |
Xi C Q, Zhou W L, Li J N. Application of multi-channel transient surface wave method in Karst grouting quality detection[J]. Journal of Suzhou University, 2016, 31(10): 123-126.
|
| [8] |
Shima H. Two-dimensional automatic resistivity inversion technique using alpha centers[J]. Geophysies, 1990, 55(6): 682-694.
|
| [9] |
Shima H. 2D and 3D resistivity image reconstruction using cross-hole data[J]. Geophysies, 1992, 57(10):1270-1281.
|
| [10] |
夏志鹏, 王树青, 徐明强, 等. 基于Tikhonov正则化迭代求解的结构损伤识别方法[J]. 振动与冲击, 2019, 38(17):251-259.
|
| [10] |
Xia Z P, Wang S Q, Xu M Q, et al. Structural damage identification method based on Tikhonov regularization iterative solution[J]. Vibration and Shock, 2019, 38(17):251-259.
|
| [11] |
Kennedy J, Eberhart R C. Particle swarm optimization[R]. Proceedings of IEEE International Conference on Neural Networks, Piscataway, NJ. 1995: 1942-1948.
|
| [12] |
Wu L H, Zuo C L, Zhang H Q. A cloud model based fruit fly optimization algorithm[J]. Knowledge-Based Systems, 2015, 89:603-617.

|
| [13] |
Venkata Rao R. Jaya: A simple and new optimization algorithm for solving constrained and unconstrained optimization problems[J]. International Journal of Industrial Engineering Computations, 1934, 7:19-34.
|
| [14] |
Jain M, Singh V, Rani A. A novel nature-inspired algorithm for optimization: Squirrel search algorithm[J]. Swarm and Evolutionary Computation, 2018:44.
|
| [15] |
Jensi R, Jiji G W. An enhanced particle swarm optimization with Lévy flight for global optimization[J]. Applied Soft Computing, 2016, 43:248-261.

|
|
|
|

