|
|
|
| Three-component responses of axially anisotropic formations using the transient electromagnetic method |
GUO Jian-Lei( ) ) |
| Xi'an Research Institute, China Coal Technology and Engineering Group, Xi'an 710077, China |
|
|
|
|
Abstract The conductivity of most formations and fractured water areas is anisotropic, while the anisotropy of formations has great impacts on transient electromagnetic observations, especially on the characteristics of horizontal components. To study the three-component responses of axially anisotropic formations using the transient electromagnetic method, this study introduced a conductivity tensor to construct the governing equation to achieve the three-dimensional three-component forward modeling of the axially anisotropic conductivity using the transient electromagnetic method based on the finite-difference time-domain (FDTD) algorithm. This study verified the accuracy of the three-component forward modeling by comparing the three-dimensional three-component forward modeling results with the one-dimensional analytical results of the isotropic and anisotropic half-space models. Meanwhile, this study established the anisotropic half-space, layered, and water-bearing models and calculated loop-source three-component responses of the transient electromagnetic method. The results are as follows. The horizontal conductivity anisotropy greatly affected the three-component responses. The x-axis anisotropy had greater effects on the ∂By/∂t component response than those on ∂Bx/∂t component response, the y-axis anisotropy had greater effects on the ∂Bx/∂t component response than those on the ∂By/∂t component response, while the z-axis anisotropy had almost no effect on the three-component responses. Moreover, the three-component responses were primarily affected by conductivity anisotropy of shallow formations. The x-axis anisotropy had greater effects on the three-component responses than the y-axis anisotropy when collection points were closer to an anomaly center in the x-direction than in the y-direction, and vice versa. The results of this study provide some valuable theoretical references for the three-component processing and interpretation of the transient electromagnetic method of anisotropic formations.
|
|
Received: 03 July 2021
Published: 28 June 2022
|
|
|
|
|
|
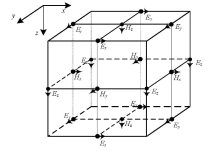
|
Schematic diagram of Yee unit cell meshing
|
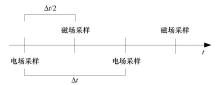
|
Schematic diagram of time sampling distribution of electromagnetic field
|

|
Isotropic half-space model vertical component magnetic field response (a) and relative error (b)
|
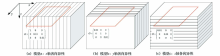
|
Anisotropic half-space models
|

| 模型 | 电导率/(S·m-1) | | x轴 | y轴 | z轴 | | a | 1 | 0.01 | 0.01 | | b | 0.01 | 1 | 0.01 | | c | 0.01 | 0.01 | 1 |
|
Axial conductivity of the Fig.4 model
|

|
Anisotropic half-space model vertical component magnetic field response (a) and relative error (b)
|

|
Three-component TEM response of anisotropic half-space models
|

|
Ground three-component magnetic field distribution at 0.1 ms
|

| 各向异性类别 | 电导率/(S·m-1) | | x轴 | y轴 | z轴 | | x轴各向异性 | 1 | 0.01 | 0.01 | | y轴各向异性 | 0.01 | 1 | 0.01 | | z轴各向异性 | 0.01 | 0.01 | 1 |
|
Anisotropy parameters of axial conductivity
|
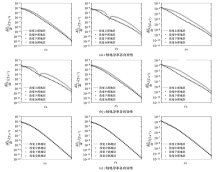
|
Three-component TEM response of anisotropic layered models
|

| 各向异性类别 | 电导率/(S·m-1) | | x轴 | y轴 | z轴 | | 各向同性 | 1 | 1 | 1 | | x轴各向异性 | 10 | 1 | 1 | | y轴各向异性 | 1 | 10 | 1 | | z轴各向异性 | 1 | 1 | 10 |
|
Anisotropy parameters of axial conductivity
|

|
Top view of the position of the hydrate relative to the loop source
|

|
Transient electromagnetic three-component response of anisotropic aquifer
|

|
x,y,z axis anisotropic transient electromagnetic horizontal component response comparison diagram
|
| [1] |
Kunz K S, Moran J H. Some effects of formation anisotropy on resistivity measurements in boreholes[J]. Geophysics, 1958, 23(4): 770-794.

|
| [2] |
张晖, 高原, 石玉涛, 等. 鄂尔多斯块体北缘与西缘地区地壳各向异性特征[J]. 地球物理学报, 2020, 63(6):2230-2247.
|
| [2] |
Zhang H, Gao Y, Shi Y T, et al. Crustal seismic anisotropy beneath the northern and western margins of the Ordos block[J]. Chinese Journal of Geophysics, 2020, 63(6): 2230-2247.
|
| [3] |
邓少贵, 刘天淋, 王磊, 等. 双轴各向异性介质多分量感应测井响应快速计算[J]. 地球物理学报, 2020, 63(1):362-373.
|
| [3] |
Deng S G, Liu T L, Wang L, et al. Analytical solution of multicomponent induction logging response in biaxial anisotropic medium[J]. Chinese Journal of Geophysics, 2020, 63(1): 362-373.
|
| [4] |
刘云鹤, 殷长春, 蔡晶, 等. 电磁勘探中各向异性研究现状和展望[J]. 地球物理学报, 2018, 61(8):3468-3487.
|
| [4] |
Liu Y H, Yin C C, Cai J, et al. Review on research of electrical anisotropy in electromagnetic prospecting[J]. Chinese Journal of Geophysics, 2018, 61(8): 3468-3487.
|
| [5] |
张韬. 中国主要聚煤期沉积环境与聚煤规律[M]. 北京: 地质出版社, 1992.
|
| [5] |
Zhang T. Depositional environment and coal-accumulating regularities of main coal-accumulating stages in China[M]. Beijing: Geological Publishing House, 1992.
|
| [6] |
伍宇明, 兰恒星, 黄为清. 龙马溪页岩弹性各向异性与矿物分布之间的关系探讨[J]. 地球物理学报, 2020, 63(5):1856-1866.
|
| [6] |
Wu Y M, Lan H X, Huang W Q. Discussion on the relationship between elastic anisotropy and mineral distribution of Longmaxi Shale[J]. Chinese Journal of Geophysics, 2020, 63(5): 1856-1866.
|
| [7] |
Yin C C, Fraser D C. The effect of the electrical anisotropy on the response of helicopter-borne frequency-domain electromagnetic systems[J]. Geophysical Prospecting, 2004, 52(5): 399-416.

|
| [8] |
孙英峰, 赵毅鑫, 王欣, 等. 基于同步辐射装置定量表征煤孔隙结构非均质性和各向异性[J]. 石油勘探与开发, 2019, 46(6):1128-1137.
|
| [8] |
Sun Y F, Zhao Y X, Wang X, et al. Synchrotron radiation facility-based quantitative evaluation of pore structure heterogeneity and anisotropy in coal[J]. Petroleum Exploration and Development, 2019, 46(6): 1128-1137.
|
| [9] |
王玉涛, 刘震. 深部煤层非充分采动下覆岩裂隙场可视化探测研究[J]. 煤炭科学技术, 2020, 48(3):197-204.
|
| [9] |
Wang Y T, Liu Z. Study on visual exploration of fissure field of overlying strata in deep coal seam under subcritical extraction[J]. Coal Science and Technology, 2020, 48(3): 197-204.
|
| [10] |
解滔, 卢军. 含裂隙介质中的视电阻率各向异性变化[J]. 地球物理学报, 2020, 63(4):1675-1694.
|
| [10] |
Xie T, Lu J. Apparent resistivity anisotropic variations in cracked medium[J]. Chinese Journal of Geophysics, 2020, 63(4): 1675-1694.
|
| [11] |
申涛, 袁峰, 宋世杰, 等. P波各向异性检测在采空区导水裂隙带探测中的应用[J]. 煤炭学报, 2017, 42(1):197-202.
|
| [11] |
Shen T, Yuan F, Song S J, et al. Application of P-wave anisotropy detection in detecting the conducting fracture zone[J]. Journal of China Coal Society, 2017, 42(1): 197-202.
|
| [12] |
周建美, 刘文韬, 李貅, 等. 双轴各向异性介质中回线源瞬变电磁三维拟态有限体积正演算法[J]. 地球物理学报, 2018, 61(1):368-378.
|
| [12] |
Zhou J M, Liu W T, Li X, et al. Research on the 3D mimetic finite volume method for loop-source TEM response in biaxial anisotropic formation[J]. Chinese Journal of Geophysics, 2018, 61(1): 368-378.
|
| [13] |
刘亚军, 胡祥云, 彭荣华, 等. 回线源瞬变电磁法有限体积三维任意各向异性正演及分析[J]. 地球物理学报, 2019, 62(5):1954-1968.
|
| [13] |
Liu Y J, Hu X Y, Peng R H, et al. 3D forward modeling and analysis of the loop-source transient electromagnetic method based on the finiye-colume method for an arbitrarily anisotropic medium[J]. Chinese Journal of Geophysics, 2019, 62(5): 1954-1968.
|
| [14] |
程久龙, 黄少华, 温来福, 等. 矿井全空间三维主轴各向异性介质瞬变电磁场响应特征研究[J]. 煤炭学报, 2019, 44(1):278-286.
|
| [14] |
Cheng J L, Huang S H, Wen L F, et al. Response characteristics of three-dimensional axial anisotropic media for transient electromagnetic method in underground whole-space[J]. Journal of China Coal Society, 2019, 44(1): 278-286.
|
| [15] |
赵慧楠. 瞬变电磁三分量接收系统设计与实现[D]. 长春: 吉林大学, 2015.
|
| [15] |
Zhao H N. Design and implementation of three-component transient electromagnetic receiving system[D]. Changchun: Jilin University, 2015.
|
| [16] |
戚志鹏, 智庆全, 李貅, 等. 大定源瞬变电磁三分量全域视电阻率定义与三分量联合反演[J]. 物探与化探, 2014, 38(4):742-749.
|
| [16] |
Qi Z P, Zhi Q Q, Li X, et al. The definition of the full-zone apparent resistivity and the constrained inversion of the three components of fixed source TEM[J]. Geophysical & Geochemical Exploration, 2014, 38(4): 742-749.
|
| [17] |
智庆全, 武军杰, 王兴春, 等. 三分量定源瞬变电磁解释技术及其在金属矿区的实验[J]. 物探与化探, 2016, 40(4):798-803.
|
| [17] |
Zhi Q Q, Wu J J, Wang X C, et al. Three-component interpretation technique of fixed source TEM and its experimental application in metallic ore district[J]. Geophysical & Geochemical Exploration, 2016, 40(4): 798-803.
|
| [18] |
武军杰, 李貅, 智庆全, 等. 电性源地—井瞬变电磁全域视电阻率定义[J]. 地球物理学报, 2017, 60(4):1595-1605.
|
| [18] |
Wu J J, Li X, Zhi Q Q, et al. Full field apparent resistivity definition of borehole TEM with electric source[J]. Chinese Journal of Geophysics, 2017, 60(4): 1595-1605.
|
| [19] |
王鹏. 井—地瞬变电磁法浮动系数空间交汇与等效电流环反演方法研究[D]. 武汉: 中国地质大学(武汉), 2017.
|
| [19] |
Wang P. Study on floating coefficient space intersection and equivalent current loop inversion of downhole TEM[D]. Wuhan: China University of Geosciences(Wuhan) 2017.
|
| [20] |
杨海燕, 李锋平, 岳建华, 等. 基于“烟圈”理论的圆锥型场源瞬变电磁优化反演[J]. 中国矿业大学学报, 2016, 45(6):1230-1237.
|
| [20] |
Yang H Y, Li F P, Yue J H, et al. Optimal transient electromagnetic inversion of conical source based on smoke ring theory[J]. Journal of China University of mining & Technology, 2016, 45(6): 1230-1237.
|
| [21] |
范涛. 矿井巷道—钻孔瞬变电磁二维拟地震反演方法及应用[J]. 煤炭学报, 2019, 44(6):1804-1816.
|
| [21] |
Fan T. Method and application on 2D pseudo-seismic inversion of roadway-borehole transient electromagnetic detection in coal mine[J]. Journal of China Coal Society, 2019, 44(6): 1804-1816.
|
| [22] |
孙怀凤, 李貅, 李术才, 等. 考虑关断时间的回线源激发TEM三维时域有限差分正演[J]. 地球物理学报, 2013, 56(3):1049-1064.
|
| [22] |
Sun H, Li X, Li S C, et al. Three-dimensional FDTD modeling of TEM excited by a loop source considering ramp time[J]. Chinese Journal of Geophysics, 2013, 56(3): 1049-1064.
|
| [23] |
卢绪山. 隧道TBM机瞬变电磁响应三维并行模拟及干扰去除研究[D]. 西安: 长安大学, 2014.
|
| [23] |
Lu X S. Three dimensional parallel simulation of transient electromagnetic response of tunnel boring machine and the elimination of its response[D]. Xi'an: Chang’an University, 2014.
|
| [24] |
李展辉, 黄清华. 复频率参数完全匹配层吸收边界在瞬变电磁法正演中的应用[J]. 地球物理学报, 2014, 57(4):1292-1299.
|
| [24] |
Li Z H, Huang Q H. Application of complex frequency shifted perfectly matched layer absorbing boundary conditions in transient electromagnetic method modeling[J]. Chinese Journal of Geophysics, 2014, 57(4): 1292-1299.
|
| [25] |
孙怀凤, 程铭, 吴启龙, 等. 瞬变电磁三维FDTD正演多分辨网格方法[J]. 地球物理学报, 2018, 61(12):5096-5104.
|
| [25] |
Sun H F, Cheng M, Wu Q L, et al. A multi-scale grid scheme in three-dimensional transient electromagnetic modeling using FDTD[J]. Chinese Journal of Geophysics, 2018, 61(12): 5096-5104.
|
|
|
|

