|
|
|
| One-dimensional Occam's inversion for transient electromagnetic data excited by a loop source |
XING Tao1( ), YUAN Wei2, LI Jian-Hui3( ), YUAN Wei2, LI Jian-Hui3( ) ) |
1. Beijing Exploration Resources Technology Co., Ltd., Beijing 100071, China
2. Inner Mongolia Geological Engineering Co., Ltd., Hohhot 010010, China
3. Institute of Geophysics and Geomatics, China University of Geosciences(Wuhan), Wuhan 430074, China |
|
|
|
|
Abstract A 1D inversion code is developed for the loop-source transient electromagnetic method (TEM) based on the open-source code Dipole1D and Occam's algorithm. This code is tested by a four-layer stratified model. Then, the model with a tilted earth-air interface is considered, for which the synthetic data are calculated by 3D finite-element method. The inversion results show that 1D inversion can be directly used for the scenario with tilted interface. Finally, this 1D inversion code is used for a field case, in which TEM is employed to delineate the 3D distributed domains of a basalt which intruded into shale and sandstone. The inversion result shows that the thickness of the basalt coincides with the drilling data, and the shape of the basalt like a pot bottom.
|
|
Received: 26 February 2021
Published: 15 December 2021
|
|
|
|
Corresponding Authors:
LI Jian-Hui
E-mail: 156663062@qq.com;ljhiiicumt@126.com
|
|
|
|
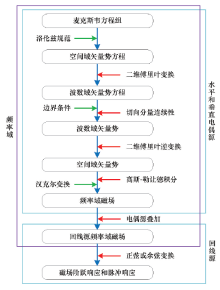
|
The framework of 1D forward modeling for loop-source transient electromagnetic methods
|
|
The inversion geo-electric model for the loop-center point and for 4-layer model
|
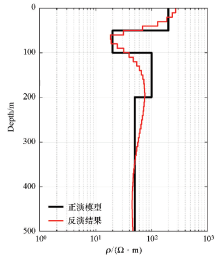
|
The data computed from the inversion model
|
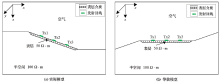
|
The sketch map for the tilted-surface model
|
|
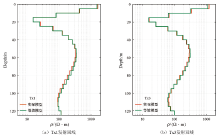
Geoelectric model obtained by inversion of data at the center of the loop( inversion schemes 1)
|
|
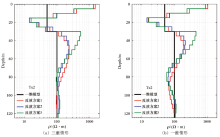
The inversion geo-electric models obtained from different inversion schemes
|
|
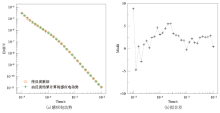
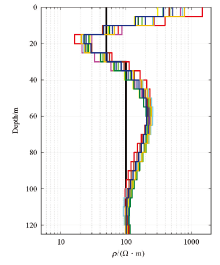
Under the influence of random noise, the inversion geoelectric model of the actual model (Tx2 loop)
The black line denotes the realistic model, the color lines denote the inversion models
|
|
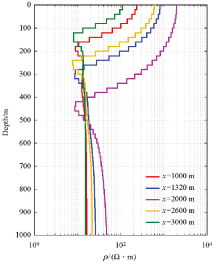
The inversion geo-electric models for five survey points
|
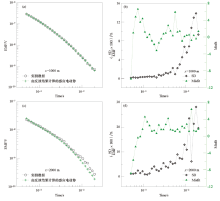
|
The data computed from the inversion model for x=1 000 m and 2 000 m
a、c—EMF curves at different measuring points; b、d—Misfit curver and the standard deviation curves of measured data
|
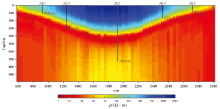
|
The section view stitched from the single-point 1D inversion models for survey line 1
|
| [1] |
Flores C, Peralta-Ortega S A. Induced polarization with in-loop transient electromagnetic soundings: A case study of mineral discrimination at El Arco porphyry copper, Mexico[J]. Journal of Applied Geophysics, 2009, 68(3):423-436.

|
| [2] |
Xue G Q, Qin K Z, Li X, et al. Discovery of a large-scale porphyry molybdenum deposit in Tibet through a modified TEM exploration method[J]. Journal of Environmental and Engineering Geophysics, 2012, 17(1):19-25.

|
| [3] |
Yang D, Oldenburg D W. Three-dimensional inversion of airborne time-domain electromagnetic data with applications to a porphyry deposit[J]. Geophysics, 2012, 77(2):B23-B34.

|
| [4] |
Scholl C, Helwig S L, Tezkan B, et al. 1-D multimodel joint inversion of TEM-data over multidimensional structures[J]. Geophysical Journal International, 2009, 176(1):81-94.

|
| [5] |
Kirkegaard C, Auken E. A parallel, scalable and memory efficient inversion code for very large-scale airborne electromagnetics surveys[J]. Geophysical Prospecting, 2015, 63(2):495-507.

|
| [6] |
孙怀凤, 张诺亚, 柳尚斌, 等. 基于L1范数的瞬变电磁非线性反演[J]. 地球物理学报, 2019, 62(12):4860-4873.
|
| [6] |
Sun H F, Zhang N Y, Liu S B, et al. L1-norm based nonlinear inversion of transient electromagnetic data[J]. Chinese J. Geophys., 2019, 62(12):4860-4873.
|
| [7] |
Liu Y, Yin C, Qiu C, et al. 3-D inversion of transient EM data with topography using unstructured tetrahedral grids[J]. Geophysical Journal International, 2019, 217(1):301-318.

|
| [8] |
Auken E, Christiansen A V, Kirkegaard C, et al. An overview of a highly versatile forward and stable inverse algorithm for airborne, ground-based and borehole electromagnetic and electric data[J]. Exploration Geophysics, 2015, 46(3):223-235.

|
| [9] |
Raiche A P, Jupp D L B, Ruter H, et al. The joint use of coincident loop transient electromagnetic and Schlumberger sounding to resolve layered structures[J]. Geophysics, 1985, 50(10):1618-1627.

|
| [10] |
黄皓平, 王维中. 时间域航空电磁数据的反演[J]. 地球物理学报, 1990, 33(1):87-97.
|
| [10] |
Huang H P, Wang W Z. Inversion of time-domain airborne electromagnetic data[J]. Chinese J. Geophys., 1990, 33(1):87-97.
|
| [11] |
Farquharson C G, Oldenburg D W. Inversion of time-domain electromagnetic data for a horizontally layered earth[J]. Geophysical Journal International, 1993, 114(3):433-442.

|
| [12] |
Effersø F, Auken E, Sørensen K I. Inversion of band-limited TEM responses[J]. Geophysical Prospecting, 1999, 47(4):551-564.

|
| [13] |
Auken E, Christiansen A V. Layered and laterally constrained 2D inversion of resistivity data[J]. Geophysics, 2004, 69(3):752-761.

|
| [14] |
Auken E, Christiansen A V, Jacobsen L H, et al. A resolution study of buried valleys using laterally constrained inversion of TEM data[J]. Journal of Applied Geophysics, 2008, 65(1):10-20.

|
| [15] |
Viezzoli V, Christiansen A V, Auken E, et al. Quasi-3D modeling of airborne TEM data by spatially constrained inversion[J]. Geophysics, 2008, 73(3):F105-F113.

|
| [16] |
Constable S C, Parker R L, Constable C G. Occam’s inversion: A practical algorithm for generating smooth models from electromagnetic sounding data[J]. Geophysics, 1987, 52(3):289-300.

|
| [17] |
Sudha , Tezkan B, Siemon B. Appraisal of a new 1D weighted joint inversion of ground based and helicopter-borne electromagnetic data[J]. Geophysical Prospecting, 2014, 62(3):597-614.

|
| [18] |
毛立峰, 王绪本, 陈斌. 直升机航空瞬变电磁自适应正则化一维反演方法研究[J]. 地球物理学进展, 2011, 26(1):300-305.
|
| [18] |
Mao L F, Wang X B, Chen B. Study on an adaptive regularized 1D inversion method of helicopter TEM data[J]. Progress in Geophysics, 2011, 26(1):300-305.
|
| [19] |
齐彦福, 殷长春, 王若, 等. 多通道瞬变电磁m序列全时正演模拟与反演[J]. 地球物理学报, 2015, 58(7):2566-2577.
|
| [19] |
Qi Y F, Yin C C, Wang R, et al. Multi-transient EM full-time forward modeling and inversion of m-sequences[J]. Chinese J. Geophys., 2015, 58(7):2566-2577.
|
| [20] |
李海, 薛国强, 钟华森, 等. 多道瞬变电磁法共中心点道集数据联合反演[J]. 地球物理学报, 2016, 59(12):4439-4447.
|
| [20] |
Li H, Xue G Q, Zhong H S, et al. Joint inversion of CMP gathers of multi-channel transient electromagnetic data[J]. Chinese J. Geophys., 2016, 59(12):4439-4447.
|
| [21] |
Li M, Cheng J, Wang P, et al. Transient electromagnetic inversion based on the PSO-DLS combination algorithm[J]. Exploration Geophysics, 2019, 50(5):472-480.

|
| [22] |
Key K. 1D inversion of multicomponent, multifrequency marine CSEM data: Methodology and synthetic studies for resolving thin resistive layers[J]. Geophysics, 2009, 74(2):F9-F20.

|
| [23] |
Guptasarma D, Singh B. New digital linear filters for Hankel J0 and J1 transforms[J]. Geophysical Prospecting, 1997, 45(5):745-762.

|
| [24] |
Anderson W L. Fourier cosine and sine transforms using lagged convolutions in double-precision (subprograms DLAGF0/DLAGF1) [R]. U.S. Geological Survey, 1983.
|
| [25] |
Li J, Lu X, Farquharson C G, et al. A finite-element time-domain forward solver for electromagnetic methods with complex-shaped loop sources[J]. Geophysics, 2018, 83(3):E117-E132.

|
| [1] |
YOU Xi-Ran, ZHANG Ji-Feng, SHI Yu. Artificial neural network-based transient electromagnetic imaging[J]. Geophysical and Geochemical Exploration, 2023, 47(5): 1206-1214. |
| [2] |
QUE Ze-Sheng, LI Guan-Chao, HU Ying, JIAN Rui-Min, LIU Bing. GIS-based assessment of the radioactivity levels and risks of soil environment[J]. Geophysical and Geochemical Exploration, 2023, 47(5): 1336-1347. |
|
|
|
|

