大地电磁交错采样有限差分二维正反演研究

doi:10.11720/wtyht.2021.1280

Abstract
Figure/Table
References
Related Citation (15)

Download: PDF (3443 KB) HTML (0 KB)
Export: BibTeX | EndNote (RIS)

Abstract

The staggered sampling grid can automatically ensure that the electromagnetic field distribution obeys the law of energy conservation. Based on the staggered sampling grid, the authors deduced the two-dimensional finite difference forward process of magnetotelluric survey, and realized the two-dimensional forward program. Compared with one-dimensional analytical solution, the algorithm is proved to be correct and has high accuracy. Then, using the finite memory quasi Newton optimization algorithm, the authors realized the staggered sampling grid finite difference two-dimensional inversion. The correctness of the inversion algorithm was verified by theoretical model inversion, which shows that the efficiency of quasi Newton inversion with finite memory is better than that of nonlinear conjugate gradient. Finally, the deep structure of the survey area was found through the inversion and interpretation of the magnetotelluric data from Guanegou in Dangchang County, which shows that the algorithm has strong practicability.

Key words： magnetotelluric interleaved sampling two-dimensional forward modeling LBFGS

Received: 01 June 2020 Published: 29 April 2021

ZTFLH:

P319.1+9

Corresponding Authors: LUO Wei E-mail: 532954771@qq.com;luovitas@qq.com

	Service

	E-mail this article
	Add to my bookshelf
	Add to citation manager
	E-mail Alert
	RSS
	Articles by authors
	Wu ZHOU
	Wei LUO
	Xing LAN
	Xing-Xiang JIAN

Cite this article:

Wu ZHOU,Wei LUO,Xing LAN, et al. Two-dimensional magnetotelluric forward and inverse analysis of the finite-difference method with staggered sampling[J]. Geophysical and Geochemical Exploration, 2021, 45(2): 458-465.

URL:

https://www.wutanyuhuatan.com/EN/10.11720/wtyht.2021.1280 OR https://www.wutanyuhuatan.com/EN/Y2021/V45/I2/458

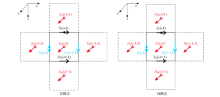
MT 2-D staggered grid finite difference separation diagram

模式位置	顶边界 (z=z_min)	底边界 (z=z_max)	侧边界 (y=y_min\|y_max)
TE模式	E_y=1	$? E y ? z$ =iωμ $E y Z bottom$	$? E y ? x$ =0
TM模式	H_y=1	$? H y ? z$ =σ $H y Z bottom$	$? H y ? x$ =0

Forms of boundary conditions

Apparent resistivity and impedance phase of 2-D forward modeling center of layered model

Anomalous body model

Forward section of abnormal body model

2-D inversion step length and fitting difference curve of abnormal body model

2-D inversion of anomalous body model

模式	$迭代 10 次耗时 / s NLCGLBFGS$		$拟合差 < 1 的耗时 / s NLCGLBFGS$
TE	75	59	175	125
TM	57	45	92	73
TE+TM	133	88	506	371

Comparison of inversion efficiency between LBFGS and NLCG

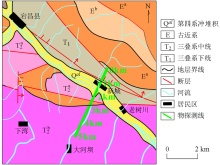
MT line distribution

MT inversion results

[1]	胡祥云, 霍光谱, 高锐, 等. 大地电磁各向异性二维模拟及实例分析[J]. 地球物理学报, 2013,56(12):4268-4277.
[1]	Hu X Y, Huo G P, Gao R, et al. Two dimensional simulation and case analysis of magnetotelluric anisotropy[J]. Journal of Geophysics, 2013,56(12):4268-4277.
[2]	童孝忠, 吴思洋, 谢维. 基于有限差分法的大地电磁二维倾子响应计算[J]. 工程地球物理学报, 2018,15(4):93-99.
[2]	Tong X Z, Wu S Y, Xie W. Calculation of magnetotelluric two-dimensional tilter response based on finite difference method[J]. Journal of Engineering Geophysics, 2018,15(4):93-99.
[3]	张弘宇, 温建亮, 张富明. 有限差分法二维地电构造模型大地电磁法正演模拟[J]. 矿产勘查, 2019,10(8):1988-1992.
[3]	Zhang H Y, Wen J L, Zhang F M. Forward modeling of two-dimensional geoelectric structural model by finite difference method[J]. Mineral Exploration, 2019,10(8):1988-1992.
[4]	Mitsuhata Y, Uchida T. 3D magnetotelluric modeling using the T-Ω finite-element method[J]. Geophysics, 2004,69(1):108-119.
[5]	谭捍东, 余钦范, Booker J, 等. 大地电磁法三维交错采样有限差分数值模拟[J]. 地球物理学报, 2003,46(5):705-711.
[5]	Tan H D, Yu Q F, Booker J, et al. Three dimensional staggered sampling finite difference numerical simulation of magnetotelluric method[J]. Chinese Journal of Geophysics, 2003,46(5):705-711.
[6]	李焱, 胡祥云, 杨文采, 等. 大地电磁三维交错网格有限差分数值模拟的并行计算研究[J]. 地球物理学报, 2012,55(12):160-167.
[6]	Li Y, Hu X Y, Yang W C, et al. Research on parallel computing of three-dimensional staggered grid finite difference numerical simulation of magnetotelluric[J]. Chinese Journal of Geophysics, 2012,55(12):160-167.
[7]	韩波. 大地电磁二维拟牛顿反演研究 [D]. 武汉:中国地质大学(武汉), 2012.
[7]	Han B. Quasi-Newton method for two-dimensional magnetotelluric inversion [D]. Wuhan:China University of Geosciences(Wuhan), 2012.
[8]	Constable S C, Parker R L, Constable C G. Occam's inversion: A practical algorithm for generating smooth models from electromagnetic sounding data[J]. Geophysics, 1987,52(3):289-300.
[9]	Rodi W, Mackie R L. Nonlinear conjugate gradients algorithm for 2-D magnetotelluric inversion[J]. Geophysics, 2001,66(1):174-187.
[10]	Dennis J E, Schnabel R I. Numerical methods for unconstrained optimization and nonlinear equations[M]. Upper Saddle River: Prentice-Hall, 1983.
[11]	阮帅. 三维大地电磁有限内存拟牛顿反演[D]. 成都:成都理工大学, 2015.
[11]	Ruan S. 3D magnetotelluric finite memory quasi Newton inversion[D]. Chengdu: Chengdu University of Technology, 2015.
[12]	王堃鹏. 张量CSAMT三维主轴各向异性正反演研究 [D]. 北京:中国地质大学(北京), 2017.
[12]	Wang K P. Research on the forward and inverse anisotropy of three-dimensional principal axis of tensor CSAMT [D]. Beijing: China University of Geosciences(Beijing), 2017.
[13]	凡友华, 刘雪峰, 陈晓非. 面波频散反演地下层状结构的拟牛顿法[J]. 物探与化探, 2006,10(5):83-86.
[14]	Tikhonov A N, Arsenin V Y. Solutions of Ill-posed problems[M]. Washington DC: Winston and Sons, 1977.
[14]	Fan Y H, Liu X F, Chen X F. Quasi Newton method for surface wave dispersion inversion of underground layered structure[J]. Geophysical and Geochemical Exploration, 2006,20(5):83-86.
[15]	Egbert G D, Kelbert A. Computational recipes for electromagnetic inverse problems[J]. Geophysical Journal International, 2012,189(1):251-267.