|
|
|
| The application of Mahalanobis distance to the delineation of multivariate outliers in the East Kunlun Mountains |
GENG Guo-Shuai1,2( ), YANG Fan3,4( ), YANG Fan3,4( ) ) |
1. School of Earth Sciences and Resources, China University of Geosciences, Beijing 100083, China
2. Geophysical Survey Center, China Geological Survey, Langfang 065000, China
3. Beijing Institute of Geology for Mineral Resources, Beijing 100012, China
4. Research Center of Geochemical Survey and Assessment on Land Quality, China Geological Survey, Langfang 065000, China |
|
|
|
|
Abstract Mahalanobis distance is a multivariate outlier detection method. At present, there are many outlier detection methods based on Mahalanobis distance. The purpose of this paper is to compare the advantages/disadvantages of various Mahalanobis distances in identifying multivariate outliers and to select a more suitable method for identifying multivariate anomalies. The authors selected 1∶500 000 stream sediment data in the East Kunlun Mountains of Qinghai Province to compare the effects of four methods: classical Mahalanobis distance, robust Mahalanobis distance based on minimum variance determinant (FMCD), robust mahalanobis distance based on Adaptive minimum variance determinant (Adaptive), and robust mahalanobis distance based on Comedian (Comedian) in identifying Cu, Co, Cr, Ni, V, Fe; Cd, Cu, Mo, Pb, Zn, Ag and three association outliers of Au, As, Sb. The result shows that the Comedian method is the superior, while the classical method is the worst. So Comedian method is the most effective multivariate outlier detection method in this area.
|
|
Received: 06 February 2020
Published: 29 April 2021
|
|
|
|
Corresponding Authors:
YANG Fan
E-mail: hnsmxggs@163.com;yangfan@igge.cn
|
|
|
|
|
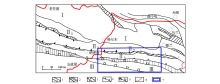
The map of geotectonic units in the study area
1—main structure zone; 2—secondary structure zone; 3—Neoproterozoic-early Paleozoic combined belt subduction direction(one-way subduction with teeth on one side and two-way subduction with teeth on both sides); 4—subduction direction of late Paleozoic and early Mesozoic suture belt; 5—A type subduction zones; 6—high way; 7—location of study area; Ⅰ—Qaidam massif; Ⅱ—East Kunlun orogenic belt; Ⅱ1—East Kunbei early paleozoic back-arc rife (Kunbei belt); Ⅱ2—East Kunzhong magmatic arc zone(Kunzhong belt); Ⅱ3—East-Kunnan tectonomagmatic belt(Kunnan belt); Ⅲ—Bayan Kara orogenic belt (Beiba belt)
|

| 组合 | 类型 | 有用组分 | 矿床(点) | | VHMS型 | Cu、Co、S(Au) | 督冷沟、驼路沟 | | 与基性岩有关的矿床组合 | SEDEX型 | Cu、Co、Pb、Zn(S、Ag、Au) | 纳赤台 | | 沉积变质型 | Fe、Mn | 洪水河、清水河 | | 与中酸性岩浆岩有关矿床组合 | 斑岩型 | Cu(Mo,Au) | 托克妥 | | 矽卡岩型 | Fe、Pb、Zn、Co、Cu、Au | 白石崖 | | 造山型金矿组合 | 蚀变岩型 | Au、As、Sb | 五龙沟、小干沟、东大滩、西藏大沟、大场 | | 石英脉型 | Au、Sb、As | 开荒北 |
|
Different type of ore deposits in the study area
|

|
The comparison of classical and robust mahalanobis distance from three element associations
|

| 元素组合 | 常规 | FMCD | Adaptive | Comedian | | 异常下限 | 异常个数 | 异常下限 | 异常个数 | 异常下限 | 异常个数 | 异常下限 | 异常个数 | | Cu、Co、Cr、Ni、V、Fe | 3.8 | 238 | 3.8 | 747 | 4.06 | 642 | 5.31 | 617 | | Cd、Cu、Mo、Pb、Zn、Ag | 3.8 | 192 | 3.8 | 710 | 4.15 | 592 | 4.92 | 703 | | Au、As、Sb | 3.06 | 173 | 3.06 | 753 | 3.4 | 658 | 3.85 | 793 |
|
Statistics of threshold and outliers determined by four methods
|
|
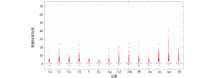
Boxplot for elements of standardized data
|
|
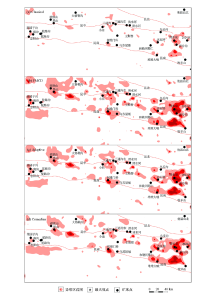
Multivariate outlier delineation for Co,Cr,Cu,V,Ni and Fe from four mahalanobis diatance methods in study area
|
|
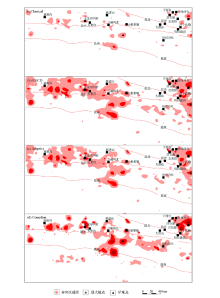
Multivariate outlier delineation for Cd,Cu,Mo,Pb,Zn and Ag from four mahalanobis diatance methods in study area
|
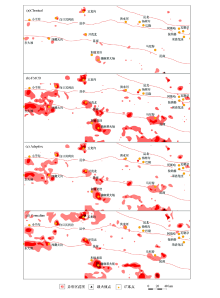
|
Multivariate outlier delineation for Au,As,Sb from mahalanobis distance methods in study area
|

| 元素组合 | Adaptive | Comedian | both | | 异常点数 | 占比/% | 异常点数 | 占比/% | 异常点数 | 占比/% | | Cu、Co、Cr、Ni、V、Fe | 233 | 27.61 | 201 | 23.82 | 410 | 48.58 | | Cd、Cu、Mo、Pb、Zn、Ag | 275 | 28.19 | 387 | 39.53 | 316 | 32.28 | | Au、As、Sb | 211 | 21.79 | 356 | 35.11 | 437 | 43.10 |
|
Statistics of outlier detection using Adaptive and Comedian methods
|

|
Outliers distribution of Co,Cr,Cu,Ni,V,Fe association using Adaptive and Comedian methods
|
| [1] |
Lindqvist L, Lundholm I, Nisca D, et al. Multivariate geochemical modeling and integration with petrophysical[J]. Geochemical Explor, 1987,29:279-294.

|
| [2] |
Rose A W, Hawkes H E, Webbs J S. Geochemistry in mineral exploration[M]. London: Academic Press, 1979: 657.
|
| [3] |
Stanely C R, Sinclair A J. Anomaly recognition for multi-element geochemical—A background characterization approach[J]. Geochemical Explor, 1987,29:333-353.

|
| [4] |
Govett G J S. Rock geochemistry in mineral exploration, Vol.3 of handbook of exploration geochemistry[M]. New York:Elsevier Science, 1983: 462.
|
| [5] |
Rocke D M, Woodruff D L. Identification of outliers in multivariate data[J]. Journal of the American Statistical Association, 1996,91:1047-1061.

|
| [6] |
Yeager M, Gregory B, Key C, et al. On using robust Mahalanobis distance estimations for feature discrimination in a damage detection scenario[J]. Structural Health Monitoring, 2019,18(1):245-253.
|
| [7] |
Xu L, Songren D, Lifang L, et al. Outlier detection based on robust mahalanobis distance and its application[J]. Open Journal of Statistics, 2019,9:15-26.
|
| [8] |
Hubert M, Rousseeuw P J, Van Aelst S. High-breakdown robust multivariate methods[J]. Statistical Science, 2008,23:92-119.
|
| [9] |
Mutalib S A, Ibrahim K. Identification of outliers: A simulation study[J]. Journal of Engineering and Applied Science, 2015,10(1):326-330.
|
| [10] |
Werner M. Idetification of multivariate outliers in large data sets[D]. Denver:University of Colorado, 2003.
|
| [11] |
Barnett V, Lewis T. Outliers in statistical data(3rd edition)[M]. New York:Wiley & Sons, 1994.
|
| [12] |
Rousseeuw P J, Zomeren B C. Unmasking multivariate outliers and leverage points[J]. Journal of the American statistical association, 1990,85(411):633-639.

|
| [13] |
宋运红, 李振祥, 李连辉, 等. 马氏距离与欧氏距离方法在地球化学异常处理中的对比[J]. 吉林地质, 2008,27(4):117-121.
|
| [13] |
Song Y H, Li Z X, Li L H, et al. Contrast between Mahalanobis distance and Eucliean distance in geochemical exploration processing[J]. Jinlin Gology, 2008,27(4):117-121.
|
| [14] |
Roberson G. Multiple outlier detection and cluster analysis of multivariate normal data[D]. Stellenbosch:University of Stellenbosch, 2003.
|
| [15] |
Pearson E, Chandra Sekar C. The efficiency of statistical tools and a criterion for the rejection of outlying observations[J]. Biometrika, 1936,28:308-320.
|
| [16] |
Chork C Y. Unmasking multivariate anomalous observations in exploration geochemical data from sheetedvein tin mineralisation near Emmaville, N.S.W[J]. Journal of Geochemical Exploration, 1990,37(2):205-223.
|
| [17] |
Hadi A S. Identifying multiple outliers in multivariate data[J]. Journal of the Royal Statistical Society, Series B, 1992,54(3):761-771.
|
| [18] |
Chork C Y, Salminen R. Interpreting exploration geochemical data from Outukumpu, Finland: A MVE-robust factor analysis[J]. Journal of Geochemical Exploration, 1993,48(1):1-20.
|
| [19] |
Hardin J, Rocke D M. The distribution of robust distances[J]. Journal of Computational and Graphical Statistics, 2005,14:910-927.
|
| [20] |
Hampel F R, Ronchetti E M, Rousseeuw P J, et al. Robust statistics:The approach based on influence functions[M]. New Jersey:John Wiley & Sons, 1986.
|
| [21] |
Hubert M, Rousseeuw P J, Van Aelst S. High-breakdown robust multivariate methods. Statistical[J]. Science, 2008,23:92-119.

|
| [22] |
Rousseeuw P J, Driessen K V. Algorithm for the Minimum covariance determinant estimator[J]. Technometrics, 1999,41(3):212-223.
|
| [23] |
Majewska J. Identification of multivariate outliers-problems and challenges of visualization methods[J]. Informatykai Ekonometria, 2015,247(4):69-83.
|
| [24] |
Filzmoser P, Garrett R G, Reimann C. Multivariate outlier detection in exploration geochemistry[J]. Compurers & Geosciences, 2005,31:579-587.
|
| [25] |
Sajesh T A, Srinivasan M R. outlier detection for high dimensional data using the comedian approach[J]. Journal of Statistical Computation and Simulation, 2012,82(5):745-757.
|
| [26] |
张德全. 东昆仑地区综合找矿预测与突破[M]. 北京: 地质出版社, 2003.
|
| [26] |
Zhang D Q. Comprehensive prospecting prediction and breakthrough in Dongkunlun area of Qinghai Province[M]. Beijing: Geological Publishing House, 2003.
|
| [27] |
丁清峰. 东昆仑造山带区域成矿作用与矿产资源评价[D]. 长春:吉林大学, 2004.
|
| [27] |
Ding Q F. Metallogenesis and mineral resources assessment in East Kunlun Orogenic belt[D]. Changchun:Jilin University, 2004.
|
| [28] |
田立明. 青海省东昆仑成矿带区域地球化学数据处理及靶区优选[D]. 武汉:中国地质大学(武汉), 2017.
|
| [28] |
Tian L M. Geochemical data processing and targets optimization in Eastern Kunlun orogenic belt, Qinghai province[D]. Wuhan:China University of Geosciences(Wuhan), 2017.
|
| [29] |
Mahalanobis P C. On the generalized distance in statistics[J]. National Institute of Science of India, 1936,2:49-55.
|
| [30] |
张文秦, 汪彩芳, 刘成东. 依据化探成果对东昆仑地质背景的讨论[J]. 现代地质, 2002,16(3):257-262.
|
| [30] |
Zhang W Q, Wang C F, Liu C D. A discussion on geological based on background of the East Kunlun area by geochemical exploration data[J]. Geoscience, 2002,16(3):257-262.
|
| [31] |
安国英. 青海省东昆仑地区地球化学异常特征及金矿找矿靶区筛选与评价[J]. 物探与化探, 2013,37(2):218-223.
|
| [31] |
An G Y. Geochemical characteristics and gold metallogenic target area selection and evaluation in east Kunlun region, Qinghai Province[J]. Geophysical and Geochemical Exploration, 2013,37(2):218-223.
|
| [32] |
安国英. 青海省东昆仑中段地区构造地球化学特征及地质意义[J]. 物探与化探, 2015,39(1):69-75.
|
| [32] |
An G Y. Tectonic geochemistry of the central segment of the East Kunlun Mountains in Qinghai Province and its geological significance[J]. Geophysical and Geochemical Exploration, 2015,39(1):69-75.
|
| [33] |
Maronna R A, Yohai V J. Robust and efficient estimation of multivariate scatter and location[J]. Computational Statistics & Data Analysis, 2017,109:64-75.
|
|
|
|

