|
|
|
| Elastic wave propagation simulation in anisotropic media and random media using high-order difference method of rotation staggered grids based on convolutional perfectly matched layer |
| De-Shan FENG1,2, Xiang-Yu WANG1,2 |
1. School of Geosciences and Info-Physics,Central South University,Changsha 410083,China
2. Key Laboratory of Non-ferrous Resources and Geological Detection of Hunan Province,Changsha 410083,China |
|
|
|
|
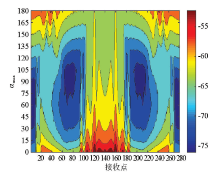
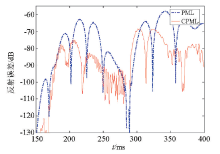
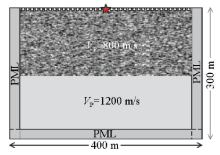
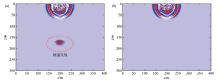
Abstract On the basis of the first-order velocity-stress elastic wave equation,a finite-difference discretization scheme with 2M-order accuracy of second-order space accuracy is deduced based on rotational staggered grid.The principle of recursive convolutional complex frequency shift perfectly matched layer (CPML) boundary condition is expounded,and the recurrence formula of first order velocity-stress elastic wave high order difference CPML boundary condition is established.The selection of the key parameter m,and sum of CPML boundary is carried out.By analyzing the distribution of reflection error,the optimal parameters of CPML boundary condition are selected.Both global reflection errors and wavefield snapshots indicate that CPML has better absorption properties than evanescent waves.On the basis of the Matlab platform,a program of elastic staggered forward simulation of rotating staggered grid based on CPML boundary is developed.The program is used to simulate the anisotropic medium and random medium.The seismic wave forward record and wavefield snapshot are obtained.The forward propagation profile and the wavefield snapshots can be used to better understand the propagation characteristics of seismic waves in anisotropic media and random media and to guide the interpretation of seismic exploration data in heterogeneous media.
|
|
Received: 17 July 2017
Published: 03 August 2018
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|

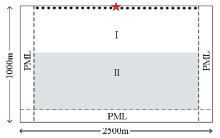
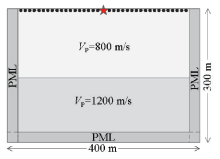
| 介质层 | C11 | C13 | C33 | C44 | ε | δ | ρ/(kg/m3) | | Ⅰ | 18.1 | 7.11 | 9.68 | 1.7 | 0.43 | 0.09 | 2250 | | Ⅱ | 25.5 | 5.0 | 18.4 | 5.6 | 0.19 | -0.11 | 2440 |
|
|
|
|
|
|

|
|
|

|
|
|

|
|
|
|
|
|

|
|
|
|
|
|

|
|
|

|
|
|

|
|
|

|
|
|
|
|
|
| [1] |
董良国, 马在田, 曹景忠 , 等. 一阶弹性波方程交错网格高阶差分解法[J]. 地球物理学报, 2000,43(3):411-419.
|
| [2] |
董良国, 马在田, 曹景忠 . 一阶弹性波方程交错网格高阶差分解法稳定性研究[J]. 地球物理学报, 2000,43(6):856-864.
|
| [3] |
Madariaga R . Dynamics of an expanding circular fault[J]. Bulletin of the Seismological Society of America, 1976,66(3):163-182.
|
| [4] |
Virieux J . P-SV wave propagation in heterogeneous media:Velocity stress finite-difference method[J]. Geophysics, 1986,51(4):889-901.

|
| [5] |
Virieux J . SH-wave propagation in heterogeneous media:Velocity stress finite-difference method[J]. Geophysics, 1984,51(4):1933-1942.
|
| [6] |
裴正林 . 双相各向异性介质弹性波传播交错网格高阶有限整分法模拟[J]. 石油地球物理勘探, 2006,41(2):137-143.

|
| [7] |
裴正林 . 三维双相各向异性介质弹性波方程交错网格高阶有限差分法模拟[J]. 中国石油大学学报:自然科学版, 2006,30(2):16-20.

|
| [8] |
孙卫涛, 杨慧珠 . 双相各向异性介质弹性波场有限差分正演模拟[J]. 固体力学学报, 2004,25(1):21-28.

|
| [9] |
陈祖银, 王用军, 彭达 . 弹性波波场分离数值模拟[J]. 中国石油勘探, 2014,19(6):47-53.
|
| [10] |
Chen K Y . Finite-difference simulation of elastic wave with separation in pure P-and S-modes[J]. Journal of Computation methods in Physics, 2014,( 3):1-14.

|
| [11] |
奚先, 姚姚 .二维弹性随机介质中的波场特征[J].地球物理学进展, 2005, 20(1): 147-154 .
|
| [12] |
奚先, 姚姚 . 随机介质模型的模拟与混合型随机介质[J]. 中国地质大学学报:地球科学, 2002,27(1):67-71.

|
| [13] |
奚先, 姚姚 . 二维随机介质及波动方程正演模拟[J]. 石油地球物理勘探, 2001,31(5):546-552.

|
| [14] |
陈浩, 王秀明, 赵海波 . 旋转交错网格有限差分及其完全匹配层吸收边界条件[J]. 科学通报, 2006,51(17):1950-1994.

|
| [15] |
Berenger J P . A perfectly matched layer for the absorption of electromagnetic waves[J]. Journal of Computational Physics, 1994,114(2):185-200.

|
| [16] |
Berenger J P . Three-dimensional perfectly matched layer for the absorption of electromagnetic waves[J]. Journal of Computational Physics, 1996,127(2):363-379.

|
| [17] |
Li J, Zeng Z F, Huang L , et al. GPR simulation based on complex frequency shifted recursive integration PML boundary of 3D high order FDTD[J]. Computers & Geosciences, 2012,49(4):121-130.
|
| [18] |
Hastings F D, Schneider J B, Broschat S L . Application of the perfectly matched layer (PML) absorbing boundary condition toelastic wave propagation[J]. Journal of the Acoustical Society of America, 1996,100(5):3061-3069.

|
| [19] |
Drossaert F H, Giannopoulos A . A nonsplit complex frequency-shifted PML based on recursive integration for FDTD modeling of elastic waves[J]. Geophysics, 2007,72(2):9-17.
|
| [20] |
Drossaert F H, Giannopoulos A . Complex frequency shifted convolution PML for FDTD modeling of elastic waves[J]. Wave Motion, 2007,44(7-8):593-604.

|
| [21] |
Zhang W, Shen Y . Unsplit complex frequency-shifted PML implementation using auxiliary differential equations for seismic wave modeling[J]. Geophysics, 2010,75(4):141-154.

|
| [22] |
Martin R, Komatitsch D, Gedney S D , et al. A high-order time and space formulation of the unsplit perfectly matched layer for the seismic wave equation using auxiliary differential equations (ADE-PML)[J]. CMES, 2010,56(1):17-40.
|
| [23] |
张显文, 韩立国, 黄玲 , 等. 基于递归积分的复频移PML弹性波方程交错网格高阶差分法[J]. 地球物理学报, 2009,52(7):1800-1807.

|
| [24] |
Roden J, Gedney S D. Convolution(PMLCPML):an effcient FDTD implementation of the CFS-PML for arbitrary media[J]. Microwave & Optical Technology Letters, 2000,27(5):334-339.
|
| [25] |
张鲁新, 符力耘, 裴正林 . 不分裂卷积完全匹配层与旋转交错网格有限差分在孔隙弹性介质模拟中的应用[J]. 地球物理学报, 2010,53(10):2470-2483.

|
| [26] |
Saenger E H, Gold N, Shapiro S A . Modeling the propagation of elastic waves using a modified finite-difference grid[J]. Wave Motion, 2000,31(1):77-92.

|
| [27] |
Kuzuoglu M, Mittra R . Frequency dependence of the constitutive parameters of causal perfectly matched anisotropic absorbers[J]. IEEE Microwave and Guided Wave Letters, 1996,6(12):447-449.

|
| [1] |
SUN Si-Yuan, YU Xue-Zhong, XIE Ru-Kuan, HE Yi-Yuan, SHAN Xi-Peng, LI Shi-Jun. Capabilities of airborne electromagnetic methods to detect permafrost[J]. Geophysical and Geochemical Exploration, 2022, 46(1): 104-113. |
| [2] |
WANG Bo, GUO Liang-Hui, CUI Ya-Tong, Wang Xiang. The approach to gravity forward calculation of 3D Tesseroid mesh model and its parallel algorithm[J]. Geophysical and Geochemical Exploration, 2021, 45(6): 1597-1605. |
|
|
|
|
