0 引言
南海是中国近海中面积最大的海区,位于欧亚板块、太平洋板块和印度洋板块的交汇部位,其地质构造复杂,富含大量海洋油气矿产资源,是国内外地球科学研究的热点区域。我国多家调查机构先后在南海开展历经数十年的地球物理勘查工作,积累了大量的历史测量数据,随着对南海研究的深入,除开展新的勘查测量外,对历史测量数据的信息挖掘工作也尤为重要。在对南海海域历史磁测数据进行整编的过程中,发现南海南部某区块历史采集的磁测数据精度较差,对整编效果也产生了严重影响,同时该部分数据包含的信息对南海构造演化研究意义重大,因此急需对该组数据开展重处理工作,以期提升数据精度,为后续的数据整编及科学研究提供基础。
依据规范[1]要求,海洋磁测数据的主要处理内容包括日变改正、探头位置改正、船磁影响改正、地磁正常场计算、交点差平差,由此可将获得每个测点处的地磁异常值,其中,日变改正是磁测数据处理中最重要的环节。通过翻阅上述历史数据的处理记录,并对历史处理成果数据进行分析,发现数据误差最大的来源为日变改正,主要是由于受当时的测量及处理方法技术手段的限制,而无法获取工区附近的地磁日变数据所导致,因此需要开展对日变改正方法的针对性研究,旨在解决该组数据日变改正误差大的问题。
国内外对于磁测数据日变改正方法的研究主要有地磁区域变化场特性分析、地磁日变数据模拟、地磁变化场建模、日变改正基值确定等内容,本次数据重处理将主要结合地磁变化场特征对地磁日变数据模拟方法进行研究改进。姚俊杰等[2]在2002年对地磁日变观测数据进行了理论分析;边刚等[3]在2009年对加权平均法和函数拟合法进行了分析,通过实例验证了该方法可不考虑经度效应的影响,只使用纬度方向的距离来计算某点的日变改正值;卞光浪等[4]在2010年利用纬差加权法进行多站地磁日变改正值计算,将日变数据的差异只建立在纬度差关系上,通过实例进行计算验证,证实该方法较距离加权法效果更好;张向宇等[5]在2016年根据地磁变化场特性,利用回归分析法推算某处地磁日变数据,通过实例分析,验证了该方法的可靠性;牛超等[6-
本文将根据区域特点,重新收集相关地磁观测台站数据,并根据地磁变化场特性以及收集数据的情况,分别使用回归分析法和CM4模型法,以及结合两种算法的特点形成的以CM4模型数据为样本控制下的回归分析法进行日变数据推算,对历史实测数据进行日变改正重处理,同时引入地磁指数对因磁扰引起的交点差的时段数据进行细致删减,得到重处理后的磁测成果数据,较历史数据精度有较大提升,解决了因日变改正误差大而导致的数据精度差的问题。
1 历史数据分析
1.1 野外采集情况
历史磁测数据是在2013年6月~11月期间采集的,共45条测线,其中主测线为EW向,共17条,检查线共28条,测网共173个交点,测量区域为4°~8°N,108°~114°E,测量船速为8 kn,均保持匀速直线航行,野外未布设日变站。
1.2 历史数据的处理情况
2013年11月开展对该批采集磁测数据的处理工作,并于该年12月完成处理。处理时,先按照采集仪器分布情况,采用拖曳概算法进行磁力探头位置改正;选择距离工区最近的越南DLT地磁台站(11.9°N,108.5°E)的观测数据做日变改正;因野外未进行船磁方位试验,故不进行船磁影响的改正;采用国际地磁参考场(IGRF)值作正常场改正,采用国际地磁与高空物理协会于 2010年发表的系数,球谐分析的阶次计算到13阶,在各项改正完成后,进行测线系统差调整,得到磁异常值,最终计算得到的磁异常交点差的最大值为84.61 nT,中误差为17.41 nT。
1.3 数据误差分析
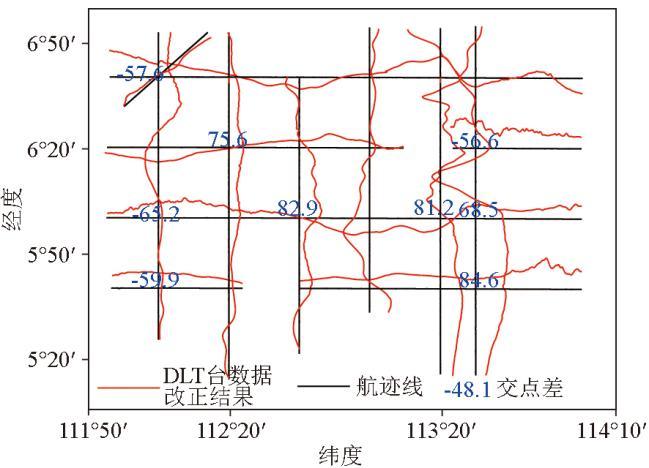
从上述处理情况可以看到,处理后数据误差较大,其中磁力探头位置改正、日变改正和船磁影响改正都将对结果产生较大影响。探头位置改正是通过算法将导航定位位置改正到探头处,所采用的拖曳概算法假定船只保持高速匀速直线的情况,计算误差较小。野外未进行船磁试验,将导致无法进行船磁影响改正,但本次采集测线均为直线,船磁影响改正值与航向相关,则同一测线上改正值相同,通过后续的系统差调整可将其消除掉,对最终数据精度影响较小。同时,因地磁参考场变化较小,故正常场改正带来的误差也较小。而处理时选择距离工区中心位置超过500 km的DLT地磁台站数据进行日变改正,因距离已超过台站有效控制距离,导致日变改正误差较大,也是最终数据误差的最大来源。图1是截取的某几条测线的平剖图,这几条测线位于工区东部,距离DLT地磁台站1 000 km,图中蓝色数字标识了历史数据处理后交点差(调差前)分布情况(只显示绝对值大于50 nT的交点差),该区域共存在24个交点,其中9个交点的交点差值超过50 nT,而全测区共5个交点的交点差超过80 nT,仅该区域中就存在3个。其误差主要由地磁台站距离测点较远所导致,且部分测线作业时发生磁扰,亦可对改正结果产生一定误差。因此,想提升该批数据的精度,需主要针对日变改正进行改进,利用日变数据模拟算法推算出工区内地磁的日变数据,以期达到对全测区进行有效控制的目的,可减小日变改正误差,提升磁测数据精度。
图1
1.4 数据重处理方案
根据对历史数据的分析情况,制定相应的数据重处理方案:首先重新整理历史成果数据,保留原来的探头位置改正结果,在此基础上重新进行日变改正、正常场计算和系统差调整。其中正常场值将采用国际地磁与高空物理协会于2020年发表的系数进行重算,日变改正将分别采用CM4模型法、回归分析法和CM4模型数据为样本控制下的回归分析法这3种方法推算的日变数据进行计算,对重新计算后的3组数据分别进行系统差调整,比较各组数据的精度,并与历史处理后的成果数据进行对比,选择精度最高的数据作为最终处理结果。
2 数据重处理
2.1 地磁日变数据收集情况
根据工区的位置和野外测量时间重新收集了相关地磁观测台站数据,具体信息见表1。
表1 地磁观测台站下载数据信息统计
Table 1
| 台站名称 | 台站类型 | 位置 | 数据覆盖时间 | 数据来源 |
|---|---|---|---|---|
| DLT | 陆地 | 11.95°N, 108.5°E | 2021.6.23~2021.11.3 2021.8.15~2021.9.30 | 网上下载 |
| PHU | 陆地 | 21.03°N, 105.96°E | 2021.6.23~2021.11.3 2021.8.15~2021.9.30 | 网上下载 |
| HD | 海底 | 6.64°N, 109.75°E | 2021.8.15~2021.9.30 | 自主采集 |
2.2 日变数据推算
根据工区位置和收集数据的情况,分别采用CM4模型法、回归分析法和以CM4模型数据为样本控制下的回归分析法推算不同位置处的日变数据。
2.2.1 CM4模型法
CM4模型将场源分为内源场与外源场,内源场包括主磁场和地壳场;外源场包括磁层场、磁层感应场、电离层场、电离层感应场及环形场,模型适用时间为1960年1月~2002年6月。推算时间在CM4模型适用时间以内时,可直接使用CM4模型计算内源场与外源场;在模型适用时间以外时,将使用IGRF模型计算内源场,CM4模型计算外源场。内源场和外源场计算出的结果均为X、Y、Z三分量数据,所以可将内外源场各个分量分别相加后,得到X、Y、Z三分量值后,再由F=(X2+Y2+Z2)1/2计算出最终的总场值。
本次推算时间在模型适用时间以外,故分别采用IGRF模型和CM4模型计算外源场和内部场,根据工区位置和范围,选择计算位置(6°N,111°E)(工区中心)处的地磁日变数据。
2.2.2 回归分析法
根据对地磁场分布规律的相关研究可知,地磁日变值随纬度呈现幅值差异,随经度呈现相位差异,即存在时差。其中,地磁场总强度F值随磁纬度变化规律为:在日变场为N向时,数值随磁纬度增加而减小,日变场为S向时,数值随磁纬度增加而增大;在小范围内(纬度差不超过10°)可认为日变值随纬度呈线性变化[15],即线性相关的。则据此规律,可引入统计学中常用的回归分析法来拟合关系式并推算日变数据。地磁台站间日变数据呈线性关系,可用如下方程式表示:
式中:a、b为常数;ΔT1、ΔT2分别为2个基站台的地磁场值;ΔT为待推算位置处地磁场值。式(1)的关键在于如何求取参数a和b的值,当可以收集到相同时间段内ΔT、ΔT1、ΔT2的参数作为样本时,则可利用最小二乘法对式(1)中的参数a、b进行无偏估计,最终得到一个确定的回归方程。由此可知,在可获取两个经度相近(5°以内)且纬度差距不超过10°的地磁台站观测数据(F值)的情况下,可据式(1)推算任意纬度处的地磁日变数据,推算以内插推算结果误差较小,外推计算时将随着待推算位置纬度较最近台站纬度差距加大而增大,使用时应以内插计算为主。
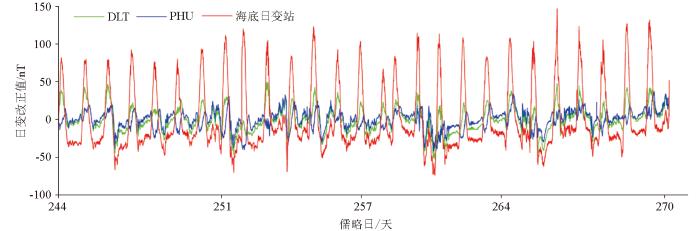
图2
图2
2021年某航次测量时段内日变数据对比
Fig.2
Comparison chart of diural variation data during the measurement time of a certain period in 2021
2.2.3 CM4模型数据为样本控制下的回归分析法
基于上述两种方法,更进一步地结合两种算法优化推算方法,可获得以CM4模型数据为样本控制下的回归分析法,即以计算得到的CM4模型法推算数据为样本,以DLT和PHU地磁台数据为基础,采用回归分析法拟合出3台站之间的关系式,并采用该关系式计算得到日变数据。因CM4模型法和回归分析法均在磁扰时段推算误差增大,则在计算时需选取连续的磁平静日数据作为样本,以期减小计算的误差。
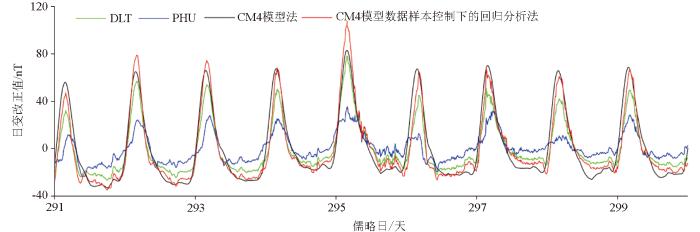
本次推算选取2021-10-18~2021-10-26时间段内由CM4模型法推算数据为样本,经统计,该时段内地磁指数Kp值范围为0°~2°+,Ap值范围为0~9,为连续地磁平静时,同时选取DLT和PHU台站为基台站,通过回归分析法拟合出关系式,从而推算整个测量时段的日变数据,根据样本情况和方法原理可知,推算数据位置与CM4模型法推算位置一致,即为(6°N,111°E)处,将样本时段内样本数据和推算数据及两个基台站数据共同成图显示,如图3所示。
图3
图3
样本时段内不同方法推算结果对比
Fig.3
Comparison chart of results calculated by different methods in the sample period
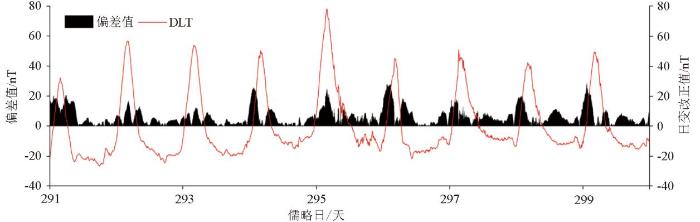
图4
图4
样本时段内不同方法推算结果偏差值示意
Fig.4
Diagram of deviation values of results calculated by different methods in the sample period
从图4中看出,两组方法推算结果偏差的较大值多集中在日变曲线的峰值附近,即每天23时~次日11时,且在日变曲线的拐点处偏差最大,这与两种推算方法原理不同有关。
2.2.4 推算结果分析
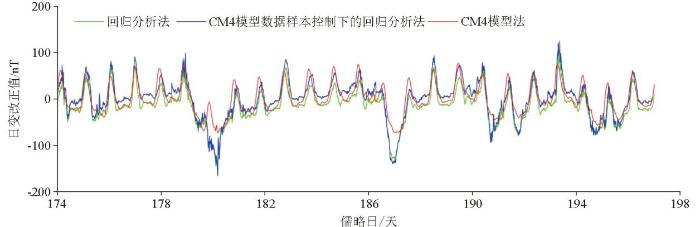
通过由以上3种方法,并选取合适的参数和样本数据,得到2013年航次某测量时段内工区中心位置处的3组推算数据,结果见图5所示。
图5
图5
2013年航次某测量时段内3组推算结果对比
Fig.5
Comparison chart of three sets of calculation results during a certian measuement period in 2013
表2 3种方法计算结果偏差统计
Table 2
| 方法一 | 方法二 | 偏差最大值 /nT | 偏差均值 /nT | 偏差均方根 差值/nT |
|---|---|---|---|---|
| 回归分析法 | CM4模型数据 样本控制下的 回归分析法 | 29.39 | 15.28 | 5.67 |
| 回归分析法 | CM4模型法 | 98.91 | 17.03 | 15.60 |
| CM4模型数据 样本控制下的 回归分析法 | CM4模型法 | 106.93 | 16.07 | 14.25 |
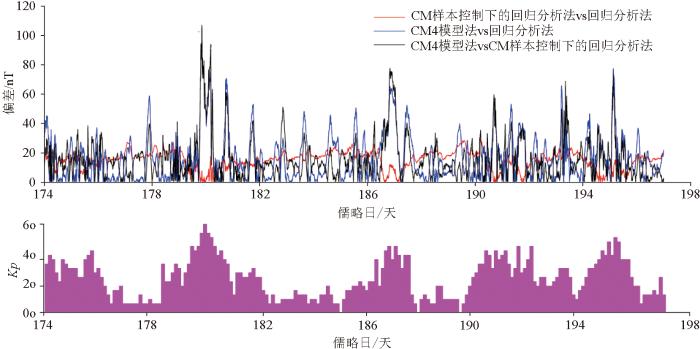
图6
图6
3种方法计算结果偏差对比
Fig.6
Comparison chart of three methods for calculating result deviation
2.2.5 工区数据重处理
依据本文制定的数据重处理方案对2013年采集的磁测数据进行重处理,其中日变改正分别采用上述3种推算方法得到的计算结果进行改正,统计处理后得到的磁异常交点差,结果见表3中“数据删减前”数据列所示。
表3 处理后磁异常交点差统计
Table 3
| 数据删减前 | 数据删减后 | ||||
|---|---|---|---|---|---|
| 所用日变数据 | 交点差最大值/nT | 交点差中误差/nT | 交点差最大值/nT | 交点差中误差/nT | 备注 |
| DLT台站数据 | 8.43 | 17.41 | 46.10 | 1.15 | 重处理前结果 |
| 回归分析法计算结果 | 66.03 | 1.07 | 30.10 | 9.61 | 重处理后结果 |
| CM4模型数据样本控制下的 回归分析法计算结果 | 64.93 | 1.91 | 29.57 | 9.33 | 重处理后结果 |
| CM4模型计算结果 | 90.65 | 18.84 | 6.11 | 17.78 | 重处理结果 |
从表3中看出,2013年处理时因技术方法的限制,使用DLT地磁台数据进行改正,该台站距离工区角点最远达到2 000 km,远超单一地磁台站控制范围,故改正后交点差较大,而通过运用3种不同方法推算工区内地磁日变数据的方法重新进行日变改正后,根据磁异常交点差统计情况可知,以CM4模型数据为样本控制下的回归分析法得到的日变数据做日变改正得到的数据精度最高,相较2013年以DLT地磁台数据改正后的处理结果,交点差的中误差提升了4.5 nT,数据精度得到了有效提升,但交点差的中误差依旧较大。该工区测线作业时间共持续62天,查询这62天的地磁指数Kp指数,发现其中有24天的Kp指数范围为4o~6o+,为中小幅度磁扰。进一步查询交点差详细分布情况,发现交点差大的交点多分布于上述所述磁扰时段,对该部分磁扰影响时段数据进行适量删减,经统计删减后共减少30个交点,删减后重新进行数据系统差调差处理,得到交点差统计情况见表3中“数据删减后”数据列所示。
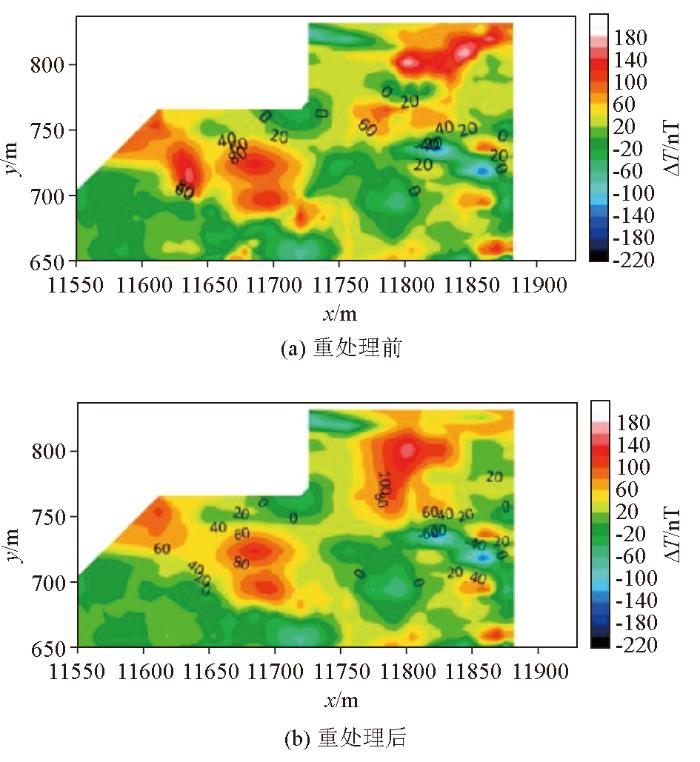
经数据删减并重新调整系统差后得到的各组成果数据精度均有所提升,其中由以CM4模型数据为样本控制下的回归分析法数据进行日变改正的成果数据精度提升至9.33 nT,为4组数据中精度最高的数据,而由回归分析法得到的数据精度与之较为接近。将重处理前后的工区磁异常平面等值线进行对比,见图7所示,图中可以看到重处理前数据(图7)中包含多个较为明显的沿测线方向分布的“串珠”状异常,这是由于这些位置处的交点误差较大导致的,而重处理后结果(图7b)中则不再存在这样由误差导致的异常条带,重处理效果显现。同时从图7中看到,重处理前后工区磁异常分布总体特征相似,但存在一些局部细节上的差异。在图7和图7b中该区域都显示为磁异常高,异常值指数范围也大致相同,但其分布范围和形态有所差异,这会导致后期不同的地质解释结论。这种差异对工区大范围区域地质构造研究影响较小,但对于局部区域地质解释则会导致不同的分析结果,在后期解释工作时应参考区域更多的地质取样、钻井等结果进行综合分析解释。
图7
图7
重处理前后工区磁异常平面等值线
Fig.7
Contour map of magnetic anomaly in the research area before and after reprocessing
为进一步定量评估重处理后的数据精度,将由以CM4模型数据为样本控制下的回归分析法数据进行日变改正的成果数据与该工区范围内在2023年采集的磁测数据求取交点差,计算两组数据外符合精度评估结果,2023年度采集数据时,在工区内投放了海底日变站,共采集74条测线,有420个交点,其处理后交点差最大值为23.86 nT,中误差为4.5 nT,数据质量较好,适宜用作外符合精度统计用。经统计,两组数据共有206个交点,交点差最大值为32.57 nT,中误差为7.86 nT,这也说明采用本文所研究的推算数据进行日变改正后的结果与真实值较为接近,从而证明了方法的可靠性。
3 结论
本文对南海南部某区历史磁测数据重处理过程及结果进行了对比分析,重点解决历史数据日变改正效果差的问题,根据重处理后的结果,有以下结论:
1)根据所搜集的地磁日变数据的情况,选择使用CM4模型法、回归分析法以及CM4模型数据样本控制下的回归分析法进行数据推算,分别运用3组推算结果进行日变改正重计算,其中以CM4模型数据样本控制下的回归分析法所得改正效果最佳;
2)CM4模型数据样本控制下的回归分析法是结合了CM4模型法和回归分析法各自特点形成的,其所得推算结果不仅较CM4模型法更高,同时又摆脱了回归分析法受样本数据获取方法限制的问题,该方法对解决南海南部区域磁测数据日变改正难度大的问题有显著效果;
3)在使用推算数据重新进行日变改正后数据交点差的中误差仍旧偏大,需结合地磁指数对磁扰发生时段的数据进行适当删减,以最大限度减小磁扰对数据精度的影响,经删减后数据交点的中误差提升,最终重处理后数据交点中误差为9.33 nT,较历史数据处理精度提升了4.5 nT,精度提升幅度较大,达到了数据重处理的预期效果;
4)通过结合重处理后数据的内符合精度和外符合精度评估结果,可知本文所采用的CM4模型数据样本控制下的回归分析法具有可靠性。
综上,本文通过采用地磁日变数据推算的方法解决南海南部区域数据重处理中日变改正误差大的难题,取得了较好的应用效果,并完成了对工区数据的重处理工作,达到了通过数据重处理工作提升历史数据精度的目的,为后续该历史数据的应用打下了良好基础,同时也为相关磁测数据处理方法研究提供了更多参考依据。
参考文献
地磁日变数据幅值关系分析与应用
[J].
Analyzingand applying the relation of amplitude value between the magnetic diurnal variations
[J].
海洋磁力测量中多站地磁日变改正值计算方法研究
[J].
Research on computation method of multi-station diurnal variation correction in marine magnetic surveys
[J].
基于纬差加权法的海洋磁力测量多站地磁日变改正值计算
[J].
Diurnal geomagnetic correction with multi-observatories in marine magnetic surveying
[J].
回归分析法在日变数据推算中的应用
[J].
The application of regression to estimating geomagnetic data
[J].
基于EEMD和改进Elman神经网络的地球变化磁场短时预测
[J].
Prediction of the geomagnetic variation field based on modified ensemble empirical mode decomposition and modified Elman neural network
[J].
地磁变化场的MEEMD-样本熵-LSSVM预测模型
[J].
Forecasting model of geomagnetic variation field based on modified ensemble empirical mode decomposition-sample entropy-least square support vector machine
[J].
基于克里格重构的区域地磁变化场短时预测模型
[J].
Regional geomagnetic short-term forecasting model based on Kriging reconstruction method
[J].
磁扰日日变改正的最小二乘谐波建模实现方法
[J].
The method realizing diurnal correction with harmonic model created by least square method in magnetically disturbed day
[J].
南海北部陆海台站地磁观测与磁场模型计算的对比分析
[J].
Comparative analysis of geomagnetic observation and magnetic field model calculation for land and marine stations in the northern South China Sea
[J].
地磁场模型在海洋磁测资料处理中的应用研究
[J].
Application of geomagnetic field model to marine magnetic data processing
[J].
地磁日变数据确定中顾及纬度和经度方向影响的双因子定权方法
[J].
Bifactor weight determination method considering the influence of latitude and longitude in the calculation of diurnal variation of geomagnetic data
[J].
顾及经纬度影响的多站地磁日变改正值计算
[J].
The correction of multi-station geomagnetic diurnal variation by the position changing on the components of latitude and longitude
[J].
海洋磁测中单台站地磁数据补缺方法探讨
[J].
Discussion on the method of geomagnetic data supplement for single station in marine survey
[J].
海洋磁测日变校正的纬度改正方法研究
[J].
Study on latitude correction method of diurnal variation correction for marine magnetic survey
[J].
基于BP神经网络的地磁变化场预测研究
[J].
Forecasting of the variable geomagnetic field based on BP neural network
[J].
The three-hour-range index measuring geomagnetic activity
[J].