E-mail Alert Rss
 

物探与化探, 2025, 49(5): 1212-1220 doi: 10.11720/wtyht.2025.1400

方法研究信息处理仪器研制

CPT磁力仪拖曳式探测系统的深度残差网络磁补偿方法

徐强锋,1,2, 王学锋,1,2, 邓意成1,2, 和焕雪1,2, 张慧松1,2, 卢向东1,2

1.北京航天控制仪器研究所,北京 100854

2.中国航天科技集团有限公司 量子工程研究中心,北京 100094

Deep residual network-based magnetic compensation for a towed, CPT-based magnetometer detection system

XU Qiang-Feng,1,2, WANG Xue-Feng,1,2, DENG Yi-Cheng1,2, HE Huan-Xue1,2, ZHANG Hui-Song1,2, LU Xiang-Dong1,2

1. Beijing Institute of Aerospace Control Devices, Beijing 100854, China

2. Quantum Engineering Research Center, China Aerospace Science and Technology Corporation, Beijing 100094, China

通讯作者: 王学锋(1974-),男,研究员,主要研究方向为原子磁力仪、光纤传感等航天光学测量。Email:xuefeng_wang@sina.cn

第一作者: 徐强锋(1995-),男,博士研究生,主要从事CPT原子磁力仪工程应用的误差校准、航磁补偿、磁异探测等方面的研究工作。Email:xqfcasc13@163.com

责任编辑: 王萌

收稿日期: 2024-09-26   修回日期: 2024-11-18  

Received: 2024-09-26   Revised: 2024-11-18  

摘要

传统的TL线性模型在处理CPT原子磁力仪拖曳式探测系统中的复杂磁干扰数据时,补偿精度存在局限性。为此本文引入神经网络技术,以实现更精准的非线性补偿。然而,常规神经网络模型在参数更新过程中可能遭遇梯度消失或过拟合等问题。为应对这些挑战,本文提出了一种基于深度残差网络的磁补偿模型(MCRNet),以进一步提升吊舱内磁干扰的补偿效果。试验结果显示,与传统方法中补偿效果最优的残差反向传播网络(ResBP)相比,MCRNet模型的改善比(IR)从4.251提升至4.826,增幅达13.53%;而补偿剩磁均方根误差(RMSE)从0.2减少至0.171,降低了14.5%。该模型提升了拖曳式磁异常探测系统的磁测精度。

关键词： CPT原子磁力仪; 拖曳式探测系统; MCRNet模型; 磁干扰补偿; 神经网络

Abstract

The traditional Tolles-Lawson (TL) linear model suffers limitations of compensation precision in processing complex magnetic disturbance data obtained using a towed coherent population trapping (CPT)-based atomic magnetometer detection system. This study introduced neural network technology to achieve more precise nonlinear compensation. Given that conventional neural network models encounter issues such as gradient vanishment or overfitting during parameter updates, this study proposed a deep residual network-based magnetic compensation model (MCRNet) to further enhance the compensation effects of magnetic interference within a towed pod. Experimental results demonstrate that compared to the best traditional method—The Residual Backpropagation Network (ResBP), the proposed MCRNet model increased the improvement ratio (IR) to 4.826 from 4.251, increasing by 13.53%, and reduced the root mean square error (RMSE) of compensated residual magnetism to 0.171 from 0.2, representing a reduction of 14.5%. The proposed model enhances the magnetic survey accuracy of towed magnetic anomaly detection systems.

Keywords： CPT-based atomic magnetometer; towed detection system; MCRNet model; magnetic interference compensation; neural network

PDF (3218KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

徐强锋, 王学锋, 邓意成, 和焕雪, 张慧松, 卢向东. CPT磁力仪拖曳式探测系统的深度残差网络磁补偿方法[J]. 物探与化探, 2025, 49(5): 1212-1220 doi:10.11720/wtyht.2025.1400

XU Qiang-Feng, WANG Xue-Feng, DENG Yi-Cheng, HE Huan-Xue, ZHANG Hui-Song, LU Xiang-Dong. Deep residual network-based magnetic compensation for a towed, CPT-based magnetometer detection system[J]. Geophysical and Geochemical Exploration, 2025, 49(5): 1212-1220 doi:10.11720/wtyht.2025.1400

0 引言

机载磁异常探测技术能够高效地获取区域地磁数据,并在科学、工业等领域中发挥着重要作用,例如水下目标探测、矿产资源勘探、地质勘探和地震预报等[1-3]。根据磁异常探测系统的安装方式不同,机载磁异常探测可以分为捷联式探测和拖曳式探测两种[4-6]。捷联式探测将高精度磁力仪直接安装在飞机平台上,磁力仪探头的姿态随着飞机飞行姿态的变化而变化[7]。由于探头与飞机本体距离较近,因此捷联式探测容易受到飞机本体磁干扰的影响,飞机本体磁干扰的大小通常影响捷联式探测的最终精度和灵敏度。而拖曳式探测则是通过软绳将磁力仪吊放在直升机下方几十米处,使探头远离飞机本体,飞机磁干扰的强度与距离的三次方成反比。因此,这种探测方式能够有效降低飞机整体磁干扰的影响,甚至可忽略不计[8]。

虽然拖曳式探测基本可以消除飞机本体磁干扰的影响,但拖曳吊舱内部的磁干扰仍会影响磁测精度。通过对拖曳吊舱材料进行控制,可以显著降低材料的磁干扰。但磁力仪的电子箱通常安装在吊舱内,在工作时,探头会受到电子箱内电子器件材料和电流的影响,产生几个纳特(nT)的磁干扰。尽管这些干扰量相对较小,但仍会影响磁测精度,尤其是在要求高精度的测量任务中。为了减小这种干扰的影响,通常采用TL模型进行磁干扰补偿[9]。TL模型的原理是建立干扰场与载体固有磁场、感应磁场和涡流磁场之间的线性关系。这些磁场量均与载体的姿态密切相关,对电磁干扰项的精确建模具有很大的挑战。有些研究通过假定电子器件电流为恒定直流,通过建立电流干扰的线性项来扩展TL模型[10-11]。但在实际系统中,可能存在多种电流值或交变电流(比如光源或气室的温控电流),使电磁干扰数据呈现复杂的结构。在这种情况下,基于线性回归的最小二乘法[12]、岭回归法[13]以及自适应滤波[14-15]等方法通常表现不稳定,且曲线拟合能力较差,从而影响磁补偿的质量。考虑到神经网络强大的非线性拟合能力,Williams[16]设计了3层神经网络用于航磁补偿,但网络层数和神经元个数较少导致其补偿效果有限。随着计算机硬件技术的发展,研究者增加神经元个数和网络的层数,并提出误差反向传播网络(BP网络)补偿磁干扰,但在参数更新过程中可能会出现梯度消失或过拟合的问题[17]。Yu等[18]提出残差反向传播网络(ResBP)来减缓该问题,但由于全连接网络结构的存在,仍然有过拟合的风险。

为了克服传统补偿方法的局限性,本文提出了一种深度残差磁补偿网络(MCRNet),用于吊舱磁干扰的补偿,利用磁异常探测系统地面试验数据训练模型,使其能够补偿复杂的磁干扰。与传统补偿方法作比较,该方法不仅提高了补偿的准确性,还增强了系统在实际应用中的稳定性和可靠性。

1 磁补偿模型

1.1 吊舱磁干扰建模

CPT原子磁力仪k时刻的输出可以表示为地磁场、转向差、干扰场之和:

Bck=Bek+Bhk+Bak,

式中:Bck为CPT原子磁力仪的输出值;Bek为地磁总场的真实值;Bhk表示转向差,即CPT原子磁力仪探头光轴与磁场方向夹角不同引起的测量偏差[19-20];Bak为吊舱产生的磁干扰场,混合了多种电流磁效应,比如吊舱内电子箱的气室温控的正弦加热电流、激光器控制的锯齿扫描电流等。虽然能够运用毕奥萨伐尔定律对电磁干扰进行近似建模,但在导线的空间布局、有效距离的测量等方面仍然存在巨大挑战。

TL线性模型中忽略了非线性电流效应的影响,并假设磁干扰场Bak由永久干扰磁场、感应干扰磁场、涡流干扰磁场3部分组成,并且3种干扰场均能够线性表示[21]。式(1)可扩展为:

Bck=Bek+Bhk+uT·x1x2x3+Bek·uTx4x5x6x5x7x8x6x8x9u+Bek·uTx10x11x12x13x14x15x16x17x18u'

式中:u=[cosα,cosβ,cosγ]T,表示地磁场方向余弦,α、β、γ分别表示地磁矢量方向与吊舱载体坐标系之间的夹角;u'表示方向余弦导数;xi(i=1,…,18)为未知参数。式(2)可进一步简化表示为:

Bck=Bek+Bhk+δkx,

式中:δk=[uT,vec(Bek·uuT)1×6,vec(Bek·uu'T)1×9],x=[x1,x2,…,x18]T。

式(3)的矩阵形式为:

Bc=Be+Bh+Ax,

式中:A=[δT1,δT2,…,δTN]TN×18为TL模型系数矩阵,Bc、Be、Bh分别表示CPT原子磁力仪输出值、地磁总场和转向差序列,为N×1向量。通过求解式(4)线性方程即可得到线性磁补偿系数x。

TL模型描述的干扰项与吊舱姿态密切相关,不足以表示吊舱内电子箱产生的非线性电磁干扰项,这些干扰项难以通过表达式直接计算。神经网络模型具有学习和预测复杂非线性关系的优势,通过大量数据的训练,可在实际测量过程中补偿非线性的磁干扰项,进而提高磁补偿的精度。考虑到CPT原子磁力仪探头与磁通门磁力仪探头均处于吊舱内,磁通门磁力仪测量数据中也包含电磁干扰项数据,运用该数据计算矩阵A作为神经网络的特征输入,既包含了TL模型的线性干扰特征,也包含了非线性电流磁干扰特征。因此,基于神经网络的磁干扰模型满足以下关系:

Bc=Be+Bh+f(A),

式中:f(A)可以表示任意非线性映射,需要从数据中学习获得。

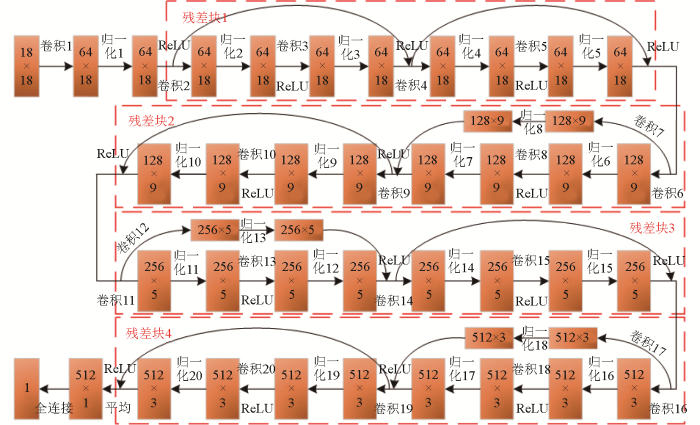
1.2 MCRNet网络结构设计

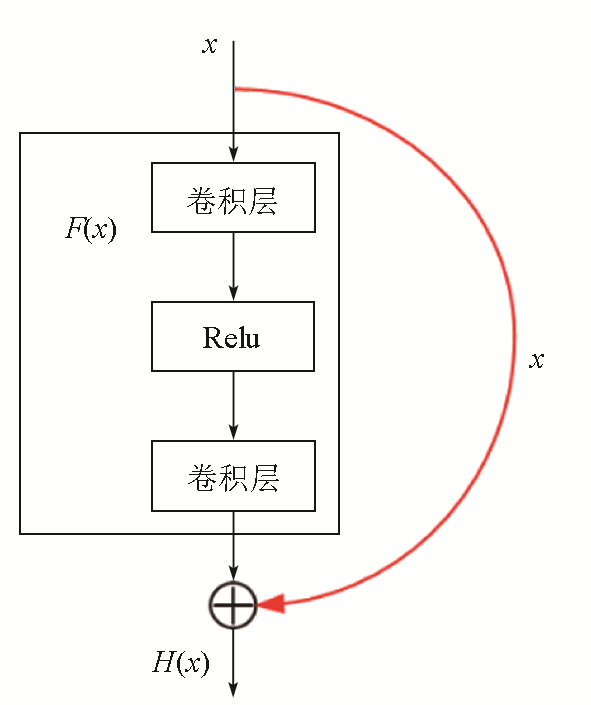
使用残差网络结构用于式(5)进行磁补偿。已有研究结果表明,残差网络能够解决由于网络深度增加而导致的精度降低问题[22]。其网络基本结构如图1所示,假设输入为x,将期望的输出映射关系表示为H(x),堆叠的非线性层表示为F(x)。如果F(x)输出的特征维度与x完全一致,则可直接通过直连边连接。因此,输出H(x)可以表示为:

H(x)=F(x)+x,

通过在非线性卷积层中增加短接边,原始目标函数H(x)的优化被转换为残差函数F(x)的优化,这种优化方式更易于学习[23]。此外,如果F(x)输出的特征维度与x不一致,则需要通过等宽卷积层连接。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   残差网络结构

Fig.1   Residual network structure


MCRNet网络模型结构基于以上残差网络结构设计,如图2所示。输入层设置为18×18的数据,第一个18表示矩阵A的18个特征,第二个18表示序列长度,该数据与后面网络的卷积层、池化层计算有关。经过卷积1层和归一化1层后转化为64×18的特征层。接下来,经过4个串联的残差块进行特征提取。残差块1包含两个带直连边的残差网络结构,残差块2、3、4的第一个残差网络结构增加了等宽卷积层和归一化层,以保持输出与输入特征结构的一致性,第二个残差网络结构为带直连边的残差网络结构。整个网络中的卷积层和归一化层的参数设置如表1所示。在残差块输出后,数据经过平均层将特征转化为512×1,最终通过线性层输出预测值。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   MCRNet磁补偿神经网络模型

Fig.2   MCRNet magnetic compensation neural network model


表1   MCRNet参数设置

Table 1  MCRNet parameter settings

卷积层卷积核尺寸步长填充归一化层特征
1、2、3、4、5、8、9、10、
13、14、15、18、19、20		3111、2、3、4、564
6、11、163216、7、8、9、10128
7、12、1712011、12、13、14、15256
----16、17、18、19、20512

新窗口打开| 下载CSV


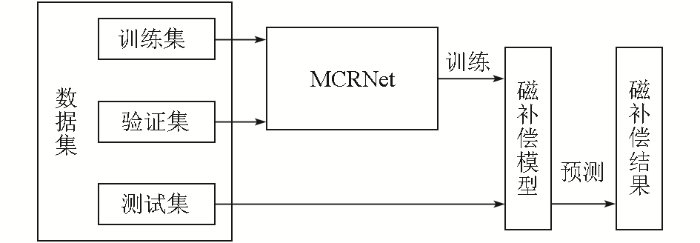
模型的训练和超参数调节是确保模型性能的关键步骤。整个模型训练与预测流程如图3所示。数据集被划分为训练集、验证集和测试集,这三者互不重叠。首先,训练集用于训练MCRNet网络模型。通过在训练集上的多次迭代,模型能够逐步学习数据的特征和模式。验证集在训练过程中发挥重要作用,它用于实时监测模型的误差,以便在模型过拟合或欠拟合时能及时调整超参数。超参数的调整可以显著影响模型的收敛速度和最终性能。最后,测试集用于评估经过训练的模型的实际性能。测试集中的数据在训练过程中未曾使用,因此可以客观地反映模型在处理新数据时的表现。通过在测试集上进行预测,可以检验模型在磁干扰补偿时的准确性和效果。通过上述方法和流程,可以不断优化MCRNet网络模型,使其在预测磁干扰方面达到更高的准确性和鲁棒性。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   模型训练与预测流程

Fig.3   Flowchart of model training and prediction


2 拖曳式探测地面磁补偿试验

2.1 地面试验系统及组成

与捷联式探测方案相比,拖曳式探测飞机与磁力仪之间仅通过软绳连接,因此磁力仪的姿态变化较大,通常要求高精度标量磁力仪没有方向盲区,并且具备自主全向适应能力,以适应拖曳式探测中吊舱姿态的变化。传统的光泵磁力仪在原理上存在方向盲区,因此通常需要通过复杂的多探头组合设计和数据切换来解决这一问题[24]。尽管Overhauser磁力仪没有方向盲区,但其采样率低导致空间磁测分辨率较低[25],不适合应用于航空磁探。相较之下,CPT原子磁力仪是一款高精度、无方向盲区的标量原子磁力仪[26]。通过优化控制算法,CPT磁力仪能够实现自主全向适应,即磁场方向与探头光轴成任意角度下无需工作模式切换,探头都可进行磁场测量,并且其采样率可达50 Hz以上,特别适用于地磁场测量和航空航天等领域[27]。

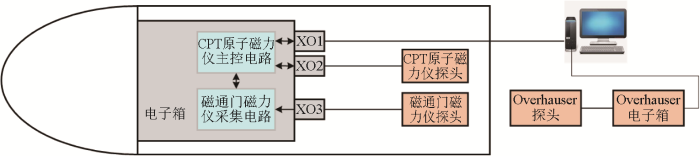
基于CPT原子磁力仪的拖曳式磁异常探测系统试验框架如图4所示。内部结构包括一个电子箱和两个磁力仪探头,整体精密布置以优化性能。磁通门磁力仪探头在y轴方向与CPT原子磁力仪探头光轴方向保持平行,可通过磁通门磁力仪输出数据得到CPT原子磁力仪探头光轴与磁场方向夹角信息。磁通门磁力仪通过XO3接口采集三轴磁场数据,并将这些数据传输到CPT原子磁力仪的主控电路。该主控电路通过XO2接口控制CPT原子磁力仪探头的信号和磁场数据采集。数据总包最终通过XO1接口输出至计算机进行处理和分析。图中Overhauser磁力仪电子箱和探头放置在吊舱外部,用于监测地磁场的长期变化,通过将CPT原子磁力仪的数据和Overhauser磁力仪的数据作差,可以获得不受地磁变化而影响的磁测数据。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   拖曳式磁异探测吊舱框架

Fig.4   Frame of the towed magnetic anomaly detection pod


在地磁场环境下,所用CPT原子磁力仪的灵敏度达到8 pT/Hz1/2,非线性度为1.3 ppm,并具备自主全向适应能力。此外,磁通门磁力仪探头采用了Bartington公司的Mag690-FL100型号,正交误差小于0.5°。Overhauser磁力仪是加拿大GEM公司生产的GSM-19型号,该设备具有±0.1 nT的绝对精度,确保了地磁场测量数据的高准确度。

2.2 数据采集

为降低环境磁干扰对磁补偿精度的影响,选在野外空旷地区进行试验和数据采集,试验实景如图5所示。Overhauser电子箱与计算机连接,以便与磁异探测系统同步数据采集和处理。标准的航磁补偿通常是飞机采用FOM飞行模式采集数据并运用TL模型求解磁补偿系数,然后将系数用于其他飞行数据磁补偿。FOM飞行包括4个方向的机动,每个方向包括一组±5°偏航、±5°俯仰和±10°翻滚组合动作。由于拖曳式磁异探测系统实际作业时空中姿态不可控,通过地面试验的方式,采取人工驱动的俯仰、偏航和翻滚动作来模拟吊舱在空中的运动。分段多次采集数据,以保证每次地磁场以及吊舱运动的姿态不同,从而丰富数据集的信息量。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   拖曳式吊舱探测试验环境

Fig.5   Test environment for towed pod detection


地面共开展了7次模拟机动测试,7次模拟机动的数据拼接后的结果如图6a所示。在俯仰、偏航和翻滚动作的驱动下,每次试验CPT原子磁力仪输出表现为几个纳特(nT)的波动,该部分需要进行补偿。相比之下,Overhauser磁力仪输出较为稳定,可以作为地磁场参考。此外,图中跳跃点表示分段数据的起始或末尾,不同段数据的台阶现象可能是由于不同时间段移动设备产生的磁梯度或者场地固有磁异常所导致。图6b表示磁通门磁力仪三轴输出数据,该数据可用于提供吊舱姿态信息。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   磁力仪实测数据

Fig.6   Magnetometer measured data


3 数据分析与处理

3.1 数据处理流程

在使用神经网络模型对吊舱磁干扰场进行补偿之前,必须先制作数据集,高质量的数据集是神经网络成功训练和准确预测的关键。图7为数据集制作的流程。CPT原子磁力仪与Overhauser磁力仪同步采集磁场数据,两者差值可以有效抵消环境磁场变化对测量结果的影响。CPT原子磁力仪转向差标定是指:磁补偿试验前,获取转向差值与探头轴向和磁场方向夹角之间的经验曲线。磁通门磁力仪校准后能够获取高精度的地磁场方位信息[28-30]。根据实时姿态信息并查询转向差经验曲线可以有效补偿CPT原子磁力仪转向差[31]。此外,校准后的磁通门磁力仪三轴数据通过TL模型计算矩阵A可作为神经网络特征输入。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   数据集制作流程

Fig.7   Block of the data set production process


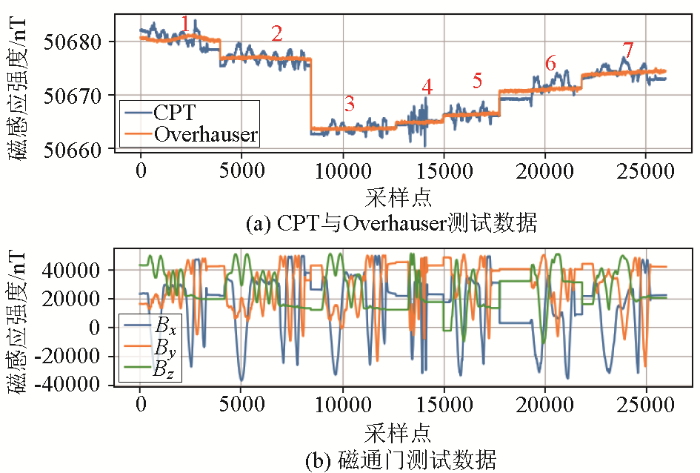
CPT原子磁力仪的标量场输出与Overhauser磁力仪输出、CPT转向差项之差以及特征输入数据共同构成数据集。在将数据输入神经网络之前,需要先对数据进行标准化,这不仅可以加快神经网络的计算速度,还能提高算法的精度。然后,将数据集1、4、5、6、7(如图6a所示)作为训练集,用于参数学习,数据集2作为验证集,用于模型验证及参数调整,数据集3作为测试集,用于评估训练后的模型性能。

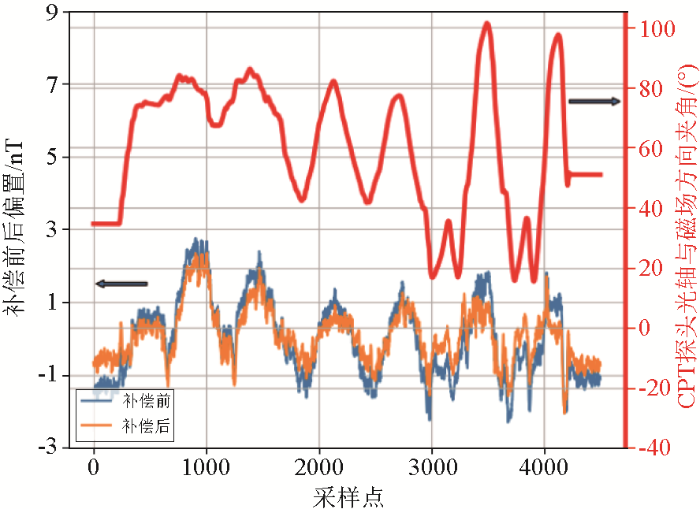
以数据集2为例,CPT原子磁力仪的转向差补偿结果如图8所示。横轴表示采样数据点,左边纵轴表示CPT原子磁力仪转向差补偿前后的偏置项,已减去Overhauser磁力仪参考值。可以看出转向差补偿后偏置项峰峰值变小,降低了由传感器方向变化引起的测量误差。右边纵轴表示不同采样数据点对应的CPT原子磁力仪探头光轴与地磁场方向之间的夹角,主要为转向差补偿提供依据。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   CPT原子磁力仪转向差校准

Fig.8   Heading error compensation of the CPT atomic magnetometer


参数学习的过程属于监督式学习,需要根据数据集制作网络的输入和标签值。式(5)矩阵A的每一行18个元素与测量值差值向量(Bc-Be-Bh)一一对应,为了实现数据之间更有效的特征提取,设置序列长度参数也为18,即抽取矩阵A的18行作为网络输入,取抽取的第18行对应的测量差值作为标签值。

3.2 MCRNet网络分析

3.2.1 训练、验证及测试

神经网络训练过程中,采取批处理的方式每次随机的从训练集中抽取n个不同输入和标签值用于模型训练和优化,损失函数采用均方损失,并采用Adam优化器来训练神经网络[32]。直至所有训练集均输入至网络,完成一次训练。则该次训练误差表示为均方损失的平均值:

Ltrainloss(k)=1mn∑i=1m∑j=1n(y︿ij-yij)2,

式中:m表示每次训练过程中训练集批量抽取的总次数;y︿ij和yij分别表示第i批次第j个样本的预测值和标签值。

在每次训练完成后,使用更新的模型计算验证误差。同样采取批量抽取的方式,然后计算每批次均方损失的平均值作为该次训练结果的验证误差:

Lvalidloss(k)=1pn∑i=1p∑j=1n(fk(xij)-yij)2,

式中:p表示每次训练过程中验证集批量抽取的总次数;xij和yij分别表示第i批次第j个输入和相应的标签值;fk(·)表示第k次训练的模型。

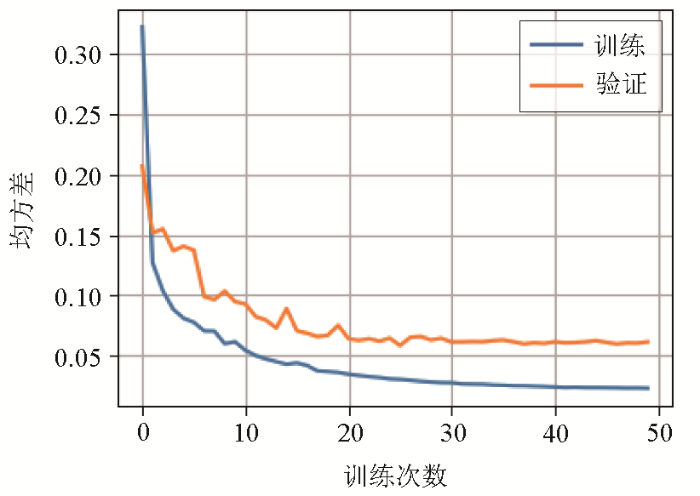
设置n=64,k=50,m、p可以根据实际数据长度计算。MCRNet网络训练过程的损失曲线如图9所示。从图中可以看出,在训练50次时,MCRNet网络模型的两条误差曲线趋于稳定,训练误差低于0.03,验证误差低于0.07。由于验证误差没有出现明显反常现象,因此模型训练没有过拟合。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   模型训练与验证过程

Fig.9   Model training and validation process


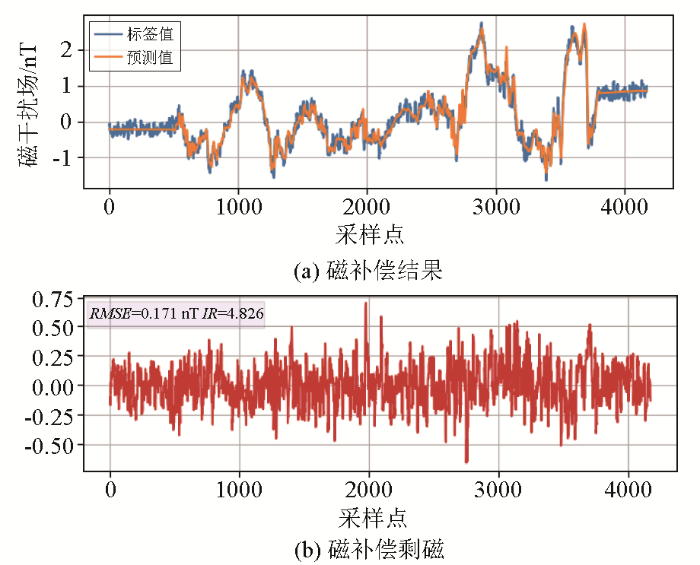
将训练好的模型分别用于测试集,使用补偿剩磁均方根(RMSE)和改善比(IR)来评估模型性能,RMSE越小且IR越大,模型性能越好。RMSE与IR指标定义如下:

RMSE=STD(ytest-fM(xtest)),
IR=STD(ytest)/RMSE,

式中:fM(·)表示训练完成的模型;xtest、ytest分别表示测试集输入和标签值。

图10a、b分别为MCRNet模型用于测试数据集磁补偿以及补偿剩磁的结果。通过式(9)、式(10)评估准则,MCRNet的RMSE为0.171 nT,IR为4.826。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   测试集预测结果

Fig.10   Test set prediction results


评估模型时,使用了浮点运算次数(FLOPs)、参数总数(parameter count,PC)、训练时间(training time,TT)以及预测时间(prediction time,PT)作为关键指标。FLOPs用于衡量模型的计算复杂度,而PC代表模型中的参数数量,它直接影响模型的复杂性及其过拟合的风险。TT则指训练模型所需的总时间,尤其在处理大型数据集和复杂模型时尤为重要。PT反映模型对新数据进行预测时的响应速度,这对于实时应用至关重要。所有的训练时间和预测时间均在配备NVIDIA GeForce RTX 4060 Laptop GPU的笔记本上完成。表2为MCRNet模型的相关指标信息,显示出其较高的FLOPs和PC,表明该模型具备较高的复杂度,因此训练时间TT也相对较长。同时,模型的PT为61.272 μs,远低于20 ms(对应50 Hz采样率),因此MCRNet模型能够适用于实时系统中。

表2   模型参数

Table 2  Parameters of the model

指标FLOPsPCTT/sPT/μs
MCRNet14.927M3.847M332.88261.272

新窗口打开| 下载CSV


从试验结果来看,MCRNet模型能够有效缓解深层神经网络中梯度消失和梯度爆炸问题,使得模型能够构建更深的层次而不过拟合。残差块的设计使模型能够专注于学习数据中的细微干扰特征,从而提升泛化能力,避免对训练数据的过度拟合,使其在测试集上表现出良好的性能和稳定性。在后续工作中,可以在保持模型高泛化能力和精度的前提下进一步优化其结构,减少模型复杂度,以降低计算资源消耗和训练时间。为此,可以考虑精简网络层数、应用参数剪枝、量化或知识蒸馏等技术,这将有助于提高模型在实际应用中的效率和适用性,特别是在实时处理需求高或计算资源受限的场景中。

3.2.2 与其他算法比较

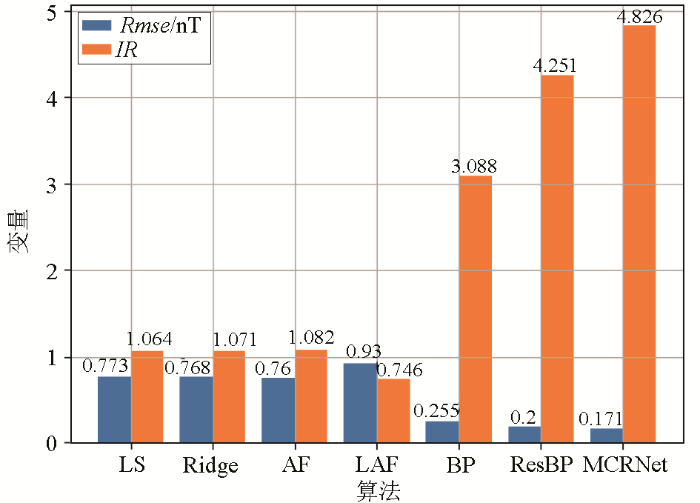
为进一步说明MCRNet模型的性能,将其与几种经典的线性模型算法及神经网络模型进行对比。对比算法包括:最小二乘法(LS)[12]、岭回归(Ridge)[13]、自适应滤波(AF)[13]、局部自适应滤波(LAF)[15],以及基于传统神经网络的BP网络[17]和ResBP网络[18]。评估指标则选用补偿后的剩磁均方根误差(RMSE)和改善比(IR),以全面衡量各模型的补偿效果和性能提升。

将训练集用于式(4)中的TL线性磁补偿模型,进行模型参数估计后,使用估计得到的参数在测试集上进行磁干扰补偿,按照式(9)和式(10)计算补偿剩磁均方根误差(RMSE)和改善比(IR)。图11为不同算法模型在这两个指标上的比较结果。从图中可以看出,LS算法在训练集中学习的全局最优参数在测试集中的磁补偿效果较差。相比之下,Ridge算法通过引入惩罚项防止过拟合,预测性能有所提升,但由于惩罚项系数固定,效果有限。AF算法能够动态调整惩罚项系数,进一步提高了预测性能,但整体改善仍不明显。LAF算法通过滑动窗口匹配训练集中与测试集最相似的部分,进行局部磁补偿,然而在本实验中的效果不佳,表明训练集与测试集的重叠部分较少。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11   不同算法模型比较

Fig.11   Comparison of different algorithms


相比线性模型补偿方法,基于神经网络的磁补偿方法表现出更优的性能。BP网络在IR和RMSE指标上有显著提升,加入残差结构后的ResBP网络性能进一步改善。而本文提出的深度残差网络MCRNet模型在RMSE和IR指标上表现最佳。与传统方法中效果最好的ResBP网络相比,MCRNet模型将IR从4.251提升至4.826,增幅13.53%,同时将RMSE从0.2降低至0.171,减少了14.5%。

4 结论

本文针对基于CPT原子磁力仪的拖曳式磁异常探测系统中的磁补偿问题展开研究。传统的TL模型由于其线性特性,难以有效应对复杂的磁干扰,补偿效果有限;同时,常规神经网络在参数更新过程中易出现梯度消失或过拟合问题。为此,本文提出了一种基于深度学习的深度残差磁补偿模型(MCRNet),并应用于拖曳吊舱中的复杂磁干扰补偿。试验结果显示,与传统效果最佳的ResBP网络相比,MCRNet的磁补偿性能显著提升,IR从4.251提高至4.826,增幅13.53%,RMSE则从0.2降至0.171,减少了14.5%,显著提升了拖曳式磁探测系统的精度。这一成果将有助于地质勘探、海洋调查和国防安全等领域的高精度磁异常探测。未来的研究将聚焦于优化模型的计算复杂度和参数量,并探索其与其他深度学习方法或物理模型的结合,以进一步提升系统在实际磁异常探测任务中的抗干扰能力和探测精度。

参考文献

彭翔, 郭弘.

光泵原子磁力仪技术

[J]. 导航与控制, 2022, 21(S2):101-121,198.

[本文引用: 1]

Peng X, Guo H.

Techniques in optically-pumped atomic magnetometer

[J]. Navigation and Control, 2022, 21(S2):101-121,198.

[本文引用: 1]

Gnadt A R, Wollaber A B, Nielsen A P.

Derivation and extensions of the tolles-lawson model for aeromagnetic compensation

[EB/OL]. 2022:2212.09899,2022-12-19. https://arxiv.org/abs/2212.09899v1.

URL     [本文引用: 1]

邱锡鹏. 神经网络与深度学习[M]. 北京: 机械工业出版社, 2020.

[本文引用: 1]

Qiu X P. Neural networks and deep learning[M]. Beijing: China Machine Press, 2020.

[本文引用: 1]

He K M, Zhang X Y, Ren S Q, et al.

Deep residual learning for image recognition

[C]// 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR),IEEE,2016.

[本文引用: 1]

Wang H, Du C P, Wang H D, et al.

Aeromagnetic compensation with suppressing heading error of the scalar atomic magnetometer

[J]. IEEE Geoscience and Remote Sensing Letters, 2020, 17(7):1134-1138.

DOI:10.1109/LGRS.2019.2940824      [本文引用: 1]

Scalar atomic magnetometer (SAM) with high sensitivity is designed to measure the total magnetic field and has been widely applied in aeromagnetic surveys. However, the measured total magnetic field of SAM is influenced by the magnetic disturbances due to the permanent, induced and eddy-current fields of the aircraft and heading errors of SAM. To reduce the magnetic disturbances caused by the aircraft maneuvers, a model was proposed by Tolles and Lawson and has been used in aeromagnetic compensation. However, the heading error of SAM deviates the compensation coefficients estimated by the Tolles-Lawson model. In this letter, we propose a linear model of heading error for multi-cell SAMs and analyze the new aeromagnetic compensation model in which the geomagnetic gradient and heading error are both taken into account. With using a He-4 magnetometer consisting of three orthogonal cells, the experimental results show that our proposed model has better performances than the previous model in terms of the figure of merit (FOM) and standard deviation (STD).

Fan S F, Chen S D, Zhang S, et al.

An improved Overhauser magnetometer for Earth’s magnetic field observation

[C]// Earth Observing Systems XXI,SPIE, 2016.

[本文引用: 1]

Zhang X N, Kou J, Li J, et al.

An omnidirectional measurement technology of CPT magnetometer based on coupling of the dark state

[C]// Fourth Seminar on Novel Optoelectronic Detection Technology and Application,SPIE, 2018.

[本文引用: 1]

王学锋, 邓意成, 徐强锋, 等.

宇航用原子磁力仪研究与应用进展

[J]. 前瞻科技, 2022, 1(1):159-168.

DOI:10.3981/j.issn.2097-0781.2022.01.013      [本文引用: 1]

磁场的测量对科学研究和人类生活具有重要作用,如地磁变化与地震关系、心脑磁场分布变化与心脑健康关系等。原子磁力仪是一类高精度的磁力仪,已经发展了多个原理的传感器,性能不断提升。文章主要论述了原子磁力仪的研究进展、应用现状、存在的问题和宇航用原子磁力仪发展建议,认为应进一步提高精度和灵敏度、加强轻小型化、标定测试方法和张量测量等研究,以促进中国磁场测量科学进步和应用对社会的贡献。

Wang X F, Deng Y C, Xu Q F, et al.

Research and application progress of atomic magnetometers for aerospace

[J]. Science and Technology Foresight, 2022, 1(1):159-168.

DOI:10.3981/j.issn.2097-0781.2022.01.013      [本文引用: 1]

The measurement of magnetic fields plays an important role in scientific research and human life. For example, geomagnetic variations can be used in earthquake prediction, and the changes in heart and brain magnetic field distributions contribute to the diagnosis of cardiovascular and cerebrovascular diseases. Characterized by high precision, several kinds of atomic magnetometers with different principles have been developed, and their performance keeps improving. This paper mainly discusses the key technologies, research progress, existing gap and development suggestions concerning atomic magnetometers. Future research of atomic magnetometers for aerospace should focus on accuracy and sensitivity improvements, miniaturization, calibration and tensor measurement to promote the advancement in magnetic field measurement and application in China.

Vasconcelos J F, Elkaim G, Silvestre C, et al.

Geometric approach to strapdown magnetometer calibration in sensor frame

[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(2):1293-1306.

[本文引用: 1]

Wu Y, Shi W.

On calibration of three-axis magnetometer

[J]. IEEE Sensors Journal, 2015, 15(11):6424-6431.

Merayo J M G, Brauer P, Primdahl F, et al.

Scalar calibration of vector magnetometers

[J]. Measurement Science and Technology, 2000, 11(2):120-132.

[本文引用: 1]

徐强锋, 王学锋, 邓意成, 等.

CPT原子磁力仪转向差及其标定补偿

[J]. 空间科学与试验学报, 2024, 24(1):95-101.

[本文引用: 1]

Xu Q F, Wang X F, Deng Y C, et al.

Heading error calibration and compensation of CPT atomic magnetometer

[J]. Journal of Space Science and Experiment, 2024, 24(1):95-101.

[本文引用: 1]

Xu Q F, Wang X F, Deng Y C, et al.

Heading error calibration and compensation of CPT atomic magnetometer

[J]. Journal of Space Science and Experiment, 2024, 1(1):95-101.

DOI:10.19963/j.cnki.2097-4302.2024.01.011      [本文引用: 1]

The CPT atomic magnetometer exhibits characteristics such as dead-zone-free operation, and continuous measurement capability without the need for mode switching when the magnetic field direction changes. This makes it particularly suitable for applications on satellites, helicopters, and other platforms. However, the CPT atomic magnetometer is prone to heading errors, and sensor remanence can adversely affect the accuracy of heading error compensation. This paper analyzes the heading error mechanism of the CPT atomic magnetometer and establishes a sensor remanence compensation model. Particle Swarm Optimization (PSO) is employed to estimate the remanence parameters, and the heading error curve is derived using cubic spline interpolation. Experimental results demonstrate that the algorithm estimates the projected component of sensor remanence on the rotating surface to be 0.344 nT, perpendicular to the sensor axis. After compensating for remanence, the standard deviation of residual error following heading error compensation decreases from 0.288 nT to 0.132 nT, marking a 54% reduction. This method effectively enhances the application performance of the CPT atomic magnetometer.

Kingma D P, Ba J.

Adam:A method for stochastic optimization

[C]// The 3rd International Conference for Learning Representations, 2015.

李晨, 周建军.

航磁探测水下目标关键技术发展及应用

[J]. 舰船电子工程, 2023, 43(6):184-188.

[本文引用: 1]

Li C, Zhou J J.

Key technology development and application on aeromagnetic detection of target underwater

[J]. Ship Electronic Engineering, 2023, 43(6):184-188.

[本文引用: 1]

殷长春, 张博, 刘云鹤, 等.

航空电磁勘查技术发展现状及展望

[J]. 地球物理学报, 2015, 58(8):2637-2653.

DOI:10.6038/cjg20150804     

航空电磁作为一种高效的地球物理勘查技术手段, 其发展在国外(加拿大、澳大利亚等国家)已十分成熟.然而, 在我国该项技术仍处于发展当中, 在国内目前尚未形成具有实际探测能力的航空电磁系统和解释手段.这一现状严重影响了我国对地形地质条件复杂区域(比如广大西部地区)矿产资源勘查的需求.本文旨在通过系统介绍航空电磁勘查技术中的基础理论、关键技术、仪器系统、数据处理、解释及应用, 并对未来我国航空电磁勘查技术的发展提出建议, 使读者了解该技术未来发展方向和研究热点, 以期该项技术在我国得到快速发展并获得广泛应用.

Yin C C, Zhang B, Liu Y H, et al.

Review on airborne EM technology and developments

[J]. Chinese Journal of Geophysics, 2015, 58(8):2637-2653.

魏征, 杜度, 刘洋, 等.

美国反潜装备技术发展研究

[J]. 舰船科学技术, 2019, 41(17):154-157.

[本文引用: 1]

Wei Z, Du D, Liu Y, et al.

Research on the development of anti-submarine equipment and technology

[J]. Ship Science and Technology, 2019, 41(17):154-157.

[本文引用: 1]

Reeves C. Aeromagnetic surveys: principles,

practice and interpretation

[M]. Washington:Geosoft, 2005.

[本文引用: 1]

黄岩, 罗丁, 冯自成, 等.

无人直升机航磁测量系统集成及应用

[J]. 物探与化探, 2019, 43(2):386-392.

Huang Y, Luo D, Feng Z C, et al.

Unmanned helicopter aeromagnetic measurement system and its application

[J]. Geophysical and Geochemical Exploration, 2019, 43(2):386-392.

西永在, 路宁, 张兰, 等.

基于无人直升机平台的航磁系统集成与应用

[J]. 物探与化探, 2019, 43(1):125-131.

[本文引用: 1]

Xi Y Z, Lu N, Zhang L, et al.

Integration and application of an aeromagnetic survey system based on unmanned helicopter platform

[J]. Geophysical and Geochemical Exploration, 2019, 43(1):125-131.

[本文引用: 1]

Dou Z J, Han Q, Niu X M, et al.

An aeromagnetic compensation coefficient-estimating method robust to geomagnetic gradient

[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(5):611-615.

[本文引用: 1]

Zheng Y X, Li S Y, Xing K, et al.

Unmanned aerial vehicles for magnetic surveys:A review on platform selection and interference suppression

[J]. Drones, 2021, 5(3):93.

[本文引用: 1]

Tolles W E, Lawson J D.

Magnetic compensation of MAD equipped aircraft

[J]. Airborne Instruments Lab.Inc., 1950, 201(1):1-5.

[本文引用: 1]

刘宇欣, 李雯, 魏东岩, 等.

一种顾及舱内OBE干扰的改进航磁补偿方法

[J]. 导航定位与授时, 2024, 11(4):38-46.

[本文引用: 1]

Liu Y X, Li W, Wei D Y, et al.

A modified aeromagnetic compensation method robust to in-cabin OBE interferences

[J]. Navigation Positioning and Timing, 2024, 11(4):38-46.

[本文引用: 1]

Zhang C, Du C P, Peng X, et al.

An aeromagnetic compensation method for suppressing the magnetic interference generated by electric current with vector magnetometer

[J]. Sensors, 2022, 22(16):6151.

[本文引用: 1]

Li H, Ge J, Dong H B, et al.Aeromagnetic compensation of rotor UAV based on least squares[C]// 2018

37th Chinese Control Conference (CCC)

IEEE,2018.

[本文引用: 2]

Su Z N, Jiao J, Zhou S, et al.

Aeromagnetic compensation method based on ridge regression algorithm

[J]. Global Geology, 2022, 25(1):41-48.

[本文引用: 3]

Noriega G, Marszalkowski A.

Adaptive techniques and other recent developments in aeromagnetic compensation

[J]. First Break, 2017, 35(9):31-38.

[本文引用: 1]

Dou Z J, Liu C H, Wang J R, et al.

An adaptive aeromagnetic compensation method based on local linear regression

[J]. IOP Conference Series:Earth and Environmental Science, 2021, 783(1):012090.

[本文引用: 2]

Williams P M.

Aeromagnetic compensation using neural networks

[J]. Neural Computing & Applications, 1993, 1(3):207-214.

[本文引用: 1]

Zhou S, Yang C C, Su Z N, et al.

An aeromagnetic compensation algorithm based on radial basis function artificial neural network

[J]. Applied Sciences, 2023, 13(1):136.

[本文引用: 2]

Yu P, Bi F Y, Jiao J, et al.

An aeromagnetic compensation algorithm based on a residual neural network

[J]. Applied Sciences, 2022, 12(21):10759.

[本文引用: 2]

Oelsner G, Schultze V, IJsselsteijn R, et al.

Sources of heading errors in optically pumped magnetometers operated in the Earth’s magnetic field

[J]. Physical Review A, 2019,99:013420.

[本文引用: 1]

/

〈 〉

京ICP备05055290号-3
版权所有 © 2021《物探与化探》编辑部
通讯地址：北京市学院路29号航遥中心 邮编：100083
电话：010-62060192；62060193 E-mail：whtbjb@sina.com , whtbjb@163.com