反射波时频域地震波形反演方法

doi:10.11720/wtyht.2025.0043

反射波时频域地震波形反演方法

汪昆^,, 吴国忱^,, 贾宗锋, 杨凌云

中国石油大学 (华东) 地球科学与技术学院,山东青岛 266580

Reflection waveform inversion in the time-frequency domain

WANG Kun^,, WU Guo-Chen^,, JIA Zong-Feng, YANG Ling-Yun

School of Geosciences,China University of Petroleum(East China),Qingdao 266580,China

通讯作者: 吴国忱(1965-),男,教授,博士生导师,现从事地球物理方面的教学和科研工作。Email :guochenwu@upc.edu.cn

第一作者: 汪昆(1998-),男,硕士研究生,2020年毕业于长安大学,获地球物理学学士学位;现于中国石油大学(华东)攻读地质工程专业硕士学位,主要从事地震波正演模拟方面的学习和研究工作。Email:1514073707@qq.com

责任编辑: 叶佩

收稿日期: 2025-02-25 修回日期: 2025-07-3

基金资助:

国家自然科学基金重点项目“深部裂缝储层地震预测理论方法及关键技术研究”(42430809)

Received: 2025-02-25 Revised: 2025-07-3

摘要

反射波形反演通过交替更新模型中的中低波数组分和高波数组分为全波形反演提供良好的初始模型。但时域反射波形反演需要存储整个时间序列的震源背景波场与接收点散射波场互相关求取梯度,占用巨量的计算机存储空间。频域反射波形反演虽然有多尺度特性,但对计算机运算内存要求高。本文通过离散傅里叶变换,从时域波场提取对应的频域波场进行多尺度的时频域反演,仅需存储数片单频波场,在存储需求方面明显优于传统的时域反演,运算成本方面明显优于频率域,结合了时域反演的高效性和频域反演多尺度的特性。针对实际地震资料低频地震数据易缺失的问题,进一步结合包络反射波反演,在重构中深层地下介质低频信息的基础上进行逐级优化反演,降低对低频长偏移地震数据的要求。最后本文通过数值算例验证了基于包络数据的时频域反射波形反演方法对低频信息恢复的有效性。

关键词： 全波形反演; 反射波反演; 时频域; 包络反演

Abstract

Reflection waveform inversion(RWI) provides an effective initial model for full waveform inversion(FWI) by alternately updating the low-to-intermediate and high wavenumber components in the model.However,time-domain RWI requires storing the cross-correlation between the source background wavefield and the receiver scattered wavefield over the entire time series to compute gradients,demanding substantial computational storage.Although frequency-domain RWI exhibits multi-scale properties,it also imposes high demands on computational memory.Based on the discrete Fourier transform,this study proposed a RWI method that extracts frequency-domain wavefields from corresponding time-domain wavefields for multi-scale inversion in the time-frequency domain.The proposed method requires storing only a few single-frequency wavefield snapshots,showing significantly lower storage demands compared to conventional time-domain RWI and reduced computational costs relative to frequency-domain RWI.Therefore,the proposed method effectively combines the computational efficiency of time-domain RWI with the multi-scale properties of frequency-domain RWI.Considering the frequently missing low-frequency data in actual seismic data,this study further integrated envelope-based RWI to reconstruct low-frequency information for medium-deep subsurface structures.This enables stage-wise optimization of the inversion process,reducing the dependency on low-frequency long-offset data.Finally,numerical examples validate the effectiveness of the time-frequency domain RWI method based on envelope data in recovering low-frequency information.

Keywords： full waveform inversion(FWI); reflection waveform inversion(RWI); time-frequency domain; envelope inversion

PDF (2790KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

汪昆, 吴国忱, 贾宗锋, 杨凌云. 反射波时频域地震波形反演方法[J]. 物探与化探, 2025, 49(5): 1155-1163 doi:10.11720/wtyht.2025.0043

WANG Kun, WU Guo-Chen, JIA Zong-Feng, YANG Ling-Yun. Reflection waveform inversion in the time-frequency domain[J]. Geophysical and Geochemical Exploration, 2025, 49(5): 1155-1163 doi:10.11720/wtyht.2025.0043

0 引言

全波形反演因其可以充分利用地震资料中的运动学和动力学信息成为目前研究的热点。Lailly^[1]和Tarantola^[2]以Born近似为基础,建立了全波形反演的基础理论框架,至此全波形反演取得了长足的发展。经典的全波形反演方法对地震数据要求苛刻,需要含有大偏移距和可靠低频成分的地震数据。但由于偏移距有限,使得在传统全波形反演的初始阶段所利用的透射波无法达到深层,导致深层反演效果较差。地下介质中深层构造信息主要由反射波中所携带的中低波组分提供,常规FWI难以利用反射波更新背景速度,且对初始模型有强依赖性。目前已经有许多方法来降低全波形反演对初始模型的依赖性,比如层析反演^[3]、多尺度反演^[4]以及本文所提及的包络反演和反射波形反演方法,即利用反射波构造透射路径补充深层信息,把反射波地震波形反演结果作为初始模型来提升反演精度。Xu等^[5]给出了基于偏移/反偏移技术提取反射波的反射波波形反演方法。Wang等^[6]实现了频率域的反射波波形反演,验证了反射波反演也需要低频的地震信息。Chi等^[7]和Luo等^[8]采用走时目标函数缓解反射波波形反演的多解性。姚刚等^[9]对反射波波形的反演方法进行总结,提供了一种稳定普遍的适用于全波形反演的方法。Guo等^[10]和Wang等^[11]将反射波理论进一步推广应用到弹性介质中。Li等^[12]提出了变密度弹性反射波形反演解决实际情况中需要考虑的变密度问题。李青阳等^[13]利用Gadrner公式实现了速度—密度联合反演的互相关反射波波形反演,进一步提升了反演的可靠性。

时间域波形反演相对于频率域波形反演没有明显的多尺度特性,在缺少含有低频信息的准确的地下介质参数初始模型的情况下,直接进行波形反演极易陷入局部极值。而频率域反演虽然在小尺度模型有一定优势,但在大模型反演时对计算机的内存和运算能力要求较为苛刻。Bunks等^[14]和Boonyasiriwat等^[15]提出了利用汉明窗低通滤波器对地震子波和数据进行时间尺度上的分解,首次实现了时间域多尺度反演。相对于时间域,Pratt等^[16-17]提出频率域全波形反演可以更直观地从低频到高频多尺度递进反演,但运算成本要求高。Operto等^[18]提出了利用离散傅里叶变换从时域波场中提取单频波场来替代频率域正演,以解决频率域正演计算量大,无法运用到大尺度模型或者三维模型中的问题。Fichtner等^[19]提出了时频域声波全波形反演并应用到实际,验证其相对于时域算法的优势。王官超^[20]实现了在弹性介质下时频域多尺度反演。胡勇等^[21]提出基于相位校正的时频域多尺度全波形反演来缓解地震反演中的周波跳跃问题。Wang等^[22]提出了在反射波波动方程走时反演(wave equation traveltime inversion for reflected waves,WRTI)时用单频波场保存数据的主要成分,无需存储正传和反传的波场快照,显著降低了对计算机的内存需求和计算成本。

通过离散傅里叶变换,可以从时域反射波场提取对应的频域波场进行多尺度的时频域反演,其最大的优点就是可以通过一次正演求取任意所需的波场值,且无需存储时间域的波场序列。和频率域反演相比,时频域在计算效率上有着显著优势;和时域相比,又有着从分频递进多尺度反演的特点,缓解易陷入局部极值的问题。虽然时频域反射波波形反演采用多尺度反演策略,但本质上仍需低频信息,Wu等^[23]和Chi等^[24]提出了包络反演来恢复大尺度的背景模型。梁展源等^[25]提出了通过改变包络反演的目标函数的频移包络反演,减少了计算成本。Luo等^[26]提出了在弹性介质下的直接包络反演方法。但传统包络反演所提取的超低频信息主要存在于直达波与折射波中,主要更新浅中层大尺度背景模型,包络反射波进一步利用反射波所携带的超低频信息更新中深层区域。利用包络数据的优势来重建地震数据中的超低频信息来进行时频域反射波形反演,进一步缓解了对低频长偏移地震数据的要求。

为此本文提出了时频域反射波形反演方法,通过从时域波场中做离散傅里叶变换提取相应的频率成分,计算对应不同频率成分的梯度向量,将反射波梯度核做尺度分解为低频、中频、高频,从低频到高频递进反演。采用层状模型和Sigebee2A速度模型对该方法进行测试,实验结果表明时频域反射波形反演有效地恢复了地下介质中深层低频信息,为全波形反演提供了良好的初始模型,从而实现高分辨率的反演结果。在面对低频缺失时,时频域多尺度反演的适用性显著降低,反演易陷入局部极值。对比缺失低频和利用包络反演的时频域多尺度反演结果,验证本文方法在缺失低频信息时依然可以较好地恢复模型的中低波数组分,提高反演的收敛性。

1 方法原理

反射波形反演基本框架基于全波形反演发展而来,选取L₂范数目标函数分别推导时频域反射波波形反演和包络反射波波形反演目梯度表达式。

1.1 时频域反射波波形反演基本理论

二阶声波方程为:

(1)

(\frac{1}{v^{2} (x)} \frac{\partial^{2}}{\partial t^{2}} - \nabla^{2}) p (x, t; x_{s}) = f (t; x_{s})

式中:p(x,t;x_s)是震源项f(t;x_s)引起的激发的全波场。v(x)为准确速度场,反射波波形反演基于偏移/反偏移理论,利用反偏移获取模拟反射波。将速度模型分为长波长分量的背景速度v₀(x)和短波长分量的扰动速度δv(x):

(2)

v (x) = v_{0} (x) + δ v (x)

。

对应在此速度场模型中所激发的波场也可分解为在背景模型中传播产生的背景波场P₀(x,t;x_s)和在扰动速度模型中传播产生的扰动波场δP(x,t;x_s):

(3)

P (x, t; x_{s}) = P_{0} (x, t; x_{s}) + δ P (x, t; x_{s})

。

将式(2)和(3)代入式(1)中,此时声波波动方程可以变形为:

(4)

\begin{array}{c} \{\frac{1}{{[v_{0} (x) + δ v (x)]}^{2}} \frac{\partial^{2}}{\partial t^{2}} - \nabla^{2}\} [p_{0} (x, t; x_{s}) + \\ δ p (x, t; x_{s})] = f (t; x_{s}) \end{array}

为计算扰动波场,对速度介质做泰勒展开:

(5)

\frac{1}{[v_{0} (x) + δ v {(x)]}^{2}} = \frac{1}{v_{0}^{2} (x)} - \frac{2 δ v (x)}{v_{0}^{3} (x)} + ο [δ v^{2} (x)] 。

将式(5)代入式(4)中,可以得到散射波动方程:

(6)

\begin{array}{c} (\frac{1}{v_{0}^{2} (x)} \frac{\partial^{2}}{\partial t^{2}} - \nabla^{2}) δ p (x, t; x_{s}) = \frac{2 δ v (x)}{v_{0}^{3} (x)} \frac{\partial^{2} p_{0} (x, t; x_{s})}{\partial t^{2}} + \\ \frac{2 δ v (x)}{v_{0}^{3} (x)} \frac{\partial^{2} δ p (x, t; x_{s})}{\partial t^{2}} \end{array}

。

式中:右端的第一项为一次散射波(初次散射),右端第二项为高阶散射项(多次波),通常能量相对于第一项非常弱。在扰动速度较小的情况下,应用Born近似忽略右端高阶项可以得到扰动波场波动方程:

(7)

(\frac{1}{v_{0}^{2} (x)} \frac{\partial^{2}}{\partial t^{2}} - \nabla^{2}) δ p (x, t; x_{s}) = 2 \frac{δ v (x)}{v_{0}^{3} (x)} \frac{\partial^{2} p_{0} (x, t; x_{s})}{\partial t^{2}} 。

式中:右端震源项由扰动速度与背景波场相乘组成,但在实际的反演过程中,扰动速度δv(x)是未知的。通常利用逆时偏移结果替代模型的高频速度扰动δv(x)。逆时偏移成像结果与扰动速度的空间位置是一致的,所以可以利用最小二乘逆时偏移结果替代速度扰动,并通过反偏移的方法获取模拟反射波。整理可得反偏移的计算过程:

(8)

\{\begin{array}{c} (\frac{1}{v_{0}^{2} (x)} \frac{\partial^{2}}{\partial t^{2}} - \nabla^{2}) P_{0} (x, t; x_{s}) = f (t; x_{s}) \\ (\frac{1}{v_{0}^{2} (x)} \frac{\partial^{2}}{\partial t^{2}} - \nabla^{2}) δ p (x, t; x_{s}) = 2 \frac{δ v (x)}{v_{0}^{3} (x)} \frac{\partial^{2} p_{0} (x, t; x_{s})}{\partial t^{2}} \\ d_{c a l} (x_{g}, r; x_{s}) = δ p (x_{g}, r; x_{s}) \end{array}

时频域反射波波形反演通过最小化观测反射数据和反偏移模拟反射数据的残差平方和寻找最优解,基于L₂范数表示的目标函数如下:

(9)$E=\sum_{s, g} \int_{0}^{t_{\max }}\left|p_{\bmod }\left(x_{g}, t ; x_{s}\right)-p_{\text {obs }}\left(x_{g}, t ; x_{s}\right)\right|^{2} \mathrm{~d} t,$

式中:p_mod为通过正演模拟得到的地震数据;p_obs为检波器观测得到的地震观测记录。

Xu等^[5]推导反射波路径核函数可以表示为:

(10)

\begin{array}{c} K^{r e f} (x, x_{s}, x_{g}) = \frac{1}{v^{3} (x)} \frac{\partial^{2}}{\partial t^{2}} [G_{0} (x, t; x_{s}) G_{s} (x_{g}, t; x) + \\ G_{s} (x, t; x_{s}) G_{0} (x_{g}, t; x)] \end{array}

式中:G₀(x,t;x_s)和G_s(x_g,t;x)分别为震源点入射波场和检波点反传散射波场;G_s(x,t;x_s)和G₀(x_g,t;x)分别为震源点反射波场和检波点的反射波场。

反射波波形反演的时域梯度可以表示为:

(11)

\begin{array}{c} \frac{\partial E}{\partial v} = \frac{2}{v^{3} (x)} \sum_{s, g}^{} \int_{0}^{t_{m a x}} [\frac{\partial^{2} p_{0} (x, t, x_{s})}{\partial t^{2}} \cdot δ p (x_{g}, t; x_{s}) + \\ \frac{\partial^{2} p_{0} (x, t, x_{s})}{\partial t^{2}} \cdot δ p (x_{g}, t; x_{s})] d t \end{array}

式中:p₀(x,t,x_s)为正传背景波场;δp(x_g,t;x_s)为伴随残差扰动波场;p₀(x,t,x_s)为正传扰动波场;δp(x_g,t;x_s)为伴随残差背景波场。其中扰动波场的求取参考式(8)给出的反偏移算子。

时间域梯度运算需要震源背景波场的时间二阶导数与接收点扰动波场零延迟互相关,包括3个步骤:①计算正传背景波场和反传背景波场;②计算正向扰动波场和反向扰动波场;③同一时刻零延迟互相关计算梯度。在这种直接实现方式中,需要同时存储震源波场和接收器波场,这必然要求将震源波场存储在内存中,从而导致大量的内存消耗。所需的内存量级为ο(N_x×N_z×N_t),其中N_t是时间样本的数量,N是x、z方向上的长度。高内存需求限制了时间域全波形反演在实际大规模反演中的应用。

时频域波场可以通过对每个时间步长上的时间域波场进行离散傅里叶变换(DFT)得到:

(12)

P (ω) = \sum_{i_{t} = 0}^{N_{t} - 1} p (i_{t}) e^{2 j π ω i_{t} / N_{t}}

。

对式(11)做离散傅里叶变换得到时频域反射波梯度:

(13)$\begin{array}{c}\frac{\partial E}{\partial v}=\sum_{s, g} \int_{0}^{\omega} \operatorname{Re}\left\{\frac { \omega ^ { 2 } } { v _ { 0 } ^ { 2 } ( x ) } \left[p_{0}\left(x, \omega ; x_{s}\right) \cdot \delta p\left(x_{g}, \omega ; x_{s}\right)+\right.\right. \\\left.\left.\delta_{p}\left(x, \omega ; x_{s}\right) \cdot p_{0}\left(x_{g}, \omega ; x_{s}\right)\right]\right\} \mathrm{d} \omega\end{array}$。

时频域梯度和时间域梯度算法不同,时频域梯度只需要进行一次波场正传和一次残差波场反传,离散傅里叶变换可以伴随时间波场外推的过程中求解所需的单频频域波场计算梯度。在完成时域波场求解的同时,也完成时频域波场的求解。相对在频率域中计算单频波场,只需要耗费较小的计算量就可以得到任意所需要的单频波场。在计算机存储方面,只需要存储数片频率片,无需存储时间波场序列,所需的内存量级仅为ο(N_x×N_z),显著降低了对计算机存储的要求。具体反演流程如下:

1)输入反演的参数信息:迭代次数,误差上限,野外观测地震数据,初始速度模型,正演模拟参数。

2)利用偏移和反偏移原理,模拟反射波。

3)时域计算震源背景场、震源扰动场并提取所需的频率组。

4)时域计算残差背景场、残差扰动场并提取所需的频率组。

5)选取合适的频率组,互相关求取梯度。

6)更新速度模型,如果收敛,则结束循环。

7)输出最终反演结果。

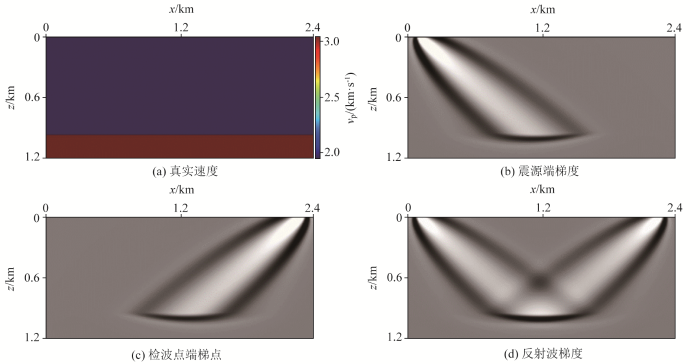
为了直观地分析反射波梯度中各项的贡献,选取一个简单层状模型分析反射波梯度响应,如图1a所示,图1b是正传背景波场和伴随残差扰动波场的互相关表示反射波震源端路径,图1c是正传扰动波场和伴随残差背景波场的互相关表示检波点端反射波路径,图1d为式(8)计算的反射波路径,呈兔耳朵状,背景波场与扰动波场互相关的夹角约为180°,主要恢复模型中的低波数背景速度。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 反射波路径示意

Fig.1 Schematic of the reflected wave path

1.2 时频域包络反射波波形反演基本理论

基于L₂范数的包络反射波波形反演目标函数通过观测模拟包络数据与观测数据包络之间的平方差来体现最优化过程:

(14)$C_{e}(\boldsymbol{m})=\frac{1}{2} \sum_{r=1}^{R} \sum_{s=1}^{S}\left|e_{\mathrm{cal}}^{m}-e_{\mathrm{obs}}^{m}\right|^{2} \mathrm{~d} t,$

在包络反演中,e_cal为模拟地震数据的包络,由模拟地震数据d_cal和模拟地震数据的希尔伯特变换H[d_cal(t)]做求模运算,$e_{\text {cal }}(t)= \sqrt{d_{\text {cal }}^{2}(t)+\left(H\left\{d_{\text {cal }}(t)\right\}\right)^{2}}$。e_obs为观测地震数据的包络,由观测地震数据d_obs和观测地震数据的希尔伯特变换H{d_obs(t)}做求模运算,即$e_{\mathrm{obs}}(t)= \sqrt{d_{\mathrm{obs}}^{2}(t)+\left(H\left\{d_{\mathrm{obs}}(t)\right\}\right)^{2}} $。

(15)$ 。\begin{array}{c}C_{e}(m)=\frac{1}{2} \sum_{r=1}^{R} \sum_{s=1}^{S} \int_{0}^{T}\left|e_{\mathrm{cal}}^{m}-e_{\mathrm{obs}}^{m}\right|^{2} \mathrm{~d} t= \\\left.\frac{1}{2} \sum_{r=1}^{R} \sum_{s=1}^{S} \int_{0}^{T} \right\rvert\,\left(\sqrt{d_{\mathrm{cal}}^{2}(t)+\left[H\left(d_{\mathrm{cal}}(t)\right)\right]^{2}}\right)^{m}- \\\left.\left(\sqrt{d_{\mathrm{obs}}^{2}(t)+\left[H\left(d_{\mathrm{obs}}(t)\right)\right]^{2}}\right)^{m}\right|^{2} \mathrm{~d} t= \\\frac{1}{2} \sum_{r=1}^{R} \sum_{s=1}^{S} \int_{0}^{T} E^{2} \mathrm{~d} t\end{array}$,

式中:E为包络数据的残差;t为时间;s为震源;r为检波点。

在包络反演的过程中引入幂指数m作为包络能量的调节因子,该参数取值范围为任意正整数。随着m值增大,包络数据在中浅层的能量越强。研究表明,当m=2时包络反演效果达到最优,既保证了反演过程的稳定性,又能在不同深度区间实现包络能量的合理配置。基于此,本文中m都取值2。

包络反演目标函数对模型参数求导得:

(16)$\begin{array}{c}\frac{\partial C_{e}(\boldsymbol{m})}{\partial \boldsymbol{m}}=m \sum_{r=1}^{R} \sum_{s=1}^{S} \int_{0}^{T}\left[E(t) d_{\mathrm{cal}}(t) e_{\mathrm{obs}}^{m-2}(t)-\right. \\\left.H\left\{E(t) d_{\mathrm{cal}}(t) e_{\mathrm{cal}}^{m-2}(t)\right\}\right] \frac{\partial u(t)}{\partial \boldsymbol{m}} \mathrm{d} t\end{array}, $

式中:$\frac{\partial u(t)}{\partial \boldsymbol{m}}$为Fréchet导数矩阵,利用伴随状态法来计算梯度。采用速度参数来描述地下介质模型,则目标函数关于速度的梯度可以具体表示为:

(17)

J = \frac{\partial d (t)}{\partial m}

(18)$\eta=E(t) d_{\mathrm{cal}}(t) e_{\mathrm{obs}}^{m-2}(t)-H\left\{E(t) d_{\mathrm{cal}}(t) e_{\mathrm{cal}}^{m-2}(t)\right\}。$

因此,梯度公式可以化简为:

(19)$\frac{\partial C_{e}(\boldsymbol{m})}{\partial \boldsymbol{m}}=J^{\mathrm{T}} \boldsymbol{\eta},$

式中:J是雅克比矩阵;η是包络反传残差。从上述公式可以看出,包络波形反演方法和常规波形反演在整体形式方面大致相似,两者之间仅有的差异体现在伴随源的计算公式上。对式(11)反射波梯度中的伴随源变形,可得时频域包络反射波梯度:

(20)$\begin{array}{c}\frac{\partial E}{\partial v}=\sum_{s, g} \int_{0}^{\omega} \operatorname{Re} \\\left\{\frac { \omega ^ { 2 } } { v _ { 0 } ^ { 2 } ( x ) } \left(p_{0} \cdot\left\{\delta p\left(\frac{E_{\text {cal }}-E_{\text {obs }}}{E_{\text {cal }}}\right)-H\left[\delta p^{H}\left(\frac{E_{\text {cal }}-E_{\text {obs }}}{E_{\text {cal }}}\right)\right]\right\}+\right.\right. \\\left.\delta p \cdot\left\{p_{0}\left(\frac{E_{\text {cal }}-E_{\text {obs }}}{E_{\text {cal }}}\right)-H\left[p_{0}^{H}\left(\frac{E_{\text {cal }}-E_{\text {obs }}}{E_{\text {cal }}}\right)\right]\right\}\right\} \mathrm{d} \omega\end{array}$。

2 数值模拟计算

2.1 时频域正演和频率域正演对比

正演是反演的基础,为了验证时频域方法求解的单频波场,即对时域波场做离散傅里叶变换获取的单频波场能否代替频率域求解的单频波场,满足时频域反演的需求。采用层状模型测试时频域提取的单频波解精度和频率域正演模拟得到的单频波解精度的拟合程度。以下在时间域上正演模拟均采取时间二阶导数,空间十阶导数有限差分。在频率域采用最优9点法有限差分法正演模拟。第一层速度为2 000 m/s,第二层速度为3 000 m/s(图2)。该模型网格大小200×200,空间采样步长均为10 m。震源是主频为25 Hz的雷克子波。时间采样间隔为1 ms,时间采样长度为2 s。炮点位于模型顶部中心点,位于(1 000 m,10 m)处,检波点均匀覆盖模型表面。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 层状模型

Fig.2 Layered model

如图3所示分别为在时频域和频率域所求的频率为20 Hz的单频波场,图中可以清楚看出模型反射轴的空间位置。为了更加直观地对比波场解的吻合程度,分别抽取第50、90、130和150道处单道进行对比,如图4所示时频域与频率域单频波场抽道对比,其中红色虚线为时频域所求单频波场,蓝色实线为频率域单频波场,从结果对比来看,其振幅和相位吻合较好,具有较高的模拟精度。因为频率域解假设无限时间序列的积分,但是时间域记录的时间只有2 s,所以两种方法存在轻微误差,但整体精度满足时频域反演的需求。利用时域波场做离散傅里叶变换求取所需的频率组,代替频率域正演,显著地降低了计算量。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 时频域与频率域单频波场对比

Fig.3 Comparative analysis of single-frequency wavefield characteristics in time-frequency and frequency domains

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 时频域与频率域单频波场抽道对比

Fig.4 Comparison of wavefield extraction between time-frequency domain and monochromatic frequency domain

2.2 时频域反射波形反演

为了验证本文算法的有效性,设计了两个模型。模型一为简单的层状模型,该模型网格大小为300×150,空间采样步长均为10 m。震源是主频为25 Hz的雷克子波。时间采样间隔为1 ms,时间采样长度为1.8 s。总共激发30炮,起始炮点位于(10 m,10 m)处,炮检距为100 m,布置300个检波点均匀覆盖地表。

真实速度模型(图5a)速度从上往下依次是2 500、3 000 m/s,初始线性速度模型如图5b所示。图5c和图5d分别呈现第一次和第十次迭代的偏移成像,对反射波波形反演的速度模型进行偏移成像来检验反演的结果(图5d),可以发现反射轴相对于图5c的反射轴与层状模型产生的反射轴位置更加吻合,层位更加准确。由于速度模型第三层没有反射波的产生,如图5e所示梯度在1 km以下的速度场没有更新。图5f是迭代10次反射波反演结果,可以看出经过反射波形反演,速度界面信息和低波数成分得到了有效的恢复。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 平层速度模型

Fig.5 Schematic diagram of plane wave excitation and reception

为了验证复杂模型的适用性,截取部分sigebee2A模型作为真实模型进行本文方法测试(图6),该模型网格大小350×180,空间采样步长均为10 m。震源是主频为25 Hz的雷克子波。时间采样间隔为0.8 ms,总时长为1.56 s。总共激发35炮,起始炮点位于(1 m,50 m)处,炮间距为100 m,检波点均匀覆盖模型表面。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 Sigebee2A速度模型

Fig.6 Sigebee2A velocity model

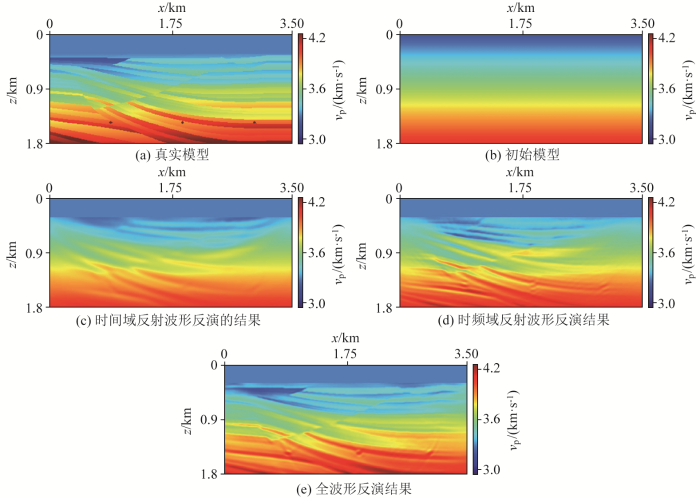
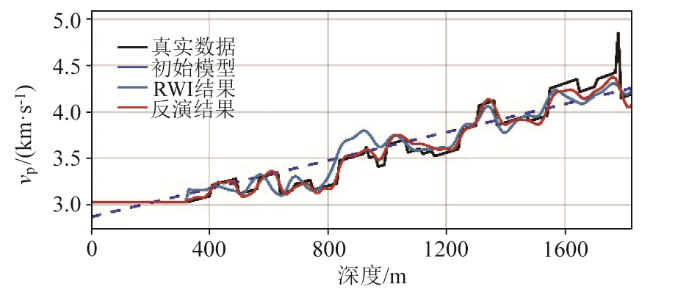
在时频域反射波形反演过程中,选取4个频率组,即(4 Hz,8 Hz),(8 Hz,13.6 Hz),(13.6 Hz,20 Hz),(20 Hz,25.6 Hz),频率间隔为0.8 Hz,将上一组频率的反演结果作为下一组频率反演的初始模型,每个频段迭代5次。图7是分别抽取真实速度(图6a)、初始速度(图6b)、时频域反射波波形反演的速度单道(图6d)和以图6d为初始模型的全波形反演的速度单道(图6e)在1 750 m处的速度曲线,反演结果与真实速度模型趋势高度吻合,通过从时域波场提取从低频到高频的频率组逐级递进反演,有效地刻画出中深层构造中的大尺度信息,验证了时频域反射波波形反演的有效性。在此基础上做全波形反演恢复速度模型的高波数组分,速度曲线几乎贴合真实速度曲线,经过反射波形反演恢复速度模型的中低波数组分,反演结果更接近真实速度模型。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 单道速度反演结果对比

Fig.7 Comparison of single-track velocity inversion results

为了测试时间域和时频域反射波形反演所需的时间和内存,下面对第一次反演迭代时的各参数进行对比,由于时频域反演需要在正演中对波场做离散傅里叶变化,导致正演所需的时间比时间域略长。但时频域反演只需要存储数片单频波场,大大减少了对计算机存储空间的需求,同时也避免了海量的波场数据读写,所以该反演方法在模型较大和三维模型上具有显著存储优势(表1)。

表1 效率测试

Table 1 Testing efficiency

	单核/min	十核/min	存储/GB
时间域	185.3	16.3	85.8
时频域	197.9	17.5	14.1

新窗口打开| 下载CSV

时频域反射波形反演将梯度核依次分解为低、中、高频进行多尺度反演,逐级有效地恢复地下介质信息,为后续全波形反演提供良好的初始模型,但本质上还需依赖地震数据中所包含的低频信息,在实际数据采集过程中,低频成分往往很难被接收。

在没有低频地震数据的情况下,即使采用多尺度反演策略,反射波形反演也无法完全避免陷入局部极小值的问题。这时,利用包络调解出原始地震数据隐藏的低频信息,结合反射波形反演,利用这些超低频信息来更新模型大尺度背景信息,就能降低对低频地震数据的依赖度。

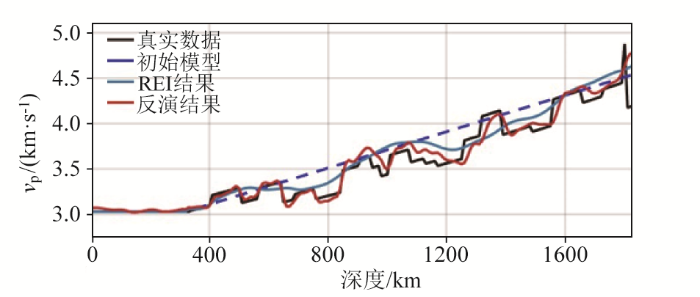
图8a为线性初始模型,其整体速度略高于真实速度。图8b是缺失4 Hz以下低频信息情况下,在时频域下采用反射波形反演与全波形反演联合反演的结果。可以看出当地震资料缺失低频数据时,即使采用了时频域多尺度的反演策略,波形反演也会陷入局部极值。图8c是时频域反射波包络反演结果,经过时频域反射波包络反演可以较好地恢复背景速度,反演趋势与真实模型速度趋势相吻合。图8d是经过反射波包络反演恢复低频信息后进行全波形反演的结果,对比图8b和图8d反演结果,可以看出经过反射波包络弥补低频信息缺失后,反演结果构造更加精细。分别抽取其在1 750 m处速度单道进行对比如图9所示,经过反射波包络弥补地震数据中的低频缺失后,反演结果明显更贴近于真实速度曲线,中深部明显吻合更好,有效地缓解了波形反演易陷入局部极值的问题。增加了时频域多尺度联合反演的适用性,减少了低频地震数据的依赖性,更加适用于低频资料缺失的反演。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 复杂速度模型

Fig.8 Complex velocity model

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 单道速度反演结果对比

Fig.9 Comparison of single-track velocity inversion results

3 结论与认识

本文提出了时频域反射波形反演方法,从低频到高频递进反演,实现多尺度反射波形反演来恢复地下介质背景速度。并利用包络反演调解出原始地震数据中隐藏的低频信息,在低频数据缺失时依然可以为全波形反演提供良好的初始模型。通过理论推导和数值实验得到以下几点结论以及认识:

1)时频域反射波形反演利用离散傅里叶变化从时域波场提取对应的频域波场进行多尺度反演,仅需存储数片单频波场,无须存储时间域的波场序列,在内存需求方面明显优于传统的时域反演,运算成本方面明显优于频率域,结合了时域正演的高效性和频域反演多尺度的特性。

2)通过将反射波梯度核依次分解为低、中、高频进行多尺度反演,有效降低了反演对初始模型的依赖性,逐级有效地恢复地下介质信息,缓解了反演的非线性。

3)反射波波形反演在地震资料缺少低频数据时,仍易陷入局部极值,利用反射波包络数据重建中深层地下介质地震数据中的低频信息后进行多尺度反演,有效地避免了陷入局部极值。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[23]

R S

, Luo

J R

, Wu

B Y

Seismic envelope inversion and modulation signal model

[J]. Geophysics, 2014, 79(3):WA13-WA24.