0 引言
利用地震反演的手段对储层岩石物理参数进行估计进而开展流体识别及储层表征是勘探地震学中的一个重要研究方向,能够为储层的含油气性评价提供明确的引导作用[1 5] 。
依托岩石物理理论研究,选择并构建相应的储层敏感参数岩石物理模型进而开展地球物理反演,对地下岩性以及流体类型进行判断,已经成为了目前储层描述以及含油气评价的一项重要手段。Grana等[6 ] 利用贝叶斯框架建立了相应的储层物性参数目标函数,并提出了统计学理论下的岩石物理建模及储层物性参数反演方法,以及岩性流体聚类策略。宗兆云等[7 ] 利用Gassmann方程推导了纵、横波模量相关的储层流体识别反射系数方程,并发展了一种叠前弹性阻抗反演储层流体敏感参数的新方法。随着地球物理理论的快速发展以及勘探工区的日益复杂,考虑砂岩致密特征的岩石物理模型及反演逐步成为了研究的焦点。卢明辉等[8 ] 在对比和分析等效介质理论中获得了能够描述致密砂岩孔隙结构的岩石物理模型。基于Biot相洽理论,印兴耀等[9 ] 发展了一种针对裂缝型致密砂岩的弹性参数估计方法,为致密砂岩弹性性质的分析开辟了新的途径。刘倩等[10 ] 在考虑孔隙连通性的基础上建立了含不连通孔隙度影响下的岩石物理模型,并对其储层的弹性特征进行了研究。针对含气致密砂岩储层,Fan等[11 ] 将统一岩石骨架模型与Sun模型相结合,得到了新的孔隙结构计算方法,并对致密砂岩孔隙结构参数进行了贝叶斯概率化反演。上述岩石物理理论驱动下的反演方法为致密砂岩储层表征提供了可靠的解决方案,但是,由于大多数反演算法为基于线性近似式的线性反演,当储层复杂性变高、纵横向变化剧烈,且勘探精度要求较高时,线性反演结果难以给出可靠的储层弹性或者物性参数预测结果。为此,寻找更为合适的反演方法以提高反演结果的准确性是目前需要解决的一项重点问题。
线性反演在保证一定的反演精度的前提下,可以为储层预测提供一种高效、快捷的指导方式[12 -13 ] 。非线性反演在极大提高反射系数方程的同时,能够进一步改善线性反演受到多种假设条件的影响,为复杂油藏的精细刻画及高精度识别提供了有效的解决方案。Yin等[14 ] 给出了一种基于Zoeppritz方程的新型精确PP反射系数并将其应用于地震数据及叠前非线性AVO反演。该方法在非线性反问题的求解中使用了蒙特卡洛求解策略的逆算子估计算法,克服了线性方程所存在的局限性,并减少待反演参数的数量,为相对值的精确反演提供了理论支撑。Cheng等[15 ] 推导了拉梅参数和密度相关三阶Zoeppritz非线性近似方程,该研究为反演过程引入了一种逆算子估计算法,结合L1 范数的约束,利用非线性反演逆算子优化反演算法提高了拉梅参数反演稳定性和准确性。逆算子优化算法在求解L1 范数提升反演分辨率与准确性方面具有较强的优势,但在求解过程中具有较低的速度,时间成本更高。Zhou等[16 ] 在精确Zoeppritz方程的基础上,提出了一种新的Russell孔隙流体因子相关方程的非线性纵横波组合反演方法,利用梯度下降反演算法,其方法在较大程度上克服了流体因子估计精度的限制,更符合地球物理反演问题的本质,且具有较高的运算速度,时间成本较低。但梯度下降优化算法适用于L2 范数的求解,难以提高反演结果的分辨率,同时,待反演参数梯度下降的过程中容易陷入局部极小值,影响反演的准确性与稳定性。非线性方程反演算法的蓬勃发展得益于反演优化算法的不断进步,因此,选择合理、稳定的优化算法开展非线性反演对致密砂岩储层进行预测,能够为提高致密砂岩储层反演结果的准确性与可靠性提供技术支撑。
考虑到上述所描述的致密砂岩岩石物理建模理论在直接反演中具有较多的参数以及较高的复杂性,不利于储层参数的稳定提取,且基于梯度类的非线性求解方法容易在优化过程中陷入局部极小值,收敛性较差。为此,本文对提高致密砂岩储层参数的叠前反演精度进行了深入研究,具体如下:首先利用岩石物理理论及Kuster-Toksöz(KT)模型[17 -18 ] 下的球形包含物模型建立纵横波速、度密度与Kf 、密度以及孔隙度之间的定量关系,之后,将此关系代入精确Zoeppritz方程[19 ] ,建立含3参数的新非线性精确反射系数方程,采用L1 范数建立反演目标函数,采用麻雀搜索算法[20 ] 进行优化求解得到目标函数取得极小值时的Kf 、密度以及孔隙度的数值解。该方法在精度测试和模型测试中表现出了较高的合理性和可靠性,并且在鄂尔多斯盆地的致密砂岩储层的实际应用中获得了高精度、高分辨率的勘探效果。
1 理论与方法
1.1 致密砂岩储层岩石物理模型构建
考虑到Gassmann流体替换方程[21 ] 联系了连通孔隙低频近似下的饱和岩石骨架、基质及赋存流体之间的定量关系,作为致密砂岩岩石物理模型,由于其孔隙的不连通特征使得常规的Gassmann流体替换方程不再适用。因此Kuster-Toksöz(KT) 模型[17 -18 ] 为计算具有可变孔隙度的多孔岩石的有效体积模量K eff 和有效剪切模量μ eff 的计算提供了一种新的解决方案:
(1) $\left(K_{\mathrm{eff}}-K_{m}\right)\left(\frac{K_{m}+\frac{4}{3} \mu_{m}}{K_{\mathrm{eff}}+\frac{4}{3} \mu_{m}}\right)=\sum_{i=1}^{n_{i}} x_{i}\left(K_{i}-K_{m}\right) P_{i},$
(2) $\left(\mu_{\mathrm{eff}}-\mu_{m}\right)\left(\frac{\mu_{m}+\zeta_{m}}{\mu_{\mathrm{eff}}+\zeta_{m}}\right)=\sum_{i=1}^{n_{i}} x_{i}\left(\mu_{i}-\mu_{m}\right) Q_{i},$
(3) $\zeta_{m}=\frac{\mu_{m}}{6} \frac{9 K_{m}+8 \mu_{m}}{K_{m}+2 \mu_{m}},$
式中:Pi 和Qi 分别表示不同类型包含物的几何因子;Km 和μm 分别表示岩石基质的体积模量和剪切模量;n 和x 分别表示包含物的数量和体积分数;Ki 与μi 则分别表示第i 类包含物的体积模量和剪切模量。假设包含物形状为球体,且岩石孔隙由流体完全填充(Ki =Kf ,μi =0),由此可得饱和致密砂岩的模量如下:
(4) $K_{\mathrm{sat}}=\frac{4 K_{m} \mu_{m}+3 K_{f} K_{m}+4 K_{f} \mu_{m} \phi-4 K_{m} \mu_{m} \phi}{3 K_{m} \phi+4 \mu_{m}+3 K_{f}-3 K_{f} \phi},$
(5) $\mu_{\mathrm{sat}}=\mu_{\mathrm{dry}}=\frac{\mu_{m}\left(9 K_{m}+8 \mu_{m}\right)(1-\phi)}{9 K_{m}+8 \mu_{m}+6\left(K_{m}-2 K_{m}\right) \phi},$
式中:K sat 和μ sat 分别代表饱和流体填充孔隙下的致密砂岩体积模量和剪切模量,由式(4)和式(5)可计算饱和流体填充状态下的致密砂岩的纵横波速度表达式如下:
(6) $V_{\mathrm{p}}=\sqrt{\frac{K_{\text {sat }}+\frac{4}{3} \mu_{\text {sat }}}{\rho}},$
(7) $V_{\mathrm{s}}=\sqrt{\frac{\mu_{\mathrm{sat}}}{\rho}},$
式中:V p 、V s 和ρ 分别代表纵、横波速度和密度。上述岩石物理模型建立了孔隙流体体积模量以及孔隙度与岩石弹性参数(纵、横波速度)之间的定量联系,为后续采用非线性反射系数方程直接反演致密砂岩储层的物性以及含流体性质参数奠定了基础。
1.2 非线性精确反射系数方程构建
Zoeppritz方程[19 ] 阐明了各向同性完全弹性假设下地震波能量在界面处的分布,并为反射系数随入射角的变化提供了精确的描述,Aki等[22 ] 给出了纵波入射、纵波反射的反射系数表达式如下:
(8) $R_{\mathrm{pp}}=\left(E^{-} F^{+}-G^{+} H^{-} p^{2}\right) / D$
(9) D = E + F + + G - H - p 2
(10) $E^{+}=b \frac{\cos \alpha}{V_{\mathrm{p} 1}}+c \frac{\cos \alpha^{\prime}}{V_{\mathrm{p} 2}},$
(11) $E^{-}=b \frac{\cos \alpha}{V_{\mathrm{p} 1}}-c \frac{\cos \alpha^{\prime}}{V_{\mathrm{p} 2}}$
(12) $F^{+}=b \frac{\cos \beta}{V_{\mathrm{s} 1}}+c \frac{\cos \beta^{\prime}}{V_{\mathrm{s} 2}},$
(13) $G^{+}=a+d \frac{\cos \alpha}{V_{\mathrm{p} 1}} \frac{\cos \beta^{\prime}}{V_{\mathrm{s} 2}},$
(14) $G^{-}=a-d \frac{\cos \beta}{V_{\mathrm{p} 1}} \frac{\cos \beta^{\prime}}{V_{\mathrm{s} 2}},$
(15) $H^{-}=a-d \frac{\cos \alpha^{\prime}}{V_{\mathrm{p} 2}} \frac{\cos \beta}{V_{\mathrm{s} 1}},$
(16) $a=\rho_{2}\left(1-2 V_{\mathrm{s} 2}^{2} p^{2}\right)-\rho_{1}\left(1-2 V_{\mathrm{s} 1}^{2} p^{2}\right),$
(17) $b=\rho_{2}\left(1-2 V_{\mathrm{s} 2}^{2} p^{2}\right)+2 \rho_{1} V_{\mathrm{s} 1}^{2} p^{2},$
(18) $c=\rho_{2}\left(1-2 V_{\mathrm{s} 1}^{2} p^{2}\right)+2 \rho_{1} V_{\mathrm{s} 2}^{2} p^{2},$
(19) $d=2 \rho_{2} V_{\mathrm{s} 2}^{2}-2 \rho_{1} V_{\mathrm{s} 1}^{2},$
式(8)~(19)中:R pp 代表反射系数;p 为射线参数;α 、α' 、β 以及β' 分别表示纵波入射角或反射角、纵波透射角、横波反射角以及横波透射角;V p 、V s 和ρ 的下标1和2则分别表示所在的上层和下层介质。联立式(4)~(19),考虑基质模量Km 及μm 为常数,可得致密砂岩背景下的3个参数(Kf 、ϕ 和ρ )非线性精确反射系数方程如下(反射系数方程的推导过程及具体表达见附录A):
(20) $R_{\mathrm{pp}}=f\left(K_{f, 1}, K_{f, 2}, \phi_{1}, \phi_{2}, \rho_{1}, \rho_{2}\right),$
式中:f 代表反射系数与流体体积模量Kf 、孔隙度ϕ 以及密度ρ 之间的非线性映射关系,变量中的下标1和2分别表示反射界面所在处的上层与下层介质。反射系数方程建立的地层界面处的纵波反射系数R pp 与界面两侧的流体体积模量、孔隙度和密度之间的非线性映射,并写成了下标1和2的形式。值得注意的是,基于致密砂岩岩石物理模型推导的反射系数方程仍然包含3个独立的待反演参数,当待反演参数序列长度为N 时,纵波反射系数的长度为N -1,其非线性表征了一个N 对N -1的非线性映射,当反射界面的采样点数加1,上一个采样点处的反射界面下层介质将变成新反射界面处的上层介质。新方程相比于线性近似的优点在于不受地层弱对比度变化以及小角度入射的使用限制,相比线性近似,能够更加准确地反映地层的真实地震响应随不同储层参数的变化。
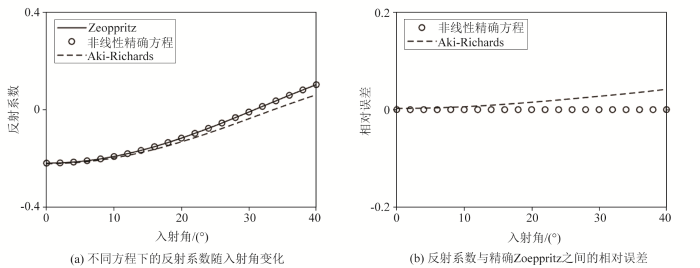
为测试新推导的非线性反射系数方程用于非线性反演的可行性,设计了模型参数如表1 所示的双层模型对其进行精度测试,模型假设各向同性完全弹性,且上下层介质分别设置为含气砂岩和泥岩,测试结果如图1 所示。
图1
图1
反射系数方程精度测试结果
Fig.1
The precision test results of reflection coefficient equations
图1a 中,黑色直线代表精确Zoeppritz,空心圆圈和黑色虚线分别代表表1 所示的模型参数下,本文所推导得到的非线性精确方程和Aki-Richards线性近似的反射系数随入射角的变化关系。图1b 则计算了图1a 中的非线性精确方程和Aki-Richards线性近似与精确Zoeppritz的反射系数的相对误差(误差绝对值)。可以看出,由于新方程的推导源于精确Zoeppritz,未受到线性化近似对方程精度的影响,使得新推导的非线性反射系数方程的精度与精确Zoeppritz几乎一致,相比于Aki-Richards线性近似,其方程精度特别是在大角度入射情况下明显提高。该测试结果为新方程能够应用于叠前反演来获取致密砂岩储层相关参数并提高反演的分辨率的可行性提供了理论支撑。
1.3 麻雀搜索算法与非线性反演
利用褶积模型对地震数据进行正演模拟,能够生成合成地震记录。褶积模型描述如下:
(21) $d_{t}(\theta)=w_{t}(\theta) * R_{\mathrm{pp}, t}(\theta), $
式中:θ 为入射角;*表示褶积算子;dt (θ )、wt (θ )、R pp, t θ )分别表示合成地震记录、地震子波以及反射系数。将式(21)所示的褶积运算写成矩阵形式:
(22) $S=W \cdot \boldsymbol{R}_{\mathrm{pp}}+\text { noise }, $
式中:R pp 为地层不同反射界面处的非线性反射系数;S 为地震记录向量;W 为子波矩阵;noise 表示噪声项。基于褶积模型构建观测数据与正演合成数据的残差项,并结合正则化约束进一步提高算法的鲁棒性,降低优化求解过程中出现过拟合现象,同时为保障反演结果的分辨率,我们将采用强调求解结果稀疏性L1 范数[23 25] 建立反演的目标函数:
(23) J = S - W · R p p | + m - m 0 |
式中:||代表L1 范数,m 与m 0 分别为3个待反演参数(Kf 、ϕ 、ρ )以及其初始模型值向量,其详细表达形式如下:
(24) R p p = [ R p p , 1 ( θ 1 ) , R p p , 2 ( θ 1 ) , … , R p p , N - 1 ( θ 1 ) , R p p , 1 ( θ 2 ) , R p p , 2 ( θ 2 ) , … , R p p , N - 1 ( θ 2 ) , R p p , 1 ( θ 3 ) , R p p , 2 ( θ 3 ) , … , R p p , N - 1 ( θ 3 ) ] T
(25) S = [ S 1 ( θ 1 ) , S 2 ( θ 1 ) , … , S N - 1 ( θ 1 ) , S 1 ( θ 2 ) , S 2 ( θ 2 ) , … , S N - 1 ( θ 2 ) , S 1 ( θ 3 ) , S 2 ( θ 3 ) , … , S N - 1 ( θ 3 ) ] T
(26) $\boldsymbol{W}=\left[\begin{array}{ccccccccccc}w_{1}\left(\theta_{1}\right) & 0 & \cdots & 0 & & & & & & & \\w_{2}\left(\theta_{1}\right) & w_{1}\left(\theta_{1}\right) & \cdots & 0 & & & & & & & \\\vdots & \vdots & \ddots & \vdots & & & & & & & \\w_{N / 2}\left(\theta_{1}\right) & w_{N / 2-1}\left(\theta_{1}\right) & \cdots & w_{1}\left(\theta_{1}\right) & & & & & & & \\0 & w_{N / 2}\left(\theta_{1}\right) & \cdots & w_{2}\left(\theta_{1}\right) & & & & & & & \\\vdots & \vdots & \ddots & \vdots & & & & & & & \\0 & 0 & \cdots & w_{N-1}\left(\theta_{1}\right) & & & & & & & \\& & & & w_{1}\left(\theta_{2}\right) & 0 & \cdots & 0 & & & \\& & & & w_{2}\left(\theta_{2}\right) & w_{1}\left(\theta_{2}\right) & \cdots & 0 & & & \\& & & & \vdots & \vdots & \ddots & \vdots & & & \\& & & & w_{N / 2}\left(\theta_{2}\right) & w_{N / 2-1}\left(\theta_{2}\right) & \cdots & w_{1}\left(\theta_{2}\right) & & & \\& & & & 0 & w_{N / 2}\left(\theta_{2}\right) & \cdots & w_{2}\left(\theta_{2}\right) & & & \\& & & & \vdots & \vdots & \ddots & \vdots & & & \\& & & & 0 & 0 & \cdots & w_{N-1}\left(\theta_{2}\right) & & & \\& & & & & & & & w_{1}\left(\theta_{3}\right) & 0 & \cdots & 0 \\& & & & & & & & w_{2}\left(\theta_{3}\right) & w_{1}\left(\theta_{3}\right) & \cdots & 0 \\& & & & & & & & \vdots & \vdots & \ddots & \vdots \\& & & & & & & & w_{N / 2}\left(\theta_{3}\right) & w_{N / 2-1}\left(\theta_{3}\right) & \cdots & w_{1}\left(\theta_{3}\right) \\& & & & & & & & 0 & w_{N / 2}\left(\theta_{3}\right) & \cdots & w_{2}\left(\theta_{3}\right) \\& & & & & & & & \vdots & \vdots & \ddots & \vdots \\& & & & & & & & 0 & 0 & \cdots & w_{N-1}\left(\theta_{3}\right)\end{array}\right]$
(27) m = [ K f , 1 , K f , 2 , … , K f , N , ϕ 1 , ϕ 2 , … , ϕ N , ρ 1 , ρ 2 , … , ρ N ] T
(28) m 0 = [ K f 0 , 1 , K f 0 , 2 , … , K f 0 , N , ϕ 0,1 , ϕ 0,2 , … , ϕ 0 , N , ρ 0,1 , ρ 0,2 , … , ρ 0 , N ] T
考虑到式(23)所示的目标函数具有强非线性及涉及到L1 范数的求解,使得常规梯度类型的反演算法难以获得可靠的数值解,为此,我们采用麻雀搜索算法(SSA)来求解此类非线性L1 范数问题。相比于常规梯度下降算法,SSA优化求解算法作为一种启发式算法,其不受目标函数可微、可导及连续性的限制,可以有效避免搜索陷入局部极小值,同时,其能够优化L1 范数目标函数,具有较高的鲁棒性和较好的收敛性,为得到分辨率更高、准确性更好的孔隙流体体积模量、孔隙度以及密度反演结果提供了算法基础。求解过程阐述如下:
令不同待反演参数序列md =[Kf ,1 ,Kf ,2 ,…,Kf , N ϕ 1 ,ϕ 2 ,…,ϕN ,ρ 1 ,ρ 2 ,…,ρN ]=[md ,1 ,md ,2 ,…,md , l Jd (md ,1 ,md ,2 ,…,md , l d S -WR pp |+|m -m 0 |)作为相应种群的适应度(目标函数越小代表适应度越强)。
首先,初始化麻雀种群,设定种群数量为h ,将待反演参数种群矩阵m * 中的各分量mi , j md 首次迭代值的位置矩阵m * :
(29) m * = m T 1 m T 2 ︙ m T h = m 1,1 m 1,2 … m 1 , l m 2,1 m 2,2 … m 2 , l ︙ ︙ ⋱ ︙ m h , 1 m h , 2 … m h , l
式中:l 为待反演参数序列的长度,其长度l =3N 。基于目标函数J ,可建立初始麻雀种群的适应度矩阵如下:
(30) J * = J 1 ( m 1,1 m 1,2 … m 1 , l ) J 2 ( m 2,1 m 2,2 … m 1 , l ) ︙ J h ( m h , 1 m h , 2 … m h , l )
将初始化得到的麻雀种群按照适应度从大到小进行排序后,开始进行麻雀种群的更新,优化过程首先对发现者进行更新,公式如下:
(31) $m_{i, j}^{t+1}=\left\{\begin{array}{cl}m_{i, j}^{t} \cdot \exp \left(\frac{-i}{a \cdot \text { iter }_{\max }}\right) & \text { if } R_{2}<S T, \\m_{i, j}^{t}+\Gamma \cdot \boldsymbol{L} & \text { if } \mathrm{R}_{2} \geqslant \mathrm{ST}\end{array}\right.$
式中:t 和iter max 分别代表当前迭代和最大迭代次数;a 为0~1之间的随机数;Γ为基于高斯分布的随机数;L 为长度为l 的各元素数值为1的列向量;R 2 和ST 则分别为介于0~1以及0.5~1之间的“警告值”和“安全阈值”常数。之后,将对跟随着的位置进行更新,迭代公式如下:
(32) $m_{i, j}^{\iota+1}=\left\{\begin{array}{cc}\Gamma \cdot \exp \left(\frac{m_{\text {worst }}-m_{i, j}^{t}}{i^{2}}\right) & \text { if } i>d / 2 \\m_{p}^{\iota+1}+\left|m_{i, j}^{\iota}-m_{p}^{\iota+1}\right| \cdot \boldsymbol{A}^{+} \cdot \boldsymbol{L} & \text { 其他。 }\end{array}\right.$
式中:mp 与m worst 分别为发现者中的最佳位置以及全局的最差位置;A+ =A T (AA T )-1 ,为每个元素被随机分配为1或-1的长度为l 的列向量A 的广义逆。最后,基于两类种群的更新,将进行随机危险预警,其迭代公式如下:
(33) $m_{i, j}^{t+1}=\left\{\begin{array}{cl}m_{\text {best }}^{t}+b \cdot\left|m_{i, j}^{t}-m_{\text {best }}^{t}\right| & \text { if } J_{i}>J_{g} \\m_{i, j}^{t}+\mathrm{K} \cdot\left(\frac{\left|m_{i, j}^{t}-m_{\text {worst }}^{t}\right|}{\left(J_{i}-J_{w}\right)+\varepsilon}\right) & \text { 其他。 }\end{array}\right.$
式中:Ji ,Jg 以及Jw 分别为当前、全局最优以及最差的适应度值;K为-1~1之间的随机数;b 为满足均值为0方差为1的高斯分布的随机数;ε 作为一个极小的常数,防止分母为零。利用式(23)所建立的目标函数,联合式(29)、(30),对式(31)~(33)进行多次迭代,直至满足输出条件(最佳适应度Jg 收敛至接近零值或达到最大迭代次数),即可求解得到目标函数取得极小时的全局最佳适应度Jg 所对应的待反演参数m T g Kf ,1 ,Kf ,2 ,…,Kf , N ϕ 1 ,ϕ 2 ,…,ϕN ,ρ 1 ,ρ 2 ,…,ρN ]=[mg ,1 ,mg ,2 ,…,mg , l
2 模型测试
本文将采用图2 所示的岩石物理模型,对所设计的反演方法进行模型测试,以此验证新方法所得的反演结果的合理性和有效性。
图2
图2
岩石物理模型
Fig.2
The rock physical models
图2 展示了用于模型测试的Kf 、孔隙度以及密度3个参数的岩石物理模型。图3 则展示了模型测试所用的无噪和信噪比为5的正演合成地震记录。图4 和图5 分别展示了以图3a 和图3b 为观测数据的无噪和信噪比为5的地震记录下不同反演方法下的3个参数反演结果。在图4 与图5 中,红色曲线代表真实模型,青色曲线代表初始模型,蓝色曲线和绿色曲线分别代表新非线性反演方法和常规梯度下降反演方法(梯度下降反演算法的目标函数及算法流程见附录C)下的反演结果。
图3
图3
正演合成的地震记录
Fig.3
The synthesized seismogram
图4
图4
无噪声合成地震记录下的反演结果
Fig.4
The inversion results of the synthesized seismogram with noise free
图5
图5
合成地震记录信噪比为5情况下的反演结果
Fig.5
The inversion results of the synthesized seismogram with signal-to-noise ratio of 5
不难看出,合成地震记录无噪情况下的反演结果与真实模型的吻合度较高,其中新非线性方法相比于常规方法,其结果与真实模型更为接近,此结果证明了所推导的非线性方程拥有较高的精度,能够用于合理有效地反演致密砂岩储层的岩石物理参数,且新方法由于采用了L1 范数约束下的麻雀搜索算法进行求解,其结果相比于常规方法更接近真实值,进一步证实了反演算法对于进一步提升反演精度的有效性。通过观察合成地震记录信噪比为5的含噪声反演结果可以看出新提出的反演算法相比于常规方法的准确性更高,具有更好的抗噪性,证实了新方法在提升含噪声复杂影响下的反演结果可靠性较高。
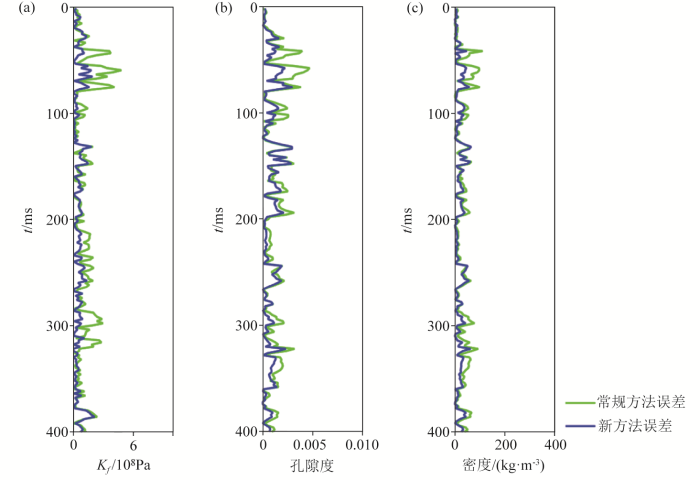
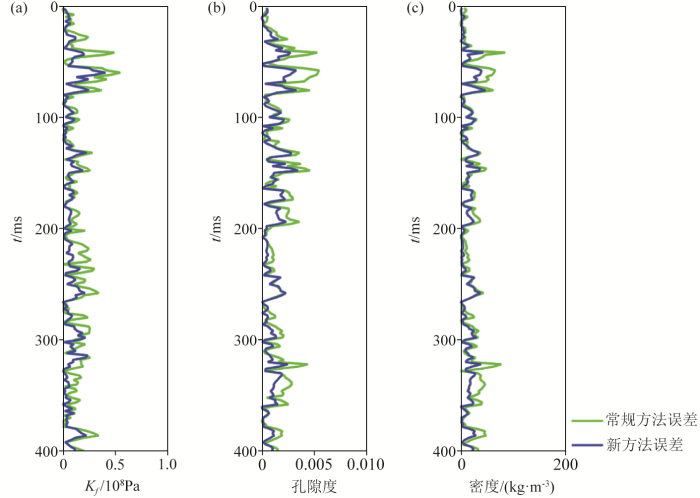
为进一步量化反演结果与真实模型之间的吻合度,图6 与图7 分别展示了合成地震记录无噪声反演结果与合成地震记录信噪比为5时的反演结果与真实模型之间的误差绝对值。通过观察能够发现,采用新方法的无噪声合成地震记录反演结果其误差绝对值基本小于常规方法,随着合成地震记录噪声的增加,反演结果的误差将增大,但由于新方法采用了L1 范数约束以及具有高鲁棒性的SSA优化求解算法,其反演结果的绝对误差小于常规方法,反演稳定性更强。
图6
图6
无噪声合成地震记录下反演结果与真实模型的误差绝对值
Fig.6
The absolute error between the inversion results and the true model under noise-free synthetic seismogram
图7
图7
合成地震记录信噪比为5情况下反演结果与真实模型的误差绝对值
Fig.7
The absolute error between the inversion results and the true model under a synthetic seismogram with a signal-to-noise ratio of 5
模型测试结果通过对比不同反演优化方法,不仅验证了所推导的反射系数方程的精度,更证实了所采用的L1 范数约束的麻雀搜索算法在提高反演准确性与稳定性方面的优势。为所提出反演方法应用于致密砂岩储层实际地震资料的非线性反演及岩石物理模型参数的准确提取奠定了理论基础。
3 实际资料测试
为测试所提出的非线性反演方法的实用性和可靠性,本文将选用中国中部鄂尔多斯盆地某致密砂岩勘探工区实际资料开展反演测试研究。
图8 展示了用于实际地震资料测试的3个角度部分叠加的过井地震剖面,地震剖面经过精细处理,保证了其能够反映振幅随入射角变化的纯波剖面。图中的黑色竖线位置代表测井所在位置。图9a~c 分别展示了L1 范数约束下的以麻雀搜索算法优化求解得到的Kf 、孔隙度和密度的非线性反演结果。图10a~c 分别展示了采用常规梯度下降求解算法进行反演所得到的Kf 、孔隙度以及密度的反演结果。在图9 和图10 中,图中的测井所在位置分别展示了相应的滤波后的变密度显示的测井曲线。可以看出,3个参数的反演结果在两种方法下都能够在测井所在位置与测井结果有较高的吻合度。对比两种反演方法,新方法所得到的反演结果能在箭头所指示的位置处对地层参数的变化描述表现出更好的效果,其反演结果的连续性、准确性以及分辨率都优于常规方法,对于复杂情况下的薄储层能够给出更好的展布刻画效果,能够改善现有方法勘探精度方面的不足,从而提升含油气储层的识别精度。为量化不同方法反演结果之间的差异,图11 展示了不同反演方法下实际地震资料井旁道反演结果与滤波后测井曲线的对比情况。不难看出,基于L1 范数约束的SSA优化算法得到的非线性反演结果相比于常规梯度下降算法的反演结果与滤波后的测井曲线吻合度更高,反演结果在储层参数预测精度方面更具优势。表2 统计了利用式(27)计算的实际资料井旁道反演结果与滤波后测井曲线的归一化均方根误差(normalized root mean square error,NRMSE ):
(34) $N R M S E=\frac{\sqrt{(\text { 反演值 }- \text { 滤波后井曲线值 })^{\mathrm{T}} \times(\text { 反演值 }- \text { 滤波后井曲线值 }) / N}}{\max (\text { 滤波后井曲线值 })-\min (\text { 滤波后井曲线值 })}$。
图8
图8
部分叠加的实际地震剖面
Fig.8
The partial stacked real seismic profiles
图9
图9
新非线性方法下的实际地震资料反演结果
Fig.9
The inversion results of real seismic data under the new nonlinear method
图10
图10
常规方法下的实际地震资料反演结果
Fig.10
The inversion results of real seismic data under the conventional method
图11
图11
不同反演方法下实际地震资料井旁道反演结果与滤波后测井曲线对比
Fig.11
Comparison of the well bypass inversion results of actual seismic data under different inversion methods and the filtered logging curves
可以看出,无论是新SSA反演方法还是常规梯度下降反演方法,其反演结果与滤波后的测井曲线都具有相对较小的归一化均方根误差值,验证了所建立的岩石物理模型的可靠性以及所推导的反射系数方程的准确性。对比新方法、常规方法与滤波后测井曲线的归一化均方根误差,新方法对孔隙流体体积模量Kf 、孔隙度ϕ 以及密度ρ 这3个储层参数的预测结果相比于常规方法均具有更小的均方根误差,反演结果的精度更高,验证了本研究所提出的反演算方法在提升反演准确性方面的优势,为提升储层表征的合理性奠定了基础。
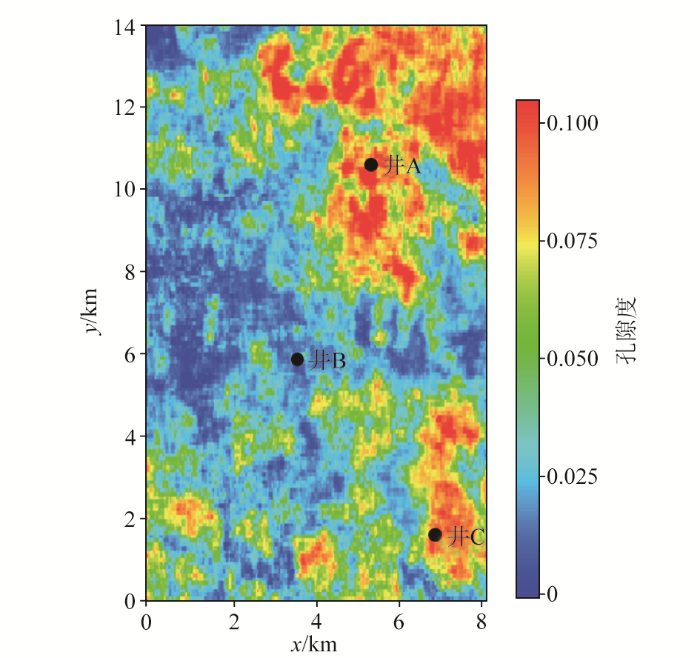
上述不同反演方法间的对比分析证实了所提方法在实际工区应用是有效的以及新方法在提升反演结果分辨率和准确性方面的优势,本文进一步将新方法应用于鄂尔多斯盆地三维致密砂岩工区,以测试其在三维工区的应用效果。图12 与图13 分别给出了新方法在三维工区反演的Kf 与孔隙度结果的沿层切片。在该三维工区中,有3口盲井(井A、井B以及井C),其中井A与井C在该层段测井解释含油,而井B在该层段不含油。通过观察切片结果的低Kf 与高孔隙度异常位置,能够清晰反映含油砂岩储层的横向展布预测,预测结果与测井所在位置是否含油气解释结果能够吻合,为利用本文方法进行致密砂岩储层精确预测给予了新的方案。
图12
图12
新非线性方法下的Kf 反演结果沿层切片
Fig.12
The interlayer slice of the real seismic data Kf inversion result under the new nonlinear method
图13
图13
新非线性方法下的孔隙度反演结果沿层切片
Fig.13
The interlayer slice of the real seismic data porosity inversion result under the new nonlinear method
实际地震资料的反演结果首先证明了所建立的岩石物理模型以及所推导的反射系数方程能够用于实际工区反演得到合理、可靠的反演结果。其次,通过不同反演方法的对比,证明了新方法能够进一步提高反演结果的精度,进而满足鄂尔多斯盆地致密砂岩储层实际工区勘探精度的需要。该方法在鄂尔多斯盆地致密砂岩储层实际二维及三维工区的应用中,利用所预测的储层参数得到了准确的致密砂岩相对高孔隙度含油气储层的分布,为该方法应用于鄂尔多斯盆地致密砂岩工区进行储层表征奠定了方法基础。
4 结论
本文针对致密砂岩储层背景下勘探精度与分辨率提升的需要,采用Kuster-Toksöz (KT)模型联系了饱和岩石的纵横波速度、密度以及储层岩石物理参数,基于精确Zoepprtiz,推导得到了非线性精确反射系数方程,方程相比于Aki-Richards线性近似实现了反射系数精度的提升,并联系了反射系数与储层孔隙流体体积模量与孔隙度,为储层物性参数的直接反演预测提供理论依据。
以褶积模型为依托,采用L1 范数约束下的麻雀搜算算法作为求解方法,发展了一种高精度非线性AVO反演方法,该方法相比于常规梯度下降算法能够进一步提升致密砂岩储层孔隙流体体积模量、孔隙度和密度反演结果的精度和分辨率,为提高储层表征的可靠性提供了技术基础。
将所提出的方法应用在鄂尔多斯盆地致密砂岩工区,得到了合理、可靠的孔隙流体体积模量与孔隙度预测结果,并在复杂致密砂岩的相对高孔隙度含油储层预测与展布刻画中得到了可靠的预测结果,为提升复杂致密砂岩储层实际勘探的准确性和分辨率给予了新的方案。
附录A
含孔隙流体体积模量Kf 、孔隙度ϕ 以及密度ρ 的非线性三参数反射系数方程的推导首先将建立纵波速度V p 、横波速度V s 与3个待反演参数之间的非线性联系,将式(4)、(5)代入式(6)、(7),可得:
(A-1) V p = 4 K m μ m + 3 K f K m + 4 K f μ m ϕ - 4 K m μ m ϕ 3 ρ ( K m ϕ + 4 μ m + 3 K f - 3 K f ϕ ) + 4 μ m 9 K m + 8 μ m ) ( 1 - ϕ ) 3 ρ 9 K m + 8 μ m + 6 ( K m - 2 K m ) ϕ )
(A-2) V s = μ m 9 K m + 8 μ m ) ( 1 - ϕ ) 9 ρ ( K m + 8 μ m + 6 ( K m - 2 K m ) ϕ )
考虑反射系数方程中反射界面两侧的上、下层介质,将式(A-1)、(A-2)代入式(8)~(19),可得含Kf 、ϕ 和ρ 的非线性三参数反射系数方程如下:
(A-3) R p p = f ( K f , 1 , K f , 2 , ϕ 1 , ϕ 2 , ρ 1 , ρ 2 ) = ( E - F + - G + H - p 2 ) / D
(A-4) D = E + F + + G - H - p 2
(A-5) $E^{+}=b \frac{\cos \alpha}{V_{\mathrm{p} 1}}+c \frac{\cos \alpha^{\prime}}{V_{\mathrm{p} 2}},$
(A-6) $E^{-}=b \frac{\cos \alpha}{V_{\mathrm{p} 1}}-c \frac{\cos \alpha^{\prime}}{V_{\mathrm{p} 2}}$
(A-7) $F^{+}=b \frac{\cos \beta}{V_{\mathrm{s} 1}}+c \frac{\cos \beta^{\prime}}{V_{\mathrm{s} 2}},$
(A-8) $G^{+}=a+d \frac{\cos \alpha}{V_{\mathrm{p} 1}} \frac{\cos \beta^{\prime}}{V_{\mathrm{s} 2}},$
(A-9) $G^{-}=a-d \frac{\cos \beta}{V_{\mathrm{p} 1}} \frac{\cos \beta^{\prime}}{V_{\mathrm{s} 2}},$
(A-10) $H^{-}=a-d \frac{\cos \alpha^{\prime}}{V_{\mathrm{p} 2}} \frac{\cos \beta}{V_{\mathrm{s} 1}},$
(A-11) $a=\rho_{2}\left(1-2 V_{\mathrm{s} 2}^{2} p^{2}\right)-\rho_{1}\left(1-2 V_{\mathrm{s} 1}^{2} p^{2}\right),$
(A-12) $b=\rho_{2}\left(1-2 V_{\mathrm{s} 2}^{2} p^{2}\right)+2 \rho_{1} V_{\mathrm{s} 1}^{2} p^{2},$
(A-13) $c=\rho_{2}\left(1-2 V_{\mathrm{s} 1}^{2} p^{2}\right)+2 \rho_{1} V_{\mathrm{s} 2}^{2} p^{2},$
(A-14) $d=2 \rho_{2} V_{\mathrm{s} 2}^{2}-2 \rho_{1} V_{\mathrm{s} 1}^{2},$
(A-15) $V_{\mathrm{p} 1}=\sqrt{\frac{4 K_{m} \mu_{m}+3 K_{f 1} K_{m}+4 K_{f 1} \mu_{m} \phi_{1}-4 K_{m} \mu_{m} \phi_{1}}{3 \rho_{1}\left(K_{m} \phi_{1}+4 \mu_{m}+3 K_{f 1}-3 K_{f 1} \phi_{1}\right)}+\frac{4 \mu_{m}\left(9 K_{m}+8 \mu_{m}\right)\left(1-\phi_{1}\right)}{3 \rho_{1}\left[9 K_{m}+8 \mu_{m}+6\left(K_{m}-2 K_{m}\right) \phi_{1}\right]}},$
(A-16) $V_{\mathrm{p} 2}=\sqrt{\frac{4 K_{m} \mu_{m}+3 K_{f 2} K_{m}+4 K_{f 2} \mu_{m} \phi_{2}-4 K_{m} \mu_{m} \phi_{2}}{3 \rho_{2}\left(K_{m} \phi_{2}+4 \mu_{m}+3 K_{f 2}-3 K_{f 2} \phi_{2}\right)}+\frac{4 \mu_{m}\left(9 K_{m}+8 \mu_{m}\right)\left(1-\phi_{2}\right)}{3 \rho_{2}\left[9 K_{m}+8 \mu_{m}+6\left(K_{m}-2 K_{m}\right) \phi_{2}\right]}},$
(A-17) $V_{\mathrm{s} 1}=\sqrt{\frac{\mu_{m}\left(9 K_{m}+8 \mu_{m}\right)\left(1-\phi_{1}\right)}{9 \rho_{1}\left[K_{m}+8 \mu_{m}+6\left(K_{m}-2 K_{m}\right) \phi_{1}\right]}},$
(A-18) $V_{\mathrm{s} 2}=\sqrt{\frac{\mu_{m}\left(9 K_{m}+8 \mu_{m}\right)\left(1-\phi_{2}\right)}{9 \rho_{2}\left[K_{m}+8 \mu_{m}+6\left(K_{m}-2 K_{m}\right) \phi_{2}\right]}},$
式中:Kf 1 、ϕ 1 、ρ 1 分别表示反射界面上层的孔隙流体体积模量、孔隙度和密度;Kf 2 、ϕ 2 、ρ 2 分别表示反射界面下层的孔隙流体体积模量、孔隙度和密度。
附录B
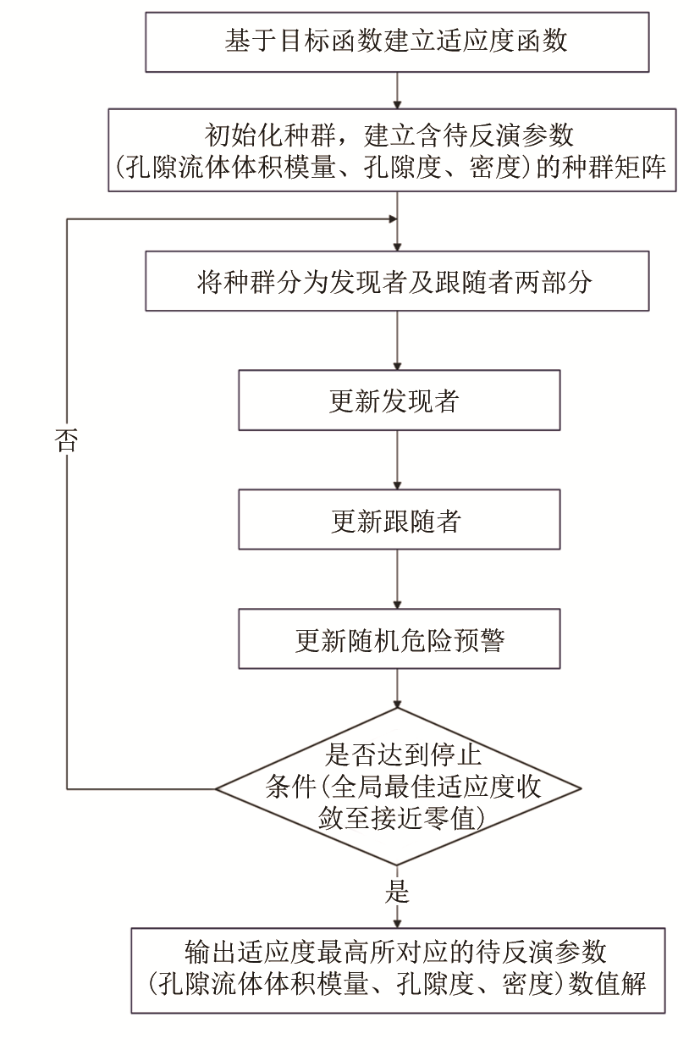
基于SSA算法的叠前非线性反演孔隙流体体积模量Kf 、孔隙度ϕ 以及密度ρ 的算法流程图描述如图B-1 。
图B-1
图B-1
基于SSA算法的叠前非线性反演流程
Fig.B-1
The flow chart of pre-stack nonlinear inversion on the basies of SSA algorithm
附录C
依托式(22)所示的褶积模型,基于褶积模型构建观测数据与正演合成数据的残差项,并采用常规L2 范数正则化约束进一步提高算法的抗噪性并降低优化求解过程中出现过拟合现象,建立基于梯度下降反演算法的目标函数建立如下:
(C-1) J G = S - W · R p p ‖ + m - m 0 ‖
式中:‖‖代表L2 范数, m 与m 0 分别表示3个待反演参数(Kf ,ϕ ,ρ )以及其初始模型值向量,式(C-1)中的各项详细表达描述如下:
(C-2) $\begin{aligned}\boldsymbol{R}_{\mathrm{pp}}= & {\left[R_{\mathrm{pp}, 1}\left(\theta_{1}\right), R_{\mathrm{pp}, 2}\left(\theta_{1}\right), \cdots, R_{\mathrm{pp}, N-1}\left(\theta_{1}\right), R_{\mathrm{pp}, 1}\left(\theta_{2}\right), R_{\mathrm{pp}, 2}\left(\theta_{2}\right), \cdots, R_{\mathrm{pp}, N-1}\left(\theta_{2}\right), R_{\mathrm{pp}, 1}\left(\theta_{3}\right), R_{\mathrm{pp}, 2}\left(\theta_{3}\right),\right.} \\ & \left.\cdots, R_{\mathrm{pp}, N-1}\left(\theta_{3}\right)\right]^{\mathrm{T}},\end{aligned}$
(C-3) $\boldsymbol{S}=\left[\mathrm{S}_{1}\left(\theta_{1}\right), \mathrm{S}_{2}\left(\theta_{1}\right), \cdots, \mathrm{S}_{N-1}\left(\theta_{1}\right), \mathrm{S}_{1}\left(\theta_{2}\right), \mathrm{S}_{2}\left(\theta_{2}\right), \cdots, \mathrm{S}_{N-1}\left(\theta_{2}\right), \mathrm{S}_{1}\left(\theta_{3}\right), \mathrm{S}_{2}\left(\theta_{3}\right), \cdots, \mathrm{S}_{N-1}\left(\theta_{3}\right)\right]^{\mathrm{T}},$
(C-4) $W=\left[\begin{array}{ccccccccccc}\\w_{1}\left(\theta_{1}\right) & 0 & \cdots & 0 & & & & & & & \\w_{2}\left(\theta_{1}\right) & w_{1}\left(\theta_{1}\right) & \cdots & 0 & & & & & & & \\\vdots & \vdots & \ddots & \vdots & & & & & & & \\w_{N / 2}\left(\theta_{1}\right) & w_{N / 2-1}\left(\theta_{1}\right) & \cdots & w_{1}\left(\theta_{1}\right) & & & & & & & \\0 & w_{N / 2}\left(\theta_{1}\right) & \cdots & w_{2}\left(\theta_{1}\right) & & & & & & & \\\vdots & \vdots & \ddots & \vdots & & & & & & & \\0 & 0 & \cdots & w_{N-1}\left(\theta_{1}\right) & & & & & & & \\& & & & w_{1}\left(\theta_{2}\right) & 0 & \cdots & 0 & & & \\& & & & w_{2}\left(\theta_{2}\right) & w_{1}\left(\theta_{2}\right) & \cdots & 0 & & & \\& & & & \vdots & \vdots & \ddots & \vdots & & & \\& & & & w_{N / 2}\left(\theta_{2}\right) & w_{N / 2-1}\left(\theta_{2}\right) & \cdots & w_{1}\left(\theta_{2}\right) & & & \\& & & & 0 & w_{N / 2}\left(\theta_{2}\right) & \cdots & w_{2}\left(\theta_{2}\right) & & & \\& & & & \vdots & \vdots & \ddots & \vdots & & & \\& & & & 0 & 0 & \cdots & w_{N-1}\left(\theta_{2}\right) & & & \\& & & & & & & w_{1}\left(\theta_{3}\right) & 0 & \cdots & 0\\& & & & & & & w_{2}\left(\theta_{3}\right) & w_{1}\left(\theta_{3}\right) & \cdots & 0 \\& & & & & & & \vdots & \vdots & \ddots & \vdots \\& & & & & & & w_{N / 2}\left(\theta_{3}\right) & w_{N / 2-1}\left(\theta_{3}\right) & \cdots & w_{1}\left(\theta_{3}\right) \\& & & & & & & 0 & w_{N / 2}\left(\theta_{3}\right) & \cdots & w_{2}\left(\theta_{3}\right) \\& & & & & & &\vdots & \vdots & \ddots & \vdots \\& & & & & & & 0 & 0 & \cdots & w_{N-1}\left(\theta_{3}\right)\end{array}\right]$
(C-5) m = [ K f , 1 , K f , 2 , … , K f , N , ϕ 1 , ϕ 2 , … , ϕ N , ρ 1 , ρ 2 , … , ρ N ] T
(C-6) m 0 = [ K f 0 , 1 , K f 0 , 2 , … , K f 0 , N , ϕ 0,1 , ϕ 0,2 , … , ϕ 0 , N , ρ 0,1 , ρ 0,2 , … , ρ 0 , N ] T
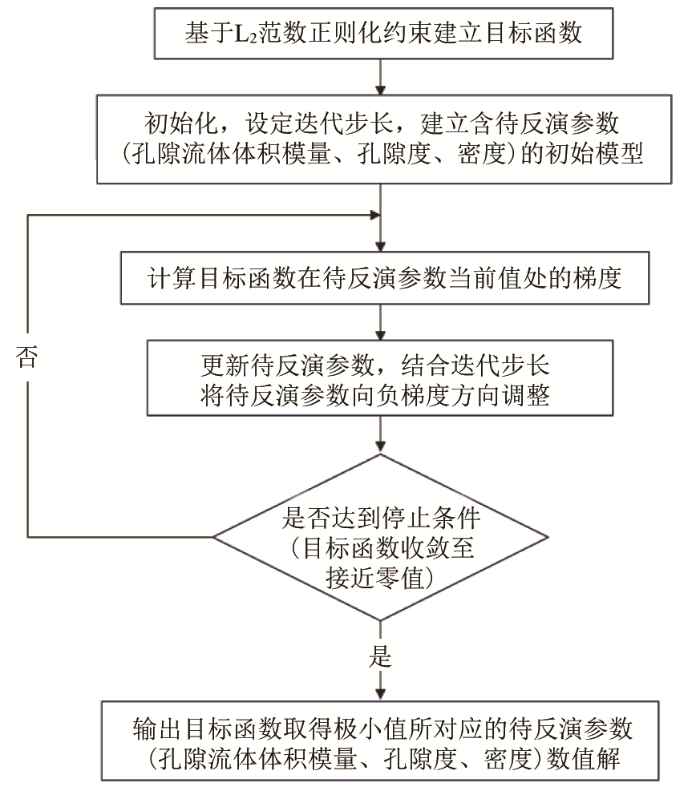
采用梯度下降算法[16 ,26 ] 求解式(C-1)所建立的目标函数,进行多次迭代,直至满足输出条件(目标函数JG 收敛至接近零值或达到最大迭代次数),即可求解得到目标函数取得极小时时对应的待反演参数m =[Kf ,1 ,Kf ,2 ,…,Kf , N ϕ 1 ,ϕ 2 ,…,ϕN ,ρ 1 ,ρ 2 ,…,ρN ]T 的数值解。梯度下降算法优化求解流程如图C-1 。
图C-1
图C-1
基于梯度下降算法的叠前非线性反演流程
Fig.C-1
The flow chart of pre-stack nonlinear inversion on the basies of gradient descent algorithm
参考文献
View Option
[1]
Bosch M Carvajal C Rodrigues J et al . Petrophysical seismic inversion conditioned to well-log data:Methods and application to a gas reservoir
[J]. Geophysics , 2009 , 74 (2 ):O1-O15.
[本文引用: 1]
[2]
Ran B Linearized orthorhombic AVAZ inversion:Theoretical and practical consideration
[C]// Denver:SEG Technical Program Expanded Abstracts 2014 , Society of Exploration Geophysicists ,2014:528 -532 .
[3]
Zong Z Y Yin X Y Wu G C Geofluid discrimination incorporating poroelasticity and seismic reflection inversion
[J]. Surveys in Geophysics , 2015 , 36 (5 ):659 -681 .
[4]
Pan X P Zhang G Z Model parameterization and PP-wave amplitude versus angle and azimuth(AVAZ) direct inversion for fracture quasi-weaknesses in weakly anisotropic elastic media
[J]. Surveys in Geophysics , 2018 , 39 (5 ):937 -964 .
[5]
Zong Z Y Zhang J L Chen F B Seismic prediction for formation pressure considering diagenesis effect
[J]. IEEE Transactions on Geoscience and Remote Sensing , 2024 ,62:4508813.
[本文引用: 1]
[6]
Grana D Della Rossa E Probabilistic petrophysical-properties estimation integrating statistical rock physics with seismic inversion
[J]. Geophysics , 2010 , 75 (3 ):O21-O37.
[本文引用: 1]
[7]
宗兆云 , 印兴耀 , 吴国忱 . 基于叠前地震纵横波模量直接反演的流体检测方法
[J]. 地球物理学报 , 2012 , 55 (1 ):284 -292 .
[本文引用: 1]
Zong Z Y Yin X Y Wu G C Fluid detection method based on direct inversion of pre-stack seismic P-S wave modulus
[J]. Chinese Journal of Geophysics , 2012 , 55 (1 ):284 -292 .
[本文引用: 1]
[8]
卢明辉 , 巴晶 , 晏信飞 . 致密砂岩的等效介质理论研究
[C]// 中国地球物理学会 , 中国石油学会 ,2011:725 -729 .
[本文引用: 1]
Lu M Ba J Yan X F Theoretical study on equivalent medium of tight sandstone
[C]// Chinese Geophysical Society , Chinese Petroleum Society ,2011:725 -729 .
[本文引用: 1]
[9]
印兴耀 , 刘欣欣 , 曹丹平 . 基于Biot相洽理论的致密砂岩弹性参数计算方法
[J]. 石油物探 , 2013 , 52 (5 ):445 -451 ,441.
DOI:10.3969/j.issn.1000-1441.2013.05.001
[本文引用: 1]
致密砂岩储层中速度孔隙度关系复杂,针对致密砂岩中孔隙/裂隙并存的特点,提出了一种致密砂岩储层弹性参数的计算方法。根据Biot相洽理论,引入岩石骨架泊松比,在Biot相洽条件下对其进行求取,用于岩石骨架弹性模量的计算;结合约束反演求取的裂隙孔隙度,在Biot理论框架下求取孔隙和裂隙并存时致密砂岩的弹性参数。该方法无需对除裂隙以外的孔隙进行描述,避免了孔隙参数选取不合理带来的计算误差。使用该方法计算实际致密砂岩储层的弹性参数,用于横波速度计算以及流体敏感参数交会分析,取得了较好的效果,证明了方法的有效性。
Yin X Y Liu X X Cao D P Elastic parameters calculation for tight sand reservoir based on Biotconsistent theory
[J]. Geophysical Prospecting for Petroleum , 2013 , 52 (5 ):445 -451 ,441.
[本文引用: 1]
[10]
刘倩 , 印兴耀 , 李超 . 含不连通孔隙的致密砂岩储层岩石弹性模量预测方法
[J]. 石油物探 , 2015 , 54 (6 ):635 -642 .
DOI:10.3969/j.issn.1000-1441.2015.06.001
[本文引用: 1]
致密砂岩储层与常规储层相比具有低孔、低渗、连通性差等特性。针对致密砂岩储层中不连通孔隙的影响,提出了一种适用于致密砂岩储层的岩石物理模型建立方法,重点是利用Raymer公式引入不连通孔隙度的影响来修正基质模量的方法,阐述了依照连通孔隙度Gassmann方程在干岩石骨架的孔隙空间进行流体充填,分析讨论了不连通孔隙的引入对于岩石弹性模量及流体响应特征的影响。应用该方法对实验测量数据及某实际工区井资料进行试算发现,与常规有效介质模型预测结果相比,基于含不连通孔隙致密砂岩岩石物理模型估算的纵、横波速度值与测井结果吻合更好,验证了方法的合理性。
Liu Q Yin X Y Li C Prediction method of rock elastic modulus of tight sandstone reservoirs with disconnected pores
[J]. Geophysical Prospecting for Petroleum , 2015 , 54 (6 ):635 -642 .
[本文引用: 1]
[11]
Fan X G Zhang G Z Zhang J J Prediction method of pore structure parameters of tight sandstone
[C]// San Antonio:SEG Technical Program Expanded Abstracts 2019 , Society of Exploration Geophysicists ,2019:3678 -3682 .
[本文引用: 1]
[12]
Cooke D A Schneider W A Generalized linear inversion of reflection seismic data
[J]. Geophysics , 1983 , 48 (6 ):665 -676 .
[本文引用: 1]
[13]
Du B Y Yang W Y Zhang J et al . Matrix-fluid decoupling-based joint PP-PS-wave seismic inversion for fluid identification
[J]. Geophysics , 2019 , 84 (3 ):R477-R487.
[本文引用: 1]
[14]
Yin X Y Cheng G S Zong Z Y Non-linear AVO inversion based on a novel exact PP reflection coefficient
[J]. Journal of Applied Geophysics , 2018 ,159:408 -417 .
[本文引用: 1]
[15]
Cheng G S Yin X Y Zong Z Y Third-order AVO inversion for lamé parameter based on inverse operator estimation algorithm
[J]. Journal of Petroleum Science and Engineering , 2018 ,164:117 -126 .
[本文引用: 1]
[16]
Zhou L Liu X Y Li J Y et al . Robust AVO inversion for the fluid factor and shear modulus
[J]. Geophysics , 2021 , 86 (4 ):R471-R483.
[本文引用: 2]
[17]
Kuster G T Toksöz M N Velocity and attenuation of seismic waves in two-phase media:Part i.Theoretical formulations
[J]. Geophysics , 1974 , 39 (5 ):587 -606 .
[本文引用: 2]
[18]
Berryman J G Long-wavelength propagation in composite elastic media II.Ellipsoidal inclusions
[J]. Acoustical Society of America Journal , 1980 , 68 (6 ):1820 -1831 .
[本文引用: 2]
[19]
Zoeppritz K Erdbebnenwellen V On the reflection and penetration of seismic waves through unstable layers
[J]. Gottinger Nachrichten , 1919 , 1 (5 ):66 -84 .
[本文引用: 2]
[20]
Xue J K Shen B A novel swarm intelligence optimization approach:Sparrow search algorithm
[J]. Systems Science & Control Engineering , 2020 , 8 (1 ):22 -34 .
[本文引用: 1]
[21]
Gassmann F Elastic waves through a packing of spheres
[J]. Geophysics , 1951 , 16 (4 ):673 -685 .
[本文引用: 1]
[22]
Aki K Richards P Quantitative seismology:Theory and methods [M]. W.H. Freeman and Co. ,1980.
[本文引用: 1]
[23]
印兴耀 , 邓炜 , 宗兆云 . 基于逆算子估计的AVO反演方法研究
[J]. 地球物理学报 , 2016 , 59 (4 ):1457 -1468 .
DOI:10.6038/cjg20160426
[本文引用: 1]
传统反演算法以优化算法为主,而基于逆算子估计的AVO反演算法则利用了直接求逆的思路.算法的关键在于寻找存在逆函数的子域,进而可以在子域内直接求逆,这种解决反问题的思路不同于一般的优化类算法所采用的直接搜索解的方式,具有更高的效率.AVO反演利用了振幅随着偏移距的变化特征,反演的精度受到地震资料质量的影响,通过加入L1范数约束以及合理的初始模型有助于提高反演的稳定性以及准确度.模型测算和实际应用表明,基于逆算子估计的AVO反演方法具有较高的精确程度和可靠性.
Yin X Y Deng W Zong Z Y AVO inversion based on inverse operator estimation
[J]. Chinese J. Geophys. , 2016 , 59 (4 ):1457 -1468 .
[本文引用: 1]
[24]
邓炜 , 印兴耀 , 宗兆云 , 等 . 基于逆算子估计的高阶AVO非线性反演
[J]. 石油地球物理勘探 , 2016 , 51 (5 ):955 -964 ,837.
Deng W Yin X Y Zong Z Y et al . High-order nonlinear AVO inversion based on estimated inverse operator
[J]. Oil Geophysical Prospecting , 2016 , 51 (5 ):955 -964 ,837.
[25]
Cheng G S Yin X Y Zong Z Y Nonlinear amplitude-variation-with-offset inversion for Lamé parameters using a direct inversion method
[J]. Interpretation , 2017 , 5 (3 ):SL57-SL67.
[本文引用: 1]
[26]
Luo C Li X Y Huang G T Pre-stack AVA inversion by using propagator matrix forward modeling
[J]. Pure and Applied Geophysics , 2019 , 176 (10 ):4445 -4476 .
DOI:10.1007/s00024-019-02157-9
[本文引用: 1]
Most existing amplitude variation with angle (AVA) inversions are based on the exact Zoeppritz equation or its approximations. These modeling methods, which are ray-tracing-based and describe P-wave primary reflections only, lead to exacting requirements for pre-processing of the input data. Current processing is inadequate to satisfy these demands, especially for removing the effects of transmission losses, P-wave multiples and various converted-wave modes. By using input data with processing errors, inversion results of primary-only methods are predictably not accurate enough. The propagator matrix (PM), like the reflectivity method, uses an analytical solution to the wave equation and considers full-wave propagation effects in horizontal or nearly horizontal multilayered earth models. The numerical examples verify that a PM can effectively estimate transmission losses, multi-reflections and the comprehensive responses of thin interbedded layers, and also has higher reflection sensitivities to P-wave and S-wave velocity and density, as compared with raytracing-based AVA modelling. A pre-stack AVA three-parameter inversion by using a PM as the forward engine is proposed. Following a Bayesian approach, the inversion is stabilized by including the correlation of P-wave velocity, S-wave velocity and density. For inversion accuracy, the limited-memory Broyden-Fletcher-Goldfarb-Shanno (L-BFGS) optimization method is used to solve the augmented function, and the generalized cross-validation (GCV) criterion (Huang et al. in J Geophys Eng 14(1):100-112, 2017) is introduced to adaptively acquire the regularization parameter. Theoretical model inversion analysis shows that the proposed inversion can make use of transmission losses, P-wave multiples and converted wave modes, which not only cost-effectively simplifies the pre-processing, but also generates reasonable inverted results for multilayered conditions. The proposed inversion is then applied to a set of real data, and a comparison with Zoeppritz equation-based inversion demonstrates that PM inversion is clearly superior to Zoeppritz equation-based inversion in terms of stability and accuracy.
Petrophysical seismic inversion conditioned to well-log data:Methods and application to a gas reservoir
1
2009
... 利用地震反演的手段对储层岩石物理参数进行估计进而开展流体识别及储层表征是勘探地震学中的一个重要研究方向,能够为储层的含油气性评价提供明确的引导作用[1 5 ] . ...
Linearized orthorhombic AVAZ inversion:Theoretical and practical consideration
0
Geofluid discrimination incorporating poroelasticity and seismic reflection inversion
0
2015
Model parameterization and PP-wave amplitude versus angle and azimuth(AVAZ) direct inversion for fracture quasi-weaknesses in weakly anisotropic elastic media
0
2018
Seismic prediction for formation pressure considering diagenesis effect
1
2024
... 利用地震反演的手段对储层岩石物理参数进行估计进而开展流体识别及储层表征是勘探地震学中的一个重要研究方向,能够为储层的含油气性评价提供明确的引导作用[1 5 ] . ...
Probabilistic petrophysical-properties estimation integrating statistical rock physics with seismic inversion
1
2010
... 依托岩石物理理论研究,选择并构建相应的储层敏感参数岩石物理模型进而开展地球物理反演,对地下岩性以及流体类型进行判断,已经成为了目前储层描述以及含油气评价的一项重要手段.Grana等[6 ] 利用贝叶斯框架建立了相应的储层物性参数目标函数,并提出了统计学理论下的岩石物理建模及储层物性参数反演方法,以及岩性流体聚类策略.宗兆云等[7 ] 利用Gassmann方程推导了纵、横波模量相关的储层流体识别反射系数方程,并发展了一种叠前弹性阻抗反演储层流体敏感参数的新方法.随着地球物理理论的快速发展以及勘探工区的日益复杂,考虑砂岩致密特征的岩石物理模型及反演逐步成为了研究的焦点.卢明辉等[8 ] 在对比和分析等效介质理论中获得了能够描述致密砂岩孔隙结构的岩石物理模型.基于Biot相洽理论,印兴耀等[9 ] 发展了一种针对裂缝型致密砂岩的弹性参数估计方法,为致密砂岩弹性性质的分析开辟了新的途径.刘倩等[10 ] 在考虑孔隙连通性的基础上建立了含不连通孔隙度影响下的岩石物理模型,并对其储层的弹性特征进行了研究.针对含气致密砂岩储层,Fan等[11 ] 将统一岩石骨架模型与Sun模型相结合,得到了新的孔隙结构计算方法,并对致密砂岩孔隙结构参数进行了贝叶斯概率化反演.上述岩石物理理论驱动下的反演方法为致密砂岩储层表征提供了可靠的解决方案,但是,由于大多数反演算法为基于线性近似式的线性反演,当储层复杂性变高、纵横向变化剧烈,且勘探精度要求较高时,线性反演结果难以给出可靠的储层弹性或者物性参数预测结果.为此,寻找更为合适的反演方法以提高反演结果的准确性是目前需要解决的一项重点问题. ...
基于叠前地震纵横波模量直接反演的流体检测方法
1
2012
... 依托岩石物理理论研究,选择并构建相应的储层敏感参数岩石物理模型进而开展地球物理反演,对地下岩性以及流体类型进行判断,已经成为了目前储层描述以及含油气评价的一项重要手段.Grana等[6 ] 利用贝叶斯框架建立了相应的储层物性参数目标函数,并提出了统计学理论下的岩石物理建模及储层物性参数反演方法,以及岩性流体聚类策略.宗兆云等[7 ] 利用Gassmann方程推导了纵、横波模量相关的储层流体识别反射系数方程,并发展了一种叠前弹性阻抗反演储层流体敏感参数的新方法.随着地球物理理论的快速发展以及勘探工区的日益复杂,考虑砂岩致密特征的岩石物理模型及反演逐步成为了研究的焦点.卢明辉等[8 ] 在对比和分析等效介质理论中获得了能够描述致密砂岩孔隙结构的岩石物理模型.基于Biot相洽理论,印兴耀等[9 ] 发展了一种针对裂缝型致密砂岩的弹性参数估计方法,为致密砂岩弹性性质的分析开辟了新的途径.刘倩等[10 ] 在考虑孔隙连通性的基础上建立了含不连通孔隙度影响下的岩石物理模型,并对其储层的弹性特征进行了研究.针对含气致密砂岩储层,Fan等[11 ] 将统一岩石骨架模型与Sun模型相结合,得到了新的孔隙结构计算方法,并对致密砂岩孔隙结构参数进行了贝叶斯概率化反演.上述岩石物理理论驱动下的反演方法为致密砂岩储层表征提供了可靠的解决方案,但是,由于大多数反演算法为基于线性近似式的线性反演,当储层复杂性变高、纵横向变化剧烈,且勘探精度要求较高时,线性反演结果难以给出可靠的储层弹性或者物性参数预测结果.为此,寻找更为合适的反演方法以提高反演结果的准确性是目前需要解决的一项重点问题. ...
基于叠前地震纵横波模量直接反演的流体检测方法
1
2012
... 依托岩石物理理论研究,选择并构建相应的储层敏感参数岩石物理模型进而开展地球物理反演,对地下岩性以及流体类型进行判断,已经成为了目前储层描述以及含油气评价的一项重要手段.Grana等[6 ] 利用贝叶斯框架建立了相应的储层物性参数目标函数,并提出了统计学理论下的岩石物理建模及储层物性参数反演方法,以及岩性流体聚类策略.宗兆云等[7 ] 利用Gassmann方程推导了纵、横波模量相关的储层流体识别反射系数方程,并发展了一种叠前弹性阻抗反演储层流体敏感参数的新方法.随着地球物理理论的快速发展以及勘探工区的日益复杂,考虑砂岩致密特征的岩石物理模型及反演逐步成为了研究的焦点.卢明辉等[8 ] 在对比和分析等效介质理论中获得了能够描述致密砂岩孔隙结构的岩石物理模型.基于Biot相洽理论,印兴耀等[9 ] 发展了一种针对裂缝型致密砂岩的弹性参数估计方法,为致密砂岩弹性性质的分析开辟了新的途径.刘倩等[10 ] 在考虑孔隙连通性的基础上建立了含不连通孔隙度影响下的岩石物理模型,并对其储层的弹性特征进行了研究.针对含气致密砂岩储层,Fan等[11 ] 将统一岩石骨架模型与Sun模型相结合,得到了新的孔隙结构计算方法,并对致密砂岩孔隙结构参数进行了贝叶斯概率化反演.上述岩石物理理论驱动下的反演方法为致密砂岩储层表征提供了可靠的解决方案,但是,由于大多数反演算法为基于线性近似式的线性反演,当储层复杂性变高、纵横向变化剧烈,且勘探精度要求较高时,线性反演结果难以给出可靠的储层弹性或者物性参数预测结果.为此,寻找更为合适的反演方法以提高反演结果的准确性是目前需要解决的一项重点问题. ...
致密砂岩的等效介质理论研究
1
... 依托岩石物理理论研究,选择并构建相应的储层敏感参数岩石物理模型进而开展地球物理反演,对地下岩性以及流体类型进行判断,已经成为了目前储层描述以及含油气评价的一项重要手段.Grana等[6 ] 利用贝叶斯框架建立了相应的储层物性参数目标函数,并提出了统计学理论下的岩石物理建模及储层物性参数反演方法,以及岩性流体聚类策略.宗兆云等[7 ] 利用Gassmann方程推导了纵、横波模量相关的储层流体识别反射系数方程,并发展了一种叠前弹性阻抗反演储层流体敏感参数的新方法.随着地球物理理论的快速发展以及勘探工区的日益复杂,考虑砂岩致密特征的岩石物理模型及反演逐步成为了研究的焦点.卢明辉等[8 ] 在对比和分析等效介质理论中获得了能够描述致密砂岩孔隙结构的岩石物理模型.基于Biot相洽理论,印兴耀等[9 ] 发展了一种针对裂缝型致密砂岩的弹性参数估计方法,为致密砂岩弹性性质的分析开辟了新的途径.刘倩等[10 ] 在考虑孔隙连通性的基础上建立了含不连通孔隙度影响下的岩石物理模型,并对其储层的弹性特征进行了研究.针对含气致密砂岩储层,Fan等[11 ] 将统一岩石骨架模型与Sun模型相结合,得到了新的孔隙结构计算方法,并对致密砂岩孔隙结构参数进行了贝叶斯概率化反演.上述岩石物理理论驱动下的反演方法为致密砂岩储层表征提供了可靠的解决方案,但是,由于大多数反演算法为基于线性近似式的线性反演,当储层复杂性变高、纵横向变化剧烈,且勘探精度要求较高时,线性反演结果难以给出可靠的储层弹性或者物性参数预测结果.为此,寻找更为合适的反演方法以提高反演结果的准确性是目前需要解决的一项重点问题. ...
致密砂岩的等效介质理论研究
1
... 依托岩石物理理论研究,选择并构建相应的储层敏感参数岩石物理模型进而开展地球物理反演,对地下岩性以及流体类型进行判断,已经成为了目前储层描述以及含油气评价的一项重要手段.Grana等[6 ] 利用贝叶斯框架建立了相应的储层物性参数目标函数,并提出了统计学理论下的岩石物理建模及储层物性参数反演方法,以及岩性流体聚类策略.宗兆云等[7 ] 利用Gassmann方程推导了纵、横波模量相关的储层流体识别反射系数方程,并发展了一种叠前弹性阻抗反演储层流体敏感参数的新方法.随着地球物理理论的快速发展以及勘探工区的日益复杂,考虑砂岩致密特征的岩石物理模型及反演逐步成为了研究的焦点.卢明辉等[8 ] 在对比和分析等效介质理论中获得了能够描述致密砂岩孔隙结构的岩石物理模型.基于Biot相洽理论,印兴耀等[9 ] 发展了一种针对裂缝型致密砂岩的弹性参数估计方法,为致密砂岩弹性性质的分析开辟了新的途径.刘倩等[10 ] 在考虑孔隙连通性的基础上建立了含不连通孔隙度影响下的岩石物理模型,并对其储层的弹性特征进行了研究.针对含气致密砂岩储层,Fan等[11 ] 将统一岩石骨架模型与Sun模型相结合,得到了新的孔隙结构计算方法,并对致密砂岩孔隙结构参数进行了贝叶斯概率化反演.上述岩石物理理论驱动下的反演方法为致密砂岩储层表征提供了可靠的解决方案,但是,由于大多数反演算法为基于线性近似式的线性反演,当储层复杂性变高、纵横向变化剧烈,且勘探精度要求较高时,线性反演结果难以给出可靠的储层弹性或者物性参数预测结果.为此,寻找更为合适的反演方法以提高反演结果的准确性是目前需要解决的一项重点问题. ...
基于Biot相洽理论的致密砂岩弹性参数计算方法
1
2013
... 依托岩石物理理论研究,选择并构建相应的储层敏感参数岩石物理模型进而开展地球物理反演,对地下岩性以及流体类型进行判断,已经成为了目前储层描述以及含油气评价的一项重要手段.Grana等[6 ] 利用贝叶斯框架建立了相应的储层物性参数目标函数,并提出了统计学理论下的岩石物理建模及储层物性参数反演方法,以及岩性流体聚类策略.宗兆云等[7 ] 利用Gassmann方程推导了纵、横波模量相关的储层流体识别反射系数方程,并发展了一种叠前弹性阻抗反演储层流体敏感参数的新方法.随着地球物理理论的快速发展以及勘探工区的日益复杂,考虑砂岩致密特征的岩石物理模型及反演逐步成为了研究的焦点.卢明辉等[8 ] 在对比和分析等效介质理论中获得了能够描述致密砂岩孔隙结构的岩石物理模型.基于Biot相洽理论,印兴耀等[9 ] 发展了一种针对裂缝型致密砂岩的弹性参数估计方法,为致密砂岩弹性性质的分析开辟了新的途径.刘倩等[10 ] 在考虑孔隙连通性的基础上建立了含不连通孔隙度影响下的岩石物理模型,并对其储层的弹性特征进行了研究.针对含气致密砂岩储层,Fan等[11 ] 将统一岩石骨架模型与Sun模型相结合,得到了新的孔隙结构计算方法,并对致密砂岩孔隙结构参数进行了贝叶斯概率化反演.上述岩石物理理论驱动下的反演方法为致密砂岩储层表征提供了可靠的解决方案,但是,由于大多数反演算法为基于线性近似式的线性反演,当储层复杂性变高、纵横向变化剧烈,且勘探精度要求较高时,线性反演结果难以给出可靠的储层弹性或者物性参数预测结果.为此,寻找更为合适的反演方法以提高反演结果的准确性是目前需要解决的一项重点问题. ...
基于Biot相洽理论的致密砂岩弹性参数计算方法
1
2013
... 依托岩石物理理论研究,选择并构建相应的储层敏感参数岩石物理模型进而开展地球物理反演,对地下岩性以及流体类型进行判断,已经成为了目前储层描述以及含油气评价的一项重要手段.Grana等[6 ] 利用贝叶斯框架建立了相应的储层物性参数目标函数,并提出了统计学理论下的岩石物理建模及储层物性参数反演方法,以及岩性流体聚类策略.宗兆云等[7 ] 利用Gassmann方程推导了纵、横波模量相关的储层流体识别反射系数方程,并发展了一种叠前弹性阻抗反演储层流体敏感参数的新方法.随着地球物理理论的快速发展以及勘探工区的日益复杂,考虑砂岩致密特征的岩石物理模型及反演逐步成为了研究的焦点.卢明辉等[8 ] 在对比和分析等效介质理论中获得了能够描述致密砂岩孔隙结构的岩石物理模型.基于Biot相洽理论,印兴耀等[9 ] 发展了一种针对裂缝型致密砂岩的弹性参数估计方法,为致密砂岩弹性性质的分析开辟了新的途径.刘倩等[10 ] 在考虑孔隙连通性的基础上建立了含不连通孔隙度影响下的岩石物理模型,并对其储层的弹性特征进行了研究.针对含气致密砂岩储层,Fan等[11 ] 将统一岩石骨架模型与Sun模型相结合,得到了新的孔隙结构计算方法,并对致密砂岩孔隙结构参数进行了贝叶斯概率化反演.上述岩石物理理论驱动下的反演方法为致密砂岩储层表征提供了可靠的解决方案,但是,由于大多数反演算法为基于线性近似式的线性反演,当储层复杂性变高、纵横向变化剧烈,且勘探精度要求较高时,线性反演结果难以给出可靠的储层弹性或者物性参数预测结果.为此,寻找更为合适的反演方法以提高反演结果的准确性是目前需要解决的一项重点问题. ...
含不连通孔隙的致密砂岩储层岩石弹性模量预测方法
1
2015
... 依托岩石物理理论研究,选择并构建相应的储层敏感参数岩石物理模型进而开展地球物理反演,对地下岩性以及流体类型进行判断,已经成为了目前储层描述以及含油气评价的一项重要手段.Grana等[6 ] 利用贝叶斯框架建立了相应的储层物性参数目标函数,并提出了统计学理论下的岩石物理建模及储层物性参数反演方法,以及岩性流体聚类策略.宗兆云等[7 ] 利用Gassmann方程推导了纵、横波模量相关的储层流体识别反射系数方程,并发展了一种叠前弹性阻抗反演储层流体敏感参数的新方法.随着地球物理理论的快速发展以及勘探工区的日益复杂,考虑砂岩致密特征的岩石物理模型及反演逐步成为了研究的焦点.卢明辉等[8 ] 在对比和分析等效介质理论中获得了能够描述致密砂岩孔隙结构的岩石物理模型.基于Biot相洽理论,印兴耀等[9 ] 发展了一种针对裂缝型致密砂岩的弹性参数估计方法,为致密砂岩弹性性质的分析开辟了新的途径.刘倩等[10 ] 在考虑孔隙连通性的基础上建立了含不连通孔隙度影响下的岩石物理模型,并对其储层的弹性特征进行了研究.针对含气致密砂岩储层,Fan等[11 ] 将统一岩石骨架模型与Sun模型相结合,得到了新的孔隙结构计算方法,并对致密砂岩孔隙结构参数进行了贝叶斯概率化反演.上述岩石物理理论驱动下的反演方法为致密砂岩储层表征提供了可靠的解决方案,但是,由于大多数反演算法为基于线性近似式的线性反演,当储层复杂性变高、纵横向变化剧烈,且勘探精度要求较高时,线性反演结果难以给出可靠的储层弹性或者物性参数预测结果.为此,寻找更为合适的反演方法以提高反演结果的准确性是目前需要解决的一项重点问题. ...
含不连通孔隙的致密砂岩储层岩石弹性模量预测方法
1
2015
... 依托岩石物理理论研究,选择并构建相应的储层敏感参数岩石物理模型进而开展地球物理反演,对地下岩性以及流体类型进行判断,已经成为了目前储层描述以及含油气评价的一项重要手段.Grana等[6 ] 利用贝叶斯框架建立了相应的储层物性参数目标函数,并提出了统计学理论下的岩石物理建模及储层物性参数反演方法,以及岩性流体聚类策略.宗兆云等[7 ] 利用Gassmann方程推导了纵、横波模量相关的储层流体识别反射系数方程,并发展了一种叠前弹性阻抗反演储层流体敏感参数的新方法.随着地球物理理论的快速发展以及勘探工区的日益复杂,考虑砂岩致密特征的岩石物理模型及反演逐步成为了研究的焦点.卢明辉等[8 ] 在对比和分析等效介质理论中获得了能够描述致密砂岩孔隙结构的岩石物理模型.基于Biot相洽理论,印兴耀等[9 ] 发展了一种针对裂缝型致密砂岩的弹性参数估计方法,为致密砂岩弹性性质的分析开辟了新的途径.刘倩等[10 ] 在考虑孔隙连通性的基础上建立了含不连通孔隙度影响下的岩石物理模型,并对其储层的弹性特征进行了研究.针对含气致密砂岩储层,Fan等[11 ] 将统一岩石骨架模型与Sun模型相结合,得到了新的孔隙结构计算方法,并对致密砂岩孔隙结构参数进行了贝叶斯概率化反演.上述岩石物理理论驱动下的反演方法为致密砂岩储层表征提供了可靠的解决方案,但是,由于大多数反演算法为基于线性近似式的线性反演,当储层复杂性变高、纵横向变化剧烈,且勘探精度要求较高时,线性反演结果难以给出可靠的储层弹性或者物性参数预测结果.为此,寻找更为合适的反演方法以提高反演结果的准确性是目前需要解决的一项重点问题. ...
Prediction method of pore structure parameters of tight sandstone
1
... 依托岩石物理理论研究,选择并构建相应的储层敏感参数岩石物理模型进而开展地球物理反演,对地下岩性以及流体类型进行判断,已经成为了目前储层描述以及含油气评价的一项重要手段.Grana等[6 ] 利用贝叶斯框架建立了相应的储层物性参数目标函数,并提出了统计学理论下的岩石物理建模及储层物性参数反演方法,以及岩性流体聚类策略.宗兆云等[7 ] 利用Gassmann方程推导了纵、横波模量相关的储层流体识别反射系数方程,并发展了一种叠前弹性阻抗反演储层流体敏感参数的新方法.随着地球物理理论的快速发展以及勘探工区的日益复杂,考虑砂岩致密特征的岩石物理模型及反演逐步成为了研究的焦点.卢明辉等[8 ] 在对比和分析等效介质理论中获得了能够描述致密砂岩孔隙结构的岩石物理模型.基于Biot相洽理论,印兴耀等[9 ] 发展了一种针对裂缝型致密砂岩的弹性参数估计方法,为致密砂岩弹性性质的分析开辟了新的途径.刘倩等[10 ] 在考虑孔隙连通性的基础上建立了含不连通孔隙度影响下的岩石物理模型,并对其储层的弹性特征进行了研究.针对含气致密砂岩储层,Fan等[11 ] 将统一岩石骨架模型与Sun模型相结合,得到了新的孔隙结构计算方法,并对致密砂岩孔隙结构参数进行了贝叶斯概率化反演.上述岩石物理理论驱动下的反演方法为致密砂岩储层表征提供了可靠的解决方案,但是,由于大多数反演算法为基于线性近似式的线性反演,当储层复杂性变高、纵横向变化剧烈,且勘探精度要求较高时,线性反演结果难以给出可靠的储层弹性或者物性参数预测结果.为此,寻找更为合适的反演方法以提高反演结果的准确性是目前需要解决的一项重点问题. ...
Generalized linear inversion of reflection seismic data
1
1983
... 线性反演在保证一定的反演精度的前提下,可以为储层预测提供一种高效、快捷的指导方式[12 -13 ] .非线性反演在极大提高反射系数方程的同时,能够进一步改善线性反演受到多种假设条件的影响,为复杂油藏的精细刻画及高精度识别提供了有效的解决方案.Yin等[14 ] 给出了一种基于Zoeppritz方程的新型精确PP反射系数并将其应用于地震数据及叠前非线性AVO反演.该方法在非线性反问题的求解中使用了蒙特卡洛求解策略的逆算子估计算法,克服了线性方程所存在的局限性,并减少待反演参数的数量,为相对值的精确反演提供了理论支撑.Cheng等[15 ] 推导了拉梅参数和密度相关三阶Zoeppritz非线性近似方程,该研究为反演过程引入了一种逆算子估计算法,结合L1 范数的约束,利用非线性反演逆算子优化反演算法提高了拉梅参数反演稳定性和准确性.逆算子优化算法在求解L1 范数提升反演分辨率与准确性方面具有较强的优势,但在求解过程中具有较低的速度,时间成本更高.Zhou等[16 ] 在精确Zoeppritz方程的基础上,提出了一种新的Russell孔隙流体因子相关方程的非线性纵横波组合反演方法,利用梯度下降反演算法,其方法在较大程度上克服了流体因子估计精度的限制,更符合地球物理反演问题的本质,且具有较高的运算速度,时间成本较低.但梯度下降优化算法适用于L2 范数的求解,难以提高反演结果的分辨率,同时,待反演参数梯度下降的过程中容易陷入局部极小值,影响反演的准确性与稳定性.非线性方程反演算法的蓬勃发展得益于反演优化算法的不断进步,因此,选择合理、稳定的优化算法开展非线性反演对致密砂岩储层进行预测,能够为提高致密砂岩储层反演结果的准确性与可靠性提供技术支撑. ...
Matrix-fluid decoupling-based joint PP-PS-wave seismic inversion for fluid identification
1
2019
... 线性反演在保证一定的反演精度的前提下,可以为储层预测提供一种高效、快捷的指导方式[12 -13 ] .非线性反演在极大提高反射系数方程的同时,能够进一步改善线性反演受到多种假设条件的影响,为复杂油藏的精细刻画及高精度识别提供了有效的解决方案.Yin等[14 ] 给出了一种基于Zoeppritz方程的新型精确PP反射系数并将其应用于地震数据及叠前非线性AVO反演.该方法在非线性反问题的求解中使用了蒙特卡洛求解策略的逆算子估计算法,克服了线性方程所存在的局限性,并减少待反演参数的数量,为相对值的精确反演提供了理论支撑.Cheng等[15 ] 推导了拉梅参数和密度相关三阶Zoeppritz非线性近似方程,该研究为反演过程引入了一种逆算子估计算法,结合L1 范数的约束,利用非线性反演逆算子优化反演算法提高了拉梅参数反演稳定性和准确性.逆算子优化算法在求解L1 范数提升反演分辨率与准确性方面具有较强的优势,但在求解过程中具有较低的速度,时间成本更高.Zhou等[16 ] 在精确Zoeppritz方程的基础上,提出了一种新的Russell孔隙流体因子相关方程的非线性纵横波组合反演方法,利用梯度下降反演算法,其方法在较大程度上克服了流体因子估计精度的限制,更符合地球物理反演问题的本质,且具有较高的运算速度,时间成本较低.但梯度下降优化算法适用于L2 范数的求解,难以提高反演结果的分辨率,同时,待反演参数梯度下降的过程中容易陷入局部极小值,影响反演的准确性与稳定性.非线性方程反演算法的蓬勃发展得益于反演优化算法的不断进步,因此,选择合理、稳定的优化算法开展非线性反演对致密砂岩储层进行预测,能够为提高致密砂岩储层反演结果的准确性与可靠性提供技术支撑. ...
Non-linear AVO inversion based on a novel exact PP reflection coefficient
1
2018
... 线性反演在保证一定的反演精度的前提下,可以为储层预测提供一种高效、快捷的指导方式[12 -13 ] .非线性反演在极大提高反射系数方程的同时,能够进一步改善线性反演受到多种假设条件的影响,为复杂油藏的精细刻画及高精度识别提供了有效的解决方案.Yin等[14 ] 给出了一种基于Zoeppritz方程的新型精确PP反射系数并将其应用于地震数据及叠前非线性AVO反演.该方法在非线性反问题的求解中使用了蒙特卡洛求解策略的逆算子估计算法,克服了线性方程所存在的局限性,并减少待反演参数的数量,为相对值的精确反演提供了理论支撑.Cheng等[15 ] 推导了拉梅参数和密度相关三阶Zoeppritz非线性近似方程,该研究为反演过程引入了一种逆算子估计算法,结合L1 范数的约束,利用非线性反演逆算子优化反演算法提高了拉梅参数反演稳定性和准确性.逆算子优化算法在求解L1 范数提升反演分辨率与准确性方面具有较强的优势,但在求解过程中具有较低的速度,时间成本更高.Zhou等[16 ] 在精确Zoeppritz方程的基础上,提出了一种新的Russell孔隙流体因子相关方程的非线性纵横波组合反演方法,利用梯度下降反演算法,其方法在较大程度上克服了流体因子估计精度的限制,更符合地球物理反演问题的本质,且具有较高的运算速度,时间成本较低.但梯度下降优化算法适用于L2 范数的求解,难以提高反演结果的分辨率,同时,待反演参数梯度下降的过程中容易陷入局部极小值,影响反演的准确性与稳定性.非线性方程反演算法的蓬勃发展得益于反演优化算法的不断进步,因此,选择合理、稳定的优化算法开展非线性反演对致密砂岩储层进行预测,能够为提高致密砂岩储层反演结果的准确性与可靠性提供技术支撑. ...
Third-order AVO inversion for lamé parameter based on inverse operator estimation algorithm
1
2018
... 线性反演在保证一定的反演精度的前提下,可以为储层预测提供一种高效、快捷的指导方式[12 -13 ] .非线性反演在极大提高反射系数方程的同时,能够进一步改善线性反演受到多种假设条件的影响,为复杂油藏的精细刻画及高精度识别提供了有效的解决方案.Yin等[14 ] 给出了一种基于Zoeppritz方程的新型精确PP反射系数并将其应用于地震数据及叠前非线性AVO反演.该方法在非线性反问题的求解中使用了蒙特卡洛求解策略的逆算子估计算法,克服了线性方程所存在的局限性,并减少待反演参数的数量,为相对值的精确反演提供了理论支撑.Cheng等[15 ] 推导了拉梅参数和密度相关三阶Zoeppritz非线性近似方程,该研究为反演过程引入了一种逆算子估计算法,结合L1 范数的约束,利用非线性反演逆算子优化反演算法提高了拉梅参数反演稳定性和准确性.逆算子优化算法在求解L1 范数提升反演分辨率与准确性方面具有较强的优势,但在求解过程中具有较低的速度,时间成本更高.Zhou等[16 ] 在精确Zoeppritz方程的基础上,提出了一种新的Russell孔隙流体因子相关方程的非线性纵横波组合反演方法,利用梯度下降反演算法,其方法在较大程度上克服了流体因子估计精度的限制,更符合地球物理反演问题的本质,且具有较高的运算速度,时间成本较低.但梯度下降优化算法适用于L2 范数的求解,难以提高反演结果的分辨率,同时,待反演参数梯度下降的过程中容易陷入局部极小值,影响反演的准确性与稳定性.非线性方程反演算法的蓬勃发展得益于反演优化算法的不断进步,因此,选择合理、稳定的优化算法开展非线性反演对致密砂岩储层进行预测,能够为提高致密砂岩储层反演结果的准确性与可靠性提供技术支撑. ...
Robust AVO inversion for the fluid factor and shear modulus
2
2021
... 线性反演在保证一定的反演精度的前提下,可以为储层预测提供一种高效、快捷的指导方式[12 -13 ] .非线性反演在极大提高反射系数方程的同时,能够进一步改善线性反演受到多种假设条件的影响,为复杂油藏的精细刻画及高精度识别提供了有效的解决方案.Yin等[14 ] 给出了一种基于Zoeppritz方程的新型精确PP反射系数并将其应用于地震数据及叠前非线性AVO反演.该方法在非线性反问题的求解中使用了蒙特卡洛求解策略的逆算子估计算法,克服了线性方程所存在的局限性,并减少待反演参数的数量,为相对值的精确反演提供了理论支撑.Cheng等[15 ] 推导了拉梅参数和密度相关三阶Zoeppritz非线性近似方程,该研究为反演过程引入了一种逆算子估计算法,结合L1 范数的约束,利用非线性反演逆算子优化反演算法提高了拉梅参数反演稳定性和准确性.逆算子优化算法在求解L1 范数提升反演分辨率与准确性方面具有较强的优势,但在求解过程中具有较低的速度,时间成本更高.Zhou等[16 ] 在精确Zoeppritz方程的基础上,提出了一种新的Russell孔隙流体因子相关方程的非线性纵横波组合反演方法,利用梯度下降反演算法,其方法在较大程度上克服了流体因子估计精度的限制,更符合地球物理反演问题的本质,且具有较高的运算速度,时间成本较低.但梯度下降优化算法适用于L2 范数的求解,难以提高反演结果的分辨率,同时,待反演参数梯度下降的过程中容易陷入局部极小值,影响反演的准确性与稳定性.非线性方程反演算法的蓬勃发展得益于反演优化算法的不断进步,因此,选择合理、稳定的优化算法开展非线性反演对致密砂岩储层进行预测,能够为提高致密砂岩储层反演结果的准确性与可靠性提供技术支撑. ...
... 采用梯度下降算法[16 ,26 ] 求解式(C-1)所建立的目标函数,进行多次迭代,直至满足输出条件(目标函数JG 收敛至接近零值或达到最大迭代次数),即可求解得到目标函数取得极小时时对应的待反演参数m =[Kf ,1 ,Kf ,2 ,…,Kf , N ϕ 1 ,ϕ 2 ,…,ϕN ,ρ 1 ,ρ 2 ,…,ρN ]T 的数值解.梯度下降算法优化求解流程如图C-1 . ...
Velocity and attenuation of seismic waves in two-phase media:Part i.Theoretical formulations
2
1974
... 考虑到上述所描述的致密砂岩岩石物理建模理论在直接反演中具有较多的参数以及较高的复杂性,不利于储层参数的稳定提取,且基于梯度类的非线性求解方法容易在优化过程中陷入局部极小值,收敛性较差.为此,本文对提高致密砂岩储层参数的叠前反演精度进行了深入研究,具体如下:首先利用岩石物理理论及Kuster-Toksöz(KT)模型[17 -18 ] 下的球形包含物模型建立纵横波速、度密度与Kf 、密度以及孔隙度之间的定量关系,之后,将此关系代入精确Zoeppritz方程[19 ] ,建立含3参数的新非线性精确反射系数方程,采用L1 范数建立反演目标函数,采用麻雀搜索算法[20 ] 进行优化求解得到目标函数取得极小值时的Kf 、密度以及孔隙度的数值解.该方法在精度测试和模型测试中表现出了较高的合理性和可靠性,并且在鄂尔多斯盆地的致密砂岩储层的实际应用中获得了高精度、高分辨率的勘探效果. ...
... 考虑到Gassmann流体替换方程[21 ] 联系了连通孔隙低频近似下的饱和岩石骨架、基质及赋存流体之间的定量关系,作为致密砂岩岩石物理模型,由于其孔隙的不连通特征使得常规的Gassmann流体替换方程不再适用.因此Kuster-Toksöz(KT) 模型[17 -18 ] 为计算具有可变孔隙度的多孔岩石的有效体积模量K eff 和有效剪切模量μ eff 的计算提供了一种新的解决方案: ...
Long-wavelength propagation in composite elastic media II.Ellipsoidal inclusions
2
1980
... 考虑到上述所描述的致密砂岩岩石物理建模理论在直接反演中具有较多的参数以及较高的复杂性,不利于储层参数的稳定提取,且基于梯度类的非线性求解方法容易在优化过程中陷入局部极小值,收敛性较差.为此,本文对提高致密砂岩储层参数的叠前反演精度进行了深入研究,具体如下:首先利用岩石物理理论及Kuster-Toksöz(KT)模型[17 -18 ] 下的球形包含物模型建立纵横波速、度密度与Kf 、密度以及孔隙度之间的定量关系,之后,将此关系代入精确Zoeppritz方程[19 ] ,建立含3参数的新非线性精确反射系数方程,采用L1 范数建立反演目标函数,采用麻雀搜索算法[20 ] 进行优化求解得到目标函数取得极小值时的Kf 、密度以及孔隙度的数值解.该方法在精度测试和模型测试中表现出了较高的合理性和可靠性,并且在鄂尔多斯盆地的致密砂岩储层的实际应用中获得了高精度、高分辨率的勘探效果. ...
... 考虑到Gassmann流体替换方程[21 ] 联系了连通孔隙低频近似下的饱和岩石骨架、基质及赋存流体之间的定量关系,作为致密砂岩岩石物理模型,由于其孔隙的不连通特征使得常规的Gassmann流体替换方程不再适用.因此Kuster-Toksöz(KT) 模型[17 -18 ] 为计算具有可变孔隙度的多孔岩石的有效体积模量K eff 和有效剪切模量μ eff 的计算提供了一种新的解决方案: ...
On the reflection and penetration of seismic waves through unstable layers
2
1919
... 考虑到上述所描述的致密砂岩岩石物理建模理论在直接反演中具有较多的参数以及较高的复杂性,不利于储层参数的稳定提取,且基于梯度类的非线性求解方法容易在优化过程中陷入局部极小值,收敛性较差.为此,本文对提高致密砂岩储层参数的叠前反演精度进行了深入研究,具体如下:首先利用岩石物理理论及Kuster-Toksöz(KT)模型[17 -18 ] 下的球形包含物模型建立纵横波速、度密度与Kf 、密度以及孔隙度之间的定量关系,之后,将此关系代入精确Zoeppritz方程[19 ] ,建立含3参数的新非线性精确反射系数方程,采用L1 范数建立反演目标函数,采用麻雀搜索算法[20 ] 进行优化求解得到目标函数取得极小值时的Kf 、密度以及孔隙度的数值解.该方法在精度测试和模型测试中表现出了较高的合理性和可靠性,并且在鄂尔多斯盆地的致密砂岩储层的实际应用中获得了高精度、高分辨率的勘探效果. ...
... Zoeppritz方程[19 ] 阐明了各向同性完全弹性假设下地震波能量在界面处的分布,并为反射系数随入射角的变化提供了精确的描述,Aki等[22 ] 给出了纵波入射、纵波反射的反射系数表达式如下: ...
A novel swarm intelligence optimization approach:Sparrow search algorithm
1
2020
... 考虑到上述所描述的致密砂岩岩石物理建模理论在直接反演中具有较多的参数以及较高的复杂性,不利于储层参数的稳定提取,且基于梯度类的非线性求解方法容易在优化过程中陷入局部极小值,收敛性较差.为此,本文对提高致密砂岩储层参数的叠前反演精度进行了深入研究,具体如下:首先利用岩石物理理论及Kuster-Toksöz(KT)模型[17 -18 ] 下的球形包含物模型建立纵横波速、度密度与Kf 、密度以及孔隙度之间的定量关系,之后,将此关系代入精确Zoeppritz方程[19 ] ,建立含3参数的新非线性精确反射系数方程,采用L1 范数建立反演目标函数,采用麻雀搜索算法[20 ] 进行优化求解得到目标函数取得极小值时的Kf 、密度以及孔隙度的数值解.该方法在精度测试和模型测试中表现出了较高的合理性和可靠性,并且在鄂尔多斯盆地的致密砂岩储层的实际应用中获得了高精度、高分辨率的勘探效果. ...
Elastic waves through a packing of spheres
1
1951
... 考虑到Gassmann流体替换方程[21 ] 联系了连通孔隙低频近似下的饱和岩石骨架、基质及赋存流体之间的定量关系,作为致密砂岩岩石物理模型,由于其孔隙的不连通特征使得常规的Gassmann流体替换方程不再适用.因此Kuster-Toksöz(KT) 模型[17 -18 ] 为计算具有可变孔隙度的多孔岩石的有效体积模量K eff 和有效剪切模量μ eff 的计算提供了一种新的解决方案: ...
1
... Zoeppritz方程[19 ] 阐明了各向同性完全弹性假设下地震波能量在界面处的分布,并为反射系数随入射角的变化提供了精确的描述,Aki等[22 ] 给出了纵波入射、纵波反射的反射系数表达式如下: ...
基于逆算子估计的AVO反演方法研究
1
2016
... 式中:R pp 为地层不同反射界面处的非线性反射系数;S 为地震记录向量;W 为子波矩阵;noise 表示噪声项.基于褶积模型构建观测数据与正演合成数据的残差项,并结合正则化约束进一步提高算法的鲁棒性,降低优化求解过程中出现过拟合现象,同时为保障反演结果的分辨率,我们将采用强调求解结果稀疏性L1 范数[23 25 ] 建立反演的目标函数: ...
基于逆算子估计的AVO反演方法研究
1
2016
... 式中:R pp 为地层不同反射界面处的非线性反射系数;S 为地震记录向量;W 为子波矩阵;noise 表示噪声项.基于褶积模型构建观测数据与正演合成数据的残差项,并结合正则化约束进一步提高算法的鲁棒性,降低优化求解过程中出现过拟合现象,同时为保障反演结果的分辨率,我们将采用强调求解结果稀疏性L1 范数[23 25 ] 建立反演的目标函数: ...
基于逆算子估计的高阶AVO非线性反演
0
2016
基于逆算子估计的高阶AVO非线性反演
0
2016
Nonlinear amplitude-variation-with-offset inversion for Lamé parameters using a direct inversion method
1
2017
... 式中:R pp 为地层不同反射界面处的非线性反射系数;S 为地震记录向量;W 为子波矩阵;noise 表示噪声项.基于褶积模型构建观测数据与正演合成数据的残差项,并结合正则化约束进一步提高算法的鲁棒性,降低优化求解过程中出现过拟合现象,同时为保障反演结果的分辨率,我们将采用强调求解结果稀疏性L1 范数[23 25 ] 建立反演的目标函数: ...
Pre-stack AVA inversion by using propagator matrix forward modeling
1
2019
... 采用梯度下降算法[16 ,26 ] 求解式(C-1)所建立的目标函数,进行多次迭代,直至满足输出条件(目标函数JG 收敛至接近零值或达到最大迭代次数),即可求解得到目标函数取得极小时时对应的待反演参数m =[Kf ,1 ,Kf ,2 ,…,Kf , N ϕ 1 ,ϕ 2 ,…,ϕN ,ρ 1 ,ρ 2 ,…,ρN ]T 的数值解.梯度下降算法优化求解流程如图C-1 . ...