0 引言
区域地磁场模型的构建方法主要包括球谐分析、球冠谐分析、等效源等方法[5-6]。其中,球谐分析是当前全球和区域地磁场建模的主要手段,通过有限阶球谐函数的叠加来求解球谐系数,使地磁场数据达到最佳拟合[7]。然而,由于球谐级数截断阶数的限制,该方法在空间分辨率方面存在局限性。例如,NGDC720模型尽管采用了720阶截断,但其空间分辨率仅为50 km,远不能满足精细探测的需求。此外,提高截断阶数虽然能提升分辨率,但会导致球谐系数的数量急剧增加,高低阶项系数相差悬殊,导致法方程矩阵高度病态,影响计算稳定性和解算精度[8]。球冠模型在处理局部区域磁场时具有一定优势,但其建模效果依赖于球冠半角的选择,截断阶数的增大会导致级数收敛缓慢甚至失去物理意义,同时难以准确模拟磁场的径向变化,影响上下延拓的效果[5]。
相比之下,等效源方法为区域地磁场建模提供了一种有效的替代方案。该方法通过在地下或地表设置等效源场源体,并求解其物性参数,使其能够拟合观测的磁场数据,进而重构磁场分布[9]。依据高斯通量定理,理论上在满足位场不变的条件下,可以通过等效源重构地磁场模型,从而实现对区域地磁场的高精度建模。若等效源分布合理,重构磁场的精度可接近真实磁场分布。然而,该方法针对海域实际应用的特殊性仍然面临诸多挑战:首先,观测数据有限且离散,不合理的等效源布设可能会导致位场信号的“泄漏”,即尽管观测数据拟合精度较高,但未观测点的重构磁场误差较大[10];其次,观测数据通常含有噪声,若等效源模型未能有效抑制噪声,可能会放大噪声影响,降低模型精度;另外,海域地质模型和观测条件的特殊性,也为等效源的构建增加了难度;最后,为了获得高精度和高分辨率的磁异常模型,需要构建大量等效源单元体,存储大规模系数矩阵,并求解大型线性方程组,计算效率和稳定性成为关键问题[11]。因此,合理构造等效源布设方案,提高计算效率并增强模型稳定性,是等效源方法在区域地磁场建模中取得良好效果的关键。
本文围绕等效源方法在海域区域地磁场建模中的关键技术问题,探讨其理论基础、建模方法及优化策略,为构建高精度区域磁场模型及后续应用提供技术支撑。
1 等效源方法原理
1.1 理论基础
式中:d为M×1维的观测数据向量;S为M×N阶的核函数矩阵;m为N×1维的模型参数向量。假设测点在地表规则分布,那么观测数据就可以表示为:
式中:ΔTM表示第M个观测点的磁场值,M为观测点的个数。
假设等效源模型单元体在地下规则分布,那么等效源模型单元体的物性参数可以表示为:
式中:mN表示第N个等效源模型单元体的物性参数,N为等效源模型单元体的个数。
求解式(1),可以表示为:
式中:m1、m2、…、mN为未知参数,即等效源模型单元体的物性参数。基于获得的等效源参数,可以构建不同空间位置的三维地磁场模型。
1.2 等效源的等效性分析
理论上,若设置的等效场源与真实场源十分接近,将会得到高精度的重构与转换结果。由于反演计算具有多解性,尽管通过高精度拟合观测数据可以构建不同的等效场源,但不是所有的等效源都可以得到高精度的建模结果。一般使用均方误差RMS评价计算结果的精度:
式中:ΔT为理论数据;ΔT'为计算结果;N为数据量。但均方误差难以反映误差相对于理论值的大小,故采用理论值的振幅对均方误差进行归一化,得到归一化均方误差NRMS:
式中:ΔTmax为最大值理论;ΔTmin为最小值理论。
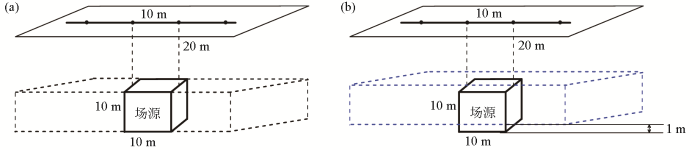
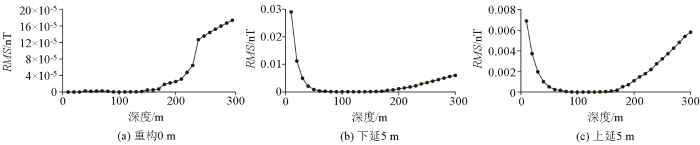
基于单个棱柱体模型分析等效源的等效性(模型一,图1a):模型尺寸为10 m×10 m×10 m,顶深为20 m,磁偏角0°,磁倾角50°,与地磁场方向一致;观测面位于0 m,网度为10 m×10 m。按照测网的网度设置了一层直立六面体等效源,单个等效源体的深度和尺寸与场源相同,等效源的磁化方向与场源相同。利用0 m观测面的数据反演等效源参数,进而计算上延5 m与下延5 m的结果。从图2a可以看出,重构得到的等效源模型能够完全重现场源特征,观测数据重构NRMS为9.39×10-10;此时,上延NRMS为2.82×10-10,下延NRMS为3.59×10-9,两者与观测面重构结果基本处于同一误差水平。这表明当等效源设置合理时,其能够完全等效场源。
图1
图1
单个棱柱体模型与等效源设置方式
a—等效源设置与实际场源一致的模型;b—等效源设置与实际场源存在偏差的模型
Fig.1
Single prism model and equivalent source setting method
a—set a model that is consistent with the actual field source for equivalent sources; b—set a model that deviates from the actual field source for equivalent sources
图2
图2
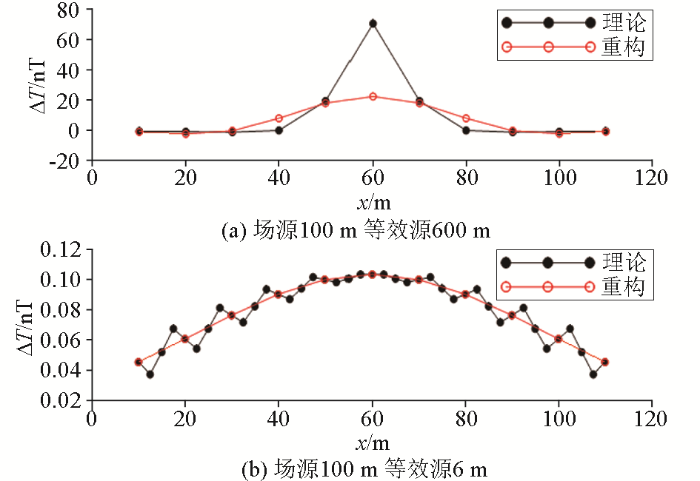
基于模型一开展等效源等效性分析的结果
a—等效源位置与实际情况一致时的计算结果;b—上移1 m等效源的计算结果;a1、b1—与原始数据的拟合差;a2、b2—下延5 m误差;a3、b3—上延5 m误差;a4、b4—反演重构的等效源
Fig.2
Results of equivalent source equivalence analysis based on model 1
a—the calculation result when the equivalent source position is consistent with the actual situation; b—calculation result of moving up 1 m equivalent source; a1, b1—poor fitting of raw data; a2, b2—downward 5 m error; a3, b3—upward 5 m error; a4, b4—equivalent sources for inversion reconstruction
2 海域地磁场建模的特殊性
基于观测面以下介质的磁性特征,海平面以下大致分为3层:海水层、沉积层和地壳。海水层和沉积层的分界面为海底,沉积层和地壳的分界面为基底。其中,磁性成分主要分布在地壳中,海水层和沉积层基本无磁性。基于公开数据,建立如图3所示的海域磁性地质模型。其中,海底地形采用GEBCO-2020网格,空间分辨率为15″×15″;基底深度基于NGDC发布的GlobSedV3构建,空间分辨率为5'×5'。
图3
图4
海域地磁场三维建模的目标是利用船测或航磁观测数据构建海平面上、下一定范围内的三维地磁场模型,类似于位场数据的向上延拓与向下延拓。本文以海平面以上0~500 m高程地磁场建模为目标开展相关研究,并利用“上延”与“下延”的结果评价建模的精度。基于位场延拓理论分析,大陆坡与大洋底模型在250 m下延深度条件下,其延拓面与海底场源间距保持较大(延拓距离远小于源—观测面间距),使得向下延拓误差较小;然而大陆架模型因浅水地质特征导致同尺度向下延拓距离相对于源—观测面间距不可忽视,引发边界效应非线性放大问题,其最大相对误差显著增大,这成为浅海区高精度地磁场建模的关键技术瓶颈[14]。
3 模型设置与参数试验
3.1 等效源模型选择
在模型一的基础上,考虑一个深度更大的单个棱柱体模型(模型二),模型顶深为95 m,其他参数不变。分别利用偶极子等效源模型和直立六面体等效源模型进行延拓误差分析。从图5可以看出,直立六面体模型的延拓误差小于偶极子模型,尤其是上延误差。因此,采用直立六面体构建等效源模型更加符合实际地质情况,延拓结果具有更好的保幅性。
图5
图5
模型二偶极子和直立六面体等效源模型延拓精度对比
Fig.5
Comparison of extension accuracy between model two dipole and prism equivalent source models
3.2 等效源深度设置
等效源的深度是等效源布设中的关键参数。图6为模型二等效源放置在不同深度时,延拓误差的变化曲线。从图中可以看出:等效源放置在不同深度时,对应的延拓精度有差异;当等效源设置深度与场源接近时,拟合误差与延拓误差最小,即存在最佳设置深度;且随着等效源深度与场源深度的偏差增大,误差有增大的趋势,即过浅或过深都会导致误差增大。
图6
图6
模型二不同深度等效源的误差统计
Fig.6
Error statistics of equivalent sources at different depths in model 2
图7
图7
不同等效源深度0 m平面的重构数据
Fig.7
Reconstructed data of 0 m plane with different equivalent source depths
因此,等效源深度参数的优化配置对位场延拓精度具有重要的影响,当其深度设置接近真实场源分布时,可得到高精度的重构和延拓结果,且当深度偏离场源实际位置时,延拓误差将呈非线性增长。特别地,等效源深度必须同时满足双重约束条件——既不能超过场源地质界面深度,又需大于5倍测点距,否则延拓结果中会产生高频噪声。
3.3 等效源磁化方向设置
由于磁异常数据不仅与磁性场源的物性参数和几何参数有关系,还受到场源磁化方向的影响。利用模型二产生的磁异常数据,我们对比了不同磁化方向模型进行延拓的误差(图8)。其中,地磁场方向与等效源的磁化方向设置相同,均为50°。可以看出,当等效源磁化方向与真实场源磁化方向一致时(等效源顶深设置为95 m,图8a1),计算误差会达到最小;且随着等效源磁化方向与场源磁化方向的偏差增大,计算误差有增大的趋势。但需要指出的是,当等效源深度设置与场源深度一致时,合理设置等效源磁化方向的优势明显;但是当等效源深度设置与场源深度不一致时(等效源顶深设置为35 m,图8b2),磁化方向的影响变小。根据等效源深度设置结论,在实际工作中,为保证高频信息的拟合,等效源设置一般偏浅。因此,与等效源设置深度相比,磁化方向的影响明显更小。
图8
图8
无磁(a)和存在剩磁(b)时不同磁化方向的延拓误差
Fig.8
Extension errors of different magnetization directions in the absence of remanence (a) and the presence of remanence (b)
考虑到自然界中存在的退磁与剩磁现象,会使地磁场方向与磁性场源真实的磁化方向不一致。将模型二中棱柱体场源模型的有效磁化方向的倾角设置为20°,地磁场仍为50°,开展等效源不同磁化方向延拓误差分析。结果表明,采用地磁场磁化方向和有效磁化方向设置等效源的延拓误差都不是最小的(图8b),最佳磁化方向介于有效磁化方向和地磁场磁化方向之间。
因此,与等效源深度设置相比,磁化方向的设置对延拓精度影响相对较小;当不存在剩磁影响时,等效源磁化方向设置为地磁场方向可以获得最小的延拓误差;当存在剩磁影响时,最佳磁化方向介于有效磁化方向和地磁场磁化方向之间。
4 等效源延拓精度分析
当依据观测磁场反演获得等效源参数后,上延与下延具有不同的误差规律。通过分析影响上延与下延精度的因素,进而提高建模的精度。
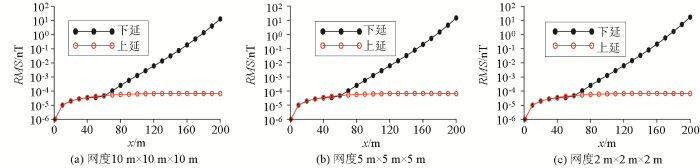
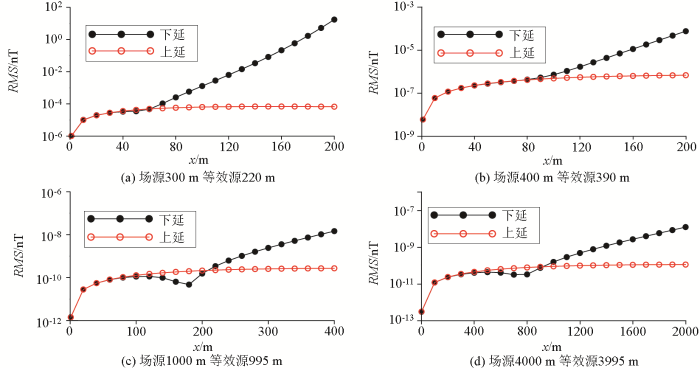
建立顶深为295 m的单个棱柱体(模型三),尺寸为10 m×10 m×10 m,磁偏角0°,磁倾角50°。正演计算棱柱体模型在0 m平面的磁异常,观测网度为10 m×10 m。在设置等效源层时,每个测点下方放置一个直立六面体等效源。等效源的横向尺寸与测网相同,厚度为10 m,顶深215 m。通过反演等效源参数,进而计算上延0~200 m与下延0~200 m的磁异常。从图9a可以看出:①当延拓距离小于60 m时,上延与下延误差大致相当;②当延拓距离大于60 m后,上延误差趋于稳定,下延误差快速增大,即下延存在误差明显增大的转折点。因此,如何提高建模精度,尤其是降低下延误差是重要的问题。
图9
图9
等效源磁场建模中不同观测网度对建模精度的影响
Fig.9
The influence of different observation network sizes on modeling accuracy in equivalent source magnetic field modeling
4.1 不同观测网度
针对模型三,我们测试了不同观测网度的结果。观测范围不变,观测网度分别为5 m×5 m和2 m×2 m。每个测点下方放置一个直立六面体等效源。
等效源的横向尺寸与测网相同,厚度均为10 m,顶深为215 m。由图9可以看出:不同网度的误差变化规律是相似的,且下延中误差增大转折点的位置并不受观测网度的影响。
4.2 不同等效源深度
基于模型三,通过改变场源的深度,我们测试了不同深度等效源的延拓结果,观测网度为5×5 m。测试中遵循本文提出的深度设置原则。从图10可以看出:不同等效源深度模型的计算结果具有相似特征,但随着等效源深度(顶深)的增大,转折点向后偏移,即能够保证下延精度的延拓距离与等效源的深度有关。通过对多个模型的结果进行线性拟合,在观测面附近一定范围内(0.23h,h为等效源的顶深)上延和下延精度大致相当。
图10
图10
不同等效源深度对建模精度的影响
Fig.10
The influence of different equivalent source depths on modeling accuracy
4.3 不同等效源厚度
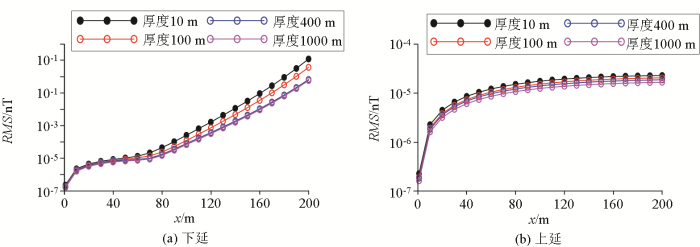
针对模型三,我们测试了等效源不同厚度对延拓的影响,观测网度为5 m×5 m。从图11可以看出:与顶深相比,等效源的厚度对延拓精度的影响较小。但是,增大厚度能在一定程度上提高延拓精度。这表明更大的等效源厚度能够吸收更多长波信息,且在延拓过程中表现出更缓的衰减特性。
图11
图11
不同等效源厚度对建模精度的影响
Fig.11
The influences of different equivalent source thicknesses on modeling accuracy
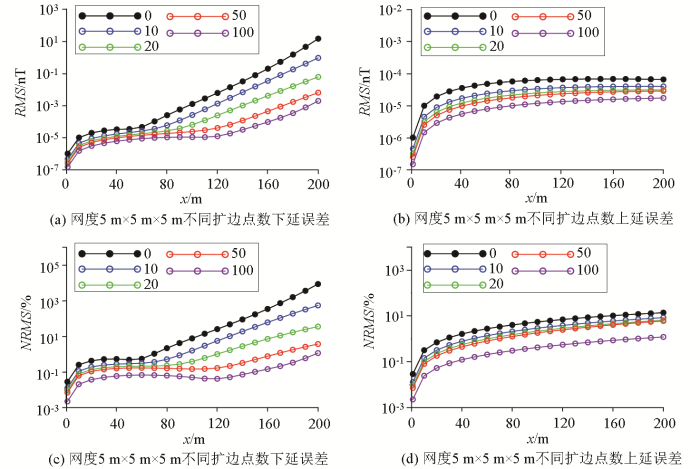
4.4 不同扩边点数
图12
图12
不同扩边点数对建模精度的影响
Fig.12
The influence of different edge expansion points on modeling accuracy
5 等效源高效构建策略研究
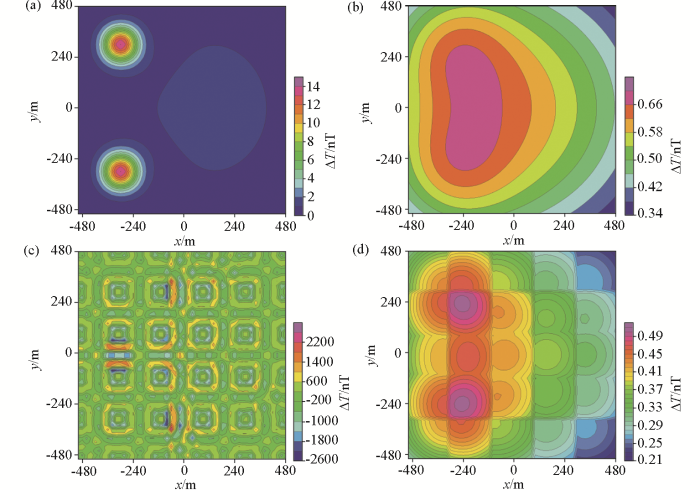
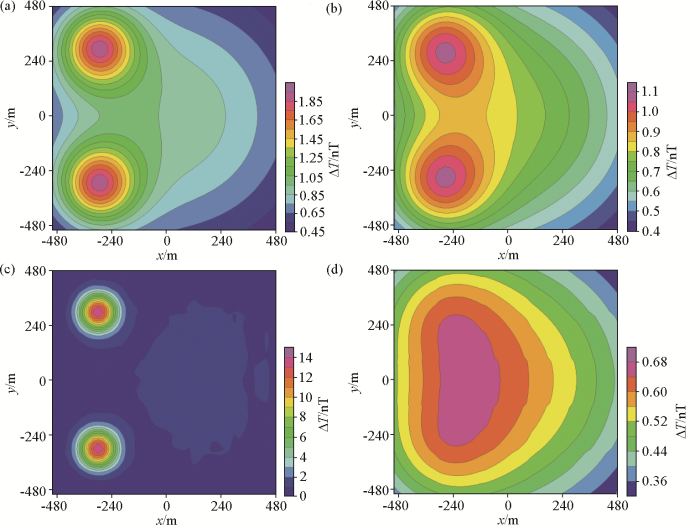
基于等效源方法的地磁场建模过程中,求取等效源的物性参数(式(4))是计算的主体,这是一项基于大量数据的最优化问题。其一,在等效源构建方面,核矩阵S内元素数据量为N2,存储数据会占用很大的内存空间,影响计算速度;其二,在应用角度方面,基于构建的等效源重建磁场模型时,调用全部的核函数和等效源参数也会导致计算速度的下降。传统方法将观测数据分割为若干个块,每个块单独进行等效源计算。以大陆架模型为例,将测区划分为25个区块,采用传统的分块方法进行试算。当延拓距离为50 m时,延拓结果与理论值相近;但当延拓200 m时,延拓结果已经完全失真(图13)。
图13
图13
大陆架模型传统分块法延拓200 m的结果
a—下延理论;b—上延理论;c—下延模拟;d—上延模拟
Fig.13
Results of traditional block method for extending the continental shelf model by 200 meters
a—downward extension theory; b—upward extension theory; c—downward simulation; d—upstream simulation
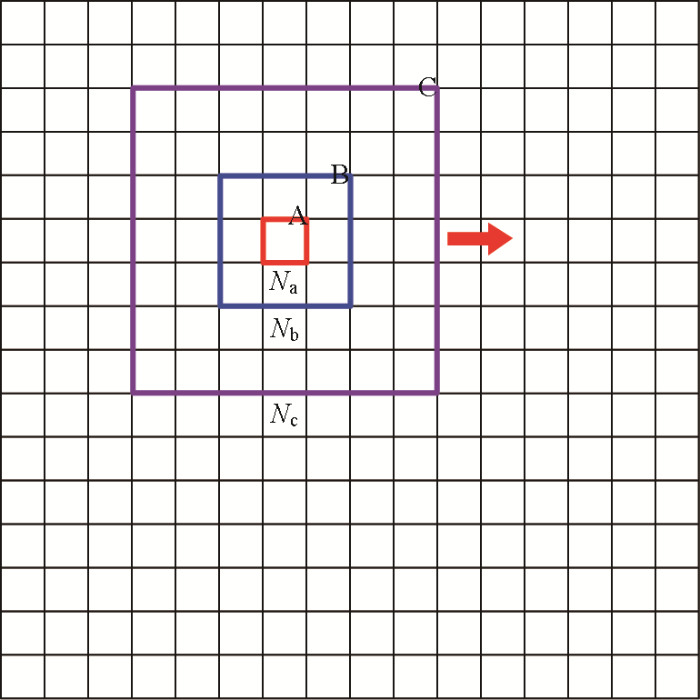
为了解决简单分块方法带来的拼接问题,提高延拓精度,我们对分块计算方法进行了改进。如图14所示,采用窗口覆盖的方式进行分块计算:在进行反演计算时,为构建(延拓)区域A小范围的磁场数据,使用区域B中等范围的观测数据和区域C较大范围的等效源。计算完成之后,需要针对区域A保存区域C的等效源参数,并利用区域C的等效源参数实现区域A磁场的建模。区域C的等效源能够保证区域B观测数据的高精度重构。区域B观测数据能够保证区域A延拓数据的连续性。通过整体滑动,实现整个区域的建模。与整体算法相比,尽管窗口覆盖的方式会使很多数据重复参与计算,并增大了等效源参数的存储量,但是可以大大提高计算结果的精度。另外,该方法通过将整体数据剖分成多个小块,避免了整体核函数矩阵的计算与存储,在重构磁场时,也仅需要局部小窗口的等效源参与计算,提高了计算效率,尤其是在大规模数据的计算时,优势更为明显。
图14
图14
窗口覆盖滑动窗口示意
红框—区域A,延拓数据范围;蓝框—区域B,观测数据范围;紫框—区域C,等效源
Fig.14
Schematic diagram of window overlay sliding window
red box—region A, extended data range; blue box—area B, observation data range; purple box—region C, equivalent source
图15
图15
改进分块方法延拓50 m和200 m的结果
a—下延50 m;b—上延50 m;c—下延200 m;d—上延200 m
Fig.15
Improved block method for extending 50 meters and 200 meters results
a—extend 50 m downwards; b—extend 50 m upwards; c—extend 200 m downwards; d—extend 200 m upwards
6 海域磁测等效源设置与试算
针对海域磁测特殊的地质和观测条件,结合等效源布设原则,采用具有一定厚度的直立六面体作为等效源。理论上,等效源的深度应小于真实场源的深度,且越接近真实场源,误差越小。考虑到海底地形资料的空间分辨率和精度均高于基底深度,因此沿着海底地形设置起伏的等效源层。以250 m飞行为例,当测线距抽稀到50 m间距时,在海底布设等效源层始终能够满足等效源深度大于5倍测点距的要求。
利用本文给出的等效源构建方案,针对图4中大陆架、大陆坡和大洋底3种模型开展试算。海底以下75 m存在两个尺寸均为100 m×100 m×10 m的棱柱体;深部存在1个尺寸为500 m×250 m×50 m的棱柱体,距海底顶深为1 155 m(图4);观测面位于海平面以上200 m。磁偏角0°,磁倾角50°。沿海底每个测点下方放置1个等效源体,单个等效源尺寸为20 m×20 m×1 000 m,等效源向4个方向分别扩边50个点。反演等效源参数,进而生成海平面以上0~500 m范围内的磁异常。另外,考虑到剩磁的影响,我们计算了等效源磁倾角为90°的误差,见表1所示。从计算结果可以看出,通过合理的场源布设,可以将误差控制在5%以内;其中在大陆坡区域,由于海底较浅,误差稍大;在大陆架和大洋底,随着海底深度的增加,建模精度较高。
表1 不同模型最大误差对比
Table 1
| NRMS/% | 大陆架模型 | 大陆坡模型 | 大洋底模型 | |||
|---|---|---|---|---|---|---|
| 上延 | 下延 | 上延 | 下延 | 上延 | 下延 | |
| 实际50° 采用90° | 2.22 | 0.35 | 0.69 | 0.27 | 0.33 | 0.21 |
| 实际50° 采用50° | 2.39 | 0.4 | 0.54 | 0.21 | 0.02 | 0.01 |
7 结论
1)通过对比分析发现,等效源几何参数与空间配置策略显著影响磁场模型精度。针对海域等效源地磁场建模的特殊性,详细分析了等效源模型的选择、模型参数的设置等问题,提出了地形跟随式直立六面体等效源的配置方案。
2)在算法实现层面,基于滑动窗口的覆盖式计算方案有效解决了大规模磁测数据的高精度处理瓶颈。实验结果表明,该方法既可保证拼接边界连续性,又能维持较好计算性能。
参考文献
中国及邻区高分辨率三维岩石圈磁场修正球冠谐模型(CUG_CLMFM3Dv1)
[J].
CUG_CLMFM3Dv1:A high-resolution revised spherical cap harmonic model of three-dimensional lithospheric magnetic field over China and surroundings
[J].
多地磁特征量对飞行器匹配导航定位精度的提高
[J/OL].
Improving the positioning accuracy of aircraft matching navigation by multiple geomagnetic features
[J/OL].
潜艇目标态势对航空磁探测的影响分析
[J].
Analysis of influence of submarine target posture on aeromagnetic detection
[J].
地磁场模型及在海洋环境中的应用需求研究
[J].
Research on geomagnetic field models and its application requirement in marine environment
[J].
地磁场全球建模和局域建模
[J].
Geomagnetic field modelling for the globe and a limited region
[J].
全球岩石圈地磁梯度张量场椭球谐模型构建方法与评估
[J].
Construction method and evaluation of ellipsoidal harmonic model of global lithospheric geomagnetic gradient tensor field
[J].
利用球谐分析方法构建局部重力场模型的可行性分析
[J].
DOI:10.6038/pg2025II0047
[本文引用: 1]

局部重力场理论相关的技术问题包括大地水准面精化、重力异常向下延拓、局部模型构建等,均会面临着具有较强的边界效应、局部积分代替全球积分、近似计算、积分离散化误差等诸多问题.针对这些问题,本文利用块对角最小二乘方法快速实现超高阶次的球谐分析,并将其引入局部重力场数据的处理及模型的构建,同时使用中低阶卫星重力场模型和GNSS/水准测量数据作为控制,可做到5400阶的全球球谐分析完成2'分辨率的局部重力场的数据处理和建模,算法精度造成的重力异常误差 < 1 mGal、(似)大地水准面误差 < 1 cm、垂线偏差误差 < 0.4″.同时球谐分析还可用于航空重力异常数据的稳定向下延拓,是一种简单易操作的方法,在精度和稳定性方面具有非常好的表现,所以球谐分析方法在局部重力场建模和数据处理中值得推广应用.
Feasibility analysis of constructing a regional gravitational model using the method of spherical harmonics analysis
[J].
DOI:10.6038/pg2025II0047
[本文引用: 1]

Technical methods related to the regional gravity fields, include precise geoid determination, downward continuation of gravity anomalies, and construction of regional models, which are greatly faced with challenges, such as low accuracy or efficiency, computation approximations, instability, and lack of criterion. This study introduces the fast implementation technique of ultra-high degree spherical harmonics analysis into the construction of regional gravity field, combined with satellite gravity field models of low to medium frequency spectrum and GNSS/leveling data. By employing a 5400-degree spherical harmonics analysis (SHA), it is possible to achieve a regional gravity field reconstruction with a resolution of 2 arc-minutes and an error less than 1 mGal for gravity anomalies, less than 1 cm for (quasi) geoid, and less than 0.4 arc-seconds for vertical deflection. Meanwhile, SHA can also be used for stable downward continuation of airborne gravity anomalies, which is verified to be more simple, accurate, and stable. Therefore, SHA is worth promoting and applying in the modeling of regional gravity fields and related data processing problems.
基于卫星磁测数据的全球岩石圈磁场建模进展与展望
[J].
Progress and outlook in global lithospheric magnetic field modelling by satellite magnetic measurements
[J].
多层等效源曲面磁异常转换方法
[J].
DOI:10.6038/cjg2018L0362
[本文引用: 2]

在磁异常数据处理中,利用等效源技术重构磁异常场具有较好的稳定性和较高的计算精度,因而被广泛应用.传统方法是采用设置在近地表的单层等效源拟合实测磁异常数据,尽管拟合精度很高,但向上延拓之后往往会出现较大的拟合误差,即可能存在磁异常信号的"泄漏",尤其在原始数据中存在背景场时更容易出现此种误差.本文提出一种多层等效源技术方案,应用分布于不同深度范围内的等效源模拟实测数据,减少了等效源参数设置的盲目性.理论模型试验表明,采用多层等效源方法重构的磁异常及其梯度与分量,较单层等效源方法具有更高精度,可以吸收更完整的实测磁异常信息.论文详细地讨论了如何优化多层等效源设置、等效源参数选择以及计算方法,通过二维和三维理论模型试验,验证了在复杂条件下多层等效源方法的可行性和适应性,并且将该方法应用于广西某地的实测磁异常数据转换之中,取得了较好的应用效果.
Transformation of magnetic anomaly data on an arbitrary surface by multi-layer equivalent sources
[J].
一种改进的等效源模型设置方案
[J].
Improved equivalent source model setting scheme
[J].
基于等效源法的低纬度地区曲面磁异常化极、分量及张量转换研究
[J].
Reduction-to-the-pole,component and tensor conversion of surface magnetic anomalies at low latitudes based on the equivalent source method
[J].
空间域和频率域平面位场延拓影响因素和稳定性分析
[J].
Influence factors and stability analysis of plane potential field continuation in space and frequency domains
[J].
Using an equivalent source with positivity for low-latitude reduction to the pole without striation
[J].
综合利用位场及其垂直梯度的快速样条曲化平方法
[J].
Fast splines conversion of curvedsurface potential field and vertical gradient data into horizontal-plane data
[J].
频率域偶层位曲面位场处理和转换方法试验研究
[J].
Experimental research using the frequency-domain dipole layer method for the processing and transformation of potential field on curved surface
[J].