随着社会的不断发展,各类工程建设及城市地下空间开发、城市地质灾害防治等对于浅地表地质结构探测的需求也越来越大。瞬态瑞利面波(以下简称瞬态面波)方法作为地球物理方法中的一种,具有抗干扰能力强、对地下层状介质及不均匀体具有频散特性等优点,因此在浅层地质结构探测中有较好的应用效果^[1-8]。尽管近年来微动(也称被动源面波)方法成为面波研究的热点^[9-14],但通过方法原理可知,2种方法都是利用面波信号计算频散曲线,通过反演获得不同深度的横波速度来探测地下地质结构。2种方法的区别主要在于瞬态面波采用锤击等人工源激发获得地震波,其激发的面波频率为几赫兹到上百赫兹,而微动采用环境背景噪声作为震源,其接收到的面波频率比瞬态面波低,因此探测深度大,一般根据接收微动面波频率的不同,探测深度从几十米到几千米^[15-18]。对于浅地表深度小于二三十米的地下地质结构的探测,采用瞬态面波法,无论是在探测精度还是探测效率方面,一般都优于微动方法。

瞬态面波法在野外数据采集时主要采用锤击震源,因此该方法操作简单、设备轻便、易于现场实施^[19]。然而,在瞬态面波数据采集中偏移距的选择是一个关键的因素。有学者通过理论分析得到了最佳偏移距公式,该公式与探测深度、纵横波速度相关^[20],但在实际采集中这些参数都是未知的。另一方面,在实际应用中发现不同位置锤击采集的面波数据所计算出的频散曲线在部分频段存在差异,以往针对这种情况,一般是在多个频散曲线中挑选一个连续性较好的进行反演,然而频散曲线选取的不同可能导致探测结果与实际地质结构不符。

本文通过理论及数值模拟分析,研究了影响面波频散谱计算的因素,进一步通过野外试验研究了锤击震源激发特性及不同重量锤击的频散曲线特征。针对不同震源位置激发采集的瞬态面波数据计算出的频散曲线存在差异的问题,提出了瞬态面波探测多频散谱融合方法,该方法能够降低不同位置激发时频散谱特征差异的影响,对于利用瞬态面波探测浅地表地质结构具有较好的实际应用价值。

目前,多道瞬态面波法在提取频散曲线时常用相移法计算频散谱。相移法是1998年由Park等^[21]提出的一种计算多道瞬态面波频散曲线的方法,该方法具有简单、高效、高频频散曲线清晰等特点。式(1)为根据相移法推导出的频散谱计算公式:

式中:φ=$\frac{\omega }{{v}_{\omega }}$,v_ω为频率ω所对应的相速度; U(x,ω)为时间域—空间域的地震信号u(x,t)沿着时间t方向作一维傅里叶变换的结果。式(1)中所表示的积分变换是在给定角频率ω和相速度v_ω后对所有偏移距x求和,因此,每一个ω在F内对应的最大值处的v_ω就是该频率所求得的相速度。通过这种计算方式就可以对一个地震记录计算出频散谱,进而拾取每个频率对应频散谱中最大值处的相速度值,就得到该地震记录的频散曲线。

通过式(1)可以看出,在将每一道面波数据做傅里叶变换后,时间域面波信号中不同频率的信息已经被分为振幅谱与相位谱,其中振幅谱包含振幅衰减、球面扩散、各向异性等信息,频散信息包含于相位谱中,振幅谱中不包含面波频散信息。而在面波频散曲线的提取过程中,最为重要的是相位谱信息,振幅谱可以忽略,因此,利用面波数据计算频散曲线时,只要噪声信号对不同频率的相位信息没有产生较大的干扰,就可以计算出准确的频散曲线。

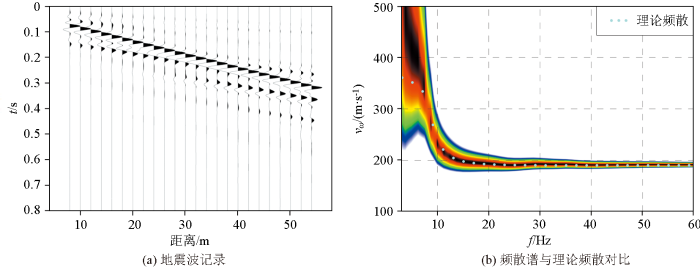
为了进一步分析相移法计算多道瞬态面波频散曲线时不同程度干扰波对频散谱的影响,设计了两层层状介质模型,利用高阶有限差分进行数值模拟^[22],然后通过增加不同强度的噪声来计算频散谱并与理论频散曲线进行对比,从而分析不同强度的噪声对面波频散谱的影响。两层介质模型大小为80 m×30 m,第一层介质参数为:纵波速度v_P1=800 m/s,横波速度v_S1=200 m/s,密度ρ₁=2.0 g/cm³,厚度5 m;第二层介质参数为:v_P2=1 200 m/s,v_S2=400 m/s,ρ₂=2.0 g/cm³。正演模拟时偏移距15 m,采样间隔0.1 ms,网格间距0.5 m,采样长度0.8 s,震源采用25 Hz雷克子波。图1a为模拟得到的多道面波记录,对该模拟数据利用相移法计算出的频散谱与理论频散曲线对比如图1b所示。从图中可以看出在无噪声情况下模拟数据频散谱中最大值与理论频散曲线基本一致,这也说明了数值模拟的正确性。

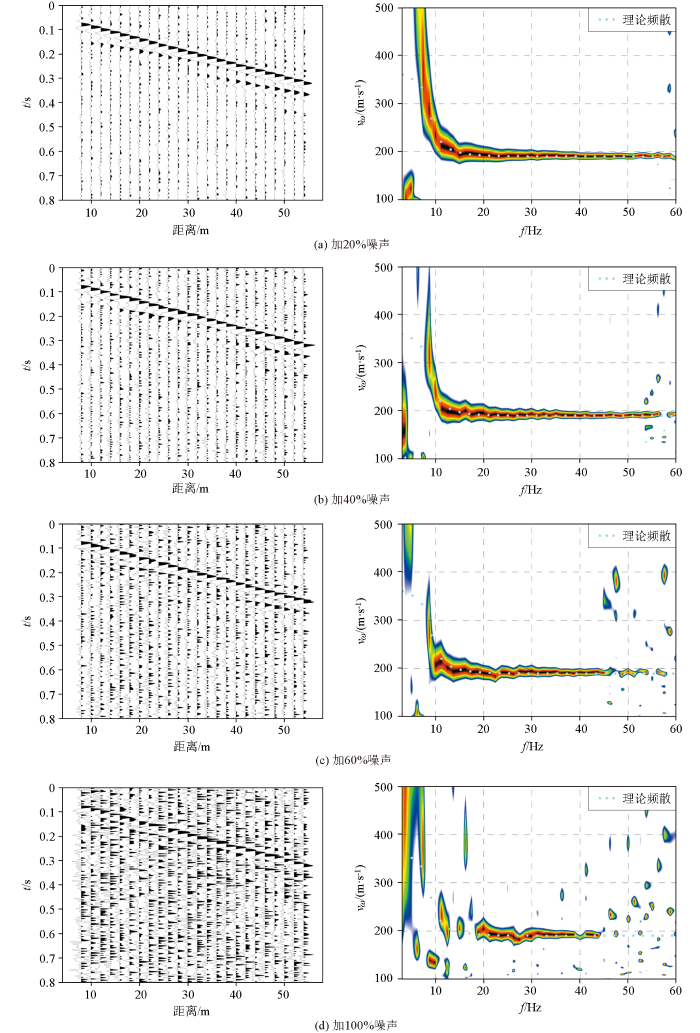
为了进一步研究噪声对频散谱的影响,特在模拟的面波记录中增加了不同强度的噪声。由于常规的随机噪声表现为高频特征,与实际面波探测中所接收到的干扰波有所不同,因此本次设置的噪声数据采用多个频率、不同初始相位的正弦波叠加,其中频率范围设定在1~120 Hz,初始相位在0~2π,随机抽取300组不同频率和相位合成噪声数据。图2为添加不同噪声情况下的地震面波记录以及计算出的频散谱与理论频散值对比。在图2a、b的地震记录中可以明显看出有效面波信号;从其频散谱中可以看出仅在图2d的58 Hz附近频散谱有断开,但总体频散谱中能量最强分布与理论频散曲线基本对应,这也说明添加20%、40%噪声对计算频散曲线基本没有影响。图2c中添加了60%的噪声,从记录中基本能够看到面波信号,同时噪声也相对增强,频散谱中在9 ~10 Hz段能量谱有所变形,在48~60 Hz段能量谱不连续,但总体趋势未发生较大改变。图2d中添加了100%的噪声,即噪声信号和有效面波信号的能量一样,此时从面波记录中勉强能看到具有线性特征的面波信号;而频散谱显示仅在19~43 Hz段与理论频散曲线基本一致,其余频段仅有部分频点能计算出正确的频散谱。

通过上述数值模拟测试可以看出,面波具有较强的抗噪声能力,一般情况下在地震波记录中只要能够看出面波信号,在面波信号强度大于2倍噪声(信噪比为3 dB)时,利用多道面波分析方法就能够计算出有效的频散曲线。

为了进一步研究面波频散谱计算时震源的影响,选取了一处试验场地,开展了不同偏移距、不同重量大锤激发实验(图3)。试验场地地层从上而下分别为填土层、粉质黏土、圆砾和泥质粉砂岩,基岩面埋深约12 m。试验采用4.5 Hz垂直检波器,道间距2 m,采样间隔0.2 ms,采样长度0.8 s。震源采用16磅、32磅大锤和200磅重锤3种,200磅重锤由50 kg重锤加16根弹簧组成(图3b),其激发能量可达到200磅重物下落所产生的能量。按照图4所示的观测系统,利用不同重量的锤击震源在排列两端分别以不同的偏移距(5 m、8 m和15 m)激发并接收地震波。

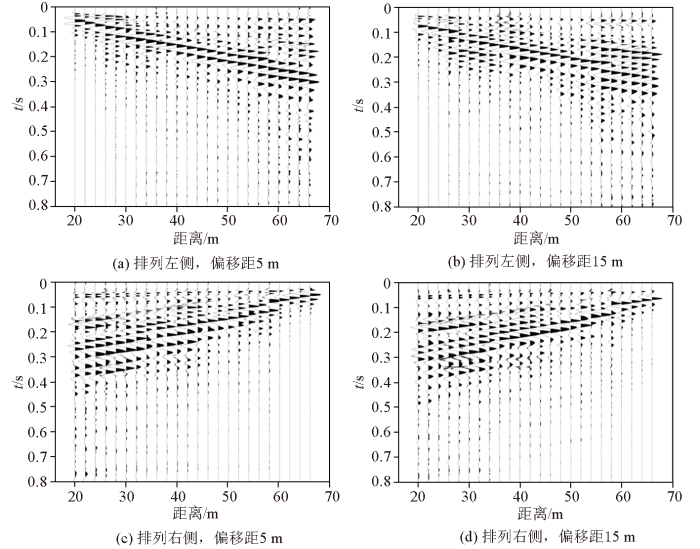
图5为16磅大锤激发得到的不同偏移距的地震波波场记录(地震波记录基本相似,为了节约篇幅仅展示2个偏移距),从左右两边5 m和15 m的地震记录中可以明显看出面波非常发育,面波所特有的低频、低速、强能量以及扫把状的频散特征都有很好的反映。在不同偏移距的地震波场记录中能够看出波组特征稍有不同,在排列右侧激发所接收到的地震波场波组多于左侧所激发的地震波波组。

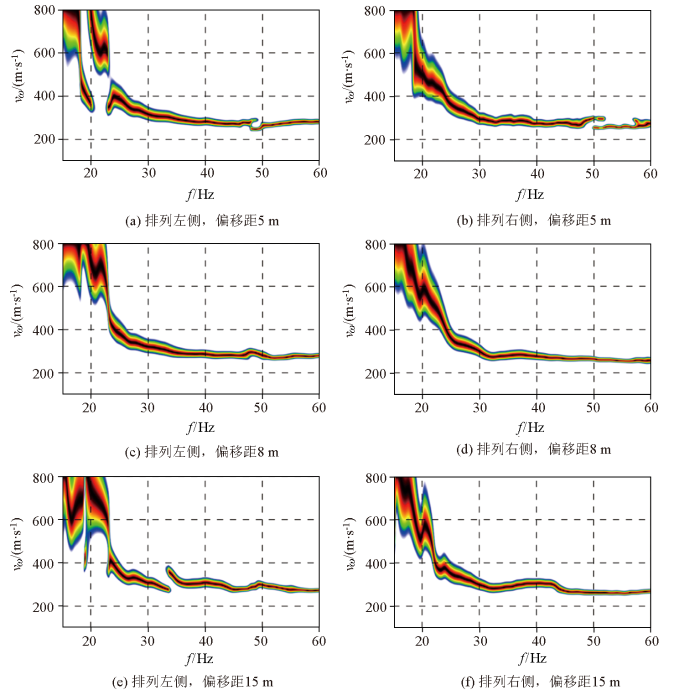
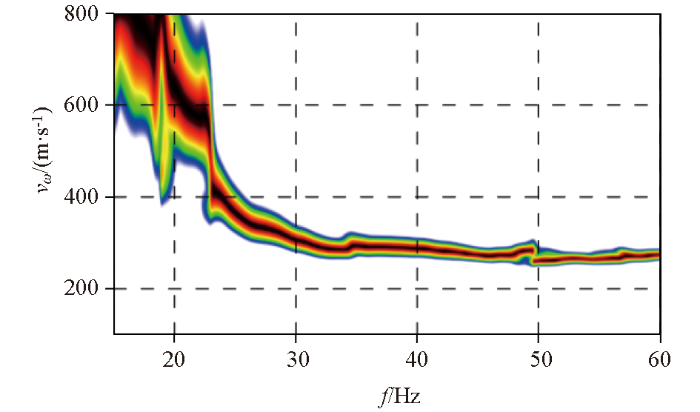
对于震源在不同偏移距位置激发所接收到的地震波,利用相移法计算其频散谱,结果如图6所示。从图中可以看出:不同偏移距的面波数据都能够用于频散谱的计算,所得到的频散谱连续性较好,其有效频段在20~60 Hz之间,低频段(深部)相速度较高,高频段(浅部)相速度较低,这也与实际地层特征一致。进一步分析可以看出,在排列左侧,不同偏移距激发所得到的频散谱在20~24 Hz频段的相速度为400~700 m/s,而在排列右侧该数据为400~500 m/s,这表明在排列两端激发时所获得的频散谱有一定的差异;在24~60 Hz频段,相速度整体在260~400 m/s,相对而言差异较小。

图6中可以看出不同位置激发得到的频散谱会有一定的差异,这一现象在多次面波探测中都有发现,即便是在偏移距足够大、符合面波探测要求的情况下也会发生,这说明面波的激发与激发位置所在的地表介质有很大关系。但是,从宏观上观察发现不了地表介质的差异,至于机理方面的研究,目前还无法深入进行。

Xu等^[20]通过简化的两层模型给出了瞬态面波在数据采集时最小偏移距公式:

式中:x为最小偏移距,h为第一层厚度,v_P和v_S分别为第一层的纵波和横波速度。在实际瞬态面波数据采集中,层厚和纵波、横波速度是未知的,因此该公式在实际面波探测中实用性不强。目前,常规做法是在数据采集时采用多个不同偏移距激发,在数据处理时从多个数据中挑选一个频散谱,相对连续提取频散曲线,但这样的处理方式有可能得到的结果与实际的地下结构有所差异。

针对目前瞬态瑞利面波存在的不同震源位置激发对频散谱的影响,本文提出了一种多频散谱融合的方案,即在面波采集时在排列两端不同位置激发地震波并采集多个偏移距面波数据,将多个面波数据计算的频散谱根据不同的权重按式(3)进行叠加融合,最后再对叠加融合后的频散谱提取频散曲线并做反演。

式中:F_m(ω,v_ω)为N个不同偏移距激发所计算出的叠加融合频散谱;W_i为不同偏移距频散曲线的权重,权重在0~1之间,权重的大小可根据单个频散曲线频散谱质量给予赋值;F_i(ω,v_ω)为单个震源激发所计算出的频散谱。

对于文中试验所计算出的单个频散谱,在计算叠加谱时权重全部为1,利用式(3)进行叠加融合得到如图7所示的融合频散谱。从图7中可以看出叠加融合的频散谱连续且能量集中,这样就可以提取到较稳定的频散曲线。

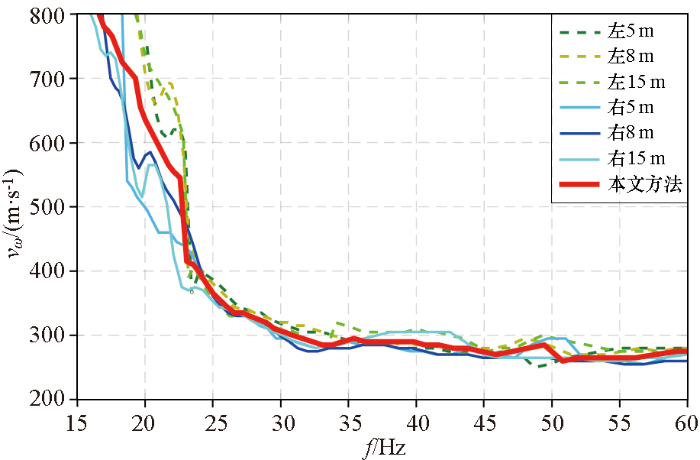
相比于频散曲线的叠加平均,利用多频散谱进行叠加融合的优势在于不受单个频散异常值的影响,能够融合多个偏移距的相速度。图8为不同偏移距频散曲线与叠加融合后的频散曲线对比,从图中可以清晰看出:在16~22 Hz段,排列左右两端激发得到的相速度值有差别,在排列左侧激发计算得到的相速度(虚线表示)大于右侧激发的相速度(实线表示),且两边不同偏移距都表现出同样特征;与平均值相比,左右两边相速度差值在21 Hz处最大,达到37%,而在22~60 Hz段左右两边激发得到的相速度值相差较小,最大处也仅有10%。图8中红色线为利用本文所提出的叠加融合方法所提取的频散曲线,与单个偏移距频散曲线对比可以看出,叠加融合所获得的相速度值介于左右两侧激发所计算得到相速度值之间,也就是对不同偏移距所得频散曲线做了综合处理,这样就避免了常规处理只取某一侧一个偏移距激发所得到的频散曲线进行反演时产生误差。从试验结果可以看出,本文所提出的多偏移距频散谱融合叠加方法可以减小由于震源激发所产生的频散曲线差异,从而更加准确地获得地下地质结构信息。

在面波勘探时,采用多大质量的震源、如何判定采集数据质量都是大家所关心的。本文通过不同质量锤击震源试验来分析频散谱,结合前面的数值模拟测试来进一步分析瞬态面波数据采集时锤击质量的选择及面波记录是否符合要求。试验参数除激发位置外其余都与前文相同,由于试验场地覆盖层相对较薄,因此在激发时增大了偏移距。激发位置在排列右侧86 m处(偏移距20 m),分别用16磅、30磅和200磅重锤激发,最大炮检距为66 m。

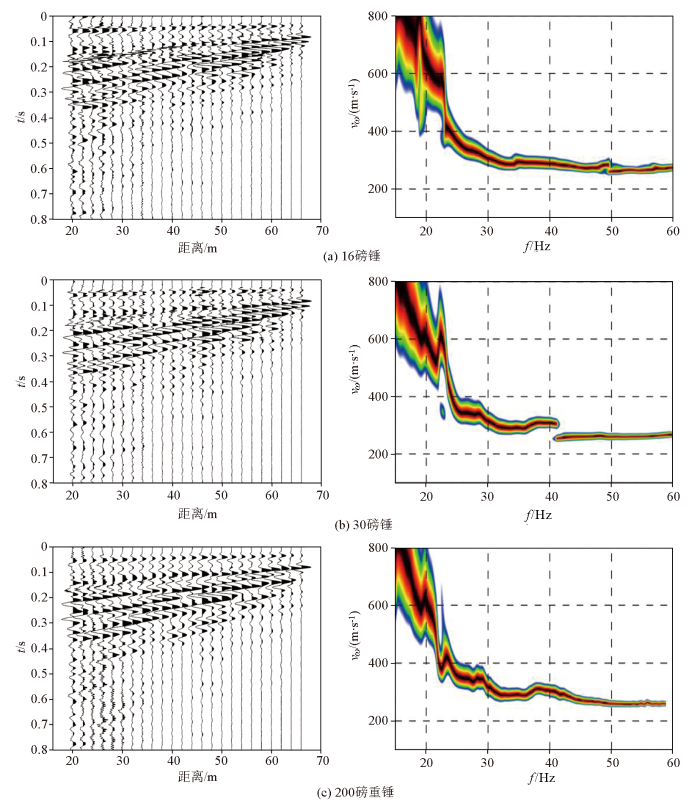
图9为不同质量锤击震源激发得到的地震波波场记录及利用相移法计算的频散谱(地震记录在成图时做了道归一化)。从地震记录中可以看出,直达波、折射波和面波都比较清晰,面波成扫把状且能量强于体波;由于试验场地距离马路约100 m,马路与测线平行,路上车辆较多,因此在面波后续还能看到一些噪声。

从3种不同质量震源激发得到的地震波记录看,200磅重锤的地震记录干扰最小,初至清晰,面波受到的干扰最小;相比而言,16磅大锤激发得到的地震波记录中噪声相对较强,但也能够看出面波特征,尤其是在离震源最远的一道也能够分辨出面波信号;30磅大锤所得到的地震记录质量介于两者之间。从频散谱图中可以看出,3个地震记录都能够获得较好的频散谱且频散特征基本一致,尤其是16磅大锤所激发的面波记录中虽然噪声相对较大,但也能计算出较好的频散谱。这一结果与前面相移法理论分析及模拟测试结果一致,即对于多道面波计算频散谱时相位信息最为关键,只要采集的面波信噪比达到一定要求,能够准确识别出相位信息,就能计算出较准确的频散曲线。在这种情况下,增大锤击质量对于提高频散曲线的精度所能发挥的作用是有限的,但对于覆盖层较厚、干扰较大的情况而言,则需要使用更大质量的锤击震源,以满足面波数据采集时能够采集到较高信噪比数据的要求。

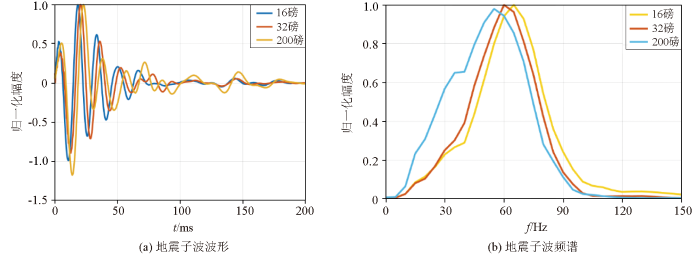
为了分析不同质量锤击震源所激发地震波的特性,将不同质量锤击所接收到的地震记录中离震源最近的一道(本文测试中采用图9地震波记录的第24道)来提取地震子波^[23]。从图10a可以看出:3种子波为最小相位子波,形态基本相似,但周期略有差异,重锤子波周期最大,16磅锤子波周期最小。将3个子波信号做频谱分析,从图10b中可以看出:重锤所激发的地震子波频段相对较低且宽,16磅锤和30磅锤所激发的地震子波频谱宽度基本相同,但频谱峰值频率16磅锤为65 Hz,而30磅锤为60 Hz。从不同质量锤击所获得的地震子波分析可知,锤的重量越大,所激发出的地震信号的频率相对就低,面波频率越低则探测深度越深。因此,对于覆盖层较厚或探测目标体较深的情况,采用质量较大的锤击震源能够采集到较好的面波数据。

在野外面波数据采集时,一般情况下面波信号的能量大于2倍噪声能量就能够计算出较好的频散谱,因此,数据采集所需要的震源质量需要根据采集面波波场记录来选择,如果小锤采集的面波记录能够满足前面所述的要求,则一般不需要更大质量的震源。虽然重锤所激发的地震子波频率相对较低,但频散谱的计算主要是与信号相位密切相关,采集到的面波信号满足信噪比需求后,再增大震源的重量,对于频散谱的质量没有更大的提升作用。

根据式(2),一般情况下面波探测表层为土层或全风化层,如果泊松比给定为0.4,则v_P/v_S=2.45,将其代入最小偏移距公式则得到x≈h。这样可以简化认为当表层为土层或全风化层、其泊松比为0.4时,面波采集的最小偏移距约等于探测的目的层深度。

结合本文研究结果,对于瞬态瑞利面波野外采集的最佳方案推荐如下。

1)瞬态面波野外数据采集时,在检波器排列两端采用多个偏移距(偏移距大于所要探测的目的层深度)激发并采集瞬态面波,具体震源激发位置数量可根据现场采集条件确定,但最少要在排列左右两端各有一个点激发。

2)如果场地条件较好,可以多采集几个不同偏移距的瞬态面波记录,在数据处理时采用多频散谱叠加融合方法可以提高频散曲线精度,从而提高瞬态面波探测的准确度。

3)对于震源质量选择,可以通过查看最大偏移距所采集的波形记录中能否分辨出面波信号来确定。尤其是距离震源最远的检波器信号,如果在采集数据时不能有效识别出面波信号,则需要增大震源质量。

针对瞬态面波数据采集时震源在不同偏移距激发所采集的面波数据计算出的频散曲线存在差异这一问题,通过理论分析、数值模拟及野外试验等方式,研究了不同激发位置对面波频散曲线的影响并提出了相关的解决方案,从而提高了瞬态面波法在浅层地质结构探测中的探测效果。通过本文研究可以得到如下结论:

1)瞬态面波法在数据采集时,不同位置激发所采集的面波数据计算的频散谱,在某些频带其相速度值有所差异,这一差异产生的原因主要与震源位置的地下介质相关。

2)针对震源位置不同所获得频散曲线存在差异的问题,提出了基于多偏移距频散谱叠加融合的方法,该方法能够有效减小频散曲线提取的误差,提高面波勘探的准确性。

3)频散谱计算与面波信号的相位最为相关,与振幅关系相对较小,在瞬态面波采集时,选择的锤击质量能够激发的面波信号能量大于2倍噪声(信噪比大于3 dB)时就能计算出较好的频散谱。