0 引言
近年来,我国油气勘探技术逐步成熟,石油生产单位的勘探要求和地质构造目标日益复杂。高陡构造、高速盐丘体等复杂构造需要更加完善的勘探成像技术。面向复杂地质目标的成像将是未来的突破方向,决定着石油工业生产的质量和效率,影响着油气藏开发和城市建设中的地下构造勘探。传统地震勘探对地下构造的刻画要求较低,只需处理一次反射波的地震信号。但随着勘探向深海深地发展,如济阳和玉门等地采集的地震数据中出现了大量多次波,特别是在海上勘探中,海底和海面强反射面导致地震数据受多次波影响明显。因此,从实际工业生产角度出发,必须考虑多次波的影响。
多次波是地震波经过地下界面反射的真实波形,包含丰富的地下构造信息。由于多次波在地下传播路径更长、反射角更小,其照明范围更广,成像分辨率更高,特别是存在盐丘等高速高陡构造时,多次波成像能够获取更细致的地下构造信息。随着地震波传播与成像理论的进步,多次波逐渐成为研究热点。传统多次波成像通过表层多次波去除或聚焦变换分离后进行。本文提出利用地震干涉理论的新方法,通过对接收到的地震信号进行互相关、褶积等运算,直接预测多次波,再进行多次波逆时偏移成像。
逆时偏移主要用于盐丘等高陡构造以及横向速度剧烈变化的地区。该技术基于双程波动方程,最早由Whitmore于1949年提出[1 ] 。国内对多次波逆时偏移也有许多研究:2008年,刘伊克等[2 ] 在成像域成功压制表层多次波与层间多次波,发现多次波含有丰富的小角度信息,能够提供更广的成像范围。2011年,郭书娟等[3 ] 实现了一次波和表层多次波联合成像,将含有多次波和震源脉冲的炮记录作为震源波场,压制了常规多次波成像噪声。Wang等[4 ] 改变传统做法,将含有一次波和多次波的地震数据记录作为震源波场和检波波场,提高了成像分辨率,但不恰当的子波选择可能导致信息覆盖。2013年,Li等[5 ] 提出了基于SRME和聚焦变换的一次波和各阶表层多次波分离方法。2014年,Wang等[6 ] 将一次波和表面多次波分别作为震源波场和检波波场,通过互相关成像,并创新性引入共角度域成像点道集,有效改善了多次波逆时偏移中的噪声问题。该方法不需要对多次波进行预测,可以进行浅层目标的成像,但会在成像区域内产生广泛且能量较强的串扰噪声,这是由于逆时偏移成像机制中需要对震源波场正传和检波波场反传后进行互相关运算所导致,该问题一直是多次波成像领域研究的重点。2015年,宋鹏等[7 ] 分析了多次波成像过程中的串扰噪声机制,创新性地应用SRME理论进行多次波分阶逆时偏移,有效压制了串扰噪声问题。2015年,朱博等[8 ] 引入多卡GPU集群加速技术,显著提高了多次波成像的计算效率。同年,Berkhout[9 ] 提出全波场偏移算法,将全波数据视为地震数据,并利用伴随方法实现了层间多次波的成像;2016年,刘学建等[10 ] 将逆散射级数方法预测的层间多次波当作逆时偏移的反传数据,并结合波场分离实现了层间多次波的偏移。2017年,Li等[11 ] 提出基于SRME与聚焦变换的分阶多次波逆时偏移,进一步压制串扰噪声并提高成像分辨率。然而,多次波成像中仍存在不相干同相轴噪声的问题,有待进一步研究。2018年,刘伊克等[12 ] 结合多次波成像与分阶思想,提出可控阶多次波成像算法:在成像前将不同阶数多次波提取出来,并将n 阶、n +1阶多次波分别当作虚震源与地震记录,应用成像条件获取n +1阶多次波的成像结果,随后叠加各阶多次波成像结果获取最终偏移结果。2022年黄建东等[13 ] 对单程波偏移方法进行了拓展,提出层间多次波傅里叶有限差分偏移。
地震干涉技术的提出对于地震波传播与成像规律的认识与研究做出了巨大的贡献,也为多次波成像提供了全新的研究思路,本文基于地震干涉理论对多次波成像作进一步研究,因此下面介绍对地震干涉理论的研究现状。
1968年,地震干涉技术由Claerbout[14 ] 提出,并在水平层状介质下验证了其正确性,同时他进一步猜想该技术在三维各向异性介质下同样适用。2001年,Schuster[15 ] 正式将这一技术方法命名为“地震干涉技术”。2002年,Wapenaar等[16 ] 对地震干涉方法进行了深入研究,并通过数学原理验证了地震干涉理论,发现其对不同的非衰减介质及震源条件均表现出很强的适应性,同时也验证了Clearbout关于三维各向异性介质的猜想。值得一提的是,Sheng等[17 ] 在2001年就应用了地震干涉技术对地下介质进行成像,并取得了显著的成像效果,且该方法不受震源条件的限制。
自2002年起,Snieder等[18 ] 开始研究地震干涉技术在尾波提取有用信息上的应用,并在2007年总结了不同条件下的地震干涉基本原理[19 ] 。2008年,Wapenaar等[20 ] 提出了多维反褶积技术,并将其应用于被动源数据,推导了多维反褶积格林函数,成功从噪声数据中提取了面波信息。
地震干涉技术在勘探地震领域应用广泛,它能够将地表激发地下接收的地震信号转化为地下激发地下接收的地震信号,从而避开上覆介质的影响,且无需考虑上覆介质的速度模型,因此也被称为“虚震源法”。Calvert等[21 ] 在2004年将VSP数据转化为SWP单井剖面记录;Mehta等[22 ] 在2007年先对地震数据进行波场分离,再运用地震干涉技术,取得了显著效果;Gaiser等[23 ] 在2010年应用折射波干涉技术从OBS数据中提取了P波和S波信息;Bharadwaj等[24 ] 在2012年改进了折射波干涉技术,提高了成像精度;Wapenaar等[25 ] 在2014年应用地震干涉技术从反射波中提取出了格林函数。此外,地震干涉技术在电磁法勘探中也有诸多应用进展。
国内对地震干涉技术的研究同样取得了显著进展。齐诚等[26 ] 在2007年首次在国内提出利用地震噪声对地下介质进行成像;王宝善等[27 ] 在2009年利用云南固定台站观测到的背景噪声进行互相关分析,得到了格林函数,并成功估计了地震速度的变化及波速变化;陶毅等[28 ] 在2010年对地震干涉技术进行了详细概述,并进一步阐明了未来的研究方向;朱恒等[29 ] 在2012年将地震干涉理论与Radon变换相结合,与传统时空域地震干涉方法相比,该方法去除了大量虚假信息,并通过了大量的理论及实际数据验证;2015年,朱恒等[30 ] 又分别提出了线性Radon域和抛物Radon域的地震干涉技术,显著提高了虚拟震源地震数据记录的质量;程浩[31 ] 在2016年进行了被动源地震干涉一次波估计,并对“稳相点”进行了深入探讨;孙宇等[32 ] 在2018年提出了基于Bayes算法的线性Radon域地震干涉技术,能够对层间多次波进行较好的预测和压制;王立歆等[33 ] 在2021年运用CURTIS炮—检地震干涉技术,研发了可控震源散射面波干涉匹配与预测技术,并将其应用于解决沙漠地区常见的严重黑三角噪声问题。该方法依靠实际地震数据驱动,无需速度模型,能够有效消除散射面波。但黑三角区域内的噪声种类过多,噪声压制机制仍需进一步研究;阮小敏等[34 ] 在2023年研究了多种地震干涉方法,构建了虚拟炮记录,并将其应用于多次波的压制。该方法能够在面波主导的背景噪声中提取有效信号,对被动源原始数据的预处理做出了重要贡献。
传统地震勘探技术通常将多次波视为成像的干扰加以压制,主要通过SRME(表面相关多次波消除)或Radon变换分离多次波。然而,这些方法在实际应用中存在局限性:例如,SRME需要准确的震源子波信息,对噪声和非理想观测条件较为敏感;Radon变换在复杂地质条件下的分离效果有限,且计算成本较高。此外,传统方法通常仅利用一次波进行成像,忽略了多次波在复杂地下构造成像中的潜力。本文则创新性地提出了一种基于地震干涉理论的方法,将多次波直接用于成像,避免了传统方法中多次波分离和压制的步骤。地震干涉理论通过互相关和褶积型互易定理构建多次波,充分利用多次波在传播路径长和反射角小方面的优势,为复杂构造成像提供了更广的照明范围和更高的分辨率。具体有以下几部分内容:
1)本文基于地震干涉技术理论,推导了互易定理以及“稳相点”,并创新性推导地震干涉技术中的褶积型互易定理,直接进行预测合成多次波,实现了多次波的直接成像,避免了传统成像中的多次波压制和分离阶段,提高了成像效率;
2)通过对多次波成像条件的研究以及噪声分析,发现多次波成像过程中由于不相干同相轴互相关导致的噪声问题严重。本文提出基于地震干涉理论进行分阶多次波逆时偏移,有效解决了不相干同相轴噪声问题,提高了盐下成像分辨率;
3)通过模型试算,证明了本文提出的基于地震干涉的分阶多次波逆时偏移成像方法可以精细描绘地下构造,尤其对于盐下构造成像效果好,能够有效改善多次波成像中的串扰噪声问题,提高了成像分辨率。
1 地震干涉的基本原理
1.1 格林函数
格林函数指的是点源引起的波场扰动,在本文特指地震波的传播过程,也就是应力值。本文研究的是二维声波介质下的格林函数,但其原理可以较为容易地推广到三维声波介质。
本文的公式是在频率域中推导的。考虑到三维声波介质具有代表性,首先介绍三维亥姆霍兹方程:
(1) $ \left(\nabla^{2}+k^{2}\right) G(g \mid s, \omega)=-\delta(s-g),$
式中:G (g ,s |ω )表示s 作为震源波场,g 作为检波点波场的地震记录的格林函数,ω 表示角频率;k =ω/v (g ),表示波数。式(1)的微分与接收点g 的位置相对应:
(2) $ \delta(s-g)=\delta\left(x_{s}-x_{g}\right) \delta\left(y_{s}-y_{g}\right) \delta\left(z_{s}-z_{g}\right),$
式中:xs 、ys 、zs 、xg 、yg 、zg 分别表示震源和检波点的三维坐标。式(1)存在两个数值解,一个是有实际物理意义的因果格林函数G (g |s ,ω ),另一个是没有实际物理意义的非因果格林函数G (g |s ,ω )*
先考虑最简单的均匀各向同性介质,因为是均匀介质,所以只有一个速度,它的有实际物理意义的因果格林函数G (g |s ,ω )可用下式表达:
(3) $ G(g \mid s, \omega)=\frac{1}{4 \pi} \frac{\mathrm{e}^{\mathrm{i} k r}}{r},$
式中:i为虚部单位;k 为波数,且k =ω/v ;r 为激发点到接收点的直线距离,因此它的倒数1/r 可以代表介质的几何扩散程度。
式(3)表示了s 点作为震源激发点、g 点作为震源接收点所接收到的三维格林函数,并且根据互易定理,格林函数中的震源激发点和震源接收点可以互换,也就是G (g |s ,ω )=G (s |g ,ω )。
1.2 互易定理
互易定理在电磁学、光学中有诸多应用,发展到地球物理领域,主要体现为波场不变的性质,即震源激发点和接收点互换后波场不变。首先通过格林函数推导出互相关型和褶积型互易定理,为后续地震干涉理论公式的创新打下基础。
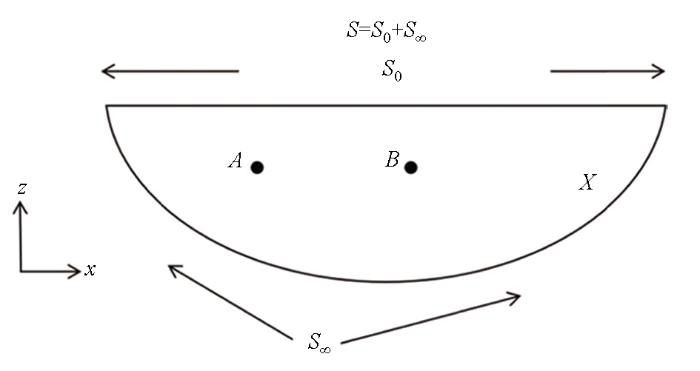
为了推导互易定理,建立互易定理模型图,如图1 所示。
图1
图1
互易定理模型
Fig.1
Model diagram for deriving reciprocity theorem
G (x |A ,ω )表示均匀介质内部A 点作为震源激发点、x 点作为震源接收点所接收到的地震波响应的格林函数。根据式(1)进行类比推导,可以得到A 、B 两点的Helmholtz方程,即:
(4) $ \left(\nabla^{2}+k^{2}\right) G(x \mid A, \omega)=-\delta(x-A),$
(5) $ \left(\nabla^{2}+k_{0}^{2}\right) G_{0}(x \mid B, \omega)=-\delta(x-B),$
式中:波数k =ω/v (x ),k 0 =ω/v 0 (x ),x ∈V ,由于介质是各向同性速度均匀的,所以如果A 、B 在介质内部,那么v (x )=v 0 (x ),在外部,则v (x )≠v 0 (x )。
(6) $G(B \mid A, \omega)-G_{0}(A \mid B, \omega)=\int_{S}\left[G_{0}(x \mid B, \omega).\right.\frac{\partial G(x \mid A, \omega)}{\partial n_{x}}-G(x \mid A, \omega) \cdot \frac{\partial G_{0}(x \mid B, \omega)}{\partial n_{x}}]\mathrm{d}^{2} x。$
式(6)被称为褶积型互易定理(详细推导见附录A),这是因为频率域的乘积运算等价于时空域的褶积运算。等式左边无需做积分运算,等式右边需要在闭合曲面S 上进行面积分运算。
G (x |A ,ω )为单极震源,它的一阶导数为偶极震源。单极震源是一种激发源的模式,特指激发区域只含有一个震源。单极震源激发模式假设初始的波场扰动只发生在一个激发点上,由这个点产生的地震波则从这个点向外扩散。该模式下生成的地震记录可以用单个震源的参数进行描述,例如震源深度、震源大小、震源机制等。单极震源模型是基于一种纯理想化的假设,只能用来简化地震波正演模拟和反演模拟,而偶极震源则是另一种激发源模式,特指激发区域内存在两个相互作用的震源,这比单极震源模式更为复杂,但也更加贴合实际情况。因此,偶极震源模式假设地震扰动波场是由两个相互作用的点源引发的,其中,每个点源都有一个独立的震源参数集合,类似于单极震源。偶极震源产生的地震波通常具有更加复杂的波形,可以用来描述更加复杂介质内地震波传播过程。当单极震源和偶极震源的相位谱叠加在一起时,有:
(7) $G \cdot \mathrm{~d} G / \mathrm{d} n=|G \cdot \mathrm{~d} G / \mathrm{d} n| \mathrm{e}^{\mathrm{i}\left(\phi_{G^{+}} \phi_{d G}\right)},$
从式(6)可以看出褶积型互易定理相较于均匀介质下的自由场格林函数
(8) $ G(x, s)=\frac{1}{4 \pi|x-s|} \mathrm{e}^{\mathrm{i} \omega|x-s| / c}$
为了简化褶积型互易定理,使其只含有由两个单极震源组成的积分核,并且更加方便理解两者的物理意义,现引入远场近似理论。均匀介质内的入射波会令散射体发生散射,在远场则可表示为:
(9) $ G(x \mid B, \omega) \sim m(\phi, \theta) \frac{\mathrm{e}^{\mathrm{i} k r}}{r}。$
类似于式(3),式(9)中r 表示三维声波介质内的接收点到激发点的距离,m (ϕ ,θ )只与空间旋转角度有关。将式(9)代入到式(8)可得:
(10) $ \begin{array}{c}\hat{n} \cdot \nabla G(x \mid A, \omega) \sim \frac{\partial G(x \mid A, \omega)}{\partial r}= \\\mathrm{i} k \frac{\mathrm{e}^{\mathrm{i} k r}}{r}-\frac{\mathrm{e}^{\mathrm{i} k r}}{r^{2}}=\frac{\mathrm{e}^{\mathrm{i} k r}}{r}\left(\mathrm{i} k-\frac{1}{r}\right),\end{array},$
(11) $ G(x \mid A, \omega)=\frac{\mathrm{e}^{\mathrm{i} k r}}{r},$
(12) $ \begin{array}{c}\hat{n} \cdot \nabla G(x \mid A, \omega) \sim \frac{\partial G(x \mid A, \omega)}{\partial r}=\mathrm{i} k G(x \mid A, \omega)- \\\frac{G(x \mid A, \omega)}{r} \approx \mathrm{i} k G(x \mid A, \omega)\end{array},$
将远场近似的结果方程(12)代入方程(13),此时nx ~r 得:
(13) $ \begin{array}{c}2 \mathrm{i} \operatorname{Im}[G(B \mid A, \omega)] \approx 2 \mathrm{i} k \int_{s_{0}} G(x \mid B, \omega) * \\G(x \mid A, \omega) \mathrm{d} x^{2},\end{array},$
(14) $ \begin{array}{c}G(B \mid A, \omega)-G_{0}(A \mid B, \omega)=\int_{S}\left[G_{0}(x \mid B, \omega) \cdot\right. \\\nabla G(x \mid A, \omega) \cdot \hat{n}-G(x \mid A, \omega) \cdot \\\left.\nabla G_{0}(x \mid B, \omega) \cdot \hat{n}\right] \mathrm{d}^{2} x\end{array}。$
1.3 “稳相点”原理
“稳相点”指的是干涉过程中循环的点数,在编程时特指震源点数和检波点数。由于地球物理勘探的观测系统本身就无法与医院的CT一样做到360°观测,所以需要尽可能的多提供震源点数和检波点数。而震源点数的增多将会导致计算量的变大,在实际勘探工作中也会增加施工成本。检波点数的增多在数值模拟中并不会产生影响,但在野外施工中会增加检波器的购买成本。
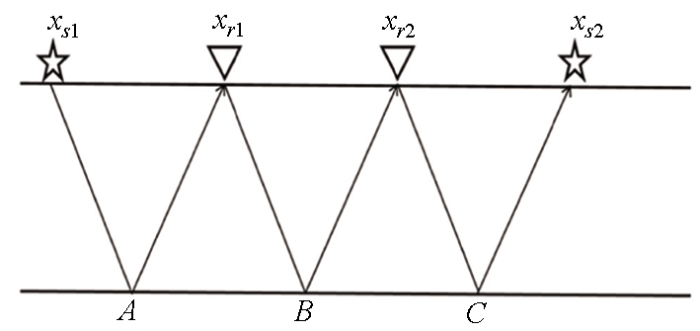
无论是褶积型还是相关型地震干涉,如果所有的地震记录都参与到虚拟地震记录的合成,那么会造成两点困扰:①计算量极大,占用的计算机内存极高,不满足工业生产的需要;②不同的地震炮记录之间进行褶积和互相关,将造成无关信号的串扰,对于后续的地震解释以及地震数据处理造成极大的困难。因此,在地震干涉中并不是全部的地震记录都参与虚拟地震记录的合成。经过地球物理界专家学者的研究,发现合成虚拟炮记录主要是“稳相点”(stationary-phase point)。如图2 所示:xs 1 、xs 2 是物理人工震源,xs 1 、xs 2 激发的地震波由地震记录检波器xr 1 、xr 2 接收。当要求取xr 1 作为虚震源,xr 2 接收的地震记录时,地震能量主要来源于xr 1 左侧的xs 1 。当利用相关型地震干涉原理时,需要对G (xr 2 |xs 2 ,ω )和G (xr 1 |xs 1 ,ω )进行互相关运算,而不是对G (xr 2 |xs 2 ,ω )和G (xr 1 |xs 2 ,ω )进行运算,这就是“稳相点”原理。
图2
图2
稳相点示意
Fig.2
Schematic diagram of stationary-phase point
2 基于地震干涉的多次波构建
2.1 地震干涉的多次波构建
基于上述格林函数、“稳相点”等基本地震干涉理论,进行褶积型互易定理多次波构建公式的推导。地震干涉本身是在垂直井间观测系统中提出的,为的是消除地下水平井以上的复杂介质对深层信号的干扰作用,其原理是基于互相关类型。而本文研究的是多次波,可以是高阶多次波,因此本文采用的是褶积型干涉公式,每一次褶积就会提高一次多次波的阶数。褶积可以在频率域中完成,也可以在时间域里完成,前者的运算效率更高。在褶积运算之前,由于地震震源激发不是立即激发,有一定的延迟时间,所以需要将炮记录中的直达波以上的零值部分去掉,在后期的成像之前再补上。在做褶积运算之前,需要将炮记录的直达波去掉,因为直达波不含有效信息,而且能量过强。
(15) $ \begin{array}{c}\rho \partial_{i}\left(\rho^{-1} \partial_{i} \hat{G}\left(x, x_{A}, \omega\right)\right)+\frac{\omega^{2}}{c^{2}} \hat{G}\left(x, x_{A}, \omega\right)= \\-i \omega \rho \delta\left(x-x_{A}\right),\end{array},$
式中:$\hat{G}$ G (x ,xA ,t )的傅里叶变换的因果时域结果,代表了震源在xA 点激发、检波器在x 处接收到的脉冲响应。式(16)~(18)表示频率域格林函数可分解为震源谱s 与介质传播响应R 的乘积:
(16) $ \hat{G}_{A}^{-}\left(x_{A}, x_{B}, \omega\right)=R\left(x, x_{A}, \omega\right) s_{A}(\omega),$
(17) $ \hat{G}_{B}^{-}\left(x_{B}, x_{C}, \omega\right)=R\left(x, x_{B}, \omega\right) s_{B}(\omega),$
(18) $ \hat{G}_{C}^{-}\left(x_{C}, x_{D}, \omega\right)=R\left(x, x_{C}, \omega\right) s_{C}(\omega)。$
因为计算机无法进行连续函数的计算,所以本文在这里引入希尔伯特变换(Hilbert Transform)来进行公式离散化:
(19) $ h(\iota)=f(\iota) \cdot g(\iota)=\int f(\tau) g(\iota-\tau) \mathrm{d} \tau。$
(20) $ H(\omega)=2 \pi F(\omega) G(\omega) ;$
(21) $ h[i]=\sum_{i^{\prime}=0}^{N-1} f\left[i^{\prime}-i\right] g\left[i^{\prime}\right]=\sum_{i^{\prime}=0}^{N-1} f\left[i^{\prime}\right] g\left[i+i^{\prime}\right] ; $
现在考虑一个二维声波波场。声波压力用p (x ,t )表示,粒子速度用vi (x ,t )表示,可得到p (x ,t )时空域的傅里叶表达式:
(22) $ \hat{p}(x, \omega)=\int_{-\infty}^{\infty} \exp (-\mathrm{i} \omega t) p(x, t) \mathrm{d} t 。$
在空间频率域内,声波压力和粒子速度在无损不均匀介质中遵循运动方程以及应力—应变方程关系分别为:
(23) $ \hat{\mathrm{i} \omega p v_{i}+\partial_{i} p=\hat{f_{i}},} $
(24) $ \hat{\mathrm{i} \omega \hat{p}+\partial_{i} \hat{v_{i}}=\hat{q}}。$
下面简单介绍交互量这一概念。交互量在物理学中通常指两个或多个系统之间相互作用的量或度量,可以用来描述声源向介质中注入声波的效果以及介质中声波的传播和反射。在本文中,交互量指声学介质和声源之间的相互作用量或相互作用强度。交互量[35 ] 可以写为:
(25) $ \hat{\partial}_{i}\left\{\hat{p}_{A} \hat{v}_{i, B}-\hat{v}_{i, A} \hat{p}_{B}\right\} $
当震源项为${\hat{f}}_{i}$ $\hat{q}$ $\hat{p}$ ${\hat{v}}_{i}$
本文研究的介质为无损介质,可以应用时间反转不变性原理[36 ] 。在频率域中,时间反转被复共轭代替。因此,当震源项为${\hat{f}}_{i}^{*}$ ${\hat{q}}^{*}$ ( *表示复共轭)时,${\hat{p}}^{*}$ ${\hat{v}}_{i}^{*}$ [37 ] :
(26) $ \begin{array}{c}\int_{D}\left\{\hat{p}_{A} \hat{q}_{B}-\hat{v}_{i, A} \hat{f}_{i, B}-\hat{q}_{A} \hat{p}_{B}+\hat{f}_{i, A} \hat{v}_{i, B}\right\} \mathrm{d}^{3} x= \\\oint_{\partial D}\left\{\hat{p}_{A} \hat{v}_{i, B}-\hat{v}_{i, A} \hat{p}_{B}\right\} n_{i} \mathrm{~d}^{2} x\end{array} 。$
假设xA 、xB 都在半无限边界D中,在两种状态下外部力都可以看作是0。因此,A 、B 点的波场可以用声学格林函数来表示:
(27) $ \hat{p}_{A}(x, \omega)=\hat{G}\left(x, x_{A}, \omega\right),$
(28) $ \hat{v}_{i, A}(x, \omega)=-[i \omega \rho(x)]^{-1} \partial_{i} \hat{G}\left(x, x_{A}, \omega\right),$
(29) $ \hat{p}_{B}(x, \omega)=\hat{G}\left(x, x_{B}, \omega\right),$
(30) $ \hat{v}_{i, B}(x, \omega)=-[\mathrm{i} \omega \rho(x)]^{-1} \partial_{i} \hat{G}\left(x, x_{B}, \omega\right) 。$
$\hat{G}$ ( x ,xA ,ω )是G (x ,xA ,ω )的傅里叶变换的因果时域结果,代表了xA 激发,x 接收到的脉冲响应。联立式(26)及(30),就可以得到褶积型声波互易定理:
(31) $ \begin{array}{c}\hat{G}_{h}\left(x_{B}, x_{A}, \omega\right)=\oint_{\partial} \frac{-1}{i \omega \rho(x)}\left[\hat{G}\left(x, x_{A}, \omega\right) \partial_{i} \hat{G}\left(x, x_{B}, \omega\right)\right. \\\left.-\partial_{i} \hat{G}\left(x, x_{A}, \omega\right) \hat{G}\left(x, x_{B}, \omega\right)\right] n_{i} \mathrm{~d}^{2} x,\end{array} $
(32) $ \hat{G}_{h}\left(x_{A}, x_{B}, \omega\right)=\hat{G}\left(x_{B}, x_{A}, \omega\right)+\hat{G}\left(x_{A}, x_{B}, \omega\right) 。$
联立式(16)~(18)和式(31),即可得到地震干涉褶积型互易定理用于多次波的构建公式:
(33) $ \begin{array}{c}\hat{G}_{h}\left(x_{C}, x_{A}, \omega\right)=\oint_{\partial D} \frac{-1}{\mathrm{i} \omega \rho(x)}\left[\oint _ { \partial D } \frac { - 1 } { \mathrm { i } \omega \rho ( x ) } \left(\hat{G}_{A x} \partial_{i} \hat{G}_{B x}-\right.\right. \\\left.\partial_{i} \hat{G}^{A x} \hat{G}_{B x}\right) n_{i} \mathrm{~d}^{2} x_{A} \cdot \partial_{i} \hat{G}_{B C}-\partial_{j} \oint_{\partial D} \frac{-1}{\mathrm{i} \omega \rho(x)}\left(\hat{G}_{A x} \partial_{i} \hat{G}_{B x}-\right. \\\left.\left.\partial_{i} \hat{G}_{A x} \hat{G}_{B x}\right) n_{i} \mathrm{~d}^{2} x_{A} \cdot \hat{G}_{B C}\right] n_{j} \mathrm{~d}^{2} x_{B}。\end{array} $
${\hat{G}}_{h}$ ( xC ,xA ,ω )的离散形式L ${\hat{G}}_{h}$ ( xC ,xA ,ω )如下:
(34) $ \begin{array}{c}L \hat{G}_{h}^{j}\left(x_{C}, x_{A}, \omega\right)=\sum_{j} \frac{n_{j} x_{B C}^{2}}{\mathrm{i} \omega \rho_{j}} L \hat{G}_{h}^{j}\left(x_{B}, x_{A}, \omega\right) \cdot \\\frac{\hat{G}_{B C}^{j+1}-\hat{G}_{B C}^{j}}{n_{j}}-\frac{L \hat{G}_{h}^{j+1}\left(x_{B}, x_{A}, \omega\right)-L \hat{G}_{h}^{j}\left(x_{B}, x_{A}, \omega\right)}{n_{j}} \cdot \hat{G}_{B C}^{j},\end{array} $
(35) $ \begin{aligned}L \hat{G}_{h}^{i}\left(x_{B}, x_{A}, \omega\right)= & \sum_{i} \frac{n_{i} x_{A B}^{2}}{\mathrm{i} \omega \rho_{i}} \hat{G}_{h}^{i}\left(x, x_{A}, \omega\right) \cdot \frac{\hat{G}_{B x}^{i+1}-\hat{G}_{B x}^{i}}{n_{i}}- \\& \frac{\hat{G}_{A x}^{i+1}-\hat{G}_{A x}^{i}}{n_{i}} \cdot \hat{G}_{B x}^{i}。\end{aligned} $
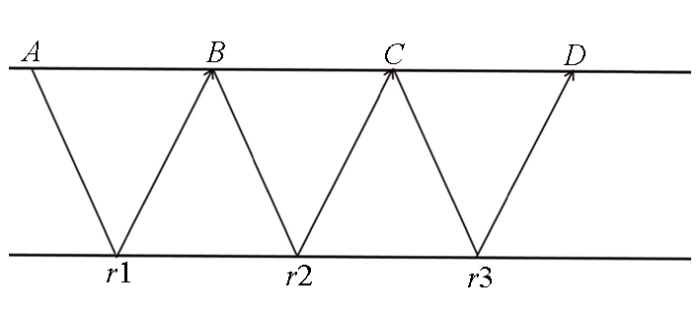
通过褶积型互易定理,可以将路径分别为AB 、BC 的地震记录相加得到路径为AC 的地震记录,从而达到多次波构建的目的。图3 为基于地震干涉的多次波构建。
图3
图3
基于地震干涉的多次波构建原理
Fig.3
Schematic of multiple construction based on seismic interference
2.2 模型试算
2.2.1 层状模型
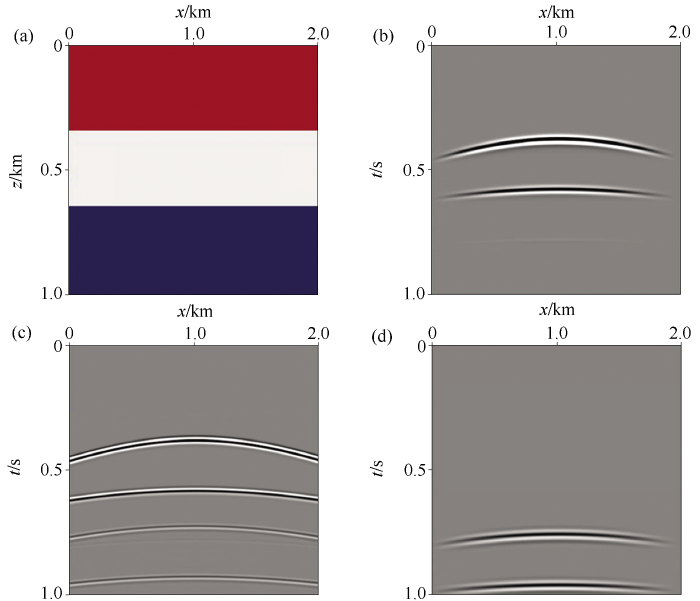
下面通过模型以及数值试验对本文所提方法的可行性进行验证。层状速度模型如图4a 所示,该层状模型的参数:第一层为速度2 000 m/s、厚度为350 m的低速层,第二层速度3 000 m/s、厚度为300 m,第三层速度2 000 m/s、厚度为350 m。模型网格个数为201×201,纵、横向网格步长均为10 m,采样间隔为0.5 ms,总记录时间为1 s。本次模拟震源采用主频为30 Hz的雷克子波,检波器为全接收排列,每个检波器间隔10 m。
图4
图4
层状模型的测试结果
a—层状速度模型;b—一次波炮记录;c—原始记录;d—预测多次波炮记录
Fig.4
Test results of layered model
a—layered velocity model;b—primary shot record;c—original record;d—predicted multiples shot record
简单层状模型采用自由地表吸收边界条件模拟出来的中间激发全接收的单炮记录见图4b ,该数据记录只含有一次波;简单层状模型采用地表吸收边界条件模拟出来的中间激发全接收的单炮记录见图4c ,该数据记录包含有一次波和多次波;通过褶积型地震干涉预测出来的多次波见图4d 。通过与原始记录的对比,发现该方法能够完全正确地预测多次波,并且预测出的多次波同相轴清晰可见;分离的一次波、多次波成分与原始记录相比,相位一致,分离的多次波记录中同相轴纵向分辨率得到提升。
需要注意的是,在进行地震数据处理过程中,常规预测出来的多次波虽然同相轴清晰可见且准确,但是存在噪声问题。本文引入了汉宁窗(Hanning window)对图像处理过程中的边界效应进行处理,处理后边界处能量稍有下降,但噪声问题得到明显改善。同时,增加接收时间能够更好地反映地下信息,也就是说,接收的时间越长,合成记录的能量越强,因而能够反映更多的信息。因此在实际工作中,可以通过加大接收时间的方法来增加虚拟反射波的能量,提高虚震源记录的信噪比,从而提高地震资料的分辨率。
2.2.2 非层状模型
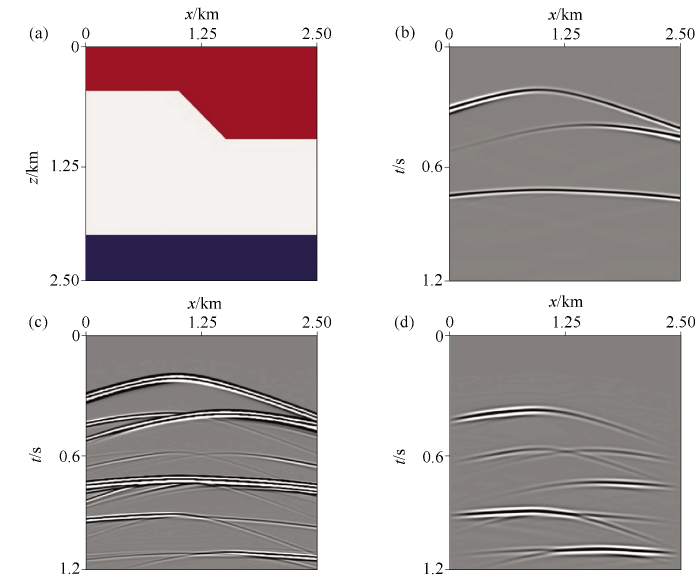
通过层状模型对基于地震干涉的多次波预测方法进行了简单验证。由于多次波主要发育在速度变化大的区域,所以通过一个斜状的非层状模型的设计来对基于地震干涉的多次波的有效性以及正确性进行进一步的测试。非层状模型见图5a ,模型网格个数为251×251,纵、横向网格步长均为10 m,采样间隔为0.5 ms,总记录时间为1.2 s。本次模拟震源采用主频为30 Hz的雷克子波,检波器为全接收排列,每个检波器间隔15 m。
图5
图5
非层状模型的测试结果
a—非层状速度模型;b—一次波炮记录;c—原始记录;d—预测多次波炮记录
Fig.5
Test results of non-layered model
a—non-layered velocity model;b—primary shot record;c—original record;d—predicted multiples shot record
非层状模型采用自由地表吸收边界条件模拟出来的中间激发全接收的单炮记录见图5b ,该数据记录只含有一次波;非层状模型采用地表吸收边界条件模拟出来的中间激发全接收的单炮记录见图5c ,该数据记录包含有一次波和多次波;通过褶积型地震干涉预测出来的多次波见图5d ,通过与原始记录的对比,该方法能够完全正确地预测多次波,并且预测出的多次波同相轴清晰可见。借助汉宁窗处理后的多次波记录边界能量稍有下降,但减少了噪声干扰。对比层状模型与非层状模型结果可见,在接收时间较长的情况下,被动源成像技术可以用来对起伏界面进行准确的探测。
2.2.3 Sigsbee2B模型
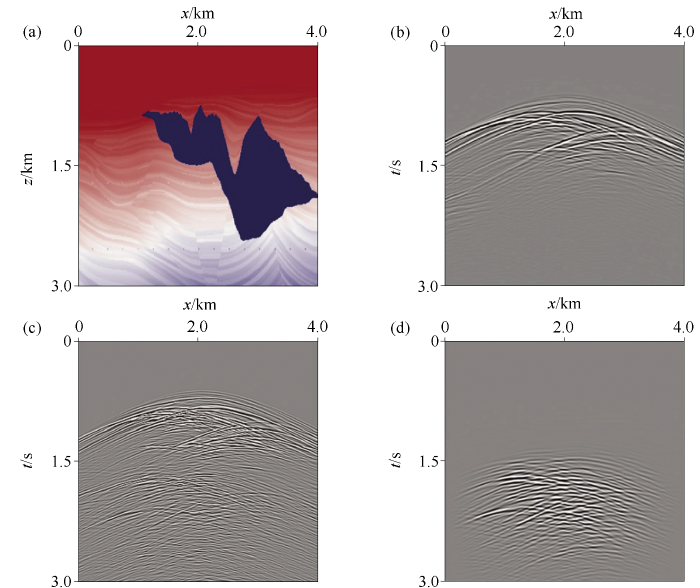
上述层状以及非层状模型都经过了数值试验的测试。SigsbeeB模型因为存在起伏海底和盐丘等高陡构造,在国际上作为通用的多次波测试数据模型,因此最后经过对Sigsbee2B模型的验算来证明预测结果。Sigsbee2B模型如图6a 所示,模型大小为401×301,纵、横向网格步长均为10 m,采样间隔为0.5 ms,总记录时间为3 s。本次模拟震源采用主频为30 Hz的雷克子波,检波器为全接收排列,每个检波器间隔10 m。
图6
图6
Sigsbee2B模型的测试结果
a—Sigsbee2B模型;b—一次波炮记录;c—原始记录;d—预测多次波炮记录
Fig.6
Test results of Sigsbee2B model
a—Sigsbee2B model;b—primary shot record;c—original record;d—predicted multiples shot record
Sigsbee2B模型采用地表吸收边界条件模拟出来的中间激发全接收的单炮记录见图6b ,该数据记录包含有一次波和多次波;Sigsbee2B模型采用自由地表吸收边界条件模拟出来的中间激发全接收的单炮记录见图6c ,该数据记录只含有一次波;通过褶积型地震干涉预测出来的多次波见图6d ,通过与原始记录的对比,发现该方法能够较好地预测多次波。该方法在Sigsbee2B模型上对多次波的正确预测,给后续多次波的成像打下了基础。另外,需要指出的是:在图6d 中预测出的多次波存在同相轴粗的问题,这是基于地震干涉方法进行多次波预测构建所不可避免的[38 ] ,后续将继续在该方向进行研究、完善。
3 基于地震干涉的分阶多次波逆时偏移
在多次波成像的过程中,不同阶多次波引起的不相关轴互相关对多次波的成像造成了不良影响,不匹配的多次波能量互相关将会造成严重的构造假象。目前针对多次波成像中该类问题的压制主要分为以下两种:一种是通过最小二乘逆时偏移进行多次波成像,但是该方法的计算成本过高;另一种是通过分离各阶多次波再进行常规多次波逆时偏移。本文基于地震干涉理论进行多次波预测,将预测出的多次波直接进行多次波逆时偏移,避免了传统的多次波分离技术,提高了成像效率,成像分辨率也有所改善,这为改善多次波成像中串扰噪声问题提供了新的研究思路。针对多次波成像中噪声问题,本文从多次波成像条件入手,对成像中噪声产生的机制进行了详细研究,并根据其产生机制,创新性提出基于地震干涉的分阶多次波逆时偏移,对多次波成像中的噪声问题进行了改善。
3.1 多次波成像条件与噪声分析
类似于逆时偏移将震源波场和检波器波场同时外推进行成像的偏移方法的应用其实很多,逆时偏移主要基于双程波动方程,可以在盐丘等倾角比较陡的地方进行比较好的成像,并且可以有效处理多个初至波的地震波。为了将地下介质反射的多次波信息有效应用,多次波逆时偏移原理可以简述为将正向外推的同时含有一次波和多次波的地震记录和反向反推的多次波进行互相关处理。
多次波成像的基本原理可以表达为震源波场和检波点波场的零延时互相关:
(36) $\begin{aligned}\operatorname{Image}(x, y, z, t)= & \sum_{t=0}^{t_{\max }}\left\{P_{F}(x, y, z, t)+M_{F}(x, y, z, t)\right\} \\・& M_{B}(x, y, z, t)\end{aligned}$
式中:Image (x ,y ,z ,t )是点(x ,y ,z ,t )处的成像值;t max 是总记录时间。数据D (z 0 ,z 0 )分为一次波数据PF (x ,y ,z ,t )和多次波数据MF (x ,y ,z ,t ),D (z 0 ,z 0 )作为震源波场正向外推的同时,检波器接收的多次波波场MB (x ,y ,z ,t )反向外推。
表层多次波是指地震波经过地下介质的反射后返回地表,在自由地表又产生了向下的反射传播,又经过地下介质的反射向上传播到地表被检波器接收到的多次波。根据其在自由地表的反射次数,又可以将表层多次波分为不同阶层的多次波,因此它由各种不同阶的多次波组成:
(37) $\begin{aligned}M(x, y, z)= & M^{1}(x, y, z, t)+M^{2}(x, y, z, t)+ \\& M^{3}(x, y, z, t)+\cdots,\end{aligned},$
式中:M 1 (x ,y ,z ,t )、M 2 (x ,y ,z ,t )和M 3 (x ,y ,z ,t )分别表示为一阶、二阶和三阶多次波。因此式(36)可以写为:
(38) $\operatorname{Image}(x, y, z)=\sum_{t=0}^{t_{\max }}\left[\begin{array}{c}S_{F}(x, y, z, t) \\P_{F}(x, y, z, t) \\M_{F}^{1}(x, y, z, t) \\M_{F}^{2}(x, y, z, t) \\M_{F}^{3}(x, y, z, t) \\\vdots\end{array}\right] \cdot\left[\begin{array}{c}P_{B}(x, y, z, t) \\M_{B}^{1}(x, y, z, t) \\M_{B}^{2}(x, y, z, t) \\M_{B}^{3}(x, y, z, t) \\\vdots\end{array}\right]。$
当PF (x ,y ,z ,t )、${M}_{F}^{i}$ ( x ,y ,z ,t )和${M}_{B}^{i}$ ( x ,y ,z ,t )在地下介质中传播时,会产生上下行一次波和上下行多次波。将公式(38)进行扩展,得到式(39):
(39) $\begin{array}{c}\operatorname{Image}(x, y, z)=\sum_{t=0}^{t_{\max }}\left\{S _ { F } ( x, y, z, t ) \cdot \left[M_{B}^{1}(x, y, z, t)+\right.\right. \\\left.M_{B}^{2}(x, y, z, t)+M_{B}^{3}(x, y, z, t)+\cdots\right]+ \\P_{F}(x, y, z, t) \cdot\left[M_{B}^{1}(x, y, z, t)+M_{B}^{2}(x, y, z, t)+\right. \\\left.M_{B}^{3}(x, y, z, t)+\cdots\right]+ \\M_{F}^{1}(x, y, z, t) \cdot\left[M_{B}^{1}(x, y, z, t)+M_{B}^{2}(x, y, z, t)+\right. \\\left.M_{B}^{3}(x, y, z, t)+\cdots\right]+M_{F}^{2}(x, y, z, t) \cdot\left[M_{B}^{1}(x, y, z, t)+M_{B}^{2}(x, y, z, t)+\right. \\\left.M_{B}^{3}(x, y, z, t)+\cdots\right]+ \\M_{F}^{3}(x, y, z, t) \cdot\left[M_{B}^{1}(x, y, z, t)+M_{B}^{2}(x, y, z, t)+\right. \\\left.\left.M_{B}^{3}(x, y, z, t)+\cdots\right]+\cdots\right\},\end{array}$
(40) ${Image}_{(x,y,z)}=\sum _{t=0}^{{t}_{max}}\left[\begin{array}{l}{S}_{F}(x,y,z,t){P}_{B}(x,y,z,t)+\\ {P}_{F}(x,y,z,t){M}_{B}^{1}(x,y,z,t)+\\ {M}_{F}^{1}(x,y,z,t){M}_{B}^{2}(x,y,z,t)+\\ {M}_{F}^{2}(x,y,z,t){M}_{B}^{3}(x,y,z,t)+\dots \end{array}\right]+\sum _{t=0}^{{t}_{max}}\left[\begin{array}{l}{S}_{F}(x,y,z,t){M}_{B}^{1}(x,y,z,t)+\dots \\ {P}_{F}(x,y,z,t){M}_{B}^{2}(x,y,z,t)+\dots \\ +{M}_{F}^{1}(x,y,z,t){M}_{B}^{3}(x,y,z,t)+\dots \\ +{M}_{F}^{2}(x,y,z,t){M}_{B}^{4}(x,y,z,t)+\dots \end{array}\right]+\sum _{t=0}^{{t}_{max}}\left[\begin{array}{l}{P}_{F}(x,y,z,t){P}_{B}(x,y,z,t)+\\ {M}_{F}^{1}(x,y,z,t){M}_{B}^{1}(x,y,z,t)+\\ {M}_{F}^{2}(x,y,z,t){M}_{B}^{1}(x,y,z,t)+\\ {M}_{F}^{2}(x,y,z,t){M}_{B}^{2}(x,y,z,t)\\ {M}_{F}^{3}(x,y,z,t){M}_{B}^{1}(x,y,z,t)+\\ {M}_{F}^{3}(x,y,z,t){M}_{B}^{2}(x,y,z,t)+\\ {M}_{F}^{3}(x,y,z,t){M}_{B}^{3}(x,y,z,t)\dots \end{array}\right]$
在式(40)中,第一项是地下构造的成像,第二项是假象,第三项不产生任何图像。下面对式(40)中的3个中括号进行详细阐述。第一个中括号表示震源波场能量正向外推与检波点波场逆向外推进行互相关后的成像值,包括脉冲震源和一次波SF ·PB 互相关得到的一次波成像结果,一次波和一阶多次波PF ·${M}_{B}^{1}$ ${M}_{F}^{1}$ ${M}_{B}^{2}$ n 阶多次波与n +1阶多次波做互相关成像;第1个中括号代表的是地层处的反射能量,具有物理意义。第2个中括号代表的是非地层处的反射能量,没有实际物理意义。所以会在非反射层深度产生成像,这也是在图像处理过程中需要解决的问题,这部分能量在公式中表现为脉冲震源和一次波SF ·${M}_{B}^{1}$ PF ·${M}_{B}^{2}$ ${M}_{F}^{1}$ ${M}_{B}^{3}$
经过上述对多次波成像过程串扰噪声产生的分析,理论推导发现不同阶多次波分别进行互相关运算后再求和,即可得到不含串扰噪声的成像结果。为了压制多次波成像过程中由于不相干同相轴进行互相关成像所导致的串扰噪声,本文提出利用地震干涉理论对多次波进行预测,预测出的多次波用于后续的分阶多次波成像处理,有效地解决了多次波成像过程中由于不同阶多次波互相关导致的串扰噪声问题。
3.2 基于地震干涉的分阶多次波逆时偏移
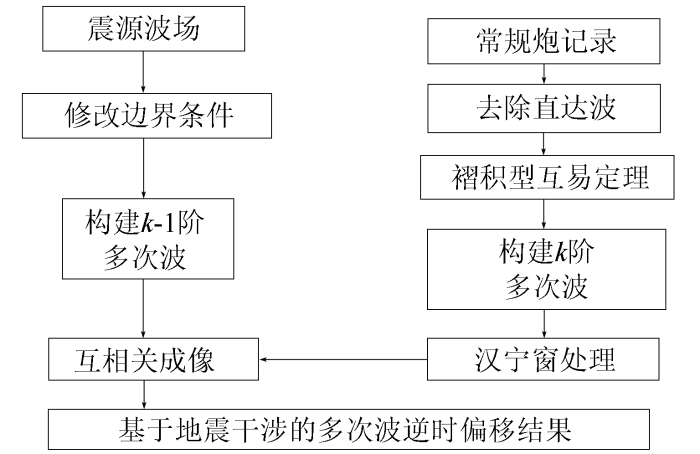
多次波逆时偏移的成像原理是进行波场的正向延拓以及反向延拓,然后将两者互相关得到成像结果。只有地震记录的k -1阶多次波和k 阶多次波互相关才能成像。多次波分阶逆时偏移的步骤如图7 所示。
图7
图7
多次波分阶逆时偏移步骤
Fig.7
Steps for order-separated reverse time migration of multiples
1)自由地表边界原始炮记录得到的是一次波和多次波的混合波,本文方法使用地表吸收边界原始炮记录只得到一次波进行后续的处理操作;
2)基于一次波记录,应用褶积型地震干涉预测一阶多次波,在预测一阶多次波的基础上预测二阶多次波,依此类推出N 阶多次波;
3)以零阶多次波和一阶多次波为基础,作为正向波场和反向波场进行偏移计算,得到一阶多次波逆时偏移成像剖面;
4)分别用k -1阶多次波和k 阶多次波作为正向波场和反向波场进行偏移计算,直到k =N ,即可得到各阶多次波逆时偏移成像剖面。
分阶多次波逆时偏移的公式以及各阶多次波的成像条件可表示为:
(41) $\begin{array}{c}\text { Image }(x, z, t)=M_{F}^{m}(x, z, t) * M_{B}^{m}(x, z, t), \\(1 \leqslant m \leqslant N),\end{array}$
3.3 模型试算
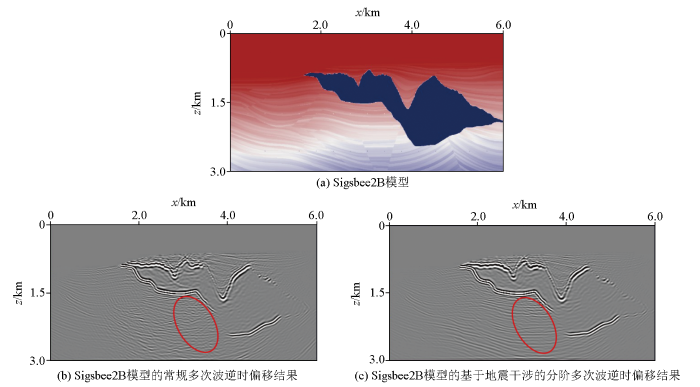
Sigsbee2B模型网格个数为601×301,纵、横向网格步长均为10 m,采样间隔为0.5 ms,总记录时间为4 s。本次模拟震源采用主频为30 Hz的雷克子波,总共201炮,炮间隔30 m,检波器为全接收排列,每个检波器间隔10 m。图8 分别展示了Sigsbee2B模型、常规多次波逆时偏移结果以及本文使用的基于地震干涉的分阶多次波逆时偏移成像结果,发现基于地震干涉的分阶多次波逆时偏移能够对盐下的复杂构造进行比较好的成像。与之前一次波逆时偏移成果和常规多次波逆时偏移结果相比,盐下构造分辨率更高(图中红框区域),并且对于多次波成像中的串扰噪声问题进行了有效的改善,对于实际生产具有重大意义。
图8
图8
基于Sigsbee2B模型的多次波逆时偏移结果对比
Fig.8
Comparison of reverse time migration results for multiples based on the Sigsbee2B model
基于地震干涉的分阶多次波逆时偏移的成像结果如图8c 所示,对比Sigsbee2B模型的一次波逆时偏移、常规多次波逆时偏移成像结果可知:一次波成像在地下层面的分界处、盐丘下断层处以及散射点的成像优于多次波成像,这是由于多次波成像本身的互相关成像带来的不可避免的串扰噪声导致;而对于一次波照明成像效果不佳的盐丘边界、盐下等区域,多次波成像则能够发挥多次波传播路径长、反射角小的优势,对Sigsbee2B模型盐丘上部凹陷和盐丘2 000~2 500 m处的边界进行比较好的成像。
3.4 实际资料应用
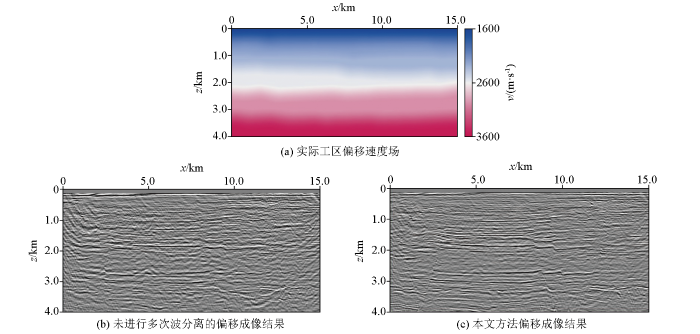
实测资料来自工区A,该工区长15 km,深4 km。偏移速度场如图9a 所示,传统未进行多次波分离的偏移成像结果如图9b 所示,本文基于干涉理论多次波分离的偏移成像结果如图9c 所示。与传统一次波逆时偏移结果作对比,发现本文方法的多次波逆时偏移结果清晰,地下构造刻画效果更好,分辨率更高。
图9
图9
实际工区偏移结果对比
Fig.9
Comparison of migration results of the actual work area
4 结论
本文系统性地研究了基于地震干涉的分阶多次波逆时偏移技术,并通过理论推导、数值模拟以及实际数据测试,证明了其在复杂地下构造成像中的显著优势。总结如下:
1)利用地震干涉理论直接预测多次波,并基于分阶思想将多次波逆时偏移成像逐步推广,实现了多次波成像精度和计算效率的显著提高,避免了传统方法中对多次波进行压制和分离的繁琐步骤。
2)基于地震干涉的分阶多次波逆时偏移方法,通过分阶处理不同阶次的多次波,实现了对成像中串扰噪声的有效压制,进一步提高了成像分辨率和盐下构造的成像效果。
3)在层状模型、非层状模型以及国际标准Sigsbee2B模型中均验证了本文方法的有效性和优越性,尤其是在复杂盐丘和高陡构造的成像中,能够显著改善传统一次波和多次波成像结果。
4)在中国某实际工区的应用中,本文方法的成像效果优于传统一次波逆时偏移结果,展现了其在实际油气勘探中的重要潜力,为复杂地下构造的准确成像提供了重要的技术支持。
综上所述,基于地震干涉的分阶多次波逆时偏移方法为复杂地下构造的地震成像提供了新的解决途径,通过充分挖掘多次波的成像潜力,该方法不仅显著提高了成像分辨率,还在抑制成像噪声、优化计算效率方面表现出卓越的优势。未来,可进一步结合人工智能和大规模计算技术,推动该方法在更多复杂场景中的应用与推广,为油气勘探及地质构造研究提供更强有力的技术支撑。
附录A
(A 1) $\left(\nabla^{2}+k^{2}\right) G(x \mid A, \omega)=-\delta(x-A),$
(A 2) $\left(\nabla^{2}+k_{0}^{2}\right) G_{0}(x \mid B, \omega)=-\delta(x-B),$
式中:波数k =ω/v (x ),k 0 =ω/v 0 (x ),x ∈V ;由于介质是各向同性速度均匀的,所以如果A 、B 在介质内部,那么v (x )=v 0 (x ),在外部,则v (x )≠v 0 (x )。
将式(A1)左右两侧同时乘以G 0 (x |B ,ω ),式(A2)左右两侧同时乘以G (x |A ,ω )后相减,可得:
(A 3) $\begin{array}{c}G_{0}(x \mid B, \omega) \nabla^{2} G(x \mid A, \omega)-G(x \mid A, \omega) \cdot \\\nabla^{2} G_{0}(x \mid B, \omega)=G(x \mid A, \omega) \delta(x-B)- \\G_{0}(x \mid B, \omega) \delta(x-A)=G(B \mid A, \omega)- \\G_{0}(A \mid B, \omega)。\end{array}$
(A 4) $\begin{array}{c}G(x \mid A, \omega) \nabla^{2} G_{0}(x \mid B, \omega)=\nabla \cdot[G(x \mid A, \omega) \cdot \\\left.\nabla G_{0}(x \mid B, \omega)\right]-\nabla G(x \mid A, \omega) \cdot \\\nabla G_{0}(x \mid B, \omega),\end{array}$
(A 5) $\begin{array}{c}G_{0}(x \mid B, \omega) \nabla^{2} G(x \mid A, \omega)=\nabla \cdot\left[G_{0}(x \mid B, \omega) \cdot\right. \\\nabla G(x \mid A, \omega)]-\nabla G_{0}(x \mid B, \omega) \cdot \\\nabla G(x \mid A, \omega)。\end{array}$
式(A4)和式(A5)的右端都含有ÑG 0 (x |B ,ω )·ÑG (x |A ,ω )。将式(A4)和式(A5)代入式(A3),可得:
(A 6) $\begin{array}{c}G(B \mid A, \omega)-G_{0}(A \mid B, \omega)=\nabla \cdot\left[G_{0}(x \mid B, \omega) \cdot\right. \\\nabla G(x \mid A, \omega)]-\nabla \cdot[G(x \mid A, \omega) \\\left.\nabla G_{0}(x \mid B, \omega)\right]。\end{array}$
(A 7) $\int_{V} \nabla^{2} f(x) \mathrm{d} x^{3}=\int_{S} \nabla f(x) \cdot \hat{n} \mathrm{~d} x^{2},$
(A 8) $\begin{array}{c}G(B \mid A, \omega)-G_{0}(A \mid B, \omega)=\int_{S}\left[G_{0}(x \mid B, \omega) \cdot\right. \\\nabla G(x \mid A, \omega) \cdot \hat{n}-G(x \mid A, \omega)· \\\left.\nabla G_{0}(x \mid B, \omega) \hat{n}\right] \mathrm{d}^{2} x,\end{array}$
式中:$\hat{n}$ S 边界的单位外法向量。
(A 9) $\frac{\partial G_{0}(x \mid B, \omega)}{\partial n_{x}}=\hat{n} \cdot \nabla G_{0}(x \mid B, \omega) ;$
(A 10) $\frac{\partial G(x \mid A, \omega)}{\partial n_{x}}=\hat{n} \cdot \nabla G(x \mid A, \omega)。$
(A 11) $\begin{array}{l}G(B \mid A, \omega)-G_{0}(A \mid B, \omega)=\int_{S}\left[G_{0}(x \mid B, \omega) \cdot\right. \\\left.\frac{\partial G(x \mid A, \omega)}{\partial n_{x}}-G(x \mid A, \omega) \frac{\partial G_{0}(x \mid B, \omega)}{\partial n_{x}}\right] \mathrm{d}^{2} x 。\end{array}$
参考文献
View Option
[1]
Whitmore N D Iterative depth migration by backward time propagation
[C]// SEG Technical Program Expanded Abstracts 1983 , Society of Exploration Geophysicists ,1983:382 -385 .
[本文引用: 1]
[2]
刘伊克 , 常旭 , 王辉 , 等 . 波路径偏移压制层间多次波的理论与应用
[J]. 地球物理学报 , 2008 , 51 (2 ):589 -595 .
[本文引用: 1]
Liu Y K Chang X Wang H et al . Internal multiple removal and its application by wavepath migration
[J]. Chinese Journal of Geophysics , 2008 , 51 (2 ):589 -595 .
[本文引用: 1]
[3]
郭书娟 , 李振春 , 仝兆岐 , 等 . 基于广义的炮偏移方法实现地表多次波和一次波联合成像
[J]. 地球物理学报 , 2011 , 54 (4 ):1098 -1105 .
[本文引用: 1]
Guo S J Li Z C Tong Z Q et al . Joint imaging of primaries and surface-related multiples based on generalized shot-profile migration
[J]. Chinese Journal of Geophysics , 2011 , 54 (4 ):1098 -1105 .
[本文引用: 1]
[4]
Wang Y B Chang X Hu H Simultaneous reverse time migration of primaries and free-surface related multiples without multiple prediction
[J]. Geophysics , 2014 , 79 (1 ):S1-S9.
[本文引用: 1]
[5]
Li Z N Li Z C Wang P et al . Multiple attenuation using λ-f domain high-resolution Radon transform
[J]. Applied Geophysics , 2013 , 10 (4 ):433 -441 .
[本文引用: 1]
[6]
Wang Y B Zheng Y K Zhang L L et al . Reverse time migration of multiples:Eliminating migration artifacts in angle domain common image gathers
[J]. Geophysics , 2014 , 79 (6 ):S263-S270.
[本文引用: 1]
[7]
宋鹏 , 朱博 , 李金山 , 等 . 多次波分阶逆时偏移成像
[J]. 地球物理学报 , 2015 , 58 (10 ):3791 -3803 .
DOI:10.6038/cjg20151029
[本文引用: 1]
本文深入分析了多次波逆时偏移的成像原理和串扰假象产生机制,并提出了多次波分阶逆时偏移策略,即首先应用自由界面多次波衰减方法对原始炮集记录中的多次波进行剔除得到一次波记录,然后应用一次波记录预测获得各阶多次波记录,最后将各阶多次波记录分别进行逆时偏移成像.模型实验结果表明,多次波分阶逆时偏移其各阶多次波成像剖面均可对真实界面正确成像且其能够有效压制串扰假象,其中一阶多次波逆时偏移剖面的成像精度最高,其深层成像质量明显优于常规多次波逆时偏移.
Song P Zhu B Li J S et al . Reverse time migration of divided-order multiples
[J]. Chinese Journal of Geophysics , 2015 , 58 (10 ):3791 -3803 .
[本文引用: 1]
[8]
朱博 , 宋鹏 , 李金山 , 等 . 基于多卡GPU集群的多次波逆时偏移成像技术
[J]. 油气地质与采收率 , 2015 , 22 (2 ):60 -65 .
[本文引用: 1]
Zhu B Song P Li J S et al . Reverse time migration of multiples based on the acceleration of multi-card GPU
[J]. Petroleum Geology and Recovery Efficiency , 2015 , 22 (2 ):60 -65 .
[本文引用: 1]
[9]
Berkhout G A J Review paper:An outlook on the future of seismic imaging,part II:Full-wavefield migration
[J]. Geophysical Prospecting , 2014 , 62 (5 ):931 -949 .
[本文引用: 1]
[10]
刘学建 , 刘伊克 . 表面多次波最小二乘逆时偏移成像
[J]. 地球物理学报 , 2016 , 59 (9 ):3354 -3365 .
DOI:10.6038/cjg20160919
[本文引用: 1]
使用相同的炮记录,多次波偏移能提供比反射波偏移更广的地下照明和更多的地下覆盖但是同时产生很多的串声噪声.相比传统逆时偏移,最小二乘逆时偏移反演的反射波成像结果具有更高的分辨率和更均衡的振幅.我们主要利用最小二乘逆时偏移压制多次波偏移产生的串声噪声.多次波最小二乘逆时偏移通常需要一定的迭代次数以较好地消除串声噪声.若提前将一阶多次波从所有阶数的多次波中过滤出来,使用相同的迭代次数,一阶多次波的最小二乘逆时偏移能够得到具有更高信噪比的成像剖面,而且能够提供与多次波最小二乘逆时偏移相似的有效地下结构成像.
Liu X J Liu Y K Least-squares reverse-time migration of surface-related multiples
[J]. Chinese Journal of Geophysics , 2016 , 59 (9 ):3354 -3365 .
[本文引用: 1]
[11]
Li Z N Li Z C Wang P et al . Reverse time migration of multiples based on different-order multiple separation
[J]. Geophysics , 2017 , 82 (1 ):S19-S29.
[本文引用: 1]
[12]
刘伊克 , 刘学建 , 张延保 . 地震多次波成像
[J]. 地球物理学报 , 2018 , 61 (3 ):1025 -1037 .
DOI:10.6038/cjg2018L0368
[本文引用: 1]
地震资料含有各种类型多次波,而传统成像方法仅利用地震一次反射波成像,在地震成像前需将多次波去除.然而,多次波携带了丰富的地下结构信息,多次波偏移能够提供除反射波外的额外地下照明.修改传统逆时偏移方法,用包含一次反射波和多次波的原始记录代替震源子波,将SRME方法预测的表面多次波代替一次反射波作为输入数据,可将表面多次波成像.多次波成像的挑战和困难在于大量串扰噪声的产生,针对表面多次波成像中的成像噪声问题,将最小二乘逆时偏移方法与多次波分阶思想结合起来,发展可控阶数的表面多次波反演成像方法,有望初步实现高精度的表面多次波成像.在消除原始记录中的表面多次波后,通过逆散射级数方法预测得到层间多次波,将层间多次波作为逆时偏移方法的输入数据可将其准确归位到地下反射位置.数值实验表明,多次波成像能够有效地为地下提供额外照明,而可控阶表面多次波最小二乘逆时偏移成像方法几乎完全避免成像噪声.
Liu Y K Liu X J Zhang Y B Migration of seismic multiple reflections
[J]. Chinese Journal of Geophysics , 2018 , 61 (3 ):1025 -1037 .
[本文引用: 1]
[13]
黄建东 , 胡天跃 , 王尚旭 . 层间多次波傅里叶有限差分偏移成像
[J]. 地球物理学报 , 2022 , 65 (11 ):4394 -4403 .
[本文引用: 1]
Huang J D Hu T Y Wang S X Fourier finite-difference migration of internal multiples
[J]. Chinese Journal of Geophysics , 2022 , 65 (11 ):4394 -4403 .
[本文引用: 1]
[14]
Claerbout J F Synthesis of a layered medium from its acoustic transmission response
[J]. Geophysics , 1968 , 33 (2 ):264 -269 .
[本文引用: 1]
[15]
Schuster G T Theory of daylight/interferometric imaging-tutorial
[C]// 63rd EAGE Conference & Exhibition . Amsterdam , Netherlands,European Association of Geoscientists & Engineers , 2001 .
[本文引用: 1]
[16]
Wapenaar K Draganov D Thorbecke J et al . Theory of acoustic daylight imaging revisited
[C]// SEG Technical Program Expanded Abstracts 2002 , Society of Exploration Geophysicists ,2002:2269 -2272 .
[本文引用: 1]
[17]
Sheng J M Migrating multiples and primaries in CDP data by crosscorrelogram migration
[C]// SEG Technical Program Expanded Abstracts 2001 , Society of Exploration Geophysicists ,2001:1297 -1300 .
[本文引用: 1]
[18]
Snieder R Grêt A Douma H et al . Coda wave interferometry for estimating nonlinear behavior in seismic velocity
[J]. Science , 2002 , 295 (5563 ):2253 -2255 .
PMID:11910107
[本文引用: 1]
In coda wave interferometry, one records multiply scattered waves at a limited number of receivers to infer changes in the medium over time. With this technique, we have determined the nonlinear dependence of the seismic velocity in granite on temperature and the associated acoustic emissions. This technique can be used in warning mode, to detect the presence of temporal changes in the medium, or in diagnostic mode, where the temporal change in the medium is quantified.
[19]
Snieder R Extracting the Green's function of attenuating heterogeneous acoustic media from uncorrelated waves
[J]. The Journal of the Acoustical Society of America , 2007 , 121 (5 Pt1 ):2637 -2643 .
[本文引用: 1]
[20]
Wapenaar K van der Neut J Ruigrok E Passive seismic interferometry by multidimensional deconvolution
[J]. Geophysics , 2008 , 73 (6 ):A51-A56.
[本文引用: 1]
[21]
Calvert R W Bakulin A Jones T C Virtual sources,a new way to remove overburden problems
[C]// 66th EAGE Conference & Exhibition . Paris,France , European Association of Geoscientists & Engineers , 2004 .
[本文引用: 1]
[22]
Mehta K Bakulin A Sheiman J et al . Improving the virtual source method by wavefield separation
[J]. Geophysics , 2007 , 72 (4 ):V79-V86.
[本文引用: 1]
[23]
Gaiser J E Vasconcelos I Elastic interferometry for ocean bottom cable data:Theory and examples
[J]. Geophysical Prospecting , 2010 , 58 (3 ):347 -360 .
[本文引用: 1]
[24]
Bharadwaj P Schuster G Mallinson I et al . Theory of supervirtual refraction interferometry
[J]. Geophysical Journal International , 2012 , 188 (1 ):263 -273 .
[本文引用: 1]
[25]
Wapenaar K Thorbecke J van der Neut J et al . Green's function retrieval from reflection data,in absence of a receiver at the virtual source position
[J]. The Journal of the Acoustical Society of America , 2014 , 135 (5 ):2847 -2861 .
[本文引用: 1]
[26]
齐诚 , 陈棋福 , 陈颙 . 利用背景噪声进行地震成像的新方法
[J]. 地球物理学进展 , 2007 , 22 (3 ):771 -777 .
[本文引用: 1]
Qi C Chen Q F Chen Y A new method for seismic imaging from ambient seismic noise
[J]. Progress in Geophysics , 2007 , 22 (3 ):771 -777 .
[本文引用: 1]
[27]
王宝善 , 葛洪魁 , 袁松湧 , 等 . 地下介质波速变化的主动和被动源监测
[C]// 中国地球物理学会第二十五届年会 ,2009:773.
[本文引用: 1]
Wang B S Ge H K Yuan S Y et al . Monitoring subsurface velocity variations with active and passive sources
[C]// The 25th Annual Meeting of the Chinese Geophysical Society ,2009:773.
[本文引用: 1]
[28]
陶毅 , 符力耘 , 孙伟家 , 等 . 地震波干涉法研究进展综述
[J]. 地球物理学进展 , 2010 , 25 (5 ):1775 -1784 .
[本文引用: 1]
Tao Y Fu L Y Sun W J et al . A review of seismic interferometry
[J]. Progress in Geophysics , 2010 , 25 (5 ):1775 -1784 .
[本文引用: 1]
[29]
朱恒 , 王德利 , 时志安 , 等 . 地震干涉技术被动源地震成像
[J]. 地球物理学进展 , 2012 , 27 (2 ):496 -502 .
[本文引用: 1]
Zhu H Wang D L Shi Z A et al . Passive seismic imaging of seismic interferometry
[J]. Progress in Geophysics , 2012 , 27 (2 ):496 -502 .
[本文引用: 1]
[30]
朱恒 , 王德利 . 抛物Radon域地震干涉技术
[J]. 世界地质 , 2015 , 34 (2 ):484 -490 .
[本文引用: 1]
Zhu H Wang D L Seismic interferometry in parabolic radon domain
[J]. Global Geology , 2015 , 34 (2 ):484 -490 .
[本文引用: 1]
[31]
程浩 . 被动源数据地震波干涉一次波估计方法研究 [D]. 长春 : 吉林大学 , 2016 .
[本文引用: 1]
Cheng H Study on primary wave estimation method of seismic wave interference from passive source data [D]. Changchun : Jilin University , 2016 .
[本文引用: 1]
[32]
孙宇 . 线性Radon域地震干涉层间多次波压制 [D]. 长春 : 吉林大学 , 2018 .
[本文引用: 1]
Sun Y Internal multiple suppression based on seismic interferometry in linear Radon domain [D]. Changchun : Jilin University , 2018 .
[本文引用: 1]
[33]
王立歆 , 陈国金 , 崔树果 , 等 . 基于地震干涉法的可控震源黑三角噪声压制技术及应用
[J]. 石油物探 , 2021 , 60 (6 ):925 -936 .
DOI:10.3969/j.issn.1000-1441.2021.06.006
[本文引用: 1]
沙漠区可控震源资料通常存在严重的高能量黑三角噪声,应用常规的转换域滤波或基于Born近似的迭代反演预测-消除方法进行去噪时,效果不理想。利用新疆某工区可控震源资料,定性分析了黑三角噪声的形成机理,主要由散射面波和可控震源与地表之间的谐振形成。针对黑三角区内的散射面波消除问题,基于炮-检地震干涉及模式的匹配相减方法,研发了可控震源散射面波干涉预测与匹配相减技术,其特点是实测地震资料驱动,无需速度模型;同时,将该技术与用于压制如谐振等不规则强噪声的异常噪声压制技术相结合,形成了可控震源黑三角综合去噪方法技术。以新疆某工区可控震源地震资料为测试资料,对比了该综合去噪技术与某商业软件的应用结果,表明该综合去噪技术能有效消除黑三角区内的强能量噪声,尤其是有效压制了散射面波,显著改善了叠前时间偏移结果,进而恢复地层真实反射特征,断裂和断溶体成像效果优于某商业软件。
Wang L X Chen G J Cui S G et al . Suppression of “black triangle” noise from vibroseis data
[J]. Geophysical Prospecting for Petroleum , 2021 , 60 (6 ):925 -936 .
[本文引用: 1]
[34]
阮小敏 , 陈明春 , 刘振东 , 等 . 被动源反射地震勘探研究进展
[J]. 地球与行星物理论评 , 2023 , 54 (2 ):150 -173 .
[本文引用: 1]
Ruan X M Chen M C Liu Z D et al . Review of progress in passive seismic reflection exploration
[J]. Reviews of Geophysics and Planetary Physics , 2023 , 54 (2 ):150 -173 .
[本文引用: 1]
[35]
de Hoop A T An elastodynamic reciprocity theorem for linear,viscoelastic media
[J]. Applied Scientific Research , 1966 , 16 (1 ):39 -45 .
[本文引用: 1]
[36]
Fink M Time-reversed acoustics
[J]. Scientific American , 1999 , 281 (5 ):91 -97 .
[本文引用: 1]
[37]
Wapenaar K Ruigrok E van der Neut J et al . Green's function representation for seismic interferometry by deconvolution
[C]// SEG Technical Program Expanded Abstracts 2010 , Society of Exploration Geophysicists ,2010:3972 -3978 .
[本文引用: 1]
[38]
刘琦 . 基于反射、散射波场分离的多次波消除方法研究 [D]. 长春 : 吉林大学 , 2009 .
[本文引用: 1]
Liu Q Research on multiple cancellation method based on separation of reflected and scattered wave fields [D]. Changchun : Jilin University , 2009 .
[本文引用: 1]
Iterative depth migration by backward time propagation
1
... 逆时偏移主要用于盐丘等高陡构造以及横向速度剧烈变化的地区.该技术基于双程波动方程,最早由Whitmore于1949年提出[1 ] .国内对多次波逆时偏移也有许多研究:2008年,刘伊克等[2 ] 在成像域成功压制表层多次波与层间多次波,发现多次波含有丰富的小角度信息,能够提供更广的成像范围.2011年,郭书娟等[3 ] 实现了一次波和表层多次波联合成像,将含有多次波和震源脉冲的炮记录作为震源波场,压制了常规多次波成像噪声.Wang等[4 ] 改变传统做法,将含有一次波和多次波的地震数据记录作为震源波场和检波波场,提高了成像分辨率,但不恰当的子波选择可能导致信息覆盖.2013年,Li等[5 ] 提出了基于SRME和聚焦变换的一次波和各阶表层多次波分离方法.2014年,Wang等[6 ] 将一次波和表面多次波分别作为震源波场和检波波场,通过互相关成像,并创新性引入共角度域成像点道集,有效改善了多次波逆时偏移中的噪声问题.该方法不需要对多次波进行预测,可以进行浅层目标的成像,但会在成像区域内产生广泛且能量较强的串扰噪声,这是由于逆时偏移成像机制中需要对震源波场正传和检波波场反传后进行互相关运算所导致,该问题一直是多次波成像领域研究的重点.2015年,宋鹏等[7 ] 分析了多次波成像过程中的串扰噪声机制,创新性地应用SRME理论进行多次波分阶逆时偏移,有效压制了串扰噪声问题.2015年,朱博等[8 ] 引入多卡GPU集群加速技术,显著提高了多次波成像的计算效率.同年,Berkhout[9 ] 提出全波场偏移算法,将全波数据视为地震数据,并利用伴随方法实现了层间多次波的成像;2016年,刘学建等[10 ] 将逆散射级数方法预测的层间多次波当作逆时偏移的反传数据,并结合波场分离实现了层间多次波的偏移.2017年,Li等[11 ] 提出基于SRME与聚焦变换的分阶多次波逆时偏移,进一步压制串扰噪声并提高成像分辨率.然而,多次波成像中仍存在不相干同相轴噪声的问题,有待进一步研究.2018年,刘伊克等[12 ] 结合多次波成像与分阶思想,提出可控阶多次波成像算法:在成像前将不同阶数多次波提取出来,并将n 阶、n +1阶多次波分别当作虚震源与地震记录,应用成像条件获取n +1阶多次波的成像结果,随后叠加各阶多次波成像结果获取最终偏移结果.2022年黄建东等[13 ] 对单程波偏移方法进行了拓展,提出层间多次波傅里叶有限差分偏移. ...
波路径偏移压制层间多次波的理论与应用
1
2008
... 逆时偏移主要用于盐丘等高陡构造以及横向速度剧烈变化的地区.该技术基于双程波动方程,最早由Whitmore于1949年提出[1 ] .国内对多次波逆时偏移也有许多研究:2008年,刘伊克等[2 ] 在成像域成功压制表层多次波与层间多次波,发现多次波含有丰富的小角度信息,能够提供更广的成像范围.2011年,郭书娟等[3 ] 实现了一次波和表层多次波联合成像,将含有多次波和震源脉冲的炮记录作为震源波场,压制了常规多次波成像噪声.Wang等[4 ] 改变传统做法,将含有一次波和多次波的地震数据记录作为震源波场和检波波场,提高了成像分辨率,但不恰当的子波选择可能导致信息覆盖.2013年,Li等[5 ] 提出了基于SRME和聚焦变换的一次波和各阶表层多次波分离方法.2014年,Wang等[6 ] 将一次波和表面多次波分别作为震源波场和检波波场,通过互相关成像,并创新性引入共角度域成像点道集,有效改善了多次波逆时偏移中的噪声问题.该方法不需要对多次波进行预测,可以进行浅层目标的成像,但会在成像区域内产生广泛且能量较强的串扰噪声,这是由于逆时偏移成像机制中需要对震源波场正传和检波波场反传后进行互相关运算所导致,该问题一直是多次波成像领域研究的重点.2015年,宋鹏等[7 ] 分析了多次波成像过程中的串扰噪声机制,创新性地应用SRME理论进行多次波分阶逆时偏移,有效压制了串扰噪声问题.2015年,朱博等[8 ] 引入多卡GPU集群加速技术,显著提高了多次波成像的计算效率.同年,Berkhout[9 ] 提出全波场偏移算法,将全波数据视为地震数据,并利用伴随方法实现了层间多次波的成像;2016年,刘学建等[10 ] 将逆散射级数方法预测的层间多次波当作逆时偏移的反传数据,并结合波场分离实现了层间多次波的偏移.2017年,Li等[11 ] 提出基于SRME与聚焦变换的分阶多次波逆时偏移,进一步压制串扰噪声并提高成像分辨率.然而,多次波成像中仍存在不相干同相轴噪声的问题,有待进一步研究.2018年,刘伊克等[12 ] 结合多次波成像与分阶思想,提出可控阶多次波成像算法:在成像前将不同阶数多次波提取出来,并将n 阶、n +1阶多次波分别当作虚震源与地震记录,应用成像条件获取n +1阶多次波的成像结果,随后叠加各阶多次波成像结果获取最终偏移结果.2022年黄建东等[13 ] 对单程波偏移方法进行了拓展,提出层间多次波傅里叶有限差分偏移. ...
波路径偏移压制层间多次波的理论与应用
1
2008
... 逆时偏移主要用于盐丘等高陡构造以及横向速度剧烈变化的地区.该技术基于双程波动方程,最早由Whitmore于1949年提出[1 ] .国内对多次波逆时偏移也有许多研究:2008年,刘伊克等[2 ] 在成像域成功压制表层多次波与层间多次波,发现多次波含有丰富的小角度信息,能够提供更广的成像范围.2011年,郭书娟等[3 ] 实现了一次波和表层多次波联合成像,将含有多次波和震源脉冲的炮记录作为震源波场,压制了常规多次波成像噪声.Wang等[4 ] 改变传统做法,将含有一次波和多次波的地震数据记录作为震源波场和检波波场,提高了成像分辨率,但不恰当的子波选择可能导致信息覆盖.2013年,Li等[5 ] 提出了基于SRME和聚焦变换的一次波和各阶表层多次波分离方法.2014年,Wang等[6 ] 将一次波和表面多次波分别作为震源波场和检波波场,通过互相关成像,并创新性引入共角度域成像点道集,有效改善了多次波逆时偏移中的噪声问题.该方法不需要对多次波进行预测,可以进行浅层目标的成像,但会在成像区域内产生广泛且能量较强的串扰噪声,这是由于逆时偏移成像机制中需要对震源波场正传和检波波场反传后进行互相关运算所导致,该问题一直是多次波成像领域研究的重点.2015年,宋鹏等[7 ] 分析了多次波成像过程中的串扰噪声机制,创新性地应用SRME理论进行多次波分阶逆时偏移,有效压制了串扰噪声问题.2015年,朱博等[8 ] 引入多卡GPU集群加速技术,显著提高了多次波成像的计算效率.同年,Berkhout[9 ] 提出全波场偏移算法,将全波数据视为地震数据,并利用伴随方法实现了层间多次波的成像;2016年,刘学建等[10 ] 将逆散射级数方法预测的层间多次波当作逆时偏移的反传数据,并结合波场分离实现了层间多次波的偏移.2017年,Li等[11 ] 提出基于SRME与聚焦变换的分阶多次波逆时偏移,进一步压制串扰噪声并提高成像分辨率.然而,多次波成像中仍存在不相干同相轴噪声的问题,有待进一步研究.2018年,刘伊克等[12 ] 结合多次波成像与分阶思想,提出可控阶多次波成像算法:在成像前将不同阶数多次波提取出来,并将n 阶、n +1阶多次波分别当作虚震源与地震记录,应用成像条件获取n +1阶多次波的成像结果,随后叠加各阶多次波成像结果获取最终偏移结果.2022年黄建东等[13 ] 对单程波偏移方法进行了拓展,提出层间多次波傅里叶有限差分偏移. ...
基于广义的炮偏移方法实现地表多次波和一次波联合成像
1
2011
... 逆时偏移主要用于盐丘等高陡构造以及横向速度剧烈变化的地区.该技术基于双程波动方程,最早由Whitmore于1949年提出[1 ] .国内对多次波逆时偏移也有许多研究:2008年,刘伊克等[2 ] 在成像域成功压制表层多次波与层间多次波,发现多次波含有丰富的小角度信息,能够提供更广的成像范围.2011年,郭书娟等[3 ] 实现了一次波和表层多次波联合成像,将含有多次波和震源脉冲的炮记录作为震源波场,压制了常规多次波成像噪声.Wang等[4 ] 改变传统做法,将含有一次波和多次波的地震数据记录作为震源波场和检波波场,提高了成像分辨率,但不恰当的子波选择可能导致信息覆盖.2013年,Li等[5 ] 提出了基于SRME和聚焦变换的一次波和各阶表层多次波分离方法.2014年,Wang等[6 ] 将一次波和表面多次波分别作为震源波场和检波波场,通过互相关成像,并创新性引入共角度域成像点道集,有效改善了多次波逆时偏移中的噪声问题.该方法不需要对多次波进行预测,可以进行浅层目标的成像,但会在成像区域内产生广泛且能量较强的串扰噪声,这是由于逆时偏移成像机制中需要对震源波场正传和检波波场反传后进行互相关运算所导致,该问题一直是多次波成像领域研究的重点.2015年,宋鹏等[7 ] 分析了多次波成像过程中的串扰噪声机制,创新性地应用SRME理论进行多次波分阶逆时偏移,有效压制了串扰噪声问题.2015年,朱博等[8 ] 引入多卡GPU集群加速技术,显著提高了多次波成像的计算效率.同年,Berkhout[9 ] 提出全波场偏移算法,将全波数据视为地震数据,并利用伴随方法实现了层间多次波的成像;2016年,刘学建等[10 ] 将逆散射级数方法预测的层间多次波当作逆时偏移的反传数据,并结合波场分离实现了层间多次波的偏移.2017年,Li等[11 ] 提出基于SRME与聚焦变换的分阶多次波逆时偏移,进一步压制串扰噪声并提高成像分辨率.然而,多次波成像中仍存在不相干同相轴噪声的问题,有待进一步研究.2018年,刘伊克等[12 ] 结合多次波成像与分阶思想,提出可控阶多次波成像算法:在成像前将不同阶数多次波提取出来,并将n 阶、n +1阶多次波分别当作虚震源与地震记录,应用成像条件获取n +1阶多次波的成像结果,随后叠加各阶多次波成像结果获取最终偏移结果.2022年黄建东等[13 ] 对单程波偏移方法进行了拓展,提出层间多次波傅里叶有限差分偏移. ...
基于广义的炮偏移方法实现地表多次波和一次波联合成像
1
2011
... 逆时偏移主要用于盐丘等高陡构造以及横向速度剧烈变化的地区.该技术基于双程波动方程,最早由Whitmore于1949年提出[1 ] .国内对多次波逆时偏移也有许多研究:2008年,刘伊克等[2 ] 在成像域成功压制表层多次波与层间多次波,发现多次波含有丰富的小角度信息,能够提供更广的成像范围.2011年,郭书娟等[3 ] 实现了一次波和表层多次波联合成像,将含有多次波和震源脉冲的炮记录作为震源波场,压制了常规多次波成像噪声.Wang等[4 ] 改变传统做法,将含有一次波和多次波的地震数据记录作为震源波场和检波波场,提高了成像分辨率,但不恰当的子波选择可能导致信息覆盖.2013年,Li等[5 ] 提出了基于SRME和聚焦变换的一次波和各阶表层多次波分离方法.2014年,Wang等[6 ] 将一次波和表面多次波分别作为震源波场和检波波场,通过互相关成像,并创新性引入共角度域成像点道集,有效改善了多次波逆时偏移中的噪声问题.该方法不需要对多次波进行预测,可以进行浅层目标的成像,但会在成像区域内产生广泛且能量较强的串扰噪声,这是由于逆时偏移成像机制中需要对震源波场正传和检波波场反传后进行互相关运算所导致,该问题一直是多次波成像领域研究的重点.2015年,宋鹏等[7 ] 分析了多次波成像过程中的串扰噪声机制,创新性地应用SRME理论进行多次波分阶逆时偏移,有效压制了串扰噪声问题.2015年,朱博等[8 ] 引入多卡GPU集群加速技术,显著提高了多次波成像的计算效率.同年,Berkhout[9 ] 提出全波场偏移算法,将全波数据视为地震数据,并利用伴随方法实现了层间多次波的成像;2016年,刘学建等[10 ] 将逆散射级数方法预测的层间多次波当作逆时偏移的反传数据,并结合波场分离实现了层间多次波的偏移.2017年,Li等[11 ] 提出基于SRME与聚焦变换的分阶多次波逆时偏移,进一步压制串扰噪声并提高成像分辨率.然而,多次波成像中仍存在不相干同相轴噪声的问题,有待进一步研究.2018年,刘伊克等[12 ] 结合多次波成像与分阶思想,提出可控阶多次波成像算法:在成像前将不同阶数多次波提取出来,并将n 阶、n +1阶多次波分别当作虚震源与地震记录,应用成像条件获取n +1阶多次波的成像结果,随后叠加各阶多次波成像结果获取最终偏移结果.2022年黄建东等[13 ] 对单程波偏移方法进行了拓展,提出层间多次波傅里叶有限差分偏移. ...
Simultaneous reverse time migration of primaries and free-surface related multiples without multiple prediction
1
2014
... 逆时偏移主要用于盐丘等高陡构造以及横向速度剧烈变化的地区.该技术基于双程波动方程,最早由Whitmore于1949年提出[1 ] .国内对多次波逆时偏移也有许多研究:2008年,刘伊克等[2 ] 在成像域成功压制表层多次波与层间多次波,发现多次波含有丰富的小角度信息,能够提供更广的成像范围.2011年,郭书娟等[3 ] 实现了一次波和表层多次波联合成像,将含有多次波和震源脉冲的炮记录作为震源波场,压制了常规多次波成像噪声.Wang等[4 ] 改变传统做法,将含有一次波和多次波的地震数据记录作为震源波场和检波波场,提高了成像分辨率,但不恰当的子波选择可能导致信息覆盖.2013年,Li等[5 ] 提出了基于SRME和聚焦变换的一次波和各阶表层多次波分离方法.2014年,Wang等[6 ] 将一次波和表面多次波分别作为震源波场和检波波场,通过互相关成像,并创新性引入共角度域成像点道集,有效改善了多次波逆时偏移中的噪声问题.该方法不需要对多次波进行预测,可以进行浅层目标的成像,但会在成像区域内产生广泛且能量较强的串扰噪声,这是由于逆时偏移成像机制中需要对震源波场正传和检波波场反传后进行互相关运算所导致,该问题一直是多次波成像领域研究的重点.2015年,宋鹏等[7 ] 分析了多次波成像过程中的串扰噪声机制,创新性地应用SRME理论进行多次波分阶逆时偏移,有效压制了串扰噪声问题.2015年,朱博等[8 ] 引入多卡GPU集群加速技术,显著提高了多次波成像的计算效率.同年,Berkhout[9 ] 提出全波场偏移算法,将全波数据视为地震数据,并利用伴随方法实现了层间多次波的成像;2016年,刘学建等[10 ] 将逆散射级数方法预测的层间多次波当作逆时偏移的反传数据,并结合波场分离实现了层间多次波的偏移.2017年,Li等[11 ] 提出基于SRME与聚焦变换的分阶多次波逆时偏移,进一步压制串扰噪声并提高成像分辨率.然而,多次波成像中仍存在不相干同相轴噪声的问题,有待进一步研究.2018年,刘伊克等[12 ] 结合多次波成像与分阶思想,提出可控阶多次波成像算法:在成像前将不同阶数多次波提取出来,并将n 阶、n +1阶多次波分别当作虚震源与地震记录,应用成像条件获取n +1阶多次波的成像结果,随后叠加各阶多次波成像结果获取最终偏移结果.2022年黄建东等[13 ] 对单程波偏移方法进行了拓展,提出层间多次波傅里叶有限差分偏移. ...
Multiple attenuation using λ-f domain high-resolution Radon transform
1
2013
... 逆时偏移主要用于盐丘等高陡构造以及横向速度剧烈变化的地区.该技术基于双程波动方程,最早由Whitmore于1949年提出[1 ] .国内对多次波逆时偏移也有许多研究:2008年,刘伊克等[2 ] 在成像域成功压制表层多次波与层间多次波,发现多次波含有丰富的小角度信息,能够提供更广的成像范围.2011年,郭书娟等[3 ] 实现了一次波和表层多次波联合成像,将含有多次波和震源脉冲的炮记录作为震源波场,压制了常规多次波成像噪声.Wang等[4 ] 改变传统做法,将含有一次波和多次波的地震数据记录作为震源波场和检波波场,提高了成像分辨率,但不恰当的子波选择可能导致信息覆盖.2013年,Li等[5 ] 提出了基于SRME和聚焦变换的一次波和各阶表层多次波分离方法.2014年,Wang等[6 ] 将一次波和表面多次波分别作为震源波场和检波波场,通过互相关成像,并创新性引入共角度域成像点道集,有效改善了多次波逆时偏移中的噪声问题.该方法不需要对多次波进行预测,可以进行浅层目标的成像,但会在成像区域内产生广泛且能量较强的串扰噪声,这是由于逆时偏移成像机制中需要对震源波场正传和检波波场反传后进行互相关运算所导致,该问题一直是多次波成像领域研究的重点.2015年,宋鹏等[7 ] 分析了多次波成像过程中的串扰噪声机制,创新性地应用SRME理论进行多次波分阶逆时偏移,有效压制了串扰噪声问题.2015年,朱博等[8 ] 引入多卡GPU集群加速技术,显著提高了多次波成像的计算效率.同年,Berkhout[9 ] 提出全波场偏移算法,将全波数据视为地震数据,并利用伴随方法实现了层间多次波的成像;2016年,刘学建等[10 ] 将逆散射级数方法预测的层间多次波当作逆时偏移的反传数据,并结合波场分离实现了层间多次波的偏移.2017年,Li等[11 ] 提出基于SRME与聚焦变换的分阶多次波逆时偏移,进一步压制串扰噪声并提高成像分辨率.然而,多次波成像中仍存在不相干同相轴噪声的问题,有待进一步研究.2018年,刘伊克等[12 ] 结合多次波成像与分阶思想,提出可控阶多次波成像算法:在成像前将不同阶数多次波提取出来,并将n 阶、n +1阶多次波分别当作虚震源与地震记录,应用成像条件获取n +1阶多次波的成像结果,随后叠加各阶多次波成像结果获取最终偏移结果.2022年黄建东等[13 ] 对单程波偏移方法进行了拓展,提出层间多次波傅里叶有限差分偏移. ...
Reverse time migration of multiples:Eliminating migration artifacts in angle domain common image gathers
1
2014
... 逆时偏移主要用于盐丘等高陡构造以及横向速度剧烈变化的地区.该技术基于双程波动方程,最早由Whitmore于1949年提出[1 ] .国内对多次波逆时偏移也有许多研究:2008年,刘伊克等[2 ] 在成像域成功压制表层多次波与层间多次波,发现多次波含有丰富的小角度信息,能够提供更广的成像范围.2011年,郭书娟等[3 ] 实现了一次波和表层多次波联合成像,将含有多次波和震源脉冲的炮记录作为震源波场,压制了常规多次波成像噪声.Wang等[4 ] 改变传统做法,将含有一次波和多次波的地震数据记录作为震源波场和检波波场,提高了成像分辨率,但不恰当的子波选择可能导致信息覆盖.2013年,Li等[5 ] 提出了基于SRME和聚焦变换的一次波和各阶表层多次波分离方法.2014年,Wang等[6 ] 将一次波和表面多次波分别作为震源波场和检波波场,通过互相关成像,并创新性引入共角度域成像点道集,有效改善了多次波逆时偏移中的噪声问题.该方法不需要对多次波进行预测,可以进行浅层目标的成像,但会在成像区域内产生广泛且能量较强的串扰噪声,这是由于逆时偏移成像机制中需要对震源波场正传和检波波场反传后进行互相关运算所导致,该问题一直是多次波成像领域研究的重点.2015年,宋鹏等[7 ] 分析了多次波成像过程中的串扰噪声机制,创新性地应用SRME理论进行多次波分阶逆时偏移,有效压制了串扰噪声问题.2015年,朱博等[8 ] 引入多卡GPU集群加速技术,显著提高了多次波成像的计算效率.同年,Berkhout[9 ] 提出全波场偏移算法,将全波数据视为地震数据,并利用伴随方法实现了层间多次波的成像;2016年,刘学建等[10 ] 将逆散射级数方法预测的层间多次波当作逆时偏移的反传数据,并结合波场分离实现了层间多次波的偏移.2017年,Li等[11 ] 提出基于SRME与聚焦变换的分阶多次波逆时偏移,进一步压制串扰噪声并提高成像分辨率.然而,多次波成像中仍存在不相干同相轴噪声的问题,有待进一步研究.2018年,刘伊克等[12 ] 结合多次波成像与分阶思想,提出可控阶多次波成像算法:在成像前将不同阶数多次波提取出来,并将n 阶、n +1阶多次波分别当作虚震源与地震记录,应用成像条件获取n +1阶多次波的成像结果,随后叠加各阶多次波成像结果获取最终偏移结果.2022年黄建东等[13 ] 对单程波偏移方法进行了拓展,提出层间多次波傅里叶有限差分偏移. ...
多次波分阶逆时偏移成像
1
2015
... 逆时偏移主要用于盐丘等高陡构造以及横向速度剧烈变化的地区.该技术基于双程波动方程,最早由Whitmore于1949年提出[1 ] .国内对多次波逆时偏移也有许多研究:2008年,刘伊克等[2 ] 在成像域成功压制表层多次波与层间多次波,发现多次波含有丰富的小角度信息,能够提供更广的成像范围.2011年,郭书娟等[3 ] 实现了一次波和表层多次波联合成像,将含有多次波和震源脉冲的炮记录作为震源波场,压制了常规多次波成像噪声.Wang等[4 ] 改变传统做法,将含有一次波和多次波的地震数据记录作为震源波场和检波波场,提高了成像分辨率,但不恰当的子波选择可能导致信息覆盖.2013年,Li等[5 ] 提出了基于SRME和聚焦变换的一次波和各阶表层多次波分离方法.2014年,Wang等[6 ] 将一次波和表面多次波分别作为震源波场和检波波场,通过互相关成像,并创新性引入共角度域成像点道集,有效改善了多次波逆时偏移中的噪声问题.该方法不需要对多次波进行预测,可以进行浅层目标的成像,但会在成像区域内产生广泛且能量较强的串扰噪声,这是由于逆时偏移成像机制中需要对震源波场正传和检波波场反传后进行互相关运算所导致,该问题一直是多次波成像领域研究的重点.2015年,宋鹏等[7 ] 分析了多次波成像过程中的串扰噪声机制,创新性地应用SRME理论进行多次波分阶逆时偏移,有效压制了串扰噪声问题.2015年,朱博等[8 ] 引入多卡GPU集群加速技术,显著提高了多次波成像的计算效率.同年,Berkhout[9 ] 提出全波场偏移算法,将全波数据视为地震数据,并利用伴随方法实现了层间多次波的成像;2016年,刘学建等[10 ] 将逆散射级数方法预测的层间多次波当作逆时偏移的反传数据,并结合波场分离实现了层间多次波的偏移.2017年,Li等[11 ] 提出基于SRME与聚焦变换的分阶多次波逆时偏移,进一步压制串扰噪声并提高成像分辨率.然而,多次波成像中仍存在不相干同相轴噪声的问题,有待进一步研究.2018年,刘伊克等[12 ] 结合多次波成像与分阶思想,提出可控阶多次波成像算法:在成像前将不同阶数多次波提取出来,并将n 阶、n +1阶多次波分别当作虚震源与地震记录,应用成像条件获取n +1阶多次波的成像结果,随后叠加各阶多次波成像结果获取最终偏移结果.2022年黄建东等[13 ] 对单程波偏移方法进行了拓展,提出层间多次波傅里叶有限差分偏移. ...
多次波分阶逆时偏移成像
1
2015
... 逆时偏移主要用于盐丘等高陡构造以及横向速度剧烈变化的地区.该技术基于双程波动方程,最早由Whitmore于1949年提出[1 ] .国内对多次波逆时偏移也有许多研究:2008年,刘伊克等[2 ] 在成像域成功压制表层多次波与层间多次波,发现多次波含有丰富的小角度信息,能够提供更广的成像范围.2011年,郭书娟等[3 ] 实现了一次波和表层多次波联合成像,将含有多次波和震源脉冲的炮记录作为震源波场,压制了常规多次波成像噪声.Wang等[4 ] 改变传统做法,将含有一次波和多次波的地震数据记录作为震源波场和检波波场,提高了成像分辨率,但不恰当的子波选择可能导致信息覆盖.2013年,Li等[5 ] 提出了基于SRME和聚焦变换的一次波和各阶表层多次波分离方法.2014年,Wang等[6 ] 将一次波和表面多次波分别作为震源波场和检波波场,通过互相关成像,并创新性引入共角度域成像点道集,有效改善了多次波逆时偏移中的噪声问题.该方法不需要对多次波进行预测,可以进行浅层目标的成像,但会在成像区域内产生广泛且能量较强的串扰噪声,这是由于逆时偏移成像机制中需要对震源波场正传和检波波场反传后进行互相关运算所导致,该问题一直是多次波成像领域研究的重点.2015年,宋鹏等[7 ] 分析了多次波成像过程中的串扰噪声机制,创新性地应用SRME理论进行多次波分阶逆时偏移,有效压制了串扰噪声问题.2015年,朱博等[8 ] 引入多卡GPU集群加速技术,显著提高了多次波成像的计算效率.同年,Berkhout[9 ] 提出全波场偏移算法,将全波数据视为地震数据,并利用伴随方法实现了层间多次波的成像;2016年,刘学建等[10 ] 将逆散射级数方法预测的层间多次波当作逆时偏移的反传数据,并结合波场分离实现了层间多次波的偏移.2017年,Li等[11 ] 提出基于SRME与聚焦变换的分阶多次波逆时偏移,进一步压制串扰噪声并提高成像分辨率.然而,多次波成像中仍存在不相干同相轴噪声的问题,有待进一步研究.2018年,刘伊克等[12 ] 结合多次波成像与分阶思想,提出可控阶多次波成像算法:在成像前将不同阶数多次波提取出来,并将n 阶、n +1阶多次波分别当作虚震源与地震记录,应用成像条件获取n +1阶多次波的成像结果,随后叠加各阶多次波成像结果获取最终偏移结果.2022年黄建东等[13 ] 对单程波偏移方法进行了拓展,提出层间多次波傅里叶有限差分偏移. ...
基于多卡GPU集群的多次波逆时偏移成像技术
1
2015
... 逆时偏移主要用于盐丘等高陡构造以及横向速度剧烈变化的地区.该技术基于双程波动方程,最早由Whitmore于1949年提出[1 ] .国内对多次波逆时偏移也有许多研究:2008年,刘伊克等[2 ] 在成像域成功压制表层多次波与层间多次波,发现多次波含有丰富的小角度信息,能够提供更广的成像范围.2011年,郭书娟等[3 ] 实现了一次波和表层多次波联合成像,将含有多次波和震源脉冲的炮记录作为震源波场,压制了常规多次波成像噪声.Wang等[4 ] 改变传统做法,将含有一次波和多次波的地震数据记录作为震源波场和检波波场,提高了成像分辨率,但不恰当的子波选择可能导致信息覆盖.2013年,Li等[5 ] 提出了基于SRME和聚焦变换的一次波和各阶表层多次波分离方法.2014年,Wang等[6 ] 将一次波和表面多次波分别作为震源波场和检波波场,通过互相关成像,并创新性引入共角度域成像点道集,有效改善了多次波逆时偏移中的噪声问题.该方法不需要对多次波进行预测,可以进行浅层目标的成像,但会在成像区域内产生广泛且能量较强的串扰噪声,这是由于逆时偏移成像机制中需要对震源波场正传和检波波场反传后进行互相关运算所导致,该问题一直是多次波成像领域研究的重点.2015年,宋鹏等[7 ] 分析了多次波成像过程中的串扰噪声机制,创新性地应用SRME理论进行多次波分阶逆时偏移,有效压制了串扰噪声问题.2015年,朱博等[8 ] 引入多卡GPU集群加速技术,显著提高了多次波成像的计算效率.同年,Berkhout[9 ] 提出全波场偏移算法,将全波数据视为地震数据,并利用伴随方法实现了层间多次波的成像;2016年,刘学建等[10 ] 将逆散射级数方法预测的层间多次波当作逆时偏移的反传数据,并结合波场分离实现了层间多次波的偏移.2017年,Li等[11 ] 提出基于SRME与聚焦变换的分阶多次波逆时偏移,进一步压制串扰噪声并提高成像分辨率.然而,多次波成像中仍存在不相干同相轴噪声的问题,有待进一步研究.2018年,刘伊克等[12 ] 结合多次波成像与分阶思想,提出可控阶多次波成像算法:在成像前将不同阶数多次波提取出来,并将n 阶、n +1阶多次波分别当作虚震源与地震记录,应用成像条件获取n +1阶多次波的成像结果,随后叠加各阶多次波成像结果获取最终偏移结果.2022年黄建东等[13 ] 对单程波偏移方法进行了拓展,提出层间多次波傅里叶有限差分偏移. ...
基于多卡GPU集群的多次波逆时偏移成像技术
1
2015
... 逆时偏移主要用于盐丘等高陡构造以及横向速度剧烈变化的地区.该技术基于双程波动方程,最早由Whitmore于1949年提出[1 ] .国内对多次波逆时偏移也有许多研究:2008年,刘伊克等[2 ] 在成像域成功压制表层多次波与层间多次波,发现多次波含有丰富的小角度信息,能够提供更广的成像范围.2011年,郭书娟等[3 ] 实现了一次波和表层多次波联合成像,将含有多次波和震源脉冲的炮记录作为震源波场,压制了常规多次波成像噪声.Wang等[4 ] 改变传统做法,将含有一次波和多次波的地震数据记录作为震源波场和检波波场,提高了成像分辨率,但不恰当的子波选择可能导致信息覆盖.2013年,Li等[5 ] 提出了基于SRME和聚焦变换的一次波和各阶表层多次波分离方法.2014年,Wang等[6 ] 将一次波和表面多次波分别作为震源波场和检波波场,通过互相关成像,并创新性引入共角度域成像点道集,有效改善了多次波逆时偏移中的噪声问题.该方法不需要对多次波进行预测,可以进行浅层目标的成像,但会在成像区域内产生广泛且能量较强的串扰噪声,这是由于逆时偏移成像机制中需要对震源波场正传和检波波场反传后进行互相关运算所导致,该问题一直是多次波成像领域研究的重点.2015年,宋鹏等[7 ] 分析了多次波成像过程中的串扰噪声机制,创新性地应用SRME理论进行多次波分阶逆时偏移,有效压制了串扰噪声问题.2015年,朱博等[8 ] 引入多卡GPU集群加速技术,显著提高了多次波成像的计算效率.同年,Berkhout[9 ] 提出全波场偏移算法,将全波数据视为地震数据,并利用伴随方法实现了层间多次波的成像;2016年,刘学建等[10 ] 将逆散射级数方法预测的层间多次波当作逆时偏移的反传数据,并结合波场分离实现了层间多次波的偏移.2017年,Li等[11 ] 提出基于SRME与聚焦变换的分阶多次波逆时偏移,进一步压制串扰噪声并提高成像分辨率.然而,多次波成像中仍存在不相干同相轴噪声的问题,有待进一步研究.2018年,刘伊克等[12 ] 结合多次波成像与分阶思想,提出可控阶多次波成像算法:在成像前将不同阶数多次波提取出来,并将n 阶、n +1阶多次波分别当作虚震源与地震记录,应用成像条件获取n +1阶多次波的成像结果,随后叠加各阶多次波成像结果获取最终偏移结果.2022年黄建东等[13 ] 对单程波偏移方法进行了拓展,提出层间多次波傅里叶有限差分偏移. ...
Review paper:An outlook on the future of seismic imaging,part II:Full-wavefield migration
1
2014
... 逆时偏移主要用于盐丘等高陡构造以及横向速度剧烈变化的地区.该技术基于双程波动方程,最早由Whitmore于1949年提出[1 ] .国内对多次波逆时偏移也有许多研究:2008年,刘伊克等[2 ] 在成像域成功压制表层多次波与层间多次波,发现多次波含有丰富的小角度信息,能够提供更广的成像范围.2011年,郭书娟等[3 ] 实现了一次波和表层多次波联合成像,将含有多次波和震源脉冲的炮记录作为震源波场,压制了常规多次波成像噪声.Wang等[4 ] 改变传统做法,将含有一次波和多次波的地震数据记录作为震源波场和检波波场,提高了成像分辨率,但不恰当的子波选择可能导致信息覆盖.2013年,Li等[5 ] 提出了基于SRME和聚焦变换的一次波和各阶表层多次波分离方法.2014年,Wang等[6 ] 将一次波和表面多次波分别作为震源波场和检波波场,通过互相关成像,并创新性引入共角度域成像点道集,有效改善了多次波逆时偏移中的噪声问题.该方法不需要对多次波进行预测,可以进行浅层目标的成像,但会在成像区域内产生广泛且能量较强的串扰噪声,这是由于逆时偏移成像机制中需要对震源波场正传和检波波场反传后进行互相关运算所导致,该问题一直是多次波成像领域研究的重点.2015年,宋鹏等[7 ] 分析了多次波成像过程中的串扰噪声机制,创新性地应用SRME理论进行多次波分阶逆时偏移,有效压制了串扰噪声问题.2015年,朱博等[8 ] 引入多卡GPU集群加速技术,显著提高了多次波成像的计算效率.同年,Berkhout[9 ] 提出全波场偏移算法,将全波数据视为地震数据,并利用伴随方法实现了层间多次波的成像;2016年,刘学建等[10 ] 将逆散射级数方法预测的层间多次波当作逆时偏移的反传数据,并结合波场分离实现了层间多次波的偏移.2017年,Li等[11 ] 提出基于SRME与聚焦变换的分阶多次波逆时偏移,进一步压制串扰噪声并提高成像分辨率.然而,多次波成像中仍存在不相干同相轴噪声的问题,有待进一步研究.2018年,刘伊克等[12 ] 结合多次波成像与分阶思想,提出可控阶多次波成像算法:在成像前将不同阶数多次波提取出来,并将n 阶、n +1阶多次波分别当作虚震源与地震记录,应用成像条件获取n +1阶多次波的成像结果,随后叠加各阶多次波成像结果获取最终偏移结果.2022年黄建东等[13 ] 对单程波偏移方法进行了拓展,提出层间多次波傅里叶有限差分偏移. ...
表面多次波最小二乘逆时偏移成像
1
2016
... 逆时偏移主要用于盐丘等高陡构造以及横向速度剧烈变化的地区.该技术基于双程波动方程,最早由Whitmore于1949年提出[1 ] .国内对多次波逆时偏移也有许多研究:2008年,刘伊克等[2 ] 在成像域成功压制表层多次波与层间多次波,发现多次波含有丰富的小角度信息,能够提供更广的成像范围.2011年,郭书娟等[3 ] 实现了一次波和表层多次波联合成像,将含有多次波和震源脉冲的炮记录作为震源波场,压制了常规多次波成像噪声.Wang等[4 ] 改变传统做法,将含有一次波和多次波的地震数据记录作为震源波场和检波波场,提高了成像分辨率,但不恰当的子波选择可能导致信息覆盖.2013年,Li等[5 ] 提出了基于SRME和聚焦变换的一次波和各阶表层多次波分离方法.2014年,Wang等[6 ] 将一次波和表面多次波分别作为震源波场和检波波场,通过互相关成像,并创新性引入共角度域成像点道集,有效改善了多次波逆时偏移中的噪声问题.该方法不需要对多次波进行预测,可以进行浅层目标的成像,但会在成像区域内产生广泛且能量较强的串扰噪声,这是由于逆时偏移成像机制中需要对震源波场正传和检波波场反传后进行互相关运算所导致,该问题一直是多次波成像领域研究的重点.2015年,宋鹏等[7 ] 分析了多次波成像过程中的串扰噪声机制,创新性地应用SRME理论进行多次波分阶逆时偏移,有效压制了串扰噪声问题.2015年,朱博等[8 ] 引入多卡GPU集群加速技术,显著提高了多次波成像的计算效率.同年,Berkhout[9 ] 提出全波场偏移算法,将全波数据视为地震数据,并利用伴随方法实现了层间多次波的成像;2016年,刘学建等[10 ] 将逆散射级数方法预测的层间多次波当作逆时偏移的反传数据,并结合波场分离实现了层间多次波的偏移.2017年,Li等[11 ] 提出基于SRME与聚焦变换的分阶多次波逆时偏移,进一步压制串扰噪声并提高成像分辨率.然而,多次波成像中仍存在不相干同相轴噪声的问题,有待进一步研究.2018年,刘伊克等[12 ] 结合多次波成像与分阶思想,提出可控阶多次波成像算法:在成像前将不同阶数多次波提取出来,并将n 阶、n +1阶多次波分别当作虚震源与地震记录,应用成像条件获取n +1阶多次波的成像结果,随后叠加各阶多次波成像结果获取最终偏移结果.2022年黄建东等[13 ] 对单程波偏移方法进行了拓展,提出层间多次波傅里叶有限差分偏移. ...
表面多次波最小二乘逆时偏移成像
1
2016
... 逆时偏移主要用于盐丘等高陡构造以及横向速度剧烈变化的地区.该技术基于双程波动方程,最早由Whitmore于1949年提出[1 ] .国内对多次波逆时偏移也有许多研究:2008年,刘伊克等[2 ] 在成像域成功压制表层多次波与层间多次波,发现多次波含有丰富的小角度信息,能够提供更广的成像范围.2011年,郭书娟等[3 ] 实现了一次波和表层多次波联合成像,将含有多次波和震源脉冲的炮记录作为震源波场,压制了常规多次波成像噪声.Wang等[4 ] 改变传统做法,将含有一次波和多次波的地震数据记录作为震源波场和检波波场,提高了成像分辨率,但不恰当的子波选择可能导致信息覆盖.2013年,Li等[5 ] 提出了基于SRME和聚焦变换的一次波和各阶表层多次波分离方法.2014年,Wang等[6 ] 将一次波和表面多次波分别作为震源波场和检波波场,通过互相关成像,并创新性引入共角度域成像点道集,有效改善了多次波逆时偏移中的噪声问题.该方法不需要对多次波进行预测,可以进行浅层目标的成像,但会在成像区域内产生广泛且能量较强的串扰噪声,这是由于逆时偏移成像机制中需要对震源波场正传和检波波场反传后进行互相关运算所导致,该问题一直是多次波成像领域研究的重点.2015年,宋鹏等[7 ] 分析了多次波成像过程中的串扰噪声机制,创新性地应用SRME理论进行多次波分阶逆时偏移,有效压制了串扰噪声问题.2015年,朱博等[8 ] 引入多卡GPU集群加速技术,显著提高了多次波成像的计算效率.同年,Berkhout[9 ] 提出全波场偏移算法,将全波数据视为地震数据,并利用伴随方法实现了层间多次波的成像;2016年,刘学建等[10 ] 将逆散射级数方法预测的层间多次波当作逆时偏移的反传数据,并结合波场分离实现了层间多次波的偏移.2017年,Li等[11 ] 提出基于SRME与聚焦变换的分阶多次波逆时偏移,进一步压制串扰噪声并提高成像分辨率.然而,多次波成像中仍存在不相干同相轴噪声的问题,有待进一步研究.2018年,刘伊克等[12 ] 结合多次波成像与分阶思想,提出可控阶多次波成像算法:在成像前将不同阶数多次波提取出来,并将n 阶、n +1阶多次波分别当作虚震源与地震记录,应用成像条件获取n +1阶多次波的成像结果,随后叠加各阶多次波成像结果获取最终偏移结果.2022年黄建东等[13 ] 对单程波偏移方法进行了拓展,提出层间多次波傅里叶有限差分偏移. ...
Reverse time migration of multiples based on different-order multiple separation
1
2017
... 逆时偏移主要用于盐丘等高陡构造以及横向速度剧烈变化的地区.该技术基于双程波动方程,最早由Whitmore于1949年提出[1 ] .国内对多次波逆时偏移也有许多研究:2008年,刘伊克等[2 ] 在成像域成功压制表层多次波与层间多次波,发现多次波含有丰富的小角度信息,能够提供更广的成像范围.2011年,郭书娟等[3 ] 实现了一次波和表层多次波联合成像,将含有多次波和震源脉冲的炮记录作为震源波场,压制了常规多次波成像噪声.Wang等[4 ] 改变传统做法,将含有一次波和多次波的地震数据记录作为震源波场和检波波场,提高了成像分辨率,但不恰当的子波选择可能导致信息覆盖.2013年,Li等[5 ] 提出了基于SRME和聚焦变换的一次波和各阶表层多次波分离方法.2014年,Wang等[6 ] 将一次波和表面多次波分别作为震源波场和检波波场,通过互相关成像,并创新性引入共角度域成像点道集,有效改善了多次波逆时偏移中的噪声问题.该方法不需要对多次波进行预测,可以进行浅层目标的成像,但会在成像区域内产生广泛且能量较强的串扰噪声,这是由于逆时偏移成像机制中需要对震源波场正传和检波波场反传后进行互相关运算所导致,该问题一直是多次波成像领域研究的重点.2015年,宋鹏等[7 ] 分析了多次波成像过程中的串扰噪声机制,创新性地应用SRME理论进行多次波分阶逆时偏移,有效压制了串扰噪声问题.2015年,朱博等[8 ] 引入多卡GPU集群加速技术,显著提高了多次波成像的计算效率.同年,Berkhout[9 ] 提出全波场偏移算法,将全波数据视为地震数据,并利用伴随方法实现了层间多次波的成像;2016年,刘学建等[10 ] 将逆散射级数方法预测的层间多次波当作逆时偏移的反传数据,并结合波场分离实现了层间多次波的偏移.2017年,Li等[11 ] 提出基于SRME与聚焦变换的分阶多次波逆时偏移,进一步压制串扰噪声并提高成像分辨率.然而,多次波成像中仍存在不相干同相轴噪声的问题,有待进一步研究.2018年,刘伊克等[12 ] 结合多次波成像与分阶思想,提出可控阶多次波成像算法:在成像前将不同阶数多次波提取出来,并将n 阶、n +1阶多次波分别当作虚震源与地震记录,应用成像条件获取n +1阶多次波的成像结果,随后叠加各阶多次波成像结果获取最终偏移结果.2022年黄建东等[13 ] 对单程波偏移方法进行了拓展,提出层间多次波傅里叶有限差分偏移. ...
地震多次波成像
1
2018
... 逆时偏移主要用于盐丘等高陡构造以及横向速度剧烈变化的地区.该技术基于双程波动方程,最早由Whitmore于1949年提出[1 ] .国内对多次波逆时偏移也有许多研究:2008年,刘伊克等[2 ] 在成像域成功压制表层多次波与层间多次波,发现多次波含有丰富的小角度信息,能够提供更广的成像范围.2011年,郭书娟等[3 ] 实现了一次波和表层多次波联合成像,将含有多次波和震源脉冲的炮记录作为震源波场,压制了常规多次波成像噪声.Wang等[4 ] 改变传统做法,将含有一次波和多次波的地震数据记录作为震源波场和检波波场,提高了成像分辨率,但不恰当的子波选择可能导致信息覆盖.2013年,Li等[5 ] 提出了基于SRME和聚焦变换的一次波和各阶表层多次波分离方法.2014年,Wang等[6 ] 将一次波和表面多次波分别作为震源波场和检波波场,通过互相关成像,并创新性引入共角度域成像点道集,有效改善了多次波逆时偏移中的噪声问题.该方法不需要对多次波进行预测,可以进行浅层目标的成像,但会在成像区域内产生广泛且能量较强的串扰噪声,这是由于逆时偏移成像机制中需要对震源波场正传和检波波场反传后进行互相关运算所导致,该问题一直是多次波成像领域研究的重点.2015年,宋鹏等[7 ] 分析了多次波成像过程中的串扰噪声机制,创新性地应用SRME理论进行多次波分阶逆时偏移,有效压制了串扰噪声问题.2015年,朱博等[8 ] 引入多卡GPU集群加速技术,显著提高了多次波成像的计算效率.同年,Berkhout[9 ] 提出全波场偏移算法,将全波数据视为地震数据,并利用伴随方法实现了层间多次波的成像;2016年,刘学建等[10 ] 将逆散射级数方法预测的层间多次波当作逆时偏移的反传数据,并结合波场分离实现了层间多次波的偏移.2017年,Li等[11 ] 提出基于SRME与聚焦变换的分阶多次波逆时偏移,进一步压制串扰噪声并提高成像分辨率.然而,多次波成像中仍存在不相干同相轴噪声的问题,有待进一步研究.2018年,刘伊克等[12 ] 结合多次波成像与分阶思想,提出可控阶多次波成像算法:在成像前将不同阶数多次波提取出来,并将n 阶、n +1阶多次波分别当作虚震源与地震记录,应用成像条件获取n +1阶多次波的成像结果,随后叠加各阶多次波成像结果获取最终偏移结果.2022年黄建东等[13 ] 对单程波偏移方法进行了拓展,提出层间多次波傅里叶有限差分偏移. ...
地震多次波成像
1
2018
... 逆时偏移主要用于盐丘等高陡构造以及横向速度剧烈变化的地区.该技术基于双程波动方程,最早由Whitmore于1949年提出[1 ] .国内对多次波逆时偏移也有许多研究:2008年,刘伊克等[2 ] 在成像域成功压制表层多次波与层间多次波,发现多次波含有丰富的小角度信息,能够提供更广的成像范围.2011年,郭书娟等[3 ] 实现了一次波和表层多次波联合成像,将含有多次波和震源脉冲的炮记录作为震源波场,压制了常规多次波成像噪声.Wang等[4 ] 改变传统做法,将含有一次波和多次波的地震数据记录作为震源波场和检波波场,提高了成像分辨率,但不恰当的子波选择可能导致信息覆盖.2013年,Li等[5 ] 提出了基于SRME和聚焦变换的一次波和各阶表层多次波分离方法.2014年,Wang等[6 ] 将一次波和表面多次波分别作为震源波场和检波波场,通过互相关成像,并创新性引入共角度域成像点道集,有效改善了多次波逆时偏移中的噪声问题.该方法不需要对多次波进行预测,可以进行浅层目标的成像,但会在成像区域内产生广泛且能量较强的串扰噪声,这是由于逆时偏移成像机制中需要对震源波场正传和检波波场反传后进行互相关运算所导致,该问题一直是多次波成像领域研究的重点.2015年,宋鹏等[7 ] 分析了多次波成像过程中的串扰噪声机制,创新性地应用SRME理论进行多次波分阶逆时偏移,有效压制了串扰噪声问题.2015年,朱博等[8 ] 引入多卡GPU集群加速技术,显著提高了多次波成像的计算效率.同年,Berkhout[9 ] 提出全波场偏移算法,将全波数据视为地震数据,并利用伴随方法实现了层间多次波的成像;2016年,刘学建等[10 ] 将逆散射级数方法预测的层间多次波当作逆时偏移的反传数据,并结合波场分离实现了层间多次波的偏移.2017年,Li等[11 ] 提出基于SRME与聚焦变换的分阶多次波逆时偏移,进一步压制串扰噪声并提高成像分辨率.然而,多次波成像中仍存在不相干同相轴噪声的问题,有待进一步研究.2018年,刘伊克等[12 ] 结合多次波成像与分阶思想,提出可控阶多次波成像算法:在成像前将不同阶数多次波提取出来,并将n 阶、n +1阶多次波分别当作虚震源与地震记录,应用成像条件获取n +1阶多次波的成像结果,随后叠加各阶多次波成像结果获取最终偏移结果.2022年黄建东等[13 ] 对单程波偏移方法进行了拓展,提出层间多次波傅里叶有限差分偏移. ...
层间多次波傅里叶有限差分偏移成像
1
2022
... 逆时偏移主要用于盐丘等高陡构造以及横向速度剧烈变化的地区.该技术基于双程波动方程,最早由Whitmore于1949年提出[1 ] .国内对多次波逆时偏移也有许多研究:2008年,刘伊克等[2 ] 在成像域成功压制表层多次波与层间多次波,发现多次波含有丰富的小角度信息,能够提供更广的成像范围.2011年,郭书娟等[3 ] 实现了一次波和表层多次波联合成像,将含有多次波和震源脉冲的炮记录作为震源波场,压制了常规多次波成像噪声.Wang等[4 ] 改变传统做法,将含有一次波和多次波的地震数据记录作为震源波场和检波波场,提高了成像分辨率,但不恰当的子波选择可能导致信息覆盖.2013年,Li等[5 ] 提出了基于SRME和聚焦变换的一次波和各阶表层多次波分离方法.2014年,Wang等[6 ] 将一次波和表面多次波分别作为震源波场和检波波场,通过互相关成像,并创新性引入共角度域成像点道集,有效改善了多次波逆时偏移中的噪声问题.该方法不需要对多次波进行预测,可以进行浅层目标的成像,但会在成像区域内产生广泛且能量较强的串扰噪声,这是由于逆时偏移成像机制中需要对震源波场正传和检波波场反传后进行互相关运算所导致,该问题一直是多次波成像领域研究的重点.2015年,宋鹏等[7 ] 分析了多次波成像过程中的串扰噪声机制,创新性地应用SRME理论进行多次波分阶逆时偏移,有效压制了串扰噪声问题.2015年,朱博等[8 ] 引入多卡GPU集群加速技术,显著提高了多次波成像的计算效率.同年,Berkhout[9 ] 提出全波场偏移算法,将全波数据视为地震数据,并利用伴随方法实现了层间多次波的成像;2016年,刘学建等[10 ] 将逆散射级数方法预测的层间多次波当作逆时偏移的反传数据,并结合波场分离实现了层间多次波的偏移.2017年,Li等[11 ] 提出基于SRME与聚焦变换的分阶多次波逆时偏移,进一步压制串扰噪声并提高成像分辨率.然而,多次波成像中仍存在不相干同相轴噪声的问题,有待进一步研究.2018年,刘伊克等[12 ] 结合多次波成像与分阶思想,提出可控阶多次波成像算法:在成像前将不同阶数多次波提取出来,并将n 阶、n +1阶多次波分别当作虚震源与地震记录,应用成像条件获取n +1阶多次波的成像结果,随后叠加各阶多次波成像结果获取最终偏移结果.2022年黄建东等[13 ] 对单程波偏移方法进行了拓展,提出层间多次波傅里叶有限差分偏移. ...
层间多次波傅里叶有限差分偏移成像
1
2022
... 逆时偏移主要用于盐丘等高陡构造以及横向速度剧烈变化的地区.该技术基于双程波动方程,最早由Whitmore于1949年提出[1 ] .国内对多次波逆时偏移也有许多研究:2008年,刘伊克等[2 ] 在成像域成功压制表层多次波与层间多次波,发现多次波含有丰富的小角度信息,能够提供更广的成像范围.2011年,郭书娟等[3 ] 实现了一次波和表层多次波联合成像,将含有多次波和震源脉冲的炮记录作为震源波场,压制了常规多次波成像噪声.Wang等[4 ] 改变传统做法,将含有一次波和多次波的地震数据记录作为震源波场和检波波场,提高了成像分辨率,但不恰当的子波选择可能导致信息覆盖.2013年,Li等[5 ] 提出了基于SRME和聚焦变换的一次波和各阶表层多次波分离方法.2014年,Wang等[6 ] 将一次波和表面多次波分别作为震源波场和检波波场,通过互相关成像,并创新性引入共角度域成像点道集,有效改善了多次波逆时偏移中的噪声问题.该方法不需要对多次波进行预测,可以进行浅层目标的成像,但会在成像区域内产生广泛且能量较强的串扰噪声,这是由于逆时偏移成像机制中需要对震源波场正传和检波波场反传后进行互相关运算所导致,该问题一直是多次波成像领域研究的重点.2015年,宋鹏等[7 ] 分析了多次波成像过程中的串扰噪声机制,创新性地应用SRME理论进行多次波分阶逆时偏移,有效压制了串扰噪声问题.2015年,朱博等[8 ] 引入多卡GPU集群加速技术,显著提高了多次波成像的计算效率.同年,Berkhout[9 ] 提出全波场偏移算法,将全波数据视为地震数据,并利用伴随方法实现了层间多次波的成像;2016年,刘学建等[10 ] 将逆散射级数方法预测的层间多次波当作逆时偏移的反传数据,并结合波场分离实现了层间多次波的偏移.2017年,Li等[11 ] 提出基于SRME与聚焦变换的分阶多次波逆时偏移,进一步压制串扰噪声并提高成像分辨率.然而,多次波成像中仍存在不相干同相轴噪声的问题,有待进一步研究.2018年,刘伊克等[12 ] 结合多次波成像与分阶思想,提出可控阶多次波成像算法:在成像前将不同阶数多次波提取出来,并将n 阶、n +1阶多次波分别当作虚震源与地震记录,应用成像条件获取n +1阶多次波的成像结果,随后叠加各阶多次波成像结果获取最终偏移结果.2022年黄建东等[13 ] 对单程波偏移方法进行了拓展,提出层间多次波傅里叶有限差分偏移. ...
Synthesis of a layered medium from its acoustic transmission response
1
1968
... 1968年,地震干涉技术由Claerbout[14 ] 提出,并在水平层状介质下验证了其正确性,同时他进一步猜想该技术在三维各向异性介质下同样适用.2001年,Schuster[15 ] 正式将这一技术方法命名为“地震干涉技术”.2002年,Wapenaar等[16 ] 对地震干涉方法进行了深入研究,并通过数学原理验证了地震干涉理论,发现其对不同的非衰减介质及震源条件均表现出很强的适应性,同时也验证了Clearbout关于三维各向异性介质的猜想.值得一提的是,Sheng等[17 ] 在2001年就应用了地震干涉技术对地下介质进行成像,并取得了显著的成像效果,且该方法不受震源条件的限制. ...
Theory of daylight/interferometric imaging-tutorial
1
2001
... 1968年,地震干涉技术由Claerbout[14 ] 提出,并在水平层状介质下验证了其正确性,同时他进一步猜想该技术在三维各向异性介质下同样适用.2001年,Schuster[15 ] 正式将这一技术方法命名为“地震干涉技术”.2002年,Wapenaar等[16 ] 对地震干涉方法进行了深入研究,并通过数学原理验证了地震干涉理论,发现其对不同的非衰减介质及震源条件均表现出很强的适应性,同时也验证了Clearbout关于三维各向异性介质的猜想.值得一提的是,Sheng等[17 ] 在2001年就应用了地震干涉技术对地下介质进行成像,并取得了显著的成像效果,且该方法不受震源条件的限制. ...
Theory of acoustic daylight imaging revisited
1
... 1968年,地震干涉技术由Claerbout[14 ] 提出,并在水平层状介质下验证了其正确性,同时他进一步猜想该技术在三维各向异性介质下同样适用.2001年,Schuster[15 ] 正式将这一技术方法命名为“地震干涉技术”.2002年,Wapenaar等[16 ] 对地震干涉方法进行了深入研究,并通过数学原理验证了地震干涉理论,发现其对不同的非衰减介质及震源条件均表现出很强的适应性,同时也验证了Clearbout关于三维各向异性介质的猜想.值得一提的是,Sheng等[17 ] 在2001年就应用了地震干涉技术对地下介质进行成像,并取得了显著的成像效果,且该方法不受震源条件的限制. ...
Migrating multiples and primaries in CDP data by crosscorrelogram migration
1
... 1968年,地震干涉技术由Claerbout[14 ] 提出,并在水平层状介质下验证了其正确性,同时他进一步猜想该技术在三维各向异性介质下同样适用.2001年,Schuster[15 ] 正式将这一技术方法命名为“地震干涉技术”.2002年,Wapenaar等[16 ] 对地震干涉方法进行了深入研究,并通过数学原理验证了地震干涉理论,发现其对不同的非衰减介质及震源条件均表现出很强的适应性,同时也验证了Clearbout关于三维各向异性介质的猜想.值得一提的是,Sheng等[17 ] 在2001年就应用了地震干涉技术对地下介质进行成像,并取得了显著的成像效果,且该方法不受震源条件的限制. ...
Coda wave interferometry for estimating nonlinear behavior in seismic velocity
1
2002
... 自2002年起,Snieder等[18 ] 开始研究地震干涉技术在尾波提取有用信息上的应用,并在2007年总结了不同条件下的地震干涉基本原理[19 ] .2008年,Wapenaar等[20 ] 提出了多维反褶积技术,并将其应用于被动源数据,推导了多维反褶积格林函数,成功从噪声数据中提取了面波信息. ...
Extracting the Green's function of attenuating heterogeneous acoustic media from uncorrelated waves
1
2007
... 自2002年起,Snieder等[18 ] 开始研究地震干涉技术在尾波提取有用信息上的应用,并在2007年总结了不同条件下的地震干涉基本原理[19 ] .2008年,Wapenaar等[20 ] 提出了多维反褶积技术,并将其应用于被动源数据,推导了多维反褶积格林函数,成功从噪声数据中提取了面波信息. ...
Passive seismic interferometry by multidimensional deconvolution
1
2008
... 自2002年起,Snieder等[18 ] 开始研究地震干涉技术在尾波提取有用信息上的应用,并在2007年总结了不同条件下的地震干涉基本原理[19 ] .2008年,Wapenaar等[20 ] 提出了多维反褶积技术,并将其应用于被动源数据,推导了多维反褶积格林函数,成功从噪声数据中提取了面波信息. ...
Virtual sources,a new way to remove overburden problems
1
2004
... 地震干涉技术在勘探地震领域应用广泛,它能够将地表激发地下接收的地震信号转化为地下激发地下接收的地震信号,从而避开上覆介质的影响,且无需考虑上覆介质的速度模型,因此也被称为“虚震源法”.Calvert等[21 ] 在2004年将VSP数据转化为SWP单井剖面记录;Mehta等[22 ] 在2007年先对地震数据进行波场分离,再运用地震干涉技术,取得了显著效果;Gaiser等[23 ] 在2010年应用折射波干涉技术从OBS数据中提取了P波和S波信息;Bharadwaj等[24 ] 在2012年改进了折射波干涉技术,提高了成像精度;Wapenaar等[25 ] 在2014年应用地震干涉技术从反射波中提取出了格林函数.此外,地震干涉技术在电磁法勘探中也有诸多应用进展. ...
Improving the virtual source method by wavefield separation
1
2007
... 地震干涉技术在勘探地震领域应用广泛,它能够将地表激发地下接收的地震信号转化为地下激发地下接收的地震信号,从而避开上覆介质的影响,且无需考虑上覆介质的速度模型,因此也被称为“虚震源法”.Calvert等[21 ] 在2004年将VSP数据转化为SWP单井剖面记录;Mehta等[22 ] 在2007年先对地震数据进行波场分离,再运用地震干涉技术,取得了显著效果;Gaiser等[23 ] 在2010年应用折射波干涉技术从OBS数据中提取了P波和S波信息;Bharadwaj等[24 ] 在2012年改进了折射波干涉技术,提高了成像精度;Wapenaar等[25 ] 在2014年应用地震干涉技术从反射波中提取出了格林函数.此外,地震干涉技术在电磁法勘探中也有诸多应用进展. ...
Elastic interferometry for ocean bottom cable data:Theory and examples
1
2010
... 地震干涉技术在勘探地震领域应用广泛,它能够将地表激发地下接收的地震信号转化为地下激发地下接收的地震信号,从而避开上覆介质的影响,且无需考虑上覆介质的速度模型,因此也被称为“虚震源法”.Calvert等[21 ] 在2004年将VSP数据转化为SWP单井剖面记录;Mehta等[22 ] 在2007年先对地震数据进行波场分离,再运用地震干涉技术,取得了显著效果;Gaiser等[23 ] 在2010年应用折射波干涉技术从OBS数据中提取了P波和S波信息;Bharadwaj等[24 ] 在2012年改进了折射波干涉技术,提高了成像精度;Wapenaar等[25 ] 在2014年应用地震干涉技术从反射波中提取出了格林函数.此外,地震干涉技术在电磁法勘探中也有诸多应用进展. ...
Theory of supervirtual refraction interferometry
1
2012
... 地震干涉技术在勘探地震领域应用广泛,它能够将地表激发地下接收的地震信号转化为地下激发地下接收的地震信号,从而避开上覆介质的影响,且无需考虑上覆介质的速度模型,因此也被称为“虚震源法”.Calvert等[21 ] 在2004年将VSP数据转化为SWP单井剖面记录;Mehta等[22 ] 在2007年先对地震数据进行波场分离,再运用地震干涉技术,取得了显著效果;Gaiser等[23 ] 在2010年应用折射波干涉技术从OBS数据中提取了P波和S波信息;Bharadwaj等[24 ] 在2012年改进了折射波干涉技术,提高了成像精度;Wapenaar等[25 ] 在2014年应用地震干涉技术从反射波中提取出了格林函数.此外,地震干涉技术在电磁法勘探中也有诸多应用进展. ...
Green's function retrieval from reflection data,in absence of a receiver at the virtual source position
1
2014
... 地震干涉技术在勘探地震领域应用广泛,它能够将地表激发地下接收的地震信号转化为地下激发地下接收的地震信号,从而避开上覆介质的影响,且无需考虑上覆介质的速度模型,因此也被称为“虚震源法”.Calvert等[21 ] 在2004年将VSP数据转化为SWP单井剖面记录;Mehta等[22 ] 在2007年先对地震数据进行波场分离,再运用地震干涉技术,取得了显著效果;Gaiser等[23 ] 在2010年应用折射波干涉技术从OBS数据中提取了P波和S波信息;Bharadwaj等[24 ] 在2012年改进了折射波干涉技术,提高了成像精度;Wapenaar等[25 ] 在2014年应用地震干涉技术从反射波中提取出了格林函数.此外,地震干涉技术在电磁法勘探中也有诸多应用进展. ...
利用背景噪声进行地震成像的新方法
1
2007
... 国内对地震干涉技术的研究同样取得了显著进展.齐诚等[26 ] 在2007年首次在国内提出利用地震噪声对地下介质进行成像;王宝善等[27 ] 在2009年利用云南固定台站观测到的背景噪声进行互相关分析,得到了格林函数,并成功估计了地震速度的变化及波速变化;陶毅等[28 ] 在2010年对地震干涉技术进行了详细概述,并进一步阐明了未来的研究方向;朱恒等[29 ] 在2012年将地震干涉理论与Radon变换相结合,与传统时空域地震干涉方法相比,该方法去除了大量虚假信息,并通过了大量的理论及实际数据验证;2015年,朱恒等[30 ] 又分别提出了线性Radon域和抛物Radon域的地震干涉技术,显著提高了虚拟震源地震数据记录的质量;程浩[31 ] 在2016年进行了被动源地震干涉一次波估计,并对“稳相点”进行了深入探讨;孙宇等[32 ] 在2018年提出了基于Bayes算法的线性Radon域地震干涉技术,能够对层间多次波进行较好的预测和压制;王立歆等[33 ] 在2021年运用CURTIS炮—检地震干涉技术,研发了可控震源散射面波干涉匹配与预测技术,并将其应用于解决沙漠地区常见的严重黑三角噪声问题.该方法依靠实际地震数据驱动,无需速度模型,能够有效消除散射面波.但黑三角区域内的噪声种类过多,噪声压制机制仍需进一步研究;阮小敏等[34 ] 在2023年研究了多种地震干涉方法,构建了虚拟炮记录,并将其应用于多次波的压制.该方法能够在面波主导的背景噪声中提取有效信号,对被动源原始数据的预处理做出了重要贡献. ...
利用背景噪声进行地震成像的新方法
1
2007
... 国内对地震干涉技术的研究同样取得了显著进展.齐诚等[26 ] 在2007年首次在国内提出利用地震噪声对地下介质进行成像;王宝善等[27 ] 在2009年利用云南固定台站观测到的背景噪声进行互相关分析,得到了格林函数,并成功估计了地震速度的变化及波速变化;陶毅等[28 ] 在2010年对地震干涉技术进行了详细概述,并进一步阐明了未来的研究方向;朱恒等[29 ] 在2012年将地震干涉理论与Radon变换相结合,与传统时空域地震干涉方法相比,该方法去除了大量虚假信息,并通过了大量的理论及实际数据验证;2015年,朱恒等[30 ] 又分别提出了线性Radon域和抛物Radon域的地震干涉技术,显著提高了虚拟震源地震数据记录的质量;程浩[31 ] 在2016年进行了被动源地震干涉一次波估计,并对“稳相点”进行了深入探讨;孙宇等[32 ] 在2018年提出了基于Bayes算法的线性Radon域地震干涉技术,能够对层间多次波进行较好的预测和压制;王立歆等[33 ] 在2021年运用CURTIS炮—检地震干涉技术,研发了可控震源散射面波干涉匹配与预测技术,并将其应用于解决沙漠地区常见的严重黑三角噪声问题.该方法依靠实际地震数据驱动,无需速度模型,能够有效消除散射面波.但黑三角区域内的噪声种类过多,噪声压制机制仍需进一步研究;阮小敏等[34 ] 在2023年研究了多种地震干涉方法,构建了虚拟炮记录,并将其应用于多次波的压制.该方法能够在面波主导的背景噪声中提取有效信号,对被动源原始数据的预处理做出了重要贡献. ...
地下介质波速变化的主动和被动源监测
1
... 国内对地震干涉技术的研究同样取得了显著进展.齐诚等[26 ] 在2007年首次在国内提出利用地震噪声对地下介质进行成像;王宝善等[27 ] 在2009年利用云南固定台站观测到的背景噪声进行互相关分析,得到了格林函数,并成功估计了地震速度的变化及波速变化;陶毅等[28 ] 在2010年对地震干涉技术进行了详细概述,并进一步阐明了未来的研究方向;朱恒等[29 ] 在2012年将地震干涉理论与Radon变换相结合,与传统时空域地震干涉方法相比,该方法去除了大量虚假信息,并通过了大量的理论及实际数据验证;2015年,朱恒等[30 ] 又分别提出了线性Radon域和抛物Radon域的地震干涉技术,显著提高了虚拟震源地震数据记录的质量;程浩[31 ] 在2016年进行了被动源地震干涉一次波估计,并对“稳相点”进行了深入探讨;孙宇等[32 ] 在2018年提出了基于Bayes算法的线性Radon域地震干涉技术,能够对层间多次波进行较好的预测和压制;王立歆等[33 ] 在2021年运用CURTIS炮—检地震干涉技术,研发了可控震源散射面波干涉匹配与预测技术,并将其应用于解决沙漠地区常见的严重黑三角噪声问题.该方法依靠实际地震数据驱动,无需速度模型,能够有效消除散射面波.但黑三角区域内的噪声种类过多,噪声压制机制仍需进一步研究;阮小敏等[34 ] 在2023年研究了多种地震干涉方法,构建了虚拟炮记录,并将其应用于多次波的压制.该方法能够在面波主导的背景噪声中提取有效信号,对被动源原始数据的预处理做出了重要贡献. ...
地下介质波速变化的主动和被动源监测
1
... 国内对地震干涉技术的研究同样取得了显著进展.齐诚等[26 ] 在2007年首次在国内提出利用地震噪声对地下介质进行成像;王宝善等[27 ] 在2009年利用云南固定台站观测到的背景噪声进行互相关分析,得到了格林函数,并成功估计了地震速度的变化及波速变化;陶毅等[28 ] 在2010年对地震干涉技术进行了详细概述,并进一步阐明了未来的研究方向;朱恒等[29 ] 在2012年将地震干涉理论与Radon变换相结合,与传统时空域地震干涉方法相比,该方法去除了大量虚假信息,并通过了大量的理论及实际数据验证;2015年,朱恒等[30 ] 又分别提出了线性Radon域和抛物Radon域的地震干涉技术,显著提高了虚拟震源地震数据记录的质量;程浩[31 ] 在2016年进行了被动源地震干涉一次波估计,并对“稳相点”进行了深入探讨;孙宇等[32 ] 在2018年提出了基于Bayes算法的线性Radon域地震干涉技术,能够对层间多次波进行较好的预测和压制;王立歆等[33 ] 在2021年运用CURTIS炮—检地震干涉技术,研发了可控震源散射面波干涉匹配与预测技术,并将其应用于解决沙漠地区常见的严重黑三角噪声问题.该方法依靠实际地震数据驱动,无需速度模型,能够有效消除散射面波.但黑三角区域内的噪声种类过多,噪声压制机制仍需进一步研究;阮小敏等[34 ] 在2023年研究了多种地震干涉方法,构建了虚拟炮记录,并将其应用于多次波的压制.该方法能够在面波主导的背景噪声中提取有效信号,对被动源原始数据的预处理做出了重要贡献. ...
地震波干涉法研究进展综述
1
2010
... 国内对地震干涉技术的研究同样取得了显著进展.齐诚等[26 ] 在2007年首次在国内提出利用地震噪声对地下介质进行成像;王宝善等[27 ] 在2009年利用云南固定台站观测到的背景噪声进行互相关分析,得到了格林函数,并成功估计了地震速度的变化及波速变化;陶毅等[28 ] 在2010年对地震干涉技术进行了详细概述,并进一步阐明了未来的研究方向;朱恒等[29 ] 在2012年将地震干涉理论与Radon变换相结合,与传统时空域地震干涉方法相比,该方法去除了大量虚假信息,并通过了大量的理论及实际数据验证;2015年,朱恒等[30 ] 又分别提出了线性Radon域和抛物Radon域的地震干涉技术,显著提高了虚拟震源地震数据记录的质量;程浩[31 ] 在2016年进行了被动源地震干涉一次波估计,并对“稳相点”进行了深入探讨;孙宇等[32 ] 在2018年提出了基于Bayes算法的线性Radon域地震干涉技术,能够对层间多次波进行较好的预测和压制;王立歆等[33 ] 在2021年运用CURTIS炮—检地震干涉技术,研发了可控震源散射面波干涉匹配与预测技术,并将其应用于解决沙漠地区常见的严重黑三角噪声问题.该方法依靠实际地震数据驱动,无需速度模型,能够有效消除散射面波.但黑三角区域内的噪声种类过多,噪声压制机制仍需进一步研究;阮小敏等[34 ] 在2023年研究了多种地震干涉方法,构建了虚拟炮记录,并将其应用于多次波的压制.该方法能够在面波主导的背景噪声中提取有效信号,对被动源原始数据的预处理做出了重要贡献. ...
地震波干涉法研究进展综述
1
2010
... 国内对地震干涉技术的研究同样取得了显著进展.齐诚等[26 ] 在2007年首次在国内提出利用地震噪声对地下介质进行成像;王宝善等[27 ] 在2009年利用云南固定台站观测到的背景噪声进行互相关分析,得到了格林函数,并成功估计了地震速度的变化及波速变化;陶毅等[28 ] 在2010年对地震干涉技术进行了详细概述,并进一步阐明了未来的研究方向;朱恒等[29 ] 在2012年将地震干涉理论与Radon变换相结合,与传统时空域地震干涉方法相比,该方法去除了大量虚假信息,并通过了大量的理论及实际数据验证;2015年,朱恒等[30 ] 又分别提出了线性Radon域和抛物Radon域的地震干涉技术,显著提高了虚拟震源地震数据记录的质量;程浩[31 ] 在2016年进行了被动源地震干涉一次波估计,并对“稳相点”进行了深入探讨;孙宇等[32 ] 在2018年提出了基于Bayes算法的线性Radon域地震干涉技术,能够对层间多次波进行较好的预测和压制;王立歆等[33 ] 在2021年运用CURTIS炮—检地震干涉技术,研发了可控震源散射面波干涉匹配与预测技术,并将其应用于解决沙漠地区常见的严重黑三角噪声问题.该方法依靠实际地震数据驱动,无需速度模型,能够有效消除散射面波.但黑三角区域内的噪声种类过多,噪声压制机制仍需进一步研究;阮小敏等[34 ] 在2023年研究了多种地震干涉方法,构建了虚拟炮记录,并将其应用于多次波的压制.该方法能够在面波主导的背景噪声中提取有效信号,对被动源原始数据的预处理做出了重要贡献. ...
地震干涉技术被动源地震成像
1
2012
... 国内对地震干涉技术的研究同样取得了显著进展.齐诚等[26 ] 在2007年首次在国内提出利用地震噪声对地下介质进行成像;王宝善等[27 ] 在2009年利用云南固定台站观测到的背景噪声进行互相关分析,得到了格林函数,并成功估计了地震速度的变化及波速变化;陶毅等[28 ] 在2010年对地震干涉技术进行了详细概述,并进一步阐明了未来的研究方向;朱恒等[29 ] 在2012年将地震干涉理论与Radon变换相结合,与传统时空域地震干涉方法相比,该方法去除了大量虚假信息,并通过了大量的理论及实际数据验证;2015年,朱恒等[30 ] 又分别提出了线性Radon域和抛物Radon域的地震干涉技术,显著提高了虚拟震源地震数据记录的质量;程浩[31 ] 在2016年进行了被动源地震干涉一次波估计,并对“稳相点”进行了深入探讨;孙宇等[32 ] 在2018年提出了基于Bayes算法的线性Radon域地震干涉技术,能够对层间多次波进行较好的预测和压制;王立歆等[33 ] 在2021年运用CURTIS炮—检地震干涉技术,研发了可控震源散射面波干涉匹配与预测技术,并将其应用于解决沙漠地区常见的严重黑三角噪声问题.该方法依靠实际地震数据驱动,无需速度模型,能够有效消除散射面波.但黑三角区域内的噪声种类过多,噪声压制机制仍需进一步研究;阮小敏等[34 ] 在2023年研究了多种地震干涉方法,构建了虚拟炮记录,并将其应用于多次波的压制.该方法能够在面波主导的背景噪声中提取有效信号,对被动源原始数据的预处理做出了重要贡献. ...
地震干涉技术被动源地震成像
1
2012
... 国内对地震干涉技术的研究同样取得了显著进展.齐诚等[26 ] 在2007年首次在国内提出利用地震噪声对地下介质进行成像;王宝善等[27 ] 在2009年利用云南固定台站观测到的背景噪声进行互相关分析,得到了格林函数,并成功估计了地震速度的变化及波速变化;陶毅等[28 ] 在2010年对地震干涉技术进行了详细概述,并进一步阐明了未来的研究方向;朱恒等[29 ] 在2012年将地震干涉理论与Radon变换相结合,与传统时空域地震干涉方法相比,该方法去除了大量虚假信息,并通过了大量的理论及实际数据验证;2015年,朱恒等[30 ] 又分别提出了线性Radon域和抛物Radon域的地震干涉技术,显著提高了虚拟震源地震数据记录的质量;程浩[31 ] 在2016年进行了被动源地震干涉一次波估计,并对“稳相点”进行了深入探讨;孙宇等[32 ] 在2018年提出了基于Bayes算法的线性Radon域地震干涉技术,能够对层间多次波进行较好的预测和压制;王立歆等[33 ] 在2021年运用CURTIS炮—检地震干涉技术,研发了可控震源散射面波干涉匹配与预测技术,并将其应用于解决沙漠地区常见的严重黑三角噪声问题.该方法依靠实际地震数据驱动,无需速度模型,能够有效消除散射面波.但黑三角区域内的噪声种类过多,噪声压制机制仍需进一步研究;阮小敏等[34 ] 在2023年研究了多种地震干涉方法,构建了虚拟炮记录,并将其应用于多次波的压制.该方法能够在面波主导的背景噪声中提取有效信号,对被动源原始数据的预处理做出了重要贡献. ...
抛物Radon域地震干涉技术
1
2015
... 国内对地震干涉技术的研究同样取得了显著进展.齐诚等[26 ] 在2007年首次在国内提出利用地震噪声对地下介质进行成像;王宝善等[27 ] 在2009年利用云南固定台站观测到的背景噪声进行互相关分析,得到了格林函数,并成功估计了地震速度的变化及波速变化;陶毅等[28 ] 在2010年对地震干涉技术进行了详细概述,并进一步阐明了未来的研究方向;朱恒等[29 ] 在2012年将地震干涉理论与Radon变换相结合,与传统时空域地震干涉方法相比,该方法去除了大量虚假信息,并通过了大量的理论及实际数据验证;2015年,朱恒等[30 ] 又分别提出了线性Radon域和抛物Radon域的地震干涉技术,显著提高了虚拟震源地震数据记录的质量;程浩[31 ] 在2016年进行了被动源地震干涉一次波估计,并对“稳相点”进行了深入探讨;孙宇等[32 ] 在2018年提出了基于Bayes算法的线性Radon域地震干涉技术,能够对层间多次波进行较好的预测和压制;王立歆等[33 ] 在2021年运用CURTIS炮—检地震干涉技术,研发了可控震源散射面波干涉匹配与预测技术,并将其应用于解决沙漠地区常见的严重黑三角噪声问题.该方法依靠实际地震数据驱动,无需速度模型,能够有效消除散射面波.但黑三角区域内的噪声种类过多,噪声压制机制仍需进一步研究;阮小敏等[34 ] 在2023年研究了多种地震干涉方法,构建了虚拟炮记录,并将其应用于多次波的压制.该方法能够在面波主导的背景噪声中提取有效信号,对被动源原始数据的预处理做出了重要贡献. ...
抛物Radon域地震干涉技术
1
2015
... 国内对地震干涉技术的研究同样取得了显著进展.齐诚等[26 ] 在2007年首次在国内提出利用地震噪声对地下介质进行成像;王宝善等[27 ] 在2009年利用云南固定台站观测到的背景噪声进行互相关分析,得到了格林函数,并成功估计了地震速度的变化及波速变化;陶毅等[28 ] 在2010年对地震干涉技术进行了详细概述,并进一步阐明了未来的研究方向;朱恒等[29 ] 在2012年将地震干涉理论与Radon变换相结合,与传统时空域地震干涉方法相比,该方法去除了大量虚假信息,并通过了大量的理论及实际数据验证;2015年,朱恒等[30 ] 又分别提出了线性Radon域和抛物Radon域的地震干涉技术,显著提高了虚拟震源地震数据记录的质量;程浩[31 ] 在2016年进行了被动源地震干涉一次波估计,并对“稳相点”进行了深入探讨;孙宇等[32 ] 在2018年提出了基于Bayes算法的线性Radon域地震干涉技术,能够对层间多次波进行较好的预测和压制;王立歆等[33 ] 在2021年运用CURTIS炮—检地震干涉技术,研发了可控震源散射面波干涉匹配与预测技术,并将其应用于解决沙漠地区常见的严重黑三角噪声问题.该方法依靠实际地震数据驱动,无需速度模型,能够有效消除散射面波.但黑三角区域内的噪声种类过多,噪声压制机制仍需进一步研究;阮小敏等[34 ] 在2023年研究了多种地震干涉方法,构建了虚拟炮记录,并将其应用于多次波的压制.该方法能够在面波主导的背景噪声中提取有效信号,对被动源原始数据的预处理做出了重要贡献. ...
1
2016
... 国内对地震干涉技术的研究同样取得了显著进展.齐诚等[26 ] 在2007年首次在国内提出利用地震噪声对地下介质进行成像;王宝善等[27 ] 在2009年利用云南固定台站观测到的背景噪声进行互相关分析,得到了格林函数,并成功估计了地震速度的变化及波速变化;陶毅等[28 ] 在2010年对地震干涉技术进行了详细概述,并进一步阐明了未来的研究方向;朱恒等[29 ] 在2012年将地震干涉理论与Radon变换相结合,与传统时空域地震干涉方法相比,该方法去除了大量虚假信息,并通过了大量的理论及实际数据验证;2015年,朱恒等[30 ] 又分别提出了线性Radon域和抛物Radon域的地震干涉技术,显著提高了虚拟震源地震数据记录的质量;程浩[31 ] 在2016年进行了被动源地震干涉一次波估计,并对“稳相点”进行了深入探讨;孙宇等[32 ] 在2018年提出了基于Bayes算法的线性Radon域地震干涉技术,能够对层间多次波进行较好的预测和压制;王立歆等[33 ] 在2021年运用CURTIS炮—检地震干涉技术,研发了可控震源散射面波干涉匹配与预测技术,并将其应用于解决沙漠地区常见的严重黑三角噪声问题.该方法依靠实际地震数据驱动,无需速度模型,能够有效消除散射面波.但黑三角区域内的噪声种类过多,噪声压制机制仍需进一步研究;阮小敏等[34 ] 在2023年研究了多种地震干涉方法,构建了虚拟炮记录,并将其应用于多次波的压制.该方法能够在面波主导的背景噪声中提取有效信号,对被动源原始数据的预处理做出了重要贡献. ...
1
2016
... 国内对地震干涉技术的研究同样取得了显著进展.齐诚等[26 ] 在2007年首次在国内提出利用地震噪声对地下介质进行成像;王宝善等[27 ] 在2009年利用云南固定台站观测到的背景噪声进行互相关分析,得到了格林函数,并成功估计了地震速度的变化及波速变化;陶毅等[28 ] 在2010年对地震干涉技术进行了详细概述,并进一步阐明了未来的研究方向;朱恒等[29 ] 在2012年将地震干涉理论与Radon变换相结合,与传统时空域地震干涉方法相比,该方法去除了大量虚假信息,并通过了大量的理论及实际数据验证;2015年,朱恒等[30 ] 又分别提出了线性Radon域和抛物Radon域的地震干涉技术,显著提高了虚拟震源地震数据记录的质量;程浩[31 ] 在2016年进行了被动源地震干涉一次波估计,并对“稳相点”进行了深入探讨;孙宇等[32 ] 在2018年提出了基于Bayes算法的线性Radon域地震干涉技术,能够对层间多次波进行较好的预测和压制;王立歆等[33 ] 在2021年运用CURTIS炮—检地震干涉技术,研发了可控震源散射面波干涉匹配与预测技术,并将其应用于解决沙漠地区常见的严重黑三角噪声问题.该方法依靠实际地震数据驱动,无需速度模型,能够有效消除散射面波.但黑三角区域内的噪声种类过多,噪声压制机制仍需进一步研究;阮小敏等[34 ] 在2023年研究了多种地震干涉方法,构建了虚拟炮记录,并将其应用于多次波的压制.该方法能够在面波主导的背景噪声中提取有效信号,对被动源原始数据的预处理做出了重要贡献. ...
1
2018
... 国内对地震干涉技术的研究同样取得了显著进展.齐诚等[26 ] 在2007年首次在国内提出利用地震噪声对地下介质进行成像;王宝善等[27 ] 在2009年利用云南固定台站观测到的背景噪声进行互相关分析,得到了格林函数,并成功估计了地震速度的变化及波速变化;陶毅等[28 ] 在2010年对地震干涉技术进行了详细概述,并进一步阐明了未来的研究方向;朱恒等[29 ] 在2012年将地震干涉理论与Radon变换相结合,与传统时空域地震干涉方法相比,该方法去除了大量虚假信息,并通过了大量的理论及实际数据验证;2015年,朱恒等[30 ] 又分别提出了线性Radon域和抛物Radon域的地震干涉技术,显著提高了虚拟震源地震数据记录的质量;程浩[31 ] 在2016年进行了被动源地震干涉一次波估计,并对“稳相点”进行了深入探讨;孙宇等[32 ] 在2018年提出了基于Bayes算法的线性Radon域地震干涉技术,能够对层间多次波进行较好的预测和压制;王立歆等[33 ] 在2021年运用CURTIS炮—检地震干涉技术,研发了可控震源散射面波干涉匹配与预测技术,并将其应用于解决沙漠地区常见的严重黑三角噪声问题.该方法依靠实际地震数据驱动,无需速度模型,能够有效消除散射面波.但黑三角区域内的噪声种类过多,噪声压制机制仍需进一步研究;阮小敏等[34 ] 在2023年研究了多种地震干涉方法,构建了虚拟炮记录,并将其应用于多次波的压制.该方法能够在面波主导的背景噪声中提取有效信号,对被动源原始数据的预处理做出了重要贡献. ...
1
2018
... 国内对地震干涉技术的研究同样取得了显著进展.齐诚等[26 ] 在2007年首次在国内提出利用地震噪声对地下介质进行成像;王宝善等[27 ] 在2009年利用云南固定台站观测到的背景噪声进行互相关分析,得到了格林函数,并成功估计了地震速度的变化及波速变化;陶毅等[28 ] 在2010年对地震干涉技术进行了详细概述,并进一步阐明了未来的研究方向;朱恒等[29 ] 在2012年将地震干涉理论与Radon变换相结合,与传统时空域地震干涉方法相比,该方法去除了大量虚假信息,并通过了大量的理论及实际数据验证;2015年,朱恒等[30 ] 又分别提出了线性Radon域和抛物Radon域的地震干涉技术,显著提高了虚拟震源地震数据记录的质量;程浩[31 ] 在2016年进行了被动源地震干涉一次波估计,并对“稳相点”进行了深入探讨;孙宇等[32 ] 在2018年提出了基于Bayes算法的线性Radon域地震干涉技术,能够对层间多次波进行较好的预测和压制;王立歆等[33 ] 在2021年运用CURTIS炮—检地震干涉技术,研发了可控震源散射面波干涉匹配与预测技术,并将其应用于解决沙漠地区常见的严重黑三角噪声问题.该方法依靠实际地震数据驱动,无需速度模型,能够有效消除散射面波.但黑三角区域内的噪声种类过多,噪声压制机制仍需进一步研究;阮小敏等[34 ] 在2023年研究了多种地震干涉方法,构建了虚拟炮记录,并将其应用于多次波的压制.该方法能够在面波主导的背景噪声中提取有效信号,对被动源原始数据的预处理做出了重要贡献. ...
基于地震干涉法的可控震源黑三角噪声压制技术及应用
1
2021
... 国内对地震干涉技术的研究同样取得了显著进展.齐诚等[26 ] 在2007年首次在国内提出利用地震噪声对地下介质进行成像;王宝善等[27 ] 在2009年利用云南固定台站观测到的背景噪声进行互相关分析,得到了格林函数,并成功估计了地震速度的变化及波速变化;陶毅等[28 ] 在2010年对地震干涉技术进行了详细概述,并进一步阐明了未来的研究方向;朱恒等[29 ] 在2012年将地震干涉理论与Radon变换相结合,与传统时空域地震干涉方法相比,该方法去除了大量虚假信息,并通过了大量的理论及实际数据验证;2015年,朱恒等[30 ] 又分别提出了线性Radon域和抛物Radon域的地震干涉技术,显著提高了虚拟震源地震数据记录的质量;程浩[31 ] 在2016年进行了被动源地震干涉一次波估计,并对“稳相点”进行了深入探讨;孙宇等[32 ] 在2018年提出了基于Bayes算法的线性Radon域地震干涉技术,能够对层间多次波进行较好的预测和压制;王立歆等[33 ] 在2021年运用CURTIS炮—检地震干涉技术,研发了可控震源散射面波干涉匹配与预测技术,并将其应用于解决沙漠地区常见的严重黑三角噪声问题.该方法依靠实际地震数据驱动,无需速度模型,能够有效消除散射面波.但黑三角区域内的噪声种类过多,噪声压制机制仍需进一步研究;阮小敏等[34 ] 在2023年研究了多种地震干涉方法,构建了虚拟炮记录,并将其应用于多次波的压制.该方法能够在面波主导的背景噪声中提取有效信号,对被动源原始数据的预处理做出了重要贡献. ...
基于地震干涉法的可控震源黑三角噪声压制技术及应用
1
2021
... 国内对地震干涉技术的研究同样取得了显著进展.齐诚等[26 ] 在2007年首次在国内提出利用地震噪声对地下介质进行成像;王宝善等[27 ] 在2009年利用云南固定台站观测到的背景噪声进行互相关分析,得到了格林函数,并成功估计了地震速度的变化及波速变化;陶毅等[28 ] 在2010年对地震干涉技术进行了详细概述,并进一步阐明了未来的研究方向;朱恒等[29 ] 在2012年将地震干涉理论与Radon变换相结合,与传统时空域地震干涉方法相比,该方法去除了大量虚假信息,并通过了大量的理论及实际数据验证;2015年,朱恒等[30 ] 又分别提出了线性Radon域和抛物Radon域的地震干涉技术,显著提高了虚拟震源地震数据记录的质量;程浩[31 ] 在2016年进行了被动源地震干涉一次波估计,并对“稳相点”进行了深入探讨;孙宇等[32 ] 在2018年提出了基于Bayes算法的线性Radon域地震干涉技术,能够对层间多次波进行较好的预测和压制;王立歆等[33 ] 在2021年运用CURTIS炮—检地震干涉技术,研发了可控震源散射面波干涉匹配与预测技术,并将其应用于解决沙漠地区常见的严重黑三角噪声问题.该方法依靠实际地震数据驱动,无需速度模型,能够有效消除散射面波.但黑三角区域内的噪声种类过多,噪声压制机制仍需进一步研究;阮小敏等[34 ] 在2023年研究了多种地震干涉方法,构建了虚拟炮记录,并将其应用于多次波的压制.该方法能够在面波主导的背景噪声中提取有效信号,对被动源原始数据的预处理做出了重要贡献. ...
被动源反射地震勘探研究进展
1
2023
... 国内对地震干涉技术的研究同样取得了显著进展.齐诚等[26 ] 在2007年首次在国内提出利用地震噪声对地下介质进行成像;王宝善等[27 ] 在2009年利用云南固定台站观测到的背景噪声进行互相关分析,得到了格林函数,并成功估计了地震速度的变化及波速变化;陶毅等[28 ] 在2010年对地震干涉技术进行了详细概述,并进一步阐明了未来的研究方向;朱恒等[29 ] 在2012年将地震干涉理论与Radon变换相结合,与传统时空域地震干涉方法相比,该方法去除了大量虚假信息,并通过了大量的理论及实际数据验证;2015年,朱恒等[30 ] 又分别提出了线性Radon域和抛物Radon域的地震干涉技术,显著提高了虚拟震源地震数据记录的质量;程浩[31 ] 在2016年进行了被动源地震干涉一次波估计,并对“稳相点”进行了深入探讨;孙宇等[32 ] 在2018年提出了基于Bayes算法的线性Radon域地震干涉技术,能够对层间多次波进行较好的预测和压制;王立歆等[33 ] 在2021年运用CURTIS炮—检地震干涉技术,研发了可控震源散射面波干涉匹配与预测技术,并将其应用于解决沙漠地区常见的严重黑三角噪声问题.该方法依靠实际地震数据驱动,无需速度模型,能够有效消除散射面波.但黑三角区域内的噪声种类过多,噪声压制机制仍需进一步研究;阮小敏等[34 ] 在2023年研究了多种地震干涉方法,构建了虚拟炮记录,并将其应用于多次波的压制.该方法能够在面波主导的背景噪声中提取有效信号,对被动源原始数据的预处理做出了重要贡献. ...
被动源反射地震勘探研究进展
1
2023
... 国内对地震干涉技术的研究同样取得了显著进展.齐诚等[26 ] 在2007年首次在国内提出利用地震噪声对地下介质进行成像;王宝善等[27 ] 在2009年利用云南固定台站观测到的背景噪声进行互相关分析,得到了格林函数,并成功估计了地震速度的变化及波速变化;陶毅等[28 ] 在2010年对地震干涉技术进行了详细概述,并进一步阐明了未来的研究方向;朱恒等[29 ] 在2012年将地震干涉理论与Radon变换相结合,与传统时空域地震干涉方法相比,该方法去除了大量虚假信息,并通过了大量的理论及实际数据验证;2015年,朱恒等[30 ] 又分别提出了线性Radon域和抛物Radon域的地震干涉技术,显著提高了虚拟震源地震数据记录的质量;程浩[31 ] 在2016年进行了被动源地震干涉一次波估计,并对“稳相点”进行了深入探讨;孙宇等[32 ] 在2018年提出了基于Bayes算法的线性Radon域地震干涉技术,能够对层间多次波进行较好的预测和压制;王立歆等[33 ] 在2021年运用CURTIS炮—检地震干涉技术,研发了可控震源散射面波干涉匹配与预测技术,并将其应用于解决沙漠地区常见的严重黑三角噪声问题.该方法依靠实际地震数据驱动,无需速度模型,能够有效消除散射面波.但黑三角区域内的噪声种类过多,噪声压制机制仍需进一步研究;阮小敏等[34 ] 在2023年研究了多种地震干涉方法,构建了虚拟炮记录,并将其应用于多次波的压制.该方法能够在面波主导的背景噪声中提取有效信号,对被动源原始数据的预处理做出了重要贡献. ...
An elastodynamic reciprocity theorem for linear,viscoelastic media
1
1966
... 下面简单介绍交互量这一概念.交互量在物理学中通常指两个或多个系统之间相互作用的量或度量,可以用来描述声源向介质中注入声波的效果以及介质中声波的传播和反射.在本文中,交互量指声学介质和声源之间的相互作用量或相互作用强度.交互量[35 ] 可以写为: ...
Time-reversed acoustics
1
1999
... 本文研究的介质为无损介质,可以应用时间反转不变性原理[36 ] .在频率域中,时间反转被复共轭代替.因此,当震源项为${\hat{f}}_{i}^{*}$ ${\hat{q}}^{*}$ ( *表示复共轭)时,${\hat{p}}^{*}$ ${\hat{v}}_{i}^{*}$ [37 ] : ...
Green's function representation for seismic interferometry by deconvolution
1
... 本文研究的介质为无损介质,可以应用时间反转不变性原理[36 ] .在频率域中,时间反转被复共轭代替.因此,当震源项为${\hat{f}}_{i}^{*}$ ${\hat{q}}^{*}$ ( *表示复共轭)时,${\hat{p}}^{*}$ ${\hat{v}}_{i}^{*}$ [37 ] : ...
1
2009
... Sigsbee2B模型采用地表吸收边界条件模拟出来的中间激发全接收的单炮记录见图6b ,该数据记录包含有一次波和多次波;Sigsbee2B模型采用自由地表吸收边界条件模拟出来的中间激发全接收的单炮记录见图6c ,该数据记录只含有一次波;通过褶积型地震干涉预测出来的多次波见图6d ,通过与原始记录的对比,发现该方法能够较好地预测多次波.该方法在Sigsbee2B模型上对多次波的正确预测,给后续多次波的成像打下了基础.另外,需要指出的是:在图6d 中预测出的多次波存在同相轴粗的问题,这是基于地震干涉方法进行多次波预测构建所不可避免的[38 ] ,后续将继续在该方向进行研究、完善. ...
1
2009
... Sigsbee2B模型采用地表吸收边界条件模拟出来的中间激发全接收的单炮记录见图6b ,该数据记录包含有一次波和多次波;Sigsbee2B模型采用自由地表吸收边界条件模拟出来的中间激发全接收的单炮记录见图6c ,该数据记录只含有一次波;通过褶积型地震干涉预测出来的多次波见图6d ,通过与原始记录的对比,发现该方法能够较好地预测多次波.该方法在Sigsbee2B模型上对多次波的正确预测,给后续多次波的成像打下了基础.另外,需要指出的是:在图6d 中预测出的多次波存在同相轴粗的问题,这是基于地震干涉方法进行多次波预测构建所不可避免的[38 ] ,后续将继续在该方向进行研究、完善. ...