0 引言
井震误差校正是深度偏移处理过程中至关重要的步骤。井震误差校正通过求取地震层位深度和井标定层位深度的误差值来对地震层位的深度进行校正,可以在求取VTI介质的Thomsen纵波各向异性参数(δ)的同时,将深度偏移得到的地震层位校正到真实的深度,δ是描述VTI介质纵波各向异性的重要参数,可以反映地震剖面层位厚度和井标定层位厚度的差异。一般来讲,地下介质并不是理想的各向同性介质,而是有不同程度的各向异性性质的介质。常见的各向异性介质有VTI介质(横向各向同性介质)、HTI介质(垂向各向同性介质)、TTI介质(对称轴不垂直的VTI介质),另外还有更为复杂的正交晶系介质和斜交晶系介质[1
常规的井震误差校正方法是在井点处求取地震层位和井标定层位的深度误差,将井点处的深度误差直接沿平面插值,然后利用插值后的井震误差求取全工区的各向异性参数,并进一步求取各向异性速度。当层位厚度变化较大时,该方法对于没有井点控制的区域可能会引起构造畸变和各向异性参数出现异常值,因此,研究人员往往需要对求取的各向异性参数场和各向异性速度场进行一定的编辑和平滑来解决该问题[1]。这种解决办法对处理人员的经验和水平依赖很大,而且会耗费更多的人力和时间。本文针对该问题,提出了一种构造导向的井震误差校正方法。该方法借助“井震误差系数”这一参数,利用层位厚度进行约束对井震误差进行插值,同时采用从浅到深,依次计算井震误差系数并插值井震误差的策略,较好地解决了地层构造复杂、地层厚度变化大引起的井震误差校正后各向异性参数异常和构造畸变的问题,避免了耗时的人工编辑和平滑的步骤。
1 井震误差校正及各向异性参数δ求取的基本原理
式中:Vs是地震成像速度;V0是垂直传播的自激自收速度;θ是入射角;δ和ε是VTI介质的Thomsen各向异性参数。
在深度偏移过程中,一般是首先利用30°入射角以内的偏移道集进行各向同性层析反演迭代,得到一个比较准确的能够拉平道集的各向同性速度,然后利用地震层位和井标定层位的深度误差求取各向异性参数δ,得到各向异性速度[11
式中:Viso为利用30°以内的入射角的CRP道集进行层析迭代得到各向同性速度,该速度可以将30°以内的CRP道集的同相轴拉平;Vvti为待求取的VTI各向异性速度;δ为待求取的各向异性参数。
在各向同性速度深度偏移剖面中,可以读取由浅到深的两套地层,深度分别为H1和H2,其对应的井标定层位的深度分别为M1和M2。地震信号从上覆地层垂直传播到下伏地层的时间为T,那么这两套地层之间的各向同性速度为:
两套地层间的各向异性速度为:
由式(2)~(4)可得:
2 常规的井震误差校正方法和构造导向的井震误差校正方法对比分析
在讨论两种井震误差校正方法时,涉及到的公式变量较多,容易引起混淆,因此,首先对变量的意义进行统一的说明。
δMm:第m套层位的各向异性参数平面分布值;
Hn,m:第n口井在第m套层位处的地震层位深度值;
HMm:第m套层位的地震层位深度平面分布值;
MISn,m:第n口井在第m套层位处的井震误差;
MISMm:第m套层位的井震误差平面分布值;
COEFn,m:第n口井在第m套层位处的井震误差系数;
COEFMm:第m套层位的井震误差系数平面分布值。
2.1 常规的井震误差校正方法
以某工区包含有N口井和M套层位为例。当工区中包含有多口井时,在求取各向异性参数和各向异性速度时,首先需要统计每口井的每套层位和对应井标定层位的深度差,该误差称为井震误差(mistie),该值为井标定层位的深度减去对应地震层位的深度,计为MISn,m;然后对每套层位的所有井的井震误差控制点进行克里金插值,得到一个井震误差平面分布值,计为MISMm。将工区的浮动面计为第0层,从上到下依次为第一层、第二层、…、第m层、…、最深的为第M层。每套层位的深度平面分布值为HMm,层位m和其上覆地层m-1层之间的地层的各向异性参数δ的平面分布值为δMm,则有:
式中:δMm为第m套层位的各向异性参数平面分布值;HMm为第m套层位的地震层位深度平面分布值;MISMm为第m套层位的井震误差平面分布值。
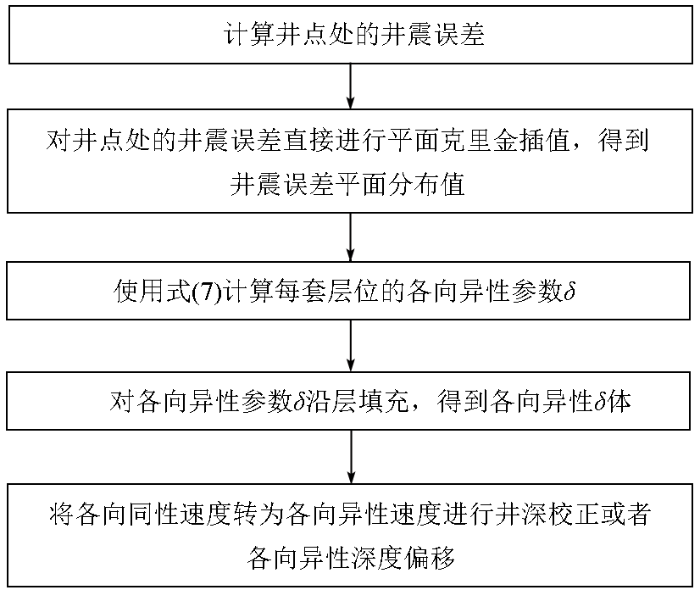
式(6)和式(5)的意义相同,唯一的区别是式(6)中的所有参数为平面分布值,而式(5)中的所有参数为井点处的数值。式(6)即为利用井点处的实测井震误差求取各个层位各向异性参数的传统方法,利用式(6)可求得各向异性参数δ在每套层位中的平面分布值。将δ的平面分布值在对应的层位之间进行填充,即可得到全工区的δ体,再利用式(2)可将全工区的各向同性速度体转为各向异性速度体。这种传统的井震误差校正方法流程如图1所示。
图1
图1
传统的井震误差校正方法流程
Fig.1
Traditional workflow of well-tie correction methodology
图2
2.2 构造导向的井震误差校正方法
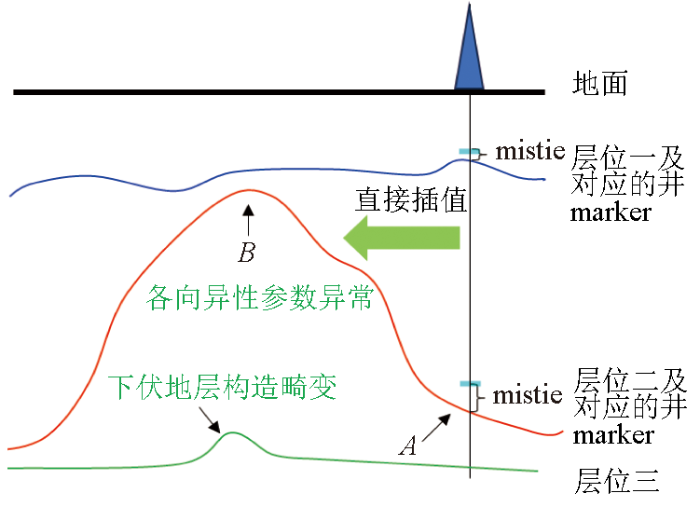
针对该问题,本文提出了一种构造导向的井震误差校正方法(图3),引入“井震误差系数”的概念,利用地层厚度对井震误差进行构造约束,可以使式(6)中的MISMm和MISMm-1的平面插值更合理,可以避免求取的各向异性参数δ出现异常值,同时避免出现构造畸变的现象。
图3
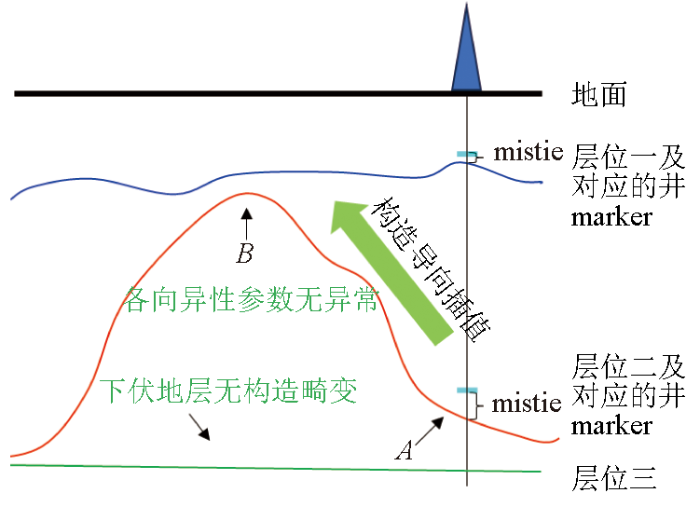
图3中使用构造导向的井震误差校正方法,将A点处的井震误差利用层位厚度约束的方法插值得到B点处的井震误差,B点处的井震误差不会偏大,因此也不会产生各向异性参数异常大值,同时不会引起下伏地层构造畸变。
仍然以某工区包含有N口井和M套层位为例进行讨论。构造导向的井震误差校正方法的第一步仍然是统计每口井的每套层位和对应井标定层位的井震误差MISn,m,然后计算每口井的第一套层位的井点处的“井震误差系数”,计为COEFn,1,计算方法是用第一套层位的井震误差减去第0套层位的井震误差,再除以第一套层位的厚度,即:
式(7)中的所有参数都是井点处的数值,而不是平面分布值。上式中,Hn,1为第n口井在第一套层位处的层位深度值,Hn,0为第n口井在第零套层位(即浮动面)处的层位深度值,二者相减即为第一套层位的厚度值;MISn,1为第n口井在第一套层位处的井震误差,MISn,0为第n口井在第零套层位(即浮动面)处的井震误差,由于浮动面处没有井标定层位,因此MISn,0=0。
求取了每个井点处的井震误差系数值后,对井震误差系数值进行克里金插值,得到第一套层位的井震误差系数在整个工区的平面分布值,表示为COEFM1。再利用COEFM1计算第一套层位的井震误差平面分布值:
式(8)中的所有参数都是平面分布值,而不是井点处的数值。上式中,HM1为第一套层位的深度平面分布值,HM0为第0套层位(即浮动面)的深度平面分布值,二者相减即为第一套层位的厚度;用第一套层位的厚度乘以第一套层位的井震误差系数COEFM1就得到了第一套层位的井震误差,再加上第0套层位的井震误差MISM0就得到了第一套层位的累积井震误差MISM1,第一套层位的累积井震误差就是第一套层位处的实测井震误差。同理,每套层位的实测井震误差都是“累积”井震误差。
式(7)和式(8)为计算第一套层位的井震误差平面分布值的方法,没有直接对第一套层位在井点处的井震误差值进行平面插值,而是先计算“井震误差系数”,对井震误差系数进行平面克里金插值,再借助地层厚度和井震误差系数反算井震误差平面分布值,其核心在于某套层位在各个井点处的实测井震误差是一个“累积”井震误差,其数值是平面分布不稳定的,因而直接进行平面克里金插值是不合理的;而某套层位在各个井点处的井震误差系数不是“累积”的,只是该套层位的地震层位厚度和测井层位厚度的差值与层位厚度的比例系数,其数值是平面分布稳定的,因而对其进行平面克里金插值也是平面分布稳定的,用平面分布稳定的井震误差系数和层位厚度反算得到的井震误差也是平面分布稳定的。
在利用式(8)求得第一套层位的井震误差值的平面分布值后,即可依次求取下面层位的井震误差值的平面分布值。首先需要求取所有井在该套层位处的井震误差系数值,方法是用该套层位的井震误差减去上面一套层位的井震误差,再除以该套层位的厚度:
式(9)和式(7)类似,其中的所有参数都是井点处的数值,而不是平面分布值。公式中的COEFn,m为第n口井在第m层处的井震误差系数。对COEFn,m进行平面插值,得到所有井在第m套层位处的井震误差系数平面分布值,表示为COEFMm,该井震误差系数在平面上是比较稳定的。再利用该套层位的井震误差系数平面分布值反算该套层位的井震误差平面分布值,方法是用该套层位的井震误差系数平面分布值乘以该套层位的厚度平面分布值,再加上上一套层位的井震误差平面分布值,即:
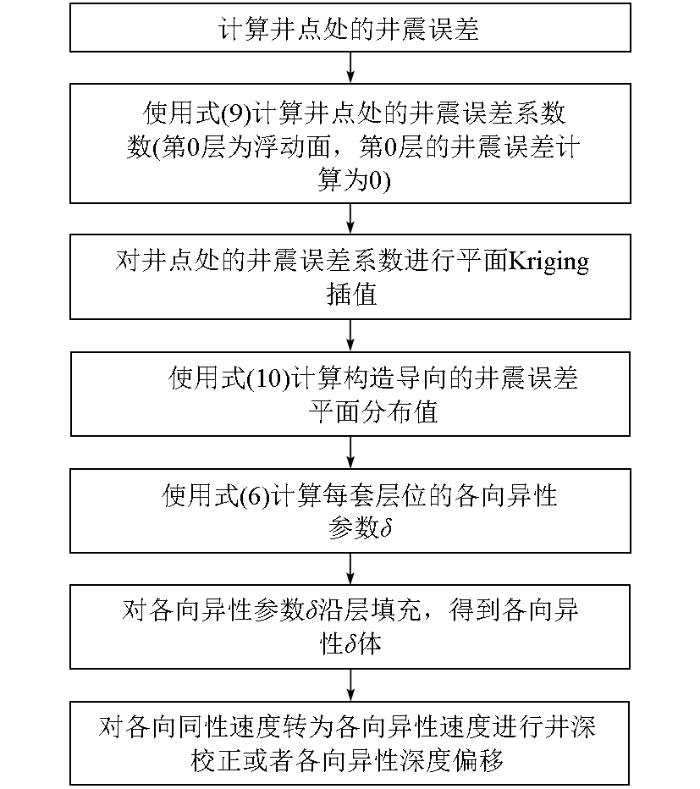
式(10)和式(8)类似,其中的所有参数都是平面分布值,而不是井点处的数值。式(10)中HMm为第m套层位的深度,HMm-1为第m-1套层位的深度,二者相减即为第m套层位的厚度,用第m套层位的厚度乘以第m套层位的井震误差系数,就得到第m套层位的井震误差,再加上上一套层位的井震误差MISMm-1,就得到了第m套层位的累计井震误差MISMm,即第m套层位的实测井震误差。以此类推,就可得到从上到下所有层位的井震误差平面分布值。用这种方法求取的井震误差平面分布值受到了地层厚度的约束,比利用井点处的井震误差值直接进行平面克里金插值更符合实际地质情况,在地层较厚的地方数值会大一些,在地层厚度小的地方数值也会相应小一些。然后,再利用式(6)就可以求取每套层位的各向异性参数δ值的平面分布,进而得到整个工区的各向异性参数δ体,最后可以进一步求得各向异性速度体。构造导向的井震误差校正过程如图4所示。
图4
图4
构造导向的井震误差校正方法流程
Fig. 4
Work flow of structure guided well-tie correction methodology
构造导向的井震误差校正方法和传统的井震误差校正方法相比,新方法没有直接对井震误差值进行平面克里金插值,而是先计算每一套层位的“井震误差系数”,对该系数进行平面插值,然后再利用井震误差系数平面分布值和层位厚度平面分布值反算每一套层位的井震误差平面分布值。这样就保证了式(6)中的分母项不会出现特别小的数值,也不会使δ出现异常大值。该方法不仅适用于构造简单、地层厚度变化不大的地层,也适用于构造复杂、地层厚度变化较大的地层。
3 应用效果
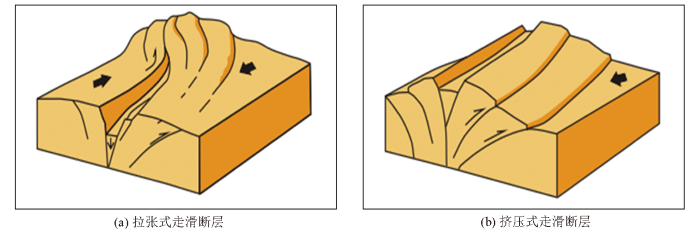
新方法在实际深度偏移项目运作过程中取得了较好的应用效果。以国外某工区为例,该工区位于走滑断裂带,构造复杂,层位厚度变化快。图5为该工区的走滑断裂构造示意,以及与走滑断裂相伴生的花状断层构造。分别应用传统井震误差校正方法和本文提出的新方法进行对比试验。
图5
图6
图6
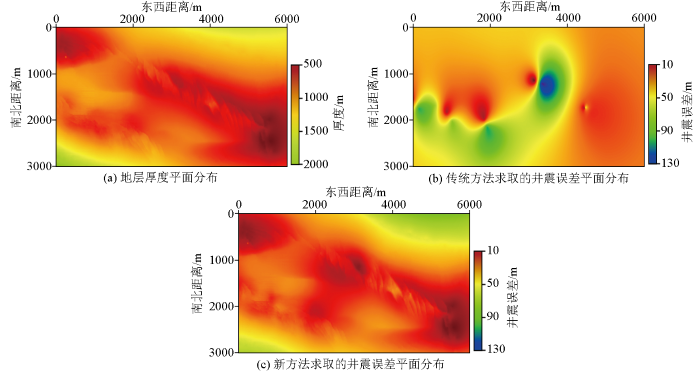
地层厚度平面分布以及新老方法求取的井震误差平面分布
Fig.6
Formation thickness map and mistie value map calculated by traditional method and new method
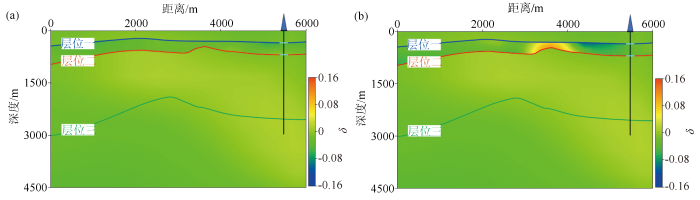
图7为传统方法求取的各向异性参数和本文方法求取的各向异性参数。可以看出,本文方法求取的各向异性参数δ无异常值,传统的井震误差校正方法求取的各向异性参数δ有异常值。
图7
图7
新(a)、老(b)方法井震误差校正后得到的各向异性参数δ剖面
Fig.7
Section of anisotropic parameter δ calculated by new method(a) and traditional method(b)
图8
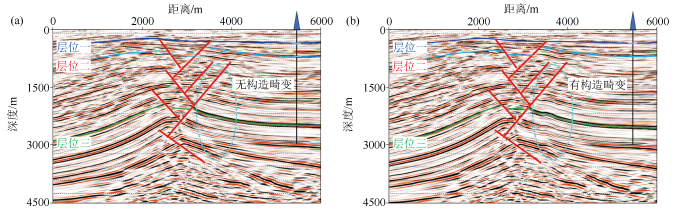
图8
新(a)、老(b)方法井震误差校正后的深度偏移剖面
Fig.8
Pre-stack depth migration section after well-tie correction calculated by new method(a) and traditional method(b)
4 结论
井震误差校正是深度偏移的重要环节。本文针对复杂构造地区井震误差校正后容易出现构造畸变和求取的各向异性参数δ容易出现异常值的问题,提出了构造导向的井震误差校正方法。本方法通过对“井震误差系数”进行插值而不是直接对“井震误差”进行插值,并且对构造层位采取从浅到深依次求取的策略,避免了在地层厚度变化较大的情况下出现构造畸变和求取的各向异性参数δ出现异常值。在实际项目中,获得了很好的应用效果。
1)本方法比传统方法计算得到的井震误差平面分布值和地层厚度的变化趋势更一致。
2)本方法比传统方法计算得到的各向异性参数δ值更合理,避免出现异常值。
3)传统方法和本方法都能校正井点处的井震误差,但是对于没有井点控制的地方,尤其是没有井点控制且地层厚度变化大的地方,构造导向的井震误差校正方法效果更好,不会产生构造畸变。
4)本方法无须地震资料处理人员对各向异性参数和速度场进行人工编辑和平滑的步骤,既节省时间,又避免误差。
参考文献
起伏地表TTI 各向异性速度建模技术在柯东复杂山地的应用
[J].
Application of irregular surface TTI anisotropic velocity modeling technology in Kedong complex mountains
[J].
VTI介质试射射线追踪
[J].
VTI medium test-firing ray tracing
[J].
TI介质各向异性速度多参数分析
[J].
Multi-parameter analysis of anisotropy velocity in TI media
[J],
浅述地震各向异性
[J].
A brief discussion on seismic anisotropy
[J].
复杂各向异性介质初至波射线追踪
[J].
DOI:10.3969/j.issn.1000-1441.2016.01.003
[本文引用: 1]

准确求取各向异性初至波走时与射线路径对偏移成像及层析反演具有重要意义,目前基于图论的最短路径方法虽然能同时得到走时与射线路径且无条件稳定,但仅适用于弱各向异性介质。利用牛顿下山法求解群相关系方程,由群角得到较为精确的相角,进而求得较为精确的群速度和走时,使得最短路径射线追踪方法可以适用于复杂各向异性介质。将此射线追踪方法应用于均匀各向异性介质及层状介质模型,并将试算结果分别与理论走时和弹性波动方程有限差分结果进行比较,验证了方法的准确性;通过复杂各向异性介质模型试算,验证了方法对复杂介质的适用性。
First arrival ray tracing in complex anisotropic medium
[J].
DOI:10.3969/j.issn.1000-1441.2016.01.003
[本文引用: 1]

The accurate calculation of anisotropic first arrival traveltime and raypath is critical for migration imaging and tomographic inversion.The shortest-path method based on graph theory can get the traveltime as well as the raypath with high stability.Thus,we proposed a new shortest-path ray tracing algorithm for anisotropic medium.To compute the traveltime in a grid,Newton downhill method is used to solve the equation relating group angle with phase angle.By this way,a more accurate phase angle can be achieved from a group angle,and then a more accurate group velocity and traveltime can be obtained.Correspondingly,the shortest-path method can be applied to strong anisotropic medium.Finally,this ray tracing algorithm was applied to homogeneous anisotropic medium,a layered model and a complex model,and its effectiveness was proved through comparing the computed traveltimes with those using the finite difference implementation of elastic wave equation.
各向异性全速度建模技术在山地地震成像中的应用
[J].
DOI:10.3969/j.issn.1000-1441.2015.02.006

针对我国南方山地探区复杂地表和复杂地下构造导致常规各向同性叠前深度偏移难以准确成像问题,研究了基于TTI各向异性的全速度建模技术,建立了一套起伏地表条件下各向异性全速度建模的技术思路和实现流程。首先采用井约束初至层析反演方法建立准确的起伏地表速度模型,将其与常规处理获得的中深层速度模型进行匹配拼接,建立起初始的各向同性起伏地表全速度模型;然后通过井震联合的方法获取各向异性参数,将其加入到各向同性起伏地表全速度模型中,结合倾角和方位角数据,实现TTI各向异性起伏地表全速度建模。四川盆地DXC工区地震资料的成像处理验证了各向异性全速度建模技术的有效性;基于TTI各向异性全速度模型的起伏地表Kirchhoff叠前深度偏移结果有效地消除了起伏地表的影响,同时降低了复杂构造与速度各向异性对地震成像的影响,使得地下构造成像更合理也更精确。
Application of anisotropic full velocity modeling in the mountainous seismic imaging
[J].
DOI:10.3969/j.issn.1000-1441.2015.02.006

The complex surface and the complex underground structure lead to inaccurate image from the conventional isotropic pre-stack depth migration in the mountainous area of southern China.Aiming at the problem,a full velocity modeling technology based on TTI anisotropy was studied,a series of technical ideas and workflow of anisotropy full velocity modeling from rugged topography was established.Firstly an accurate irregular surface velocity model was built by the well-constrained first arrival tomographic inversion method.Secondly,an initial irregular surface isotropic full velocity model was built by matching and stitching the near surface model and the mid-depth velocity model was obtained by conventional data processing.Then the anisotropy parameters was obtained through borehole-seismic joint method.Finally,the TTI anisotropic irregular surface full velocity modeling was accomplished by integrating the dip,azimuth and anisotropy parameters into the existing initial irregular surface isotropic full velocity model.Apply the velocity modeling technology to the seismic image of DXC survey in the Sichuan Basin.The processing results show that anisotropic full velocity modeling can achieve available full velocity modeling in the mountainous area; TTI anisotropy velocity model based Kirchhoff pre-stack depth migration from rugged surface can eliminate the influenc of rugged topography and reduce the impact of complex structure and velocity anisotropy on the seismic imaging.
横向各向同性介质中地震波旅行时的计算
[J].
Computation of travel time in transversely isotropic media
[J].
关于横向各向同性介质中的Thomsen参数取值的讨论
[J].
Research on the values of Thomsen parameter in transversely isotropic media
[J].
VTI 介质多参数联合走时层析成像方法
[J].
DOI:10.6038/cjg20141026
[本文引用: 1]

本文基于球谐展开群速度表达式计算走时关于各向异性参数的Fréchet核函数,利用共轭梯度法对两种参数化方法进行了VTI介质中多参数联合反演方法研究.经过理论分析和数值试验发现,与经典的Thomsen参数化方法相比,垂直慢度、水平慢度与动校正慢度的参数化方式更有利于VTI介质多参数联合走时层析反演.为了克服走时对ε参数的不敏感性,我们采用了两步法进行双参数反演,理论模型试验反演得到了与垂直速度精度相当的ε参数.可以将两步法扩展到三步法以同时反演各向异性介质中的三个参数,数值试验展示了该策略的应用潜力.
Joint inversion of VTI parameters using nonlinear traveltime tomography
[J].
TTI介质各向异性参数优化提取方法
[J].
An optimized method for extracting anisotropic parameters in TTI media
[J].
VTI介质各向异性参数层析反演策略与应用
[J].
Strategy of anisotropic parameter tomography inversion in VTI medium
[J].
井控各向异性速度建模技术在YKL地区的应用
[J].
DOI:10.3969/j.issn.1000-1441.2017.03.009

YKL气藏开发迫切需要高品质地震成像资料的支撑,尤其是要求有高精度的构造成像资料。由于该区块三维地震勘探资料存在缺失近炮检距、覆盖次数低等不利因素,因此,常规单一的速度建模方法难以解决该区井震误差大的问题。为此,针对性地提出并联合应用了井控各向异性网格层析和逐层速度建模技术。在选好区内标志层、建好初始速度模型的基础上,利用区内多口已知井信息求取各向异性参数,先消除浅部大套稳定地层速度对气藏深度的影响,再由浅到深逐层对标志层反演,更新迭代各向异性参数、速度及深度成像,直至各标志层的井震误差降低到规定范围内。3口验证井的应用结果显示,实际资料最终成像成果的气藏构造深度预测值与实钻井深度误差均在5 m内,气藏构造成像的精度得到了显著提高,断裂成像也得到明显改善,降低了开发钻井的风险。
The application of well-controlled anisotropy velocity modeling in YKL region
[J].
DOI:10.3969/j.issn.1000-1441.2017.03.009

<p>The urgent demand for high quality imaging data,especially high-precision geological structure,is a key problem in the development of YKL gas field.Because of missing near-offset data and low fold of seismic data,well-seismic misfit for structural depth prediction in this region can’t meet the exploration requirement if we only use conventional velocity modeling.Therefore,well-controlled anisotropy grid-tomography technique was adopted to conduct velocity modeling layer-by-layer.Based on precise choosing the reasonable markers and building the initial velocity model in the selected area,we use known logging data to calculate anisotropic parameters within this region.Then we eliminate the influence of large set for stable formation velocity on gas reservoir depth,and from shallow to deep layer by layer inversion on marker layer,update iterative anisotropic parameters,velocity and depth migration imaging until the predicted depth errors from well log and seismic data for each marker layer to be reduced.In addition,it has been confirmed by 3 drilling wells that the misfit between the predicted structural depths respectively from the final seismic migration results and logging depth measurements in this gas reservoir are all within 5m.So we can draw a conclusion that our technique can significantly improve the imaging accuracy for structure and fracture of gas reservoir so as to reduce the risk of production drilling.</p>
井震联合构建三维地质导向模型关键技术研究
[J].
DOI:10.3969/j.issn.1672-9803.2018.02.007

地质导向是水平井钻井中保障沿着优质储集层钻进的重要支撑手段。传统的基于地层对比的地质导向技术所构建的导向模型通常难以提供精细且具有预测能力的地层构造模型、岩性分布模型及含油性分布模型,往往使导向工作出现偏差,引发优质储集层钻遇率低的问题。地震数据纵向分辨率虽低但具有层面横向控制能力,测井数据纵向层位虽精细但因井位少使其纵向地层延展性控制能力差,基于二者优点的井震联合构建三维地质导向模型技术,则可以提供更准确的三维地层模型和剖面导向模型,进一步结合随钻数据实时校正模型,即能够确保钻井轨迹位于薄砂层目的层中,指导钻井施工实现精准地质导向。三维建模技术、地层剖面建模与分析技术以及模型更新技术研究结果表明,在勘探开发中后期,钻井、测井、录井资料丰富的情况下,基于井震联合三维地质导向模型构建的地层剖面模型能够满足地质导向的精度要求,有效提高油气层钻遇率。
Research on key technologies of joint construction of three-dimensional geological guidance model by well and seismology
[J].
DOI:10.3969/j.issn.1672-9803.2018.02.007

Geosteering is an important support to ensure drilling along high quality reservoirs in horizontal well drilling. The guidance model constructed by the traditional geosteering technology based on stratigraphic correlation is difficult to provide a fine and predictive stratal configuration model, lithologic distribution model and oil-bearing distribution model. It often leads to deviation in guiding work and causes low rate in drilling high-quality reservoirs. Vertical resolution of seismic data is low but has horizontal control ability. Log data are precise in the vertical horizon, but the control ability of their vertical formation ductility is poor due to the lack of well location. 3D geosteering model technology was constructed jointly based on the advantages of well logging and seismic. It can provide more accurate 3D stratigraphic model and profile guidance model and further combine with data while drilling to real-time correct model, that is, it can ensure that the drilling track is located in the target bed of thin sand layer, and guide drilling operation. The accurate geosteering is realized. The study results of 3D modeling technology, stratigraphic profile modeling and analysis technology and model updating technology show that stratigraphic profile model based on 3D geological model of well logging and seismic combination can meet the precision requirement of geosteering with abundant drilling, well logging and mud logging data in the middle and late stages of exploration and development, effectively improving the rate of drilling oil and gas reservoirs.
井震联合处理技术在川西南部地区的应用
[C]//
Application of well-seismic joint processing technology in the Southern Sichuan Basin
[C]//
井震联合深层区域勘探构造建模技术研究
[J].
Research on structural modeling technology for deep regional exploration combined with well and earthquake
[J].
巴楚夏河工区的三维速度建模方法
[J].
3-D velocity model-building method in Bachuxia river work zone
[J].
渤南洼陷井—震速度误差分析和速度模型的建立及应用
[J].
DOI:10.3969/j.issn.1000-1441.2014.02.010
[本文引用: 1]

高精度速度场的建立对渤南洼陷隐蔽油气藏勘探十分重要。综合大量测井、测试和地震资料,分析和讨论了测井、VSP和地面地震速度间的差异;利用VSP测井优化技术,对叠前偏移速度做了标定和校正,在此基础上对离散速度数据进行空间插值,获得了全区地震层速度、均方根速度三维数据体。不同类型速度资料的对比分析表明,研究区浅层的井孔速度大于井旁地震层速度,中、深层则呈现正好相反的特点;浅层速度弥散、深层介质的各向异性是导致井、震速度误差的主要原因。利用VSP速度对地震层速度的局部误差进行闭合差校正,经空间插值后建立的全区速度模型可从任意方向切片观察速度空间展布。三维速度资料为研究渤南洼陷整体的地层密度、压力系数等岩石和流体参数的空间展布和结构特征提供了可能。
The error analysis between logging and seismic velocity for 3D velocity modeling in Bonan Sag
[J].
DOI:10.3969/j.issn.1000-1441.2014.02.010
[本文引用: 1]

Seismic velocity is one of the most important parameters for subtle reservoir exploration in Bonan Sag.The difference among logging,VSP and ground seismic velocity are analyzed and discussed based on a large amount of logging,testing and seismic data.On the basis of analysis for discrete velocity in target area,a method with VSP logging optimum technique is proposed to calibrate and correct prestack migration velocity, and the 3D data volume of seismic interval velocity and RMS velocity is obtained.Comparison between different types of velocity data reveals that,velocity obtained from borehole is larger than seismic interval velocity in the upper stratum,of which the fact is opposite in the middle and deep stratum.Velocity dispersion of upper stratum and rock anisotropy of deep stratum could explain the cause of the logging and seismic velocity error.The local error of seismic interval velocity is conducted mis-tie correction by using VSP velocity.By spatial interpolation,we get an overall velocity 3D model and it offers a comprehensive understanding of velocity distribution at any direction slice.3D velocity data reveals an overall variation view of formation density,pressure parameters and some other spatial distribution as well as structural characteristics of rock and fluid.
多波地震地层各向异性的初步研究和探讨
[J].
A preliminary discussion on the application of multiwave seismic data to the study of anisotropy of various formations
[J].