0 引言
在山前带、黄土塬、沙漠等近地表条件复杂地区,起伏地形和低降速带剧烈的纵、横向速度变化使得在地表接收的地震记录中反射波同相轴发生明显的扭曲[1 ⇓ -3 ] 。对地震记录进行静校正,可以有效地消除起伏地形和低降速带对反射波同相轴的不良影响,提高成像质量[4 -5 ] 。
在地震资料处理中,常规静校正方法包括高程静校正[6 -7 ] 、折射静校正[8 -9 ] 和层析静校正等[10 -11 ] 。高程静校正将炮点和检波点从地表校正到同一高程的基准面,消除了起伏地形对地震记录中反射波同相轴的影响。然而,高程静校正没有考虑低降速带内速度的纵、横向变化,在近地表复杂工区的应用效果较差[6 ] 。折射静校正方法利用初至折射波走时信息直接计算长波长静校正量。在近地表速度结构简单的工区,初至折射波连续、明显,折射静校正方法可以取得较好的静校正应用效果[11 -12 ] 。然而,在低降速带较厚、速度横向变化剧烈、折射界面不稳定等近地表条件复杂地区,该类方法不再适用[2 ,13 -14 ] 。层析静校正方法首先利用大量的初至走时信息通过多次迭代修正初始速度模型从而获得高精度的近地表速度模型,然后基于该近地表模型计算长波长静校正量。层析静校正方法不强调初至波一定是折射波,也不要求折射界面稳定和低降速带速度横向变化小。该方法是近地表条件复杂地区应用效果最佳和最广泛的静校正方法[2 ,4 ] 。
对于三维高密度地震资料,初至走时数据量极其庞大。这导致传统初至走时层析需要进行非常多次的射线追踪,耗时极大。为了提高近地表速度建模的效率,Shi等[5 ] 利用水平地表下的回折波走时和射线方程,从地表向下逐层确定介质的速度分布。相比于传统初至走时层析方法,该方法无需进行射线追踪计算初至波路径,其计算效率提高了近百倍。然而,在地表高程起伏较大的工区,其反演模型的精度较低,难以解决实测陆地地震资料的静校正问题。
为了提高三维高密度地震资料的近地表速度建模效率且解决长波长静校正问题,本文提出了一种利用起伏地形下的回折波走时信息快速建立三维近地表速度模型的方法。该方法考虑了起伏地形和低降速带速度纵横向变化对回折波走时及射线方程的影响,适用于复杂近地表速度建模。理论模型合成数据测试和实测地震资料应用验证了本文方法的有效性和高效性。
1 方法原理
本文采用层剥离的策略快速建立三维近地表速度模型。其速度建模流程主要包含3个步骤。第一步,采用起伏观测面下的回折波走时和射线方程,计算最小偏移距数据集中每个炮检对的回折点位置和速度。第二步,计算所有回折点构成的界面位置及地表至该界面的速度分布。第三步,将其他共偏移距数据集中的炮点和检波点延拓至第二步确定的界面,并将该界面作为新的地表,然后重复第一步和第二步,直到完成所有共偏移距数据集的处理。整个速度建模过程无需进行常规的射线追踪,显著地提高了建模效率。采用起伏观测面下的回折波走时和射线方程,结合层剥离的策略,确保了速度建模的精度。
1.1 起伏观测面下回折点位置和速度计算方法
在观测面高程起伏较大且介质速度横向变化剧烈时,基于水平观测面和一维速度模型的回折波走时和射线方程不再适用[5 ] 。为此,本文采用起伏观测面下的回折波走时和射线方程。将回折波经过的区域分为两部分:炮点至回折点所在区域和回折点至检波点所在区域。炮点至回折点所在区域内速度随深度线性递增,速度梯度为λ s ,炮点所在地表的速度为v 0s ;检波点至回折点所在区域内速度随深度线性递增,速度梯度为λ r ,检波点所在地表的速度为v 0r 。观测面处的速度可以通过近地表调查或直达波走时信息计算得到。
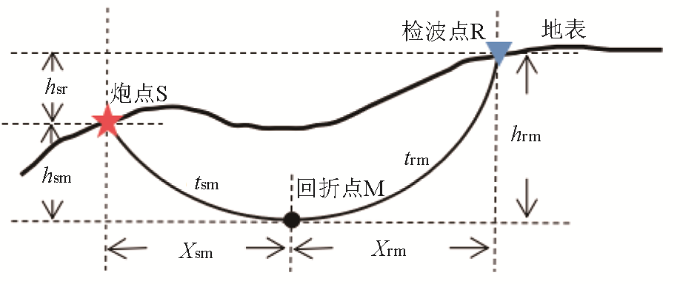
起伏观测面下回折波传播路径如图1 所示。回折波从炮点传播至回折点,走时和射线方程可以表示为[15 -16 ] :
(1) t s m = 1 λ s l n v m + v m 2 - v 0 s 2 v 0 s ,
(2) X s m = v m 2 - v 0 s 2 λ s ,
(3) h s m = v m - v 0 s λ s ,
式中:t sm 为回折波从炮点至回折点的旅行时间,v m 为回折点处的速度,v 0s 为炮点位置地表的速度,λ s 为炮点至回折点所在区域内的速度梯度,X sm 为炮点和回折点之间的水平距离,h sm 为炮点至回折点的垂直距离。同理可得回折波从回折点传播至检波点的走时和射线方程。根据回折波的走时和射线方程及炮检点之间的几何关系,可得炮点至回折点所在区域内的速度梯度λ s 和检波点至回折点所在区域内的速度梯度λ r [15 ⇓ -17 ] 。
图1
图1
起伏观测面下回折波传播路径示意
Fig.1
The ray path of the diving wave propagating in heterogeneous media with undulant topography
然后,利用式(2)、(3),计算回折点的空间位置,如下:
(4) x m = x s + X s m c o s β ,
(5) y m = y s + X s m s i n β ,
(6) z m = z s - h s m ,
式中:x m 、y m 和z m 分别是回折点的x 、y 和z 坐标,z 轴表示高程,x s 、y s 和z s 分别是炮点的x 、y 和z 坐标,β 是炮检点连线与x 轴的夹角。
1.2 地表与回折点构成的界面之间介质速度的计算方法
对于三维高密度地震初至走时数据,最小偏移距数据集中存在若干炮检对,每个炮检对都对应一个回折点。利用求得的所有回折点位置和速度信息,即可确定一个空间连续的速度界面,记为l。界面l的高程通过反距离加权算法求得,可以表示为:
(7) z l ( x , y ) = ∑ i = 1 N w i z m i ( x m i , y m i ) 。
式中:z l 表示速度界面l的z 坐标,x m 、y m 和z m 分别表示回折点的x 、y 和z 坐标,w 表示权重,i 表示回折点的序号,N 表示回折点的总数。权重的计算公式如下:
(8) w i = 1 ( x - x m i ) 2 + ( y - y m i ) 2 + ε ∑ j = 1 N 1 ( x - x m j ) 2 + ( y - y m j ) 2 + ε 。
式中:ε 为阻尼系数,用于避免插值出现“牛眼”现象。
(9) v l ( x , y ) = ∑ i = 1 N w i v m i ( x m i , y m i ) 。
采用线性插值的方法求取地表和界面l之间介质的速度,可以表示为:
(10) v ( x , y , z ) = v 0 ( x , y ) + z - z 0 ( x , y ) z l ( x , y ) - z 0 ( x , y ) · [ v l ( x , y ) - v 0 ( x , y ) ] 。
式中:v 0 表示地表速度,z 0 表示地表高程。地表速度通过近地表调查或直达波走时信息计算得到。
1.3 层剥离方法
同一个偏移距数据集内所有初至走时数据对应的回折点共同确定了一个“层界面”。该层界面不是物理上真实的速度界面,而是本文方法用于从浅至深速度建模的深度界面。对于速度随深度逐渐增加的介质,回折点的深度随偏移距的增大而增大。故从最小偏移距数据集开始,逐步使用更大偏移距数据集,即可从地表向下逐层确定介质的速度分布。
除最小偏移距数据集以外,将其余道集内的炮点和检波点延拓至界面l,就可以消除界面l上覆地层对回折波射线路径及走时的影响[5 ] 。将延拓后的初至走时数据作为新的观测数据,将界面l作为新的地表,采用前述的方法即可确定新地表至新界面之间的速度。对所有的共偏移距数据集进行类似处理,即可自浅至深逐步建立三维近地表速度模型。
基于回折波走时和射线方程[5 ,16 ] ,将炮点延拓至界面l附近可以表示为:
(11) x ' s = x s ± c o s β [ z l ( x s , y s ) - z 0 ( x s , y s ) ] p [ v l ( x s , y s ) - v 0 ( x s , y s ) ] [ 1 - p 2 v 0 2 ( x s , y s ) - 1 - p 2 v l 2 ( x s , y s ) ]
(12) y ' s = y s ± s i n β [ z l ( x s , y s ) - z 0 ( x s , y s ) ] p [ v l ( x s , y s ) - v 0 ( x s , y s ) ] [ 1 - p 2 v 0 2 ( x s , y s ) - 1 - p 2 v l 2 ( x s , y s ) ]
(13) z ' s = z s - [ 1 - p v 0 ( x s , y s ) ] [ z l ( x s , y s ) - z 0 ( x s , y s ) ] p [ v l ( x s , y s ) - v 0 ( x s , y s ) ]
式中:x 's 、y 's 和z 's 分别表示延拓后炮点的x 、y 和z 坐标。当炮点x 坐标小于检波点x 坐标时,式(11)中等号右端取正号,否则取负号。类似地,当炮点y 坐标小于检波点y 坐标时,式(12)中等号右端取正号,否则取负号。
(14) x ' r = x r ± c o s β [ z l ( x r , y r ) - z 0 ( x r , y r ) ] p [ v l ( x r , y r ) - v 0 ( x r , y r ) ] [ 1 - p 2 v 0 2 ( x r , y r ) - 1 - p 2 v l 2 ( x r , y r ) ]
(15) y ' r = y r ± s i n β [ z l ( x r , y r ) - z 0 ( x r , y r ) ] p [ v l ( x r , y r ) - v 0 ( x r , y r ) ] [ 1 - p 2 v 0 2 ( x r , y r ) - 1 - p 2 v l 2 ( x r , y r ) ]
(16) z ' r = z r - [ 1 - p v 0 ( x r , y r ) ] [ z l ( x r , y r ) - z 0 ( x r , y r ) ] p [ v l ( x r , y r ) - v 0 ( x r , y r ) ]
式中:x 'r 、y 'r 和z 'r 分别表示延拓后检波点的x 、y 和z 坐标。当检波点x 坐标小于炮点x 坐标时,公式(14)中等号右端取正号,否则取负号。当检波点y 坐标小于炮点y 坐标时,式(15)中等号右端取正号,否则取负号。
(17) t ' s r = t s r - [ z l ( x s , y s ) - z 0 ( x s , y s ) ] [ v l ( x s , y s ) - v 0 ( x s , y s ) ] l n v l ( x s , y s ) ( 1 + 1 - p 2 v 0 2 ( x s , y s ) ) v 0 ( x s , y s ) ( 1 + 1 - p 2 v l 2 ( x s , y s ) ) - [ z l ( x r , y r ) - z 0 ( x r , y r ) ] [ v l ( x r , y r ) - v 0 ( x r , y r ) ] l n v l ( x r , y r ) ( 1 + 1 - p 2 v 0 2 ( x r , y r ) ) v 0 ( x r , y r ) ( 1 + 1 - p 2 v l 2 ( x r , y r ) )
2 模型测试
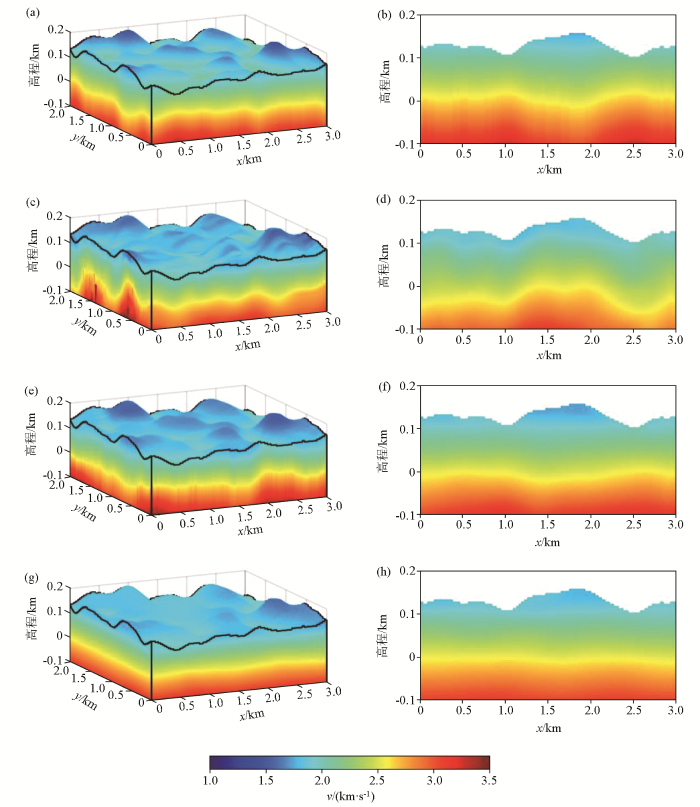
为了测试本文方法的正确性,建立了一个地形起伏且速度纵横向变化的理论速度模型,如图2a 所示。模型大小为3 km×2 km×0.3 km。地表最大高程差为120 m。理论模型的最小和最大速度分别为1 440 m/s和4 000 m/s。图2b 为理论模型在y =1 km处沿x 方向的速度切片。从速度切片中可以看出,近地表速度在纵横向均变化,且在横向的速度变化趋势与地形起伏不是正相关的。
图2
图2
速度模型
a—理论速度模型;c—基于水平地表假设的初至走时层析反演模型;e—菲涅尔体初至走时层析反演模型;g—本文方法反演模型;b、d、f、h—左侧三维模型在y =1 km处的速度切片
Fig.2
Velocity models
a—the theoretical velocity model;c—models constructed by the first-arrival traveltime inversion based on horizontal observation surface;e—Fresnel first-arrival traveltime tomography model;g—model invesed by the proposed method;b、d、f、h—the velocity slices at y =1 km corresponding to the 3D velocity models shown at the left column
在地表沿x 方向布设10条炮线,20条检波点线。炮线距和检波点线距分别设置为200 m和100 m。每条炮线共有60个炮点,炮间距为50 m。每条检波点线共有120个检波点,检波点间距为25 m。采用边长5 m的规则立方体单元离散速度模型,利用二阶声波方程正演模拟获得地震记录并从中拾取初至走时数据。
为了客观而充分地展示本文方法的优缺点,分别使用现有的基于水平地表假设的初至走时层析方法[5 ] 、菲涅尔体初至走时层析方法[14 ] 和本文方法反演拾取的初至走时数据。
图2c、d 分别为基于水平地表假设的初至走时层析反演模型及其在y =1 km处沿x 方向的速度切片。对比图2b、d ,可以发现基于水平地表假设的初至走时层析反演模型与理论模型相差较大,特别是两者在x 方向的速度变化趋势不一致。这表明在反演过程中不考虑地形起伏会导致反演模型的速度趋势发生错误。
图2e、f 分别为菲涅尔体初至走时层析迭代30次后的反演模型及其在y =1 km处沿x 方向的速度切片。反演采用速度为3 km/s的匀速模型作为初始模型。对比图2b、f ,可以明显看出,反演模型非常接近理论模型。
图2g、h 分别为本文方法反演模型及其在y =1 km处沿x 方向的速度切片。本文方法将近偏移距的回折波走时作为直达波走时,用于估计地表速度,导致反演的地表速度略高于真实值和菲涅尔体初至走时层析反演的地表速度,如图2a、e、g 所示。此外,在缺少回折波射线覆盖的区域,两种反演方法均通过外推获得该区域内的速度。然而,两种反演方法在原理和编程实现上存在一定差异,导致外推的速度不同。
对比图2b、f、h 所示的y =1 km处的速度切片,可以发现,本文方法和菲涅尔体初至走时层析反演模型在浅部(z >0 km)与理论模型非常接近。在深部(z <0 km),菲涅尔体初至走时层析反演模型略好于本文方法反演模型。
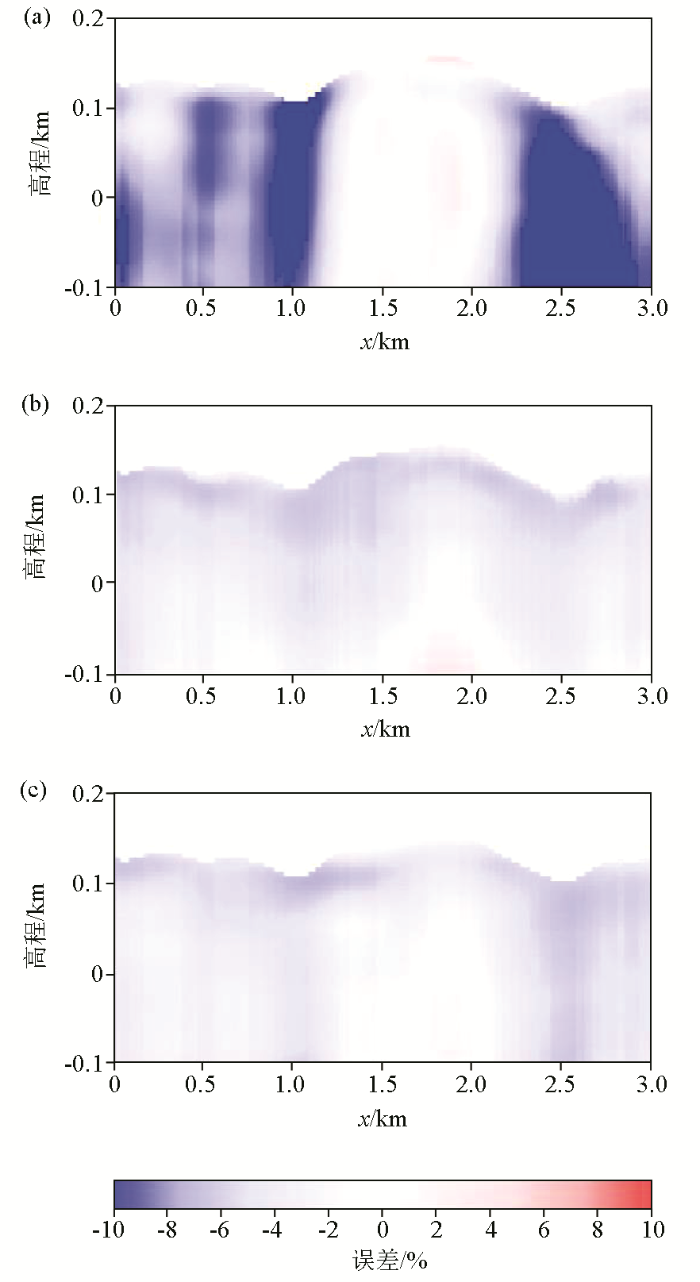
图3a~c 分别是基于水平地表假设的初至走时层析、菲涅尔体初至走时层析和本文方法反演模型在y =1 km处的相对误差切片。从图3 中可以看出,基于水平地表假设的初至走时层析反演模型的相对误差最大,部分区域的相对误差超过20%。菲涅尔体初至走时层析和本文方法反演模型的相对误差相当,两者的平均相对误差分别约为3.6%和3.8%。
图3
图3
y =1 km处的速度相对误差切片
a—基于水平地表假设的初至走时层析反演模型相对误差;b—菲涅尔体初至走时层析反演模型相对误差;c—本文方法反演模型相对误差
Fig.3
The slices of velocity relative errors at y =1 km
a—the relative errors of the velocity model inverted by the first-arrival traveltime inversion based on horizontal observation surface;b—the relative errors of the velocity model inverted by the Fresnel first-arrival traveltime tomography;c—the relative errors of the velocity model inverted by the proposed method
为了对比上述3种方法的速度建模效率,在同一Dell工作站(CPU型号:Intel(R) Xeon(R) Gold 6246R,CPU主频:3.4 GHz,内存:32 GB)上运行所有程序。基于水平地表假设的初至走时层析用1个进程耗时约114 s。菲涅尔体初至走时层析用10个进程迭代30次耗时约9 780 s,换算为1个进程耗时约为97 800 s。本文方法用1个进程耗时约为392 s。这3种方法的效率比约为1:858:3.4。相比于菲涅尔体初至走时层析,本文方法耗时提高了约252倍。
3 实际资料应用
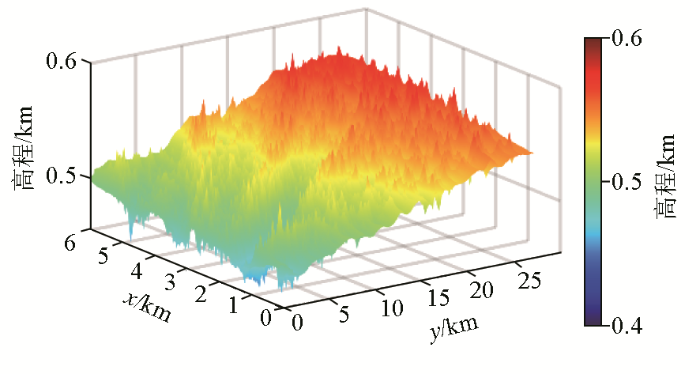
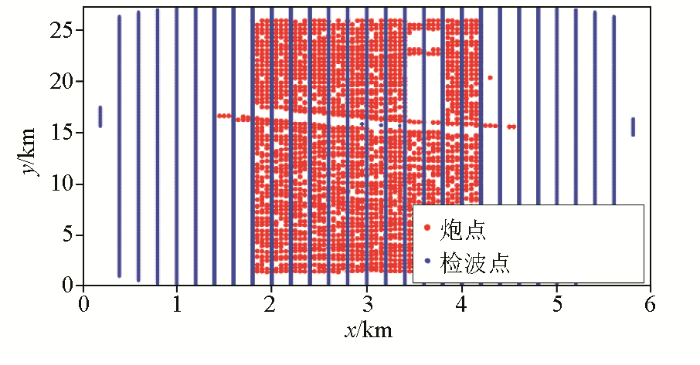
将本文方法应用于西部地区三维实测地震资料。工区东西(x )方向长约6 km,南北(y )方向长约27 km。整体上,北部地表高程大,南部地表高程小,如图4 所示。工区内地表最小和最大高程分别约为454 m和584 m。工区地形起伏剧烈,近地表条件复杂。图5 为该工区的观测系统。共有2 815个炮点,14 689个检波点。炮线距和炮点距均为50 m。检波点线距为200 m,道间距为50 m。地震记录采样间隔为1 ms,记录长度为6 s。
图4
图4
工区地形
Fig.4
The topography of the exploration area
图5
图5
观测系统
Fig.5
Observation geometry
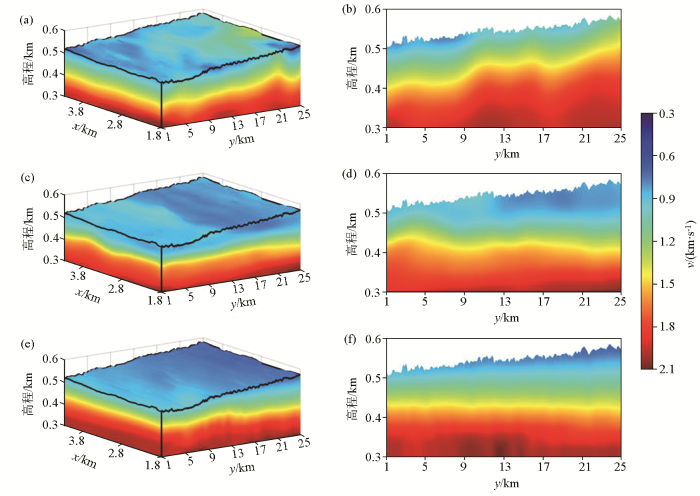
从预处理后的地震记录中拾取初至走时,并分别采用基于水平地表假设的初至走时层析、菲涅尔切片体初至走时层析和本文方法建立近地表速度模型和静校正。图6a、b 分别是基于水平地表假设的初至走时层析反演模型以及在x =3 km处的速度。图6c、d 分别是菲涅尔体初至走时层析经过30次迭代后的反演模型以及在x =3 km处的速度切片。菲涅尔体初至走时层析采用速度为2.5 km/s的匀速模型作为初始模型。图6e、f 分别是本文方法反演模型以及在x =3 km处的速度切片。对比图6b、d、f ,可以明显看出,基于水平地表假设的初至走时层析反演模型与其余两种方法反演模型明显不同,特别是宏观速度变化趋势。菲涅尔体初至走时层析和本文方法反演模型的宏观速度变化趋势一致。
图6
图6
反演速度模型及其在x =3 km处的速度切片
a—基于水平地表假设的初至走时层析模型;c—菲涅尔体初至走时层析模型;e—本文方法反演速度模型;b、d、f—左侧对应速度模型在x =3 km处的速度切片
Fig.6
Inverted velocity models and slices at x =3 km
a—the models constructed by the first-arrival traveltime inversion based on horizontal observation surface;c—Fresnel first-arrival traveltime tomography model;e—the model inverted by the proposed method;b、d、f—the slices at x =3 km corresponding to the models at the left column respectively
为了验证图6 所示速度模型的有效性,利用3种方法反演模型分别计算长波长静校正量,并对静校正后的单炮记录和叠加剖面进行对比。静校正基准面高程设置为0.6 km,替换速度设置为2 km/s。
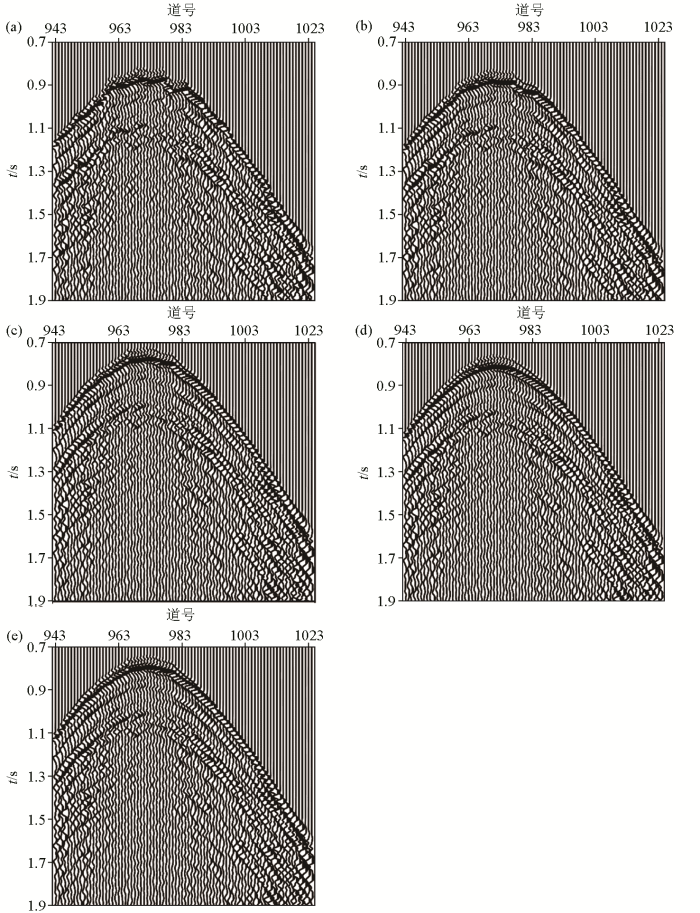
图7 为静校正前后的第1 200炮地震记录。原始地震记录如图7a 所示。可以看出,受起伏地形和近地表速度纵横向变化的影响,地震波同相轴存在严重扭曲。图7b 为高程静校正后的地震记录。地震波同相轴连续性有一定的改善,但仍然非常扭曲。这表明高程静校正难以解决近地表速度纵横向变化对地震同相轴的不良影响。图7c 为采用基于水平地表假设的初至走时层析反演模型获得的静校正后的地震记录,其静校正效果略好于高程静校正,表明基于水平地表假设的初至走时层析难以正确反演近地表速度分布。图7d 为采用菲涅尔体初至走时层析反演模型获得的静校正后的地震记录,可以看出,其初至和反射同相轴的连续性得到了显著改善。图7e 为采用本文方法反演模型获得的静校正后的地震记录,其静校正效果好于高程静校正和基于水平地表假设的初至走时层析静校正,但比菲涅尔体初至走时层析静校正效果略差。
图7
图7
第1 200炮地震记录
a—原始地震记录;b—高程校正后的地震记录;c—基于水平地表假设的初至走时层析速度模型进行长波长静校正后的地震记录;d—菲涅尔体初至走时层析速度模型进行长波长静校正后的地震记录;e—本文方法建立的速度模型进行长波长静校正后的地震记录
Fig.7
The 1 200th common shot gather
a—the original seismic gather;b—the gather with elevation correction;c—the gather with long-wavelength static correction using the model inverted by the first-arrival traveltime inversion based on horizontal observation surface;d—the gather with long-wavelength static correction using the model inverted by the Fresnel first-arrival traveltime tomography;e—the gather with long-wavelength static correction using the model inverted by the proposed method
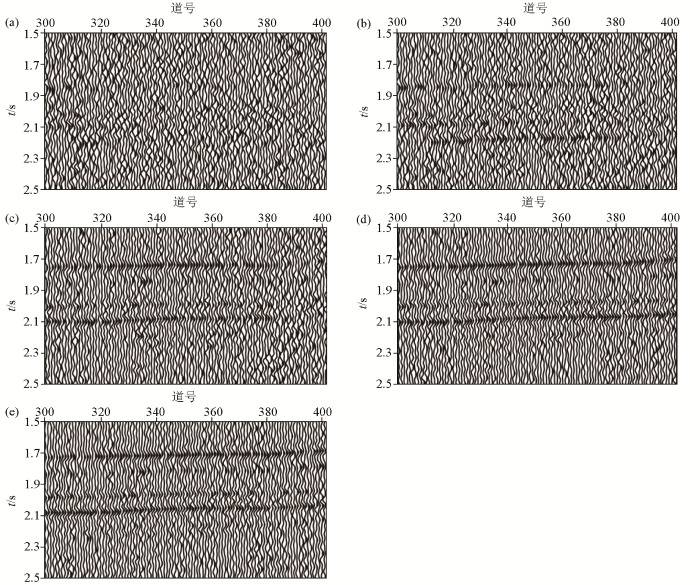
图8 是第75条CMP线的叠加剖面对比。可以看出,菲涅尔体初至走时层析和本文方法的静校正效果相当,均好于高程静校正和基于水平地表假设的初至走时层析静校正。这表明应用本文方法可以有效解决该地区长波长静校正问题。
图8
图8
静校正处理后的第75条CMP线叠加剖面
a—未做静校正的叠加剖面;b—高程校正后的叠加剖面;c—基于水平地表假设的初至走时层析速度模型进行长波长静校正后的叠加剖面;d—菲涅尔体初至走时层析速度模型进行长波长静校正后的叠加剖面;e—本文方法建立的速度模型进行长波长静校正后的叠加剖面
Fig.8
The stacked profiles of the 75th CMP line
a—the stack profile without static correction;b—the stack profile with elevation correction;c—the stack profiles with long-wavelength static correction using the model inverted by the first-arrival traveltime inversion based on horizontal observation surface;d—the stack profiles with long-wavelength static correction using the model inverted by the Fresnel first-arrival traveltime tomography;e—the stack profiles with long-wavelength static correction using the model inverted by the proposed method
为了对比3种速度建模方法的效率,在同一工作站(CPU型号:Intel(R) Xeon(R) Gold 6246R,CPU主频:3.4 GHz,内存:32 GB)上执行相关程序。基于水平地表假设的初至走时层析用1个进程耗时353 s。菲涅尔体初至走时层析用10个进程耗时35 400 s,相当于1个进程354 000 s。本文方法用1个进程耗时807 s。3种方法的耗时比约为1:1 003:2.3。基于水平地表假设的初至走时层析的近地表速度建模效率最高,但其静校正效果最差。菲涅尔体初至走时层析的静校正效果最佳,但其速度建模效率远低于其余两种方法。本文方法的静校正效果与菲涅尔体初至走时层析的静校正效果相当,然而相比于菲涅尔体初至走时层析,其速度建模效率提高了约439倍。这表明本文方法在确保近地表速度建模精度的基础上,显著提高了速度建模的效率,可以有效缩短陆地地震资料的处理周期。
4 结论
本文提出了一种起伏地形下利用回折波走时信息快速建立3D速度模型的方法。该方法考虑了起伏地形和低降速带纵横向速度变化对回折波走时和射线路径的影响。利用共偏移距数据集中的初至走时信息,采用层剥离的策略自浅至深逐步确定地下介质的速度分布。该方法不依赖于初始速度模型,无需进行射线追踪正演计算初至波路径和多次迭代更新初始速度模型。理论模型合成数据测试和实测陆地地震资料应用证明了该方法的有效性和高效性。本文方法具有极高的近地表速度建模效率,尤其是对于3D高密度地震资料。
本文方法建立的近地表速度模型通常可以较为准确地反映真实近地表速度结构的低频速度分布。然而,真实近地表速度结构的高频变化通常难以被正确反演。因此,本文方法可以有效解决山前带等地区地震资料的长波长静校正问题,无法解决短波长静校正问题。对长波长静校正后的地震资料,应用初至波短波长静校正,有望进一步提高单炮地震记录和叠加剖面的质量。
参考文献
View Option
[1]
张林 , 杨勤勇 , 张兵 , 等 . 复杂近地表初至波层析反演静校正技术研究
[J]. 地球物理学进展 , 2017 , 32 (2 ):816 -821 .
[本文引用: 1]
Zhang L Yang Q Y Zhang B , et al . Tomography inversion by first breaks in areas with complex near surface
[J]. Progress in Geophysics , 2017 , 32 (2 ):816 -821 .
[本文引用: 1]
[2]
于豪 . 折射波静校正与层析静校正技术适用性分析
[J]. 地球物理学进展 , 2012 , 27 (6 ):2577 -2584 .
[本文引用: 3]
Yu H . Applicability analysis of refraction static correction and tomographic inversion static correction
[J]. Progress in Geophysics , 2012 , 27 (6 ):2577 -2584 .
[本文引用: 3]
[3]
Cox M . Static corrections for seismic reflection surveys [M]. Tulsa : Society of Exploration Geophysicists , 1999 .
[本文引用: 1]
[4]
周衍 , 饶莹 . 黄土塬覆盖区的层析反演静校正方法研究
[J]. 地球物理学报 , 2019 , 62 (11 ):4393 -4400 .
DOI:10.6038/cjg2019N0304
[本文引用: 2]
我国北方地区黄土塬覆盖区的静校正问题是地震数据处理中的难点问题之一.黄土塬表层覆盖巨厚黄土,高差起伏较大,地震静校正问题严重;而且黄土塬覆盖区的潜水面普遍较深,常规折射静校正方法无法取得令人满意的处理效果.本文针对黄土塬覆盖区的静校正难题,研究层析反演静校正方法在黄土塬地区的适用性和可靠性.层析反演静校正利用地震波初至走时数据、通过迭代反演的方法构建速度模型,进而依据所得的近地表速度模型对地震数据进行静校正处理.本文的迭代反演采用同步迭代重构算法(SIRT),并且对同步迭代重构算法进行了改进,使得层析反演的迭代过程趋于稳定.但是,因为黄土塬覆盖区地表高程的横向变化剧烈,相邻检波点的高差及其静校正量有时差异很大,在运用层析静校正求取长波长静校正量的同时,还需采用初至波剩余静校正方法求取短波长静校正量.实例证明,综合应用依据初至波走时数据的层析静校正和剩余静校正方法,同时计算长波长和短波长的静校正量,能够有效地解决黄土塬覆盖区实际地震资料的静校正问题.
Zhou Y Rao Y . Tomographic static corrections in loess plateaus
[J]. Chinese Journal of Geophysics , 2019 , 62 (11 ):4393 -4400 .
[本文引用: 2]
[5]
Shi T K Zhang J Z Huang Z L , et al . A layer-stripping method for 3D near-surface velocity model building using seismic first-arrival times
[J]. Journal of Earth Science , 2015 , 26 (4 ):502 -507 .
[本文引用: 6]
[6]
林伯香 , 孙晶梅 , 徐颖 , 等 . 几种常用静校正方法的讨论
[J]. 石油物探 , 2006 , 45 (4 ):367 -372 ,5.
[本文引用: 2]
随着地震勘探区域地表条件复杂化,静校正在资料处理中的作用日显重要。因此,有必要对各种静校正方法的基本原理、适用条件进行系统的归纳和分析。为此,对目前常用的高程静校正、模型静校正、折射静校正和层析静校正等方法的基本理论和适用条件进行了讨论和分析,认为基于初至时间的层析静校正方法能较好地解决复杂地表区由于地形和低速带变化引起的长波长静校正问题。同时讨论了多域统计剩余静校正、相对折射法剩余静校正和反射剩余静校正等方法,认为基于初至时间的多域统计剩余静校正是解决由测量误差和表层速度模型误差引起的残留短波长静校正问题的较好方法,只要应用得当,同样适合复杂地表区的资料处理。
Lin B X Sun J M Xu Y , et al . Static correction approaches being frequently applied
[J]. Geophysical Prospecting for Petroleum , 2006 , 45 (4 ):367 -372 ,5.
[本文引用: 2]
The fundamental principles of static correction approaches being frequently applied, including elevation,model, refraction and tomography static corrections, are described and their suitability for complex near-surface conditions is discussed. The tomography static correction based on first breaking time is considered to be one of themost effectivemethods to deal with the long wavelength statics caused by variation of topography and low velocity zone (LVZ). The residual statics correction calculation based onmultiple domains statistics is thought to be a quit good approach for determining the short wavelength statics caused by geometry deviation and LVZmodel error, it is suitable for complex near-surface conditions through correct application. The conventional residual statics correction calculation based on reflection energy is of course indispensable in data processing. Time variable residual static correction can also be used if necessary. Real data examples give an explanation on above opinions.
[7]
黄明忠 , 冯泽元 , 周大同 . 炮检域迭代直接静校正方法及应用效果
[J]. 勘探地球物理进展 , 2008 , 31 (2 ):122 -128 ,87.
[本文引用: 1]
Huang M Z Feng Z Y Zhou D T . Direct statics iterated in shot and receiver domains and its application
[J]. Progress in Exploration Geophysics , 2008 , 31 (2 ):122 -128 ,87.
[本文引用: 1]
[8]
肖永新 , 杨海申 , 崔士天 , 等 . 一项高效的折射静校正技术
[J]. 石油地球物理勘探 , 2019 , 54 (4 ):768 -774 ,722.
[本文引用: 1]
Xiao Y X Yang H S Cui S T , et al . An efficient refraction statics method for massive seismic data
[J]. Oil Geophysical Prospecting , 2019 , 54 (4 ):768 -774 ,722.
[本文引用: 1]
[9]
王克斌 , 赵灵芝 , 张旭民 . 折射静校正在苏里格气田三维处理中的应用
[J]. 石油物探 , 2003 , 42 (2 ):248 -251 .
[本文引用: 1]
长庆油田苏里格气田所在地区, 地表为小沙丘, 高差不大。该区近地表存在一条深达80m的古河道, 河道中已冲填了流沙, 造成近地表局部低速层的厚度发生了巨大变化, 引起地震剖面上严重的长、短波长静校正问题。在处理中, 利用本区域折射初至比较清楚的特点, 应用三维折射静校正技术。
Wang K B Zhao L Z Zhang X M . Application of refraction statics in 3-D data processing in Sulige gas field
[J]. Geophysical Prospecting for Petroleum , 2003 , 42 (2 ):248 -251 .
[本文引用: 1]
Sandy hillocks with small height difference dot in Sulige gas field area, Changqing oilfield. Because an ancient river course of 80m thick filled with sand passes across the area, the thickness of weathering layer changes greatly, leading to serious problems of statics. On account of clear first refraction arrival in this area, 3-D refraction techniques are adopted in data processing. The serious problems of long wavelength and short wavelength statics are solved satisfactorily.
[10]
方勇 , 罗文山 , 姜翠苹 , 等 . 库车山地地震资料层析静校正方法的应用
[J]. 石油地球物理勘探 , 2017 , 52 (S1 ):23 -27 .
[本文引用: 1]
Fang Y Luo W S Jiang C P , et al . Application of tomographic static correction method for Kuqa mountain seismic data
[J]. Oil Geophysical Prospecting , 2017 , 52 (S1 ):23 -27 .
[本文引用: 1]
[11]
郝鹏亮 . 基于深度学习的复杂地表初至拾取及层析静校正应用研究 [D]. 北京 : 中国石油大学(北京) , 2023 .
[本文引用: 2]
Hao P L . Research on application of first break picking and tomographic static correction of complex surface based on deep learning [D]. Beijing : China University of Petroleum (Beijing) , 2023 .
[本文引用: 2]
[12]
Palmer D . The generalized reciprocal method:An integrated approach to shallow refraction seismology
[J]. Exploration Geophysics , 1990 , 21 (1/2 ):33 -44 .
[本文引用: 1]
[13]
井西利 , 杨长春 , 李幼铭 , 等 . 地震静校正全局最优化问题的求解
[J]. 地球物理学报 , 2002 , 45 (5 ):707 -713 .
[本文引用: 1]
Jing X L Yang C C Li Y M , et al . A global optimized algorithm for seismic residual statics corrections
[J]. Chinese Journal of Geophysics , 2002 , 45 (5 ):707 -713 .
[本文引用: 1]
[14]
Zhang J Z Shi T K Zhao Y S , et al . Static corrections in mountainous areas using Fresnel-wavepath tomography
[J]. Journal of Applied Geophysics , 2014 , 111 :242 -249 .
[本文引用: 2]
[15]
Gibson B S . Nonlinear least-squares inversion of traveltime data for a linear velocity-depth relationship
[J]. Geophysics , 1979 , 44 (2 ):185 .
[本文引用: 2]
[16]
Yang H C Zhang J Z Ren K , et al . First-arrival traveltime inversion of seismic diving waves observed on undulant surface
[J]. Geophysical Journal International , 2021 , 225 (2 ):1020 -1031 .
[本文引用: 3]
[17]
Jin C K Zhang J Z . Stereotomography of seismic data acquired on undulant topography
[J]. Geophysics , 2018 , 83 (4 ):U35 -U41.
[本文引用: 1]
复杂近地表初至波层析反演静校正技术研究
1
2017
... 在山前带、黄土塬、沙漠等近地表条件复杂地区,起伏地形和低降速带剧烈的纵、横向速度变化使得在地表接收的地震记录中反射波同相轴发生明显的扭曲[1 ⇓ -3 ] .对地震记录进行静校正,可以有效地消除起伏地形和低降速带对反射波同相轴的不良影响,提高成像质量[4 -5 ] . ...
复杂近地表初至波层析反演静校正技术研究
1
2017
... 在山前带、黄土塬、沙漠等近地表条件复杂地区,起伏地形和低降速带剧烈的纵、横向速度变化使得在地表接收的地震记录中反射波同相轴发生明显的扭曲[1 ⇓ -3 ] .对地震记录进行静校正,可以有效地消除起伏地形和低降速带对反射波同相轴的不良影响,提高成像质量[4 -5 ] . ...
折射波静校正与层析静校正技术适用性分析
3
2012
... 在山前带、黄土塬、沙漠等近地表条件复杂地区,起伏地形和低降速带剧烈的纵、横向速度变化使得在地表接收的地震记录中反射波同相轴发生明显的扭曲[1 ⇓ -3 ] .对地震记录进行静校正,可以有效地消除起伏地形和低降速带对反射波同相轴的不良影响,提高成像质量[4 -5 ] . ...
... 在地震资料处理中,常规静校正方法包括高程静校正[6 -7 ] 、折射静校正[8 -9 ] 和层析静校正等[10 -11 ] .高程静校正将炮点和检波点从地表校正到同一高程的基准面,消除了起伏地形对地震记录中反射波同相轴的影响.然而,高程静校正没有考虑低降速带内速度的纵、横向变化,在近地表复杂工区的应用效果较差[6 ] .折射静校正方法利用初至折射波走时信息直接计算长波长静校正量.在近地表速度结构简单的工区,初至折射波连续、明显,折射静校正方法可以取得较好的静校正应用效果[11 -12 ] .然而,在低降速带较厚、速度横向变化剧烈、折射界面不稳定等近地表条件复杂地区,该类方法不再适用[2 ,13 -14 ] .层析静校正方法首先利用大量的初至走时信息通过多次迭代修正初始速度模型从而获得高精度的近地表速度模型,然后基于该近地表模型计算长波长静校正量.层析静校正方法不强调初至波一定是折射波,也不要求折射界面稳定和低降速带速度横向变化小.该方法是近地表条件复杂地区应用效果最佳和最广泛的静校正方法[2 ,4 ] . ...
... [2 ,4 ]. ...
折射波静校正与层析静校正技术适用性分析
3
2012
... 在山前带、黄土塬、沙漠等近地表条件复杂地区,起伏地形和低降速带剧烈的纵、横向速度变化使得在地表接收的地震记录中反射波同相轴发生明显的扭曲[1 ⇓ -3 ] .对地震记录进行静校正,可以有效地消除起伏地形和低降速带对反射波同相轴的不良影响,提高成像质量[4 -5 ] . ...
... 在地震资料处理中,常规静校正方法包括高程静校正[6 -7 ] 、折射静校正[8 -9 ] 和层析静校正等[10 -11 ] .高程静校正将炮点和检波点从地表校正到同一高程的基准面,消除了起伏地形对地震记录中反射波同相轴的影响.然而,高程静校正没有考虑低降速带内速度的纵、横向变化,在近地表复杂工区的应用效果较差[6 ] .折射静校正方法利用初至折射波走时信息直接计算长波长静校正量.在近地表速度结构简单的工区,初至折射波连续、明显,折射静校正方法可以取得较好的静校正应用效果[11 -12 ] .然而,在低降速带较厚、速度横向变化剧烈、折射界面不稳定等近地表条件复杂地区,该类方法不再适用[2 ,13 -14 ] .层析静校正方法首先利用大量的初至走时信息通过多次迭代修正初始速度模型从而获得高精度的近地表速度模型,然后基于该近地表模型计算长波长静校正量.层析静校正方法不强调初至波一定是折射波,也不要求折射界面稳定和低降速带速度横向变化小.该方法是近地表条件复杂地区应用效果最佳和最广泛的静校正方法[2 ,4 ] . ...
... [2 ,4 ]. ...
1
1999
... 在山前带、黄土塬、沙漠等近地表条件复杂地区,起伏地形和低降速带剧烈的纵、横向速度变化使得在地表接收的地震记录中反射波同相轴发生明显的扭曲[1 ⇓ -3 ] .对地震记录进行静校正,可以有效地消除起伏地形和低降速带对反射波同相轴的不良影响,提高成像质量[4 -5 ] . ...
黄土塬覆盖区的层析反演静校正方法研究
2
2019
... 在山前带、黄土塬、沙漠等近地表条件复杂地区,起伏地形和低降速带剧烈的纵、横向速度变化使得在地表接收的地震记录中反射波同相轴发生明显的扭曲[1 ⇓ -3 ] .对地震记录进行静校正,可以有效地消除起伏地形和低降速带对反射波同相轴的不良影响,提高成像质量[4 -5 ] . ...
... 在地震资料处理中,常规静校正方法包括高程静校正[6 -7 ] 、折射静校正[8 -9 ] 和层析静校正等[10 -11 ] .高程静校正将炮点和检波点从地表校正到同一高程的基准面,消除了起伏地形对地震记录中反射波同相轴的影响.然而,高程静校正没有考虑低降速带内速度的纵、横向变化,在近地表复杂工区的应用效果较差[6 ] .折射静校正方法利用初至折射波走时信息直接计算长波长静校正量.在近地表速度结构简单的工区,初至折射波连续、明显,折射静校正方法可以取得较好的静校正应用效果[11 -12 ] .然而,在低降速带较厚、速度横向变化剧烈、折射界面不稳定等近地表条件复杂地区,该类方法不再适用[2 ,13 -14 ] .层析静校正方法首先利用大量的初至走时信息通过多次迭代修正初始速度模型从而获得高精度的近地表速度模型,然后基于该近地表模型计算长波长静校正量.层析静校正方法不强调初至波一定是折射波,也不要求折射界面稳定和低降速带速度横向变化小.该方法是近地表条件复杂地区应用效果最佳和最广泛的静校正方法[2 ,4 ] . ...
黄土塬覆盖区的层析反演静校正方法研究
2
2019
... 在山前带、黄土塬、沙漠等近地表条件复杂地区,起伏地形和低降速带剧烈的纵、横向速度变化使得在地表接收的地震记录中反射波同相轴发生明显的扭曲[1 ⇓ -3 ] .对地震记录进行静校正,可以有效地消除起伏地形和低降速带对反射波同相轴的不良影响,提高成像质量[4 -5 ] . ...
... 在地震资料处理中,常规静校正方法包括高程静校正[6 -7 ] 、折射静校正[8 -9 ] 和层析静校正等[10 -11 ] .高程静校正将炮点和检波点从地表校正到同一高程的基准面,消除了起伏地形对地震记录中反射波同相轴的影响.然而,高程静校正没有考虑低降速带内速度的纵、横向变化,在近地表复杂工区的应用效果较差[6 ] .折射静校正方法利用初至折射波走时信息直接计算长波长静校正量.在近地表速度结构简单的工区,初至折射波连续、明显,折射静校正方法可以取得较好的静校正应用效果[11 -12 ] .然而,在低降速带较厚、速度横向变化剧烈、折射界面不稳定等近地表条件复杂地区,该类方法不再适用[2 ,13 -14 ] .层析静校正方法首先利用大量的初至走时信息通过多次迭代修正初始速度模型从而获得高精度的近地表速度模型,然后基于该近地表模型计算长波长静校正量.层析静校正方法不强调初至波一定是折射波,也不要求折射界面稳定和低降速带速度横向变化小.该方法是近地表条件复杂地区应用效果最佳和最广泛的静校正方法[2 ,4 ] . ...
A layer-stripping method for 3D near-surface velocity model building using seismic first-arrival times
6
2015
... 在山前带、黄土塬、沙漠等近地表条件复杂地区,起伏地形和低降速带剧烈的纵、横向速度变化使得在地表接收的地震记录中反射波同相轴发生明显的扭曲[1 ⇓ -3 ] .对地震记录进行静校正,可以有效地消除起伏地形和低降速带对反射波同相轴的不良影响,提高成像质量[4 -5 ] . ...
... 对于三维高密度地震资料,初至走时数据量极其庞大.这导致传统初至走时层析需要进行非常多次的射线追踪,耗时极大.为了提高近地表速度建模的效率,Shi等[5 ] 利用水平地表下的回折波走时和射线方程,从地表向下逐层确定介质的速度分布.相比于传统初至走时层析方法,该方法无需进行射线追踪计算初至波路径,其计算效率提高了近百倍.然而,在地表高程起伏较大的工区,其反演模型的精度较低,难以解决实测陆地地震资料的静校正问题. ...
... 在观测面高程起伏较大且介质速度横向变化剧烈时,基于水平观测面和一维速度模型的回折波走时和射线方程不再适用[5 ] .为此,本文采用起伏观测面下的回折波走时和射线方程.将回折波经过的区域分为两部分:炮点至回折点所在区域和回折点至检波点所在区域.炮点至回折点所在区域内速度随深度线性递增,速度梯度为λ s ,炮点所在地表的速度为v 0s ;检波点至回折点所在区域内速度随深度线性递增,速度梯度为λ r ,检波点所在地表的速度为v 0r .观测面处的速度可以通过近地表调查或直达波走时信息计算得到. ...
... 除最小偏移距数据集以外,将其余道集内的炮点和检波点延拓至界面l,就可以消除界面l上覆地层对回折波射线路径及走时的影响[5 ] .将延拓后的初至走时数据作为新的观测数据,将界面l作为新的地表,采用前述的方法即可确定新地表至新界面之间的速度.对所有的共偏移距数据集进行类似处理,即可自浅至深逐步建立三维近地表速度模型. ...
... 基于回折波走时和射线方程[5 ,16 ] ,将炮点延拓至界面l附近可以表示为: ...
... 为了客观而充分地展示本文方法的优缺点,分别使用现有的基于水平地表假设的初至走时层析方法[5 ] 、菲涅尔体初至走时层析方法[14 ] 和本文方法反演拾取的初至走时数据. ...
几种常用静校正方法的讨论
2
2006
... 在地震资料处理中,常规静校正方法包括高程静校正[6 -7 ] 、折射静校正[8 -9 ] 和层析静校正等[10 -11 ] .高程静校正将炮点和检波点从地表校正到同一高程的基准面,消除了起伏地形对地震记录中反射波同相轴的影响.然而,高程静校正没有考虑低降速带内速度的纵、横向变化,在近地表复杂工区的应用效果较差[6 ] .折射静校正方法利用初至折射波走时信息直接计算长波长静校正量.在近地表速度结构简单的工区,初至折射波连续、明显,折射静校正方法可以取得较好的静校正应用效果[11 -12 ] .然而,在低降速带较厚、速度横向变化剧烈、折射界面不稳定等近地表条件复杂地区,该类方法不再适用[2 ,13 -14 ] .层析静校正方法首先利用大量的初至走时信息通过多次迭代修正初始速度模型从而获得高精度的近地表速度模型,然后基于该近地表模型计算长波长静校正量.层析静校正方法不强调初至波一定是折射波,也不要求折射界面稳定和低降速带速度横向变化小.该方法是近地表条件复杂地区应用效果最佳和最广泛的静校正方法[2 ,4 ] . ...
... [6 ].折射静校正方法利用初至折射波走时信息直接计算长波长静校正量.在近地表速度结构简单的工区,初至折射波连续、明显,折射静校正方法可以取得较好的静校正应用效果[11 -12 ] .然而,在低降速带较厚、速度横向变化剧烈、折射界面不稳定等近地表条件复杂地区,该类方法不再适用[2 ,13 -14 ] .层析静校正方法首先利用大量的初至走时信息通过多次迭代修正初始速度模型从而获得高精度的近地表速度模型,然后基于该近地表模型计算长波长静校正量.层析静校正方法不强调初至波一定是折射波,也不要求折射界面稳定和低降速带速度横向变化小.该方法是近地表条件复杂地区应用效果最佳和最广泛的静校正方法[2 ,4 ] . ...
几种常用静校正方法的讨论
2
2006
... 在地震资料处理中,常规静校正方法包括高程静校正[6 -7 ] 、折射静校正[8 -9 ] 和层析静校正等[10 -11 ] .高程静校正将炮点和检波点从地表校正到同一高程的基准面,消除了起伏地形对地震记录中反射波同相轴的影响.然而,高程静校正没有考虑低降速带内速度的纵、横向变化,在近地表复杂工区的应用效果较差[6 ] .折射静校正方法利用初至折射波走时信息直接计算长波长静校正量.在近地表速度结构简单的工区,初至折射波连续、明显,折射静校正方法可以取得较好的静校正应用效果[11 -12 ] .然而,在低降速带较厚、速度横向变化剧烈、折射界面不稳定等近地表条件复杂地区,该类方法不再适用[2 ,13 -14 ] .层析静校正方法首先利用大量的初至走时信息通过多次迭代修正初始速度模型从而获得高精度的近地表速度模型,然后基于该近地表模型计算长波长静校正量.层析静校正方法不强调初至波一定是折射波,也不要求折射界面稳定和低降速带速度横向变化小.该方法是近地表条件复杂地区应用效果最佳和最广泛的静校正方法[2 ,4 ] . ...
... [6 ].折射静校正方法利用初至折射波走时信息直接计算长波长静校正量.在近地表速度结构简单的工区,初至折射波连续、明显,折射静校正方法可以取得较好的静校正应用效果[11 -12 ] .然而,在低降速带较厚、速度横向变化剧烈、折射界面不稳定等近地表条件复杂地区,该类方法不再适用[2 ,13 -14 ] .层析静校正方法首先利用大量的初至走时信息通过多次迭代修正初始速度模型从而获得高精度的近地表速度模型,然后基于该近地表模型计算长波长静校正量.层析静校正方法不强调初至波一定是折射波,也不要求折射界面稳定和低降速带速度横向变化小.该方法是近地表条件复杂地区应用效果最佳和最广泛的静校正方法[2 ,4 ] . ...
炮检域迭代直接静校正方法及应用效果
1
2008
... 在地震资料处理中,常规静校正方法包括高程静校正[6 -7 ] 、折射静校正[8 -9 ] 和层析静校正等[10 -11 ] .高程静校正将炮点和检波点从地表校正到同一高程的基准面,消除了起伏地形对地震记录中反射波同相轴的影响.然而,高程静校正没有考虑低降速带内速度的纵、横向变化,在近地表复杂工区的应用效果较差[6 ] .折射静校正方法利用初至折射波走时信息直接计算长波长静校正量.在近地表速度结构简单的工区,初至折射波连续、明显,折射静校正方法可以取得较好的静校正应用效果[11 -12 ] .然而,在低降速带较厚、速度横向变化剧烈、折射界面不稳定等近地表条件复杂地区,该类方法不再适用[2 ,13 -14 ] .层析静校正方法首先利用大量的初至走时信息通过多次迭代修正初始速度模型从而获得高精度的近地表速度模型,然后基于该近地表模型计算长波长静校正量.层析静校正方法不强调初至波一定是折射波,也不要求折射界面稳定和低降速带速度横向变化小.该方法是近地表条件复杂地区应用效果最佳和最广泛的静校正方法[2 ,4 ] . ...
炮检域迭代直接静校正方法及应用效果
1
2008
... 在地震资料处理中,常规静校正方法包括高程静校正[6 -7 ] 、折射静校正[8 -9 ] 和层析静校正等[10 -11 ] .高程静校正将炮点和检波点从地表校正到同一高程的基准面,消除了起伏地形对地震记录中反射波同相轴的影响.然而,高程静校正没有考虑低降速带内速度的纵、横向变化,在近地表复杂工区的应用效果较差[6 ] .折射静校正方法利用初至折射波走时信息直接计算长波长静校正量.在近地表速度结构简单的工区,初至折射波连续、明显,折射静校正方法可以取得较好的静校正应用效果[11 -12 ] .然而,在低降速带较厚、速度横向变化剧烈、折射界面不稳定等近地表条件复杂地区,该类方法不再适用[2 ,13 -14 ] .层析静校正方法首先利用大量的初至走时信息通过多次迭代修正初始速度模型从而获得高精度的近地表速度模型,然后基于该近地表模型计算长波长静校正量.层析静校正方法不强调初至波一定是折射波,也不要求折射界面稳定和低降速带速度横向变化小.该方法是近地表条件复杂地区应用效果最佳和最广泛的静校正方法[2 ,4 ] . ...
一项高效的折射静校正技术
1
2019
... 在地震资料处理中,常规静校正方法包括高程静校正[6 -7 ] 、折射静校正[8 -9 ] 和层析静校正等[10 -11 ] .高程静校正将炮点和检波点从地表校正到同一高程的基准面,消除了起伏地形对地震记录中反射波同相轴的影响.然而,高程静校正没有考虑低降速带内速度的纵、横向变化,在近地表复杂工区的应用效果较差[6 ] .折射静校正方法利用初至折射波走时信息直接计算长波长静校正量.在近地表速度结构简单的工区,初至折射波连续、明显,折射静校正方法可以取得较好的静校正应用效果[11 -12 ] .然而,在低降速带较厚、速度横向变化剧烈、折射界面不稳定等近地表条件复杂地区,该类方法不再适用[2 ,13 -14 ] .层析静校正方法首先利用大量的初至走时信息通过多次迭代修正初始速度模型从而获得高精度的近地表速度模型,然后基于该近地表模型计算长波长静校正量.层析静校正方法不强调初至波一定是折射波,也不要求折射界面稳定和低降速带速度横向变化小.该方法是近地表条件复杂地区应用效果最佳和最广泛的静校正方法[2 ,4 ] . ...
一项高效的折射静校正技术
1
2019
... 在地震资料处理中,常规静校正方法包括高程静校正[6 -7 ] 、折射静校正[8 -9 ] 和层析静校正等[10 -11 ] .高程静校正将炮点和检波点从地表校正到同一高程的基准面,消除了起伏地形对地震记录中反射波同相轴的影响.然而,高程静校正没有考虑低降速带内速度的纵、横向变化,在近地表复杂工区的应用效果较差[6 ] .折射静校正方法利用初至折射波走时信息直接计算长波长静校正量.在近地表速度结构简单的工区,初至折射波连续、明显,折射静校正方法可以取得较好的静校正应用效果[11 -12 ] .然而,在低降速带较厚、速度横向变化剧烈、折射界面不稳定等近地表条件复杂地区,该类方法不再适用[2 ,13 -14 ] .层析静校正方法首先利用大量的初至走时信息通过多次迭代修正初始速度模型从而获得高精度的近地表速度模型,然后基于该近地表模型计算长波长静校正量.层析静校正方法不强调初至波一定是折射波,也不要求折射界面稳定和低降速带速度横向变化小.该方法是近地表条件复杂地区应用效果最佳和最广泛的静校正方法[2 ,4 ] . ...
折射静校正在苏里格气田三维处理中的应用
1
2003
... 在地震资料处理中,常规静校正方法包括高程静校正[6 -7 ] 、折射静校正[8 -9 ] 和层析静校正等[10 -11 ] .高程静校正将炮点和检波点从地表校正到同一高程的基准面,消除了起伏地形对地震记录中反射波同相轴的影响.然而,高程静校正没有考虑低降速带内速度的纵、横向变化,在近地表复杂工区的应用效果较差[6 ] .折射静校正方法利用初至折射波走时信息直接计算长波长静校正量.在近地表速度结构简单的工区,初至折射波连续、明显,折射静校正方法可以取得较好的静校正应用效果[11 -12 ] .然而,在低降速带较厚、速度横向变化剧烈、折射界面不稳定等近地表条件复杂地区,该类方法不再适用[2 ,13 -14 ] .层析静校正方法首先利用大量的初至走时信息通过多次迭代修正初始速度模型从而获得高精度的近地表速度模型,然后基于该近地表模型计算长波长静校正量.层析静校正方法不强调初至波一定是折射波,也不要求折射界面稳定和低降速带速度横向变化小.该方法是近地表条件复杂地区应用效果最佳和最广泛的静校正方法[2 ,4 ] . ...
折射静校正在苏里格气田三维处理中的应用
1
2003
... 在地震资料处理中,常规静校正方法包括高程静校正[6 -7 ] 、折射静校正[8 -9 ] 和层析静校正等[10 -11 ] .高程静校正将炮点和检波点从地表校正到同一高程的基准面,消除了起伏地形对地震记录中反射波同相轴的影响.然而,高程静校正没有考虑低降速带内速度的纵、横向变化,在近地表复杂工区的应用效果较差[6 ] .折射静校正方法利用初至折射波走时信息直接计算长波长静校正量.在近地表速度结构简单的工区,初至折射波连续、明显,折射静校正方法可以取得较好的静校正应用效果[11 -12 ] .然而,在低降速带较厚、速度横向变化剧烈、折射界面不稳定等近地表条件复杂地区,该类方法不再适用[2 ,13 -14 ] .层析静校正方法首先利用大量的初至走时信息通过多次迭代修正初始速度模型从而获得高精度的近地表速度模型,然后基于该近地表模型计算长波长静校正量.层析静校正方法不强调初至波一定是折射波,也不要求折射界面稳定和低降速带速度横向变化小.该方法是近地表条件复杂地区应用效果最佳和最广泛的静校正方法[2 ,4 ] . ...
库车山地地震资料层析静校正方法的应用
1
2017
... 在地震资料处理中,常规静校正方法包括高程静校正[6 -7 ] 、折射静校正[8 -9 ] 和层析静校正等[10 -11 ] .高程静校正将炮点和检波点从地表校正到同一高程的基准面,消除了起伏地形对地震记录中反射波同相轴的影响.然而,高程静校正没有考虑低降速带内速度的纵、横向变化,在近地表复杂工区的应用效果较差[6 ] .折射静校正方法利用初至折射波走时信息直接计算长波长静校正量.在近地表速度结构简单的工区,初至折射波连续、明显,折射静校正方法可以取得较好的静校正应用效果[11 -12 ] .然而,在低降速带较厚、速度横向变化剧烈、折射界面不稳定等近地表条件复杂地区,该类方法不再适用[2 ,13 -14 ] .层析静校正方法首先利用大量的初至走时信息通过多次迭代修正初始速度模型从而获得高精度的近地表速度模型,然后基于该近地表模型计算长波长静校正量.层析静校正方法不强调初至波一定是折射波,也不要求折射界面稳定和低降速带速度横向变化小.该方法是近地表条件复杂地区应用效果最佳和最广泛的静校正方法[2 ,4 ] . ...
库车山地地震资料层析静校正方法的应用
1
2017
... 在地震资料处理中,常规静校正方法包括高程静校正[6 -7 ] 、折射静校正[8 -9 ] 和层析静校正等[10 -11 ] .高程静校正将炮点和检波点从地表校正到同一高程的基准面,消除了起伏地形对地震记录中反射波同相轴的影响.然而,高程静校正没有考虑低降速带内速度的纵、横向变化,在近地表复杂工区的应用效果较差[6 ] .折射静校正方法利用初至折射波走时信息直接计算长波长静校正量.在近地表速度结构简单的工区,初至折射波连续、明显,折射静校正方法可以取得较好的静校正应用效果[11 -12 ] .然而,在低降速带较厚、速度横向变化剧烈、折射界面不稳定等近地表条件复杂地区,该类方法不再适用[2 ,13 -14 ] .层析静校正方法首先利用大量的初至走时信息通过多次迭代修正初始速度模型从而获得高精度的近地表速度模型,然后基于该近地表模型计算长波长静校正量.层析静校正方法不强调初至波一定是折射波,也不要求折射界面稳定和低降速带速度横向变化小.该方法是近地表条件复杂地区应用效果最佳和最广泛的静校正方法[2 ,4 ] . ...
2
2023
... 在地震资料处理中,常规静校正方法包括高程静校正[6 -7 ] 、折射静校正[8 -9 ] 和层析静校正等[10 -11 ] .高程静校正将炮点和检波点从地表校正到同一高程的基准面,消除了起伏地形对地震记录中反射波同相轴的影响.然而,高程静校正没有考虑低降速带内速度的纵、横向变化,在近地表复杂工区的应用效果较差[6 ] .折射静校正方法利用初至折射波走时信息直接计算长波长静校正量.在近地表速度结构简单的工区,初至折射波连续、明显,折射静校正方法可以取得较好的静校正应用效果[11 -12 ] .然而,在低降速带较厚、速度横向变化剧烈、折射界面不稳定等近地表条件复杂地区,该类方法不再适用[2 ,13 -14 ] .层析静校正方法首先利用大量的初至走时信息通过多次迭代修正初始速度模型从而获得高精度的近地表速度模型,然后基于该近地表模型计算长波长静校正量.层析静校正方法不强调初至波一定是折射波,也不要求折射界面稳定和低降速带速度横向变化小.该方法是近地表条件复杂地区应用效果最佳和最广泛的静校正方法[2 ,4 ] . ...
... [11 -12 ].然而,在低降速带较厚、速度横向变化剧烈、折射界面不稳定等近地表条件复杂地区,该类方法不再适用[2 ,13 -14 ] .层析静校正方法首先利用大量的初至走时信息通过多次迭代修正初始速度模型从而获得高精度的近地表速度模型,然后基于该近地表模型计算长波长静校正量.层析静校正方法不强调初至波一定是折射波,也不要求折射界面稳定和低降速带速度横向变化小.该方法是近地表条件复杂地区应用效果最佳和最广泛的静校正方法[2 ,4 ] . ...
2
2023
... 在地震资料处理中,常规静校正方法包括高程静校正[6 -7 ] 、折射静校正[8 -9 ] 和层析静校正等[10 -11 ] .高程静校正将炮点和检波点从地表校正到同一高程的基准面,消除了起伏地形对地震记录中反射波同相轴的影响.然而,高程静校正没有考虑低降速带内速度的纵、横向变化,在近地表复杂工区的应用效果较差[6 ] .折射静校正方法利用初至折射波走时信息直接计算长波长静校正量.在近地表速度结构简单的工区,初至折射波连续、明显,折射静校正方法可以取得较好的静校正应用效果[11 -12 ] .然而,在低降速带较厚、速度横向变化剧烈、折射界面不稳定等近地表条件复杂地区,该类方法不再适用[2 ,13 -14 ] .层析静校正方法首先利用大量的初至走时信息通过多次迭代修正初始速度模型从而获得高精度的近地表速度模型,然后基于该近地表模型计算长波长静校正量.层析静校正方法不强调初至波一定是折射波,也不要求折射界面稳定和低降速带速度横向变化小.该方法是近地表条件复杂地区应用效果最佳和最广泛的静校正方法[2 ,4 ] . ...
... [11 -12 ].然而,在低降速带较厚、速度横向变化剧烈、折射界面不稳定等近地表条件复杂地区,该类方法不再适用[2 ,13 -14 ] .层析静校正方法首先利用大量的初至走时信息通过多次迭代修正初始速度模型从而获得高精度的近地表速度模型,然后基于该近地表模型计算长波长静校正量.层析静校正方法不强调初至波一定是折射波,也不要求折射界面稳定和低降速带速度横向变化小.该方法是近地表条件复杂地区应用效果最佳和最广泛的静校正方法[2 ,4 ] . ...
The generalized reciprocal method:An integrated approach to shallow refraction seismology
1
1990
... 在地震资料处理中,常规静校正方法包括高程静校正[6 -7 ] 、折射静校正[8 -9 ] 和层析静校正等[10 -11 ] .高程静校正将炮点和检波点从地表校正到同一高程的基准面,消除了起伏地形对地震记录中反射波同相轴的影响.然而,高程静校正没有考虑低降速带内速度的纵、横向变化,在近地表复杂工区的应用效果较差[6 ] .折射静校正方法利用初至折射波走时信息直接计算长波长静校正量.在近地表速度结构简单的工区,初至折射波连续、明显,折射静校正方法可以取得较好的静校正应用效果[11 -12 ] .然而,在低降速带较厚、速度横向变化剧烈、折射界面不稳定等近地表条件复杂地区,该类方法不再适用[2 ,13 -14 ] .层析静校正方法首先利用大量的初至走时信息通过多次迭代修正初始速度模型从而获得高精度的近地表速度模型,然后基于该近地表模型计算长波长静校正量.层析静校正方法不强调初至波一定是折射波,也不要求折射界面稳定和低降速带速度横向变化小.该方法是近地表条件复杂地区应用效果最佳和最广泛的静校正方法[2 ,4 ] . ...
地震静校正全局最优化问题的求解
1
2002
... 在地震资料处理中,常规静校正方法包括高程静校正[6 -7 ] 、折射静校正[8 -9 ] 和层析静校正等[10 -11 ] .高程静校正将炮点和检波点从地表校正到同一高程的基准面,消除了起伏地形对地震记录中反射波同相轴的影响.然而,高程静校正没有考虑低降速带内速度的纵、横向变化,在近地表复杂工区的应用效果较差[6 ] .折射静校正方法利用初至折射波走时信息直接计算长波长静校正量.在近地表速度结构简单的工区,初至折射波连续、明显,折射静校正方法可以取得较好的静校正应用效果[11 -12 ] .然而,在低降速带较厚、速度横向变化剧烈、折射界面不稳定等近地表条件复杂地区,该类方法不再适用[2 ,13 -14 ] .层析静校正方法首先利用大量的初至走时信息通过多次迭代修正初始速度模型从而获得高精度的近地表速度模型,然后基于该近地表模型计算长波长静校正量.层析静校正方法不强调初至波一定是折射波,也不要求折射界面稳定和低降速带速度横向变化小.该方法是近地表条件复杂地区应用效果最佳和最广泛的静校正方法[2 ,4 ] . ...
地震静校正全局最优化问题的求解
1
2002
... 在地震资料处理中,常规静校正方法包括高程静校正[6 -7 ] 、折射静校正[8 -9 ] 和层析静校正等[10 -11 ] .高程静校正将炮点和检波点从地表校正到同一高程的基准面,消除了起伏地形对地震记录中反射波同相轴的影响.然而,高程静校正没有考虑低降速带内速度的纵、横向变化,在近地表复杂工区的应用效果较差[6 ] .折射静校正方法利用初至折射波走时信息直接计算长波长静校正量.在近地表速度结构简单的工区,初至折射波连续、明显,折射静校正方法可以取得较好的静校正应用效果[11 -12 ] .然而,在低降速带较厚、速度横向变化剧烈、折射界面不稳定等近地表条件复杂地区,该类方法不再适用[2 ,13 -14 ] .层析静校正方法首先利用大量的初至走时信息通过多次迭代修正初始速度模型从而获得高精度的近地表速度模型,然后基于该近地表模型计算长波长静校正量.层析静校正方法不强调初至波一定是折射波,也不要求折射界面稳定和低降速带速度横向变化小.该方法是近地表条件复杂地区应用效果最佳和最广泛的静校正方法[2 ,4 ] . ...
Static corrections in mountainous areas using Fresnel-wavepath tomography
2
2014
... 在地震资料处理中,常规静校正方法包括高程静校正[6 -7 ] 、折射静校正[8 -9 ] 和层析静校正等[10 -11 ] .高程静校正将炮点和检波点从地表校正到同一高程的基准面,消除了起伏地形对地震记录中反射波同相轴的影响.然而,高程静校正没有考虑低降速带内速度的纵、横向变化,在近地表复杂工区的应用效果较差[6 ] .折射静校正方法利用初至折射波走时信息直接计算长波长静校正量.在近地表速度结构简单的工区,初至折射波连续、明显,折射静校正方法可以取得较好的静校正应用效果[11 -12 ] .然而,在低降速带较厚、速度横向变化剧烈、折射界面不稳定等近地表条件复杂地区,该类方法不再适用[2 ,13 -14 ] .层析静校正方法首先利用大量的初至走时信息通过多次迭代修正初始速度模型从而获得高精度的近地表速度模型,然后基于该近地表模型计算长波长静校正量.层析静校正方法不强调初至波一定是折射波,也不要求折射界面稳定和低降速带速度横向变化小.该方法是近地表条件复杂地区应用效果最佳和最广泛的静校正方法[2 ,4 ] . ...
... 为了客观而充分地展示本文方法的优缺点,分别使用现有的基于水平地表假设的初至走时层析方法[5 ] 、菲涅尔体初至走时层析方法[14 ] 和本文方法反演拾取的初至走时数据. ...
Nonlinear least-squares inversion of traveltime data for a linear velocity-depth relationship
2
1979
... 起伏观测面下回折波传播路径如图1 所示.回折波从炮点传播至回折点,走时和射线方程可以表示为[15 -16 ] : ...
... 式中:t sm 为回折波从炮点至回折点的旅行时间,v m 为回折点处的速度,v 0s 为炮点位置地表的速度,λ s 为炮点至回折点所在区域内的速度梯度,X sm 为炮点和回折点之间的水平距离,h sm 为炮点至回折点的垂直距离.同理可得回折波从回折点传播至检波点的走时和射线方程.根据回折波的走时和射线方程及炮检点之间的几何关系,可得炮点至回折点所在区域内的速度梯度λ s 和检波点至回折点所在区域内的速度梯度λ r [15 ⇓ -17 ] . ...
First-arrival traveltime inversion of seismic diving waves observed on undulant surface
3
2021
... 起伏观测面下回折波传播路径如图1 所示.回折波从炮点传播至回折点,走时和射线方程可以表示为[15 -16 ] : ...
... 式中:t sm 为回折波从炮点至回折点的旅行时间,v m 为回折点处的速度,v 0s 为炮点位置地表的速度,λ s 为炮点至回折点所在区域内的速度梯度,X sm 为炮点和回折点之间的水平距离,h sm 为炮点至回折点的垂直距离.同理可得回折波从回折点传播至检波点的走时和射线方程.根据回折波的走时和射线方程及炮检点之间的几何关系,可得炮点至回折点所在区域内的速度梯度λ s 和检波点至回折点所在区域内的速度梯度λ r [15 ⇓ -17 ] . ...
... 基于回折波走时和射线方程[5 ,16 ] ,将炮点延拓至界面l附近可以表示为: ...
Stereotomography of seismic data acquired on undulant topography
1
2018
... 式中:t sm 为回折波从炮点至回折点的旅行时间,v m 为回折点处的速度,v 0s 为炮点位置地表的速度,λ s 为炮点至回折点所在区域内的速度梯度,X sm 为炮点和回折点之间的水平距离,h sm 为炮点至回折点的垂直距离.同理可得回折波从回折点传播至检波点的走时和射线方程.根据回折波的走时和射线方程及炮检点之间的几何关系,可得炮点至回折点所在区域内的速度梯度λ s 和检波点至回折点所在区域内的速度梯度λ r [15 ⇓ -17 ] . ...