基于Shearlet变换的三维地震数据重建

doi:10.11720/wtyht.2025.1271

基于Shearlet变换的三维地震数据重建

黄伟鸿^,, 张华^,, 武召祺, 戴梦雪, 鲍兴悦, 蒋伟龙, 邱修权

东华理工大学核资源与环境国家重点实验室,江西南昌 330013

3D seismic data reconstruction based on Shearlet transform

HUANG Wei-Hong^,, ZHANG Hua^,, WU Zhao-Qi, DAI Meng-Xue, BAO Xing-Yue, JIANG Wei-Long, QIU Xiu-Quan

State Key Laboratory of Nuclear Resources and Environment, East China University of Technology, Nanchang 330013, China

通讯作者: 张华(1979-),男,教授,博士生导师,研究方向为地震数据处理方法技术以及自然灾害探测与评估。Email:zhhua1979@163.com

第一作者: 黄伟鸿(2000-),男,硕士研究生,主要研究方向为地震勘探数据重建和去噪方法。Email:1372296255@qq.com

责任编辑: 沈效群

收稿日期: 2024-06-26 修回日期: 2024-11-3

基金资助:

国家自然科学基金项目(42304145)
国家自然科学基金项目(41874126)
江西省自然科学基金项目(20232BAB213077)
江西省自然科学基金项目(20242BAB26051)

Received: 2024-06-26 Revised: 2024-11-3

摘要

在地震勘探中,受采集成本或地形环境的限制,地震数据往往存在缺失,因此数据重建是地震数据预处理的关键步骤。本文基于压缩感知理论框架,对合成数据进行二维随机欠采样,将三维地震数据划分为一系列时间切片,随后引入Shearlet稀疏变换,结合凸集投影(POCS)算法逐次对每个时间切片进行数据重建,从而实现了基于Shearlet变换的三维地震数据时间域重建方法。数值试验和实测数据结果表明,相对于Curvelet变换的重建方法,本文所提出的重建方法的信噪比更高,计算速度更快,效果更好。

关键词： Shearlet变换; 地震数据重建; 压缩感知; 凸集投影算法

Abstract

Seismic data collected in the field frequently suffer from missing values due to constraints of acquisition cost or terrain. Data reconstruction is a critical step in seismic data preprocessing. Based on the compressed sensing theoretical framework, this study subsampled synthesized data using the 2D random undersampling technique. Then, the 3D seismic data were divided into a series of time slices. By introducing the sparse Shearlet transform and using the convex set projection (POCS) algorithm, this study conducted sequential data reconstruction for various time slices. As a result, a Shearlet transform-based time-domain 3D seismic data reconstruction method was developed. Numerical experiments and measured results demonstrate that the proposed reconstruction method exhibits a higher signal-to-noise ratio, a higher computational speed, and better effects than a Curvelet transform-based approach.

Keywords： Shearlet transform; seismic data reconstruction; compression sensing; convex set projection algorithm

PDF (6054KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

黄伟鸿, 张华, 武召祺, 戴梦雪, 鲍兴悦, 蒋伟龙, 邱修权. 基于Shearlet变换的三维地震数据重建[J]. 物探与化探, 2025, 49(2): 394-403 doi:10.11720/wtyht.2025.1271

HUANG Wei-Hong, ZHANG Hua, WU Zhao-Qi, DAI Meng-Xue, BAO Xing-Yue, JIANG Wei-Long, QIU Xiu-Quan. 3D seismic data reconstruction based on Shearlet transform[J]. Geophysical and Geochemical Exploration, 2025, 49(2): 394-403 doi:10.11720/wtyht.2025.1271

0 引言

在野外数据采集过程中,受到地形、地貌、仪器故障等因素的限制,地震勘探数据在空间方向上常呈现不规则采样,导致地震波场信息不完整,从而出现空间假频现象,影响高分辨率地震勘探的准确性^[1-2]。此外,即使按照传统的奈奎斯特定理进行理想采样,但在后续的某些地震处理方法中,地震数据仍存在采样不足的情况,难以满足特定处理方法的要求,在这种情况,需要发展快速高精度叠前数据重建方法,重建出高密度地震数据,以减轻地震数据采样不足对后续处理方法的影响。

目前主要存在5类地震数据重建方法。第一类是基于滤波器的方法,这类方法通过插值滤波来实现数据重建,但对于不均匀网格采样的数据,规则化处理可能导致较大误差。第二类是波场延拓方法^[3],这类方法需要利用地下信息,但由于地下结构的先验信息通常不明确且计算量巨大,难以应用于实际工作中。第三类是快速降秩方法^[4-5],该类方法将插值问题转化为图像填充问题,速度快,参数简单,但在非均匀网格采样下有不规则缺失数据现象,在反假频能力方面也存在一定不足。第四类是稀疏变换的方法,该类方法将地震数据从时间域转换到变换域,利用变换域的信号特征进行插值;这一类方法无需先验地下信息,可以重建规则和不规则的缺失地震道,计算速度快,精度高。第五类是人工智能重建方法^[6],根据地震数据本身的特征进行自我学习,从而恢复缺失道信息,如:有监督学习、无监督学习、自监督学习等。

由于不规则采样数据产生的混叠噪声较少,因此重建不规则采样数据的难度低于重建规则采样数据的难度^[7]。针对不规则数据的重建,稀疏促进重建是应用最为广泛的方法之一。压缩感知理论提供了一个很好的机会来解决地震数据重建问题,指出可以用低于奈奎斯特采样率的非自适应测量来处理信号,将地震数据重建问题转化为稀疏优化问题,利用稀疏变换来区分有用信号和缺失信号^[8]。目前,对于稀疏变换的研究已取得了大量成果,如早期的傅里叶变换^[9]、小波变换^[10],以及众多具有更好方向表示能力的类小波变换:Contourlet变换、Curvelet变换^[11-12]、Shearlet变换等^[13-14]。Shearlet变换是一种与多尺度和多分辨率分析密切相关的多维函数逼近方法^[15],该变换的基函数可以通过膨胀、剪切和平移构造在频域中逐层细分,从而使得其比小波变换更为稀疏。值得一提的是,该变换的分解方向数量和支撑基的规模没有明确限制。现如今Curvelet变换已被广泛应用于地震数据重建和去噪领域,但Shearlet变换在地震数据处理领域中尚未得到广泛应用。

在所有数据插值算法中,凸集投影算法(POCS)因其高效率和高性能的优势而被广泛应用于图像重建和不规则数据绘制^{[16⇓⇓⇓⇓-21]}。Gao等^[22]结合傅里叶变换与POCS算法对不规则地震数据进行插值。基于傅里叶变换重建能较好地处理近似线性同相轴的地震数据,但处理非线性同相轴的效果不佳。Curvelet变换^[23]有局部化识别能力,于是被用于地震数据重建。张华等^[12]基于Curvelet变换和POCS算法,通过对时间切片处理实现三维地震数据重建。

在前人研究基础上,本文采用Shearlet变换基作为稀疏表示基,对地震数据进行二维随机欠采样,并通过POCS算法对时间切片进行重建,在时间域实现了基于Shearlet变换的三维地震数据重建,这种方法降低了地震数据的维数,提高了计算效率,节省内存空间。研究结果表明,Shearlet变换相较于Curvelet变换不仅运算速度更快,而且重建效果更好。

1 理论原理

1.1 压缩感知基本理论

由完整地震数据d和实测数据y组成的地震正演模型可以表示为

(1)y=Md,

式中:y∈Rⁿ,d∈R^N,其中R为实数集,N、n为数据维度,且N>n;M为随机采样矩阵。

S为一种稀疏变换,且有S^HS=I,则d在变换域中的稀疏表示为

(2)y=Ax且A=MS^H,

式中,S^H是S的共轭转置矩阵。地震数据重建问题就是把实际采集的数据d重建回完整的数据y,这是一个欠定的反演问题。获得稀疏表示后,该问题可以转化为L₀范数最小化问题:

(3)

\tilde{x}

\underset{x}{m i n}

‖x‖₀ s.t. y=Ax 。

式中: $\tilde{x}$ 为重建后的地震数据稀疏表示。当数据量加剧时,该问题变得不可解。但在压缩感知理论中指出,信号若能稀疏表示和采样矩阵满足有限等距条件(RIP)时^[24],即可求得唯一解。地震勘探中,所使用的随机采样矩阵(数据缺失位置对应元素为0,采集的数据对应元素为1)能满足以上条件。这时,求解L₀范数最小化问题等价于求解L₁范数最小化问题,这样就转化为一个线性规划凸优化问题:

(4)

\tilde{x}

\underset{x}{m i n}

‖x‖₁ s.t. y=Ax;

其目标函数形式为

(5)

\tilde{x}

\underset{x}{m i n}

ψ(x)且ψ(x)=

‖ y - A x ‖_{2}^{2}

+λ‖x‖₁ ;

得到重建后完整的数据:

(6)

\tilde{d}

=S^H

\tilde{x}

。

1.2 Shearlet变换基本理论

稀疏变换是压缩感知的一个主要环节,其中Shearlet变换是一种多维函数稀疏表示方法,具有比曲波更敏感的方向性和更稀疏的表现形式。当维度为2时,shearlet系统的形式为

(7)

\begin{array}{l} S H (ψ) = {ψ_{i, j, k} (x) = | d e t A |^{i / 2} ψ (S_{j} A_{i} x - k) : \\ i, j \in Z, k \in Z^{2}}, \end{array}

式中: $ψ \in L^{2} (R^{2})$ ; $ψ_{i, j, k} (x)$ 为Shearlet函数;A_i为各向异性膨胀矩阵;S_j为剪切矩阵;i、j、k分别为尺度参数、剪切参数和平移参数,对∀i>0,j∈R,有:

(8)A_i=

(\begin{array}{l} i & 0 \\ 0 & \sqrt{i} \end{array})

, S_j=

(\begin{array}{l} 1 & j \\ 0 & 1 \end{array})

。

另外,对于任意ξ=(ξ₁,ξ₂)∈R²,ξ₁≠0,ψ满足:

(9)

\hat{ψ} (ξ) = {\hat{ψ}}_{1} (ξ_{1}) {\hat{ψ}}_{2} (\frac{ξ_{2}}{ξ_{1}}),

式中: $\hat{ψ}$ 为ψ的傅里叶变换; ${\hat{ψ}}_{1}$ ∈C^∞(R)且supp ${\hat{ψ}}_{1}$ ⊂ $[- 2, - \frac{1}{2}]$ ∪ $[\frac{1}{2}, 2]$ ; ${\hat{ψ}}_{2}$ ∈C^∞(R)且supp ${\hat{ψ}}_{2}$ ⊂[-1,1]。于是,由母函数ψ、各向异性膨胀矩阵A_i和剪切矩阵S_j可以得到Shearlet系统:

(10)

\begin{array}{l} {ψ_{i, j, k} (x) = i^{- 3 / 4} ψ (A_{i}^{- 1} S_{j}^{- 1} (x - k)) : \\ i \in R^{+}, j \in R, s \in R^{2}} 。 \end{array}

1.3 POCS算法

由压缩感知理论得到,利用随机欠采样可以将信号的重建问题转化为去噪问题。本文采用凸集投影算法进行数据重建,在每次迭代过程中,将空间域的地震数据转换到变换域,通过设置阈值保留有效信号,然后把有效信号进行反剪切波变换,最后把原始待重建的地震数据置换到反剪切波后的数据中。反复重复以上步骤,直到缺失的地震数据得到最佳恢复,迭代公式为

(11)

{\tilde{d}}_{k + 1} = y + (I - M) S^{H} T_{λ_{k}} S {\tilde{d}}_{k} 。

式中:S表示稀疏变换;y为缺失数据; ${\tilde{d}}_{k}$ 是第k次迭代后恢复的值。阈值收缩算子 $T_{λ_{k}}$ 表示为

(12)

T_{λ_{k}} (x) = \{\begin{array}{l} 1, & | x_{k} | \geq λ_{k}; \\ 0, & | x_{k} | < λ_{k} 。 \end{array}

式中的阈值表达式为

(13)‖Sy‖_∞=λ₁>λ₂>…λ_k…>ε,

其中,ε是几乎为零的最小阈值,其大小和数据中噪声的能量有关;λ_k为第k次迭代后的阈值,可以根据阈值模型选择λ_k。为了使计算速度更快,本文引用以指数形式 $e^{- \sqrt{x}}$ 衰减的新型阈值模型^[12]:

(14)

λ_{k} = m \cdot e x p [\sqrt{\frac{k - 1}{N - 1}} (l n ε - l n m)]

式中:m=|Sy|_max,表示稀疏变换系数绝对值的最大值。

2 模型数据重建试验

为了评价地震数据重建后的质量,本文定义的信噪比(SNR)公式为

(15)

S N R = 20 l g (‖ d_{0} ‖_{2} / ‖ d - d_{0} ‖_{2}),

式中:d₀为原始数据;d为重建后的数据。SNR值越高,表示重建结果与原始数据越接近,效果越好。

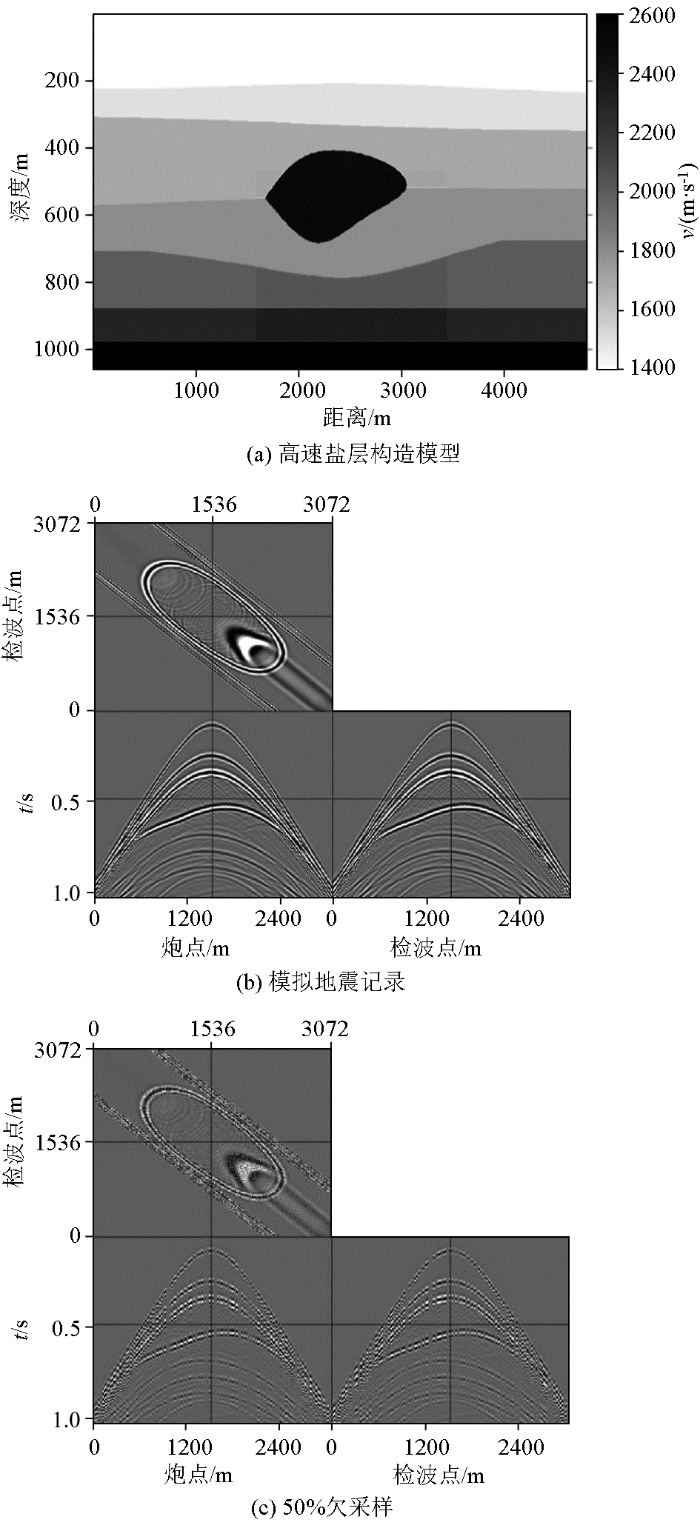
为了恢复缺失的地震数据、提高数据质量,以满足后续处理、反演和解释工作的要求,进行叠前数据重建是不可缺少的一环。首先设计如图1a所示的速度模型,该模型由沉积物层包围的高速盐层组成;然后使用声波方程有限差分法进行模拟,从而得到一个理论的合成数据,并将其按检波器、炮点和时间采样点方向排列成三维数据体,如图1b所示。该合成的数据包括256炮,每一炮有256个检波器,炮间距与检波距都为12 m。其中每个检波器都包含256个时间采样点,时间采样间隔为4 ms,采样时长为1.024 s。图1c为50%二维随机欠采样记录,抽取共炮点第128炮(1 536 m),共检波器第128道(1 536 m),时间0.48 s进行展示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 合成数据及相应速度模型

Fig.1 Synthesize data and corresponding speed model

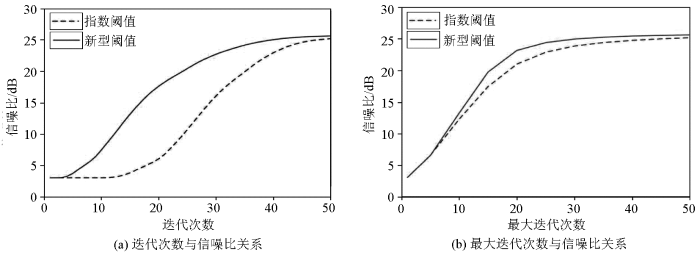
阈值模型的选择影响算法的收敛速度。为了比较本文方法在不同模型下的运算效果,随机抽取任意一时间切片进行计算。图2a为最大迭代次数固定为50次、迭代次数与两种阈值模型重建后的信噪比关系图,图2b为不同的最大迭代次数、两种不同阈值模型重建后的信噪比曲线。从图2中可以看出,无论是固定迭代次数还是不同的最大迭代次数,两者在迭代次数为50时均已收敛,但新型阈值模型的收敛速度更具有优势,在迭代次数少的情况下,重建后的信噪比更高。因此,在后续的模型试验中,选择新型阈值模型和迭代次数为50次进行数据重建试验。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 指数和新型阈值模型的重建信噪比曲线

Fig.2 Reconstructed SNR curves of the index and the new threshold model

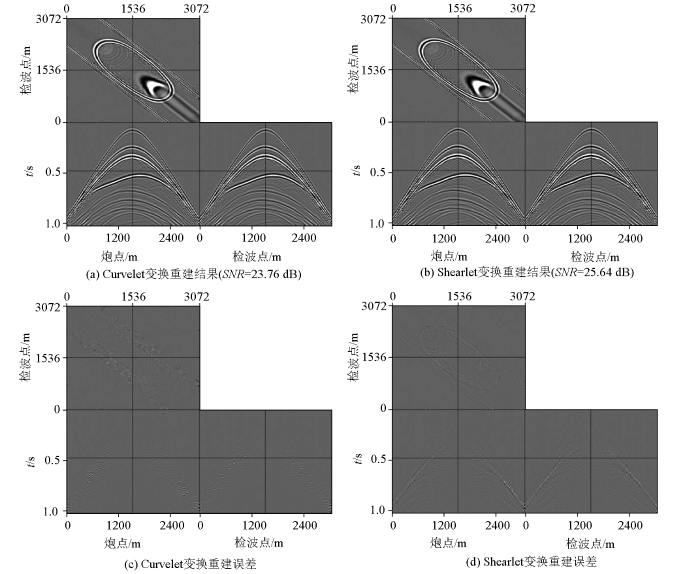
本文采用50%随机欠采样的地震数据进行重建。图3a~d分别为基于Curvelet变换和Shearlet 变换的重建结果以及重建后与完整数据的误差,工程方法重建后的SNR分别为23.76 dB和25.64 dB。重建结果表明:两种方法都获得了较好的插值结果,相比之下,基于Shearlet变换重建后的同相轴恢复得更完整,重建误差更小,信噪比更高。值得一提的是,Shearlet变换相比Curvelet变换,仅需一半的时间就完成了数据的重建,大大提高了重建速度。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 Curvelet变换和Shearlet变换重建结果及其误差

Fig.3 The reconstructed results and error by Curvelet and Shearlet

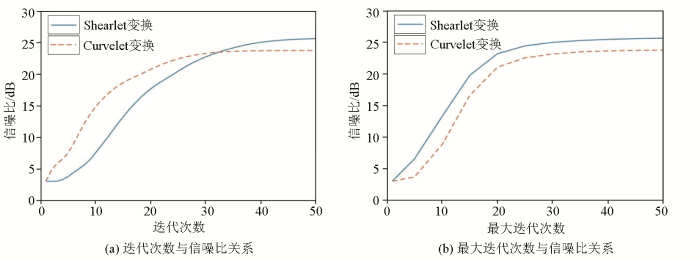
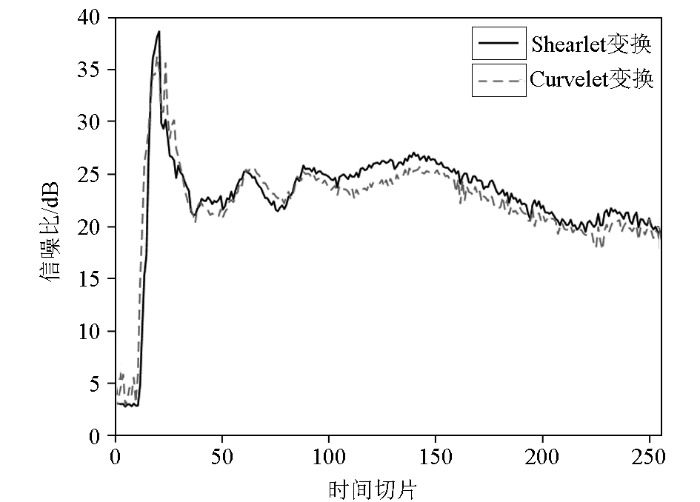
图4a为最大迭代次数固定为50次、迭代次数与重建后的信噪比关系曲线,可以看出:在初期基于Curvelet变换重建的收敛速度快、信噪比较高,但后期收敛慢;在第32次迭代后的迭代过程中,基于Shearlet变换重建后的精度更高。图4b为计算不同最大迭代次数与重建后的信噪比关系曲线,可以发现在1~50的最大迭代次数中,Shearlet变换的重建效果都优于Curvelet变换。经对比,信噪比达到23 dB时,Curvelet变换要迭代30次,而Shearlet仅需要迭代20次即可,所用的时间更少,在效率上更具有优势,这说明Shearlet变换具有一定的实际意义。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 Curvelet变换和Shearlet变换重建信噪比曲线

Fig.4 Reconstructed SNR curves by Curvelet and Shearlet

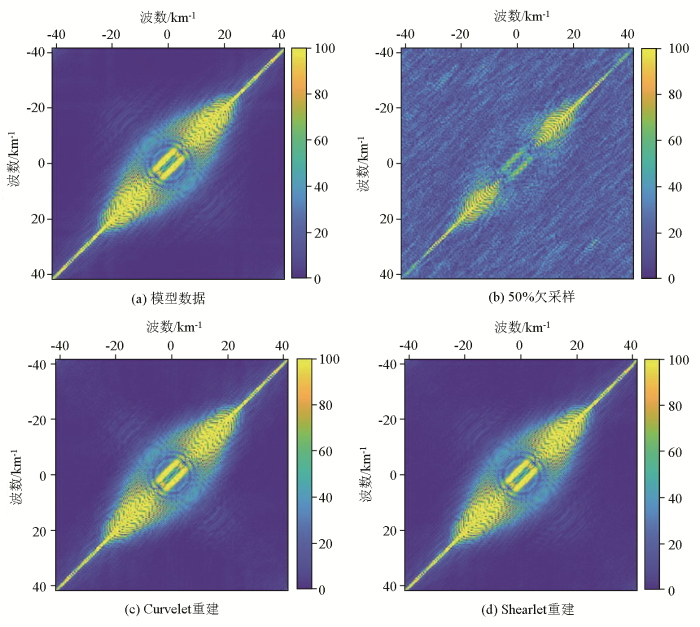
图5a~d分别为图1b~c和图3a~b对应时间切片的f-k频谱图,可以看到由于随机缺失的存在,原始时间切片的能量发生了泄露,导致在整个频谱中出现类似随机噪声出现的采样噪声。经过重建后有效波的能量更加集中,有了更明显的收敛,不相干的随机噪声得到了有效压制。基于Shearlet变换重建后的频谱与原始时间切片的频谱的相似度更高,几乎无差别。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 二维随机欠采样重建结果f-k谱

Fig.5 f-k spectrum of 2D random under-sampling reconstruction results

为了更好地从细节处对比两种变换方法的重建效果,从重建后的三维数据中提取2条单道曲线进行对比。图6是炮点为第90道、检波器为第60道和炮点为第60道、检波器为第94道的重建前后对比曲线,时窗为0~0.8 s。可以看到两种变换重建后与原始数据的单道曲线都吻合较好,都具有良好的插值精度。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 重建结果与误差的单道显示

1—原始记录;2—Curvelet变换重建曲线;3—Shearlet变换重建曲线;4—Curvelet变换的误差曲线;5—Shearlet变换的误差曲线

Fig.6 Single channel display of reconstruction results and errors

1—original record;2—Curvelet reconstruction results;3—Shearlet reconstruction results;4—Curvelet errors; 5—Shearlet errors

为了更加直观地对比两种变换方法在时间方向上的重建结果,图7给出了在50%欠采样率下,逐时间切片(4 ms一个切片)的重建后的信噪比。可以发现:在1~36和60~80时间切片中,基于Curvelet变换方法重建的信噪比略高;在其余时间切片中,基于Shearlet变换方法的重建精度略高。即经过对比,占比76.92%的基于Shearlet的时间切片重建效果略高于基于Curvelet变换方法的。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 Curvelet变换和Shearlet变换重建结果和各时间切片信噪比

Fig.7 Reconstruction results of curved and shear wave bases and SNR of each time slice

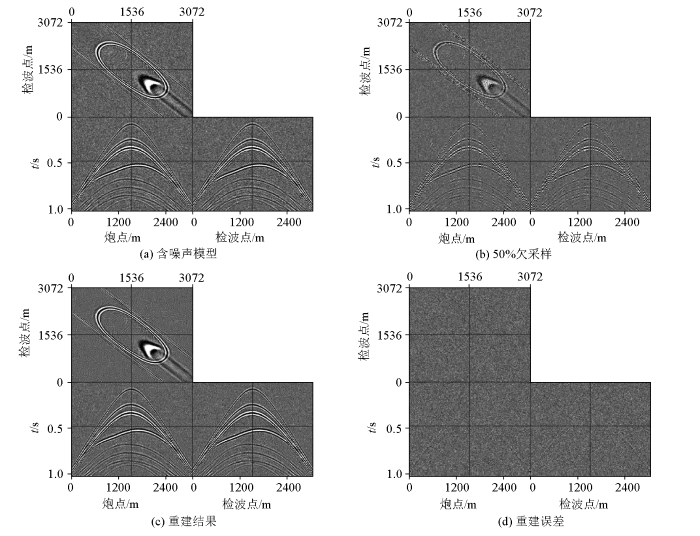
通常实测地震数据中都含有噪声,因此本文检验了基于Shearlet变换在随机欠采样下用POCS重建算法的抗噪声能力。在图1b模型中加入高斯随机噪声进行抗噪声地震数据重建试验(图8)。经对比可以发现,重建后的有效波同相轴几乎相同,损失的有效信息较少,数据的重建效果较好,说明Shearlet变换重建方法有着不错的抗噪声能力,可以进行实际地震资料的数据处理。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 含噪声数据二维随机欠采样重建结果及其误差

Fig.8 Reconstruction results of two-dimensional random under-sampling of noisy data and its error diagram

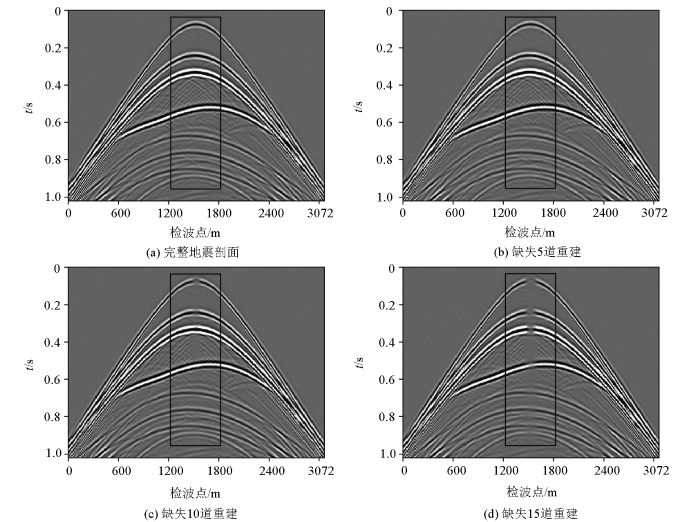
为了检验本文方法对于连续缺失不同地震道数据的重建效果,从三维地震数据抽取128炮进行处理(图9a),并以128道(1 536 m)为中心点,分别连续缺失5、10和15道,然后采用本文方法进行重建。由图9分析可得,连续缺失5道时所有同相轴能完好重建,连续缺失10道时重建效果相对较好,但当缺失道数为15道时,重建后的同相轴不完整,特别是能量较弱的缺失道,重建误差相对较大。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 连续缺失地震道重建

Fig.9 Continuous missing seismic trace reconstruction

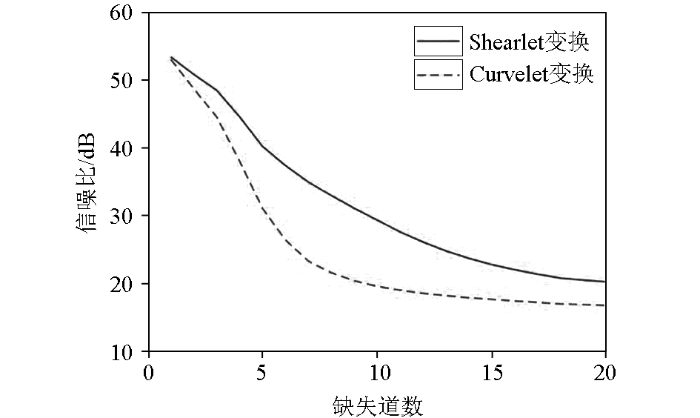
为了进一步测试本文方法与Curvelet的重建效果,将图9a连续缺失2~20道,然后分别使用Curvelet和Shearlet变换方法进行重建,重建后的信噪比曲线如图10所示。可以看到:随着连续缺失道增多,两种方法重建后的信噪比都是逐渐降低,且变化趋势一致,但相比较而言,本文方法重建后的信噪比更高,表明重建效果更佳。综合图9与图10的结果可以推断,本文方法对于连续缺失10道以内的地震数据可以有效地重建出来。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 连续缺失地震道数与重建后信噪比曲线

Fig.10 Continuous missing trace number and reconstructed SNR

3 实测数据应用

实测数据为某海上二维高密度地震资料,道间距为25 m,采样率为4 ms,180道接收,检波点和炮点移动一个检波器的距离。把检波器、炮点和时间采样点方向排列成三维数据体,截取了其中的180道、180炮和采样长度为2 s的数据体进行计算,由于在时间方向上采样是连续不断的,为了加快计算速度,把三维数据体在时间方向上进行切片处理。

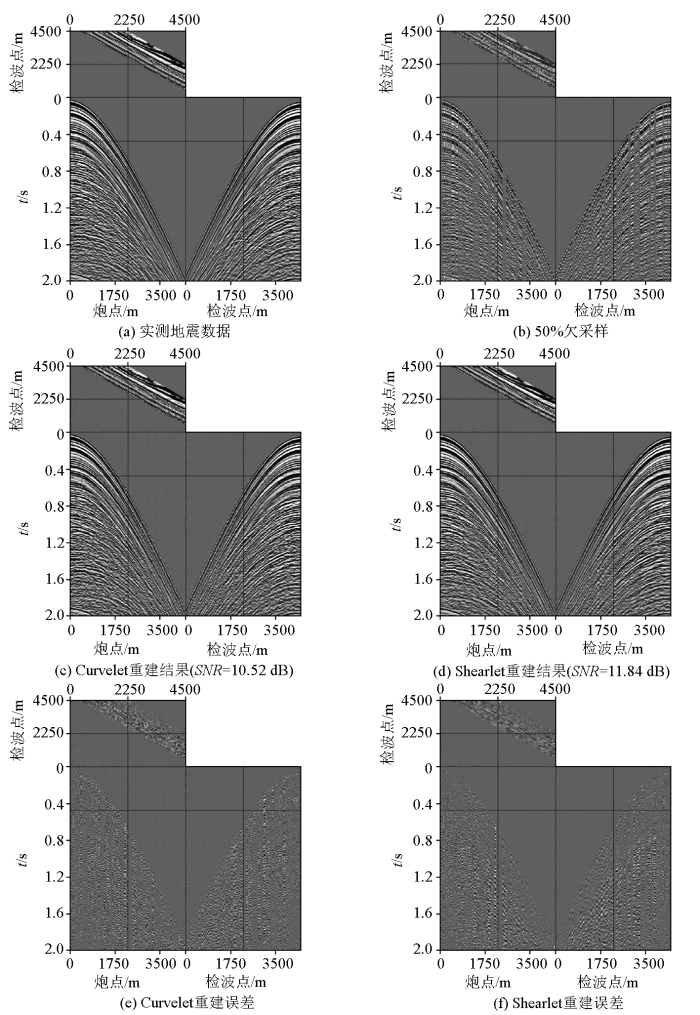
图11a为共炮点距离和共检波点距离为2 250 m、时间切片为0.48 s的实际采样数据,图11b为实际采样数据的50%二维随机欠采样;然后利用POCS算法迭代计算进行数据重建(图11c~f)。可以看出:在50%欠采样下,基于Shearlet变换重建后的局部细节恢复得更好、误差更小,在精度上略优于Curvelet变换方法;在计算速度方面,Shearlet变换比Curvelet变换的计算速度快一倍。这表明当处理大量的地震数据时,本文所提出的方法更具有优势。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 实测数据重建结果

Fig.11 Reconstruction results of measured data

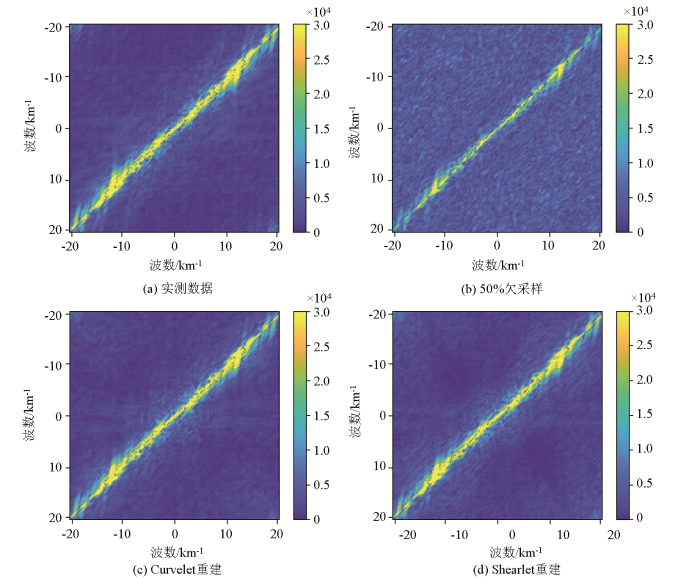
图12为图11a~d时间切片的f-k频谱图。图12b出现了能量泄露的迹象,产生了白色噪点,经过重建后有效波的能量有了明显的收敛。经对比,基于Curvelet变换重建后的频谱图还存在少量的噪点,而基于Shearlet变换重建后的频谱更接近于原始的实际采样数据。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 实测数据重建结果f-k谱

Fig.12 f-k spectrum of reconstructed measured data

4 结论

基于压缩感知理论的知识框架,在随机欠采样情况下运用Shearlet变换和凸集投影算法进行了三维地震数据重建。通过模型试验、加入随机噪声实验、最大连续缺失道重建试验和实际数据应用,验证了基于Shearlet变换相较于Curvelet变换在地震数据重建中表现更优,从重建后的剖面、误差剖面和f-k频谱图等对比观察,基于Shearlet变换的精度略高。

从计算效率上看,基于Shearlet变换的重建速度比Curvelet变换快一倍,但在处理更大数据体时,计算效率仍然是个挑战。未来需要发展其他快速算法或者在频率域中进行快速计算,在保证精度的前提下进一步提高计算速度。

在实际勘探中,可以利用目标测区的地质先验信息,因此,下一步的研究工作将采用基于先验信息的采样方式。本文方法是基于均匀网格情形,然而在实际采样工作中常常遇到复杂地形情况,均匀网格不一定适用。因此,未来的研究方向之一是发展基于非均匀Shearlet变换的三维地震数据重建方法,以应对实际采样工作中遇到的挑战。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

霍志周, 熊登, 张剑锋.

地震数据重建方法综述

[J]. 地球物理学进展, 2013, 28(4):1749-1756.