0 引言
斜率层析成像利用局部相干反射波的走时和斜率(射线参数)反演地下介质的背景速度[1 ⇓ -3 ] 。在地质构造简单工区,斜率层析反演模型的精度较高,能够满足叠前深度偏移成像的需求[4 ⇓ -6 ] 。然而,在地质构造复杂(如存在纵、横向速度突变)的工区,斜率层析反演模型的误差较大,尤其是在速度突变界面附近区域[7 ] 。
为了提高斜率层析成像在地质构造复杂工区的速度建模精度,研究人员尝试利用先验信息对反演进行约束[8 -9 ] 。Costa等[10 ] 利用反射角信息对反演模型进行空间平滑约束,他们通过理论模型测试表明不同平滑约束对反演速度模型的影响较大,但对深度偏移剖面的影响较小,这主要是由于平滑约束难以降低强波阻抗界面两侧的速度误差。Guillaume等[11 ] 利用偏移后的局部反射同相轴的倾角对斜率层析反演进行约束,克服了浅层局部速度异常体对反演中深部地层速度的不良影响。Yang等[7 ] 和张力起等[9 ] 利用反射点的空间位置信息对反演的速度模型进行约束,获得了良好的应用效果[6 ] 。然而,这类方法严重依赖于初始反射点的空间位置,故对低信噪比资料和地质构造复杂工区资料的适用性较低。此外,一些学者尝试利用非震资料对斜率层析反演进行约束[6 ] ,从而提高反演模型精度,但联合多种地球物理资料进行反演会增加反演未知量个数,导致反演多解性增强[12 ⇓ ⇓ -15 ] 。上述方法利用先验信息或非震资料改善了斜率层析反演模型,然而由于反演固有的空间平滑效应,导致速度突变界面附近区域的速度难以得到准确反演。
近年来,研究人员尝试利用深度学习技术建立高精度的速度模型,如:采用卷积神经网络建立共炮域道集与地下速度分布的非线性映射关系[16 ⇓ ⇓ -19 ] ;以炮域和检波点域道集作为所提出的SeisInvNet的输入,以理论速度模型作为标签[20 -21 ] ;将共中心点道集作为卷积神经网络的输入[22 -23 ] ;将共成像点道集作为卷积神经网络的输入[24 ] ;采用偏移后的共偏移距道集作为卷积神经网络的输入[25 ] 。这些研究表明,通过大量的、多种类型的样本训练神经网络,可以建立从地震数据到速度模型的非线性映射关系。然而,当训练样本中的速度模型与实际速度分布差别较大时,网络预测模型往往与实际速度分布不一致。
为此,本文提出一种基于深度学习的斜率层析反演模型误差校正方法。该方法以斜率层析反演模型作为神经网络输入、对应的理论模型作为标签,通过训练神经网络,建立从斜率层析反演模型到理论模型的非线性映射。为了确保训练后的神经网络适用于实测地震资料,基于实测资料反演模型和偏移剖面生成训练样本。本文通过理论模型合成数据测试和实际资料应用验证了所提方法的正确性和有效性。
1 方法原理
1.1 斜率层析成像
斜率层析成像利用叠前地震资料中局部相干反射波的走时和斜率反演地下介质的宏观速度背景[1 -2 ] ,其目标函数可以表示为[7 ,26 ]
(1) E ( [ v i ] i = 1 M , [ x c , j ] j = 1 N , [ z c , j ] j = 1 N ) = 1 2 σ T 2 ∑ j = 1 N ( T j - T j * ) 2 + 1 2 σ P 2 ∑ j = 1 N ( P s , j - P s , j * ) 2 + 1 2 σ P 2 ∑ j = 1 N ( P r , j - P r , j * ) 2
式中:vi 表示第i 个模型离散单元的速度;M 表示模型离散单元的总数;xc , j zc , j j 个反射点的水平距离和深度;N 表示反射波数据的总数;T 表示反射波双程走时;Ps 和Pr 分别表示反射波炮点端和检波点端的走时斜率;上标*表示观测数据;σT 和σP 分别表示反射波双程走时和斜率的标准差,其计算公式为[10 ⇓ -12 ]
(2) σ T = ∑ j = 1 N ( T j * - T - * ) 2 N - 1 ,
(3) σ P = ∑ j = 1 N ( P s , j * - P - * ) 2 + ∑ j = 1 N ( P r , j * - P - * ) 2 2 N - 1 ,
式中:T - * P - *
本文采用有限差分法计算炮点端和检波点端的走时斜率Ps 和Pr [26 ] ,采用基于直线叠加能量扫描的方法自动拾取局部反射同相轴的斜率P s * [4 ] 。在进行斜率拾取之前,需要对共炮域和共检波点域的地震数据进行预处理,主要包括剔除野值、压制噪声、去除多次波等非一次反射波。
为了最小化式(1)所示的目标函数,通常采用梯度类局部最优化算法[1 ,3 ] ,本文采用共轭梯度法。速度和反射点坐标的更新过程可以表示为[27 ]
(4) v i k + 1 = v i k + α v k d v i k ,
(5) x c , j k + 1 = x c , j k + α c k d x c , j k ,
(6) z c , j k + 1 = z c , j k + α c k d z c , j k ,
式中:k 表示当前迭代次数;αv 和αc 分别表示速度模型和反射点空间坐标的更新步长;d v i d x c , j d z c , j x 和z 坐标的共轭梯度。更新步长αv 和αc 采用线性搜索方法计算[28 ] 。速度模型、反射点空间x 和z 坐标的共轭梯度由当前迭代的梯度和前一次迭代的共轭梯度计算得到,计算公式如下[7 ]
(7) d v i k = - ∂ E k ∂ v i k , k = 1 - ∂ E k ∂ v i k + β v k d v i k - 1 , k > 1
(8) d x c , j k = - ∂ E k ∂ x c , j k , k = 1 - ∂ E k ∂ x c , j k + β c k d x c , j k - 1 , k > 1
(9) d z c , j k = - ∂ E k ∂ z c , j k , k = 1 - ∂ E k ∂ z c , j k + β c k d z c , j k - 1 , k > 1
式中:βv 和βc 分别是使速度模型和反射点坐标相邻两次共轭梯度正交的系数,采用Dai等[27 ] 提出的方法计算获得。
(10) ∂ E ∂ v i = 1 σ T 2 ∑ j = 1 N ∂ T j ∂ v i ( T j - T j * ) + 1 σ P 2 ∑ j = 1 N ∂ P s , j ∂ v i · ( P s , j - P s , j * ) + 1 σ P 2 ∑ j = 1 N ∂ P r , j ∂ v i ( P r , j - P r , j * ) 。
从式(10)中可以看出,所有射线路径经过第i 个模型离散单元的反射波数据拟合误差共同决定了该单元的反演速度,这导致反演的速度模型非常光滑,在强波阻抗界面附近区域的速度误差较大。
式(8)和(9)中目标函数对反射点空间x 和z 坐标的梯度可以分别表示为[7 ]
(11) ∂ E ∂ x c , j = ∂ T j ∂ x c , j T j - T j * σ T 2 + ∂ P s , j ∂ x c , j P s , j - P s , j * σ P 2 + ∂ P r , j ∂ x c , j P r , j - P r , j * σ P 2 ,
(12) ∂ E ∂ z c , j = ∂ T j ∂ z c , j T j - T j * σ T 2 + ∂ P s , j ∂ z c , j P s , j - P s , j * σ P 2 + ∂ P r , j ∂ z c , j P r , j - P r , j * σ P 2 。
式(11)和(12)表明,目标函数对第j 个反射点的x 、z 坐标的梯度只与该反射点对应的走时和斜率拟合误差相关,而与其他反射波数据拟合误差无关。
1.2 反演模型误差校正方法
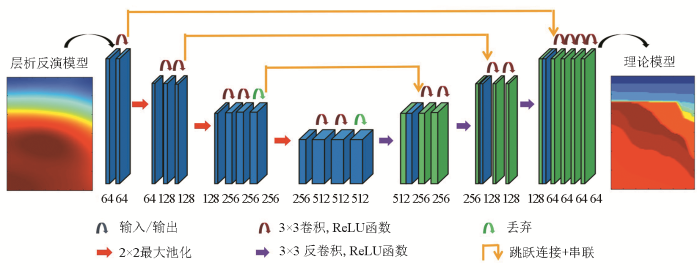
为了提高斜率层析反演模型的精度,本文采用深度学习方法建立反演模型的误差校正算子。采用U-net卷积神经网络[19 ] 建立从反演模型到理论模型的非线性映射,网络结构如图1 所示。网络前半部分的编码器使用卷积和最大池化操作进行特征提取,卷积核尺寸越大,越有益于从输入的反演模型中提取大尺度的结构信息,反之,越容易提取细节信息[29 ] 。本文将卷积核大小设置为3×3,使神经网络尽可能地从输入的层析反演模型中提取关于速度突变界面的细节信息。激活函数为修正线性单元(Rectified linear unit,ReLU)。为保证卷积前后的矩阵尺寸不变,在卷积之前进行了填充操作,最大池化为2×2,移动步幅为2,移动步幅与最大池化操作的矩阵大小对应。网络后半部分的解码器进行特征定位,以反卷积恢复数据维度并获得特征,并通过跳跃连接与浅层提取到的特征结合来提高空间分辨率。网络的通道数随着层数增加逐渐倍增,依次为64、128、256、512。此外,设置丢弃层以提高网络的稳定性,选取系数为0.5。
图1
图1
本文采用的U-net神经网络结构
Fig.1
Architecture of the U-net in this paper
(13) E ~ = ∑ l = 1 L v t r u λ - N e t v t o m λ ; Θ 2 ,
式中:L 表示训练样本总数;v tru 和v tom 分别表示理论速度模型和对应的斜率层析反演速度模型;λ 表示归一化因子,其作用是使网络输入和标签数据均介于0~1之间;Θ 表示神经网络参数。
为了降低神经网络训练阶段对计算机内存的需求,采用随机梯度下降算法迭代更新神经网络参数[30 ] 。神经网络参数迭代更新过程可以表示为
(14) Θ k + 1 = Θ k - η k Δ E ~ k ,
式中:k 表示当前迭代次数;η 表示迭代更新步长(学习率);ΔE ~
(15) v p r e = λ N e t v i n v λ ; Θ ~ ,
式中:v pre 表示网络预测模型;v inv 表示实测地震资料斜率层析反演速度模型;Θ ~
1.3 反演模型的误差校正流程
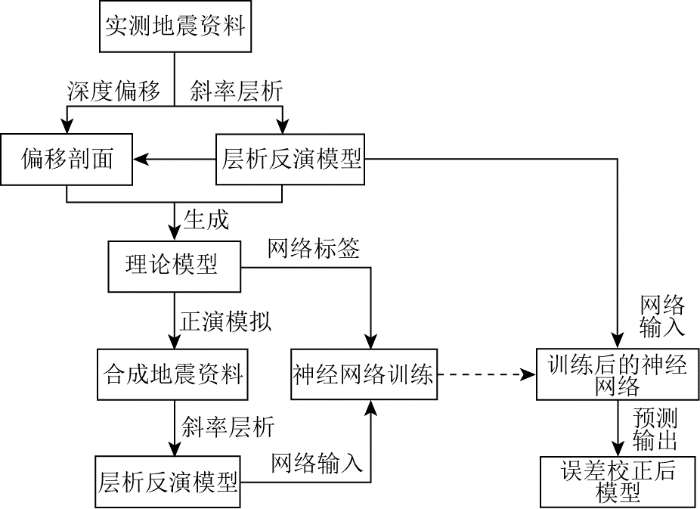
本文提出的斜率层析反演模型误差校正流程如图2 所示。该流程分为两个部分。第一部分是对神经网络进行训练,网络标签是根据实测资料反演模型和偏移剖面生成的理论模型,网络输入是理论模型对应的层析反演模型。第二部分是神经网络预测,向训练后的神经网络输入实测资料反演模型,网络预测输出即为误差校正后的模型。
图2
图2
层析反演模型误差校正流程
Fig.2
Error-correction process for tomographic models
2 样本构建
为使神经网络能够从网络输入中学习到实际地下介质速度分布的特征,基于实测地震资料反演模型和对应的偏移剖面构建理论速度模型。样本构建流程共包含两个步骤:首先采用斜率层析成像反演实测资料,获得反演速度模型和对应的深度偏移剖面,然后基于反演模型和偏移剖面,生成层状理论模型;使用理论模型合成理论地震资料,并进行斜率层析反演,获得对应反演模型。理论模型和对应的反演模型就是本文构建的训练样本,具体构建流程如下。
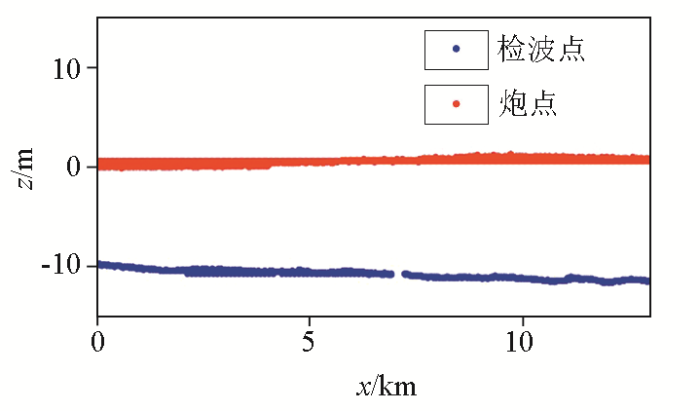
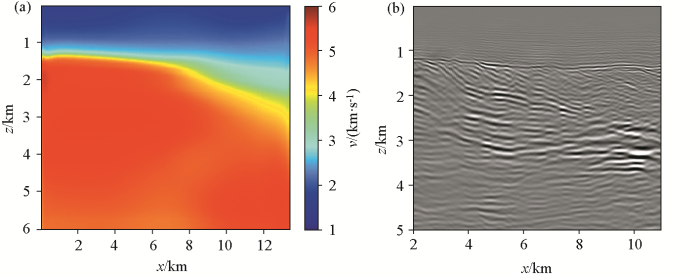
第一步,根据实测2D滩浅海地震资料(图3 )进行斜率层析成像和深度偏移。测线共498炮,炮间距和道间距均为25 m,最小和最大偏移距分别约为25 m和4.2 km。
图3
图3
测线观测系统
Fig.3
The geometry of the survey line
从实测共炮域和共检波点域道集中拾取反射波走时和斜率,共获得110 550组数据。采用速度随深度线性递增的速度模型作为斜率层析反演的初始模型。初始模型的速度可以表示为
(16) v i n i ( z ) = 1.5 + 0.5 z ,
式中:z 表示深度,单位为km;v ini 表示初始模型的速度,单位为km/s。
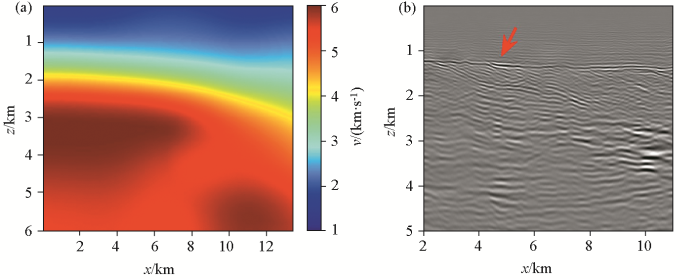
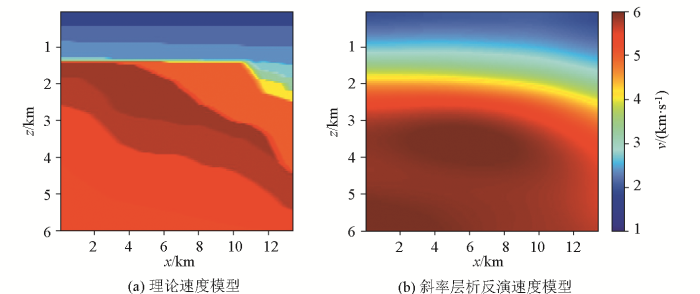
采用边长0.2 km的正方形网格离散初始速度模型。经过30次迭代后,获得反演速度模型如图4a 所示,可以看出斜率层析反演速度模型非常光滑。利用反演速度模型进行深度偏移,获得偏移成像剖面(图4b )。其中,在深度约1.2 km处存在一个强波阻抗界面(红色箭头所示),结合测井和地质资料,该界面上下两侧分别为新近系沉积层和中—古生界地层,它们之间的速度差极大。然而,图4a 中所示的反演速度在该强波阻抗界面两侧连续变化,不符合实际情况,因此导致深度偏移剖面质量不佳。
图4
图4
实测资料反演模型(a)和深度偏移剖面(b)
Fig.4
Tomographic model (a) and depth-domain migration image (b) of the field seismic data
第二步,根据图4 所示的反演速度模型和深度偏移剖面建立一个训练样本。首先,根据深度偏移剖面(图4b )进行标志层位拾取(如红色箭头所示强波阻抗界面),再根据反演速度模型(图4a )构建一个理论层状速度模型,如图5a 所示。可以看出,构建的理论模型与实测资料反演模型较为相似。
利用图5a 所示理论模型合成理论地震资料,并从合成资料中拾取局部相干反射波的走时和斜率。采用步骤一中斜率层析反演参数和初始模型反演理论地震资料,获得反演速度模型如图5b 所示。图5 显示反演速度模型与理论速度模型相差较大,尤其是在深度1~2 km范围内。
图5
图5
构建的训练样本
Fig.5
A training sample constructed
图5 所示的理论和反演的速度模型分别作为神经网络训练的一个标签和输入,对其进行扰动获得额外499个训练样本。扰动为深度和速度的同步扰动,从而让实际速度分布位于构建的理论速度模型空间之内。这个扰动可以表示为
(17) v ' ( x , z ) = ( 1 + 0.2 μ 1 ) v ( x , z + 0.5 μ 2 ) + 0.5 μ 3 ,
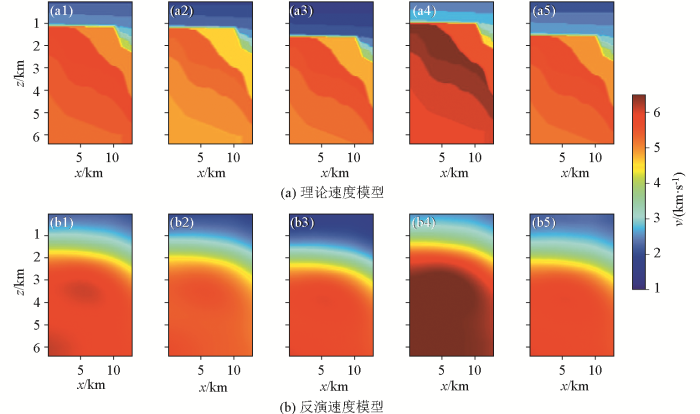
式中:v 和v '分别表示扰动前和扰动后的速度模型;x 表示水平距离;μ 1 、μ 2 和μ 3 均为0~1之间的随机数。图6 是其中5个有代表性的训练样本,可以看出不同样本的速度值和速度界面深度不同。
图6
图6
5个有代表性的训练样本
Fig.6
Five representative training samples
本文共合成了500个不同的训练样本。所有理论速度模型中均含有速度突变界面,且界面深度在强波阻抗界面附近扰动。所有反演模型的速度在图4a 所示模型的速度附近扰动,故实际速度分布与某些合成样本足够接近。样本中模型的最小和最大速度分别约为0.98 km/s和7.40 km/s,样本中的所有速度模型均重采样为256×128=32 768个离散网格单元。
3 网络训练与测试
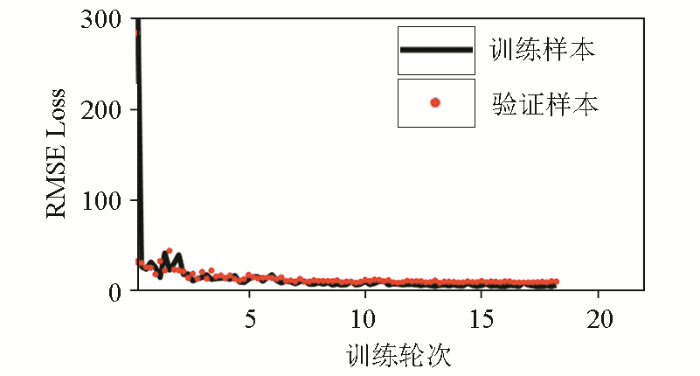
采用Adam算法训练神经网络[31 -32 ] 。从生成的500个样本中随机选择400、50和50个样本分别作为训练样本、验证样本和测试样本。神经网络训练的最大轮数设置为30,批量大小设置为4,每个轮次的迭代次数为100。归一化因子λ 设置为7.5 km/s。网络训练的终止条件是连续5次验证样本的目标函数值均大于当前最小目标函数值或达到最大轮数。图7 给出了神经网络训练的目标函数值(RMSE Loss)。图中显示目标函数值在第1轮下降最快,随后缓慢下降;训练样本和验证样本的最终目标函数值分别约为初始值的1.66%和3.89%。这表明训练后神经网络的输出与标签之间的差异非常小。
图7
图7
神经网络训练的目标函数值
Fig.7
The objective function values of the network training
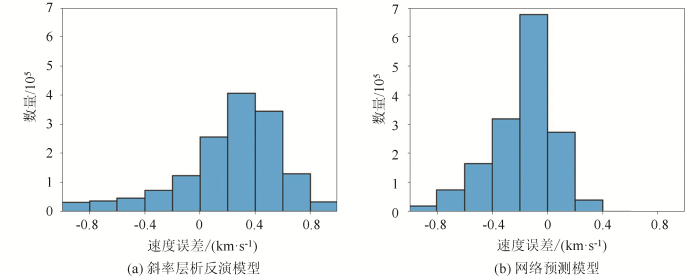
利用50个随机选择的测试样本检验训练后的神经网络性能(图8 )。图8 表明:斜率层析反演模型的误差主要集中于0~0.6 km/s,而网络预测模型的误差主要介于-0.4~0.2 km/s;斜率层析反演的和网络预测的速度误差介于-0.2~0.2 km/s的个数分别约为总数的23.12%和57.81%;网络预测速度模型的精度提高约250%。这表明采用本文提出的方法可以显著提高测试样本中斜率层析反演模型的精度。
图8
图8
测试样本中所有离散网格单元的速度误差分布
Fig.8
The velocity error distributions of all discrete grids of the testing samples
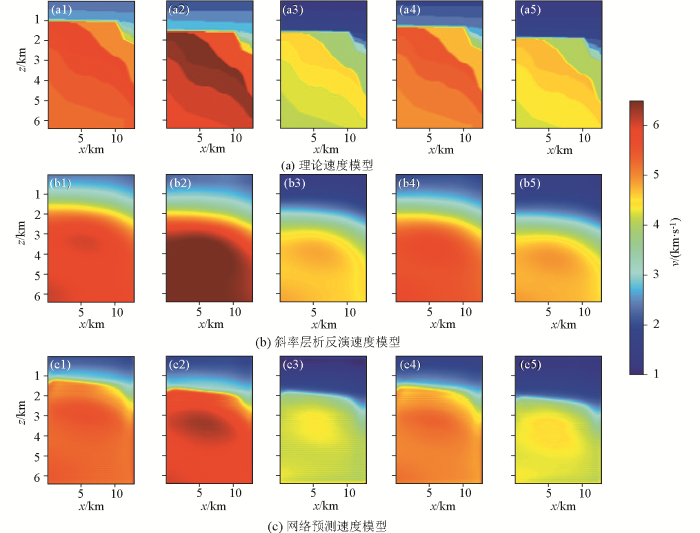
图9 给出了5个有代表性测试样本的理论、斜率层析反演和网络预测的速度模型。可以看出,网络预测模型中浅部的速度突变界面非常明显,界面附近区域的速度值明显比斜率层析反演的速度值更接近理论速度值。这表明训练后的神经网络可以校正斜率层析反演模型在浅层速度突变界面附近区域的速度误差,从而获得更高精度、更高分辨率的速度模型。
图9
图9
5个有代表性的测试样本
Fig.9
Five representative testing samples
4 实测资料应用
将训练后的神经网络应用于图4a 所示的实测资料斜率层析反演模型,获得网络预测模型如图10a 所示。对比图4a 和图10a 可以看出,网络预测模型在深度约为1.3 km处的速度突变界面非常明显,斜率层析反演和网络预测的该界面两侧的速度存在显著差异。图10b 是利用网络预测模型获得的深度偏移成像剖面。对比图4b 和图10b 可以明显看出,采用网络预测模型获得的深度偏移剖面质量明显高于斜率层析反演模型对应的深度偏移剖面。
图10
图10
实测资料的网络预测模型(a)及其对应的深度偏移剖面(b)
Fig.10
Nefword predicted model for measured data (a) and its corresponding depth-domain migration image (b)
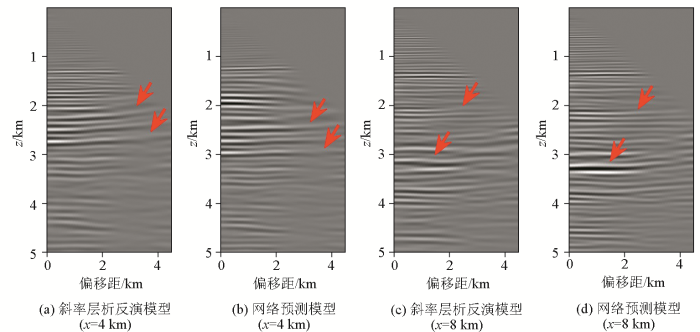
为了进一步验证网络预测模型的准确性,计算了水平方向4 km和8 km处的共成像点道集,如图11 所示。图11a 中深度2~3 km内的同相轴存在明显的上翘,而图11b 中对应同相轴的上翘程度很低(如红色箭头所示);图11c 中深度2~3.5 km内的同相轴能量较弱且同相轴存在扭曲,而图11d 中对应同相轴的能量更强且同相轴更平直。这表明网络预测模型比斜率层析反演模型更加准确,且预测速度值与理论值非常接近。
图11
图11
不同距离、不同模型计算的共成像点道集
Fig.11
Common imaging point gathers calculated by different distances and methods
5 结论
斜率层析成像在速度变化剧烈区域的建模效果欠佳,为此,提出一种基于深度学习的斜率层析反演模型误差校正方法。该方法以斜率层析反演模型作为神经网络输入,以对应理论模型作为标签,通过训练神经网络建立从反演模型到理论模型的非线性映射关系。理论模型合成数据测试表明,本文提出的方法可以显著降低斜率层析反演模型在速度纵向突变区域的误差,获得更高精度和分辨率的网络预测模型。将训练后的神经网络应用于实测地震资料,获得了更加准确的速度模型和更高质量的深度偏移剖面。
基于实测资料反演模型和偏移剖面构建理论模型,确保理论模型与实际速度分布较为接近,使训练后的神经网络适用于实测地震资料。本文所提方法仅需要少量的训练样本且无需输入地震记录,易于拓展到三维实测地震资料的速度建模。在渤海和南黄海等地区,新近系沉积层和下覆中—古生界地层之间广泛存在速度突变,本文方法对这些地区的速度建模工作具有重要参考意义。
参考文献
View Option
[1]
Billette F Lambaré G . Velocity macro-model estimation from seismic reflection data by stereotomography
[J]. Geophysical Journal International , 1998 , 135 (2 ):671 -690 .
[本文引用: 3]
[2]
Jin C K Zhang J Z . Stereotomography of seismic data acquired on undulant topography
[J]. Geophysics , 2018 , 83 (4 ):U35 -U41 .
[本文引用: 2]
[3]
Sambolian S Operto S Ribodetti A , et al . Parsimonious slope tomography based on eikonal solvers and the adjoint-state method
[J]. Geophysical Journal International , 2019 , 218 (1 ):456 -478 .
DOI:10.1093/gji/ggz150
[本文引用: 2]
Velocity macromodel building is an essential step of the seismic imaging workflow. Indeed, obtaining acceptable results through migration or full waveform inversion is highly dependent on the kinematic accuracy of the background/initial velocity model. Two decades ago, stereotomography was proposed as an alternative to reflection traveltime tomography, the first relying on semi-automatic picking of locally coherent events associated with small reflection or diffraction segments tied to scatterers in depth by a pair of rays, while the latter on interpretive picking of laterally continuous reflections. The flexibility of stereotomography paved the way for many developments that have shown the efficiency of the method whilst emphasizing on the complementary information carried out by traveltimes and slopes of locally coherent events. A recent formulation recast stereotomography under a matrix-free formulation based on eikonal solvers and the adjoint-state method. In the latter, like in the previous works, the scatterer positions and the velocity field are updated jointly to tackle the ill-famed velocity-position coupling in reflection tomography. Following on from this adjoint-state formulation, we propose a new parsimonious formulation of slope tomography that offers the chance to restrain the problem to minimizing the residuals of a single data class being a slope, in search of a sole parameter class being the subsurface velocity field. This parsimonious formulation results from a variable projection, which is implemented by enforcing a consistency between the scatterer coordinates and the velocity macromodel through migration of kinematic attributes. We explain why the resulting reduced-parametrization inversion is more suitable for tomographic problems than the most common joint inversion strategy. We benchmark our method against the complex Marmousi model along with a validation through time domain full waveform inversion and then present the results of a field data case study.
[4]
金昌昆 , 张建中 . 地震立体层析成像的实现方法及效果分析
[J]. CT理论与应用研究 , 2014 , 23 (6 ):939 -950 .
[本文引用: 2]
Jin C K Zhang J Z . Implementation methods of stereotomography and analysis of influence factors on its results
[J]. Computerized Tomography Theory and Applications , 2014 , 23 (6 ):939 -950 .
[本文引用: 2]
[5]
叶云飞 , 孙建国 , 张益明 , 等 . 基于立体层析反演的低频模型构建在深水区储层反演中的应用:以南海深水W构造为例
[J]. 吉林大学学报:地球科学版 , 2018 , 48 (4 ):1253 -1259 .
[本文引用: 1]
Ye Y F Sun J G Zhang Y M , et al . Construction of low-frequency model with three-dimensional tomographic velocity inversion and application in deep-water bock W of South China Sea
[J]. Journal of Jilin University:Earth Science Edition , 2018 , 48 (4 ):1253 -1259 .
[本文引用: 1]
[6]
Liu J Zhang J Z . Joint inversion of seismic slopes,traveltimes and gravity anomaly data based on structural similarity
[J]. Geophysical Journal International , 2022 , 229 (1 ):390 -407 .
[本文引用: 3]
[7]
Yang H C He W L Ma F , et al . Slope tomography dynamically weighted according to the locations of the reflection points
[J]. IEEE Transactions on Geoscience and Remote Sensing , 2024 , 62 :5905311 .
[本文引用: 6]
[8]
熊凯 , 杨锴 , 邢逢源 , 等 . 联合结构张量与运动学反偏移的立体层析数据空间提取与反演策略研究Ⅱ:实践
[J]. 石油物探 , 2018 , 57 (2 ):254 -261 ,273.
DOI:10.3969/j.issn.1000-1441.2018.02.011
[本文引用: 1]
为降低立体层析反演实际应用中绕射波、多次波和侧面波等对提取最佳数据空间(炮点坐标、检波点坐标、炮点P参数、检波点P参数、旅行时)精度的影响,提出了获取更佳立体层析数据空间的两步法策略。首先利用初始速度进行叠前深度偏移,然后在成像域实施运动学反偏移以提取更佳数据空间参数。将二维叠前成像体视为三维数据,采用三维结构张量算法一步即可精确获得运动学反偏移所需的构造倾角和剩余曲率信息。不同于理论数据,对于实际数据采用了在若干不同偏移距数据体的共偏移距成像道集上分别选取有效数据点,然后分别延拓的策略,以保证通过延拓挑选出的数据点更均匀、可靠。最后,利用运动学反偏移将选出的成像域数据点的运动学信息反偏移到数据空间,获得更佳立体层析数据空间。针对南海某二维实际数据,对两步法提取的数据空间进行立体层析反演,建立偏移速度模型,最终的叠前深度偏移结果表明:两步法策略有效地提高了实际数据的反演精度,是一种获得更佳立体层析数据空间的有效途径。
Xiong K Yang K Xing F Y , et al . Inversion strategy and data space extraction for stereo-tomography based on a combination of structure tensor and kinematic demigration.Ⅱ:Practice
[J]. Geophysical Prospecting for Petroleum , 2018 , 57 (2 ):254 -261 ,273.
DOI:10.3969/j.issn.1000-1441.2018.02.011
[本文引用: 1]
<p> In stereo-tomographic inversion,diffractions,multiples and side waves have adverse impact upon optimal data space extraction (source position,receiver position,source P parameter,receiver P parameter,travel time).This paper proposes a two-step scheme to counter that.First,Prestack depth migration (PSDM) is implemented using initial velocity.Then,kinematic demigration is implemented to extract the data space parameter.We used a 3D structure tensor,with the 2D pre-stack depth-migrated dataset used as a 3D volume,to obtain residual move-out (RMO) and structural dip for kinematic demigration.For field data,a set of key horizons were selected manually in several select depth-migrated common offset gathers,and these were extrapolated along the offset axis based on the RMO chosen in advance to produce reliable and well-distributed initial high-density data points.Finally,kinematic demigration was implemented to inverse the kinematic information of selected data points to obtain a refined data space for stereo-tomography.We applied the strategy to 2D field data from the South China Sea.A migration velocity model was built based on the data space achieved using the proposed scheme and then PSDM was implemented.The migration results demonstrate that the strategy is effective for achieving best data space for stereo-tomographic inversion.</p>
[9]
张力起 , 杨锴 , 邢逢源 , 等 . 地层格架正则化约束下的二维立体层析反演
[J]. 地球物理学报 , 2019 , 62 (2 ):634 -647 .
DOI:10.6038/cjg2019L0568
[本文引用: 2]
通过把地层格架信息作用于立体层析Fréchet导数矩阵,使得更新后的速度模型呈现出符合地质规律的块状特征.地层格架信息基于立体层析反演中得到的反射点位置进行非规则B样条插值拟合得到,因此在反演中它将会随着反射点位置的更新自然得到更新.与前人提出的保边缘层析算法或多层立体层析算法相比,本文提出的地层格架正则化无需引入混合正则化项或定义某种复杂的混合速度格式,更为直接也更容易实现.理论和实际数据算例证实了该正则化技巧的稳健性和可靠性,能够得到与实际地质构造特征更为一致的地质一致性反演结果.
Zhang L Q Yang K Xing F Y , et al . 2D stereo-tomography inversion constrained by regularization of stratum framework
[J]. Chinese Journal of Geophysics , 2019 , 62 (2 ):634 -647 .
[本文引用: 2]
[10]
Costa J C da Silva F J Gomes E N , et al . Regularization in slope tomography
[J]. Geophysics , 2008 , 73 (5 ):VE39 -VE47.
[本文引用: 2]
[11]
Guillaume P Reinier M Lambaré G , et al . Dip constrained non-linear slope tomography
[C]// SEG Technical Program Expanded Abstracts 2013,Society of Exploration Geophysicists , 2013 :4811 -4815 .
[本文引用: 2]
[12]
Kurose T Yamanaka H . Joint inversion of receiver function and surface-wave phase velocity for estimation of shear-wave velocity of sedimentary layers
[J]. Exploration Geophysics , 2006 , 37 (1 ):93 -101 .
[本文引用: 2]
[13]
张佩 , 宋晓东 , 熊奥林 . 重震联合反演方法及其应用进展
[J]. 地球物理学进展 , 2019 , 34 (5 ):1818 -1825 .
[本文引用: 1]
Zhang P Song X D Xiong A L . Advancement of joint inversion of gravity and seismic data and its application
[J]. Progress in Geophysics , 2019 , 34 (5 ):1818 -1825 .
[本文引用: 1]
[14]
相鹏 , 王金铎 , 谭绍泉 , 等 . 一种变密度—速度关系的重力与地震同步联合反演方法
[J]. 石油地球物理勘探 , 2020 , 55 (3 ):686 -693 ,474.
[本文引用: 1]
Xiang P Wang J D Tan S Q , et al . Simultaneous and joint inversion of gravity and seismic data based on variable density-velocity relation
[J]. Oil Geophysical Prospecting , 2020 , 55 (3 ):686 -693 ,474.
[本文引用: 1]
[15]
刘洁 , 张建中 . 重震联合中速度—密度耦合研究综述
[J]. 地球物理学进展 , 2020 , 35 (3 ):976 -986 .
[本文引用: 1]
Liu J Zhang J Z . Review of velocity-density coupling in joint inversion of seismic and gravity data
[J]. Progress in Geophysics , 2020 , 35 (3 ):976 -986 .
[本文引用: 1]
[16]
Yang H C Li P Ma F , et al . Building near-surface velocity models by integrating the first-arrival traveltime tomography and supervised deep learning
[J]. Geophysical Journal International , 2023 , 235 (1 ):326 -341 .
[本文引用: 1]
[17]
Araya-Polo M Jennings J Adler A , et al . Deep-learning tomography
[J]. The Leading Edge , 2018 , 37 (1 ):58 -66 .
[本文引用: 1]
[18]
Araya-Polo M Farris S Florez M . Deep learning-driven velocity model building workflow
[J]. The Leading Edge , 2019 , 38 (11 ):872a1 -872 a9.
[本文引用: 1]
[19]
Wang W L Ma J W . Velocity model building in a crosswell acquisition geometry with image-trained artificial neural networks
[J]. Geophysics , 2020 , 85 (2 ):U31 -U46 .
[本文引用: 2]
[20]
Li S C Liu B Ren Y X , et al . Deep-learning inversion of seismic data
[J]. IEEE Transactions on Geoscience and Remote Sensing , 2020 , 58 (3 ):2135 -2149 .
[本文引用: 1]
[21]
Liu B Yang S L Ren Y X , et al . Deep-learning seismic full-waveform inversion for realistic structural models
[J]. Geophysics , 2021 , 86 (1 ):R31 -R44 .
[本文引用: 1]
[22]
Kazei V Ovcharenko O Alkhalifah T . Velocity model building by deep learning:From general synthetics to field data application
[C]// SEG Technical Program Expanded Abstracts 2020,Virtual,Society of Exploration Geophysicists , 2020 :1561 -1565 .
[本文引用: 1]
[23]
Fabien-Ouellet G Sarkar R . Seismic velocity estimation:A deep recurrent neural-network approach
[J]. Geophysics , 2020 , 85 (1 ):U21 -U29 .
DOI:10.1190/GEO2018-0786.1
[本文引用: 1]
Applying deep learning to 3D velocity model building remains a challenge due to the sheer volume of data required to train large-scale artificial neural networks. Moreover, little is known about what types of network architectures are appropriate for such a complex task. To ease the development of a deep-learning approach for seismic velocity estimation, we have evaluated a simplified surrogate problem - the estimation of the root-mean-square (rms) and interval velocity in time from common-midpoint gathers - for 1D layered velocity models. We have developed a deep neural network, whose design was inspired by the information flow found in semblance analysis. The network replaces semblance estimation by a representation built with a deep convolutional neural network, and then it performs velocity estimation automatically with recurrent neural networks. The network is trained with synthetic data to identify primary reflection events, rms velocity, and interval velocity. For a synthetic test set containing 1D layered models, we find that rms and interval velocity are accurately estimated, with an error of less than 44 m/s for the rms velocity. We apply the neural network to a real 2D marine survey and obtain accurate rms velocity predictions leading to a coherent stacked section, in addition to an estimation of the interval velocity that reproduces the main structures in the stacked section. Our results provide strong evidence that neural networks can estimate velocity from seismic data and that good performance can be achieved on real data even if the training is based on synthetics. The findings for the 1D problem suggest that deep convolutional encoders and recurrent neural networks are promising components of more complex networks that can perform 2D and 3D velocity model building.
[24]
Geng Z C Zhao Z Y Shi Y Z , et al . Deep learning for velocity model building with common-image gather volumes
[J]. Geophysical Journal International , 2021 , 228 (2 ):1054 -1070 .
[本文引用: 1]
[25]
Muller A P O Bom C R Costa J C , et al . Deep-Tomography:Iterative velocity model building with deep learning
[J]. Geophysical Journal International , 2022 , 232 (2 ):975 -989 .
[本文引用: 1]
[26]
Tavakoli F B Operto S Ribodetti A , et al . Slope tomography based on eikonal solvers and the adjoint-state method
[J]. Geophysical Journal International , 2017 , 209 (3 ):1629 -1647 .
[本文引用: 2]
[27]
Dai Y H Yuan Y . A nonlinear conjugate gradient method with a strong global convergence property
[J]. SIAM Journal on Optimization , 1999 , 10 (1 ):177 -182 .
[本文引用: 2]
[28]
Nocedal J Wright S J . Numerical optimization,2th ed [M]. New York,NY,USA : Springer , 2006 .
[本文引用: 1]
[29]
张岩 , 孟德聪 , 宋利伟 , 等 . 基于特征强化U-Net的地震速度反演方法
[J]. 石油地球物理勘探 , 2024 , 59 (2 ):185 -194 .
[本文引用: 1]
Zhang Y Meng D C Song L W , et al . Seismic velocity inversion method based on feature enhancement U-Net
[J]. Oil Geophysical Prospecting , 2024 , 59 (2 ):185 -194 .
[本文引用: 1]
[30]
Yang F S Ma J W . Deep-learning inversion:A next-generation seismic velocity model building method
[J]. Geophysics , 2019 , 84 (4 ):R583 -R599 .
[本文引用: 1]
[31]
许祥 , 邹志辉 , 韩明亮 , 等 . 联合地震初至走时与早至波形的深度学习速度建模
[J]. 地球物理学报 , 2023 , 66 (12 ):5107 -5122 .
[本文引用: 1]
Xu X Zou Z H Han M L , et al . Deep-learning velocity model building by jointly using seismic first arrivals and early-arrival waveforms
[J]. Chinese Journal of Geophysics , 2023 , 66 (12 ):5107 -5122 .
[本文引用: 1]
[32]
杨庭威 , 曹丹平 , 杜南樵 , 等 . 基于深度学习的接收函数横波速度预测
[J]. 地球物理学报 , 2022 , 65 (1 ):214 -226 .
DOI:10.6038/cjg2022P0025
[本文引用: 1]
远震接收函数中包含了大量台站下方速度间断面所产生的Ps转换波及其多次反射波的信息,被广泛应用于反演精细的地壳及上地幔速度结构.但当地壳结构复杂如存在沉积层或高速层时,转换波和多次波震相的到时和振幅发生变化,从而导致接收函数反演存在强非唯一性.深度学习作为一种高效的特征提取方法,能够建立接收函数与横波速度在空间上的映射关系.因此,利用全球模型数据以及高质量观测接收函数建立样本库,设计了利用接收函数预测横波速度的卷积神经网络.测试集结果表明,合成数据预测的横波速度与模型拟合程度较高,在实际数据检测中预测横波速度结果与全局反演的结果基本一致,预测的横波速度间断面与传统H-κ叠加结果也基本一致.利用该方法对琉球海沟地区海底地震数据的接收函数进行反演,获得了台站下方横波速度精细结构,进一步获得了该地区更为精细的地壳结构特征.测试实验及应用表明利用卷积神经网络预测台站下方横波速度的深度学习方法不仅计算效率高,且具有较高的可靠性.
Yang T W Cao D P Du N Q , et al . Prediction of shear-wave velocity using receiver functions based on the deep learning method
[J]. Chinese Journal of Geophysics , 2022 , 65 (1 ):214 -226 .
[本文引用: 1]
Velocity macro-model estimation from seismic reflection data by stereotomography
3
1998
... 斜率层析成像利用局部相干反射波的走时和斜率(射线参数)反演地下介质的背景速度[1 ⇓ -3 ] .在地质构造简单工区,斜率层析反演模型的精度较高,能够满足叠前深度偏移成像的需求[4 ⇓ -6 ] .然而,在地质构造复杂(如存在纵、横向速度突变)的工区,斜率层析反演模型的误差较大,尤其是在速度突变界面附近区域[7 ] . ...
... 斜率层析成像利用叠前地震资料中局部相干反射波的走时和斜率反演地下介质的宏观速度背景[1 -2 ] ,其目标函数可以表示为[7 ,26 ] ...
... 为了最小化式(1)所示的目标函数,通常采用梯度类局部最优化算法[1 ,3 ] ,本文采用共轭梯度法.速度和反射点坐标的更新过程可以表示为[27 ] ...
Stereotomography of seismic data acquired on undulant topography
2
2018
... 斜率层析成像利用局部相干反射波的走时和斜率(射线参数)反演地下介质的背景速度[1 ⇓ -3 ] .在地质构造简单工区,斜率层析反演模型的精度较高,能够满足叠前深度偏移成像的需求[4 ⇓ -6 ] .然而,在地质构造复杂(如存在纵、横向速度突变)的工区,斜率层析反演模型的误差较大,尤其是在速度突变界面附近区域[7 ] . ...
... 斜率层析成像利用叠前地震资料中局部相干反射波的走时和斜率反演地下介质的宏观速度背景[1 -2 ] ,其目标函数可以表示为[7 ,26 ] ...
Parsimonious slope tomography based on eikonal solvers and the adjoint-state method
2
2019
... 斜率层析成像利用局部相干反射波的走时和斜率(射线参数)反演地下介质的背景速度[1 ⇓ -3 ] .在地质构造简单工区,斜率层析反演模型的精度较高,能够满足叠前深度偏移成像的需求[4 ⇓ -6 ] .然而,在地质构造复杂(如存在纵、横向速度突变)的工区,斜率层析反演模型的误差较大,尤其是在速度突变界面附近区域[7 ] . ...
... 为了最小化式(1)所示的目标函数,通常采用梯度类局部最优化算法[1 ,3 ] ,本文采用共轭梯度法.速度和反射点坐标的更新过程可以表示为[27 ] ...
地震立体层析成像的实现方法及效果分析
2
2014
... 斜率层析成像利用局部相干反射波的走时和斜率(射线参数)反演地下介质的背景速度[1 ⇓ -3 ] .在地质构造简单工区,斜率层析反演模型的精度较高,能够满足叠前深度偏移成像的需求[4 ⇓ -6 ] .然而,在地质构造复杂(如存在纵、横向速度突变)的工区,斜率层析反演模型的误差较大,尤其是在速度突变界面附近区域[7 ] . ...
... 本文采用有限差分法计算炮点端和检波点端的走时斜率Ps 和Pr [26 ] ,采用基于直线叠加能量扫描的方法自动拾取局部反射同相轴的斜率 P s * [4 ] .在进行斜率拾取之前,需要对共炮域和共检波点域的地震数据进行预处理,主要包括剔除野值、压制噪声、去除多次波等非一次反射波. ...
地震立体层析成像的实现方法及效果分析
2
2014
... 斜率层析成像利用局部相干反射波的走时和斜率(射线参数)反演地下介质的背景速度[1 ⇓ -3 ] .在地质构造简单工区,斜率层析反演模型的精度较高,能够满足叠前深度偏移成像的需求[4 ⇓ -6 ] .然而,在地质构造复杂(如存在纵、横向速度突变)的工区,斜率层析反演模型的误差较大,尤其是在速度突变界面附近区域[7 ] . ...
... 本文采用有限差分法计算炮点端和检波点端的走时斜率Ps 和Pr [26 ] ,采用基于直线叠加能量扫描的方法自动拾取局部反射同相轴的斜率 P s * [4 ] .在进行斜率拾取之前,需要对共炮域和共检波点域的地震数据进行预处理,主要包括剔除野值、压制噪声、去除多次波等非一次反射波. ...
基于立体层析反演的低频模型构建在深水区储层反演中的应用:以南海深水W构造为例
1
2018
... 斜率层析成像利用局部相干反射波的走时和斜率(射线参数)反演地下介质的背景速度[1 ⇓ -3 ] .在地质构造简单工区,斜率层析反演模型的精度较高,能够满足叠前深度偏移成像的需求[4 ⇓ -6 ] .然而,在地质构造复杂(如存在纵、横向速度突变)的工区,斜率层析反演模型的误差较大,尤其是在速度突变界面附近区域[7 ] . ...
基于立体层析反演的低频模型构建在深水区储层反演中的应用:以南海深水W构造为例
1
2018
... 斜率层析成像利用局部相干反射波的走时和斜率(射线参数)反演地下介质的背景速度[1 ⇓ -3 ] .在地质构造简单工区,斜率层析反演模型的精度较高,能够满足叠前深度偏移成像的需求[4 ⇓ -6 ] .然而,在地质构造复杂(如存在纵、横向速度突变)的工区,斜率层析反演模型的误差较大,尤其是在速度突变界面附近区域[7 ] . ...
Joint inversion of seismic slopes,traveltimes and gravity anomaly data based on structural similarity
3
2022
... 斜率层析成像利用局部相干反射波的走时和斜率(射线参数)反演地下介质的背景速度[1 ⇓ -3 ] .在地质构造简单工区,斜率层析反演模型的精度较高,能够满足叠前深度偏移成像的需求[4 ⇓ -6 ] .然而,在地质构造复杂(如存在纵、横向速度突变)的工区,斜率层析反演模型的误差较大,尤其是在速度突变界面附近区域[7 ] . ...
... 为了提高斜率层析成像在地质构造复杂工区的速度建模精度,研究人员尝试利用先验信息对反演进行约束[8 -9 ] .Costa等[10 ] 利用反射角信息对反演模型进行空间平滑约束,他们通过理论模型测试表明不同平滑约束对反演速度模型的影响较大,但对深度偏移剖面的影响较小,这主要是由于平滑约束难以降低强波阻抗界面两侧的速度误差.Guillaume等[11 ] 利用偏移后的局部反射同相轴的倾角对斜率层析反演进行约束,克服了浅层局部速度异常体对反演中深部地层速度的不良影响.Yang等[7 ] 和张力起等[9 ] 利用反射点的空间位置信息对反演的速度模型进行约束,获得了良好的应用效果[6 ] .然而,这类方法严重依赖于初始反射点的空间位置,故对低信噪比资料和地质构造复杂工区资料的适用性较低.此外,一些学者尝试利用非震资料对斜率层析反演进行约束[6 ] ,从而提高反演模型精度,但联合多种地球物理资料进行反演会增加反演未知量个数,导致反演多解性增强[12 ⇓ ⇓ -15 ] .上述方法利用先验信息或非震资料改善了斜率层析反演模型,然而由于反演固有的空间平滑效应,导致速度突变界面附近区域的速度难以得到准确反演. ...
... [6 ],从而提高反演模型精度,但联合多种地球物理资料进行反演会增加反演未知量个数,导致反演多解性增强[12 ⇓ ⇓ -15 ] .上述方法利用先验信息或非震资料改善了斜率层析反演模型,然而由于反演固有的空间平滑效应,导致速度突变界面附近区域的速度难以得到准确反演. ...
Slope tomography dynamically weighted according to the locations of the reflection points
6
2024
... 斜率层析成像利用局部相干反射波的走时和斜率(射线参数)反演地下介质的背景速度[1 ⇓ -3 ] .在地质构造简单工区,斜率层析反演模型的精度较高,能够满足叠前深度偏移成像的需求[4 ⇓ -6 ] .然而,在地质构造复杂(如存在纵、横向速度突变)的工区,斜率层析反演模型的误差较大,尤其是在速度突变界面附近区域[7 ] . ...
... 为了提高斜率层析成像在地质构造复杂工区的速度建模精度,研究人员尝试利用先验信息对反演进行约束[8 -9 ] .Costa等[10 ] 利用反射角信息对反演模型进行空间平滑约束,他们通过理论模型测试表明不同平滑约束对反演速度模型的影响较大,但对深度偏移剖面的影响较小,这主要是由于平滑约束难以降低强波阻抗界面两侧的速度误差.Guillaume等[11 ] 利用偏移后的局部反射同相轴的倾角对斜率层析反演进行约束,克服了浅层局部速度异常体对反演中深部地层速度的不良影响.Yang等[7 ] 和张力起等[9 ] 利用反射点的空间位置信息对反演的速度模型进行约束,获得了良好的应用效果[6 ] .然而,这类方法严重依赖于初始反射点的空间位置,故对低信噪比资料和地质构造复杂工区资料的适用性较低.此外,一些学者尝试利用非震资料对斜率层析反演进行约束[6 ] ,从而提高反演模型精度,但联合多种地球物理资料进行反演会增加反演未知量个数,导致反演多解性增强[12 ⇓ ⇓ -15 ] .上述方法利用先验信息或非震资料改善了斜率层析反演模型,然而由于反演固有的空间平滑效应,导致速度突变界面附近区域的速度难以得到准确反演. ...
... 斜率层析成像利用叠前地震资料中局部相干反射波的走时和斜率反演地下介质的宏观速度背景[1 -2 ] ,其目标函数可以表示为[7 ,26 ] ...
... 式中:k 表示当前迭代次数;αv 和αc 分别表示速度模型和反射点空间坐标的更新步长; d v i d x c , j d z c , j x 和z 坐标的共轭梯度.更新步长αv 和αc 采用线性搜索方法计算[28 ] .速度模型、反射点空间x 和z 坐标的共轭梯度由当前迭代的梯度和前一次迭代的共轭梯度计算得到,计算公式如下[7 ] ...
... 式(7)中目标函数对速度的梯度可以表示为[7 ] ...
... 式(8)和(9)中目标函数对反射点空间x 和z 坐标的梯度可以分别表示为[7 ] ...
联合结构张量与运动学反偏移的立体层析数据空间提取与反演策略研究Ⅱ:实践
1
2018
... 为了提高斜率层析成像在地质构造复杂工区的速度建模精度,研究人员尝试利用先验信息对反演进行约束[8 -9 ] .Costa等[10 ] 利用反射角信息对反演模型进行空间平滑约束,他们通过理论模型测试表明不同平滑约束对反演速度模型的影响较大,但对深度偏移剖面的影响较小,这主要是由于平滑约束难以降低强波阻抗界面两侧的速度误差.Guillaume等[11 ] 利用偏移后的局部反射同相轴的倾角对斜率层析反演进行约束,克服了浅层局部速度异常体对反演中深部地层速度的不良影响.Yang等[7 ] 和张力起等[9 ] 利用反射点的空间位置信息对反演的速度模型进行约束,获得了良好的应用效果[6 ] .然而,这类方法严重依赖于初始反射点的空间位置,故对低信噪比资料和地质构造复杂工区资料的适用性较低.此外,一些学者尝试利用非震资料对斜率层析反演进行约束[6 ] ,从而提高反演模型精度,但联合多种地球物理资料进行反演会增加反演未知量个数,导致反演多解性增强[12 ⇓ ⇓ -15 ] .上述方法利用先验信息或非震资料改善了斜率层析反演模型,然而由于反演固有的空间平滑效应,导致速度突变界面附近区域的速度难以得到准确反演. ...
联合结构张量与运动学反偏移的立体层析数据空间提取与反演策略研究Ⅱ:实践
1
2018
... 为了提高斜率层析成像在地质构造复杂工区的速度建模精度,研究人员尝试利用先验信息对反演进行约束[8 -9 ] .Costa等[10 ] 利用反射角信息对反演模型进行空间平滑约束,他们通过理论模型测试表明不同平滑约束对反演速度模型的影响较大,但对深度偏移剖面的影响较小,这主要是由于平滑约束难以降低强波阻抗界面两侧的速度误差.Guillaume等[11 ] 利用偏移后的局部反射同相轴的倾角对斜率层析反演进行约束,克服了浅层局部速度异常体对反演中深部地层速度的不良影响.Yang等[7 ] 和张力起等[9 ] 利用反射点的空间位置信息对反演的速度模型进行约束,获得了良好的应用效果[6 ] .然而,这类方法严重依赖于初始反射点的空间位置,故对低信噪比资料和地质构造复杂工区资料的适用性较低.此外,一些学者尝试利用非震资料对斜率层析反演进行约束[6 ] ,从而提高反演模型精度,但联合多种地球物理资料进行反演会增加反演未知量个数,导致反演多解性增强[12 ⇓ ⇓ -15 ] .上述方法利用先验信息或非震资料改善了斜率层析反演模型,然而由于反演固有的空间平滑效应,导致速度突变界面附近区域的速度难以得到准确反演. ...
地层格架正则化约束下的二维立体层析反演
2
2019
... 为了提高斜率层析成像在地质构造复杂工区的速度建模精度,研究人员尝试利用先验信息对反演进行约束[8 -9 ] .Costa等[10 ] 利用反射角信息对反演模型进行空间平滑约束,他们通过理论模型测试表明不同平滑约束对反演速度模型的影响较大,但对深度偏移剖面的影响较小,这主要是由于平滑约束难以降低强波阻抗界面两侧的速度误差.Guillaume等[11 ] 利用偏移后的局部反射同相轴的倾角对斜率层析反演进行约束,克服了浅层局部速度异常体对反演中深部地层速度的不良影响.Yang等[7 ] 和张力起等[9 ] 利用反射点的空间位置信息对反演的速度模型进行约束,获得了良好的应用效果[6 ] .然而,这类方法严重依赖于初始反射点的空间位置,故对低信噪比资料和地质构造复杂工区资料的适用性较低.此外,一些学者尝试利用非震资料对斜率层析反演进行约束[6 ] ,从而提高反演模型精度,但联合多种地球物理资料进行反演会增加反演未知量个数,导致反演多解性增强[12 ⇓ ⇓ -15 ] .上述方法利用先验信息或非震资料改善了斜率层析反演模型,然而由于反演固有的空间平滑效应,导致速度突变界面附近区域的速度难以得到准确反演. ...
... [9 ]利用反射点的空间位置信息对反演的速度模型进行约束,获得了良好的应用效果[6 ] .然而,这类方法严重依赖于初始反射点的空间位置,故对低信噪比资料和地质构造复杂工区资料的适用性较低.此外,一些学者尝试利用非震资料对斜率层析反演进行约束[6 ] ,从而提高反演模型精度,但联合多种地球物理资料进行反演会增加反演未知量个数,导致反演多解性增强[12 ⇓ ⇓ -15 ] .上述方法利用先验信息或非震资料改善了斜率层析反演模型,然而由于反演固有的空间平滑效应,导致速度突变界面附近区域的速度难以得到准确反演. ...
地层格架正则化约束下的二维立体层析反演
2
2019
... 为了提高斜率层析成像在地质构造复杂工区的速度建模精度,研究人员尝试利用先验信息对反演进行约束[8 -9 ] .Costa等[10 ] 利用反射角信息对反演模型进行空间平滑约束,他们通过理论模型测试表明不同平滑约束对反演速度模型的影响较大,但对深度偏移剖面的影响较小,这主要是由于平滑约束难以降低强波阻抗界面两侧的速度误差.Guillaume等[11 ] 利用偏移后的局部反射同相轴的倾角对斜率层析反演进行约束,克服了浅层局部速度异常体对反演中深部地层速度的不良影响.Yang等[7 ] 和张力起等[9 ] 利用反射点的空间位置信息对反演的速度模型进行约束,获得了良好的应用效果[6 ] .然而,这类方法严重依赖于初始反射点的空间位置,故对低信噪比资料和地质构造复杂工区资料的适用性较低.此外,一些学者尝试利用非震资料对斜率层析反演进行约束[6 ] ,从而提高反演模型精度,但联合多种地球物理资料进行反演会增加反演未知量个数,导致反演多解性增强[12 ⇓ ⇓ -15 ] .上述方法利用先验信息或非震资料改善了斜率层析反演模型,然而由于反演固有的空间平滑效应,导致速度突变界面附近区域的速度难以得到准确反演. ...
... [9 ]利用反射点的空间位置信息对反演的速度模型进行约束,获得了良好的应用效果[6 ] .然而,这类方法严重依赖于初始反射点的空间位置,故对低信噪比资料和地质构造复杂工区资料的适用性较低.此外,一些学者尝试利用非震资料对斜率层析反演进行约束[6 ] ,从而提高反演模型精度,但联合多种地球物理资料进行反演会增加反演未知量个数,导致反演多解性增强[12 ⇓ ⇓ -15 ] .上述方法利用先验信息或非震资料改善了斜率层析反演模型,然而由于反演固有的空间平滑效应,导致速度突变界面附近区域的速度难以得到准确反演. ...
Regularization in slope tomography
2
2008
... 为了提高斜率层析成像在地质构造复杂工区的速度建模精度,研究人员尝试利用先验信息对反演进行约束[8 -9 ] .Costa等[10 ] 利用反射角信息对反演模型进行空间平滑约束,他们通过理论模型测试表明不同平滑约束对反演速度模型的影响较大,但对深度偏移剖面的影响较小,这主要是由于平滑约束难以降低强波阻抗界面两侧的速度误差.Guillaume等[11 ] 利用偏移后的局部反射同相轴的倾角对斜率层析反演进行约束,克服了浅层局部速度异常体对反演中深部地层速度的不良影响.Yang等[7 ] 和张力起等[9 ] 利用反射点的空间位置信息对反演的速度模型进行约束,获得了良好的应用效果[6 ] .然而,这类方法严重依赖于初始反射点的空间位置,故对低信噪比资料和地质构造复杂工区资料的适用性较低.此外,一些学者尝试利用非震资料对斜率层析反演进行约束[6 ] ,从而提高反演模型精度,但联合多种地球物理资料进行反演会增加反演未知量个数,导致反演多解性增强[12 ⇓ ⇓ -15 ] .上述方法利用先验信息或非震资料改善了斜率层析反演模型,然而由于反演固有的空间平滑效应,导致速度突变界面附近区域的速度难以得到准确反演. ...
... 式中:vi 表示第i 个模型离散单元的速度;M 表示模型离散单元的总数;xc , j zc , j j 个反射点的水平距离和深度;N 表示反射波数据的总数;T 表示反射波双程走时;Ps 和Pr 分别表示反射波炮点端和检波点端的走时斜率;上标*表示观测数据;σT 和σP 分别表示反射波双程走时和斜率的标准差,其计算公式为[10 ⇓ -12 ] ...
Dip constrained non-linear slope tomography
2
2013
... 为了提高斜率层析成像在地质构造复杂工区的速度建模精度,研究人员尝试利用先验信息对反演进行约束[8 -9 ] .Costa等[10 ] 利用反射角信息对反演模型进行空间平滑约束,他们通过理论模型测试表明不同平滑约束对反演速度模型的影响较大,但对深度偏移剖面的影响较小,这主要是由于平滑约束难以降低强波阻抗界面两侧的速度误差.Guillaume等[11 ] 利用偏移后的局部反射同相轴的倾角对斜率层析反演进行约束,克服了浅层局部速度异常体对反演中深部地层速度的不良影响.Yang等[7 ] 和张力起等[9 ] 利用反射点的空间位置信息对反演的速度模型进行约束,获得了良好的应用效果[6 ] .然而,这类方法严重依赖于初始反射点的空间位置,故对低信噪比资料和地质构造复杂工区资料的适用性较低.此外,一些学者尝试利用非震资料对斜率层析反演进行约束[6 ] ,从而提高反演模型精度,但联合多种地球物理资料进行反演会增加反演未知量个数,导致反演多解性增强[12 ⇓ ⇓ -15 ] .上述方法利用先验信息或非震资料改善了斜率层析反演模型,然而由于反演固有的空间平滑效应,导致速度突变界面附近区域的速度难以得到准确反演. ...
... 式中:vi 表示第i 个模型离散单元的速度;M 表示模型离散单元的总数;xc , j zc , j j 个反射点的水平距离和深度;N 表示反射波数据的总数;T 表示反射波双程走时;Ps 和Pr 分别表示反射波炮点端和检波点端的走时斜率;上标*表示观测数据;σT 和σP 分别表示反射波双程走时和斜率的标准差,其计算公式为[10 ⇓ -12 ] ...
Joint inversion of receiver function and surface-wave phase velocity for estimation of shear-wave velocity of sedimentary layers
2
2006
... 为了提高斜率层析成像在地质构造复杂工区的速度建模精度,研究人员尝试利用先验信息对反演进行约束[8 -9 ] .Costa等[10 ] 利用反射角信息对反演模型进行空间平滑约束,他们通过理论模型测试表明不同平滑约束对反演速度模型的影响较大,但对深度偏移剖面的影响较小,这主要是由于平滑约束难以降低强波阻抗界面两侧的速度误差.Guillaume等[11 ] 利用偏移后的局部反射同相轴的倾角对斜率层析反演进行约束,克服了浅层局部速度异常体对反演中深部地层速度的不良影响.Yang等[7 ] 和张力起等[9 ] 利用反射点的空间位置信息对反演的速度模型进行约束,获得了良好的应用效果[6 ] .然而,这类方法严重依赖于初始反射点的空间位置,故对低信噪比资料和地质构造复杂工区资料的适用性较低.此外,一些学者尝试利用非震资料对斜率层析反演进行约束[6 ] ,从而提高反演模型精度,但联合多种地球物理资料进行反演会增加反演未知量个数,导致反演多解性增强[12 ⇓ ⇓ -15 ] .上述方法利用先验信息或非震资料改善了斜率层析反演模型,然而由于反演固有的空间平滑效应,导致速度突变界面附近区域的速度难以得到准确反演. ...
... 式中:vi 表示第i 个模型离散单元的速度;M 表示模型离散单元的总数;xc , j zc , j j 个反射点的水平距离和深度;N 表示反射波数据的总数;T 表示反射波双程走时;Ps 和Pr 分别表示反射波炮点端和检波点端的走时斜率;上标*表示观测数据;σT 和σP 分别表示反射波双程走时和斜率的标准差,其计算公式为[10 ⇓ -12 ] ...
重震联合反演方法及其应用进展
1
2019
... 为了提高斜率层析成像在地质构造复杂工区的速度建模精度,研究人员尝试利用先验信息对反演进行约束[8 -9 ] .Costa等[10 ] 利用反射角信息对反演模型进行空间平滑约束,他们通过理论模型测试表明不同平滑约束对反演速度模型的影响较大,但对深度偏移剖面的影响较小,这主要是由于平滑约束难以降低强波阻抗界面两侧的速度误差.Guillaume等[11 ] 利用偏移后的局部反射同相轴的倾角对斜率层析反演进行约束,克服了浅层局部速度异常体对反演中深部地层速度的不良影响.Yang等[7 ] 和张力起等[9 ] 利用反射点的空间位置信息对反演的速度模型进行约束,获得了良好的应用效果[6 ] .然而,这类方法严重依赖于初始反射点的空间位置,故对低信噪比资料和地质构造复杂工区资料的适用性较低.此外,一些学者尝试利用非震资料对斜率层析反演进行约束[6 ] ,从而提高反演模型精度,但联合多种地球物理资料进行反演会增加反演未知量个数,导致反演多解性增强[12 ⇓ ⇓ -15 ] .上述方法利用先验信息或非震资料改善了斜率层析反演模型,然而由于反演固有的空间平滑效应,导致速度突变界面附近区域的速度难以得到准确反演. ...
重震联合反演方法及其应用进展
1
2019
... 为了提高斜率层析成像在地质构造复杂工区的速度建模精度,研究人员尝试利用先验信息对反演进行约束[8 -9 ] .Costa等[10 ] 利用反射角信息对反演模型进行空间平滑约束,他们通过理论模型测试表明不同平滑约束对反演速度模型的影响较大,但对深度偏移剖面的影响较小,这主要是由于平滑约束难以降低强波阻抗界面两侧的速度误差.Guillaume等[11 ] 利用偏移后的局部反射同相轴的倾角对斜率层析反演进行约束,克服了浅层局部速度异常体对反演中深部地层速度的不良影响.Yang等[7 ] 和张力起等[9 ] 利用反射点的空间位置信息对反演的速度模型进行约束,获得了良好的应用效果[6 ] .然而,这类方法严重依赖于初始反射点的空间位置,故对低信噪比资料和地质构造复杂工区资料的适用性较低.此外,一些学者尝试利用非震资料对斜率层析反演进行约束[6 ] ,从而提高反演模型精度,但联合多种地球物理资料进行反演会增加反演未知量个数,导致反演多解性增强[12 ⇓ ⇓ -15 ] .上述方法利用先验信息或非震资料改善了斜率层析反演模型,然而由于反演固有的空间平滑效应,导致速度突变界面附近区域的速度难以得到准确反演. ...
一种变密度—速度关系的重力与地震同步联合反演方法
1
2020
... 为了提高斜率层析成像在地质构造复杂工区的速度建模精度,研究人员尝试利用先验信息对反演进行约束[8 -9 ] .Costa等[10 ] 利用反射角信息对反演模型进行空间平滑约束,他们通过理论模型测试表明不同平滑约束对反演速度模型的影响较大,但对深度偏移剖面的影响较小,这主要是由于平滑约束难以降低强波阻抗界面两侧的速度误差.Guillaume等[11 ] 利用偏移后的局部反射同相轴的倾角对斜率层析反演进行约束,克服了浅层局部速度异常体对反演中深部地层速度的不良影响.Yang等[7 ] 和张力起等[9 ] 利用反射点的空间位置信息对反演的速度模型进行约束,获得了良好的应用效果[6 ] .然而,这类方法严重依赖于初始反射点的空间位置,故对低信噪比资料和地质构造复杂工区资料的适用性较低.此外,一些学者尝试利用非震资料对斜率层析反演进行约束[6 ] ,从而提高反演模型精度,但联合多种地球物理资料进行反演会增加反演未知量个数,导致反演多解性增强[12 ⇓ ⇓ -15 ] .上述方法利用先验信息或非震资料改善了斜率层析反演模型,然而由于反演固有的空间平滑效应,导致速度突变界面附近区域的速度难以得到准确反演. ...
一种变密度—速度关系的重力与地震同步联合反演方法
1
2020
... 为了提高斜率层析成像在地质构造复杂工区的速度建模精度,研究人员尝试利用先验信息对反演进行约束[8 -9 ] .Costa等[10 ] 利用反射角信息对反演模型进行空间平滑约束,他们通过理论模型测试表明不同平滑约束对反演速度模型的影响较大,但对深度偏移剖面的影响较小,这主要是由于平滑约束难以降低强波阻抗界面两侧的速度误差.Guillaume等[11 ] 利用偏移后的局部反射同相轴的倾角对斜率层析反演进行约束,克服了浅层局部速度异常体对反演中深部地层速度的不良影响.Yang等[7 ] 和张力起等[9 ] 利用反射点的空间位置信息对反演的速度模型进行约束,获得了良好的应用效果[6 ] .然而,这类方法严重依赖于初始反射点的空间位置,故对低信噪比资料和地质构造复杂工区资料的适用性较低.此外,一些学者尝试利用非震资料对斜率层析反演进行约束[6 ] ,从而提高反演模型精度,但联合多种地球物理资料进行反演会增加反演未知量个数,导致反演多解性增强[12 ⇓ ⇓ -15 ] .上述方法利用先验信息或非震资料改善了斜率层析反演模型,然而由于反演固有的空间平滑效应,导致速度突变界面附近区域的速度难以得到准确反演. ...
重震联合中速度—密度耦合研究综述
1
2020
... 为了提高斜率层析成像在地质构造复杂工区的速度建模精度,研究人员尝试利用先验信息对反演进行约束[8 -9 ] .Costa等[10 ] 利用反射角信息对反演模型进行空间平滑约束,他们通过理论模型测试表明不同平滑约束对反演速度模型的影响较大,但对深度偏移剖面的影响较小,这主要是由于平滑约束难以降低强波阻抗界面两侧的速度误差.Guillaume等[11 ] 利用偏移后的局部反射同相轴的倾角对斜率层析反演进行约束,克服了浅层局部速度异常体对反演中深部地层速度的不良影响.Yang等[7 ] 和张力起等[9 ] 利用反射点的空间位置信息对反演的速度模型进行约束,获得了良好的应用效果[6 ] .然而,这类方法严重依赖于初始反射点的空间位置,故对低信噪比资料和地质构造复杂工区资料的适用性较低.此外,一些学者尝试利用非震资料对斜率层析反演进行约束[6 ] ,从而提高反演模型精度,但联合多种地球物理资料进行反演会增加反演未知量个数,导致反演多解性增强[12 ⇓ ⇓ -15 ] .上述方法利用先验信息或非震资料改善了斜率层析反演模型,然而由于反演固有的空间平滑效应,导致速度突变界面附近区域的速度难以得到准确反演. ...
重震联合中速度—密度耦合研究综述
1
2020
... 为了提高斜率层析成像在地质构造复杂工区的速度建模精度,研究人员尝试利用先验信息对反演进行约束[8 -9 ] .Costa等[10 ] 利用反射角信息对反演模型进行空间平滑约束,他们通过理论模型测试表明不同平滑约束对反演速度模型的影响较大,但对深度偏移剖面的影响较小,这主要是由于平滑约束难以降低强波阻抗界面两侧的速度误差.Guillaume等[11 ] 利用偏移后的局部反射同相轴的倾角对斜率层析反演进行约束,克服了浅层局部速度异常体对反演中深部地层速度的不良影响.Yang等[7 ] 和张力起等[9 ] 利用反射点的空间位置信息对反演的速度模型进行约束,获得了良好的应用效果[6 ] .然而,这类方法严重依赖于初始反射点的空间位置,故对低信噪比资料和地质构造复杂工区资料的适用性较低.此外,一些学者尝试利用非震资料对斜率层析反演进行约束[6 ] ,从而提高反演模型精度,但联合多种地球物理资料进行反演会增加反演未知量个数,导致反演多解性增强[12 ⇓ ⇓ -15 ] .上述方法利用先验信息或非震资料改善了斜率层析反演模型,然而由于反演固有的空间平滑效应,导致速度突变界面附近区域的速度难以得到准确反演. ...
Building near-surface velocity models by integrating the first-arrival traveltime tomography and supervised deep learning
1
2023
... 近年来,研究人员尝试利用深度学习技术建立高精度的速度模型,如:采用卷积神经网络建立共炮域道集与地下速度分布的非线性映射关系[16 ⇓ ⇓ -19 ] ;以炮域和检波点域道集作为所提出的SeisInvNet的输入,以理论速度模型作为标签[20 -21 ] ;将共中心点道集作为卷积神经网络的输入[22 -23 ] ;将共成像点道集作为卷积神经网络的输入[24 ] ;采用偏移后的共偏移距道集作为卷积神经网络的输入[25 ] .这些研究表明,通过大量的、多种类型的样本训练神经网络,可以建立从地震数据到速度模型的非线性映射关系.然而,当训练样本中的速度模型与实际速度分布差别较大时,网络预测模型往往与实际速度分布不一致. ...
Deep-learning tomography
1
2018
... 近年来,研究人员尝试利用深度学习技术建立高精度的速度模型,如:采用卷积神经网络建立共炮域道集与地下速度分布的非线性映射关系[16 ⇓ ⇓ -19 ] ;以炮域和检波点域道集作为所提出的SeisInvNet的输入,以理论速度模型作为标签[20 -21 ] ;将共中心点道集作为卷积神经网络的输入[22 -23 ] ;将共成像点道集作为卷积神经网络的输入[24 ] ;采用偏移后的共偏移距道集作为卷积神经网络的输入[25 ] .这些研究表明,通过大量的、多种类型的样本训练神经网络,可以建立从地震数据到速度模型的非线性映射关系.然而,当训练样本中的速度模型与实际速度分布差别较大时,网络预测模型往往与实际速度分布不一致. ...
Deep learning-driven velocity model building workflow
1
2019
... 近年来,研究人员尝试利用深度学习技术建立高精度的速度模型,如:采用卷积神经网络建立共炮域道集与地下速度分布的非线性映射关系[16 ⇓ ⇓ -19 ] ;以炮域和检波点域道集作为所提出的SeisInvNet的输入,以理论速度模型作为标签[20 -21 ] ;将共中心点道集作为卷积神经网络的输入[22 -23 ] ;将共成像点道集作为卷积神经网络的输入[24 ] ;采用偏移后的共偏移距道集作为卷积神经网络的输入[25 ] .这些研究表明,通过大量的、多种类型的样本训练神经网络,可以建立从地震数据到速度模型的非线性映射关系.然而,当训练样本中的速度模型与实际速度分布差别较大时,网络预测模型往往与实际速度分布不一致. ...
Velocity model building in a crosswell acquisition geometry with image-trained artificial neural networks
2
2020
... 近年来,研究人员尝试利用深度学习技术建立高精度的速度模型,如:采用卷积神经网络建立共炮域道集与地下速度分布的非线性映射关系[16 ⇓ ⇓ -19 ] ;以炮域和检波点域道集作为所提出的SeisInvNet的输入,以理论速度模型作为标签[20 -21 ] ;将共中心点道集作为卷积神经网络的输入[22 -23 ] ;将共成像点道集作为卷积神经网络的输入[24 ] ;采用偏移后的共偏移距道集作为卷积神经网络的输入[25 ] .这些研究表明,通过大量的、多种类型的样本训练神经网络,可以建立从地震数据到速度模型的非线性映射关系.然而,当训练样本中的速度模型与实际速度分布差别较大时,网络预测模型往往与实际速度分布不一致. ...
... 为了提高斜率层析反演模型的精度,本文采用深度学习方法建立反演模型的误差校正算子.采用U-net卷积神经网络[19 ] 建立从反演模型到理论模型的非线性映射,网络结构如图1 所示.网络前半部分的编码器使用卷积和最大池化操作进行特征提取,卷积核尺寸越大,越有益于从输入的反演模型中提取大尺度的结构信息,反之,越容易提取细节信息[29 ] .本文将卷积核大小设置为3×3,使神经网络尽可能地从输入的层析反演模型中提取关于速度突变界面的细节信息.激活函数为修正线性单元(Rectified linear unit,ReLU).为保证卷积前后的矩阵尺寸不变,在卷积之前进行了填充操作,最大池化为2×2,移动步幅为2,移动步幅与最大池化操作的矩阵大小对应.网络后半部分的解码器进行特征定位,以反卷积恢复数据维度并获得特征,并通过跳跃连接与浅层提取到的特征结合来提高空间分辨率.网络的通道数随着层数增加逐渐倍增,依次为64、128、256、512.此外,设置丢弃层以提高网络的稳定性,选取系数为0.5. ...
Deep-learning inversion of seismic data
1
2020
... 近年来,研究人员尝试利用深度学习技术建立高精度的速度模型,如:采用卷积神经网络建立共炮域道集与地下速度分布的非线性映射关系[16 ⇓ ⇓ -19 ] ;以炮域和检波点域道集作为所提出的SeisInvNet的输入,以理论速度模型作为标签[20 -21 ] ;将共中心点道集作为卷积神经网络的输入[22 -23 ] ;将共成像点道集作为卷积神经网络的输入[24 ] ;采用偏移后的共偏移距道集作为卷积神经网络的输入[25 ] .这些研究表明,通过大量的、多种类型的样本训练神经网络,可以建立从地震数据到速度模型的非线性映射关系.然而,当训练样本中的速度模型与实际速度分布差别较大时,网络预测模型往往与实际速度分布不一致. ...
Deep-learning seismic full-waveform inversion for realistic structural models
1
2021
... 近年来,研究人员尝试利用深度学习技术建立高精度的速度模型,如:采用卷积神经网络建立共炮域道集与地下速度分布的非线性映射关系[16 ⇓ ⇓ -19 ] ;以炮域和检波点域道集作为所提出的SeisInvNet的输入,以理论速度模型作为标签[20 -21 ] ;将共中心点道集作为卷积神经网络的输入[22 -23 ] ;将共成像点道集作为卷积神经网络的输入[24 ] ;采用偏移后的共偏移距道集作为卷积神经网络的输入[25 ] .这些研究表明,通过大量的、多种类型的样本训练神经网络,可以建立从地震数据到速度模型的非线性映射关系.然而,当训练样本中的速度模型与实际速度分布差别较大时,网络预测模型往往与实际速度分布不一致. ...
Velocity model building by deep learning:From general synthetics to field data application
1
2020
... 近年来,研究人员尝试利用深度学习技术建立高精度的速度模型,如:采用卷积神经网络建立共炮域道集与地下速度分布的非线性映射关系[16 ⇓ ⇓ -19 ] ;以炮域和检波点域道集作为所提出的SeisInvNet的输入,以理论速度模型作为标签[20 -21 ] ;将共中心点道集作为卷积神经网络的输入[22 -23 ] ;将共成像点道集作为卷积神经网络的输入[24 ] ;采用偏移后的共偏移距道集作为卷积神经网络的输入[25 ] .这些研究表明,通过大量的、多种类型的样本训练神经网络,可以建立从地震数据到速度模型的非线性映射关系.然而,当训练样本中的速度模型与实际速度分布差别较大时,网络预测模型往往与实际速度分布不一致. ...
Seismic velocity estimation:A deep recurrent neural-network approach
1
2020
... 近年来,研究人员尝试利用深度学习技术建立高精度的速度模型,如:采用卷积神经网络建立共炮域道集与地下速度分布的非线性映射关系[16 ⇓ ⇓ -19 ] ;以炮域和检波点域道集作为所提出的SeisInvNet的输入,以理论速度模型作为标签[20 -21 ] ;将共中心点道集作为卷积神经网络的输入[22 -23 ] ;将共成像点道集作为卷积神经网络的输入[24 ] ;采用偏移后的共偏移距道集作为卷积神经网络的输入[25 ] .这些研究表明,通过大量的、多种类型的样本训练神经网络,可以建立从地震数据到速度模型的非线性映射关系.然而,当训练样本中的速度模型与实际速度分布差别较大时,网络预测模型往往与实际速度分布不一致. ...
Deep learning for velocity model building with common-image gather volumes
1
2021
... 近年来,研究人员尝试利用深度学习技术建立高精度的速度模型,如:采用卷积神经网络建立共炮域道集与地下速度分布的非线性映射关系[16 ⇓ ⇓ -19 ] ;以炮域和检波点域道集作为所提出的SeisInvNet的输入,以理论速度模型作为标签[20 -21 ] ;将共中心点道集作为卷积神经网络的输入[22 -23 ] ;将共成像点道集作为卷积神经网络的输入[24 ] ;采用偏移后的共偏移距道集作为卷积神经网络的输入[25 ] .这些研究表明,通过大量的、多种类型的样本训练神经网络,可以建立从地震数据到速度模型的非线性映射关系.然而,当训练样本中的速度模型与实际速度分布差别较大时,网络预测模型往往与实际速度分布不一致. ...
Deep-Tomography:Iterative velocity model building with deep learning
1
2022
... 近年来,研究人员尝试利用深度学习技术建立高精度的速度模型,如:采用卷积神经网络建立共炮域道集与地下速度分布的非线性映射关系[16 ⇓ ⇓ -19 ] ;以炮域和检波点域道集作为所提出的SeisInvNet的输入,以理论速度模型作为标签[20 -21 ] ;将共中心点道集作为卷积神经网络的输入[22 -23 ] ;将共成像点道集作为卷积神经网络的输入[24 ] ;采用偏移后的共偏移距道集作为卷积神经网络的输入[25 ] .这些研究表明,通过大量的、多种类型的样本训练神经网络,可以建立从地震数据到速度模型的非线性映射关系.然而,当训练样本中的速度模型与实际速度分布差别较大时,网络预测模型往往与实际速度分布不一致. ...
Slope tomography based on eikonal solvers and the adjoint-state method
2
2017
... 斜率层析成像利用叠前地震资料中局部相干反射波的走时和斜率反演地下介质的宏观速度背景[1 -2 ] ,其目标函数可以表示为[7 ,26 ] ...
... 本文采用有限差分法计算炮点端和检波点端的走时斜率Ps 和Pr [26 ] ,采用基于直线叠加能量扫描的方法自动拾取局部反射同相轴的斜率 P s * [4 ] .在进行斜率拾取之前,需要对共炮域和共检波点域的地震数据进行预处理,主要包括剔除野值、压制噪声、去除多次波等非一次反射波. ...
A nonlinear conjugate gradient method with a strong global convergence property
2
1999
... 为了最小化式(1)所示的目标函数,通常采用梯度类局部最优化算法[1 ,3 ] ,本文采用共轭梯度法.速度和反射点坐标的更新过程可以表示为[27 ] ...
... 式中:βv 和βc 分别是使速度模型和反射点坐标相邻两次共轭梯度正交的系数,采用Dai等[27 ] 提出的方法计算获得. ...
1
2006
... 式中:k 表示当前迭代次数;αv 和αc 分别表示速度模型和反射点空间坐标的更新步长; d v i d x c , j d z c , j x 和z 坐标的共轭梯度.更新步长αv 和αc 采用线性搜索方法计算[28 ] .速度模型、反射点空间x 和z 坐标的共轭梯度由当前迭代的梯度和前一次迭代的共轭梯度计算得到,计算公式如下[7 ] ...
基于特征强化U-Net的地震速度反演方法
1
2024
... 为了提高斜率层析反演模型的精度,本文采用深度学习方法建立反演模型的误差校正算子.采用U-net卷积神经网络[19 ] 建立从反演模型到理论模型的非线性映射,网络结构如图1 所示.网络前半部分的编码器使用卷积和最大池化操作进行特征提取,卷积核尺寸越大,越有益于从输入的反演模型中提取大尺度的结构信息,反之,越容易提取细节信息[29 ] .本文将卷积核大小设置为3×3,使神经网络尽可能地从输入的层析反演模型中提取关于速度突变界面的细节信息.激活函数为修正线性单元(Rectified linear unit,ReLU).为保证卷积前后的矩阵尺寸不变,在卷积之前进行了填充操作,最大池化为2×2,移动步幅为2,移动步幅与最大池化操作的矩阵大小对应.网络后半部分的解码器进行特征定位,以反卷积恢复数据维度并获得特征,并通过跳跃连接与浅层提取到的特征结合来提高空间分辨率.网络的通道数随着层数增加逐渐倍增,依次为64、128、256、512.此外,设置丢弃层以提高网络的稳定性,选取系数为0.5. ...
基于特征强化U-Net的地震速度反演方法
1
2024
... 为了提高斜率层析反演模型的精度,本文采用深度学习方法建立反演模型的误差校正算子.采用U-net卷积神经网络[19 ] 建立从反演模型到理论模型的非线性映射,网络结构如图1 所示.网络前半部分的编码器使用卷积和最大池化操作进行特征提取,卷积核尺寸越大,越有益于从输入的反演模型中提取大尺度的结构信息,反之,越容易提取细节信息[29 ] .本文将卷积核大小设置为3×3,使神经网络尽可能地从输入的层析反演模型中提取关于速度突变界面的细节信息.激活函数为修正线性单元(Rectified linear unit,ReLU).为保证卷积前后的矩阵尺寸不变,在卷积之前进行了填充操作,最大池化为2×2,移动步幅为2,移动步幅与最大池化操作的矩阵大小对应.网络后半部分的解码器进行特征定位,以反卷积恢复数据维度并获得特征,并通过跳跃连接与浅层提取到的特征结合来提高空间分辨率.网络的通道数随着层数增加逐渐倍增,依次为64、128、256、512.此外,设置丢弃层以提高网络的稳定性,选取系数为0.5. ...
Deep-learning inversion:A next-generation seismic velocity model building method
1
2019
... 为了降低神经网络训练阶段对计算机内存的需求,采用随机梯度下降算法迭代更新神经网络参数[30 ] .神经网络参数迭代更新过程可以表示为 ...
联合地震初至走时与早至波形的深度学习速度建模
1
2023
... 采用Adam算法训练神经网络[31 -32 ] .从生成的500个样本中随机选择400、50和50个样本分别作为训练样本、验证样本和测试样本.神经网络训练的最大轮数设置为30,批量大小设置为4,每个轮次的迭代次数为100.归一化因子λ 设置为7.5 km/s.网络训练的终止条件是连续5次验证样本的目标函数值均大于当前最小目标函数值或达到最大轮数.图7 给出了神经网络训练的目标函数值(RMSE Loss).图中显示目标函数值在第1轮下降最快,随后缓慢下降;训练样本和验证样本的最终目标函数值分别约为初始值的1.66%和3.89%.这表明训练后神经网络的输出与标签之间的差异非常小. ...
联合地震初至走时与早至波形的深度学习速度建模
1
2023
... 采用Adam算法训练神经网络[31 -32 ] .从生成的500个样本中随机选择400、50和50个样本分别作为训练样本、验证样本和测试样本.神经网络训练的最大轮数设置为30,批量大小设置为4,每个轮次的迭代次数为100.归一化因子λ 设置为7.5 km/s.网络训练的终止条件是连续5次验证样本的目标函数值均大于当前最小目标函数值或达到最大轮数.图7 给出了神经网络训练的目标函数值(RMSE Loss).图中显示目标函数值在第1轮下降最快,随后缓慢下降;训练样本和验证样本的最终目标函数值分别约为初始值的1.66%和3.89%.这表明训练后神经网络的输出与标签之间的差异非常小. ...
基于深度学习的接收函数横波速度预测
1
2022
... 采用Adam算法训练神经网络[31 -32 ] .从生成的500个样本中随机选择400、50和50个样本分别作为训练样本、验证样本和测试样本.神经网络训练的最大轮数设置为30,批量大小设置为4,每个轮次的迭代次数为100.归一化因子λ 设置为7.5 km/s.网络训练的终止条件是连续5次验证样本的目标函数值均大于当前最小目标函数值或达到最大轮数.图7 给出了神经网络训练的目标函数值(RMSE Loss).图中显示目标函数值在第1轮下降最快,随后缓慢下降;训练样本和验证样本的最终目标函数值分别约为初始值的1.66%和3.89%.这表明训练后神经网络的输出与标签之间的差异非常小. ...
基于深度学习的接收函数横波速度预测
1
2022
... 采用Adam算法训练神经网络[31 -32 ] .从生成的500个样本中随机选择400、50和50个样本分别作为训练样本、验证样本和测试样本.神经网络训练的最大轮数设置为30,批量大小设置为4,每个轮次的迭代次数为100.归一化因子λ 设置为7.5 km/s.网络训练的终止条件是连续5次验证样本的目标函数值均大于当前最小目标函数值或达到最大轮数.图7 给出了神经网络训练的目标函数值(RMSE Loss).图中显示目标函数值在第1轮下降最快,随后缓慢下降;训练样本和验证样本的最终目标函数值分别约为初始值的1.66%和3.89%.这表明训练后神经网络的输出与标签之间的差异非常小. ...