基于标量坐标的复杂地质表面模型隐式生成方法

doi:10.11720/wtyht.2025.2573

基于标量坐标的复杂地质表面模型隐式生成方法

刘培刚^,¹, 袁昊¹, 薛开欣¹, 李兆亮²^,³, 李宗民¹

1.中国石油大学(华东) 计算机科学与技术学院,山东青岛 266580

2.中国自然资源航空物探遥感中心,北京 100083

3.自然资源部航空地球物理与遥感地质重点实验室,北京 100083

Implicit generation of complex geological surface models based on scalar coordinates

LIU Pei-Gang^,¹, YUAN Hao¹, XUE Kai-Xin¹, LI Zhao-Liang²^,³, LI Zong-Min¹

1. College of Computer Science and Technology, China University of Petroleum (East China), Qingdao 266580, China

2. China Aero Geophysical Survey and Remote Sensing Center for Natural Resources, Beijing 100083, China

3. Key Laboratory of Airborne Geophysics and Remote Sensing Geology, Ministry of Land and Resources, Beijing 100083, China

第一作者: 刘培刚(1979-),男,2017年毕业于北京大学,理学博士,主要从事人工智能、图形图像处理、数据科学及应用的研究工作。Email:dongfangwy@upc.edu.cn

责任编辑: 王萌

收稿日期: 2023-12-27 修回日期: 2024-05-14

基金资助:

国家重点研发计划项目(2019YFF0301800)
国家自然科学基金项目(61379106)

Received: 2023-12-27 Revised: 2024-05-14

摘要

地质模型的构建和呈现是三维地质建模领域的研究热点和难点之一。针对规模庞大、表面复杂、地质约束信息不足的地质体数据,本文采用基于域分解的隐式生成方法,实现大规模地质表面模型的快速构建。以径向基函数为核函数来构建隐式方程;利用重叠域分解策略,并行求解每个域内的分布函数,降低时空成本,加快求解速度;提取法向量生成控制点,构建表面波动约束,实现对模型边界的良好控制。实验结果表明,本文提出的方法能够在保证模型较高质量的前提下显著提升分布函数的求解效率。本研究有效解决地质建模中效率与精度的平衡难题,为地质表面精细化重构提供了方法理论支持。

关键词： 地质表面模型; 隐式建模; 径向基函数; 域分解

Abstract

The construction and presentation of a geological modelprove to be ahot topic and challenge in research on 3D geological modelling. Given the large scale, involvement of complex surfaces, and insufficient geological constraints of geological body data, this study achieved the rapid construction of a large-scale geological surface model using the domain decomposition-based implicit generation method. Initially, implicit functionswere constructed by taking radial basis functions as the kernel functions.Then, the distribution functions of various domainswere solved in parallel usinganoverlapping domain decompositionmethod, reducing the spatiotemporalcost and accelerating the solving process.Subsequently, normal vectors were extracted to generate control pointsand formconstraints on surface fluctuation, thereby effectively controlling the model boundaries. The experimental results indicate that the method proposed in this study can significantly improve the efficiency associated with the solving of distribution functionswhile ensuring the high quality of the model. This study effectively solves the problem of balance between efficiency and precision in geological modeling and provides methodological support for the refinement of geological surfaces.

Keywords： geological surface model; implicit modelling; radial basis function; domain decomposition

PDF (5374KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

刘培刚, 袁昊, 薛开欣, 李兆亮, 李宗民. 基于标量坐标的复杂地质表面模型隐式生成方法[J]. 物探与化探, 2025, 49(2): 349-359 doi:10.11720/wtyht.2025.2573

LIU Pei-Gang, YUAN Hao, XUE Kai-Xin, LI Zhao-Liang, LI Zong-Min. Implicit generation of complex geological surface models based on scalar coordinates[J]. Geophysical and Geochemical Exploration, 2025, 49(2): 349-359 doi:10.11720/wtyht.2025.2573

0 引言

三维地质建模的相关研究在20世纪80年代就已经开始,加拿大地质学家Simon Houlding在1993年提出了“三维地质建模”的概念^[1-2]。随着计算能力的提升,三维地质建模技术逐步应用于越来越复杂的地下场景^{[3⇓⇓⇓⇓⇓⇓⇓⇓-12]}。表面建模是三维地质建模的关键技术之一^[13],其结果将直接影响三维地质体模型的质量。

地质表面模型的构建方法主要分为显式建模^[14⇓-16]和隐式建模^[17⇓-19]。显式建模明确定义了模型中的对象^[20-21],但是这种方法需要复杂且耗时的人机交互,模型也难以进行更新。隐式建模通过插值来逼近模型形状,被广泛应用于地质建模中^{[22⇓⇓⇓-26]}。常见的插值方案分为两种:离散插值方案和连续插值方案。

离散插值方案适用于地质属性存在明显的局部变化的情况,需通过插值方法完成模型构建^{[27⇓⇓⇓-31]}。然而其相邻数据点的插值可能出现剧烈变化,并不适用于地质表面模型的生成。连续插值方案用构造连续的插值函数来描述地层的形状和属性,可以确保地质体的连续性和地层的光滑性。双克里金法或协同克里金法^{[32⇓⇓-35]}是一种基于协方差函数对随机过程或随机场进行空间建模和预测的插值方法,被用于多个地层界面的连续势场建模。Lajaunie 等^[22]提出了一种使用克里金插值的隐式势场建模方法,该方法考虑了地质界面上已知点和平面方向数据,将建模的界面表示为插值场的等值线。Calcagno 等^[24]利用协同克里金,一定程度上解决了以连续3D势场标量函数描述地质形态的问题。Gonalves等^[36]提出了一种将机器学习与势场方法相结合的新方法,使用多种分类方法解决了原始的潜在场方法可能存在的假设问题。连续插值方案的另一种方法是使用径向基函数(RBF)^[37⇓-39]对多维空间进行插值。 Hillier等^[40-41]利用开源库Surfe中的RBF提出了一种应用于多变量结构数据的广义插值框架,克服了在接触约束很少或接触的横向连续性定义不清的数据环境时的局限性。Guo等^{[42⇓⇓-45]}提出了综合三维地质建模方法,使用基于HRBF的隐式方法与蒙皮法和自由曲面方法相结合,在建模地层、断层和褶皱等结构的同时处理局部精细的结构。

针对大规模地质数据建模,求解插值函数需要大量内存空间和运行时间;同时,部分场景仅包含三维坐标,走向、倾角等地质约束信息缺乏,对模型质量控制不足。本文采用域分解策略,构建包含表面波动约束的隐式方程,求解地质表面,优化上述问题,解决的具体方法为:①基于标量坐标数据提取法向量,丰富地质约束信息;②将数据空间划分为具有重叠部分的域,降低求解规模并保证模型的连贯性;③基于控制点构建模型波动约束,控制模型质量;④求解子域分布函数,构建模型的隐式生成方程。

1 本文方法

1.1 模型构建流程

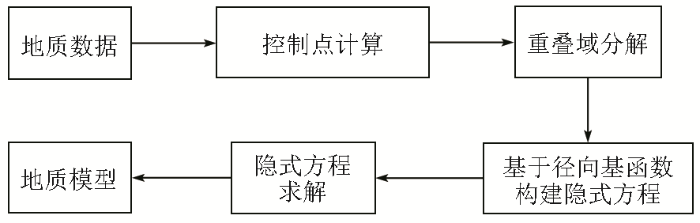
针对仅有坐标信息的数据,本文模型构建方法总结为以下3个部分:①提取法向量并生成控制点:基于局部表面拟合求解法向量并提供一种基于局部质心校正法向的方法,在此基础上生成地质表面的控制点;②对数据进行重叠域分解:域分解是一种数值求解策略,通过将复杂的计算域分割成多个子域,分别进行求解,最后将各个子域的解综合,加快整体求解过程,重叠域在高效求解的前提下,保证了域间信息的连贯性和模型表面的光滑性;③构建模型表面波动约束并求解隐式方程:表面波动约束保证了高质量的模型,利用校正后的法向量生成的地质表面控制点构建表面波动约束,对模型边界的控制起到了关键作用。模型构建流程见图1。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 模型构建流程

Fig.1 Flowchart for model construction

1.2 控制点计算

计算控制点是本文生成良好地质模型的关键因素,控制点对地质模型边界的约束起到了至关重要的作用。本文基于法向量计算控制点,主要步骤包括:①计算法向量;②种子点法向校正;③构建控制点集。

1.2.1 计算法向量

法向量是计算机视觉和三维图形处理中的关键信息,它们描述了每个点在局部表面上的方向信息。针对仅包含坐标信息的标量地质数据,提取法向量并保持方向的一致性是生成控制点的关键因素,本文使用最小二乘拟合领域平面方法求解法向量,增加地质约束信息。

1.2.2 种子点法向校正

最小二乘拟合领域平面方法,即使采用固定视点的方式也无法保证法向的一致性,因此本小节提供一种基于局部质心校正法向的方法。

1.2.2.1 法向校正思想

法向校正方法通过确定局部点云的质心,判断法向的朝向并进行校正,使其指向模型的内部。该方法核心步骤为:

1)以模型最底部的点作为初始种子点,并与单位向量(0,0,1)进行点乘运算,当结果大于0时,才能保证初始种子点法向的正确性,并将初始种子点加入到生长队列L;

2)从队列L取点x,采用K近邻方法查找x的K个邻居点,存入队列L₁。

3)遍历队列L₁,若某数据y的法向未被确定,则采用K近邻方法查找y的K个邻居点,并用队列L₂存储已确定法向的邻居点。

4)将L₂中数据的法向量乘以偏移参数,得到新的向量,将新向量和L₂对应数据的坐标相加,生成向模型内部偏移的临时控制点;翻转L₂中数据的法向,生成向模型内部偏移的临时控制点。

5)计算生成的两部分控制点的质心,同时从队列L₂取点z作为y的参考点,分别判断点z和y的法向与两者指向内外质心的向量的点乘的正负关系,若正负关系不同,则翻转y的法向,并将y加入到生长队列L中。

1.2.2.2 校正方法

种子点法向的正确性是本文建模过程中重要一环,只有保证正确的法向,才能准确生成控制点。种子点法向的校正方式见图2。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 法向校正方法

Fig.2 Normal correction method

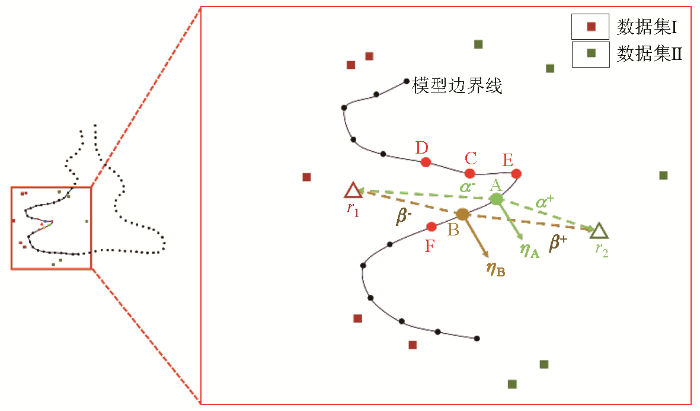
数据点A是待确定法向的种子点,数据点B是距离数据点A最近且已确定法向的邻居点,数据点C、D、E、F是种子点 A 其余邻居点,假定已确定其法向。除边界线上的数据之外,其余数据被分为两部分。数据集Ⅰ是种子点的邻居点沿着法向相反方向偏移后的数据,其质心r₁位于模型外部,数据集Ⅱ是沿着法向偏移后的数据,其质心r₂位于模型内部。α⁺,β⁺表示数据点指向内部质心的向量,α^-,β^-表示数据点指向外部质心的向量,η_A、η_B分别是点A、B对应的法向量。

(1)

\{\begin{array}{l} η_{A} \cdot α^{+} > 0 \\ η_{A} \cdot α^{-} < 0 \end{array}

\{\begin{array}{l} η_{B} \cdot β^{+} > 0 \\ η_{B} \cdot β^{-} < 0 \end{array}

。

通过判断种子点和邻居点与指向内外质心法向的一致性,校正种子点的法向,如式(1)所示,数据点B法向量η_B与指向质心r₁或质心r₂的向量β⁺、β^-点乘结果的正负,均与种子点A法向量η_A与指向两个质心的向量α⁺、α^-点乘结果正负相同,因此不用调整种子点的法向量方向。

1.2.3 构建控制点集

校正后的法向保证了计算控制点的准确性,但是在模型表面平滑的区域,相近点的法向量近似,因此可以选取部分点的法向量代表局部区域法向量,表征其局部特征:①随机筛选法向量:以整体数据为目标,按照数据在文件中存储的顺序,每隔一定的数量便读入一条数据;②以曲率为目标值进行极值抑制:设置曲率阈值,当曲率大于该阈值时,保留法向量,同时采用随机筛选法保留被过滤的法向量,确保模型在平坦的地方仍能受到较好的约束。

利用筛选的法向量生成控制点:对被保留了法向量的数据点,沿着与法向相同或相反的方向进行移动,生成控制点,表达式如式(2)和式(3)所示:

(2)x⁺=x+u=

\{(x + u_{x}), (y + u_{y}), (z + u_{z})\}

(3)x^-=x-u=

\{(x - u_{x}), (y - u_{y}), (z - u_{z})\}

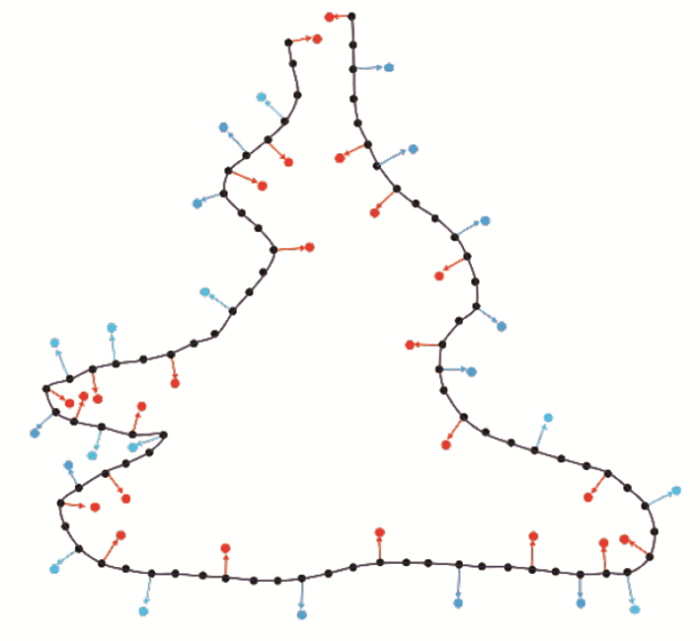
其中:x代表数据点;u为相应数据点对应的法向量;x⁺和 x^- 代表生成的控制点。生成控制点后数据集效果见图3。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 控制点二维示意(红色代表模型内部控制点,蓝色代表模型外部控制点)

Fig.3 2D schematic of control points (red for control points inside the model, blue for control points outside the model)

1.3 重叠域分解

本文采用体素化的方式对域进行划分,并在相邻域之间设置域的重叠度,以实现域间的信息传递,保证域间信息的连续变化。体素化的方式使得域在数据空间均匀分布,每个数据点所在域的坐标由式(4)和式(5)所示:

(4)

\begin{array}{l} I n d e x X = {(x - x_{m i n}) / [v_{x} \times (1.0 - ρ)]} \\ I n d e x Y = {(y - y_{m i n}) / [v_{y} \times (1.0 - ρ)]} \\ I n d e x Z = {(z - z_{m i n}) / [v_{z} \times (1.0 - ρ)]} \end{array}

(5)

\begin{array}{l} I n d e x X_{n e x t} = {(x - x_{m i n} - v_{x} \times ρ) / [v_{x} \times (1.0 - ρ)]} \\ I n d e x Y_{n e x t} = {(y - y_{m i n} - v_{y} \times ρ) / [v_{y} \times (1.0 - ρ)]} \\ I n d e x Z_{n e x t} = {(z - z_{m i n} - v_{z} \times ρ) / [v_{z} \times (1.0 - ρ)]} \end{array}

(6)v_index=IndexX+X_num×(IndexY+Y_num×IndexZ),

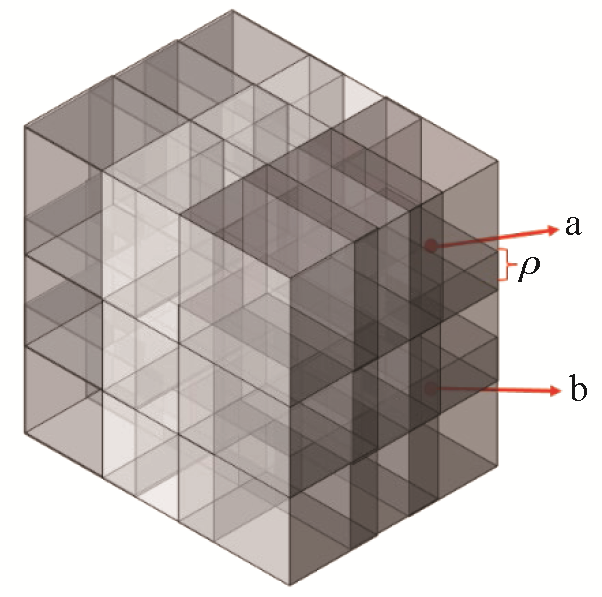
其中:IndexX、IndexY、IndexZ分别代表点所在域的坐标,IndexX_next、IndexY_next、IndexZ_next判断该点是否同时位于其他域内;ρ 代表域间重叠度;x、y、z 表示该点的坐标值;x_min、y_min、z_min表示数据在坐标轴上的最小值;v_x、v_y、v_z 表示子域的大小;X_num、Y_num表示坐标轴上域的数量;v_index是域的索引,通过式(6)进行转换。域重叠示意见图4。如图4中数据点a和数据点b处在多个域有重叠部分,因此相较于原始数据规模,参与计算的点的数量总体增加,但是由于每个域独立求解,整体计算成本比原始数据集大幅度降低。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 域重叠示意

(ρ表示域重叠部分)

Fig.4 Domain overlap

(ρ denotes domain overlap)

1.4 基于径向基函数构建隐式方程

论文采用径向基函数(radial basis function,RBF)作为核函数构建隐式方程。径向基函数的一般形式可以表示为:

(7)φ

(x)

=φ

(‖ x - x_{c} ‖)

其中:函数 φ 是一个关于距离的非线性函数,具体表现形式根据问题的要求而变化;x为输入空间中的一个数据点;x_c为径向基函数的中心点。本节基于函数 φ 构造隐式分布函数 s $(x)$ ,其中利用控制点构建模型表面波动约束,并求解子域分布函数。

1.4.1 利用控制点构建表面波动约束

广义RBF插值函数形式为:

(8)s

(x)

\overset{N}{\sum_{j = 1}}

w_jφ

(x, x')

其中:w_j是权重系数矩阵;φ(x,x') 是径向基函数。径向基函数被定义为:

(9)φ(x,x')=φ(r),r=‖x-x'‖₂,

其中:‖x-x'‖₂是R³上的欧几里得范数。

给定空间R³中仅含坐标信息的标量数据集 X= ${\{x_{i}, s (x_{i})\}}_{i = 1}^{N}$ ,通过构建空间分布函数s $(x)$ 隐式地模拟地质表面,其中x= $(x, y, z)$ 是三维空间中的标量数据点。设存在s $(x)$ ,在数据集 X 上满足:

(10)s

(x)

=0, x∈X,

令M表示函数s表征的地质表面,则函数s隐式定义M,即:

(11)M=

\{x \in R^{3}, s (x) = 0\}

因此,地质表面重建可以描述为在 M 上求解以径向基函数为核函数的标量函数 s $(x)$ 。

复杂地质表面波动幅度大,在缺少约束的情况下,会生成畸形模型。为避免该问题,通过控制点构建表面波动约束,控制模型边界。

由式(2)和式(3)生成的控制点可以详细定义为:

(12)x⁺=

\{(x_{x} + ξ \frac{\partial s (x)}{\partial x}), (x_{y} + ξ \frac{\partial s (x)}{\partial y}), (x_{z} + ξ \frac{\partial s (x)}{\partial z})\}

(13)x^-=

\{(x_{x} - ξ \frac{\partial s (x)}{\partial x}), (x_{y} - ξ \frac{\partial s (x)}{\partial y}), (x_{z} - ξ \frac{\partial s (x)}{\partial z})\}

其中:ξ 是自定义的一个空间偏移参数; $\frac{\partial s (x)}{\partial x}$ 、 $\frac{\partial s (x)}{\partial y}$ 和 $\frac{\partial s (x)}{\partial z}$ 是隐函数 s $(x)$ 在 x 的一阶偏导数。包含控制点的数据集定义为:{x_i,s(x_i) $}_{i = 1}^{u}$ ,{x_i+ξÑs(x_i),s(x_i) $}_{i = u}^{u + σ}$ ,{x_i-ξÑs(x_i),s(x_i) $}_{i = u + σ}^{u + σ + τ}$ 。

此时式(10)可以表述为:

(14)

\{\begin{array}{l} s (x) = 0, 点 x 属 于 地 质 表 面 点 \\ s (x) \neq 0, 点 x 属 于 控 制 点 \end{array}

标量函数 s $(x)$ 的取值如下:

(15)

\{\begin{array}{l} s (x_{i}) = 0, & i = 1,2, \dots, u, \\ s (x_{i}) = 0.5, & i = u + 1, u + 2, \dots, u + σ, \\ s (x_{i}) = - 0.5, & i = u + σ + 1, \dots, u + σ + τ 。 \end{array}

1.4.2 构造子域插值函数

结合式(8)和式(15),可以得到子域分布函数的详细定义:

(16)

[\begin{array}{l} φ \\ φ^{+} \\ φ^{-} \end{array}]

[\begin{array}{l} a \\ b \\ c \end{array}]

[\begin{array}{l} 0 \\ 0.5 \\ - 0.5 \end{array}]

其中,

(17)φ=

{[\begin{array}{l} φ_{11} & \dots & φ_{1 (u + σ + τ)} \\ ︙ & ⋱ & ︙ \\ φ_{u 1} & \dots & φ_{u (u + σ + τ)} \end{array}]}_{u \times (u + σ + τ)}

(18)φ⁺=

{[\begin{array}{l} φ_{(u + 1) 1} & \dots & φ_{(u + 1) (u + σ + τ)} \\ ︙ & ⋱ & ︙ \\ φ_{(u + σ) 1} & \dots & φ_{(u + σ) (u + σ + τ)} \end{array}]}_{σ \times (u + σ + τ)}

(19)φ^-=

{[\begin{array}{l} φ_{(u + σ + 1) 1} & \dots & φ_{(u + σ + 1) (u + σ + τ)} \\ ︙ & ⋱ & ︙ \\ φ_{(u + σ + τ) 1} & \dots & φ_{(u + σ + τ) (u + σ + τ)} \end{array}]}_{τ \times (u + σ + τ)}

(20)a=

{[w_{1}, \dots, w_{u}]}^{T}

(21)b=

{[g_{1}, \dots, g_{σ}]}^{T}

(22)c=

{[h_{1}, \dots, h_{τ}]}^{T}

。

本文采用Multiquadric函数作为基函数,即 φ $(r)$ = $\sqrt{ε^{2} + r^{2}}$ ,因为它适用于更广泛空间范围内的建模问题,可以适应形状复杂的地质体,能够处理地质体的边界和细节。通过求解上述的RBF线性方程得到权重系数 w,将权重系数带入到 RBF 方程中,就可以得到插值函数 s $(x)$ 。

数据空间被分解成多个子域,假定 F= $\{F_{1}, F_{2}, \dots, F_{n}\}$ ,代表数据空间中被划分的子域,上述求解权重系数的问题就变成了在每个子域 F_i求解插值函数 s_i $(x)$ :

(23)S=

\{s_{1} (x), \dots, s_{n} (x)\}

\{[\begin{array}{l} φ_{1} \\ φ_{1}^{+} \\ φ_{1}^{-} \end{array}] \cdot [\begin{array}{l} a_{1} \\ b_{1} \\ c_{1} \end{array}], \dots, [\begin{array}{l} φ_{n} \\ φ_{n}^{+} \\ φ_{n}^{-} \end{array}] \cdot [\begin{array}{l} a_{n} \\ b_{n} \\ c_{n} \end{array}]\}

2 实验结果与分析

2.1 数据简介

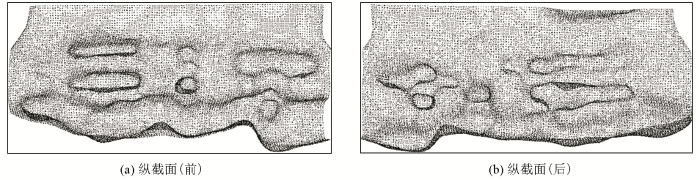
本文使用的地质数据来源于矿体,是仅包含三维坐标的标量数据,该数据集包含了824 073个数据点,空间尺度为4 720 m×9 604 m×4 450 m。本文以该标量数据集为基础,求解以径向基函数为核函数的隐式方程,点的空间分布和地质的整体形态见图5和图6。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 纵截面

Fig.5 Longitudinal section

图6

新窗口打开| 下载原图ZIP| 生成PPT

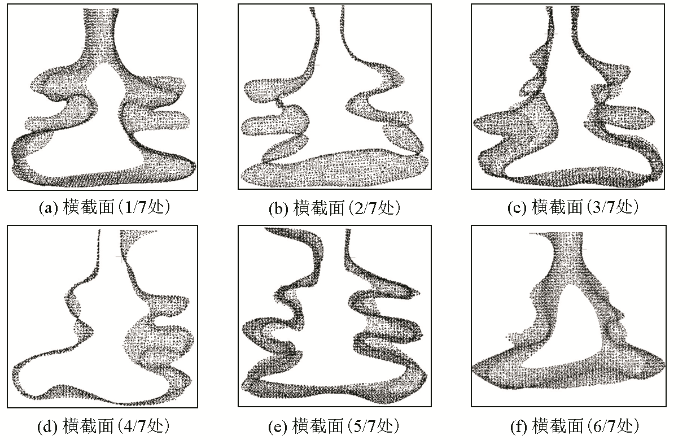
图6 横截面

Fig.6 Cross section

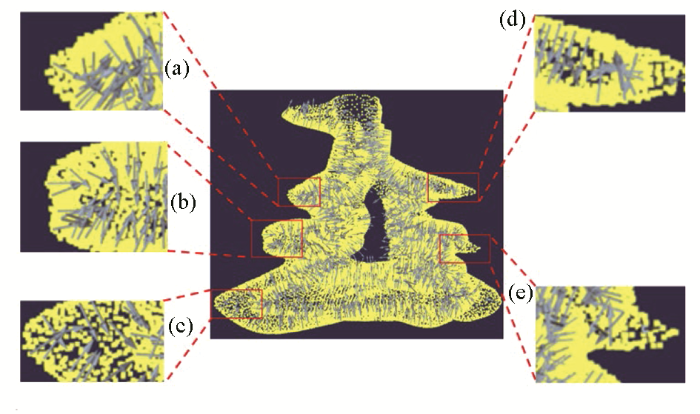
本文数据描述了一个矿体模型,点的空间分布比较均匀,但是该模型较为复杂。图5a~b以纵截面的形式展示了矿体的形态,其两侧存在较多凸出区域,并且一部分凸出区域的边界存在相交情况,该区域法向量的处理具有一定困难性。图6a~f展示了矿体不同位置的横截面形态,表明在地质体的侧面位置,表面起伏大,地质体的凸出区域明显,并且凸出区域在空间分布关系上邻近。

2.2 法向校正实验

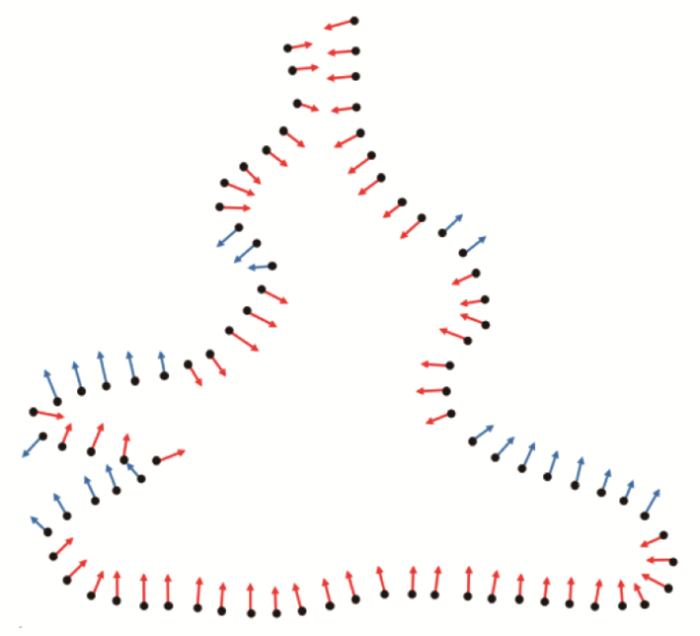
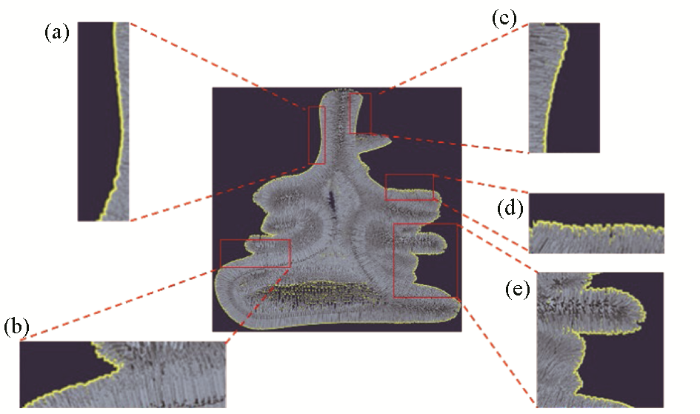
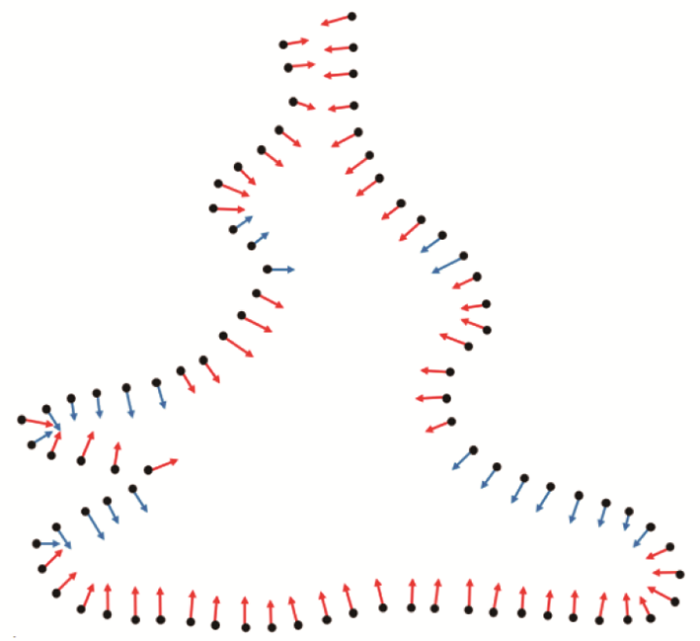
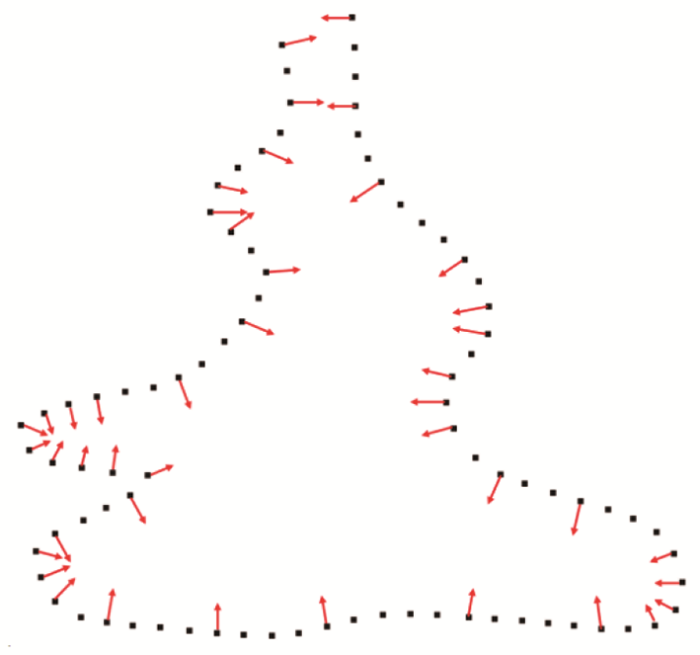
固定视点的法向量效果和示意分别见图7和图8。图7中给出了5个区域,这些区域中大部分法向均指向模型外部,需要调整该部分法向量;图8是二维的切面示意图,红色箭头代表正确的法向量,蓝色箭头代表错误的法向量。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 固定视点的法向量

(a~e为法向量指向模型外部的区域放大效果)

Fig.7 Normal vectors for fixed viewpoints

(a~e represent the amplification effect of the normal vector pointing towards the external area of the model)

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 固定视点的法向量切面示意

Fig.8 Schematic diagram of normal vector section with fixed viewpoint

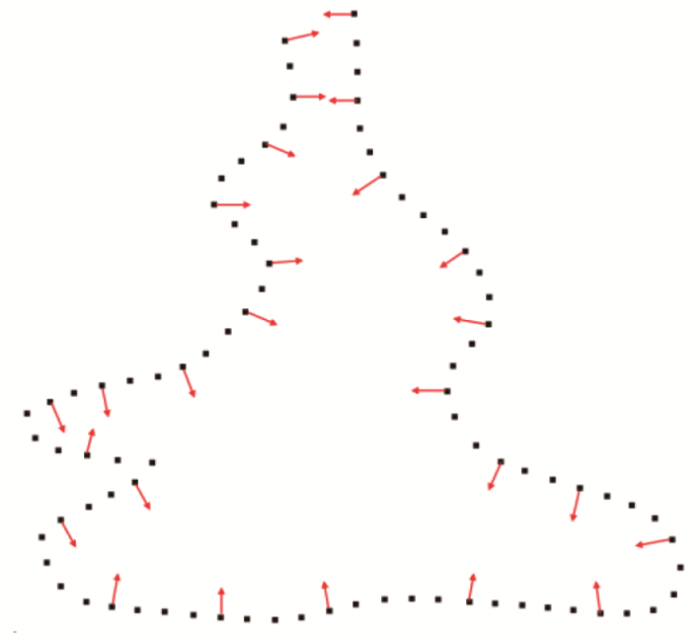
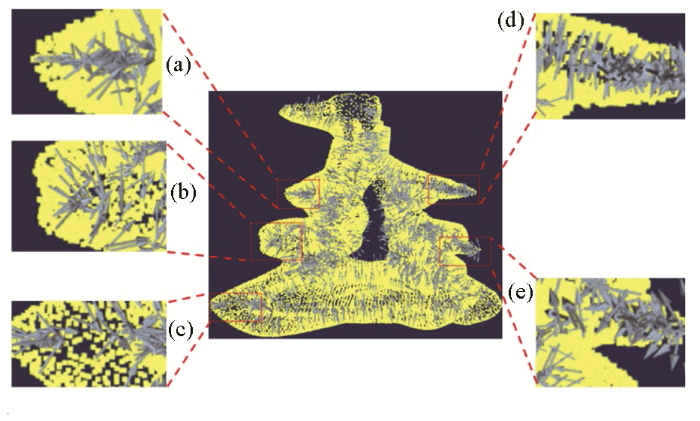
对无序的法向量进行校正后的效果和示意见图9和图10:图9中5个区域对应图7,对应模型的可视化效果。图10中,代表错误法向量的蓝色箭头得到修正,指向模型内部。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 校正的法向量

(a~e为图7对应区域校正法向后的放大效果)

Fig.9 Corrected normal vector

(a~e represent the amplification effect after correcting the normal vector in the corresponding region of Fig.7)

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 校正的法向量切面示意

Fig.10 Schematic diagram of the corrected normal vector section

通过对比图7和图9中a~e这5个区域,明显看出固定视点的方法仅仅在求法向量时将视点固定在模型的内部,实际上法线的指向仍然是无序的。图9也验证了本文提出的基于局部质心校正法向方法的有效性。

2.3 法向量筛选实验

法向量的筛选方式和模型精度有着密切关系。在表面平坦的区域,法向量的方向一定程度上是相似的,仅需选取少量的法向量即可表征该区域的特点。然而当模型有明显的突起或表面有显著弯折的情况时,该区域则需要更多的法向量对模型曲面进行质量和细节的控制。当模型表面有明显弯折情况时,随机筛选方式在该区域选取的法向量数量不足,而极值筛选方式则弥补了该缺点。

随机筛选的结果和切面示意见图11和图12,在曲面弯曲程度不同的区域,法向量的分布仍然是比较均匀的。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 法向量随机筛选

(a~e为法向量随机筛选的区域放大效果)

Fig.11 Random selection of normal vectors

(a~e are the region amplification effects of random normal vector screening)

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 法向量随机筛选切面示意

Fig.12 Schematic of a randomly selected section of a normal vector

极值筛选过滤后的法向量和切面示意见图13和图14,在曲面弯曲程度较大的区域,保留的法向量数量更多。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 法向量极值筛选

(a~e为法向量极值筛选的区域放大效果)

Fig.13 Normal vector extremum selection

(a~e are the region amplification effects of normal vector extremum screening)

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 法向量极值筛选切面示意

Fig.14 Schematic of normal vector extreme value selection cuts

以图11和图13中a~e这5个区域保留的法向量为例,相同区域法向量数量对比情况见图15,相同区域,极值筛选方式保留了更多地质弯曲程度较大区域的法向量,这对后续模型曲面质量的提高和边界控制起到了至关重要的作用。

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 5个法向量随机筛选和极值筛选区域内法向量数量

Fig.15 Number of normal vectors in the region of random and extreme selection of normal vectors

2.4 模型结果分析

本节结果分析对比分为以下几个方面:①本文提出的方法和Surfe开源库进行对比,验证本文方法的可行性;②对比法向量两种筛选、两种方法生成的模型效果图,验证极值筛选方法的有效性;③验证在极值筛选方式下,点的数量和模型效果的关系。

2.4.1 本文方法与Surfe对比

矩阵复杂度对内存占用有明显影响,当矩阵阶数增加一个数量级时,其内存占用往往呈现出幂增长趋势,同时也会显著增加程序运行时间。该小节通过对比矩阵阶数以验证本文方法在降低内存占用和减少运行时间的可行性,结果见表1。

表1 矩阵复杂度对比

Table 1 Matrix complexity comparison

方法	矩阵阶数
Surfe	(4×N)²
本文方法	(N/10)²

新窗口打开| 下载CSV

本文的矩阵阶数相比Surfe显著降低,尤其当数据量较为庞大时,本文的方法在内存占用上具有明显的优势,更便于后续求解插值矩阵。

通过与开源算法库Surfe的模型生成时间进行比较,验证本实验的可行性,结果见表2。

表2 运行时间对比

Table 2 Run time comparison

方法	不同数据量的运行时间
方法	1000	3200	5000	11000	50000
Surfe	90 s	40 min	2.5 h	22 h
本文方法 (非并行)	0.91 s	19.45 s	29.72 s	67.58 s	268.3 s
本文方法 (并行)	0.35 s	3.3 s	5.2 s	15.8 s	120.6 s

新窗口打开| 下载CSV

上述结果均在CPU型号为12th Gen Intel(R) Core(TM) i9-12900H 2.50 GHz,内存为32 GB的电脑下生成。实验证明,在相同数据规模下,本文对比Surfe开源库有了明显的速度提升,尤其是在规模比较大的数据集上,当数据量在50 000左右时,Surfe开源库会因为内存不足等原因退出程序。得益于域分解策略,该实验可以借助并行算法对隐式矩阵进行同步求解,同时仅利用部分法向量信息,减少了内存的消耗,提高了隐式方程的求解效率。

2.4.2 随机筛选和极值筛选下模型效果对比

法向量采用随机筛选法和极值筛选法生成的模型效果见图16。

图16

新窗口打开| 下载原图ZIP| 生成PPT

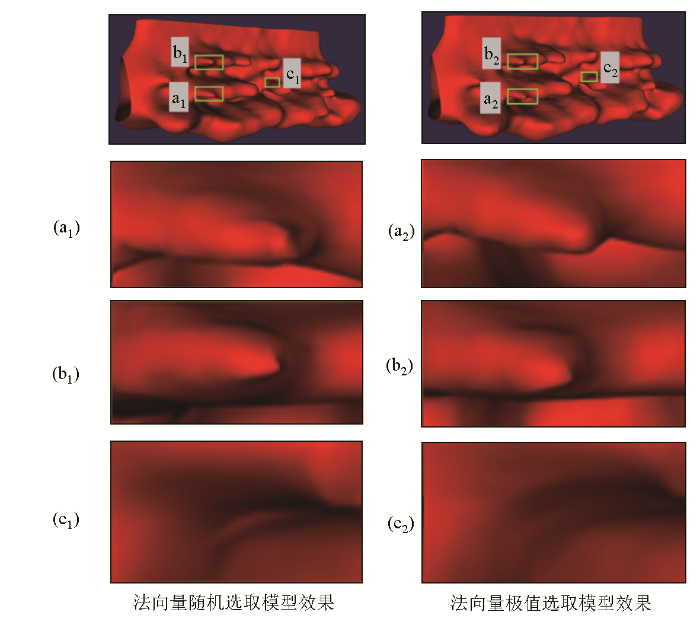
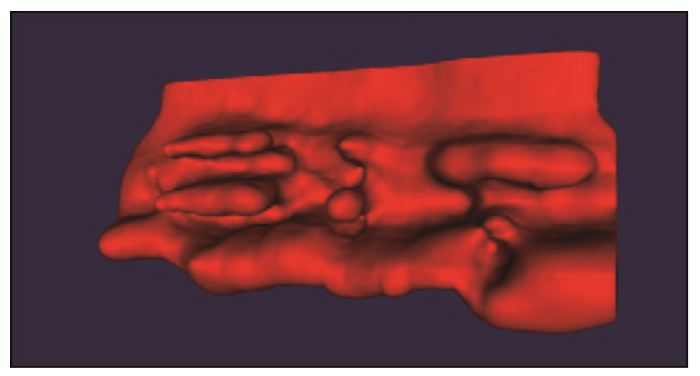
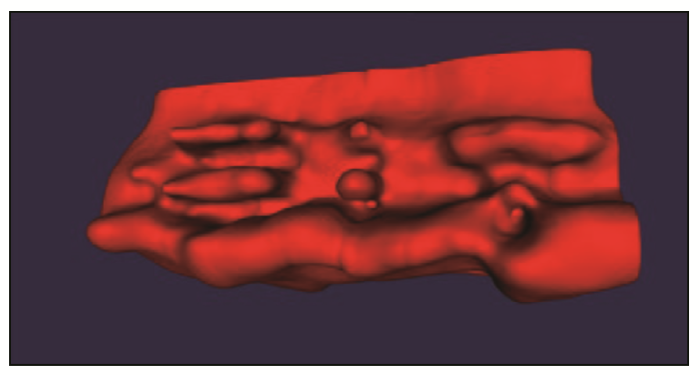
图16 法向量随机筛选和极值筛选结果对比

(a~c为局部放大区域)

Fig.16 Comparison of the results of random and extreme value selection of normal vectors

(a~c are locally enlarged areas)

使用随机筛选的法向量在模型细节处,如曲面弯折程度较大的地方有着较为明显的瑕疵:如图16中的a₁、a₂区域所示,随机筛选法生成的模型效果相较于极值筛选法,在a区域的顶端有明显的突起情况;b₁、b₂、c₁、c₂区域,极值筛选法向量的方法在曲面连接处处理效果更好,模型边界更加平滑、清晰。实验结果证明通过极值筛选的法向量,可以较好地改善随机筛选所带来的问题。

2.4.3 不同数据量下模型效果对比

本文通过对比4个不同采样规模下的数据集生成的模型平均曲率和可视化效果来验证不同规模的数据集对模型质量的影响情况。

以模型平均曲率来衡量模型的光滑程度,当模型的平均曲率较高时,说明表面起伏较大,代表着不平滑的部分;当平均曲率较低时,表示模型更加平滑。结果见表3。不同数据量下模型可视化效果见图17~20。表3和图17~20表明数据量的提升相应地改善了模型的质量,模型整体过渡更加平滑,减少了因域分解产生的表面信息不连贯的情况。

表3 不同数据量下模型的平均曲率

Table 3 Mean curvature of the model for different data volumes

参数	数据量
参数	1000	3200	5000	11000
运行时间/s	0.35	3.3	5.2	15.8
平均曲率/10^-4	8.921	4.972	3.519	1.377

新窗口打开| 下载CSV

图17

新窗口打开| 下载原图ZIP| 生成PPT

图17 1 000个数据的模型效果

Fig.17 Model effect for 1 000 data points

图18

新窗口打开| 下载原图ZIP| 生成PPT

图18 3 200个数据的模型效果

Fig.18 Model effect for 3 200 data points

图19

新窗口打开| 下载原图ZIP| 生成PPT

图19 5 000个数据的模型效果

Fig.19 Model effect for 5 000 data points

图20

新窗口打开| 下载原图ZIP| 生成PPT

图20 11 000个数据的模型效果

Fig.20 Model effect for 11 000 data points

3 总结

本文提出了一种结合域分解策略的地质表面模型隐式生成方法,该方法能够大幅度降低隐函数的计算成本。对于缺乏地质约束信息的标量数据,提取数据法向量可以建立地质约束,实现隐函数对模型边界的良好控制,避免出现畸形模型。

因此,本文针对地质模型可视化方面的工作可以分为以下几点:

1)采用重叠域分解策略,并实现并行算法,保证域边界信息的一致性、降低隐式矩阵的规模、提高建模效率。

2)提出基于局部质心的法向校正方法,统一法向量方向指向模型内部,是正确生成控制点的前提。

3)基于法向量生成控制点构建表面波动约束,为隐函数增加约束条件,确保模型具有较高质量。

本文中,域分解策略仅采用了简单的均分空间的思想,需要人工根据模型的特点进行划分,隐函数中引入的法向量信息也无法处理特定的地质现象,如断层和尖灭等。后续工作可以重点考虑域分解策略和引入额外地质信息,在域分解阶段保证数据分布的合理性,引入额外信息处理特定地质现象,保证模型效果。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

苗晋祥, 吴继臣, 朱学立, 等.

三维地质建模技术的发展历史与未来展望

[G]// 河南地球科学通报2008年卷(下册),河南省地质调查院, 2008.