0 引言
横波速度在流体识别、叠前反演、AVO分析和储层预测中是不可或缺的一个重要参数,但是在实际生产过程中,受限于生产成本以及技术条件的原因,许多井中往往缺乏横波速度信息,尤其是在老井中,在这种情况下,如何对横波速度进行高精度的预测就成了地球物理中重要研究内容之一。
目前,横波速度预测的主要方法有经验公式法、神经网络法以及岩石物理模型法[4]。经验公式法主要是基于研究工区的岩心测量实验数据和测井数据,拟合横波速度和对横波速度敏感的其他弹性参数之间的线性或者非线性关系式,Castagna等[5]、Han等[6]、Greenberg等[7]通过此方法利用拟合的关系式来对横波速度进行预测。神经网络法是利用大量的测井数据和实验数据对神经网络进行训练,可以得到横波速度和其它参数之间的非线性关系,Rajabi等[8]、王晓光[9]、Zhang等[10]利用此关系来对横波速度进行预测。岩石物理模型法是基于岩石的组成成分和结构,构建岩石弹性参数和岩石微观特征对其进行等效建模计算的方法,Xu等[11-12]、Lee等[13]、张广智等[14]利用此方法进行横波速度的预测。对比3种不同的横波预测方法,经验公式法和神经网络法都非常依赖于大量的测井数据或者岩心实验数据,都属于数据驱动的预测方法,预测结果代表了输入数据样本的规律,并没有明确的物理意义,预测结果通常都具有区域性,如果输入数据样本的数量较少或者数据质量不好,则预测结果并不可信,可推广性比较差。岩石物理建模法则是基于弹性波传播理论,根据岩石的组成成分和微观结构,基于一定的假设对岩石进行建模,基于建立的岩石物理模型对横波速度进行预测,具有明确的物理意义和推导过程,可推广性好,因此基于岩石物理模型的横波预测法已经成为了主流的横波预测方法[15]。
本文以四川盆地FL地区为例探讨岩石物理建模技术在横波预测以及后续叠前反演中的应用。首先,基于川东南地区致密砂岩特性分析,优选适用于低孔、低渗致密砂岩的岩石物理模型,并进行致密砂岩岩石物理建模;其次,将建立的致密砂岩岩石物理模型应用于实际工区,进行横波速度预测,预测误差为3.36%,此精度可以很好地应用于实际;最后,通过测井数据统计,优选对致密砂岩敏感的泊松比参数,对川东南FL地区进行高精度叠前反演,通过预测的泊松比数据体对河道砂岩内幕进行精细刻画及预测。
1 岩石物理建模流程方法
本章主要讲述了岩石物理建模的主要流程,出于对川东南致密砂岩低孔低渗、孔隙流体不均匀混合等问题的考虑,有针对性地选择合适的岩石物理模型进行建模,HS模型相比于VRH模型计算得到的上下限更加收敛,与实际测量数据更加吻合,王斌等[16]的岩石物理实验也证明了这一观点,因此本文优选HS模型进行岩石基质模量的计算。针对致密砂岩低渗透率以及孔隙流体不均匀混合的问题,优选Domenico模型进行孔隙混合流体模量的计算,其中本文中流体模量不同于其他岩石物理建模流程中选用的固定值,而是利用经验公式计算出来与深度有关的值,这样更加符合地下实际情况。针对致密砂岩低孔隙度的特征,本文优选Lee-Pride模型进行岩石骨架模量的计算,Lee-Pride模型可以通过调节固结参数α的值来描述岩石骨架和岩石基质之间的关系,并且在岩石物理实验测量结果中也表明,Krief模型和Nur模型并不能准确描述孔隙度小于15%的岩石骨架与岩石基质之间的关系,通过张佳佳等[17]的实验数据可以佐证这个结论,由于本研究工区的致密砂岩孔隙度均小于15%,因此优选Lee-Pride模型进行岩石骨架模量的计算。
1.1 岩石基质模量
在已知岩石基质组成矿物的弹性模量和体积分数的条件下,可以估算出岩石基质等效弹性模量,常用的公式有VRH公式和Hashin-Shtrikman公式[18],针对致密砂岩而言,HS公式计算出来的上下限比VRH计算出来的上下限更加收敛,与实际数据更加吻合。HS公式如下:
式中:KHS±和μHS±分别为岩石基质等效体积模量和剪切模量的上下限,下标1和2代表不同的两种矿物成分, K、μ、f分别代表矿物成分的体积模量、剪切模量和体积分数。
按照Hill取算数平均的思想[19],对HS公式的上下限取平均计算岩石基质等效弹性模量,公式如下:
式中:K0和μ0代表岩石基质等效体积模量和剪切模量,KHS+和μHS+为式(1)计算得到的上限,KHS-和μHS-为式(1)计算得到的下限。
1.2 致密砂岩孔隙流体模量
式中:Kf为混合流体等效体积模量,Kw和Kg分别为岩石孔隙中水和气的体积模量,Sw为岩石孔隙的含水饱和度。
Wood等[22]给出混合流体等效密度的计算公式如下:
式中:ρf为混合流体等效密度,ρw和ρg是岩石孔隙中水和气的密度,Sw为岩石孔隙的含水饱和度。
在常规的岩石物理建模流程中,水、气的体积模量和密度一般给的都是定值,但是在实际地下情况中,随着埋深的增加,水、气的体积模量和密度必定是随着深度和压力变化的,因此在本文岩石物理建模流程中孔隙中水和气的体积模量和密度均通过刘雯林[23]总结的关系式给出,关系式如下:
式中:H为深度,单位是km。
1.3 岩石骨架等效弹性模量
计算岩石骨架模量已有许多针对不同情况的等效模型,比如说Krief模型、Nur模型和Pride模型等[24⇓-26],针对本文研究的川东南致密砂岩低孔隙度的特征,Krief模型、Nur模型在计算孔隙度小于15%的岩石时误差均比较大,适用于孔隙度比较高的岩石,而本文研究工区中的致密砂岩的孔隙度一般都小于15%,因此Krief模型和Nur模型均不适用于计算本工区的岩石骨架模量。Pride在岩石基质中加入了孔隙影响的同时引入了固结系数的概念,这个固结系数α取决于岩石的等效压力和岩石固结程度,通过固结参数的大小来更加准确地控制岩石基质和岩石骨架的关系,Lee在Pride模型基础上进一步进行修正,得到Lee-Pride模型,针对四川盆地致密砂岩此模型计算出来的值相比于Krief模型、Nur模型更加准确,张佳佳等[27]文章中的测试结果也佐证了这一结论,因此本文采用Lee-Pride模型进行岩石骨架等效模量的计算,公式如下:
式中: Kdry和μdry分别为岩石骨架等效体积模量和剪切模量,K0和μ0分别为岩石基质等效体积模量和剪切模量,φ为孔隙度,α为固结参数,表示岩石的固结程度,这个参数与岩石孔隙形状和压力均有关,对于砂岩来说,一般取2~20。
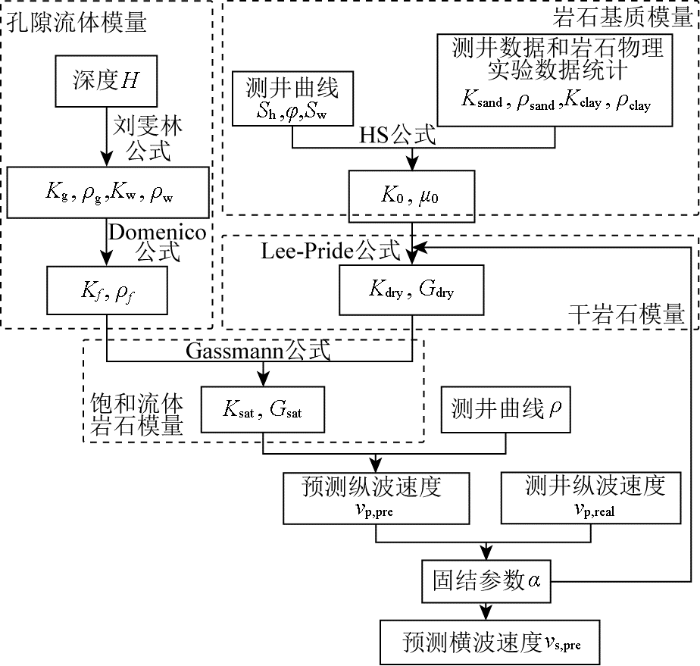
1.4 岩石物理建模流程和示意
图1
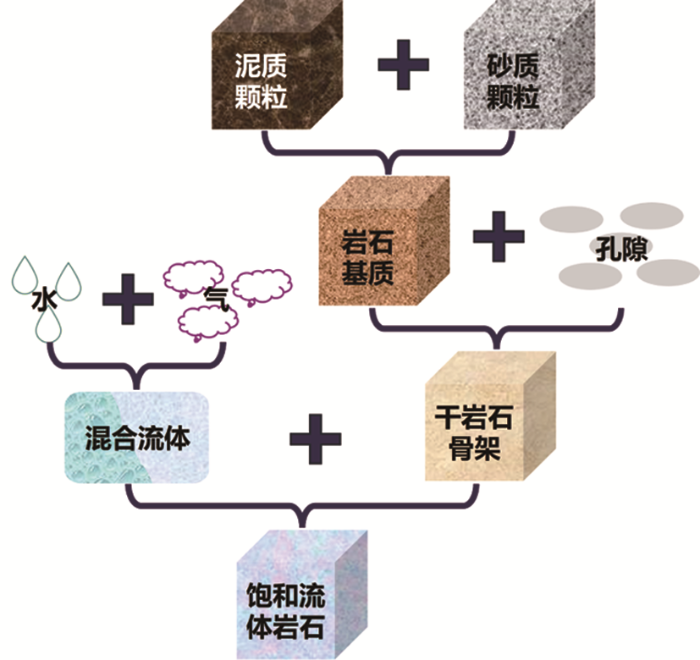
图2
2 岩石物理模型测试分析
表1 石英、黏土和流体的体积模量、剪切模量和密度
Table 1
| 类型 | 体积模量/GPa | 剪切模量/GPa | 密度/(g·cm-3) |
|---|---|---|---|
| 石英 | 52 | 31 | 2.72 |
| 黏土 | 23 | 7 | 2.54 |
| 气 | 0.001 5 | 0 | 0.002 |
| 水 | 2.2 | 0 | 1.1 |
对本工区内目的层测井数据进行统计,可以得到测井数据中的孔隙度、含水饱和度和泥质含量的最大值、最小值和平均值,具体数值如表2。
表2 测井数据中孔隙度、含水饱和度和泥质含量的最大值、最小值和平均值
Table 2
| 参数 | 最小值 | 最大值 | 平均值 |
|---|---|---|---|
| 孔隙度/% | 2.00 | 12.57 | 4.24 |
| 含水饱和度/% | 3.21 | 100 | 52.10 |
| 泥质含量/% | 1.06 | 62.19 | 21.90 |
针对砂岩Lee-Pride模型中的固结参数α的取值一般为2~20,不考虑极端情况,本文在模型测试过程中固结参数α的取值为6、10、14和18。
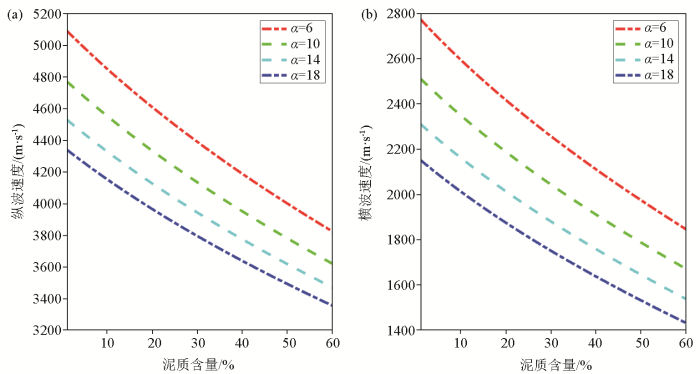
2.1 泥质含量模拟分析
图3
图3
纵波速度(a)和横波速度(b)随泥质含量和固结参数α的变化
Fig.3
Variation of longitudinal(a) and transverse(b) wave velocity with mud content and consolidation parameter α
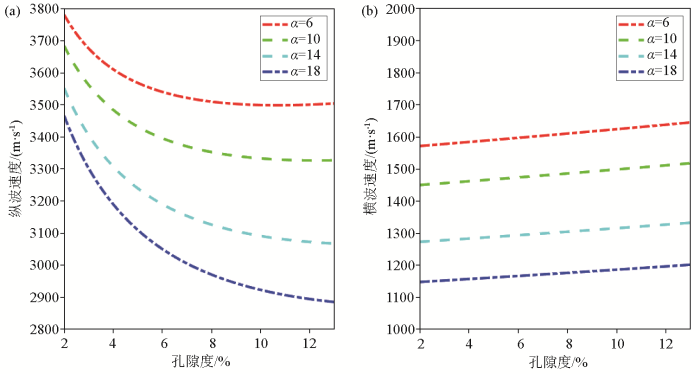
2.2 孔隙度模拟分析
图4
图4
纵波速度(a)和横波速度(b)随孔隙度和固结参数α的变化
Fig.4
Variation of longitudinal(a) and transverse(b) wave velocity with porosity and consolidation parameter α
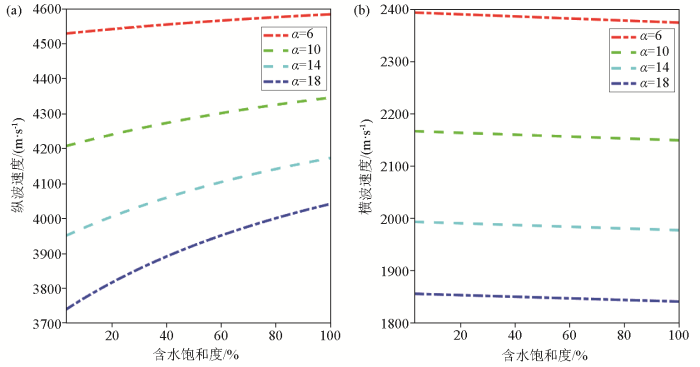
2.3 含水饱和度模拟分析
图5
图5
纵波速度(a)和横波速度(b)随含水饱和度和固结参数α的变化
Fig.5
Variation of longitudinal(a) and transverse(b) wave velocity with water saturation and consolidation parameter α
3 实例测试
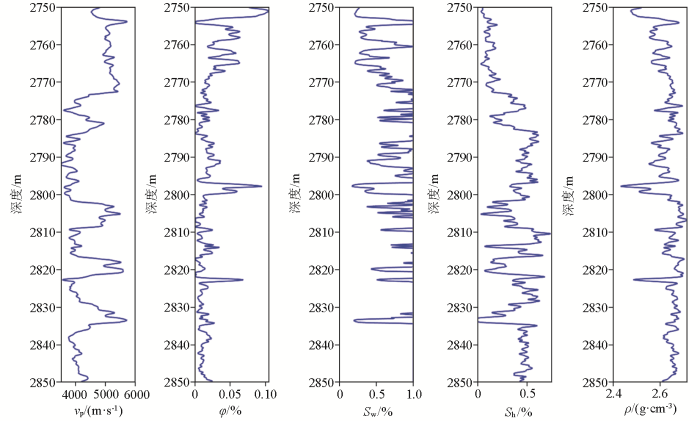
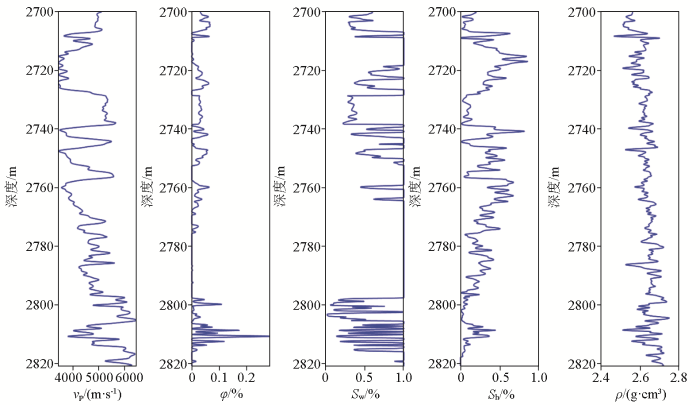
将本文建立的岩石物理模型应用于四川盆地川东南地区A井进行实际数据测试,A井构造位置位于四川盆地川东弧形高陡褶皱带万县复向斜拔山寺向斜中部,以中侏罗统凉高山组二段砂岩油气层段为主要目的层。取A井目的层及上部的围岩进行实际数据测试,深度为2 750~2 850 m,需要的测井数据为纵波速度vp、孔隙度φ、含水饱和度Sw、泥质含量Sh和密度ρ,各测井数据见图6。
图6
图6
岩石物理建模过程中需要A井中的测井数据
Fig.6
Logging data from well A is required for the petrophysical modeling process
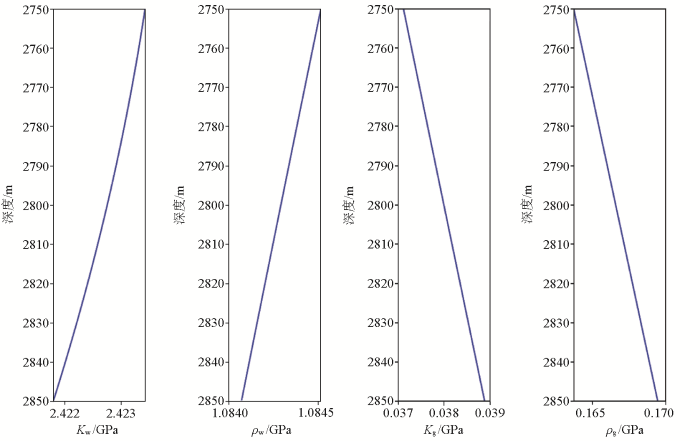
在对实际数据进行岩石物理建模过程中,岩石孔隙中的水和气的体积模量和密度是利用式(5)计算得到的,不同于模型测试过程中是通过测井数据和岩石物理实验得到的常值数据,岩石孔隙中的水和气的体积模量和密度如图7所示,从图中可以看出,孔隙中的水的体积模量Kw和密度ρw随着深度的增加而减小,孔隙中的气的体积模量Kg和密度ρg随着深度的增加而增加。
图7
图7
岩石物理建模过程中孔隙中水和气的体积模量和密度
Fig.7
Bulk modulus and density of water and gas in pores during petrophysical modeling
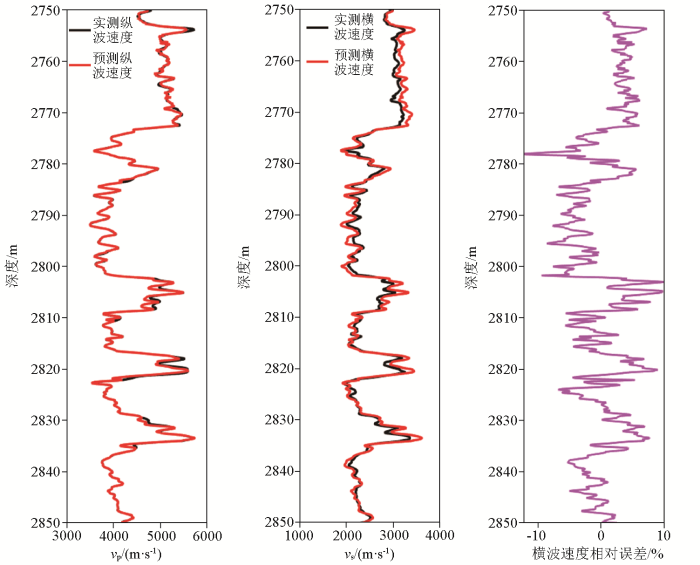
利用A井中的实际测井数据进行岩石物理建模,得到的纵波速度的实测结果和预测结果、横波速度的实测结果和预测结果以及横波速度实测结果和预测结果的相对误差(图8)。结合图6和图8进行分析,将模型的横波预测结果规律和应用于实际井的横波预测结果规律进行对比、取实际曲线中孔隙度和含水饱和度大小接近的点进行对比,可以发现横波速度随着泥质含量的增加而减小,和章节2.1模型测试的结果规律一致;取实际曲线中泥质含量和含水饱和度大小接近的点进行对比,可以发现横波速度随着孔隙度的增加而略微增加,和章节2.2模型测试的结果规律一致;取实际曲线中泥质含量和孔隙度大小接近的点进行对比,可以发现横波速度随着含水饱和度的增加而略微减小,和章节2.3模型测试的结果规律一致;因此可以看出实例测试横波预测结果和模型测试横波预测结果规律一致,交互验证了建立的岩石物理模型的有效性。
图8
图8
A井纵横波实测结果和预测结果以及横波实测结果和预测结果的相对误差
Fig.8
Relative error between measured and predicted longitudinal and transverse wave results and between measured and predicted transverse wave results for well A
对图8实例测试的纵、横波预测结果进行分析,由于是通过拟合预测的纵波速度和实测的纵波速度来得到固结参数α,所以预测的纵波速度和实测的纵波速度对应性很好。预测的横波速度和实测的横波速度吻合的也较好,趋势一致,相对误差绝对值的平均值为3.36%,表明利用此岩石物理模型预测的横波速度是有效的,建立的岩石物理模型可以应用于实际中,可以为后续岩石物理量版的建立、叠前反演以及AVO分析提供一定的指导意义。
4 实际应用
通过实例测试中四川盆地的A井可以验证本文建立的川东南致密砂岩岩石物理模型的有效性,将此方法应用到四川盆地川东南另一口B井,B井中没有实测的横波速度,在岩石物理建模的过程中需要B井中的测井数据(图9)。
图9
图9
岩石物理建模过程中需要B井中的测井数据
Fig.9
The petrophysical modeling process requires the number of logs in well B
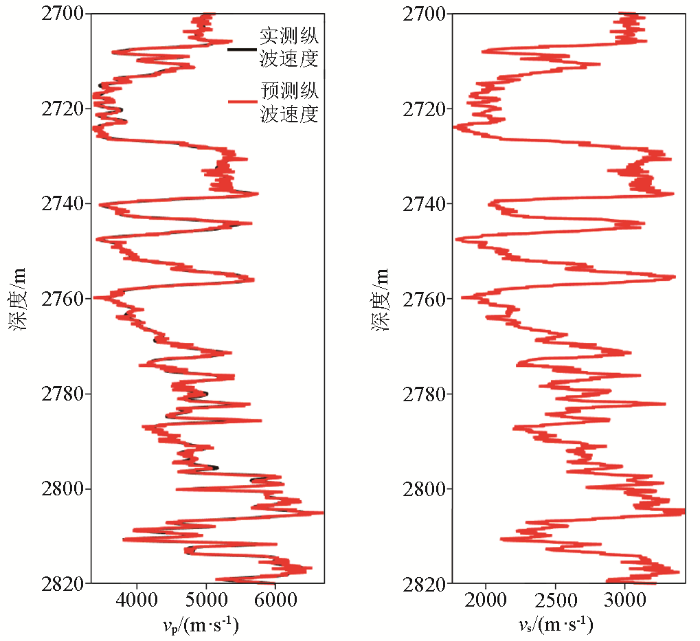
利用B井中已有的测井数据以及建立的岩石物理模型对B井的横波速度进行预测,B井实际的纵波速度、预测的纵波速度和预测的横波速度如图10所示。
图10
图10
B井纵波速度的实测结果和预测结果以及横波速度的预测结果
Fig.10
Measured and predicted longitudinal wave velocities and predicted transverse wave velocities in well B
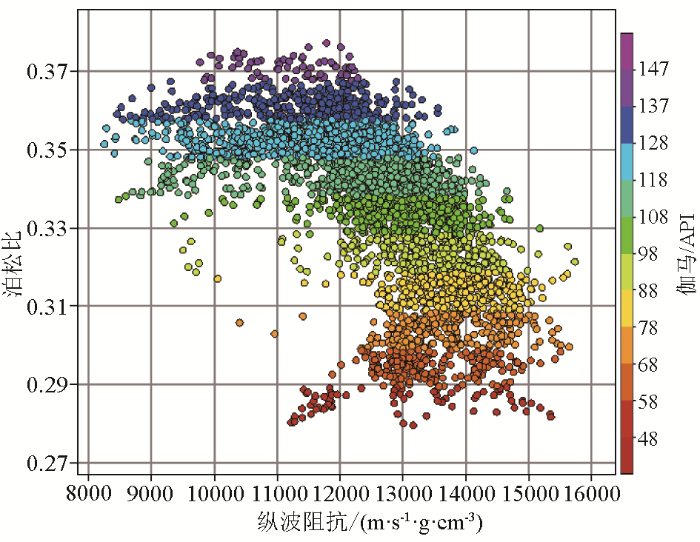
图11
图11
A井泊松比和纵波阻抗交会
Fig.11
Poisson’s ratio and longitudinal wave impedance rendezvous plot for well A
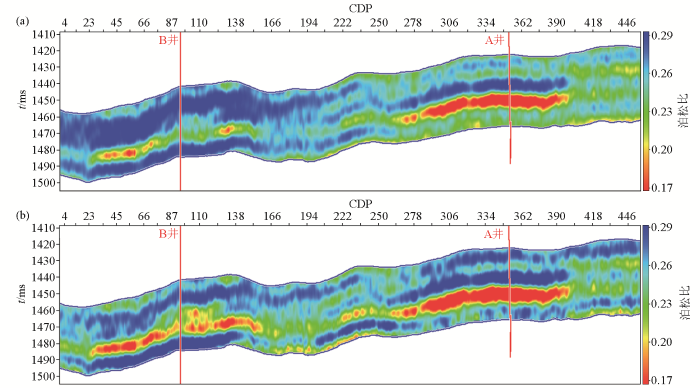
通过上面的分析对此工区进行叠前反演,第一次只使用A井进行反演,第二次同时使用A井和通过岩石物理建模进行横波预测的B井进行反演,并将反演得到的数据体转换成泊松比数据体,两次泊松比的对比结果如图12所示,其中图12a是只使用A井得到的泊松比结果,图12b是同时使用A井和B井得到的泊松比对比。对比图12a、b可以看出,只使用A井进行反演得到的结果并不能完全刻画本工区河道砂的位置以及边界,在B井所在区域周边的砂体在反演的过程中由于没有B井的控制导致边界不清晰,连续性差,而同时使用A井和B井进行反演得到的结果可以清楚地刻画本工区河道砂的边界,在B井所在区域周边的砂体在反演的过程中由于受到B井的控制导致边界清晰、连续性好,且砂体分布平面图对应性好。
图12
图12
使用A井(a)和同时使用A、B井(b)得到的泊松比反演对比
Fig.12
Comparison of Poisson’s ratio inversions obtained using well A(a) and also using well A and B(b)
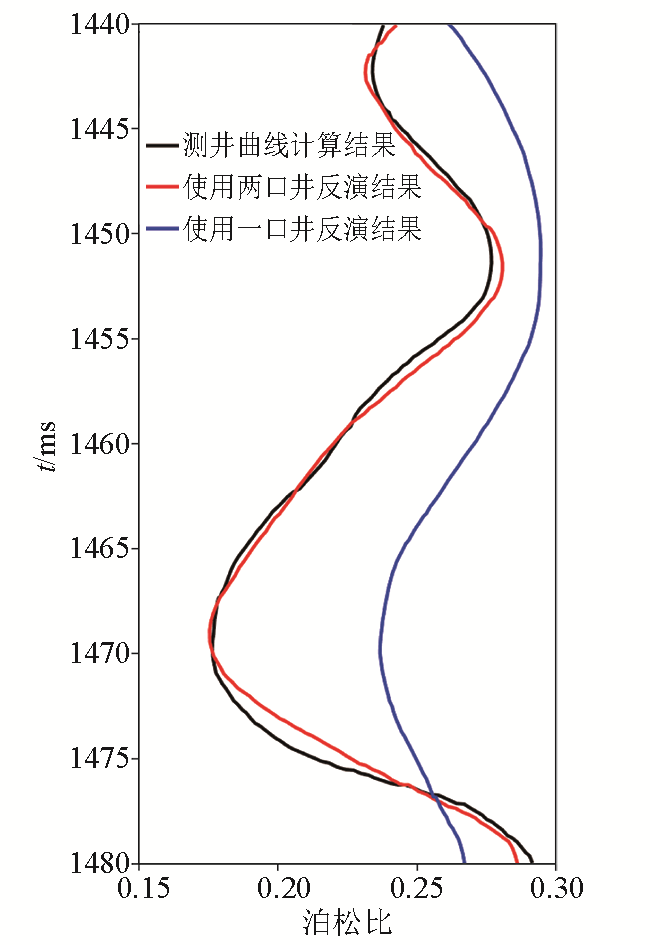
图13
图13
原始泊松比测井曲线和两次泊松比反演结果曲线对比
Fig.13
Comparison chart of original Poisson’s ratio logging curve and two Poisson’s ratio inversion result curves
5 结论
本文以川东南凉高山组致密砂岩为研究对象,基于凉高山组致密砂岩低孔低渗等特性进行岩石物理建模,并将其应用于实际工区,通过对结果分析得出以下几点结论:
1)基于致密砂岩低孔低渗的特征优选Domenico模型、Lee-Pride模型进行建模,孔隙流体模量和密度给定的是与深度有关变化的值,更加符合实际地下情况,以此为基础建立了一个适用于川东南凉高山组致密砂岩的岩石物理模型;
2)将建立的致密砂岩岩石物理模型应用于四川盆地陆相致密砂岩某口气井进行横波预测,实例井的横波预测结果规律和测试模型的横波预测结果规律一致,并且实例井实测横波和预测横波之间的误差为3.36%,这共同验证了本文建立的致密砂岩岩石物理模型的准确性以及有效性;
3)利用建立的致密砂岩岩石物理模型对此工区内的井进行横波预测,随后进行高精度叠前反演,对比两次反演剖面结果以及井上和两次反演的泊松比曲线结果,验证了建立致密砂岩岩石物理模型的有效性和必要性。
参考文献
A rock physics model for tight gas sand
[J].
Rock-physics modeling guided by depositional and burial history in low-to-intermediate-porosity sandstones
[J].
改进型随机斑块饱和模型及其在致密气层检测中的应用
[J].
Modified continuous random patchy-saturation model in tight gas detection
[J].
基于改进Xu-White模型的富有机质页岩横波预测方法研究
[J].
Research on transverse wave prediction method of organic-rich shale based on improved Xu-White model
[J].
Relationships between compressional-wave and shear-wave velocities in clastic silicate rocks
[J].
Effects of porosity and clay content on wave velocities in sandstones
[J].
Shear-wave velocity estimation in porous rocks:Theoretical formulation,preliminary verification and applications
[J].
Intelligent approaches for prediction of compressional,shear and Stoneley wave velocities from conventional well log data:A case study from the Sarvak carbonate reservoir in the Abadan Plain(Southwestern Iran)
[J].
自适应BP神经网络在横波速度预测中的应用
[J].
Application of self-adaptive BP neural network to the prediction of shear wave velocity
[J].
DOI:10.3969/j.issn.1673-8926.2013.05.015
[本文引用: 1]

Accurate shear wave velocity is the necessary information for prestack inversion and prestack attribute analysis, but it is always deficient in actual production. The prediction methods are numerous and complicated and the accuracy is difficult to ensure. By selecting the parameters such as relative natural gamma-ray value, acoustic slowness, density and resistivity, this paper used the method of self-adaptive BP neural network to establish the prediction model of shear wave velocity. The actual data in Liaohe Oilfield showthe high precision of the prediction value, and the results can meet production requirements.
Improvement of petrophysical workflow for shear wave velocity prediction based on machine learning methods for complex carbonate reservoirs
[J].
A new velocity model for clay-sand mixtu res
[J].
Modeling elastic properties in carbonate rocks
[J].
A simple method of predicting S-wave velocity
[J].
基于修正Xu-White模型的碳酸盐岩横波速度估算方法
[J].
A shear velocity estimation method for carbonate rocks based on the improved Xu-White model
[J].
富有机质泥页岩岩石物理横波速度预测方法研究
[J].
DOI:10.3969/j.issn.1000-1441.2018.05.004
[本文引用: 1]

许多实际测井资料中缺失横波速度数据,给叠前地震资料反演、脆性因子计算、应力分析和储层预测等带来不利影响。关于碎屑岩和碳酸盐岩的横波速度预测方法已日趋成熟,而关于富有机质泥页岩的横波速度预测方法的研究相对较少。基于Keys-Xu干岩石模型,引入Gassmann方程和Brown-Korringa固体替代等岩石物理理论,构建了一种包含多矿物、复杂孔隙和有机质含量的富有机质泥页岩岩石物理横波速度预测方法。该方法将富有机质泥页岩等效为由岩石基质矿物、有机质和含流体孔隙组成的混合物,将岩石中复杂的孔隙结构等效为球形孔隙与裂缝状孔隙组合的结构;利用纵波速度计算球形孔隙与裂缝状孔隙的体积分数,进而预测横波速度。将该方法应用于实验室测试数据和建南构造侏罗系下统自流井组东岳庙段富有机质泥页岩实际测井资料,预测的横波速度与实测的横波速度吻合度较高,表明该方法在预测富有机质泥页岩横波速度时适用且有效。
A new S-wave velocity estimation method for organic-enriched shale
[J].
四川盆地侏罗系致密砂岩弹性特征及岩石物理建模
[J].
DOI:10.6038/cjg2020O0346
[本文引用: 1]

近年来围绕四川盆地侏罗系陆相致密砂岩已取得了勘探突破,其中川中—川西过渡带具备形成大气田的地质条件,但对该套致密砂岩弹性性质变化规律的研究还较少,致使利用地震方法进行"甜点"储层预测的精度不高.本文利用四川盆地侏罗系沙溪庙组32块样品开展了系统的声学测量,在此基础上,分析了样品弹性性质的变化规律.结合X射线衍射矿物组分分析、扫描电镜、铸体薄片和岩石薄片特征确定了不同成岩作用对岩石储集性能的影响.研究结果表明,研究区致密砂岩储层表现为孔隙型储层,受差异性成岩作用影响,黏土含量、钙质含量和硅质含量的差异以及它们分布特征之间的差异对岩石弹性性质造成了很大的影响.在研究区对岩石物性及弹性性质有明显影响的成岩作用包括早期的钙质胶结作用、压实作用和溶蚀作用,因此针对不同时期的成岩作用对岩石弹性及物性的影响,利用接触-胶结模型、微分等效模量模型和临界孔隙度校正的Hashin-Shtrikman上限模型建立了研究区致密砂岩的岩石物理模型.
Elastic characteristics and petrophysical modeling of Jurassic tight sandstone in Sichuan Basin
[J].
基于多孔可变临界孔隙度模型的储层孔隙结构表征
[C]//
Characterization of reservoir pore structure based on porous variable critical porosity model
[C]//
A variational approach to the theory of the elastic behaviour of multiphase materials
[J].
The elastic behavior of crystalline aggregate
[J].
Elastic properties of unconsolidated porous sand reservoirs
[J].
流体体积模量计算方法研究
[J].
Research on calculation methods of fluid bulk modulus
[J].
A petrophysical interpretation using the velocities of P and S waves(full-waveform sonic)
[J].
Relationships between seismic and hydrological properties
[J].