基于压缩感知的地震数据规则化技术在塔里木区块的应用

doi:10.11720/wtyht.2025.2581

基于压缩感知的地震数据规则化技术在塔里木区块的应用

郑多明^,¹, 王德英²^,³, 吴宇兵¹, 寇龙江^,², 陈阳阳¹, 金保中²

1.中国石油塔里木油田公司,新疆库尔勒 841000

2.中国石油勘探开发研究院西北分院,甘肃兰州 730020

3.中国石油大学(华东) 地球科学与技术学院,山东青岛 257061

Application of compressed sensing-based seismic data regularization technology in the Tarim block

ZHENG Duo-Ming^,¹, WANG De-Ying²^,³, WU Yu-Bing¹, KOU Long-Jiang^,², CHEN Yang-Yang¹, JIN Bao-Zhong²

1. Tarim Oilfield Company, PetroChina,Korla 841000,China

2. Research Institute of Petroleum Exploration & Development-Northwest(NWGI),PetroChina,Lanzhou 730020,China

3. School of Geosciences,China University of Petroleum(East China),Qingdao 257061,China

通讯作者: 寇龙江(1981-),男,2007年毕业于吉林大学,获得硕士学位。2023年在中国石油天然气集团公司担任物探高级工程师,长期从事地震资料处理工作。Email:koujl@petrochina.com.cn

第一作者: 郑多明(1972-),男,本科,高级工程师,主要从事地震资料高分辨率处理、速度建模及偏移成像等领域的科研及生产工作。Email:zhengdm-tlm@petrochina.com.cn

责任编辑: 叶佩

收稿日期: 2023-12-29 修回日期: 2024-09-26

基金资助:

中国石油塔里木油田公司生产项目“地震处理质控及并行处理研究”(041023050047)

Received: 2023-12-29 Revised: 2024-09-26

摘要

塔里木盆地是中国最重要的石油勘探区之一,其盆地内沉积岩层厚,构造活动频繁,形成了大量的生油岩、储油岩和盖层,为石油等资源的生成和储存提供了良好的条件。但该地区地形起伏较大,极大地阻碍了观测系统布置和采集工程设计,同时起伏地表和地下复杂构造也对地震波的传播产生影响,从而降低地震勘探数据的质量,对数据预处理、成像及储层预测等方面造成困难。本文针对塔里木区块内由于不良采集所造成的数据缺失问题,利用压缩感知技术实现地震数据的高精度重建,希望为预处理或叠加阶段提供高完整度、高可信度和高精度的地震记录。压缩感知作为一种新型的采样技术,在数据重建领域发挥了重要作用,该理论的关键是对地震数据进行充分的稀疏表达,但Fourier和DCT等传统变换仅适用于简单的全局型构造,本文根据塔里木区块数据的高复杂型,引入Shearlet变换作为压缩感知重建的稀疏基函数并成功应用于塔里木盆地实际资料,处理结果证明所用方法在该区域具有高度准确性和适用性。

关键词： 地震资料处理; 地震数据重建; 压缩感知; 稀疏变换; 稀疏反演

Abstract

The Tarim Basin,one of China's most significant oil exploration areas,exhibits thick sedimentary rock layers and frequent tectonic movements.These characteristics have led to the formation of abundant source,reservoir,and cap rocks,creating favorable conditions for the generation and storage of resources like petroleum.However,the high topographic relief in the area poses significant challenges to observation system arrangement and acquisition engineering design.Moreover,undulating surfaces and complex subsurface structures affect the propagation of seismic waves,impairing the quality of seismic exploration data and complicating data preprocessing,imaging,and reservoir prediction.Given the data loss of the Tarim block caused by suboptimal data collection,this study conducted high-precision reconstruction of seismic data using the compressed sensing technique,aiming to provide seismic records with high integrity,reliability,and precision for the preprocessing/superimposition phase.Compressed sensing,a novel sampling technique,plays a significant role in data reconstruction.The key to this technique is the adequate sparse representation of seismic data.However,conventional transform methods like Fourier transform and discrete cosine transform(DCT) are merely applicable to simple global structures.Considering the high complexity of the Tarim block data,this study employed the Shearlet transform as the sparse basis function for data reconstruction through compressed sensing.The technology of this study was finally applied to process the actual data of the Tarim Basin,demonstrating high accuracy and applicability for the area.

Keywords： seismic data processing; seismic data reconstruction; compressed sensing; sparse transform; sparse inversion

PDF (8903KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

郑多明, 王德英, 吴宇兵, 寇龙江, 陈阳阳, 金保中. 基于压缩感知的地震数据规则化技术在塔里木区块的应用[J]. 物探与化探, 2025, 49(1): 189-199 doi:10.11720/wtyht.2025.2581

ZHENG Duo-Ming, WANG De-Ying, WU Yu-Bing, KOU Long-Jiang, CHEN Yang-Yang, JIN Bao-Zhong. Application of compressed sensing-based seismic data regularization technology in the Tarim block[J]. Geophysical and Geochemical Exploration, 2025, 49(1): 189-199 doi:10.11720/wtyht.2025.2581

0 引言

传统奈奎斯特采样定理要求在同个周期内至少保证两个采样点,导致数据采集成本提高的同时增大了数据存储与处理的难度,而压缩感知理论^[1⇓-3]为这一问题提供了很好的解决方法。根据压缩感知的稀疏表示理论^[3⇓-5],数据若具有稀疏性或在某一域中具有稀疏性,其主要信息仅保留在较大的系数中,利用这些稀疏系数可以实现压缩数据和恢复数据的目的。稀疏表示是整个重建过程的前提条件。根据稀疏表示的构成来源可以分为:采用单一的数学变换来进行处理的地震数据恢复重建方法、通过不同种类的数学变化叠加的方式来进行地震的数据恢复重建以及采用学习型字典的地震数据恢复重建方法。单一数学变换的地震数据重建可以理解为用单一的某一种固定不变的数学变换来对数据进行稀疏表示^[6-7]。Herrmann等^[8]通过对曲波变换进行了一定的改进,从而提出了一种通过稀疏促进恢复的曲波方法CRSI地震数据插值重建的方法,第一次在地震恢复重建方法中应用了压缩感知的方法;在此基础上,更多的学者尝试将更加优越的数学变换带到压缩感知体系中,并对其不断地完善。Gan等^[9]通过对快速迭代收缩阈值算法(fast iterative Shrinkage-Thresholding algorithm,FISTA)的进一步改进从而研究出快速凸集投影法(fast projections onto convex sets,FPOCS),其效果比传统的傅里叶变换重建效果有很大的提升;郭念民等^[10]采用在数学变换中比Fourier 变化更稀疏的非抽样小波变换进行地震数据的恢复重建,从而得到了更优的系数表示形式,其重建效果也有显著提升;Yang等^[11]通过改进的采样方法,采用曲波变换来进行地震数据的恢复重建,得到了比之前更好的重建效果;冯飞等^[12]将具有尺度变换且更完备的剪切波(Shearlet)变换引入地震数据的恢复重建中,得到的效果比曲波变换得到的重建效果更好,信噪比更高。

由于实际采集到的地震数据往往并不是单一特征的,所以采用单一的数学变换方法可能并不能很准确地对地震数据进行稀疏表示,鉴于此,李海山等^[13]将Starck 等建立的使用在图像处理领域的形态分量分析(morphological component analysis,MCA)方法借鉴到地震勘探领域中,用来对地震数据进行恢复重建,取得了比单一稀疏表示效果更好的恢复重建结果。形态分量分析方法的原理是对于拥有多种性质的复杂地震数据,用分而治之的策略对各种特性采用与之对应的最佳稀疏表示方法进行稀疏表示,最终将处理得到的结果进行叠加处理。正是出于这样的原因,使得MCA方法在选取稀疏表示基时,选取不同的稀疏表示基则有不同的重建效果,周亚同等^[14]在前人所做的基础上,将不同类型的稀疏表示方法进行组合,最终得出曲波(Curvelet)字典和离散余弦变换(DCT)字典的组合形式具有比其他字典组合形式更好的稀疏表示能力,可以取得更好的恢复重建效果。张凯等^[15]将Shearlet引入形态分量分析中,通过选取Shearlet字典和DCT字典组合的形式比之前组合形式更具有稀疏表示能力的方法。训练出具有理想稀疏表示能力的字典是另一个有效的稀疏表示方法,字典学习算法是根据提取的数据特征作为样本来对地震数据进行稀疏表示和重新表征的过程,最终得到的稀疏表示字典也可以很好地对数据进行恢复重建。周亚同等^[16]利用字典学习的方法训练稀疏字典,并对其不断地优化,最终取得较好的重建效果,由此K-奇异值分解(K-singular value decomposition,K-SVD)的字典学习方法正式被引入到地震数据恢复重建中来。

塔里木盆地作为中国最重要的能源基地之一,石油资源量约为160亿t,天然气资源量约为30万亿m³,其石油和天然气资源的开采和利用对中国的能源安全和经济发展具有重要意义。但由于地表和地下构造的“双复杂”问题,使得部分区块数据在处理和解释方面面临困难。该地区地形起伏较大,可能极大地阻碍了观测系统布置和采集工程设计,同时起伏地表和地下复杂构造也对地震波的传播产生影响,从而降低地震勘探数据的质量,对数据预处理、成像及储层预测等方面造成困难。本文针对塔里木区块内由于不良采集所造成的数据缺失问题,利用压缩感知技术实现地震数据的高精度重建,希望为预处理或叠加阶段提供高完整度、高可信度和高精度的地震记录,模型测试和实际资料应用结果验证了Shearlet变换在塔里木区块是适用和有效的。

1 基本理论

1.1 压缩感知重建原理

压缩感知理论利用信号的稀疏性对均匀网格下的缺失数据进行恢复重建^[17]。数据的欠采样用下式表示:

(1)

y = M x

式中:x为原始数据;y为缺失数据;M为由0和1构成的采样矩阵,0元素代表未被采样,用于去除对应位置的数据,1元素用于保留数据。

压缩感知的成立需要以下3个前提:①信号具有稀疏性或在某个变换域内其表示系数稀疏;②欠采样方法具有随机性,即M中0元素列与1元素列的分布是随机的;③迭代求解算法。对于非规则采集数据,采样方式,即采样矩阵M确定,因此在重建的过程中只需要考虑信号的稀疏性与最优化算法,也就是需要确定最合适的稀疏域的和求解方法。

由于地震数据的复杂性,数据本身并不是稀疏的,所以选择合适的、高精度的稀疏变换成为了首要考虑的问题。首先对地震数据x进行稀疏表示:

(2)

x = D α

式中:D表示为稀疏字典,α代表稀疏系数,两者共同构成原始地震数据的稀疏表示。把式(1)与式(2)合并,得到地震数据的采集与稀疏表示模型:

(3)

y = M D α = A α

式中:A通常被称为压缩感知矩阵,是采样矩阵与稀疏字典基函数在时间域中的组合形式。这里需要说明的是,为使得观测矩阵能准确区分出不同的稀疏信号映射,采样矩阵M被要求符合有限等距性质(restricted isometry property,RIP),RIP定义如下^[18]:

对于任意稀疏信号x与任意RIP常数 $δ \in (0,1)$ 需满足如下公式:

(4)

(1 - δ) {‖x‖}_{2}^{2} \leq {‖M x‖}_{2}^{2} \leq (1 + δ) {‖x‖}_{2}^{2}

。

根据压缩感知的需要,稀疏表示系数α稀疏。为得到迭代最优解,式(3)被表述为一个求解L₀范数的问题,其求解基函数如下:

(5)

δ = \underset{α}{a r g m i n} {‖α‖}_{0} s . t . ‖y - A α‖ \leq ε

式(5)是一个迭代最优化求解问题。但是L₀范数的计算量会随着字典中原子数目的增加而增大难度。用L₁范数代替L₀范数是很好的解决办法,式(5)变为:

(6)

δ = \underset{α}{a r g m i n} {‖α‖}_{1} s . t . ‖y - A α‖ \leq ε

或

(7)

δ =_{α}^{a r g m i n} {‖y - A α‖}_{1} s . t . ‖α‖ \leq ε

但是在对该问题的进一步求解中,往往会出现一定的差别。所以在对式(7)求解时用一些近似的形式来将其转化成如下最优化求解的问题:

(8)

δ = \underset{α}{a r g m i n} λ {‖y - A α‖}_{1} + P (α), P (α) = {‖α‖}_{1} o r {‖α‖}_{0}

式中:符号 $λ$ 表示拉格朗日的乘子,作为惩罚项与约束项之间的权值。

式(2)~(8)是范数约束问题,一般通过最优化算法求解,常用的迭代算法有POCS、Bregman和JRSI等,解决L₀约束问题一般使用IHT等。

凸集投影(POCS)是求解范数约束问题时常用的迭代算法,其基础公式为

(9)

x_{k + 1} = y - (I - M) D^{T} T_{τ k} D_{x_{k}}

式中: $x_{k}$ 为第 $k$ 次迭代时域的解; $D$ 和 $D^{T}$ 分别为正、反稀疏变换; $τ k$ 为阈值; $T_{τ k}$ 为硬阈值算子。其具体取值如下:

(10)

T_{τ k} = \{\begin{array}{l} x_{k} | x_{k} | \geq τ k \\ 0 | x_{k} | τ k \end{array}

IHT(iterative hard threshold)就理论而言与POCS相近,其基础公式为:

(11)

α_{k + 1} = T_{τ k} [δ k + (M D^{T})^{T} (y - M D^{T} α_{k})]

式中: $α_{k + 1}$ 为第 $k$ 次迭代稀疏域的解,将式(11)转化为:

(12)

\begin{array}{l} α_{k + 1} = T_{τ k} [α_{k} + (M D^{T})^{T} (y - M D^{T} α_{k})] = \\ T_{τ k} D [y + (I - M) x_{k}] \end{array}

(13)

x_{k + 1} = D^{T} α_{k + 1} = D^{T} T_{τ k} D [y + (I - M) x_{k}]

对比式(9)与式(11)可知,IHT相当于在POCS之后再做一次阈值滤波。若最后的 $τ k = 0$ ,则两者结果相同;若最后的 $τ k \neq 0$ ,则结果有所差异。

1.2 稀疏变换的特点分析

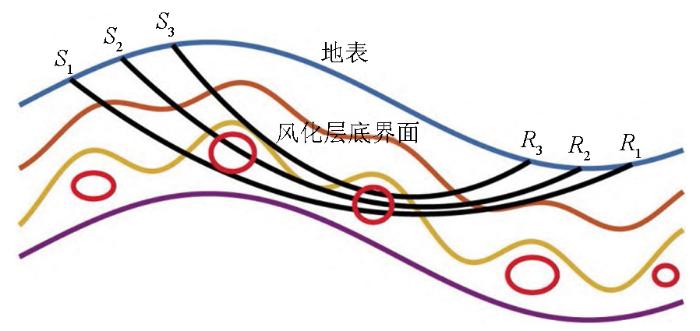
在压缩感知理论被提出开始,由于理论基础充分,计算速度快,许多学者都首先考虑Fourier变换。但Fourier变换注重信号的整体趋势,分析信号的区间是整个时间域,所以不能准确地描述局部细小构造。短时傅里叶变换对Fourier变换进行了加窗处理,有效解决了Fourier变换的全局限制,通过加窗处理把分析区间分为多个时间小段并在各个小段内做Fourier变换,这样就可以分析各个小段内的局部频率。这种方式虽然在某种意义上实现了局部刻画,但窗的形态和大小固定,不能根据所处理数据的类型自适应变化。地震记录通常是一组动态数据,地震波在传播过程中,波的形态、能量及频率振幅在各个时间段内各不相同。对于地震数据处理要求来说,对不同时刻、不同能量信号的处理要求也是不同的,通常希望高频成分的分辨率较高,而低频信号分辨率较低。小波变换很好地克服了窗口机械性的问题,虽然大小固定,但随着波的传播和频率的变化,窗口形态可自适应改变。对于分辨率的需求也正是根据频率来调整。但由于地震波多为曲线结构(图1),无论是Fourier变换还是小波变换都不能很好地表征曲状结构。Curvelet(曲波)变换由此诞生,曲波函数基由多种大小和方向不同的曲状元素组成,具有很好的多尺度性和多方向性。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 复杂近地表速度对成像的影响

蓝线—地表;橙、黄、紫线—构造地层;红线—串珠、缝洞等小尺度构造;黑线—地震波传播路径示意

Fig.1 Impact of complex near-surface velocities on imaging

blue line—surface;orange,yellow,purple line—structural layers;red line—small-scale structures such as beads and cavities;black line—schematic of seismic wave propagation paths

上面所提到的稀疏表示方法各有特点,各适用于不同特征的数据,但都属于固定的数学变换。它们的函数基已经被定义,对数据进行域的转换时是机械性的,无法根据数据特征做出相应改变。大多情况下,一种变换只适用于一种特征,而地震数据又是多特征信号,只选择一种稀疏字典进行表达难免存在误差。为了解决以上问题,目前已经出现两种解决办法:形态分量分析和字典学习。形态分量分析本着组合字典的思想,认为字典可以由多种字典组合而成,分别对数据特征进行描述。而字典学习可以根据数据本身特征,为所处理数据训练出一个专属字典,可以完全表达数据的各个形态特征。要进行固定基重建研究,表1展示了几个典型的稀疏变换方法及其特点。

表1 5种稀疏表示方法特点

Table 1 Characteristics of five sparse representation methods

稀疏变换方法	特点
傅里叶变换(Fourier)	计算速度快,识别信号的全局特征, 不能识别局部特征
离散余弦变换(DCT)	能量集中于低频,不能识别局部特征
短时傅里叶变换 (short-time Fourier)	可识别局部特征,但窗口形态固定
曲波变换(Curvelet)	多尺度性,多方向性,各向异性, 有效表征曲线特征,无自适应性
剪切波变换(Shearlet)	多尺度性,多方向性,各向异性, 有效表征曲线特征,局部特征刻画能力强,无自适应性

新窗口打开| 下载CSV

1.3 基于Shearlet变换的地震数据重建

对于本文提出的技术,我们考虑了3种常见的数学字典:Wavelat、Curvelet和Shearlet。由于只有水平和垂直基函数,Wavelat只能表示各向同性数据。Curvelet变换可以表示不同尺度和角度的各向异性数据,然而由于Curvelet变换是带限的,因此在空间域中只有有限的局部特征。Shearlet具有定向紧密支撑结构,精细尺度可以很好地表达不同频带的特性,它可以在离散和连续变化之间提供统一的转换,并且可以最好地稀疏各向异性图像,因此,本文选用Shearlet变换进行压缩感知框架下的地震数据重建。Shearlet 变换通过合成小波理论和仿射系统结合了多尺度几何分析,通过拉伸、平移和旋转基函数来生成基函数,相比Curvelet变换,具有更强的方向性和各向异性,在描述数据局部特征时,也具有更强的刻画能力。基于Shearlet的地震数据重建也会获得更高的重建质量。在 $n = 2$ 的情况下,Shearlet基函数具有膨胀的仿射系统:

(14)

\begin{array}{l} S h (D) (λ) S h {(D B)}_{d, s, t} (λ) = \\ {λ_{d, s, t} (α = d^{- 3 / 4} λ [\frac{α}{{(D B)}_{d, s}} - t] : \\ d \in R^{+}, s \in R, t \in R^{2})} \end{array}

式中: $λ \in L^{2} (R^{2})$ ; $λ_{d, s, t} (α)$ 为变换函数; $α$ 为空间函数变量; $D = (\begin{array}{l} d 0 \\ 0 \sqrt{d} \end{array})$ 为各向异性膨胀矩阵; $B = (\begin{array}{l} 1 s \\ 0 1 \end{array})$ 为剪切矩阵; $d 、 s 、 t$ 分别为尺度参数、剪切参数、平移参数。

对任意 $μ = (μ_{1}, μ_{2}) \in R^{2}, μ_{1} \neq 0$ 和任意 $λ$ ,使其满足:

(15)

λ' (μ) = λ'_{1} (μ_{1}) λ'_{2} (μ_{2} / μ_{1})

式中:λ'₁∈C(R),supλ'₁∈[-2,1/2]∪[1/2,2];λ'₂∈C(R),且supλ'₂∈[-1,1],λ'₂∈C(-1,1)>0,其中 $‖λ_{2}‖ = 1$ 。

若满足上述条件,对 $x$ 进行二维Shearlet变换就可以转变成 $x$ 与 $λ_{d, s, t}$ 做内积,即

(16)

S_{x} (d, s, t) = x, λ_{d, s, t} = \int_{R^{2}} x (α) {λ^{H}}_{d, s, t} (α) d α

式中: $S_{x} (d, s, t)$ 为Shearlet变换系数; ${λ^{H}}_{d, s, t} (α)$ 为 $λ_{d, s, t}$ 的共轭。Shearlet函数 $λ_{d, s, t}$ 通过改变尺度大小、剪切方向、平移位置实现对二维空间的基函数展开,在函数空间中是平方可积的,则有如下逆变换:

(17)

x' (α) = \sum_{d, s, t} [S_{x} (d, s, t) λ'_{d, s, t}]

式中: $λ'_{d, s, t}$ 为逆Shearlet函数; $x' (α)$ 为逆Shearlet变换结果。

在 $n = 3$ 的情况下,Shearlet变换由3个近似锥区域 $P$ 函数和1个中心区域 $C$ 函数构成:

(18)

\begin{array}{l} P_{1} = {(e_{1}, e_{2}, e_{3}) \in R^{3} : | e_{2} / e_{1} | \leq 1, | e_{3} / e_{1} | \leq 1} \\ P_{2} = {(e_{1}, e_{2}, e_{3}) \in R^{3} : | e_{1} / e_{2} | \leq 1, | e_{3} / e_{2} | \leq 1} \\ P_{3} = {(e_{1}, e_{2}, e_{3}) \in R^{3} : | e_{1} / e_{3} | \leq 1, | e_{2} / e_{3} | \leq 1} \\ C = {(e_{1}, e_{2}, e_{3}) \in R^{3} : \infty 1\} \end{array}

式中: $e_{1}, e_{2}, e_{3} \in R$ 表示三维坐标。

基于Shearlet变换重建一般通过OMP算法求解,其流程伪代码为:

输入:压缩感知矩阵A,原始数据x,总迭代次数 $K$ ;

输出: $α^{H}$ ,最终残差 $r_{k} = x - A_{k} α_{k}^{H}$ ;

初始化:初始残差 $r_{0} = x$ ,迭代次数 $k = 1 。$

1)寻找残差 $r$ 和 $A$ 的列 $θ_{J}$ 的内积的最大值 $a r g m i n_{j = 1, \dots, N} | r_{k - 1}, θ_{j} |$ ;

2)求 $x = A_{k} α_{k}$ 的最小二乘解,即 $a r g m a x {‖x - A_{k} α_{k}‖}_{2}$ ;

3)更新残差 $r_{k} = x - A_{k} α_{k}^{H}$ ;

4)增加迭代 $k = k + 1$ ;若 $k \leq K$ ,则返回1,若 $k K$ ,则继续;

5)输出最后得到的 $α^{H};$

6)根据 $y' = D^{T} α^{H}$ 得到重建数据。

2 模型测试

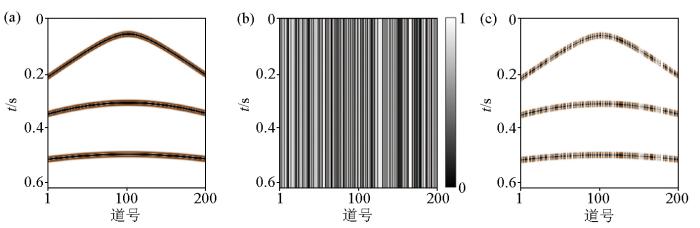
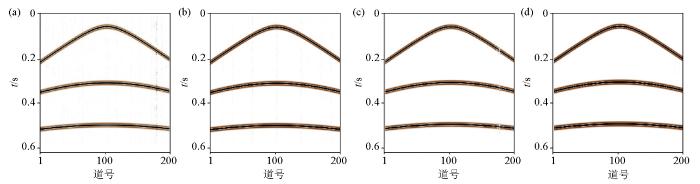
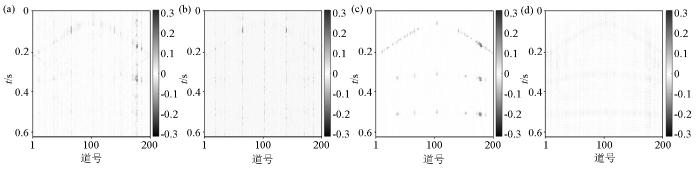
首先选用二维模型进行测试,二维合成地震记录共500道,每道800个采样点,随后进行50%的随机欠采样处理,原始数据、采样矩阵和缺失数据如图2所示。其中采样矩阵由0和1元素构成,0元素用于数据的缺失,1元素用于保留原位置上的数据。通过图3可对比分析Curvelet、Fourier、DCT和Shearlet的重建结果(4种变换方法均为二维形式),可以看出4种方法都能够在一定程度上找回丢失信息,但Fourier变换和DCT变换的重建结果包含更强的背景噪声,这可能由于字典的全局特征导致,Curvelet变换由于其对曲线特征的高适用性,对于小缺失部分可以达到很好的效果,但在连续多道缺失时其效果较差,在重建结果中呈现断轴现象。从图4中可以看出,Shearlet变换的重建误差要小于其他3种方法,说明其具有更高的准确度。通过图5可以从频率域角度看出Shearlet变换的有效性,重建后由于随机欠采样造成的频率噪声被完全消除。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 随机欠采样合成地震数据

a—合成地震数据;b—0%随机欠采样矩阵;c—0%缺失数据

Fig.2 Random undersampling of synthetic seismic data

a—synthetic seismic data;b—0% random undersampling matrix;c—0% missing data

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 4种单一变换的重建结果

a—基于Fourier变换的重建结果;b—基于DCT变换的重建结果;c—基于Curvelet变换的重建结果;d—基于Shearlet变换的重建结果

Fig.3 Reconstruction results of four single transformations

a—reconstruction result based on Fourier transform;b—reconstruction result based on DCT transform;c—reconstruction result based on Curvelet transform;d—reconstruction result based on Shearlet transform

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 4种单一变换的重建误差

a—基于Fourier变换重建误差;b—基于DCT变换的重建误差;c—基于Curvelet变换的重建误差;d—基于Shearlet变换的重建误差

Fig.4 Reconstruction error of four single transformations

a—reconstruction error based on Fourier transform;b—reconstruction error based on DCT transform;c—reconstruction error based on Curvelet transform;d—reconstruction error based on Shearlet transform

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 Shearlet重建前后频谱

a—随机缺失50%地震记录频谱;b—Shearlet重建数据频谱

Fig.5 Spectrum before and after Shearlet reconstruction

a—spectrum of seismic records with 50% random missing data;b—spectrum of Shearlet reconstructed data

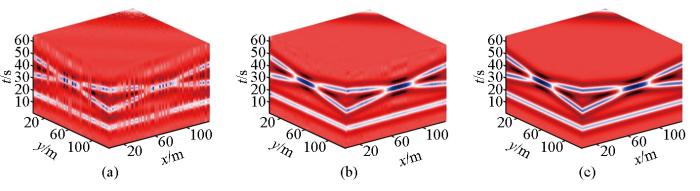
随后进行Shearlet重建在三维模型中的应用,实验选用三维合成地震记录进行对比实验来测试其适用性和有效性。数据欠采样过程如图6所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 随机欠采样三维合成地震数据

a—三维合成地震数据;b—50%随机采样矩阵;c—50%缺失数据

Fig.6 Random undersampling of 3D synthetic seismic data

a—3D synthetic seismic data;b—50% random sampling matrix;c—50% missing data

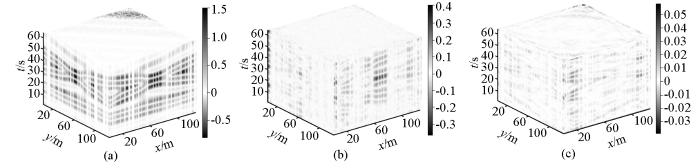
使用Fourier、DCT及Shearlet这3种字典进行对比实验。数据的采样、重建结果(3种方法均使用30次迭代)及误差如图7和图8所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 3种单一变换的重建结果

a—基于Fourier变换重建结果;b—基于DCT变换重建结果;c—基于Shearlet变换重建结果

Fig.7 Reconstruction results of three single transformations

a—reconstruction result based on Fourier transform;b—reconstruction result based on DCT transform;c—reconstruction result based on Shearlet transform

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 基于3种单一变换的重建误差

a—基于Fourier变换重建误差;b—基于DCT变换重建误差;c—基于Shearlet变换重建误差

Fig.8 Reconstruction error of three single transformations

a—reconstruction error based on Fourier transform;b—reconstruction error based on DCT transform;c—reconstruction error based on Shearlet transform

3 塔里木盆地实际数据处理

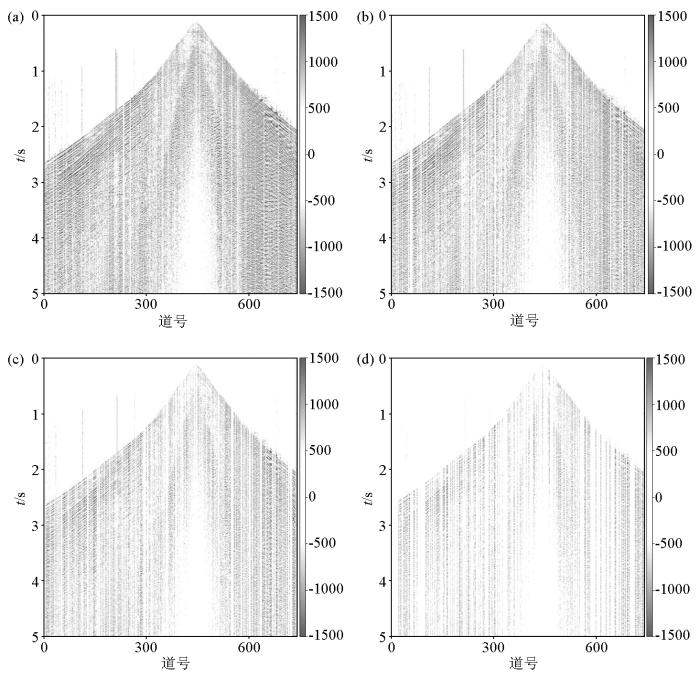
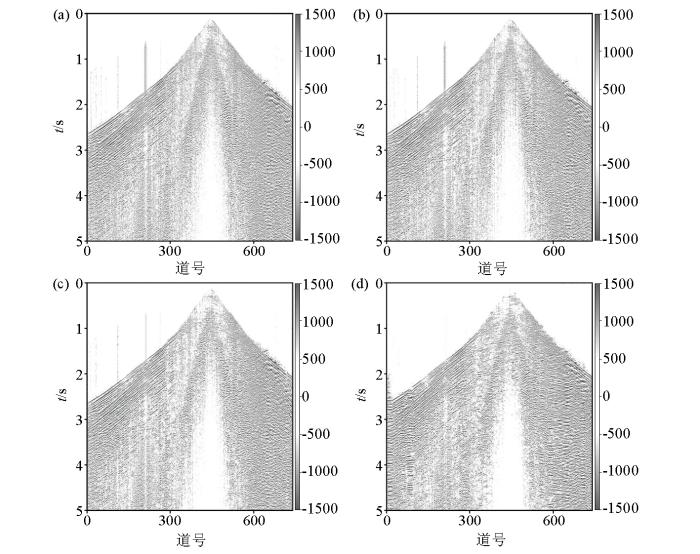
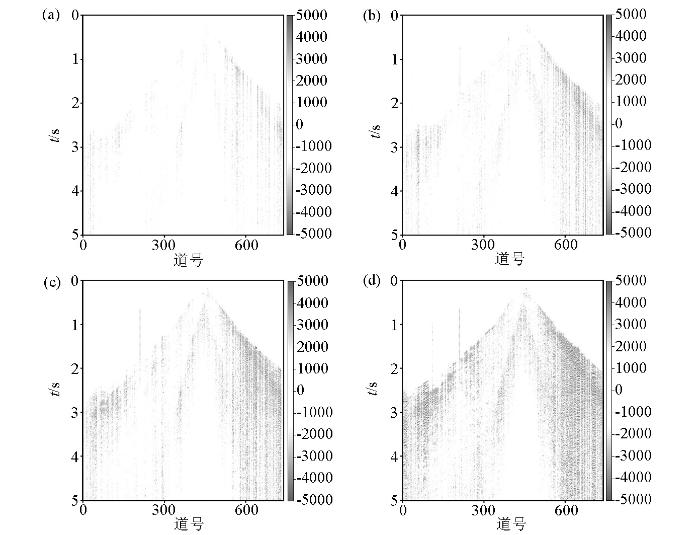
首先利用塔里木某区块数据进行缺失重建实验,为探究所用方法的重建能力,我们分别对原始数据进行不同程度的随机缺失处理,再进行恢复重建工作,其中缺失量分别为原始道数的 20%、40%、60%和 80%。图9和图10展示了原始单炮和4种缺失水平下的缺失数据。图11和图12分别展示重建数据和重建误差,从图中可以发现随着缺失数量的增加,重建效果逐渐降低,但可以保证在缺失量小于60%的情况下,所用方法可以达到令人满意的结果。当缺失量达到80%时,虽无法准确重建,但重建数据的信息仍是完整的,同相轴仍连续的,并且信噪比得到了提高。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 实际单炮

Fig.9 Real single shot

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 缺失单炮

a—随机缺失20%地震记录;b—随机缺失40%地震记录;c—随机缺失60%地震记录;d—随机缺失80%地震记录

Fig.10 Missing single shot

a—seismic records with 20% random missing data;b—seismic records with 40% random missing sata;c—seismic records with 60% random missing data;d—seismic records with 80% random missing data

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 重建单炮

a—随机缺失20%重建地震记录 (SNR=11.5 dB;PSNR=2.7 dB);b—随机缺失40%重建地震记录 (SNR=10.43 dB;PSNR=1.2 dB);c—随机缺失60%重建地震记录 (SNR=8.93 dB;PSNR=0.89 dB);d—随机缺失80%重建地震记录 (SNR=8.36 dB;PSNR=0.78 dB)

Fig.11 Reconstructed single shot

a—reconstructed seismic records with 20% random missing data(SNR=11.5 dB;PSNR=2.7 dB);b—reconstructed seismic records with 40% random missing sata(SNR=10.43 dB;PSNR=1.2 dB);c—reconstructed seismic records with 60% random missing data(SNR=8.93 dB;PSNR=0.89 dB);d—reconstructed seismic records with 80% random missing data(SNR=8.36 dB;PSNR=0.78 dB)

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 重建误差

a—随机缺失20%重建误差;b—随机缺失40%重建误差;c—随机缺失60%重建误差;d—随机缺失80%重建误差

Fig.12 Error of reconstruction

a—reconstruction error with 20% random missing data;b—reconstruction error with 40% random missing data;c—reconstruction error with 60% random missing data;d—reconstruction error with 80% random missing data

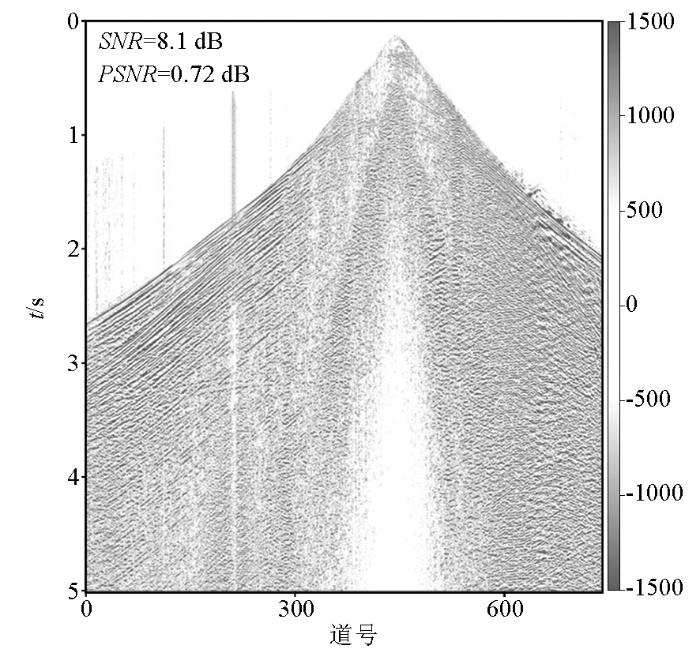
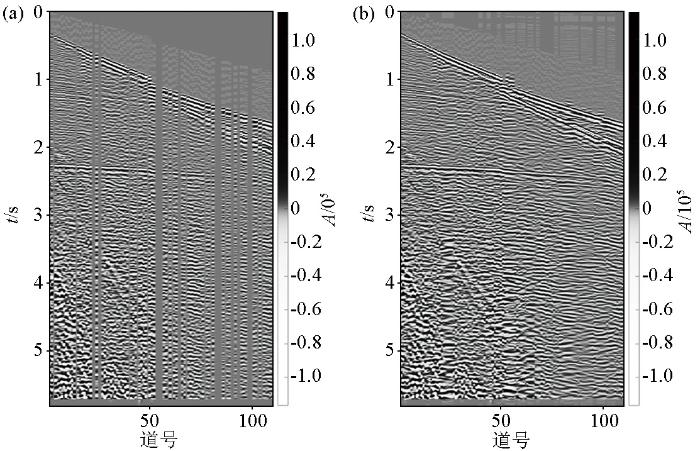
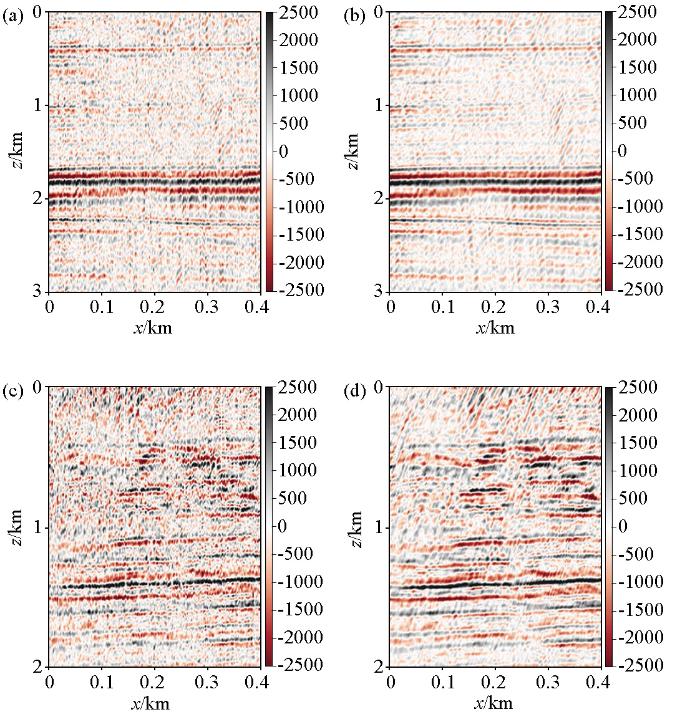
选用某区块实际炮集进行测试,图13展示单炮结果。从图13a中可以看出,该数据缺失形式呈随机缺失且缺失量较大,特别对在60道和80道左右存在连续多道缺失的情况,大大增大数据重建难度。图13b展示了Shearlet重建结果,可以看出重建后所有缺失数据被恢复,同相轴连续且光滑,同相轴弯曲程度和走向趋势并无异常,证明重建结果基本正确。另外,由于稀疏表示对随机噪声的过滤作用,重建数据的信噪比和峰值信噪比均有所提升。为进一步验证所用方法的有效性,对重建前后炮集进行叠加,叠加结果如图14所示,图中展示了叠加剖面的两个部分,通过对比发现,由于数据缺失,原始剖面无法呈现完整构造,同相轴不连续,若响应无法叠加成像,而重建数据叠加剖面很大程度改善了以上问题,构造相对成像完整,同相轴光滑连续,弱信号也得到了一定呈现。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 原始炮记录重建前后对比

a—原始单炮(SNR=5.39 dB;PSNR=0.2 dB);b—重建单炮(SNR=7.53 dB;PSNR=1.6 dB)

Fig.13 Comparison of original shot records before and after reconstruction

a—original single shot(SNR=5.39 dB;PSNR=0.2 dB);b—reconstructed single shot(SNR=7.53 dB;PSNR=1.6 dB)

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 重建前后叠加对比

a—原始数据叠加局部放大1;b—重建数据叠加局部放大1;c—原始数据叠加局部放大2;d—重建数据叠加局部放大2

Fig.14 Stacking comparison before and after reconstruction

a—original data stack with local magnification 1;b—reconstructed data stack with local magnification 1;c—original data stack with local magnification 2;d—reconstructed data stack with local magnification 2

4 结论

由于塔里木盆地的复杂地表条件,对地震数据采集造成较大困难,往往导致地震数据存在一定程度的缺失。本文基于压缩感知理论框架,利用Shearlet变换实现了塔里木盆地资料的实际应用并取得了良好效果。

本文实现了基于Shearlet变换重建的塔里木盆地资料实际应用,Shearlet变换通过合成小波理论和仿射系统结合了多尺度几何分析。它通过拉伸、平移和旋转基函数来生成基函数,相比Curvelet变换,具有更强的方向性和各向异性,在描述数据局部特征时,也具有更强的刻画能力。通过数值实验对Curvelet、Fourier、DCT和Shearlet这4种方法进行了比较,结果表明,本文方法重建结果的相对误差较小,可以很好地重建局部细节和深弱反射信号。实际资料处理结果表明,所用方法可以完全准确地重建缺失数据,且重建数据的信噪比有所提高,叠加对比也证明了方法对于后期成像工作具有重要作用。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Tseng

Applications of a splitting algorithm to decomposition in convex programming and variational inequalities

[J]. SIAM Journal on Control and Optimization, 1991, 29(1):119-138.