考虑孔隙形状的碳酸盐岩储层流体综合识别方法研究及应用——以鄂尔多斯盆地奥陶系马家沟组四段为例

doi:10.11720/wtyht.2025.1183

考虑孔隙形状的碳酸盐岩储层流体综合识别方法研究及应用——以鄂尔多斯盆地奥陶系马家沟组四段为例

王永刚^,¹^,², 姚宗惠¹^,², 杨骐羽³^,⁴, 李景叶³^,⁴, 宋炜³^,⁴

1.中国石油长庆油田分公司勘探开发研究院,陕西西安 710018

2.低渗透油气田勘探开发国家工程实验室,陕西西安 710018

3.油气资源与探测国家重点实验室,北京 102249

4.中国石油大学(北京) 地球物理学院,北京 102249

A comprehensive fluid identification method for carbonate reservoirs considering pore shapes: A case study of the fourth member of the Ordovician Majiagou Formation,Ordos Basin

WANG Yong-Gang^,¹^,², YAO Zong-Hui¹^,², YANG Qi-Yu³^,⁴, LI Jing-Ye³^,⁴, SONG Wei³^,⁴

1. Research Institute of Exploration and Development,Changqing Oilfield Company,PetroChina,Xi'an 710018,China

2. National Engineering Laboratory for Exploration and Development of Low-Permeability Oil & Gas Fields,Xi'an 710018,China

3. State Key Laboratory of Petroleum Resources and Prospecting,Beijing 102249,China

4. College of Geophysics,China University of Petroleum(Beijing),Beijing 102249,China

第一作者: 王永刚(1980-),男,汉族,陕西扶风人,硕士研究生学历,高级工程师,主要研究方向为地震资料解释、地震反演及储层预测等。Email:wangyg_cq@petrochina.com.cn

责任编辑: 叶佩

收稿日期: 2024-05-7 修回日期: 2024-11-4

基金资助:

中国石油集团公司攻关性应用性科技专项“海相碳酸盐岩油气规模增储上产与勘探开发技术研究”课题4“复杂碳酸盐岩地球物理评价关键技术研究”(2023ZZ16YJ04)

Received: 2024-05-7 Revised: 2024-11-4

摘要

鄂尔多斯盆地马四段白云岩储层具有厚度较薄、致密、孔隙形状复杂、非均质性显著、地震响应相对较弱的特征。储层地震预测机理尚存疑,流体识别具有一定困难。传统的单一属性地球物理方法未能准确预测流体,因此我们以对孔隙形状与孔隙连通性的综合考虑为基础,借助岩石物理建模和分析,结合波动理论的叠前AVO反演、流体因子的频变AVO反演与基于PNN的孔隙结构参数预测,构建了一种新的综合流体识别方法。该方法全面考虑了弹性参数、物性参数与频散属性的影响,取得了显著的效果。相对于传统单一属性流体识别方法,综合流体识别方法展现出更高的精度,尤其在含气层区域表现出显著的指示效果,充分验证了其在流体识别领域的有效性,具备广泛推广和应用的潜力。

关键词： 马家沟组四段; 岩石物理模型; 孔隙形状; 频散属性; 流体识别

Abstract

The dolomite reservoirs of the fourth member of the Majiagou Formation in the Ordos Basin are characterized by thin layers,tightness,complex pore shapes,strong heterogeneity,and relatively weak seismic responses.The mechanisms behind the seismic prediction of the reservoirs remains uncertain, making fluid identification challenging.Traditional geophysical methods based on a single attribute fail to accurately predict fluids.Therefore,by comprehensively accounting for the pore shapes and connectivity,this study proposed a new fluid identification method using petrophysical modeling and analysis,as well as wave theory-based prestack AVO inversion,frequency-dependent AVO inversion of fluid factors,and probabilistic neural network(PNN)-based prediction of pore structure parameters.This method,comprehensively considering the impacts of elastic parameters,physical parameters,and dispersion properties,achieve remarkable results.Compared to traditional single-attribute fluid identification method,the proposed method demonstrates higher accuracy,particularly for gas-bearing areas,fully verifying its effectiveness in fluid identification and highlighting its potential for widespread application.

Keywords： the fourth member of the Majiagou Formation; rock physical model; shape of pore; dispersion property; fluid recognition

PDF (7816KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

王永刚, 姚宗惠, 杨骐羽, 李景叶, 宋炜. 考虑孔隙形状的碳酸盐岩储层流体综合识别方法研究及应用——以鄂尔多斯盆地奥陶系马家沟组四段为例[J]. 物探与化探, 2025, 49(1): 177-188 doi:10.11720/wtyht.2025.1183

WANG Yong-Gang, YAO Zong-Hui, YANG Qi-Yu, LI Jing-Ye, SONG Wei. A comprehensive fluid identification method for carbonate reservoirs considering pore shapes: A case study of the fourth member of the Ordovician Majiagou Formation,Ordos Basin[J]. Geophysical and Geochemical Exploration, 2025, 49(1): 177-188 doi:10.11720/wtyht.2025.1183

0 引言

近年来,随着勘探活动的深入进行,在远离风化壳的马家沟组四段(以下简称马四段)中,发现夹在石灰岩和膏岩之间的薄层白云岩具备良好的物性和富含油气特征^[1-2]。然而,该层白云岩储层形成于膏盐岩下,其储层表现出厚度较薄、致密、孔隙形状复杂、非均质性显著,且地震响应较为微弱的特点^[1-2],这使得准确识别有利储层面临一定的挑战。

至今,国内外众多学者通过综合应用地震资料、测井资料以及地质资料,对储层的含流体性质进行了全面的表征和描述。Smith等^[3]在泥岩基线公式基础上,通过对速度参数的相对变化率进行“加权叠加”,首次提出并构建了流体因子,为流体检测提供了新的方法。Goodway等^[4]通过研究介质在含流体情况下的拉伸特性,引入了LMR(Lamé参数、密度、泊松比的联合反演)储层流体识别技术。Gray则直接将Lamé参数作为流体因子用于储层流体识别,而Smith等^[5]提出了交会图和流体因子的定义。2003年Russell等^[6]基于孔隙弹性理论,利用Biot-Gassmann方程推导出组合参数的阻抗形式表达式,将其作为孔隙流体识别因子,并于2006年提出了将Gassmann流体项直接作为流体因子的方法,同时推导出了包含流体因子的AVO近似公式,实现了流体因子直接反演^[7]。宁中华等^[8]对前人提出的流体因子进行了幂次方阻抗归纳总结,并且构建了具有较高敏感性的流体因子。此后,不少学者基于弹性参数反演,建立流体因子,开展流体识别工作^[9⇓⇓-12]。李英等^[13]考虑孔隙度对流体识别的影响,筛选出合适的弹性参数组合避免了高孔隙度的水层对流体识别的影响。Yin等^[14]在实际应用中发现,在储层固结程度较低的地区,流体因子受到固体因素的较大影响,存在流体识别的虚假现象,并于2014年提出了固液解耦的流体因子流体体积模量。付金华等^[15]通过孔隙介质等效岩石物理模型的统计分析,实现了流体体积模量的直接反演。然而,由于碳酸盐岩储层的复杂性,单一属性建立的流体因子不再适用于孔隙系统较为复杂的储层。

本文充分考虑弹性参数、物性参数与频散属性的影响,建立了一种综合流体识别方法:考虑孔隙形状与孔隙连通性建立碳酸盐岩岩石物理模型,寻找孔隙形状敏感性参数,结合波动理论反演得到的纵波速度、横波速度与密度,进一步预测孔隙形状参数;基于Ruessell方程的频变AVO反演提取高分辨率的频散因子;结合纵波速度差、孔隙形状参数、频散属性,建立多源信息融合的流体因子,应用于实际数据,在含气层区域具有一定的指示效果。

1 研究区地质概况

鄂尔多斯盆地中东部地区下古生界奥陶系中下统发育了多套膏盐岩,其分布面积广泛,封盖条件优越,奥陶系盐下马五6~10段已初步显示储量规模,马四段的风险勘探取得了显著突破,而在马三—马二段也观察到了含气迹象,揭示出盐下领域可能是该盆地一个全新的含气系统^[1-2]。马家沟组发育在低隆背景下的台内颗粒滩,是盆地东部白云岩储集层及圈闭发育的有利相带;构造上倾方向被认为是天然气运移的有利指向区,因此马四段天然气成藏具有上、下古生界双源供烃的优势^[1-2]。

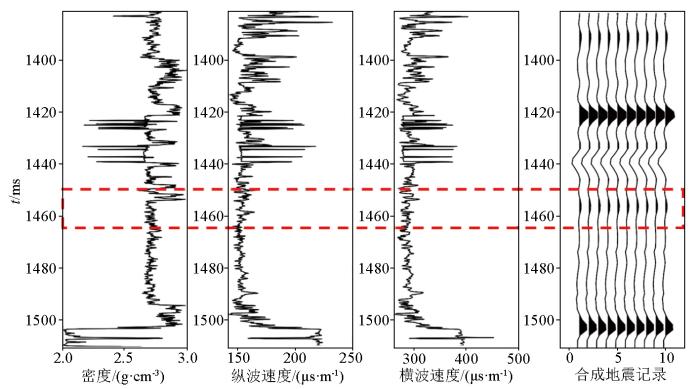
马四段主要发育台内滩相和台内丘相两类优质储层,储集空间主要由粒间孔、晶间孔和微裂缝构成,其平均孔隙度为4.95%、平均渗透率为0.090 mD,岩性主要以石灰岩、白云质石灰岩、灰质白云岩和白云岩等碳酸盐岩为主^[16-17]。井1的合成地震记录如图1所示。在井1中,马四段的厚度为183.94 m,马四段白云岩厚度薄,储层致密,且与围岩地球物理参数差异小,地震响应弱,如红色框线所示;夹层型白云岩分辨分辨难度大,储层地震预测机理尚不清晰,流体识别具有一定困难。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 井1合成记录

Fig.1 Well 1 synthetic record

2 多属性流体预测方法

基于传统AVO反演获得的弹性参数构建的流体因子虽然能够指示流体的存在,但其精度存在限制。例如,在地下地层含有流体时,纵波速度发生变化,导致含流体储层与周围岩层的纵波速度差异;由于反演结果的精度限制,若以纵波速度差作为流体指示因子,识别流体的效果并不理想。此外,流体的存在也会引起岩层中弹性模量的频变特征,使得地震信息具有频率依赖性;因此,也可以利用传统的FAVO反演技术基于不同的近似式构建不同的流体检测因子,将频散特性作为识别流体的一种属性。

本文综合考虑纵波速度差和频散因子,可以构建更为准确的流体因子。若存在较好的频散响应或流体响应,通常表明相应的储层具有较好的孔隙度。孔隙形状参数作为储层的物性属性,可用于进一步约束基于地震获取的流体因子,从而提高储层预测的准确性。得到更为精确指示流体的流体因子DCF,公式如下:

(1)

D C F = Δ V_{P} \cdot {I_{a}}^{n} \cdot E

式中:ΔV_P、 $I_{a}$ 、 $E$ 分别为纵波速度差、频散因子、孔隙结构参数,n为常数。

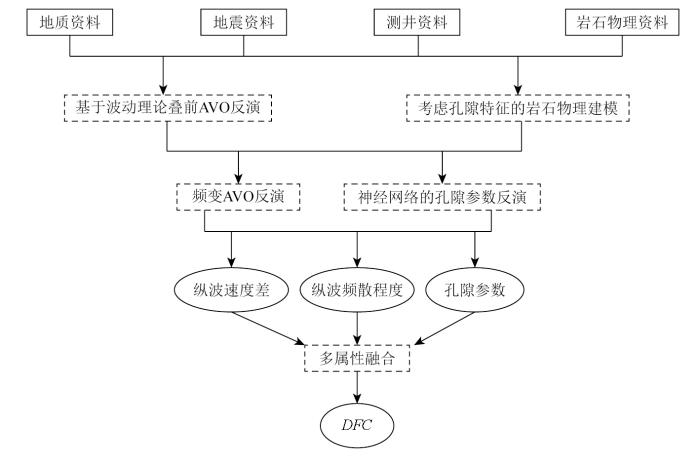
在本文中,综合流体因子预测的流程如图2所示。首先,基于波动理论进行弹性参数的预测。随后,建立了考虑孔隙形状和孔隙连通性的岩石物理模型,确定了孔隙形状敏感性参数,并利用深度学习技术建立了多元非线性关系,用于预测孔隙形状参数。最后,利用Ruessell方程的频变AVO反演进行频散因子的预测。通过综合考虑纵波速度差、频散因子以及孔隙形状参数,得到了综合流体因子DCF。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 综合流体因子预测的流程

Fig.2 Flowchart of the integrated fluid factor prediction

2.1 基于波动方程解析解的叠前反演技术

传统的Zoeppritz方程及其近似式通常假设接收到的反射振幅只包含一次反射,而忽略了波的传播效应。在复杂薄互层中,多次波、转换波和透射损失对AVO响应的影响较大,而且很难完全消除。弹性波动方程被认为是可以弥补传统AVO技术不足的一种方法。本文考虑了基于弹性波动方程的一维解析解(反射率法)的叠前AVO反演,以预测弹性参数。这种方法能够更全面地考虑复杂地层中多次波、转换波和透射损失对AVO响应的影响,从而提高了对地下岩石性质的准确性。

反射率法是在层状半空间介质中进行全波场模拟的一种有效方法。它通过在频率—慢度域直接求解完全弹性波动方程,模拟出的波场包含了各种波的传播效应。该方法基于矢量化复合矩阵求解频率波数域的一维波动方程,通过定义层传播矩阵,其总传播响应可以通过下式计算:

(2)

\begin{array}{l} v_{n} = Q_{n} v_{n + 1} \\ Q_{n} = T_{n}^{+} E_{n} T_{n}^{-} \end{array}

式中:矩阵 $E_{n}$ 描述了地震波经过第 $n$ 层界面时地震波相位的改变, $T_{n}^{-}$ 为 ${T^{+}}_{n}$ 对应的矩阵逆。由 $v_{0}$ 计算PP波在频率—波数域的总反射系数与地震记录^[18]:

(3)

R_{P P} (ω, p) = \frac{v_{0} (4)}{v_{0} (1)}

(4)

G (τ, p) = \frac{1}{2 π} \int_{- \infty}^{\infty} S (ω) R (ω, p) e^{i w t} d ω

式中: $p$ 表示水平波数,利用公式 $p = s i n θ / {\tilde{v}}_{p} (ω)$ 进行射线参数与角度的转换,获取最终共角度道集:

(5)

G (t, p) = \frac{1}{2 π} \int_{- \infty}^{\infty} S (ω) R (ω, p) e^{i w t} \int_{- \infty}^{\infty} {[\frac{v_{0} (4)}{v_{0} (1)}]}_{p_{i}} e^{i w t} d ω

。

使用贝叶斯理论,特别是在高斯先验分布的假设下,可以通过最大化后验概率来估计模型参数。这个过程可以通过建立目标函数,然后使用高斯—牛顿迭代方法来求解:

(6)

m^{k + 1} = m^{k} - η H (m^{k})^{- 1} γ (m^{k})

式中:η 为反演迭代步长, $γ$ 是 $S_{0} (m)$ 对模型参数的一阶偏导, $H$ 是 $S_{0} (m)$ 对模型参数的二阶偏导,称为海森矩阵。矩阵γ和矩阵H的表达形式如下:

(7)

\begin{array}{l} γ (m) = \frac{\partial J (m)}{\partial m} = {(\frac{\partial G (m)}{\partial m})}^{T} (G (m) - d) + \\ μ_{h} Q (m - μ) \\ H (m) \approx {(\frac{\partial G (m)}{\partial m})}^{T} \frac{\partial G (m)}{\partial m} + μ_{h} Q \end{array}

。

2.2 考虑孔隙形状的岩石物理建模

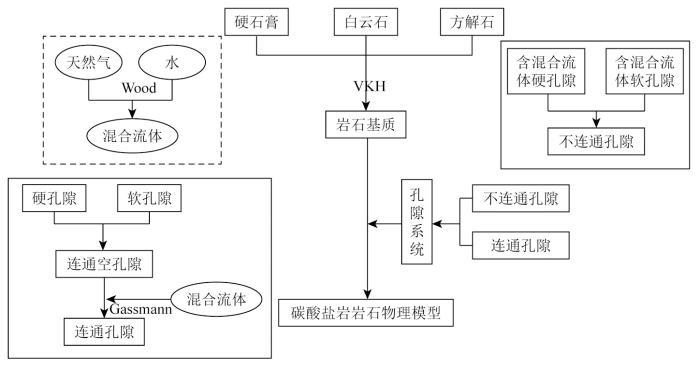
Ruiz 等^[18]构建SPM模型时将孔隙形状划分为两种类型:纵横比为0.01的裂隙状软孔隙和纵横比为1的球状硬孔隙;杨骐羽等^[19]则对孔隙形状及其类型进行了进一步细分。而王璞等^[20]将储集空间分为Gassmann模型描述的全连通孔隙和等效介质模型描述的不连通孔隙。鉴于碳酸盐岩储层物性的大幅度变化以及孔隙形状的复杂性,本文综合考虑矿物组分、混合流体与孔隙系统,建立岩石物理模型,如图3所示,具体流程如下:

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 考虑连通孔隙与孔隙形状的碳酸盐岩岩石物理模型

Fig.3 A petrophysical model of carbonate rocks considering connected pores and pore shapes

1)混合矿物的等效模量:

储层中主要包含硬石膏、白云石、方解石等多种矿物组分。使用Voight-Reuss-Hill平均方法^[21-22],计算混合矿物的等效模量,以考虑不同矿物在储层中的影响。

2)混合流体的等效模量:

孔隙中包含气体和水,Wood公式考虑了气体和水的体积分数,以及它们的声波速度,采用Wood公式^[23]求取混合流体的等效模量。

3)硬孔隙与软孔隙的分布:

参考SPM模型将孔隙分为两种类型:孔隙纵横比为1的硬孔隙和孔隙纵横比为0.01的软孔隙。KT模型通常用于描述非均质介质中的孔隙分布,而Gassmann模型则考虑了孔隙之间的连接性。结合KT模型与Gassmann模型,构建饱和流体连通孔隙与饱和流体不连通孔隙。

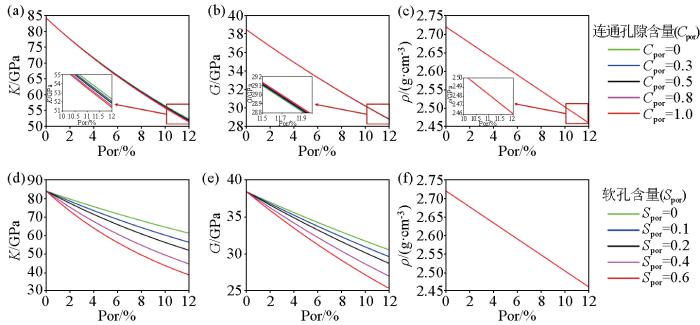
该模型引入了两个关键的孔隙参数:连通孔隙含量和软孔含量,可以更精确地刻画碳酸盐岩储层孔隙系统的复杂性,为深入分析和研究提供了便利。图4展示了不同孔隙参数对岩石弹性参数的影响。如图可知,弹性参数与孔隙度均呈负相关关系;体积模量与连通孔隙含量和软孔含量均表现为负相关关系;剪切模量与连通孔隙含量呈正相关,而与软孔含量呈负相关;由于储层各组分的组成未发生变化,在相同的孔隙度条件下,孔隙参数的变化对岩石密度没有影响。此外,随着孔隙度的增加,弹性模量对孔隙参数的变化变得更加敏感。在低孔隙度条件下(孔隙度小于10%), 弹性模量对软孔含量更为敏感。因此,在针对致密碳酸盐岩储层的研究中,孔隙形态成为描述孔隙形状系统的一个关键参数。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 基于岩石物理模型的孔隙参数对弹性模量影响分析

a—连通孔隙变化情况下孔隙参数与体积模量关系;b—连通孔隙变化情况下孔隙参数与剪切模量关系;c—连通孔隙变化情况下孔隙参数与密度关系;d—软孔含量变化情况下孔隙参数与体积模量关系;e—软孔含量变化情况下孔隙参数与剪切模量关系;f—软孔含量变化情况下孔隙参数与密度关系

Fig.4 Effect analysis of pore parameters on elastic modulus based on rock physical model

a—the relationship between pore parameters and bulk modulus when connected pores change; b—the relationship between pore parameters and shear modulus when connected pores change; c—the relationship between pore parameters and density when connected pores change; d—the relationship between pore parameters and bulk modulus when soft pore content changes; e—the relationship between pore parameters and shear modulus when soft pore content changes; f—the relationship between pore parameters and density when soft pore content changes

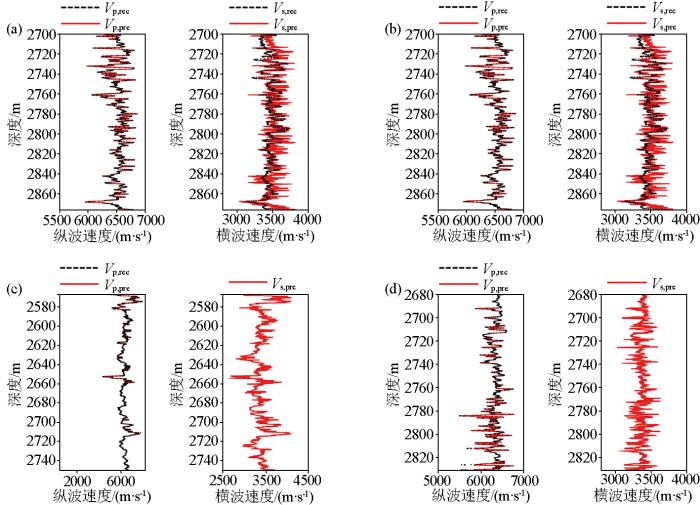
岩石物理模型建立了储层物性参数与弹性参数之间的关系,通过岩石物理建模,我们能够深入研究孔隙形状与弹性参数之间的关系。在此基础上,借助深度学习构建弹性参数与储层孔隙形状参数之间的多元非线性回归模型,预测孔隙形状参数,以进一步了解储层孔隙系统。敏感性分析通常需要考虑多个井而非单一井,因此选择了研究区内外过目的层的5口井进行分析。由于并非所有井都有横波速度数据,必须对这5口井展开横波速度的预测工作,以更好地组合各类弹性参数并进行敏感性分析。借助岩石物理模型进行了基于纵波约束的横波速度预测,结果如图5所示。其中,井I1和井I2具有横波速度作为质控井,而井1、井2没有横波速度作为预测井。图中红色曲线代表岩石物理模型计算得到的预测速度,而黑色曲线则为测井曲线。观察可知,五口井的预测纵波与实际纵波基本一致,质控井的预测横波速度与实际横波速度曲线具有较高的拟合度,预测精度在可接受范围内。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 横波速度预测结果

a—质控井I1横波预测结果;b—质控井I2横波预测结果;c—预测井1横波预测结果;d—预测井2横波预测结果

Fig.5 Shear wave velocity prediction results

a—shear wave prediction results of quality control well I1; b—shear wave prediction results of quality control well I2; c—shear wave prediction results of prediction well 1; d—shear wave prediction results of prediction well 2

2.3 孔隙结构参数预测

孔隙形状参数与弹性属性之间呈现出复杂的非线性关联,据此,可以通过弹性属性对储层孔隙形状参数进行估算。考虑到这种关系的复杂性,深度学习算法的应用显得尤为重要。采用深度学习技术,对物性参数反演进行反演分析。

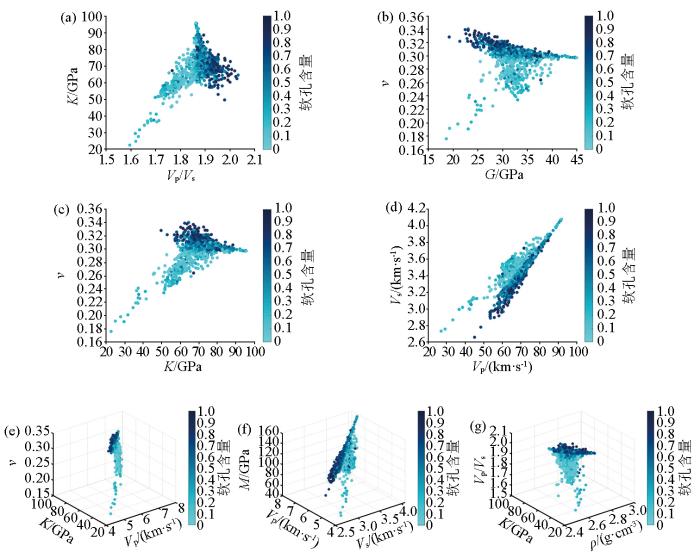
结合五口井的纵波速度 $V$ _p、横波速度 $V$ _s、密度 $ρ$ 以及体积模量 $K$ 、剪切模量 $G$ 、纵波模量 $M$ 、泊松比 $ν$ 等弹性参数曲线,开展孔隙形状参数对不同弹性参数组合的敏感性分析,为深度学习选取最优的弹性参数组合。首先进行了两参数组合的敏感性分析,其中纵横波速度比—体积模量、剪切模量—泊松比、体积模量—泊松比、纵波速度—横波速度均可较好地区分孔隙形状参数,结果如图6a所示。基于两参数组合结果,增加弹性参数的个数进一步开展三参数组合的方式进行敏感性分析,发现体积模量—纵波速度—泊松比、纵波速度—横波速度—纵波模量和体积模量—密度—纵横波速度比可以进一步区分孔隙形状参数,结果如图6b~d所示,增加弹性参数的个数能更好地区分孔隙形状参数。最终,我们选择了体积模量—纵波速度—泊松比作为弹性参数的组合,预测孔隙形状参数。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 孔隙形状参数(软孔含量)敏感性分析

a—纵横波速度比与体积模量散点分析;b—剪切模量与泊松比量散点分析;c—体积模量与泊松比散点分析;d—纵波速度与横波速度散点分析;e—体积模量、纵波速度和泊松比散点分析;f—纵波速度、横波速度和纵波模量散点分析;g—体积模量、密度和纵横波速度比散点分析

Fig.6 Sensitivity analysis of pore shape parameter(soft pore content)

a—scatter-point analysis of P-S velocity ratio and bulk modulus;b—scatter analysis of shear modulus and Poisson's ratio;c—bulk modulus and Poisson's ratio scatter analysis;d—scatter analysis of P-wave velocity and S-wave velocity;e—bulk modulus,p-wave velocity and Poisson's ratio scatter analysis;f—scatterpoint analysis of P-wave velocity,S-wave velocity and P-wave modulus;g—bulk modulus,density and P/S velocity ratio scatter analysis

本文所采用的神经网络为probabilistic neural network (PNN)。该网络通过训练同一地区地震属性和测井参数之间的关系,得到适用的网络模型,以便在只有地震数据的地区预测测井参数。该网络是全连接神经网络的一种。整体框架由输入层、隐藏层和输出层3部分构成。其中输入层为地震属性数据,隐藏层为属性数据与权重的非线性组合,输出层为预测的测井参数。神经网络模型可表示为:

(8)

y = f (\sum_{j = 1}^{p} x_{j} w_{j})

式中: $x_{j}$ 是输入数据,这里选取的是弹性参数数据, $w_{j}$ 为神经元权重, $f$ 为激活函数, $p$ 是隐藏层神经元的个数, $y$ 是输出数据,这里表示为预测的软孔含量。

为了提升网络的非线性能力,激活函数选用:

(9)

\begin{matrix} e_{i} = \frac{1}{P} \sum_{i = 1}^{p} (y_{i} - d_{i})^{2}, e = \frac{1}{N} \end{matrix} \sum_{i = 1}^{N} e_{i}

式中: $y_{i}$ 是预测结果, $d_{i}$ 表示该属性数据对应的真实测井参数。通过反传操作对神经网路权重进行更新,最小化误差则可以训练出较好的网络模型。所得到的网络模型则可以进行测井参数的预测。

2.4 基于流体因子的频散因子预测

在 Erzai 非弹性介质中,Russell 提出的纵波反射系数的近似方程^[7]如下:

(10)

R (θ, ω) = a (θ) \frac{Δ f}{f} + b (θ) \frac{Δ μ}{μ} + c (θ) \frac{Δ ρ}{ρ}

式中: $a (θ)$ 、 $b (θ)$ 、 $c (θ)$ 是与角度 $θ$ 有关的系数, $ρ$ 、 $μ$ 和 $f$ 分别为界面两侧密度、剪切模量和流体项的平均值,Δ $ρ$ 、Δ $μ$ 和Δ $f$ 分别为界面两侧密度、剪切模量和流体项的差值。

将上式在参考频率 $f_{0}$ 处进行泰勒展开,取一阶近似得到:

(11)

\begin{array}{l} R (θ, f) = A (θ) \frac{Δ V_{p}}{V_{p}} (f_{0}) + (f - f_{0}) A (θ) I_{a} + \\ B (θ) \frac{Δ V_{s}}{V_{s}} (f_{0}) + (f - f_{0}) B (θ) I_{b} \end{array}

式中: $I_{a}$ 和 $I_{b}$ 表示 $f_{0}$ 处阻抗的导数,称为反射率频散。

(12)

I_{a} = \frac{d}{d f} [\frac{Δ V_{p}}{V_{p}} (f_{0})], I_{b} = \frac{d}{d f} [\frac{Δ V_{s}}{V_{s}} (f_{0})]

对式(11)进行重新整理,得到:

(13)

R (θ, f) \approx R (θ, f_{0}) + α (θ, f)

式中:

(14)

R (θ, f_{0}) = A (θ) \frac{Δ V_{p}}{V_{p}} (f_{0}) + B (θ) \frac{Δ V_{s}}{V_{s}} (f_{0})

(15)

α (θ, f) = (f - f_{0}) A (θ) I_{a} + (f - f_{0}) B (θ) I_{b}

。

建立频变反射系数与地震数据之间的关系。将具有n道的AVO道集数据用矩阵表示为D(t,n),对数据矩阵进行谱分解得到S(t,n,f)。考虑Robinson褶积模型,地震波场 $S (θ, f)$ 相当于子波 $W (θ, f)$ 与地层反射系数 $R (θ, f)$ 的褶积,其对应的频率域表达式为:

(16)

S (θ, f) = W (θ, f) R (θ, f)

考虑地震波的频散效应,则有:

(17)

S (θ, f) = W (θ, f) [R (θ, f_{0}) + α (θ, f)]

上式在频率 $f_{0}$ 和 $f_{i}$ 处的表达式为:

(18)

S (θ, f_{0}) = W (θ, f_{0}) R (θ, f_{0})

(19)

S (θ, f_{i}) = W (θ, f_{i}) [R (θ, f_{i}) + α (θ, f_{i})]

。

由于地震子波的能量不随频率均衡分布,因此对不同频率的振幅对比,会出现“子波叠印”现象,常采用谱均衡方法进行消除。

(20)

\begin{array}{l} W (θ, f_{0}) S (θ, f_{i}) - W (θ, f_{i}) S (θ, f_{0}) = \\ W (θ, f_{0}) W (θ, f_{i}) α (θ, f_{i}) \end{array}

。

将上式简化为矩阵表达式:

(21)

S = W [\begin{array}{l} I_{a} \\ I_{b} \end{array}]

式中, $S = W_{θ_{i}}^{f_{0}} S_{θ_{i}}^{f_{j}} - W_{θ_{i}}^{f_{j}} S_{θ_{i}}^{f_{0}} (i = 1,2, \dots, n; j = 1,2, \dots, m), i 为第 i 个入射角, j 为第 j$ 个频率, $W = [W (θ, f_{0}) W (θ, f_{i}) (f_{j} - f_{0}) A (θ) W (θ, f_{0}) W (θ, f_{i}) (f_{j} - f_{0}) B (θ)]$ 。

通过最小二乘法得到 $I_{a}$ 和 $I_{b}$ :

(22)

[\begin{array}{l} I_{a} \\ I_{b} \end{array}] = (W^{T} W) W^{T} S

。

2.5 多属性融合

基于局部熵的LP-PCNN的多属性融合方法,可以在一定程度上压制单属性中存在的冗余或错误信息,提高信噪比。拉普拉斯金字塔算法(LP)可以将属性分解到多个尺度的空间频带上,通过上采样获得重建的拉普拉斯金字塔, 将高斯金字塔进行上采样, 然后进行高斯卷积滤波, 将得到的每一层图像与拉普拉斯金字塔存放的残差进行对应相加。最终,分离出细节信息的同时保护单个属性的完整性, 以确保多属性融合的准确性。利用拉普拉斯高斯金字塔进行多尺度分解(式(23))与重构(式(24))的第 $l$ 层图像 $L_{p l}$ 为:

(23)

\{\begin{array}{l} \begin{array}{l} L_{p l} = G_{l} - G_{l + 1}^{*} & 0 \leq l N \end{array} \\ \begin{array}{l} L_{P N} = G_{N} & l = N \end{array} \end{array}

(24)

\{\begin{array}{l} \begin{array}{l} G_{N} = L_{P N} & l = N \end{array} \\ \begin{array}{l} G_{l} = L_{p l} + G_{l + 1}^{*} & 0 \leq l N \end{array} \end{array}

式中:

(25)

G_{l} (i, j) = \sum_{m = - 2}^{2} \sum_{n = - 2}^{2} Ω (m, n) G_{l - 1} (2 i + m, 2 j + n)

(26)

G_{_{l}}^{*} (i, j) = 4 \sum_{m = - 2}^{2} \sum_{n = - 2}^{2} Ω (m, n) G'_{_{l}} (\frac{i + m}{2}, \frac{j + n}{2})

$Ω (m, n)$ 为具有低通滤波作用的高斯卷积核。

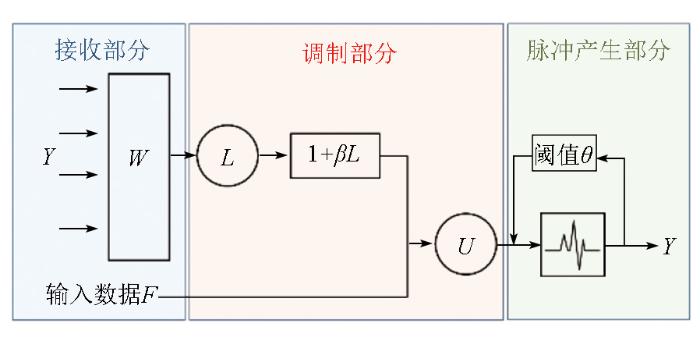
PCNN是一个由若干神经元局部互联的单层二维反馈网络,构成PCNN系统的每一个神经元都是动态的,如图7为其简化模型流程。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 PCNN模型流程

Fig.7 Flow chart of PCNN model

利用PCNN神经网络计算每个层的点火频率(FM),如式(27):

(27)

F M (i, j) = \frac{\sum_{k = 1}^{N} Y_{i j} (k)}{N}

局部熵可以用作点火频率评价因子对各尺度属性子带进行融合,如式(28):

(28)

L E (i, j) = \sum_{k = 0}^{K} p_{k} l o g_{2} p_{k}

式中:

(29)

p_{k} = h (k) / (m \times n)

。

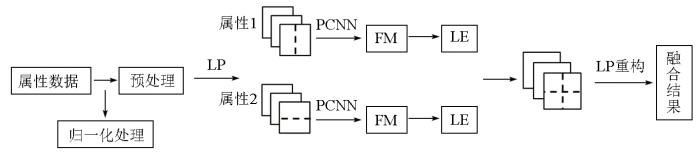
利用LP-PCNN的多属性融合方法流程如图8所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 LP-CNN多属性融合方法流程(以两种属性为例)

Fig.8 LP-CNN multi-attribute fusion process(using two attributes as an example)

2.6 模型测试

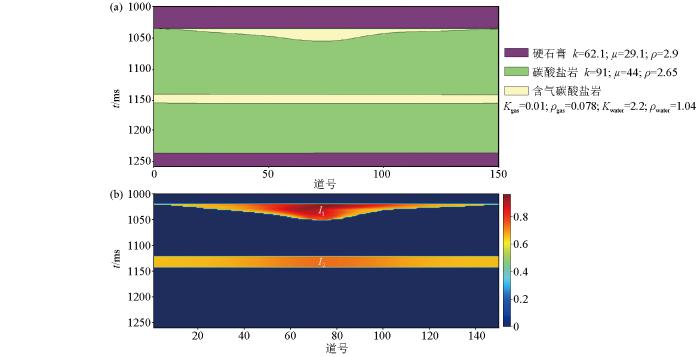
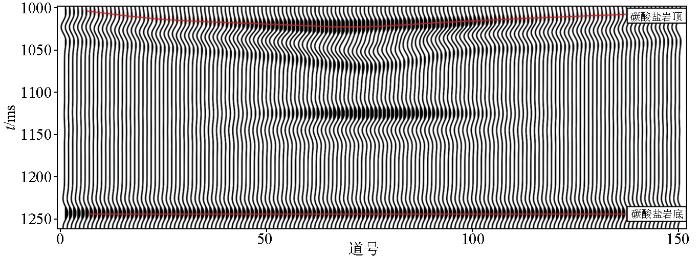
如图9建立硬石膏—碳酸盐岩—硬石膏的三层模型、碳酸盐岩储层含两段气层,其中气层 $I_{1}$ 的含气饱和度高于气层 $I_{2}$ 。地震正演记录如图10所示,可以看出碳酸盐岩顶层与底层由于岩性差异形成较为明显的强反射,距离顶界面较近的气层 $I_{1}$ 反射界面较弱,距离分界面有一定距离的气层 $I_{2}$ 有较为明显的反射。利用2.1~2.3节理论获取单一属性结果如图11所示,其中,图11a~c分别为纵波速度差、频散因子、孔隙结构参数。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 模型储层(a)及含气饱和度(b)示意

Fig.9 Model reservoir(a) and gas saturation(b) diagram

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 地震正演结果

Fig.10 Earthquake forward modeling resul

图11

新窗口打开| 下载原图ZIP| 生成PPT

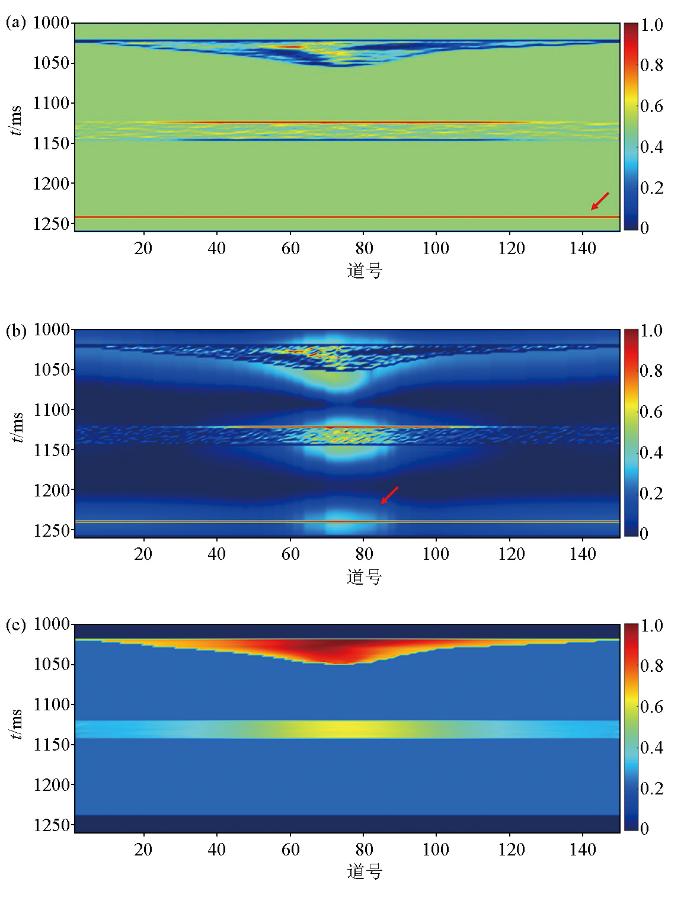
图11 单属性结果示意

a—纵波速度差(归一化结果);b—频散因子(归一化结果);c—孔隙结构参数

Fig.11 Schematic diagram of single-attribute results

a—longitudinal wave velocity difference(normalized result);b—dispersion factor(normalized result);c—pore structure parameters

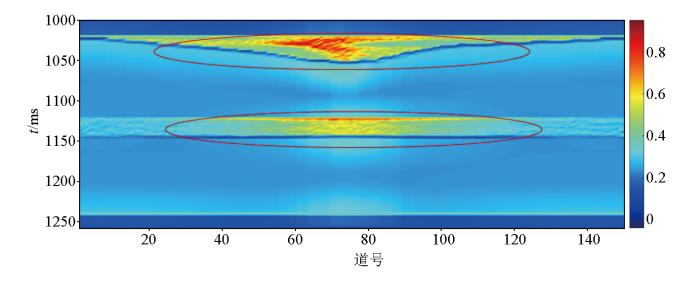
图11可以看出,纵波速度差与频散因子均在气层区域有较为明显的指示作用,由于受岩性的影响,使得其在岩性分界面处形成明显的高值区域,如图中箭头所指位置;孔隙结构参数在有利区域一般会具有高值,如图11c所示,气层中的孔隙结构参数具有明显的高值,且气层 $I_{1}$ 的孔隙结构参数高于气层 $I_{2}$ 。利用2.4节理论的多属性融合结果如图12所示,多属性融合结果结合了单属性的油气层指示作用,通过属性融合有效减少了由于岩性等因素产生的虚假指示区域,有效指示了储层含油气有利区,如图红色框线所示。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 多属性融合预测结果(归一化结果)

Fig.12 Prediction results of multi-attribute fusion(normalized results)

3 应用效果

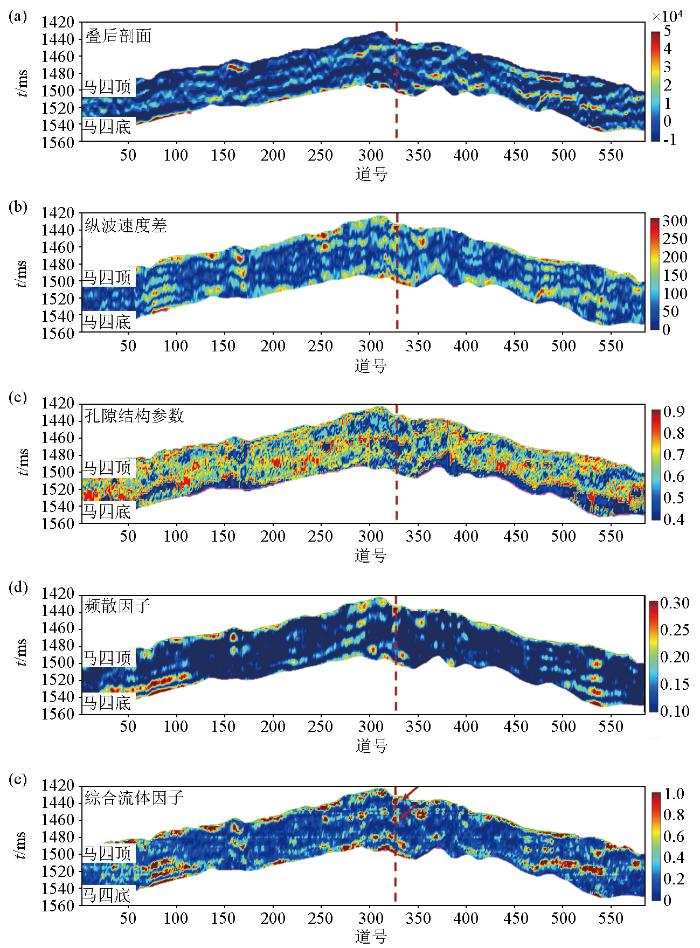
根据测井解释结构在鄂尔多斯盆地奥陶系马家沟组井1的马四段上段和中段分别有气层与含油气层显示。图13a~e分别展示了叠后剖面与各属性的预测结果,图中红色虚线位置为井1位置,图13e红色箭头所指示的位置分辨表示井1的气层与含气水层位置。本文所建立的考虑孔隙形状的综合流体因子,综合考虑弹性参数、频散属性与孔隙形状参数,相对于单一属性的流体因子(频散属性、纵波速度差等)在油气层区域具有更为明显的指示作用,使得预测剖面呈现更为清晰和明显的有利区指示效果。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 马四段预测结果示意

Fig.13 Schematic of the prediction results of the fourth section of Majiagou Formation

4 结论

单一属性的流体识别能够反映储层的流体响应,但是容易受到储层其他因素的影响,产生虚假响应。本文考虑道鄂尔多斯奥陶系马家沟组碳酸盐岩储层流体识别难点大的问题,提出了一种多属性流体综合识别的方法。储层中流体会导致纵波速度降低以及纵波速度频散特征。此外,考虑到碳酸盐岩储层孔隙结构的复杂性,建立考虑孔隙连通性与孔隙形状的岩石物理模型,正演分析发现孔隙形状对储层弹性模量的影响远大于孔隙连通性。因此,本文综合考虑储层纵波速度的变换、纵波速度的频散响应以及储层孔隙形状特征;利用LP-PCNN多属性融合方法,获得流体综合因子DFC。利用模型数据测试,研究了多属性融合的流体因子具有更高的精度。基于工区实际资料的测试,取得不错的效果。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

付金华, 刘新社, 魏柳斌, 等.

鄂尔多斯盆地奥陶系盐下马家沟组四段天然气勘探突破及意义

[J]. 中国石油勘探, 2022, 27(2):47-58.

DOI:10.3969/j.issn.1672-7703.2022.02.005 [本文引用: 4]

鄂尔多斯盆地奥陶系马家沟组发育碳酸盐岩—膏盐岩共生体系沉积，马家沟组四段(马四段)是马家沟组沉积厚度最大的一套海侵碳酸盐岩沉积层，长期以来是天然气勘探关注的重点层位。基于地球物理、钻井岩心及有机地球化学等资料，重新认识了鄂尔多斯盆地奥陶系盐下古构造、储层分布、烃源岩和圈闭等成藏条件，并取得以下成果认识：(1)盐下马四段天然气为油型气，主要来自奥陶系盐下海相烃源岩，该套烃源岩生烃母质除常规干酪根外，还发育分散有机质、有机酸盐，生烃物质丰厚，具备规模生烃潜力；（2）奥陶纪鄂尔多斯盆地中东部坳陷存在乌审旗—靖边古隆起和东部盐下低隆两大次级构造单元，分别控制了盐下马四段台内滩、台内丘白云岩储层的发育，储集空间主要为白云岩晶间孔；(3)盆地中东部盐下马四段台内滩、台内丘白云岩上覆厚层膏盐岩封盖，上倾方向致密石灰岩侧向遮挡，海相烃源岩供烃，形成了大面积分布的自生自储式岩性气藏。在新的地质理论认识的指导下，针对鄂尔多斯盆地奥陶系盐下马四段部署的风险探井MT1井钻遇气层43.4m，采用水力加砂压裂新工艺，试气获35.24×104m3/d的高产工业气流，实现了盆地战略接替领域的重大突破。

J H

, Liu

X S

, Wei

L B

, et al.

Natural gas exploration breakthrough and significance of the fourth Member of the Ordovician subsalt Majiagou Formation in Ordos Basin

[J]. China Petroleum Exploration, 2012, 27(2):47-58.

[本文引用: 4]

[2]

何海清, 郭绪杰, 赵振宇, 等.

鄂尔多斯盆地奥陶系盐下马四段天然气成藏新认识及勘探重大突破

[J]. 石油勘探与开发, 2022, 49(3):429-439.

DOI:10.11698/PED.20210659 [本文引用: 4]

基于大量钻井、测井和地震资料分析,对鄂尔多斯盆地奥陶系盐下马家沟组四段天然气地质条件与成藏主控因素开展研究,提出古隆起控相、控储、控藏新认识：①马家沟组沉积期,中央古隆起分隔盆地中东部华北海与西南缘秦祁海两大沉积体系,在马四段台缘带发育巨厚丘状颗粒滩相白云岩,同时控制盆地中东部形成“两隆两凹”古地理格局,其中水下低隆带发育台内滩相白云岩,隆间低洼区发育泥灰岩。②由中央古隆起至盆地东缘,马四段白云岩逐渐减薄并相变为灰岩,灰岩致密带侧向封挡形成大面积白云岩岩性圈闭。③加里东末期中央古隆起遭受不同程度剥蚀,面积达6×10<sup>4</sup> km<sup>2</sup>,上古生界石炭系—二叠系煤系优质烃源岩大面积披覆沉积,成为下伏奥陶系盐下白云岩岩性圈闭规模供烃主体。④印支期—燕山期盆地西倾掀斜,中央古隆起下拗转变为高效供烃窗,上古生界煤系烃源岩通过中央古隆起高孔渗白云岩体向上倾高部位侧向供烃,盐下海相烃源岩作为重要的气源补充,通过加里东期断裂、微裂缝输导供烃。以新认识为指导,转变勘探思路,综合评价优选盆地中东部马四段两大有利勘探区,部署实施两口风险探井均钻遇较厚马四段（含）气层,其中1口井获高产工业气流。该研究推动了奥陶系盐下马四段天然气勘探的历史性突破,开辟了鄂尔多斯盆地天然气勘探的重要新领域。

H Q

, Guo

X J

, Zhao

Z Y

, et al.

New understanding and exploration breakthrough of natural gas accumulation in the Fourth Member of Yanxama,Ordovician,Ordos Basin

[J]. Petroleum Exploration and Development, 2022, 49(3):429-439.

[本文引用: 4]

[3]

Smith

G C

, Gidlow

P M

Weighted stacking for rock property estimation and detection of gas

[J]. Geophysical Prospecting, 2010, 35(9):993-1014.