0 引言
重磁异常是不同地质体密度、磁性的综合反映,由不同深度、不同规模地质体叠加产生的,如何从叠加的异常中有效地分离出目标体引起的异常,是重磁数据处理与解释中的一项重要工作[1-2]。目前,位场分离方法主要分为空间域和频率域两大类。在空间域方法中,插值切割法和滑动窗口平均法广泛应用,但是窗口大小的选择具有人为性[3-4],结果受到人为因素的干扰。频率域常用的位场分离方法主要有匹配滤波、向上延拓差值场法等[5⇓⇓⇓-9],该类方法利用异常频率特征的不同来分离出区域异常和局部异常[10]。相较于传统位场分离的二分法(区域异常和局部异常),广泛应用于位场分离的小波分析方法[11-12]与功率谱分析相结合的重磁异常场分离效果较好。此外,陈召曦[13]利用位场(重磁)理论模型数据,实现了曲波变换的多方向性分析。
在位场分离过程中存在着区域场与局部场分离不足或过分离的现象,比如罗潇等[14]通过模型试验及实例应用,发现了空间域中的趋势分析法分离出的局部场中含有明显的虚假异常;任朗宁[9]通过模型试验发现,频率域中的匹配滤波在进行位场分离时存在过分离现象。而低秩稀疏分解(low-rank and spare matrix decomposition,LRSD),也叫鲁棒主成分分析(robust principal component analysis, RPCA),是一种新的矩阵分解理论,广泛应用于计算机信号处理领域。该方法在充分考虑数据矩阵特征的基础上,可以鲁棒地将矩阵分解为低秩部分和稀疏部分,低秩部分代表具有局部相关性的背景信号,稀疏部分代表中高频的局部信号。由于低秩成分可以较好地对背景信号进行建模,而稀疏分量可表示局部异常,因此在地球物理的重磁异常场分离中得到了推广应用[15⇓-17]。前人研究认为局部场的延滞矩阵具有稀疏性,区域场的延滞矩阵具有低秩性,将低秩稀疏分解用于位场分离有助于得到更高的分离精度[18⇓-20]。但在位场分离过程中存在两个问题:首先,朱丹等[18]提出了基于构造延滞矩阵的低秩分解进行位场分离的方法,但延滞矩阵维度较大,不仅需要大量内存空间用于存储,也需要更多的计算时间,比如对于M×N大小的矩阵,构造延滞矩阵后矩阵规模约增大为(M×N/2)2,增大了处理的难度与计算效率;其次在位场分离应用中,有关平衡参数选择的问题研究较少,缺乏确定平衡参数选择的依据。
朱丹等[18]为了使观测数据形成低秩结构进行了构造延滞矩阵,相当于对原始数据按照一定的分块准则进行重新排列,并未增加新的信息。重磁异常的局部场和区域场本身是具有稀疏特性和低秩特性的,具备直接进行矩阵低秩稀疏分解的前提,无需构造延滞矩阵。因此,本文研究直接针对重磁异常进行低秩分解以实现位场分离,并对影响低秩分解结果的平衡参数提出了参数最优化的方法,同时利用理论模拟与实际数据验证了本文方法的有效性。
1 方法原理
1.1 低秩稀疏分解
式中:‖A‖*表示核范数,也就是该矩阵进行奇异值分解之后得到的全部奇异值的和;‖E‖1表示L1范数,也就是该矩阵中全部元素求绝对值之后的和;λ为平衡参数。
本文采用不精确拉格朗日乘子法(Inexact augmented Lagrange multipliers, IALM)求解上式的最优化问题进行位场分离[25],该方法不需要针对增广拉格朗日函数L(A,E,Y,μ)求解最优化问题
假定E、Y和μ固定不变,则:
假定A、Y和μ固定不变,则:
Y和μ的迭代方式为
式中:Y为拉格朗日乘子;μ为补偿参数;‖ ‖F表示Frobenius范数;k为迭代次数;D、S分别表示奇异值阈值运输符、软阈值运算符;
1.2 平衡参数的选择
采用上述低秩矩阵分解时,平衡参数λ的选择直接影响到分离效果。Lin等[25]建议的平衡参数λ0=
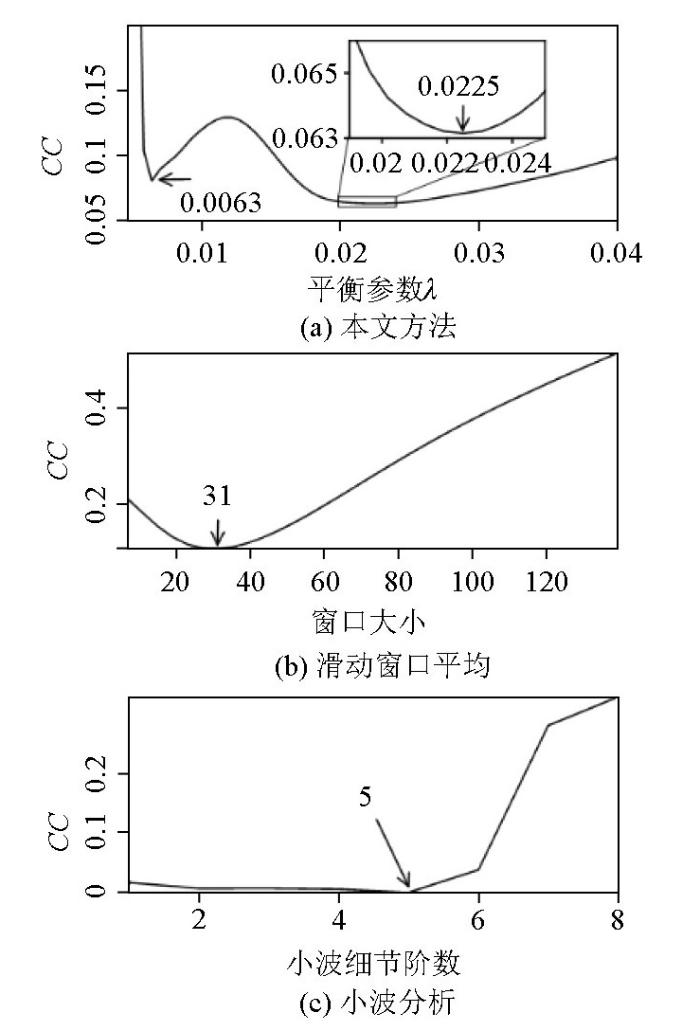
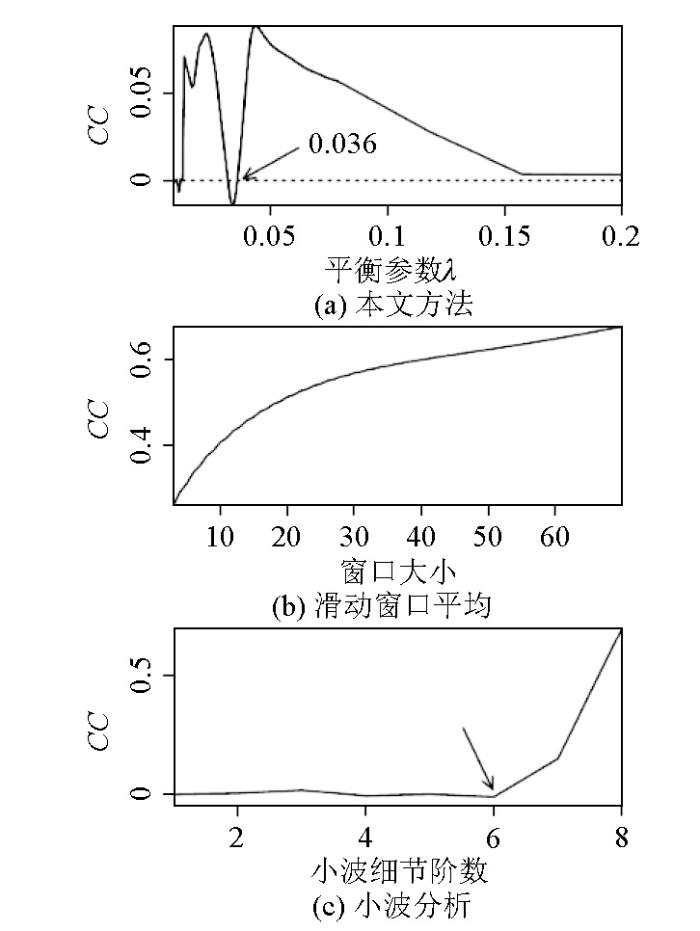
同时将此方法扩展应用于小波分析的分解阶数、滑动窗口平均的窗口大小等估计。对滑动窗口平均方法绘制窗口大小影响的相关系数曲线,当窗口过小时分离不足,产生一定的正相关,当窗口过大时导致过分离产生一定的负相关,合适的窗口产生较小的相关系数。对小波多尺度分析方法绘制分解阶数影响的相关系数曲线,分解阶数为1时细节信号主要由噪声主导,期望相关系数为零;随着分解阶数增大,局部异常逐渐被分离,此时期望相关系数依然为零;当分解阶数过大时,小波细节中包含有部分区域异常,相关系数迅速增大。因此,本文将相关系数由0迅速增大的拐点作为最优小波分解阶数。
综上所述,通过绘制不同参数分离的局部异常和区域异常的相关系数曲线,根据相关性最小或相关系数的拐点,可确定最优分离参数。
2 理论模型试验与对比分析
为了测试本文方法在重磁异常分离方面的优势,通过最优分离参数的选择方法确定参数并应用于理论模型试验中,进行低秩稀疏分解与小波分析、滑动窗口平均位场分离方法的对比分析。
2.1 磁异常模型试验与对比分析
表1 正演模型参数
Table 1
| 模型 | 中心坐标/m | 中心深度/ m | 尺寸/m | 磁化强度/ (A·m-1) |
|---|---|---|---|---|
| A:球体 | (300,750) | 50 | r=50 | 2 |
| B:球体 | (1 200,750) | 300 | r=100 | 10 |
| C:棱柱体 | (600,750) | 1200 | a=500,b=100, c=100 | 100 |
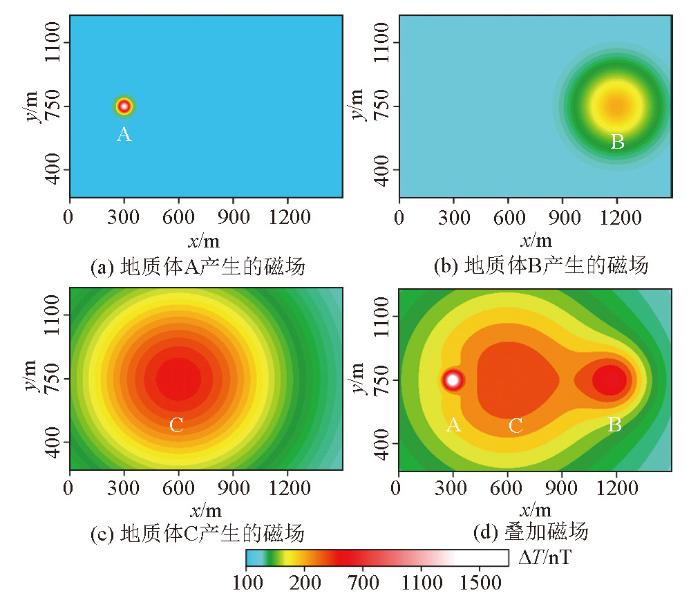
图1
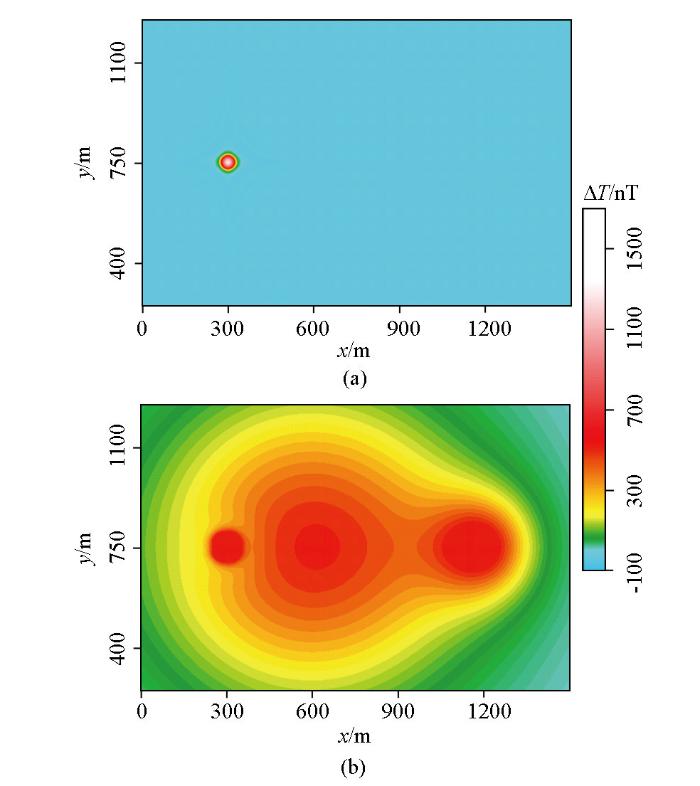
图2
图2
采用λ0=0.057 6的低秩矩阵分解得到的局部磁异常(a)和区域磁异常(b),其中(a)表示从叠加场中分离得到的A异常
Fig.2
The separated residual (a) and regional (b) anomalies by the low-rank decomposition using a balance parameter determined in the previous studies
图3
图3
根据相关系数(CC)估计分离参数
Fig.3
The correlation coefficients (CC) between the separated residual and regional fields using different parameters in the mentioned methods
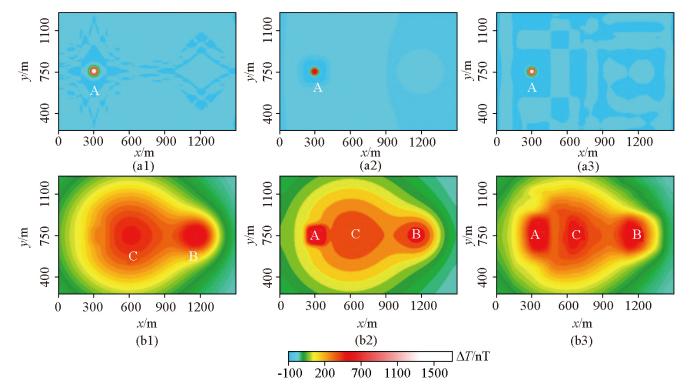
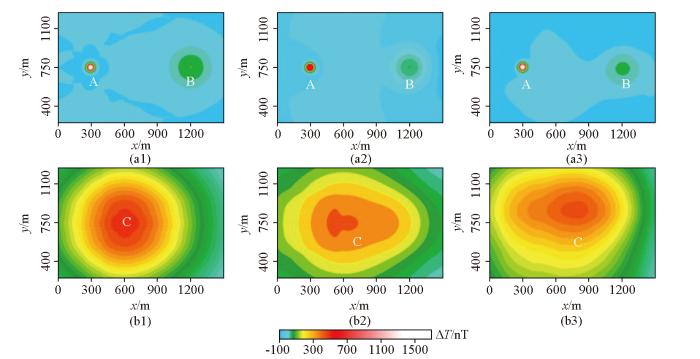
图4是采用图3估计的参数得到的磁场分离结果,其中低秩矩阵分解的平衡参数首先采用估计参数λ=0.022 5。可以看出,低秩矩阵分解将异常A从异常B和C中较好的分离;滑动窗口平均和小波多尺度分解两种方法将一部分异常A的信息分离出来,但在分离得到的区域异常中显示了显著的分离不彻底的现象。为了将A、B、C这3个异常分别分离,我们将更多的短波长异常能量进行分离,如图5所示,其中低秩矩阵分解的平衡参数采用估计参数λ=0.006 3;滑动窗口平均的窗口大小是根据多次实验选取的101×101;小波细节阶数根据试验取7。可以看出,本文方法将异常A和B从异常C中分离(图5a1、b1),分离得到的区域异常反映了异常C的特征(图5b1);而较大的窗口使得滑动窗口平均能够将局部异常A和B从异常C中分离(图5a2、b2),利用较大的小波细节也可以更好的分离异常A和B(图5a3、b3),然而在分离得到的区域异常中,由于分离不彻底或过分离显著改变了区域异常C的形态特征(图5b2、5b3)。
图4
图4
不同方法将A异常与叠加场分离得到的局部磁异常(a1~a3)和区域磁异常(b1~b3)
(a1、b1—是本文方法采用λ=0.022 5得到的结果;a2、b2—是滑动窗口平均采用窗口大小为31×31时得到的结果;a3、b3—是小波多尺度分析采用5阶小波细节得到的结果)
Fig.4
The potential field separations using different methods
(a1、b1—the residual anomalies and regional anomalies using the low-rank decomposition with a balance parameter of λ=0.022 5; a2、b2—the residual anomalies and regional anomalies using the sliding window average method with a window size of 31×31; a3、b3—the residual anomalies and regional anomalies using the wavelet analysis method with 5 orders details
图5
图5
不同方法将A、B异常与叠加场分离得到的局部磁异常(a1~a3)和区域磁异常(b1~b3)
(a1、b1—是本文方法采用λ=0.0 063得到的结果;a2、b2—是滑动窗口平均采用窗口大小为101×101时得到的结果;a3、b3—是小波多尺度分析采用7阶小波细节得到的结果)
Fig.5
The potential field separations using different methods
(a1、b1—the residual anomalies and regional anomalies using the low-rank decomposition with a balance parameter of λ=0.006 3; a2、b2—the residual anomalies and regional anomalies using the sliding window average method with a window size of 101×101; a3、b3—the residual anomalies and regional anomalies using the wavelet analysis method with 7 orders details)
图6
图6
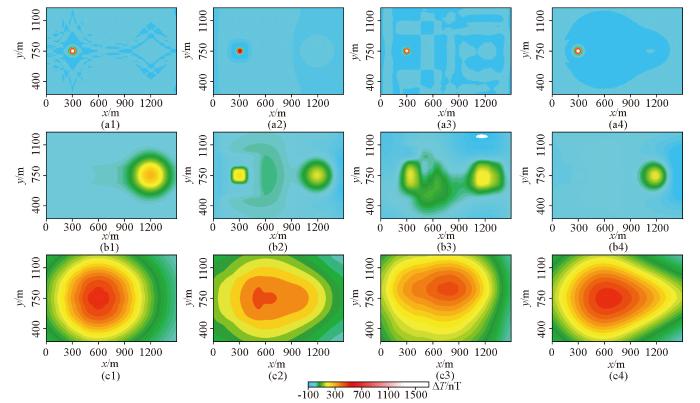
不同方法对A、B、C这3个磁异常的分离结果(a1、b1、c1—是本文方法得到的分离结果;a2、b2、c2—是滑动窗口平均得到的分离结果;a3、b3、c3—是小波多尺度分解得到的分离结果;a4、b4、c4—是采用Zhu等[19]的方法得到的分离结果)
Fig.6
The separated result of anomalies A, B, and C with different methods(a1、b1、c1—the results using the proposed method; a2、b2、c2 —the results using the sliding window average method; a3、b3、c3—the results using the wavelet analysis method; a4、b4、c4—the results using the method from Zhu et al.[19])
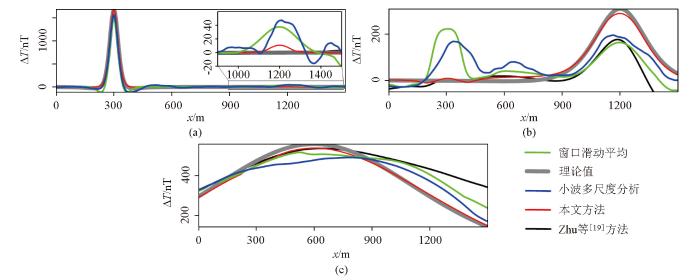
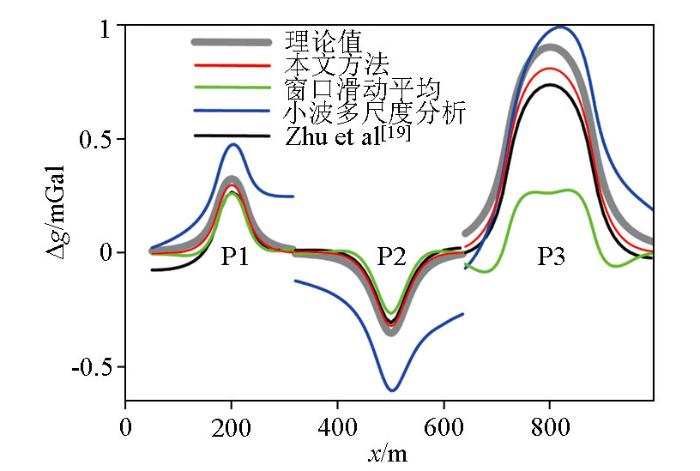
通过表2所示的4种方法进行A、B、C磁异常的分离结果与理论值之间的相关系数(CC)和最大误差(Err)分析可知,本文方法分离结果的相关系数接近1,最大误差显著低于滑动窗口平均和小波多尺度分析方法;相比Zhu等[19]采用的构造延滞矩阵的低秩分解方法,本文直接进行低秩矩阵分解的分离方法能更彻底的分离异常,其中A异常分离结果的相关系数相似,但本文方法得到的最大误差更小,对B、C这2个异常具有更高的分离精度,相关系数与最大误差均显著优于Zhu等[19]采用的方法。为了更加直观地显示不同方法分离结果的差异,选择过异常中心的剖面(y=750 m)对应的磁异常曲线进行对比(图7)。可以看出,使用本文方法分离的磁场曲线与理论曲线有较高的重合度,能够较完整地进行局部异常与区域异常的分离;滑动窗口平均方法分离出的局部异常和区域异常与真实值之间存在较大误差,主要是因为滑动窗口平均值的计算“平滑”了区域异常的幅值,使得部分区域异常的特征被当作为局部异常(如图中的绿色线所示)。小波分析方法得到的局部异常与滑动窗口平均结果相似,没有完整的将局部异常分离,局部异常中一些相对低频的信息被当作区域异常(如图中的蓝色线),存在局部异常分离不彻底的现象。而传统采用构造延滞矩阵的低秩分解(图中黑色线)没有较好的分离B异常,使得部分B异常的信息被当作C异常导致分离不彻底。
表2 位场分离结果与理论值的相关系数(CC)和最大误差(Err)
Table 2
| 本文低秩矩阵分解 | 滑动窗口平均 | 小波多尺度分析 | Zhu等[19] | |||||
|---|---|---|---|---|---|---|---|---|
| CC | Err/nT | CC | Err/nT | CC | Err/nT | CC | Err/nT | |
| 异常A | 0.99 | 30.6 | 0.92 | 201.5 | 0.93 | 131.7 | 0.99 | 64.4 |
| 异常B | 0.99 | 21.2 | 0.55 | 226.1 | 0.55 | 171.5 | 0.47 | 201.2 |
| 异常C | 1.00 | 29.9 | 0.97 | 110.0 | 0.94 | 109.5 | 0.94 | 198.2 |
图7
图7
不同方法位场分离的异常A(a)、B(b)、C(c)沿着中心剖面y=750 m对应的磁异常剖面对比
Fig.7
Comparison of the separated anomalies A (a), B (b), and C (c) along the profile y=750 m
2.2 重力异常模型试验与对比分析
图8
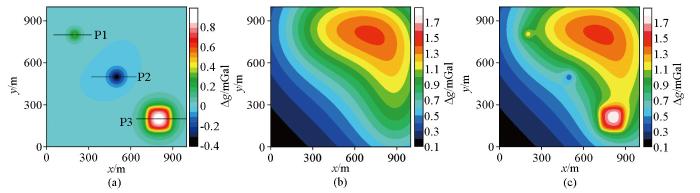
图8
理论模拟的局部重力异常(a)、区域重力异常(b)以及总重力异常(c)(图中的P1、P2、P3剖面将用于
Fig.8
The modeled residual (a), the regional (b), and the total (c) gravity anomalies(P1, P2, and P3 shown in
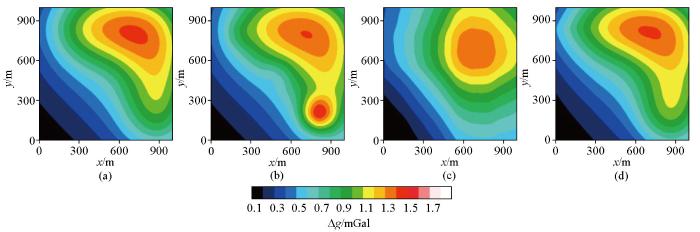
采用本文方法、窗口滑动平均、小波多尺度分析方法进行对比分析。利用相关系数准则得到的各方法的分离参数,即:λ为0.012、滑动窗口平均的窗口大小为35×35、小波细节阶数为7。图9a~c、10a~c是采用估计的参数得到的位场分离结果,图9d、10d是采用构造延滞矩阵的低秩分解方法得到的分离效果。可以看出,采用低秩分解方法能够更有效地分离局部异常和区域异常(图9a、d,图10a、d),而滑动窗口平均和小波多尺度分解两种方法都出现了一定程度的畸变(图9b、c,图10b、c)。如图11所示,采用本文方法的分离结果与Zhu 等[19]的结果总体上优于滑动窗口平均和小波多尺度分析方法;相对采用构造延滞矩阵的低秩分解方法[19](图11黑色线),本文方法分离得到的局部异常更加逼近真实值(图11红色线)。
图9
图10
图11
图11
不同方法分离的局部重力异常沿
Fig.11
Comparison of the separated anomalies along the profiles P1~P3 as shown in
3 矽卡岩型铁多金属矿区重力资料处理
图12
图12
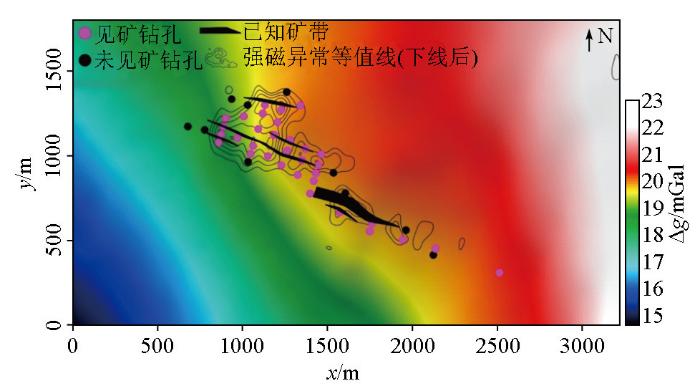
研究区1∶1万布格重力异常
Fig.12
1∶10 000 Bouguer gravity anomaly in the study area covered by the downward continued magnetic anomalies with high values
图13
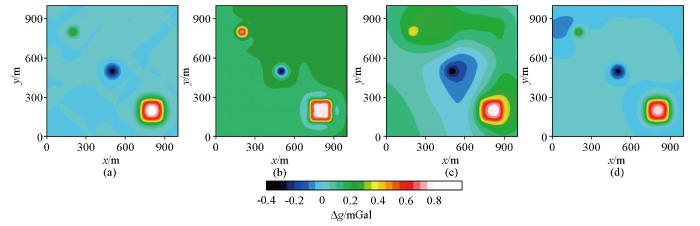
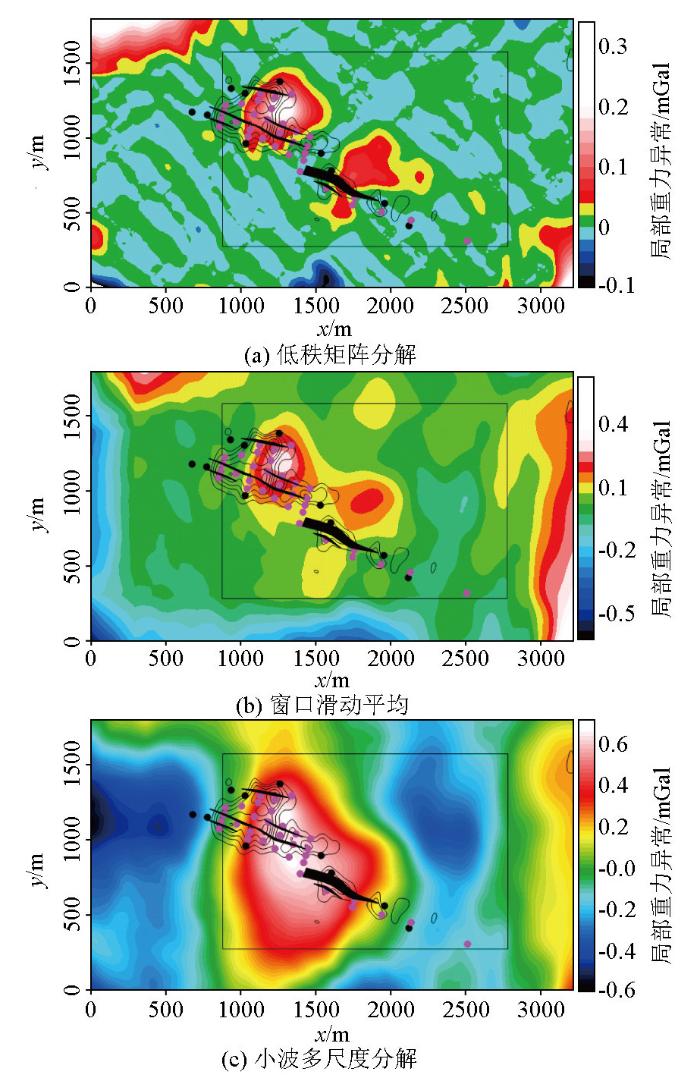
通过以上参数进行分离得到的局部布格重力异常如图14所示。总体上看,3种方法皆分离了局部高重力异常的特征,但细节部分存在显著差异。表3显示不同方法分离的局部异常与区域异常的相关性,可以看出,无论是对全区还是局部异常区,采用本文低秩矩阵分解得到的局部异常与区域异常显示较低的相关性,表明分离过程没有发生显著的分离不足或过分离。而滑动窗口平均和小波多尺度分解方法得到的局部异常和区域异常存在显著的相关性,其中滑动窗口平均分离的结果在全区显示正相关是因为窗口平均难以完全分离局部异常和区域异常,导致分离的局部异常中存在一部分区域异常的特征,因此产生较高的正相关;而滑动窗口平均和小波多尺度分解在局部异常区都显示负相关,表示局部重力异常产生了过分离。此外,图14b与14c分离的局部重力异常特征复杂,不仅有显著的局部高重力异常,也存在显著的局部低重力异常特征。本研究区局部重力异常以高密度岩矿体引起的局部高重力异常特征为主,不存在低密度岩体引起低重力异常的条件,因此推测图14b、14c中的局部低重力异常是由于分离不当引起的伪异常。
图14
图14
3种方法分离的局部重力异常成果
Fig.14
The separated residual gravity anomalies using the mentioned three methods
表3 不同方法分离的局部异常与区域异常的相关系数
Table 3
| 低秩矩阵分解 | 滑动窗口平均 | 小波多尺度分析 | |
|---|---|---|---|
| 全区 | 0 | 0.55 | 0.14 |
| 局部( 黑色线框) | -0.08 | -0.22 | -0.74 |
低秩矩阵分解主要突出了区域重力异常中位于测区中心位置的两个局部高重力异常(图14a),该局部高重力异常位于磁异常和已知磁性矿体的外围,代表低磁性高密度的岩矿体。研究区矿体类型是矽卡岩型铁多金属矿[30],伴生有钴矿、铅锌矿以及金矿等。前人根据高精度磁测在该区开展了系统工作,钻探揭示的磁铁矿体与磁异常向下延拓结果具有良好的对应关系[31-32]。伴生矿体与矽卡岩体无显著的强磁性特征,但具有显著的高密度特征,是产生局部高重力异常的主要因素,因此从观测重力异常中分离局部重力异常,对寻找高密度岩矿体与控矿构造等具有重要意义[33]。从图14a可以看出,已知矿体主要围绕该重力高异常的边部、鞍部分布,表示该重力高异常与成矿关系紧密,推测是本区重要的控矿构造或铅锌等非磁性矿体富集区。
4 结论
1)本文研究了基于低秩稀疏分解进行重磁异常场分离的方法,相较于前人提出的基于构造延滞矩阵的低秩分解方法,本文直接针对原始重磁异常进行低秩矩阵分解,无须构造延滞矩阵,有效减少了计算量。通过与前人提出的基于构造延滞矩阵的低秩分解方法相比,采用本文方法能够得到更好的位场分离结果,得到的局部异常幅值以及形态更接近真实值。
2)平衡参数是影响低秩矩阵分解方法分离效果的敏感参数,本文提出了基于相关系数最小的平衡参数最优化估计方法,避免因参数选择不当而引起的结果偏差,为方法的实践应用提供了依据。通过模型实验,表明本文方法能够较好地估计得到最优参数,没有发生显著的分离不足或过分离现象,验证了方法的有效性。
3)将本文方法应用于中国西部某矿区重力异常的处理解释,分离的局部异常较清晰地反映了本区低磁性高密度的岩矿体分布特征,通过与其他方法对比验证了该方法的实用性,值得在实践中推广应用。
致谢
感谢中国地质调查局自然资源航空物探遥感中心周文月老师提供了模型数据的匹配滤波分离结果用于对比,并为论文修改提供了宝贵意见。文中重力异常处理采用中国地质大学(武汉)开发的Gra3DPro重力异常处理软件。文中模型数据及其处理结果可与张恒磊联系获取。
参考文献
一种实测重力异常区域场的消除方法
[J].
A way of eliminating the regional field of measured gravity anomalies
[J].
插值切割位场分离方法改进及其在资料处理中的应用
[J].
The improvement of the interpolation cutting potential field separation method and its application to data processing
[J].
深源矿致异常提取方法对比及应用:以山东齐河—禹城地区航磁数据为例
[J].
Comparison and application of extraction methods for aeromagnetic anomaly caused by deep magnetite:A case study of the Qihe-Yucheng ore area,Shandong
[J].
金牛火山岩盆地重磁异常综合分析及找矿预测
[J].
Comprehensive analysis of gravity and magnetic anomalies in Jinniu volcanic basin for prediction of ore deposits
[J].
一种重力异常向上延拓高度最优化确定方法
[J].
Amethod for determining the optimal height for upward continuation of gravity anomalies
[J].
基于球面重力反演苏拉威西地区莫霍面结构
[J].
Moho structure in Sulawesi area based on spherical gravity inversion
[J].
磁异常小波多尺度分解及危机矿山的深部找矿:以大冶铁矿为例
[J].
Wavelet multi-scale decomposition of magnetic anomaly and its application in searching for deep-buried minerals in crisis mines:A case study from Daye iron mines
[J].
重力位场小波多尺度分解性质的分析与应用
[J].
Property analysis and application of multi-scale wavelet decomposition of gravity potential field
[J].
位场异常分离方法的对比分析——以江西相山铀多金属矿田为例
[J].
Comparative analysis on the methods of potential field separation:A case study of the Jiangxi Xiangshan uranium polymetallic orefield
[J].
求解二阶解耦弹性波方程的低秩分解法和低秩有限差分法
[J].
DOI:10.6038/cjg2018L0257
[本文引用: 1]

时间域的波场延拓方法在本质上都可以归结为对一个空间-波数域算子的近似.本文基于一阶波数-空间混合域象征,提出一种新的方法求解解耦的二阶位移弹性波方程.该方法采用交错网格,连续使用两次一阶前向和后向拟微分算子,推导得到了解耦的二阶位移弹性波方程的波场延拓算子.由于该混合域象征在伪谱算子的基础上增加了一个依赖于速度模型的补偿项,可以补偿由于采用二阶中心差分计算时间微分项带来的误差,有效地减少模拟结果的数值频散,提高模拟精度.然而,在非均匀介质中,直接计算该二阶的波场延拓算子,每一个时间步上需要做N次快速傅里叶逆变换,其中N是总的网格点数.为了减少计算量,提出了交错网格低秩分解方法;针对常规有限差分数值频散问题,本文将交错网格低秩方法与有限差分法结合,提出了交错网格低秩有限差分法.数值结果表明,交错网格低秩方法和交错网格低秩有限差分法具有较高的精度,对于复杂介质的地震波数值模拟和偏移成像具有重要的价值.
Solving second-order decoupled elastic wave equation using low-rank decomposition and low-rank finite differences
[J].
A tensor higher-order singular value decomposition for prestack seismic data noise reduction and interpolation
[J].
Seismic random noise attenuation using sparse low-rank estimation of the signal in the time-frequency domain
[J].
利用数据低秩性和稀疏性的位场分离
[J].
Potential field separation based on the low rank and sparse characteristics
[J].
Low-rank matrix decomposition method for potential field data separation
[J].
从压缩传感到低秩矩阵恢复:理论与应用
[J].
From compressed sensing to low-rank matrix recovery:Theory and applications
[J].
结合稀疏先验与多模式分解的低秩张量恢复方法
[J].
Low-rank tensor recovery using sparse prior and multi-modal tensor factorization
[J].
基于自适应加权低秩矩阵恢复的图像去噪
[J].
Image denoising based on adaptive weighted low-rank matrix recovery
[J].
Rank-sparsity incoherence for matrix decomposition
[J].
The augmented lagrange multiplier method for exact recovery of corrupted low-rank matrices
[J].
基于RPCA的群稀疏表示人脸识别方法
[J].
Group sparse representation face recognition method based on RPCA
[J].
基于低秩矩阵恢复的群稀疏表示人脸识别方法
[J].
Face recognition method by group sparse representation and low rank recovery
[J].
Ilvaite as a thermodynamic recorder of multistage retrograde alteration in large Galinge skarn Fe deposit,Western China
[J].
向下延拓在深部矿产勘探中的应用———以青海某矿区为例
[J].
The Application of downward continuation to deep mineral exploration:A case study of an ore distrist in QingHai Province
[J].
高精度磁测找矿效果:以青海尕林格矿区为例
[J].
Application of high-precision magnetic survey to prospecting:A case study in the Galinge deposit of Qinghai Province
[J].
基于噪声扰动下重力二阶垂向导数与归一化磁源强度的重磁相关性分析——以相山铀矿田为例
[J].
Gravity and magnetic correlation analysis based on the second-order vertical derivative of gravity anomaly and normalized source strength of magnetic anomaly with noise disturbance:A case of Xiangshan uranium orefields
[J].