基于VMD-LSTM对大地电磁信号进行噪声检测和预测重构

doi:10.11720/wtyht.2025.2309

基于VMD-LSTM对大地电磁信号进行噪声检测和预测重构

李博^,¹, 李长伟^,¹^,², 罗润林¹^,², 吕玉增¹^,², 王占¹

1.桂林理工大学地球科学学院,广西桂林 541000

2.广西隐伏金属矿产勘查重点实验室,广西桂林 541000

VMD-LSTM-based noise detection and predictive reconstruction for magnetotelluric signals

LI Bo^,¹, LI Chang-Wei^,¹^,², LUO Run-Lin¹^,², LU Yu-Zeng¹^,², WANG Zhan¹

1. College of Earth Sciences, Guilin University of Technology, Guilin 541000, China

2. Guangxi Key Laboratory of Exploration for Hidden Metallic Ore Deposits, Guilin 541000, China

通讯作者: 李长伟(1972-),女,桂林理工大学,博士,教授,研究方向为电磁地球物理方法。Email:lcw@glut.edu.cn

第一作者: 李博(1997-),男,桂林理工大学研究生,主要从事大地电磁信号处理工作。Email:1049895983@qq.com

责任编辑: 王萌

收稿日期: 2023-07-25 修回日期: 2023-10-8

基金资助:

广西自然科学基金项目(2020GXNSFAA297079)
国家自然科学基金项目(42274182)

Received: 2023-07-25 Revised: 2023-10-8

摘要

在大地电磁法中,强干扰噪声限制了该方法还原真实地下结构的精度,会对后期资料解释造成不良影响。本文基于大地电磁时间序列的特点,对不同类型噪声的特征进行分析,提出了一种基于VMD(变分模态分解)与LSTM(长短时记循环神经网络)预测重构的信号去噪技术。首先通过VMD信号分解算法对原始大地电磁数据进行去基线漂移处理,对处理好的时间序列继续通过VMD分解为多个不同的模态IMFs,选用含噪声轮廓信息的RSE分量中无干扰数据训练LSTM时间序列检测模型,对RSE分量进行识别并标记含噪时间段,计算噪声的步长,将噪声信息传递给原始信号并截断删除。最后通过对IMFs训练LSTM多维预测模型,对空缺的位置预测不同模态下的信号,将所有模态输出结果叠加可得大地电磁预测信号,重构信号后针对VMD方法识别度不高的尖脉冲噪声进行二次信噪分离即完成去噪。通过该技术可精确识别大地电磁信号中的强干扰噪声,只针对噪声发生时间段进行处理,有效保护了信号中无干扰数据,且预测数据误差可控制在大地电磁信号数据处理的误差允许范围内,去噪效果显著。

关键词： 大地电磁; 变分模态分解VMD; 长短时循环神经网络LSTM; 深度学习; 信号去噪

Abstract

In thereconstruction of actual subsurface structures, strong noise limits the accuracy of the magnetotelluric (MT) method,causing adverse effects on later data interpretation. Given this and the characteristics of the MT time series,this study analyzed different types of noise in the MT time series,proposing a signal denoising technique based on variational mode decomposition (VMD) and long short-term memory (LSTM) predictive reconstruction. First, baseline drift correctionwas performed for the original MT datausing the VMD signal decomposition algorithm. Then, the time series was further decomposed into multiple different intrinsic mode functions (IMFs) through VMD. The LSTM time series detection model was trained using interference-free data in the RSE component, which was then identified. Afterward, the time intervals containing noise weremarked, the increasement of noise was calculated, and the noise information wastransmitted to the original signal for truncation and removal. Finally, an LSTM multi-dimensional prediction model was trained for the IMFs, followed by the prediction of missing values under various modes. The predicted results under all modes were combined to obtain the final predicted MT signals. After signal reconstruction, a secondary signal-noise separationwas performed for spike-pulse noise that was not effectively identified through VMD. TheVMD-LSTM-based signal denoisingtechnique can accurately identify strong noise in MT signals by merely processing the time series intervals containing noise, thuseffectively preserving interference-free data. Moreover, its prediction errors can berestricted within the allowable error range of the data processing for MT signals. Therefore, this technique enjoys significant denoising effects.

Keywords： magnetotellurics (MT); variational mode decomposition (VMD); long short-term memory (LSTM) recurrent neural network; deep learning; signal denoising

PDF (11043KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

李博, 李长伟, 罗润林, 吕玉增, 王占. 基于VMD-LSTM对大地电磁信号进行噪声检测和预测重构[J]. 物探与化探, 2025, 49(1): 100-117 doi:10.11720/wtyht.2025.2309

LI Bo, LI Chang-Wei, LUO Run-Lin, LU Yu-Zeng, WANG Zhan. VMD-LSTM-based noise detection and predictive reconstruction for magnetotelluric signals[J]. Geophysical and Geochemical Exploration, 2025, 49(1): 100-117 doi:10.11720/wtyht.2025.2309

0 引言

大地电磁噪声通常可以分为人文环境噪声、观测系统噪声和地质噪声等^[1],其中人文环境噪声随着科技社会的发展对信号的污染也越来越严重,属于强干扰噪声,时间序列表现出形态明显、振幅突出、结构稀疏及相关性高等特征^[2]。其主要包括尖脉冲噪声、类方波噪声,类三角波噪声、类阶跃噪声等。

大地电磁信号在传统处理方法中是假设MT信号具有平稳性、线性和最小相位等特征,基于此特征提出的Fourier变换^[3]并不能准确反映出非平稳信号的局部特性;无法充分获取非线性和非高斯分布数据中的隐含信息;信号处理后无法反映原始信号的非最小相位特征。为解决该问题,许多学者尝试引入其他方法处理MT信号。汤井田等^[4]提出使用Hilbert-Huang变换处理MT数据,利用Hilbert时频能量谱筛选大地电磁信号的时段,应用经验模态分解(EMD)和多尺度滤波特征,分析MT信号的噪声分布并进行干扰抑制,有较理想的去噪效果,但是由于处理数据量大,该算法难以满足实时处理,且易出现模态混叠现象。严家斌等^[5]开始尝试小波变换来处理类脉冲电磁噪声,针对类脉冲噪声在小波域中的变化特征利用迭代回归技术来分析和压制噪声,经验证明相比传统小波阈值去噪方法该方法性能更优。但是小波滤波存在一个主要问题,即依赖于小波基函数的选择,如果选择不合适或者设置不合理的阈值,可能会导致有用信号的损失。此外,一旦小波基函数确定,在分解和重构过程中无法进行调整,缺乏自适应性。李晋^[6]提出了基于数学形态学的大地电磁强干扰分离方法,对大地电磁强干扰中的大尺度干扰和基线漂移有较好的抑制作用,能够有效改善MT数据质量、结构元素的尺寸和形状都将对形态学基本变换产生很大影响,结构元素越复杂,其滤除噪声的能力就越强,但所耗费的时间也就越长,如何设置普遍适用于大地电磁信号的结构元素是目前存在的问题。汤井田等^[7]引入了稀疏分解对MT信号处理,通过构建一种冗余字典原子,使其能够与常见典型强干扰相匹配,并且对纯净信号不敏感,利用压缩感知重构算法的方法分离大地电磁信号中的强干扰部分,但由于原子库的高冗余度,算法的执行时间较长,导致算法效率不够高。

近年来,随着人工智能的发展,对于去噪方法的研究也呈现出新的前景。利用人工智能技术,如深度学习和神经网络,已经取得了一些显著的成果,这些方法能够学习和理解噪声的特征,并自动学习生成更准确的去噪模型。许滔滔等^[8]提出了一种基于长短时记忆循环神经网络的大地电磁工频干扰压制方法,将训练好的模型输出为提取的工频噪声,和原始信号做差既完成去噪,但是该方法依赖模型的训练,对数据集的建立需要耗费大量时间,且大地电磁强干扰噪声多种多样,尤其是针对随机噪声如何构建数据集难以解决。李德伟等^[9]提出将基于BP神经网络模型的时间序列预测方法引入大地电磁数据处理中,根据已知序列样本,建立适当的神经网络模型,对缺失数据进行预测取得很好的效果,但是当缺失的数据过多,或者序列本身出现突变、跳跃等情况,预测的结果就会出现很大的偏差。上述方法都有其优点和局限性。然而,在这个领域仍然存在一些需要解决的关键问题,包括算法效率、自适应性、对有用信号的保护、随机噪声的处理以及精度不够的问题。

本文提出了一种基于变分模态分解和长短时循环神经网络的去噪方法,实现了对大地电磁测深法信号中的基线漂移现象的处理,然后对信号中的强干扰噪声进行检测后通过预测重构的方法还原数据,最后再针对尖脉冲信号进行二次信噪分离的完整去噪过程。该方法保证了只针对噪声发生的位置进行处理,通过LSTM模型对无干扰信号的信息挖掘,找出其蕴含的核心规律并且依据已知的信号特点对未来的数据做出相应的预测。在输出数据时,通过与无干扰信号的均方误差来评价预测,并用于控制预测信号的误差。该方法去噪效果显著,在对异常检测模型训练时只需要用RES分量中无干扰部分构建数据集,因此所训练出的异常检测模型复杂度低,检测精度高,同时还能识别不符合大地电磁特征的随机干扰,适合实时处理,且有效改善了上述对有用信号过处理的问题。将频率复杂的大地电磁按不同的中心频率分解,分解后每一个分量分别对LSTM-VMD时序预测模型进行训练,然后将各个频率分量的预测结果按照对应的中心频率进行合成,得到最终的大地电磁时序预测结果。相较于LSTM时序预测模型,通过VMD分解后再训练LSTM模型可以更有效捕捉大地电磁信号中的不同频率成分,提高预测的准确性和稳定性。

1 基于VMD-LSTM去噪方法

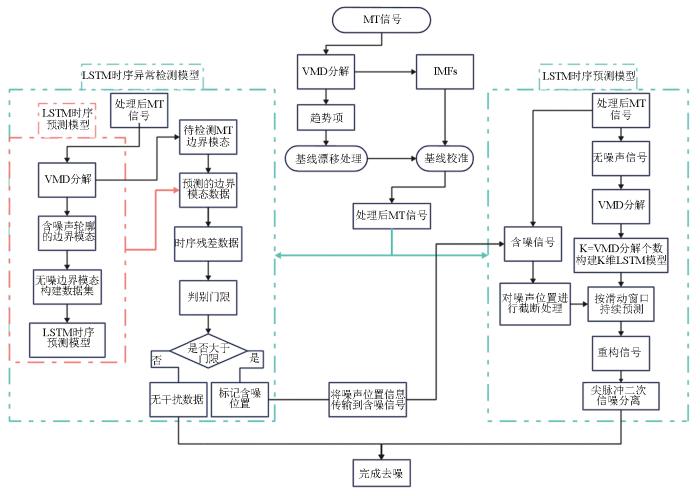
基于VMD-LSTM的大地电磁信号去噪方法流程如图1所示,该方法由时序异常检测模型和时序预测模型两部分组成。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 基于VMD-LSTM预测重构模型流程

Fig.1 Flowchart of the prediction and reconstruction model based on VMD-LSTM

时序异常检测模型用于检测时间序列数据中的异常点或异常模式,它的主要目标是确定数据中的异常行为。这些异常可能是由于仪器故障或人文干扰引起的,通过学习时间序列数据的正常行为模式,能够识别出与这些模式显著不同的数据点。这些异常点可以包括突然的偏移、震荡或其他不符合正常行为的模式,时序异常检测模型能够提供较强的噪声识别能力。

时序预测模型用于对未来的时间序列数据进行预测,它的主要目标是根据过去的数据模式和趋势来预测未来的数值,时序预测模型能够捕捉到时间序列数据中的更细微的模式和趋势。LSTM时序预测模型提供了去噪处理的精度,能还原出真实的大地电磁信号。

首先将大地电磁信号进行VMD分解成不同模态,通过设置α值使其分解出的RES(残差)分量只包含信号的趋势信息,此时称这个分量为趋势项,通过趋势项对大地电磁信号进行基线漂移处理后,依据其他IMFs中提供的基线信息进行校准,校准后的MT信号已经不存在基线漂移现象,且所有信号在同一基线上。然后构建两个LSTM模型,通过处理好的大地电磁信号去训练两个模型。其分别为LSTM时序异常检测模型和LSTM时序预测模型。最后通过两个模型所提供的信息重构信号后进行二次信噪分离,即完成去噪,去噪模型如图1所示。

1.1 LSTM时序异常检测模型

在大地电磁RSE分量信号中,存在大幅度的噪声,这些噪声或异常信号可能会对基于均值、方差等统计特征的方法产生较大的影响^[10]。由于强干扰噪声的存在,时间序列的均值可能会偏离其真实值,从而导致基于均值的异常检测方法出现错误的判断;方差也可能会偏离其真实值,使得基于方差的异常检测方法无法准确判断异常点;时间序列的分布可能会发生明显的偏斜,例如出现长尾分布,使得基于正态分布假设的异常检测方法失效。因此可以使用LSTM网络来捕捉时间序列中的动态模式和特征,从而提高异常检测的准确性。

通过设置α值和K值,使得VMD分解后的RES分量只包含信号的边界轮廓信息^[11-12],其中RSE分量中包含了强干扰噪声的形态特点,其余IMFs不参与训练模型,因此使用RSE分量对LSTM异常检测模型训练可以极大地降低模型的复杂度。由于频率组成较原信号更为简单,所以对RSE分量进行噪声检测也更为精准,模型的输出结果是对RSE分量下的含噪波段的标记。

LSTM时间序列异常检测的本质是先对时间序列预测,即使用LSTM模型对当前时刻后面的数据进行预测,然后通过比较预测值和真实值的误差来判断是否存在异常。具体步骤如下:

1)数据准备:将RSE分量下的无干扰数据按照一定的时间窗口大小分段,每个时间窗口内包含多个连续的时间点,其中最后一个时间点作为标签数据,前面的时间点作为特征数据。

2)LSTM模型训练:使用前面的时间点作为输入数据,最后一个时间点作为输出数据来训练LSTM模型。在训练过程中,LSTM模型会根据历史数据计算出当前时间点的预测值,然后通过损失函数计算预测值与真实值之间的误差,并更新模型参数以优化预测效果。

3)残差计算:利用训练好的LSTM模型对数据集中所有时间窗口进行预测,得到预测值和真实值的比较结果。由于预测值是通过历史数据计算出来的,因此预测值与真实值之间的误差即为残差。

4)异常检测:通过计算残差,从而判断是否存在异常。一般来说,当某个时间点的残差值超过一定的阈值时,就可以认为该时间点存在异常。

初始阈值需要根据实际情况逐步调整阈值以达到最佳的检测效果。本文使用基于统计规则的KSigma的方法设置阈值,当被检测值与均值的差值的绝对值在K倍序列标准差以外,则认定为异常。当K值较小时,更容易检测到较小的异常信号,但是误判率也可能会增加。反之,当K值较大时,误判率可能较低,但是也可能漏掉较小的异常信号^[13]。强噪声干扰较无噪信号幅度大很多,所以在识别强干扰噪声时,可将阈值设置适当放宽,选用K=3,同时保证了模型的检出概率和误检概率。

1.2 LSTM时序预测模型

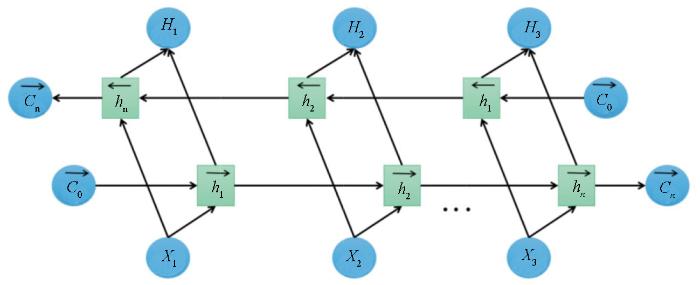
在构建LSTM预测模型的数据集时,数值较大的输入可能会降低网络的学习和收敛速度,在某些情况下会阻止网络客观地学习,因此在数据预处理时将训练数据归一化处理^[14]。由于LSTM的输入量最好不要超过400个时间步的序列,所以将数据分割成子样本。在处理时间序列时必须转换成具有输入和输出分量的样本,将上述样本按照一次相差一个时间步长进行隔断处理得到训练的输入样本和输出样本。本文采用的是BI-LSTM(双向循环神经网络)如图2所示,BI-LSTM可以看成是两层神经网络,第一层从左边作为系列的起始输入,在时间序列的处理上可以理解为从正向开始输入,第二层从右边作为系列的起始输入反向做与第一层一样的处理,这样处理不仅能保证模块能够获取当前以及过去的信息,而且还能获得未来的信息,在预测上考虑到了时间序列前后的关联性,提高了预测的准确性。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 Bi-LSTM网络结构

Fig.2 Bi-LSTM network architecture diagram

当模型训练好之后会有记忆性,因为大地电磁不同类型的噪声会发生在不同的分道中,信号的幅值有所区别,当对每一个新的序列进行预测时,需要调用初始化函数来给模型的当前状态进行初始化,目的是防止在之前的预测工作中模型记忆的数据特征会对当前预测产生不良影响,使用模型初始化函数后对新序列输入进行第一次预测,达到更新网络状态的目的,再进行多步预测。在LSTM异常检测模型输出了噪声位置信息,为截断处理提供了位置信息,同时也确定了预测步长,通过VMD-LSTM网络对空缺位置进行多步预测,然后对信号进行重构。

重构信号后由于VMD分解对于尖脉冲干扰的处理结果不佳,获得的轮廓特征中毛刺现象较为严重,因此模型在处理以后需要对信号进行二次信噪分离。根据预测模型输出最大值去设置合适的阈值,采用峰值检测的方法,随检测窗口遍厉所有数据点,超过阈值的点为异常点,根据异常点前的数据预测标记异常的点,从而完成二次信噪分离。

2 理论基础

2.1 VMD原理

VMD(variational mode decomposition)是一种基于变分原理的信号分解和处理方法。VMD将信号分解为多个固有模态函数(IMF)来实现信号的频域划分,使得每个模态函数在时域中具备局部特征,并且在频域中相互独立。VMD通过使每阶模态的估计带宽之和最小,且各模态之和等于输入信号的条件来约束,其核心思想是构建变分问题并求解,原理如式(1)所示,具体流程如下:

假设信号分解为K个本征模态函数(intrinsic mode function,IMF)分量,构造变分问题:

(1)

\underset{\{u_{k}\}, \{ω_{k}\}}{m i n} \{\sum_{k}^{} ‖ \partial t [(δ (t) + \frac{j}{π}) u_{k} (t)] e^{- j ω_{k} t} ‖_{2}^{2}\}

(2)

s . t . \sum_{k}^{} u_{k} = f

式中: $t$ 为时间; $f$ 为原始信号; $ω_{k}$ 为各模态分量实际的中心频率; $e^{- j ω_{k} t}$ 为各分量的预估中心频率; $u_{k}$ 为模态函数; $δ (t)$ 为冲击函数; $‖ \cdot ‖_{2}^{2}$ 为 $L_{2}$ 范数; $\partial t$ 为梯度运算; $j^{2} = - 1$ 。

通过引入增广拉格朗日函数,利用二次惩罚项和拉格朗日乘子法的优势,将上述问题从约束变分转化为非约束变分,得到的增广拉格朗日表达式如式(3)所示:

(3)

L (\{u_{k}\}, \{ω_{k}\}, λ) = α \sum_{k}^{} ‖ \partial t [(δ (t) + \frac{j}{π}) u_{k} (t)] e^{- j ω_{k} t} ‖_{2}^{2} + ‖f (t) - \sum_{k}^{} u_{k} (t) ‖_{2}^{2} + λ (t), f (t) - \sum_{k}^{} u_{k} (t)

式中: $λ$ 为拉格朗日乘法算子; $α$ 为二次惩罚因子; $\cdot, \cdot$ 为内积运算符。

利用交替方向乘子迭代算法结合傅里叶等距变换,得到各模态分量和中心频率,并搜寻增广拉格朗日函数的鞍点,交替寻优后 $\{u_{k}\}$ 、 $\{ω_{k}\}$ 和 $λ$ 的表达式如(4)~(6)所示:

(4)

{\overset{\land}{u}}_{k}^{n + 1} (ω) \leftarrow \frac{\overset{\land}{f} (ω) - \sum_{i \neq k} \overset{\land}{u_{i}} (ω) + \frac{\overset{\land}{λ} (ω)}{2}}{1 + 2 α (ω - ω_{k})^{2}}

(5)

ω_{k}^{n + 1} \leftarrow \frac{\int_{0}^{\infty} ω {|{\overset{\land}{u}}_{k}^{n + 1} (ω)|}^{2} d ω}{\int_{0}^{\infty} {|{\overset{\land}{u}}_{k}^{n + 1} (ω)|}^{2} d ω}

(6)

{\overset{\land}{λ}}^{n + 1} (ω) \leftarrow {\overset{\land}{λ}}^{n} (ω) + τ [\overset{\land}{f} (ω) - \sum_{k}^{} \overset{}{{\overset{\land}{u}}_{k}^{n + 1} (ω)}]

式中: $i$ 、 $n$ 为不同参数取得的任意值; $ω$ 为信号从时域 $t$ 变化到频域的符号; $\land$ 为傅里叶变换运算符; $τ$ 为噪声容忍限参数。

(7)

\sum_{k}^{} ‖ {\overset{\land}{u}}_{k}^{n + 1} - u_{k}^{n} ‖_{2}^{2} / ‖ {\overset{\land}{u}}_{k}^{n} ‖_{2}^{2} \in

式中: $\in$ 为收敛进度。

最后得到原始功率序列分解后的K个窄带IMF分量。

2.2 LSTM原理

LSTM(long short term memory network)在近些年发展迅速且应用广泛,传统的前向神经网络在解决时序相关的输入信号时,由于信息直进直出的处理特性只能对当前输入进行处理,不同的是LSTM可以对之前输入的信息有选择的记忆,从而有助于判断当前的输入,LSTM的这一特点在处理时序相关的输入时,有着很大的优势。“长期记忆”是LSTM与生俱来的结构特性,可以处理对于关联度较长的序列^[15]。LSTM 网络有一个不断重复的模块,是复杂的4个网络层,用一种特殊的方式连接在一起如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 LSTM网络结构

Fig.3 LSTM network architecture diagram

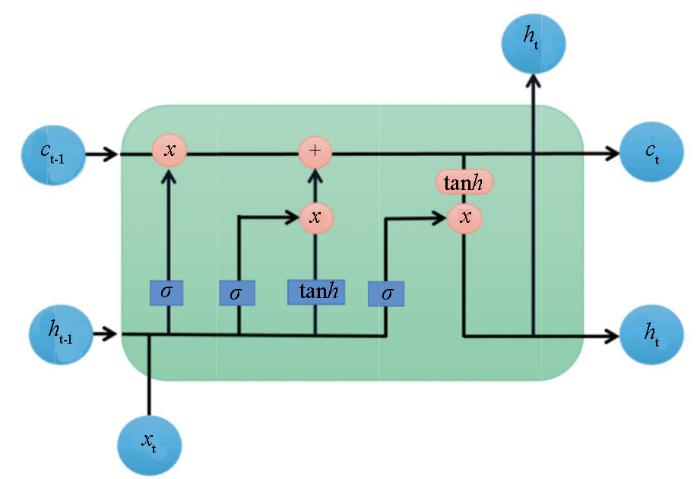
LSTM网络在处理信息时的第一步就是先选择性遗忘哪些信息,这是由 $s i g m o i d$ 层来控制,输入的 $h_{t - 1}$ 和 $x_{t}$ 会被处理成0~1的数,这些数表示从上一模块保存下来的信息的概率,表达式如下:

(8)

f_{t} = σ (W_{f} \cdot [h_{t - 1}, x_{t}] + b_{f})

接下来是要储存新的信息,同样地通过 $s i g m o i d$ 层来控制信息的选择,接下来通过一个 $t a n h$ 层创建一个新向量 $\tilde{C}$ ,分别由下式表达:

(9)

i_{t} = σ (W_{f} \cdot [h_{t - 1}, x_{t}] + b_{i})

(10)

\tilde{C} = t a n h (W_{c} \cdot [h_{t - 1}, x_{t}] + b_{c})

然后对网络的旧状态进行更新,表达式如下:

(11)

C_{t} = f_{t} \cdot C_{t - 1} + i_{t} \cdot {\tilde{C}}_{t}

。

最后通过 $s i g m o i d$ 层来决定 $C_{t}$ 中那些信息是需要被输出到下一个模块的,通过 $t a n h$ 层将值映射到 $[- 1,1]$ 之间,然后乘以 $s i g m o i d$ 层的输出,最终完成整个网络,表达式如下:

(12)

o_{t} = σ (W_{o} \cdot [h_{t - 1}, x_{t}] + b_{o})

(13)

h_{t} = o_{t} \cdot t a n h (C_{t})

其中: $h_{t - 1}$ 是上一时刻的输出值; $x_{t}$ 是当前时刻的输入值; $f_{t}$ 和 $i_{t}$ 是两个控制门; $f_{t}$ 表示有多少旧的信息会被删除; $i_{t}$ 表示有多少新的信息加入进来; $C_{t - 1}$ 是旧的网络状态; $C_{t}$ 是网络更新的信息。

3 仿真信号实验

3.1 VMD分解参数实验

在VMD算法中K(模态个数)和 $α$ (惩罚因子)这两个参数非常关键,会直接影响信号的分解效果,决定了信号的分解程度;模态的混叠程度;分解后子信号的精度。K值决定了VMD分解的层数,K值取过大或过小都会导致最终分解后得到的子信号含噪声过多,影响后续对信号的处理。 $α$ 的选取决定了分离出的各个子信号的模态函数的带宽和中心频率。

3.1.1 K值实验

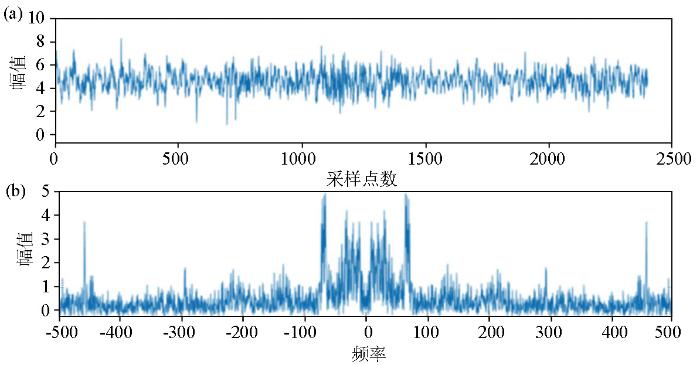
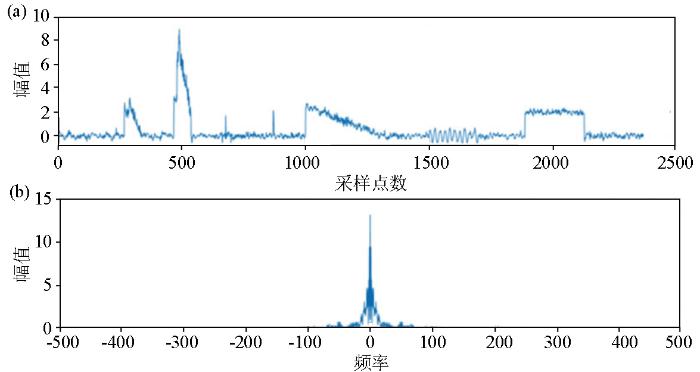
为研究VMD中参数选取对MT实测信号处理结果的影响,选取一段实测MT数据进行实验分析。如图4所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 原始MT信号时间序列(a)和原始MT信号频谱(b)

Fig.4 Time series graph of the original MT signal(a) and spectrogram of the original MT signal(b)

MT实测信号为非线性信号,且属于宽带信号,在频域没有特别明显的特征,但是若能在复杂的信号中通过VMD分解出含信号轮廓信息的低频分量,便能够满足LSTM时序异常检测模型的建模需求,即只需在RSE分量中识别出噪声发生的位置。固定设置 $α$ =2 000情况下,验证分解效果和K值对分解结果影响,对实测信号添加类三角波噪声、尖脉冲噪声、阶跃噪声、50 Hz工频干扰和类方波噪声来模拟含噪实测信号,如图5所示。分别选用K=2,3,4,5进行分解效果如图6、图7、图8、图9所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 加噪后实测信号的时间序列(a)和加噪后实测信号频谱(b)

Fig.5 Time series graph of the measured signal with added noise(a) and spectrogram of the measured signal with added noise(b)

图6

新窗口打开| 下载原图ZIP| 生成PPT

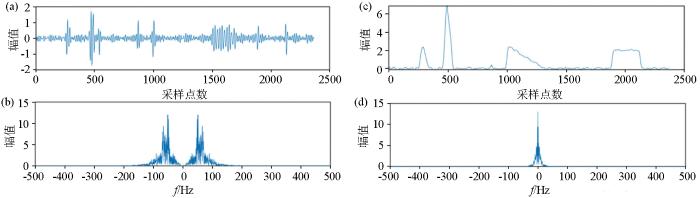
图6 K=2时对测试信号VMD分解时间序列和频谱

a—IMF1时间序列; b—IMF1频谱;c—IMF2时间序列; d—IMF2频谱

Fig.6 Time series graph and spectrogram of the VMD decomposition for the test signal with K=2

a—IMF1 time series graph;b—IMF1 spectrogram;c—IMF2 time series graph;d—IMF2 spectrogram

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 K=3时对测试信号VMD分解时域和频谱

a—IMF1时间序列; b—IMF1频谱;c—IMF2时间序列; d—IMF2频谱;e—IMF3时间序列; f—IMF3频谱

Fig.7 Time series graph and spectrogram of the VMD decomposition for the test signal with K=3

a—IMF1 time series graph; b—IMF1 spectrogram;c—IMF2 time series graph;d—IMF2 spectrogram;e—IMF3 time series graph;f—IMF3 spectrogram

图8

新窗口打开| 下载原图ZIP| 生成PPT

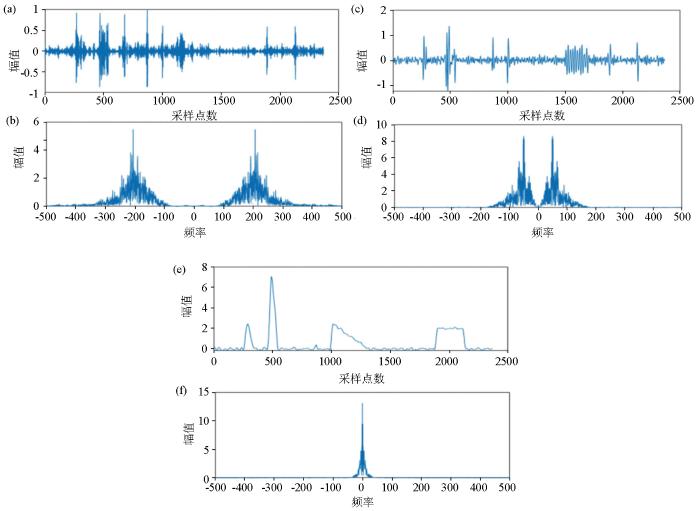
图8 K=4时对测试信号VMD分解时间序列图和频谱

a—IMF1时间序列; b—IMF1频谱;c—IMF2时间序列; d—IMF2频谱;e—IMF3时间序列; f—IMF3频谱;g—IMF4时间序列;h—IMF4频谱

Fig.8 Time series graph and spectrogram of the VMD decomposition for the test signal with K=4

a—IMF1 time series graph;b—IMF1 spectrogram;c—IMF2 time series graph;d—IMF2 spectrogram;e—IMF3 time series graph;f—IMF3 spectrogram;g—IMF4 time series graph;h—IMF4 spectrogram

图9

新窗口打开| 下载原图ZIP| 生成PPT

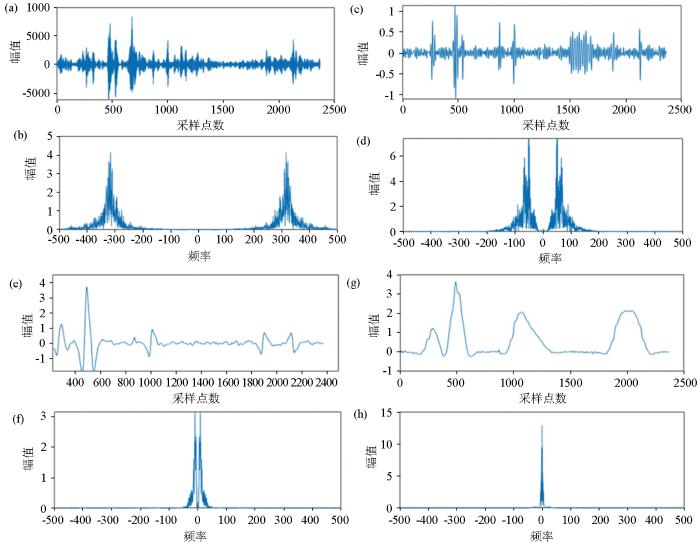
图9 K=5时对测试信号VMD分解时间序列和频谱

a—IMF1时间序列; b—IMF1频谱;c—IMF2时间序列; d—IMF2频谱;e—IMF3时间序列; f—IMF3频谱;g—IMF4时间序列; h—IMF4频谱;i—IMF5时间序列; j—IMF5频谱

Fig.9 Time series graph and spectrogram of the VMD decomposition for the test signal with K=5

a—IMF1 time series graph; b—IMF1 spectrogram;c—IMF2 time series graph;d—IMF2 spectrogram;e—IMF3 time series graph;f—IMF3 spectrogram;g—IMF4 time series graph;h—IMF4 spectrogram;i—IMF5 time series graph; j—IMF5 spectrogram

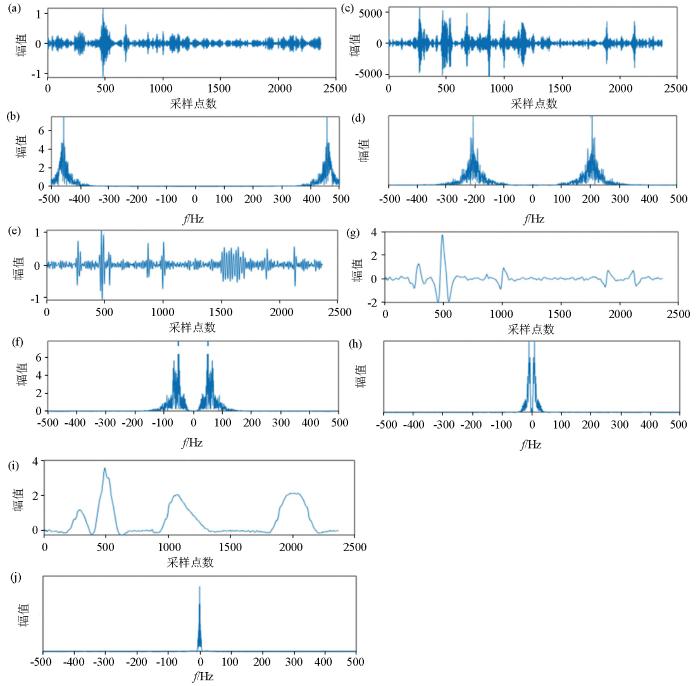
当实验选用K=2时,对测试信号进行分解,在频域上IMF2显示为低频分量,IMF1则主要为除低频外的其余频率成分,但是IMF1和IMF2在低频范围内有相同成分,出现了模态混叠现象,说明信号未完全分解,且未能表现出200 Hz以上的频率特征,在构建LSTM时间序列预测模型时,IMF1中包含过多的频率范围,所以并不能实现VMD-LSTM预测模型在预测精度上的提升。IMF2清晰地显示出了类三角波噪声、阶跃噪声、类方波噪声的轮廓,但是针对与尖脉冲噪声和50 Hz工频干扰的识别效果并不好。这是由于实验是保持在 $α$ =2 000情况下,对K值进行研究,当 $α$ =2 000时,带宽较小,50 Hz以内的的频率成分被分解在了IMF1中。因此在构建LSTM时序异常检测模型时应选用合适的 $α$ 值,以降低噪声检测模型的漏检概率。

当实验选用K=3时,测试信号进一步被分解成3个子信号,在频域上,IMF1和IMF2中同时存在50~200 Hz的相同频域成分,IMF2和IMF3中同时存在50 Hz以内的频域成分,说明当K=3时信号也并未完全分解,但是相较与K=2时,多出的一个子信号包含了K=2时未能体现的频率信息。说明随K值增大,在频域上的划分更为精细,可以提供给LSTM时序预测模型更多的频域信息,提升预测的精度。从时间序列上看,RSE分量同样缺失部分噪声信息,且表现出的轮廓幅值上有所减弱,这是因为信号中的噪声发生在不同的频率范围内,随着分解的子信号增多,导致噪声的轮廓信息混叠在其他分量中。因此随K值增大LSTM异常检测模型的性能是降低的,但LSTM时序预测模型预测性能是提升的。

当实验选用K=4、5时,分解后的测试信号在频域上按不同的中心频率进一步分解,每一个模态函数包含了更为详细的频率信息。可以更清楚,更直观地去了解测试信号的成分,但是在时间序列上,随着K值的增大,RSE分量下的噪声轮廓变得更为模糊,完全不能提供噪声的位置信息。

通过实验分析可知,在VMD算法中K值的选取非常关键,直接影响到分解结果。当K值过小时,会出现不同频率的信号被分解到同一子信号中,无法完全展示信号更多的频域信息;当K值过大时,信号会被过度分解,产生冗余分量,无法清晰地看到噪声的轮廓信息。实验表明在构建LSTM时序异常检测模型时K选择2最佳;构建LSTM时序预测模型时K值越大精度越佳。

3.1.2 α值实验

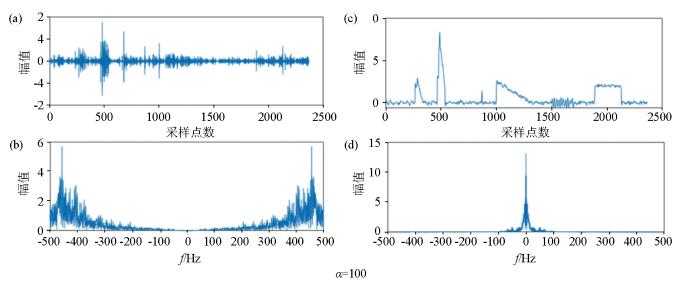
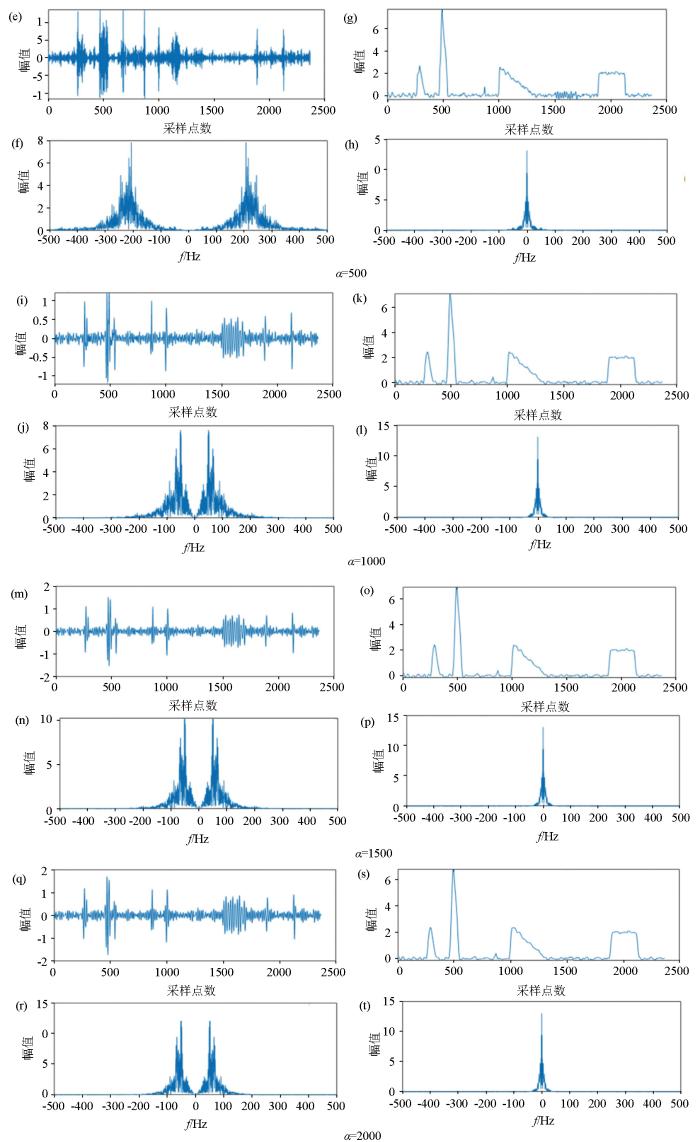
K值实验是在α=2 000进行的,为验证α是否影响RSE分量,保持K=2,选用α=100、500、1 000、2 000进行实验,所得到的IMF1和IMF2的时间序列图和频域谱如图10所示。

图10-1

新窗口打开| 下载原图ZIP| 生成PPT

图10-1 K=2时,不同α值下两个分量的时间序列图和频谱

Fig.10-1 Time series graph and spectrogram of the two components for K=2, under different α values

实验结果显示在K=2时,α=100时RSE分量轮廓最清晰,并且包含的噪声轮廓最完整。参数α控制了VMD分解中约束条件的强度。较小的α值会使约束条件更强,促使分解产生更稀疏的分量,所以在α=100时,IMF1中的带宽大,且与IMF2没有发生严重的混叠现象。随着α取值不断增大,IMF1中的带宽不断减小,与IMF2发生混叠现象越来越严重。但是VMD方法对尖脉冲噪声的处理效果并不理想,在实验中有一个尖脉冲在RSE分量下甚至无法体现。

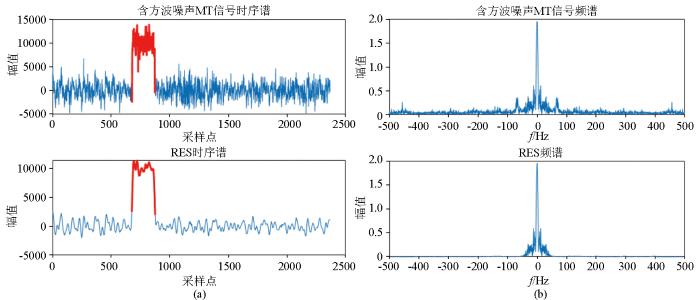
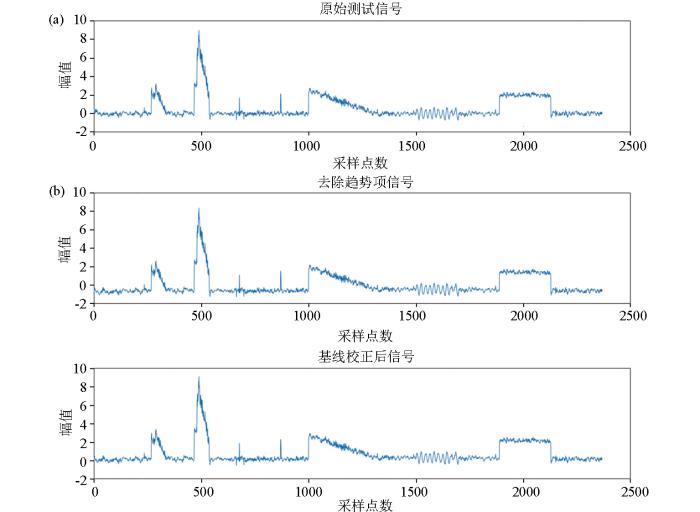
因此在构建LSTM时序异常检测模型,进行VMD处理时K=2、α=100效果最佳,既降低了模型的漏检概率又降低了模型的复杂度,针对尖脉冲噪声在后续处理中需要进行二次信噪分离。训练好的LSTM异常检测模型对RES分量进行检测,并将噪声发生的位置信息传递到含噪原始信号中。在每个噪声发生位置的左右额外传递5个步长,以降低去噪模型的漏检概率。图11a中模型准确地在原始信号中检测到了整个方波噪声的位置信息。截断后的信号除含方波噪声位置外,其他位置也保留了真实原始信号,不参与后续的处理,确保了原始信号中无干扰数据的完整性。图11b是含方波噪声的原始信号与RES分量的频谱,通过对比可发现,两个信号低频信息保持一致,RES分量中高频部分不参与检测,从而降低了异常检测的复杂度。

图10-2

新窗口打开| 下载原图ZIP| 生成PPT

图10-2 K=2时,不同α值下两个分量的时间序列和频谱

a、e、i、m、q—IMF1时间序列;b、f、j、n、r—IMF1频谱;c、g、k、o、s—IMF2时间序列;d、h、l、p、t—IMF2频谱

Fig.10-2 Time series graph and spectrogram of the two components for K=2, under different α values

a、e、i、m、q—IMF1 time series graph;b、f、j、n、r—IMF1 spectrogram;c、g、k、o、s—IMF2 time series graph;d、h、l、pt—IMF2 spectrogram

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 含噪原始信号与RES分量时序谱(a)和含噪原始信号与RES分量频谱(b)

Fig.11 Time-domain spectrogram of the noisy original signal and RES component(a) and frequency spectrum of the noisy original signal and RES component(b)

3.2 α值、K值在LSTM预测模型影响实验

对于LSTM时序预测模型,单从VMD参数实验结果看K值越大,α值越大,效果越佳,但是具体合适的参数还需要进一步实验分析。

在K值实验中,构建LSTM时序预测模型时K值越大效果越好;在α值实验中显示α越大带宽越小,提高了信号的稀疏性,即每个分量所占据的频率范围更加集中,使得分解结果更加清晰和精确。对于构建LSTM预测模型,这种更稀疏的特征有助于模型提取有效的特征信息,更好地理解和捕捉时间序列中的关键模式和变化信息。

但是较高的K值意味着模型的维度更多,会直接导致计算和存储需求大幅提升。对于每个分量都建立一个独立的模型,需要更多的资源和时间来训练和预测。由于大地电磁信号的非周期性和随机性特点,VMD分解后会存在模态混叠现象,无法将信号完全按不同中心频率进行分解,每个VMD分量或多或少都会包含一些冗余成分,这些冗余成分会对模型预测噪声产生不良影响。增加VMD分解中的K值可以提供更细粒度的分解,使得每个分量更接近原始信号的局部特征。但是,较大的K值也会增加冗余成分的数量,每个分量都可能包含来自其他频率分量的一些冗余信息。因此在VMD-LSTM预测模型中并非K值越大越好,需要通过实验分析计算时间和预测误差综合决定。通过分析大地电磁信号的带宽特点,依据经验和实验结果,本文选择α=2 000时对LSTM预测模型的预测效果最佳,并基于此进行后续对K值实验研究。

构建LSTM预测模型,数据集信息如表1所示,有A、B、C、D、E、F共6个数据集,数据集来自实测纯净的无噪信号进行VMD处理后的IMFs。6个数据集分别对应VMD分解后K=2、3、4、5、6、7,对应建立A₁、B₁、C₁、D₁、E₁、F₁共6个训练集,A₂、B₂、C₂、D₂、E₂、F₂共6个测试集,训练集和测试集的比例为7∶3。采用误差评价指标来衡量预测模型性能,评价指标计算出的误差越小,则模型预测的准确率越高,进而表示所建立的预测模型性能表现也就越好。实验选用均方根误差(RMSE)、平均绝对误差(MAE)、平均绝对百分比误差(MAPE)作为实验的评价指标,表达式如(13)~(15)所示:

(13)

R M S E = \sqrt{\frac{1}{n} \sum_{i = 1}^{n} (P_{r e a l} - P_{p r e})}

(14)

M A P E = \frac{100 %}{n} \sum_{i = 1}^{n} |\frac{P_{p r e} - P_{r e a l}}{P_{r e a l}}|

(15)

M A E = \frac{1}{n} \sum_{i = 1}^{n} |P_{r e a l} - P_{p r e}|

。

表1 实验参数

Table 1 Experimental parameters

数据集	K值	α值	模型训练个数	数据集大小
A	2	2000	2	300×2400×2
B	3	2000	3	300×2400×3
C	4	2000	4	300×2400×4
D	5	2000	5	300×2400×5
E	6	2000	6	300×2400×6
F	7	2000	7	300×2400×7

新窗口打开| 下载CSV

实验结果如表2所示,当K值从2增加到5时,RMSE由319.684降低到242.9843,然后在K值为6时再次上升。这表明,在K值增加到一定程度时,模型的预测误差变小,但当K值继续增加时,模型可能开始过拟合,导致预测误差增加。MAE在K值为3和5时相对较小,然后随着K=5后而增大。MAPE在K值为5或6时最低。随着K值的增大,模型训练的维度在不断增大,训练时间也在大幅提升。综合实验结果显示,K值并非越大对模型精度越好,选取K=5时,模型复杂度最佳的同时预测精度最佳。

表2 不同K值下模型预测误差

Table 2 Model prediction errors for different values of K

K值	2	3	4	5	6	7
RMSE	319.684	288.3506	278.5965	242.9843	286.9627	293.2542
MAE	255.3978	177.6701	216.9816	175.6035	219.5106	235.4275
MAPE	12.0185%	11.82071%	11.4593%	11.2015%	11.3134%	11.5241%
TIME	3.1h	4.4h	6.5h	9.8h	13.2h	17.6h

新窗口打开| 下载CSV

3.3 LSTM与VMD-LSTM预测精度比较实验

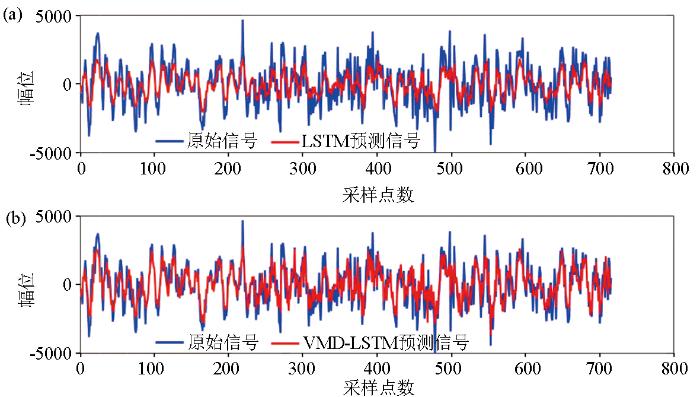
上述实验确定了VMD-LSTM预测模型中VMD分解过程中所需的K值和α值。为验证VMD-LSTM模型较LSTM模型在预测精度上的优势,在相同数据集下对两个模型进行训练,图12是原始信号分别与LSTM预测信号和VMD-LSTM预测信号的对比,图中VMD-LSTM预测信号与原始信号对比曲线更加拟合,预测出了更加细节的信息,这归因于VMD-LSTM模型能够充分利用VMD分解得到的IMFs的细节信息,能够更好地处理信号中的非线性特征,并通过LSTM网络对这些特征进行建模和预测。所以采用VMD-LSTM预测模型能够提升预测精度,从而提升去噪效果。通过实验和测试,分析综合模型的复杂性和性能表现,确定了在LSTM层中适用于大地电磁信号预测的最佳参数与模型的训练环境如表3所示。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 LSTM预测信号(a)VMD-LSTM预测信号(b)与原始信号对比

Fig.12 Comparison of LSTM predicted signal (a), VMD-LSTM predicted signal (b), and the original signal

表3 LSTM模型实验参数与训练环境

Table 3 Experimental parameters and training environment of LSTM model

隐含单元数	求解器	梯度阈值	特征维数	初始学习率	学习因子
128×3	Adam	1	50	0.1	0.3
处理器:	AMD RADEON7 5000 SERIES
显卡:	NVIDIA GeForce RTX 3060
平台:	Matlab2021a

新窗口打开| 下载CSV

3.4 基于VMD的MT信号基线漂移处理

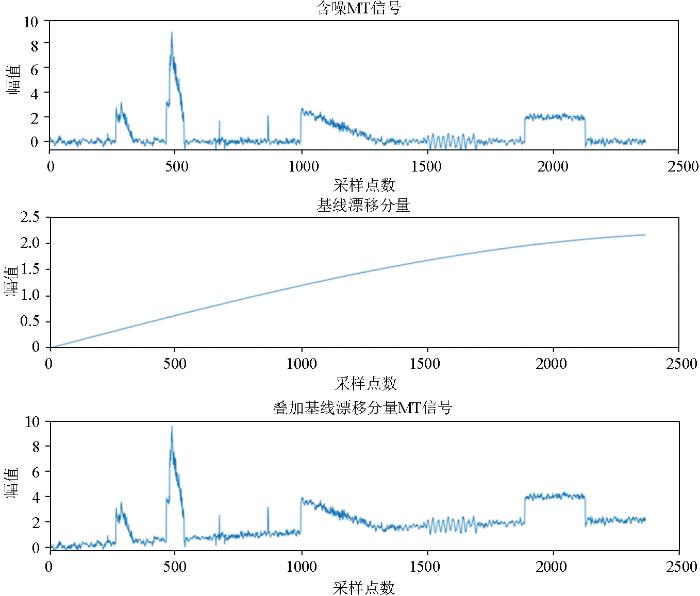
在实测大地电磁信号中往往会出现基线漂移的情况,在VMD-LSTM去噪模型处理前需要对实测信号针对基线漂移进行处理。处理后的信号再输入到VMD-LSTM去噪模型中进行信号分解和训练模型。这样可以更好地提取信号的动态特征,并减少基线漂移对LSTM模型的干扰。实验将模拟的基线漂移分量添加到测试信号中,得到同时包含基线漂移和各种强干扰噪声的信号如图13所示,并进行VMD处理。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 含噪MT信号中添加基线漂移分量

Fig.13 Addition of baseline drift component in the noisy MT signal

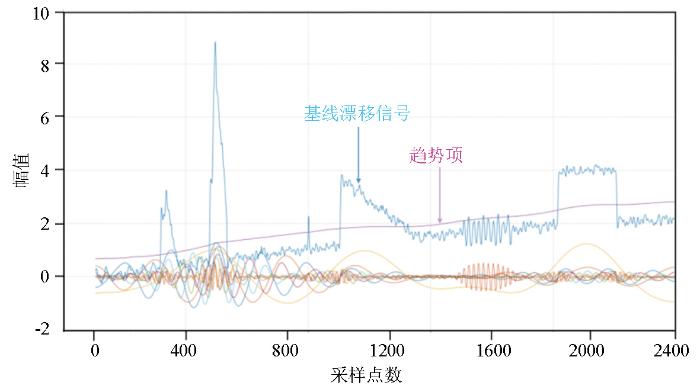
实验对K值大小进行试验时,随着K值的增大,包含趋势项的IMF与信号其他频域成分逐渐区分明显,但是不论K值取值多大,趋势项总是会发生混叠现象如图14所示。因此,在保持K值在一定数值范围内,调整α值则是实验的重点研究。

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 控制α值,K值20 000时VMD分解分解效果

Fig.14 VMD decomposition results with controlled α value, K = 20 000

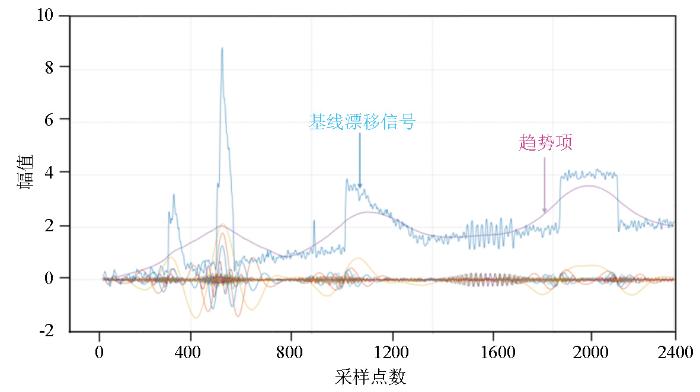
增加α值可以提高VMD分解对细节的保留能力,从而减少有用信号被误判为残差的可能性,能更好地保留有用信号。同时这也意味着,随着α的增大,趋势项的IMF所含信号的细节信息更少,更接近基线漂移分量。图15是随着α增大,叠加信号进行VMD分解后的结果,非常直观地可以看到趋势项非常接近实验模拟的基线漂移分量,且除趋势项外其余分量都没有发生基线漂移的现象。

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 控制K值取20 000,α取值逐渐增大时VMD分解效果

Fig.15 VMD decomposition results with controlled K value of 20 000 and gradually increasing α values

通过实验分析可知,足够大的K值和α值,通过VMD处理能够完全提取出信号中基线漂移的分量成分。但是提取到的分量总是整体大于实验设置的基线漂移分量,直接去除趋势项以后所得信号总是小于原始信号,如图16所示,a为原始测试信号,b为仅去除趋势项后的结果,b的基线明显低于a,这个结果是不利于信号去噪的最终效果的。

图16

新窗口打开| 下载原图ZIP| 生成PPT

图16 基线漂移处理结果

Fig.16 Result of baseline drift processing

针对对此问题可以对含准确基线信息的IMF分量,即除趋势项以外的分量进行二次分解,然后对信号进行校准。基线校准后的信号与测试信号对比如图13中a与c所示,校准后已无基线漂移现象,且与原始测试信号基线保持一致,信号其余成分得到完整的保留。

3.5 二次信噪分离

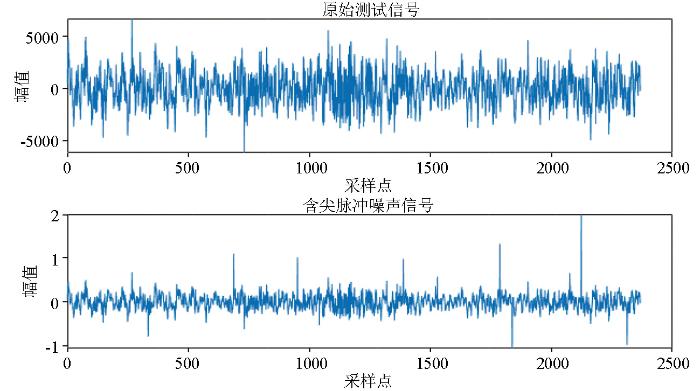
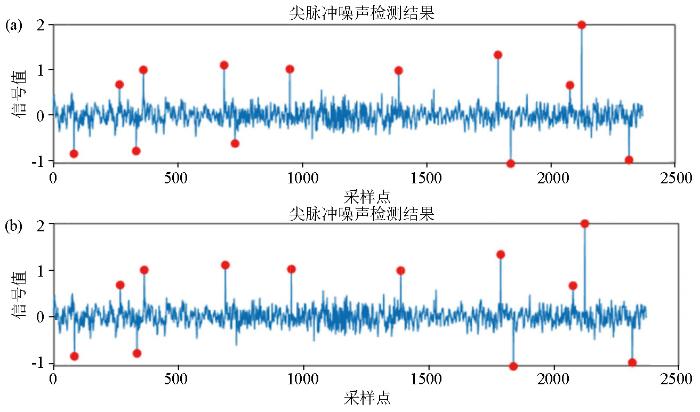
由于VMD分解对尖脉冲信号识别度不高的原因,去噪过程中还需要进行二次信噪分离。实验通过对测试信号添加10个尖脉冲噪声,如图17所示。首先实验根据LSTM预测模型的输出最大值设置了一个阈值,这个阈值是最大值的90%。然后进行峰值检测,寻找重构信号中超过阈值的点作为异常点。实验预测模型输出结果中最大值为6 383,结果显示当设置阈值为最大值的90%时,会出现误检,检出的噪声点为13个。当阈值直接取最大值6 383时,检出的噪声点为12个,如图18所示。这是因为大地电磁信号非周期且随机的性质导致LSTM预测模型的误差超出100,个别点预测出的最大值并不完全大于实际信号,但个别时间点对应的误差对整个信噪分离效果影响不大,不足以对求视电阻率和阻抗时所引起误差。

图17

新窗口打开| 下载原图ZIP| 生成PPT

图17 原始测试信号添加10个尖脉冲噪声

Fig.17 Original test signal with the addition of 10 sharp pulse noises

图18

新窗口打开| 下载原图ZIP| 生成PPT

图18 不同阈值设置下的检测结果

a—取预测最大值的90%;b—取预测最大值

Fig.18 Detection results under different threshold settings

a—threshold set at 90% of the maximum predicted value;b—threshold set at the maximum predicted value

3.6 实验结论

通过以上数值实验结果分析得出:

1)LSTM时序异常检测模型中K=2且α=100时,VMD分解后RSE分量下的轮廓最清晰且包含了除尖脉冲噪声以外的全部噪声类型。针对尖脉冲噪声,在经过VMD-LSTM去噪流程后需要进行二次信噪分离。

2)LSTM时序预测模型中K=4且α=2 000时,VMD分解后各个模态分量在频域上没有出现非常严重的模态混叠,结合计算时间,此时预测模型综合性能达到最佳。

3)VMD-LSTM模型相较于LSEM模型直接对MT这种非线性信号进行预测有更高的精度,能够更好地完成去噪系统中的预测任务。

4)MT信号中出现的基线漂移现象通过VMD分解能够很好地解决。

5)通过对LSTM预测模型输出的最大值作为阈值去检测尖脉冲噪声时,信噪分离效果较好,可以满足MT信号的去噪精度需求。

4 实测信号处理

本文选取位于陕西省安康市宁陕县东沟矿段采用V8系统采集大地电磁实测数据来检验该方法的去噪性能。由于该矿区内有大型起重设备,汽车、挖掘机等交通工具以及通讯等人文干扰,信号中含不同类型的噪声。类脉冲噪声一般在大地电磁原始数据中全频段均有出现,其影响频带范围为大地电磁数据的全频段;方波噪声在时间序列中表现为非正弦曲线的波形,呈类方波形态,其幅值很大,通常是正常信号的几个数量级;三角波噪声在时间序列中表现为非正弦曲线的锯齿波形,呈类三角形态,其幅值很大。这些噪声的存在使得信号在低频内失真,非常影响后续数据处理工作。

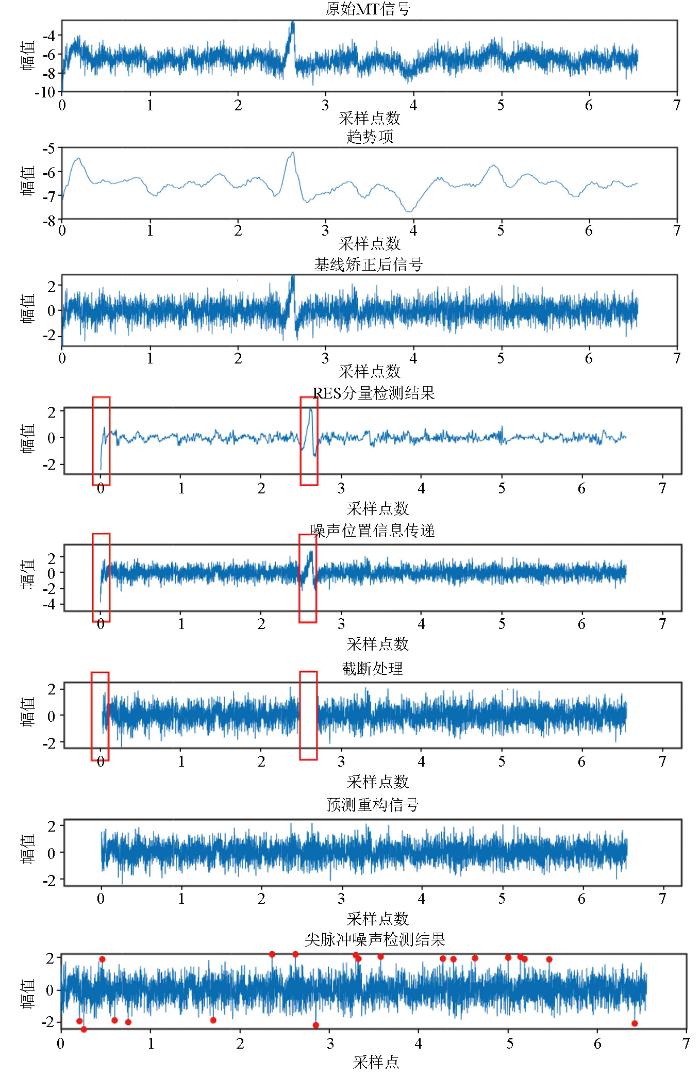
将V8系统采集的数据进行格式转换,再按照本文的去噪流程进行处理。图19是实测信号去噪的完整流程,包括基线处理、VMD分解、RES分量异常检测、噪声位置信息传递、截断处理、预测重构以及二次信噪分离。处理结果显示,原始实测信号发生了基线漂移的现象,通过VMD分解,去除趋势项后,整个信号的基线得到了很好的校正。VMD时序检测模型可以准确识别出噪声发生的位置,在实测信号中,仪器刚开始测量时,信号往往会有较大的波动,这种变化,去噪模型也可以精确的检测到,标记的位置所对应的原始信号即是强干扰噪声发生位置,只针对该位置进行预测重构,保证了噪声周边的无干扰信号在处理时不受影响。原始信号中并没有明显的尖脉冲噪声,二次信噪分离过程中,检测出的异常点为大于LSTM预测模型的预测最大值的点,在65 536个点中,仅有20个异常,所引起的误差可忽略。

图19

新窗口打开| 下载原图ZIP| 生成PPT

图19 实测含噪MT信号去噪流程

Fig.19 Denoising process of the measured noisy MT signal

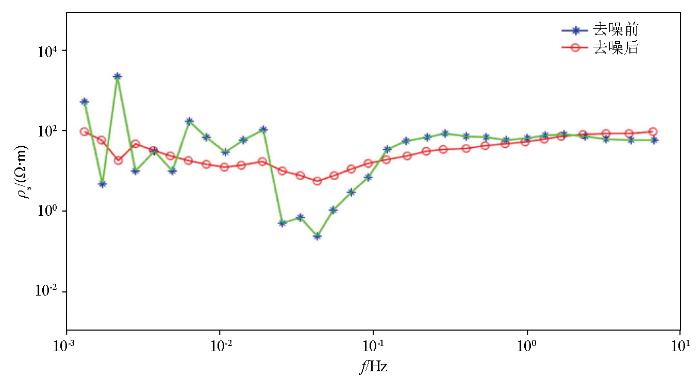
通过计算数据处理前后的卡尼亚视电阻率,可以清楚地观察到去噪后的视电阻率曲线在整个频率范围内的变化更加缓慢和稳定,没有出现剧烈的波动或快速变化,这表明在去噪的同时并没有引入显著的形变或失真。尤其值得注意的是,在低频范围内,去噪处理显著改善了视电阻率曲线中出现不稳定、快速变化或大幅度波动的情况。通过去噪处理,低频部分的曲线变得更加平缓和连续,去噪前后飞点和跳点问题得到了显著改善,视电阻率曲线能够更好地展现真实的地下介质特征,减少了近源效应对结果的影响,数据的准确性得到了保持,如图20所示。

图20

新窗口打开| 下载原图ZIP| 生成PPT

图20 实测信号去噪前后视电阻率对比

Fig.20 Comparison of apparent resistivity before and after denoising in the measured signal

5 结论

本文先利用VMD分解技术对大地电磁信号进行基线漂移处理,通过VMD-LSTM模型先对大地电磁强干扰进行识别,然后使用VMD-LSTM模型对信号预测重构,仅对信号被噪声污染的时间段进行处理,解决了在传统去噪过程中对噪声邻近的有用信号过处理的问题,仿真实验和实测数据处理证明该方法提供了很好的去噪效果,且适应大地电磁信号非周期、随机的特点。训练好的模型还可以检测出一些未知的随机干扰。数据集的构建需要依靠人工挑选无噪声的数据,这个过程需要耗费一定的人力,对于如何自动构建数据集,即如何自动识别信号当前是否含有噪声还需要继续研究。如何通过在LSTM网络模型中里添加基于大地电磁信号的频域信息的先验条件,用于提高检测性能,约束预测,提高去噪的精确性是下一步研究方向。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

孙洁, 晋光文, 白登海, 等.

大地电磁测深资料的噪声干扰

[J]. 物探与化探, 2000, 24(2):119-127.