基于高精度重力勘探对地下空洞的探测研究

doi:10.11720/wtyht.2024.0047

基于高精度重力勘探对地下空洞的探测研究

杨敏^,¹^,²^,³^,⁸, 徐新强^,¹^,⁸, 陈明⁴, 纪晓琳⁵, 王万银⁶^,⁷, 赵东明³, 周巍¹, 张义蜜⁶^,⁷

1.西安测绘总站,陕西西安 710054

2.中国地质大学(武汉) 地球物理与空间信息学院,地球内部多尺度成像湖北省重点实验室,湖北武汉 430074

3.信息工程大学地理空间信息学院,河南郑州 450001

4.广东省地质物探工程勘察院,广东广州 510000

5.空军工程大学信息与导航学院,陕西西安 710007

6.长安大学地质工程与测绘学院,陕西西安 710054

7.海洋油气勘探国家工程研究中心,北京 100028

8.智慧地球重点实验室,陕西西安 710054

Research on the detection of underground pedestrian passage by high precision gravity exploration

YANG Min^,¹^,²^,³^,⁸, XU Xin-Qiang^,¹^,⁸, CHEN Ming⁴, Ji Xiao-Lin⁵, WANG Wan-Yin⁶^,⁷, ZHAO Dong-Ming³, ZHOU Wei¹, ZHANG Yi-Mi⁶^,⁷

1. Xi’an Division of Surveying and Mapping, Xi’an 710054, China

2. Hubei Subsurface Multi-scale Imaging Key Laboratory, School of Geophysics and Geomatics, China University of Geosciences, Wuhan 430074, China

3. Institute of Geospatial Information, Information Engineering University, Zhengzhou, 450001, China

4. Guangdong Geological and Geophysical Engineering Investigation Institute, Guangzhou 510000, China

5. Information and Navigation College, Air Force Engineering University 710007, China

6. School of Geology Engineering and Geomatics, Chang’an University, Xi’an 710054, China

7. National Engineering Research Center of Offshore Oil and Gas Exploration, Beijing 100028, China

8. Key Laboratory of Smart Earth, Xi’an 710054, China

通讯作者: 徐新强(1968-),男,正高级工程师,主要从事测量数据处理理论和地球重力场方面的研究工作。Email:xaxcq@126.com

第一作者: 杨敏(1990-),女,博士后,主要从事重力数据三维物性反演研究工作。Email:yangmin@chd.edu.cn

责任编辑: 王萌

收稿日期: 2024-02-5 修回日期: 2024-04-15

基金资助:

湖北省重点实验室开放基金“地球内部多尺度成像”(SMIL-2023-06)

Received: 2024-02-5 Revised: 2024-04-15

摘要

地下空洞埋藏浅、规模小不易探测,随着重力感应技术的发展,给准确快速获取微重力变化为探测地下空洞带来新机会,对小规模地下空洞的探测能力具有广泛的研究和实用价值。本文从重力基础理论、重力探测技术、重力数据处理及反演3方面对地下空洞进行系统的分析研究。在给定形体大小、重力数据精度的情况下,通过二分法计算出了重力探测的最大埋藏深度;将高密度采集、高精度重力探测方法用于某区客运站地下人行通道实际探测,获得一套高精度重力格网数据,理论研究和实测结果表明,现有重力仪器具有探测地下空洞的能力;采用最小曲率位场分离方法、2.5D人机交互反演和靶区识别三维物性快速反演方法,得到地下人行通道近SN向的分布,埋藏深度大致2.5~5 m,这与实际情况相符。本次研究为地下空洞探测摸索出一套完整的重力勘探流程,具有一定的参考价值。

关键词： 重力勘探; 地下空洞; 客运站; 地下人行通道; 正反演研究

Abstract

Underground cavities with shallow burial and small scale are difficult to detect. With the development of gravity sensing technology, the accurate and rapid acquisition of micro-gravity variations brings new opportunities for detecting underground cavities, and it has wide research and practical value for the detection of small-scale underground cavities. This paper systematically analyzes and studies underground cavities from three aspects: gravity basic theory, gravity detection technology, and gravity data processing and inversion. Under given body size and gravity data accuracy, the maximum burial depth of gravity detection is calculated using the bisection method. High-density acquisition and high-precision gravity detection methods are applied to the actual detection of an underground pedestrian tunnel in a certain area of a passenger station. A set of high-precision gravity grid data is obtained. The theoretical research and measurement results indicate that existing gravity instruments have the ability to detect underground cavities. By using the minimum curvature potential field separation method, 2.5D interactive inversion and the target area recognition three-dimensional physical property fast inversion method, the approximate SN distribution and burial depth of the underground pedestrian tunnel are obtained, which is approximately 2.5~5 m, consistent with the actual situation. This study has developed a complete gravity exploration process for detecting underground cavities, and it has certain reference value.

Keywords： gravity exploration; underground cavities; passenger station; underground pedestrian tunnel; forward and inverse modeling research

PDF (3819KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

杨敏, 徐新强, 陈明, 纪晓琳, 王万银, 赵东明, 周巍, 张义蜜. 基于高精度重力勘探对地下空洞的探测研究[J]. 物探与化探, 2024, 48(3): 876-883 doi:10.11720/wtyht.2024.0047

YANG Min, XU Xin-Qiang, CHEN Ming, Ji Xiao-Lin, WANG Wan-Yin, ZHAO Dong-Ming, ZHOU Wei, ZHANG Yi-Mi. Research on the detection of underground pedestrian passage by high precision gravity exploration[J]. Geophysical and Geochemical Exploration, 2024, 48(3): 876-883 doi:10.11720/wtyht.2024.0047

0 引言

地下空洞指地表以下所有空洞,包括由地质作用形成的天然空洞和人工建造的地下空洞,例如煤矿采空区、岩溶空洞、山体洞库或地下巷道等,埋藏于地下数米甚至百米深处,对地下空洞分布进行透视勘查,能够有效减少地下空洞对地上建筑物的危害,服务于防灾抗灾,具有非常重要的意义,然而大多数地下空洞埋藏较浅、规模较小,探测地下空洞具有很大的挑战性。

重力勘探是传统的地球物理勘探方法,是一种无源探测方式,由重力基础理论、重力探测技术、重力数据处理及反演和重力数据应用研究4个重要部分组成。20世纪70年代至今,国内外学者在利用重力勘探探测地下空洞方面做了大量的工作取得一些进展,但仍有许多关键环节值得关注,对于探测地下空洞具有重要意义。

重力基础理论是通过假定地下空洞的埋深和形状大小(场源),分析不同埋深及形状大小引起的重力场特征、大小、分布^[1-2],随着埋深增大、形状体积变小,地下空洞引起的重力异常也随之减弱,还需进一步定量研究重力勘探对地下空洞的深度探测能力,即在现有观测数据精度下,对于固定尺寸地下空洞的最大可探测深度。

重力探测技术包括重力探测方法及数据预处理技术,研究表明高精度重力法可以用于地下空洞探测,例如已探测的侏罗系和二叠系深度大约在40 m处的喀斯特岩洞^[3-4],加州范登堡空军基地的地下导弹发射设施^[5],地下老旧防空洞^[6-7],城市地下空洞建筑^[8-9]。以上研究大都以重力剖面数据为主,较为缺乏地面实测重力格网数据。

重力数据处理及反演是进一步挖掘重力数据所包含的信息,数据处理中重力异常分离是从叠加重力异常中分离出单纯由地下空洞引起的重力异常,是重点也是难点,分离方法主要包括空间域的趋势分析^[10]、插值切割法^[11]和最小曲率位场分离方法^[12]等,频率域的小波分析^[13-14]和匹配滤波^[15-16]。数据反演是利用重力异常分离出来的重力数据,反演地下空洞特征值位置^[8,17-18]或地下空间剩余密度分布以确定地下空洞形态分布^[19-20]。以上数据处理和反演方法用于地下空洞的实测重力数据较少,大多为数值模拟研究。

针对以上情况,本文从重力基础理论、重力探测方法及数据预处理、重力数据处理及反演这3个方面对地下空洞探测进行系统研究,以某区客运站试验区地下人行通道为对象,通过实测高密度、高精度重力格网数据,探明重力勘探的探测能力,形成一套系统的重力勘探地下空洞方法技术,为地下空洞重力探测提供重要的技术支撑。

1 地下空洞重力理论基础

地下空洞通常填充空气,空气密度近似为0×10³ kg/m³,围岩密度通常为(2.0~2.6)×10³ kg/m³,地下空洞相对于围岩的剩余密度为负值,其差异是开展重力勘探工作的地球物理前提条件。

1.1 地下空洞重力异常分布特征

本次研究的地下空洞模型是依据某区客运站地下人行通道的几何参数,埋深较浅,地表为第四系松散层,密度为2.0×10³ kg/m³,因此将地下空洞模型的剩余密度设定为-2.0×10³ kg/m³,尺寸定为长30 m×宽4 m×高3 m,埋深为0~3 m^[7,9],其分布形态如图 1a所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

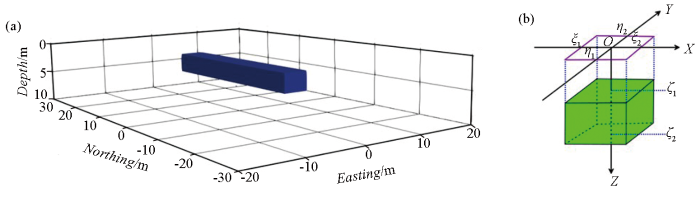
图1 地下空洞模型三维立体图(a)和坐标位置(b)

Fig.1 Three-dimensional diagram of the underground massive cavity model

以地面上某一点O为坐标原点,z轴铅垂向下为正,x,y轴在水平面内,剩余密度为 $σ$ 的地下空洞在观测点A(x,y,z)处引起的重力异常为^[21]:

(1)

Δ g_{z} = - G σ \{\begin{array}{l} (x - ξ) l n [(y - η) + r] + (y - η) l n [(x - ξ) + r] - \\ (z - ζ) a r c t a n \frac{(x - ξ) (y - η)}{(z - ζ) r} \end{array}\} |\begin{array}{l} ξ_{2} \\ ξ_{1} \end{array} |\begin{array}{l} η_{2} \\ η_{1} \end{array} |\begin{array}{l} ζ_{2} \\ ζ_{1} \end{array}

式中: $r = \sqrt{{(x - ξ)}^{2} + {(y - η)}^{2} + {(z - ζ)}^{2}}$ ,ξ、η和ζ分别表示直立六面体模型长、宽、高坐标位置,如图1b所示,重力场分布如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

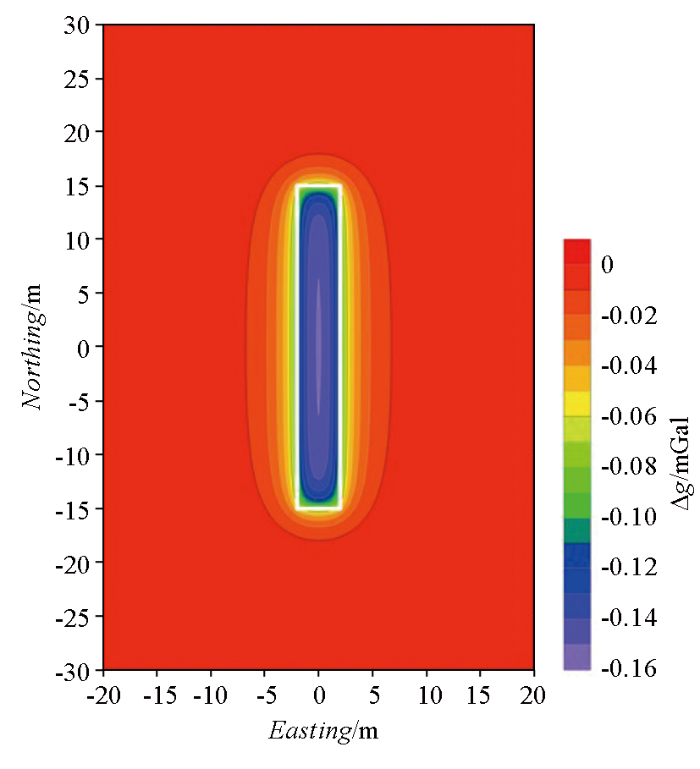
图2 地下空洞重力场

(白色边框为地下空洞模型水平位置投影)

Fig.2 Gravity data of cavity

(The white border is the horizontal projection of the cavity model)

结合地下空洞模型尺寸和剩余密度值,由图2可知地下空洞在地表引起的重力异常表现为重力低值区,空洞的边缘位置为重力异常的梯级带位置。当该地下空洞埋藏深度为0~3 m时(即贴近浅地表),重力异常最大幅值为-0.16 mGal,并且随着埋藏深度加深,重力异常最大幅值会随之减小。因此,可以利用重力异常低值区及其梯级带位置研究地下空洞的形态。

1.2 地下空洞重力探测能力研究

由于重力异常会随着地下空洞埋藏深度加深而减小,因而在实际工作中,需要明确在给定空洞尺寸情况下,不同观测重力数据精度可探测空洞的最大埋藏深度,即重力数据精度、地下空洞埋藏深度之间的关系,为重力勘探提供有效勘探深度依据。

地下空洞模型xOz截面如图3所示,在给定地下空洞尺寸,通过研究其中心位置埋深 $ζ_{c e n t r e}$ 与重力数据精度的关系,得到不同的重力数据精度对地下空洞的最大探测深度。根据图3所示,则式(1)中z方向的积分上下限分别为 $ζ_{1} = ζ_{c e n t r e} - Δ ζ / 2$ , $ζ_{2} = ζ_{c e n t r e} + Δ ζ / 2$ 。

图3

新窗口打开| 下载原图ZIP| 生成PPT

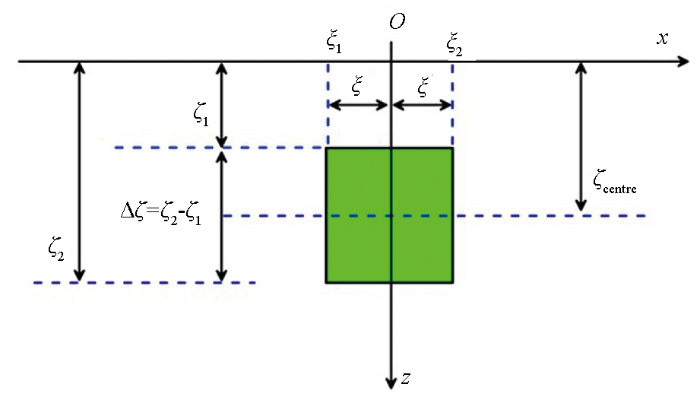
图3 地下空洞模型xOz截面深度示意图研究中心埋深ζ_centre和重力数据精度Δg_mse的关系

Fig.3 Schematic diagram of xOz section depth of the massive cavity model The relationship between the depth of the center ζ_centre and the accuracy of gravity data Δg_mseis studied

则式(1)变为:

(2)

Δ g_{z} = - G σ \{\begin{array}{l} (x - ξ) l n [(y - η) + r] + \\ (y - η) l n [(x - ξ) + r] - \\ (z - ζ) a r c t a n \frac{(x - ξ) (y - η)}{(z - ζ) r} \end{array}\} |\begin{array}{l} ξ_{2} \\ ξ_{1} \end{array} |\begin{array}{l} η_{2} \\ η_{1} \end{array} |\begin{array}{l} ζ_{c e n t r e} + Δ ζ / 2 \\ ζ_{c e n t r e} - Δ ζ / 2 \end{array}

式中: $r = \sqrt{{(x - ξ)}^{2} + {(y - η)}^{2} + {(z - ζ)}^{2}}$ ,ξ、η和ζ分别表示直立六面体模型长、宽、高坐标位置,x,y,z为计算点坐标。

分析式(2)可知,重力的幅值 $Δ g_{*}$ 与地下空洞中心位置埋深 $ζ_{c e n t r e}$ 为单调递减关系,当地下空洞引起的重力异常幅值 $Δ g_{*}$ (幅值为异常最大值 $Δ g_{z m a x}$ 与最小值 $Δ g_{z m i n}$ 之差)大于等于重力数据精度 $Δ g_{* m s e}$ 才能被识别^[22],如下式:

(3)

Δ g_{*} \geq Δ g_{* m s e}

在固定地下空洞尺寸的情况下,当重力异常幅值 $Δ g_{*}$ 等于重力数据精度 $Δ g_{* m s e}$ 时,对应的中心位置埋深 $ζ_{c e n t r e}$ 为可探测到的最大埋深,则该中心位置埋深以浅的地下空洞可被探测到,以深不可被探测,即式:

(4)

Δ g_{*} - Δ g_{* m s e} = 0

由式(4)可知 $Δ g_{* m s e}$ 和 $ζ_{c e n t r e}$ 为非线性关系,无法得到关于 $Δ g_{* m s e}$ 和 $ζ_{c e n t r e}$ 的解析表达式,因此需要求解式(4)的数值解。由于 $Δ g_{* m s e}$ 和 $ζ_{c e n t r e}$ 为单值函数,式(4)存在唯一零解,可以通过二分法得到数值解。

根据中华人民共和国地矿产业行业标准DZ/T 0171—2017《大比例尺重力勘查规范》中,应根据最小勘查对象在最大埋深条件下,与围岩的剩余密度差异,正演计算其引起的布格重力异常值,布格重力异常总精度应为勘查对象能够在地表引起布格重力异常的1/3~1/5,布格重力异常总精度与测点重力观测均方误差、布格改正均方误差、地形改正均方误差和正常场改正均方误差有关,最终布格重力异常总精度分为4个等级,分别是±0.03 mGal,±0.05 mGal,±0.1 mGal,±0.15 mGal。

根据表1可知,随着重力数据精度的提高,地下空间可探测的深度也更大,当重力数据精度为±0.03 mGal时,对于剩余密度为-2.0×10³ kg/m³,长30 m×宽4 m×高3 m的地下人行通道中心埋深不超过9.06 m,才能够被探测。而当重力数据精度为±0.15 mGal时,则已经不能探测到该地下空洞。

表1 地下空洞模型在不同重力数据精度下最大探测深度

Table 1 Maximum detection depth of underground cavity models under different gravity data accuracies

重力数据精度/mGal	0.03	0.05	0.1
最大探测深度/m	9.06	5.85	2.87

新窗口打开| 下载CSV

2 地下空洞重力观测与数据预处理

2.1 重力观测技术

近年来引进的新一代高精度重力仪CG-5或CG-6仪器分辨率为±0.001 mGal^[23],不仅可用于传统勘探应用领域,而且也可用于地下空间探测,用于寻找浅地表特殊地质目标如岩溶洞、地裂缝、地下地道、地下空洞、基岩面起伏等。通过重力场探测能力研究表明,目前高精度重力仪的精度可以满足探测地下空洞的精度要求。

本次测地工作方法试验区选为某区客运站的地下人行通道,地下人行通道埋深2~5 m,长宽高为30 m×4 m×3 m,由于地下人行通道埋藏较浅,并且探测目标体不大,通过正演计算引起的重力异常在0.085 mGal以内,适当调整中大比例尺重力测量规范中的测地工作方法技术获得高精度重力数据。

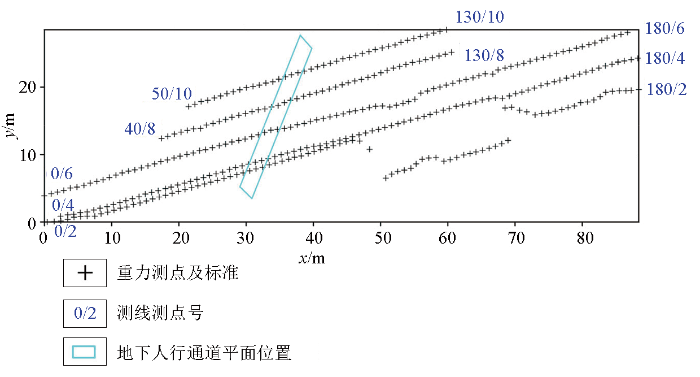
由于试验区附近进行改造施工,测线布设沿街道方向进行,沿街布设测线5条,点距1 m,测地使用GNSS RTK完成,重力点位详见图4。城市地区施工时由于人多、车多,场地晃动大,需保持场地稳定方可读取可靠数据,在该试验区附近场地进行不同采样时长的读数试验,结果表明,读数时间越短跳动越大,读数时间越长采样率越高、读数越稳、精度越高,综合考虑本次试验采集数据最佳读数时长为60 s。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 某区客运站试验区重力测点点位

Fig.4 Layout of gravity measurement points in the test area of a passenger station in a certain area

2.2 重力数据预处理

重力异常值计算需进行中间层改正,采用不同中间层密度的计算结果不同。一般采用研究区中间层密度平均值,即研究层的平均密度。实际工作中,一般在现场采集密度标本求取平均值,若存在水泥路面则按水泥混凝土的密度参与计算平均密度;若各物性层层厚差别大,宜用密度与层厚计算物性层加权平均密度。当探测浅层地质目标且工作场地不大时,应测定大比例尺地形图,以工作区外扩20 m作为地改区,采用1 m×1 m或2 m×2 m的网格高程点进行近区地改^[9]。

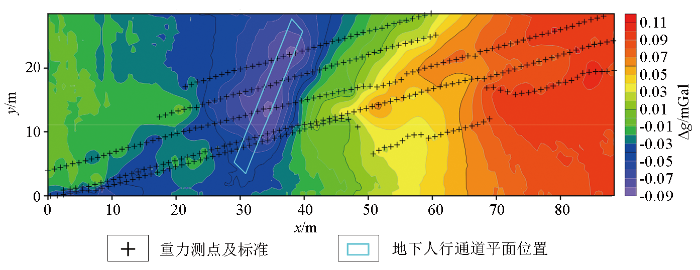
在该客运站试验时,为客运站前期建设时期,人行通道以上均平地且无建筑物影响,因此本次采集的重力格网数据主要包括地下人行通道异常场和背景场(图5),在该研究区重力异常幅值可达0.2 mGal,研究区x=[25,40]m区域分布着近SN向重力异常低值带,低值带两侧分布着明显的重力异常高值区,低值带对应的就是本次研究对象:地下人行通道,这与实际地下情况是相吻合的。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 某区客运站试验区布格重力格网数据

Fig.5 Bouguer gravity grid data in the test area of a passenger station in a certain area

3 地下空洞重力数据处理与反演

3.1 重力数据分离

采用位场分离方法技术分离出由地下目标体引起的重力异常,为确定地下目标体的位置信息和物性信息提供了更丰富的数据资料,因此,位场分离技术在重力数据处理环节中起到关键性作用。本次基于最小曲率位场分离方法^[12]对该试验区布格重力数据格网数据进行位场分离,分别得到区域布格重力格网数据(图6)和剩余布格格网数据(图 7)。区域布格重力格网数据异常整体走向近SN向,重力背景场自西向东由低值逐渐过渡为高值,剩余布格重力格网数据在x=[25,40] m区间呈现明显近SN向重力低值带,x=[40,70] m区间呈现近NE向重力高值带,与图7中地下人行通道平面位置(浅蓝色框)较为吻合。

图6

新窗口打开| 下载原图ZIP| 生成PPT

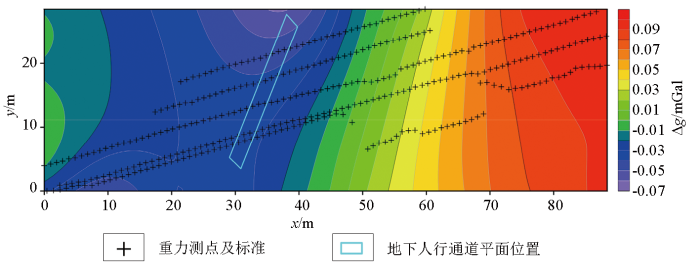
图6 某区客运站试验区区域布格重力格网数据

Fig.6 Regional Bouguer gravity grid data in the test area of a passenger station in a certain area

图7

新窗口打开| 下载原图ZIP| 生成PPT

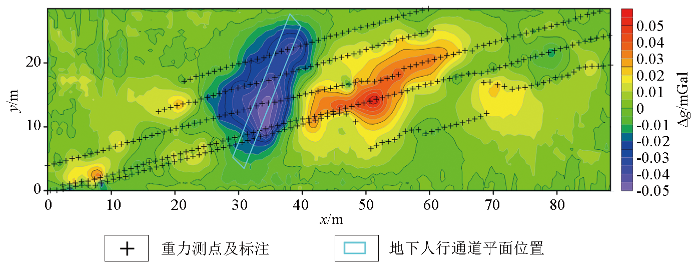
图7 某区客运站试验区剩余布格重力格网数据

Fig.7 Residual Bouguer gravity grid data in the test area of a passenger station in a certain area

3.2 重力数据反演解释

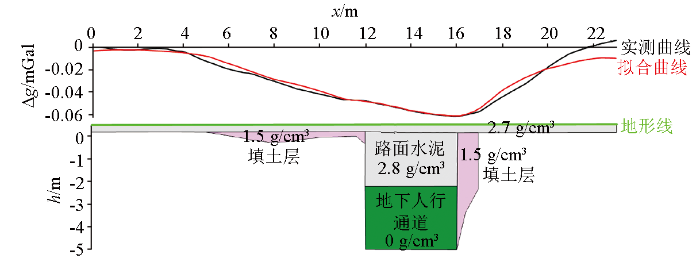
3.2.1 2.5D剖面反演技术

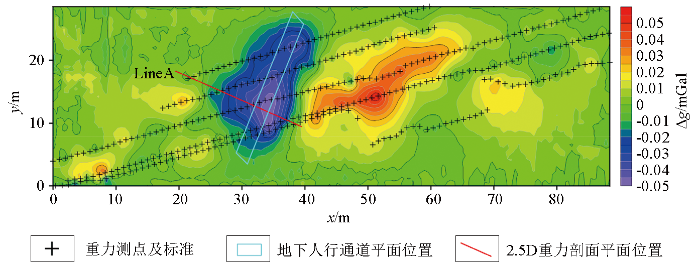
在本次试验区中,选取与地下人行通道相垂直的剖面LineA,且位于重力异常中心位置(图8),可通过对地下人行通道进行重力异常提取后再进行2.5D人机交互反演,本次采用GRIS软件进行反演,结果如图 9所示。通过人机交互反演的结果,可以得出人行通道大致位于地下2.5~5 m。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 LineA剖面线平面位置

Fig.8 Plan position of profile Line A

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 LineA 2.5D重力剖面反演结果

Fig.9 2.5D gravity profile inversion result of Line A

3.2.2 靶区识别三维物性快速反演方法

重力三维物性反演流程主要包括构置模型、构建目标函数和选取最优化方法,通过研究区地下半空间剩余密度分布的结果圈定地下空洞可能存在的位置。

构置模型是根据平面靶区优选技术^[24]实施流程,得到参与反演的靶区网格平面示意图,参与反演计算的网格三维如图 10所示。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 参与反演计算的靶区网格分布

Fig.10 Distribution of target area grids involved in the inversion calculation

构建目标函数如下:

(5)

\begin{array}{l} Φ (m) = Φ_{d} (m) + β Φ_{m} (m) = \\ ‖ W_{d} (G m - d) ‖_{2} + β‖ W_{z} (m - m_{0}) ‖^{2} \end{array}

其中: $W_{d}$ 为数据加权对角矩阵, $W_{d} = d i a g \{1 / s_{1}, 1 / s_{2}, . . ., 1 / s_{N}\}$ , $W_{z}$ 为深度加权矩阵, $β$ 为正则化参数,以调整 $Φ_{d} (m)$ 和 $Φ_{m} (m)$ 的相对重要程度。

目标函数取极值时,对应的法方程如下:

(6)

(K^{T} K + β {W^{T}}_{Z} W_{Z}) m = K^{T} d + β {W^{T}}_{Z} W_{Z} m_{0}

最优化方法选用广义最小残差法(GMRES),该方法能有效提高重力三维物性反演的求解效率^[20]。

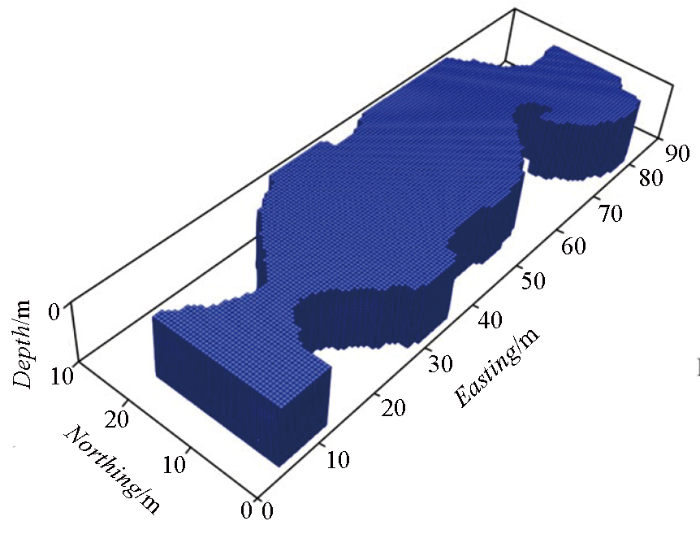
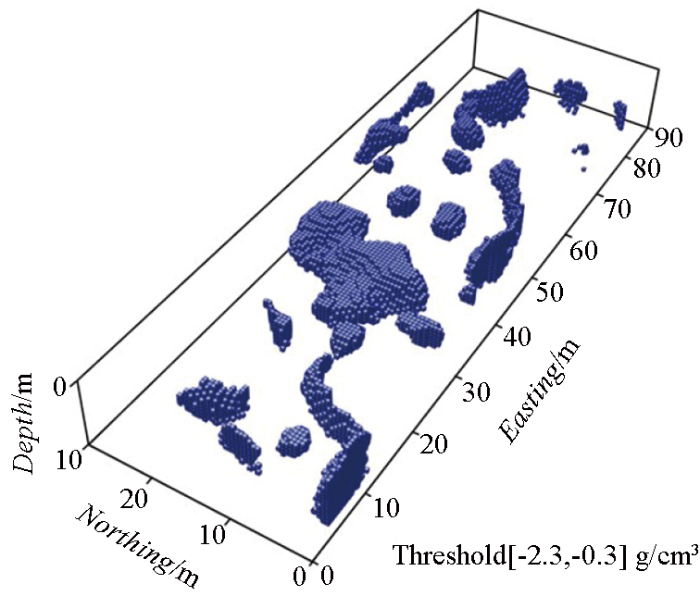
本次参与重力反演格网数据点数为148×49,共7 252个重力数据点,地下半空间剖分深度为0~10 m,网格大小为0.5 m×0.5 m×0.5 m,共119 520个网格,通过反演计算得到该客运站试验区地下半空间剩余密度分布图,图 11所示的剩余密度阈值区间选为[-2.3, -0.3] g/cm³。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 某区客运站试验区重力三维物性反演结果

Fig.11 Three-dimensional physical property inversion result of gravity in the test area of a passenger station in a certain area

该试验区重力测点沿着对角线NE向分布(图 7),数据点主要分布中部近SN向重力低值区和近NE向重力高值区,而其他位置重力测点分布稀少甚至部分没有分布测点。通过研究表明地下人行通道的重力异常表现为低值区,因此本次反演结果重点关注中部近SN向的剩余密度分布情况。根据阈值反演结果显示(图 11),地下人行通道分布在x=[30,40] m区间里,走向近SN向,与剩余重力异常走向一致,根据反演结果显示,该地下人行通道深度主要分布在2.5~5 m之间,而实际情况人行道深度分布在2~5 m,反演结果与实际情况是大体一致。

4 结论与建议

本文研究了地下空洞的探测问题,从重力基础理论、重力探测技术、重力数据处理及反演这3方面系统深入地研究,并以某客运站试验区重力格网数据为研究数据,提出一套基于重力勘探的地下空间探测方法,取得以下成果:

1)地下空洞埋藏浅但规模较小,在地表引起的重力异常较小,可以根据二分法求得给定数据观测精度下地下空洞的最大埋藏深度,有助于在重力勘探前期对探测目标、探测深度有定性认识。

2)地下空洞这一类浅层特殊地下结构,在野外实际测量阶段非常重要,数据质量直接影响了后续数据处理解释的结果,高要求测地精度、重力仪读数以及各项改正,对重力仪精度、操作员熟练程度、测量环境都有很高的需求。

3)根据重力三维物性快速反演方法得到某试验区地下人行通道的剩余密度分布结果,结果显示该人行道近SN向分布,埋藏深度在2.5~5 m之间,这与实际情况是相符的,但是三维反演结果边界比较模糊,后续需要考虑聚焦反演方法。因此,可以利用重力勘探探测地下空洞,并可以结合其他探测方法技术,利用多源数据研究地下空洞的分布。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

王庆宾, 江东, 赵东明, 等.

重力垂直梯度测量探测能力的正演

[J]. 测绘科学技术学报, 2011, 28(3):161-168.