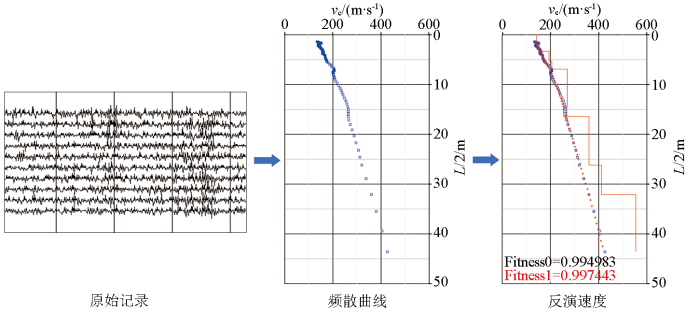
0 序言
微动勘探技术是基于面波频散的特性,一般来说,周期越长,速度越大,穿透地下的深度越深,微动勘探技术最早是利用全球中强地震所激发的面波信号来探测地球深部结构。
微动勘探具有抗干扰能力强、探测深度大、简便高效、经济环保等优势。但在进行千米深度勘探时,会存在浅部信息缺失大、深部分辨率低、现场台阵布置无法把控等问题。
本文针对地壳浅部千米深度勘探进行了试验分析与探讨来缩小浅部盲区、提高深部探测精度以及提高野外工作效率。
1 微动原理及方法
1.1 微动基本原理
图1
1.2 微动方法
本文所采用的微动方法结合了SPAC和ESPAC,既能适用于有中心点的规则台阵,也能适用于无中心点的非规则台阵。同时,相比F-K法,其低频分辨率较高,保证千米深度的探测精度。其具体数据处理步骤为:
1)对所有采集单元所采集数据进行预处理,删除有明显干扰和无效的数据;
2)对不同采集单元间距进行划分,分别进行数据处理;
3)对长时间连续记录进行分段;
4)将各数据段作FFT处理,转换成时域数据,分别提取每个频率数据;
5)将每个频率数据分别计算两两采集单元对的空间自相关系数,并将相同采集单元间距所计算的结果进行方位平均,得到此采集单元间距下的空间自相关系数;
6)重复以上步骤,计算不同采集单元间距组合的空间自相关系数;
7)固定频率,将不同采集单元间距所得空间自相关系数与第一类贝塞尔函数进行拟合,得到
8)对所得频散曲线进行反演,得到地下介质横波速度。
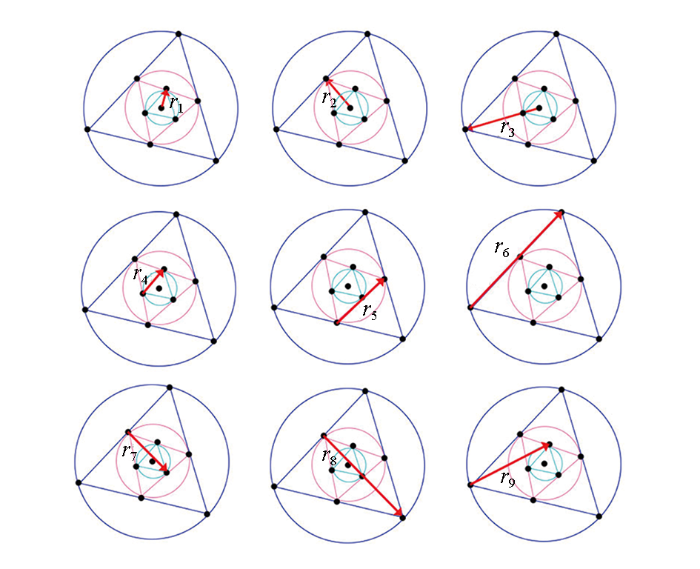
如图2所示,以三重内嵌三角形为例,其共有9组不同采集单元间距。分别计算不同采集单元间距组合下的不同频率的方位平均相关系数,再将所有频率下不同采集单元间距所得相关系数拟合贝塞尔函数确定所有频率下的面波速度,最终获得频散曲线。
图2
2 千米深度勘探的关键影响因素
2.1 台阵规模
2.1.1 采集单元数量
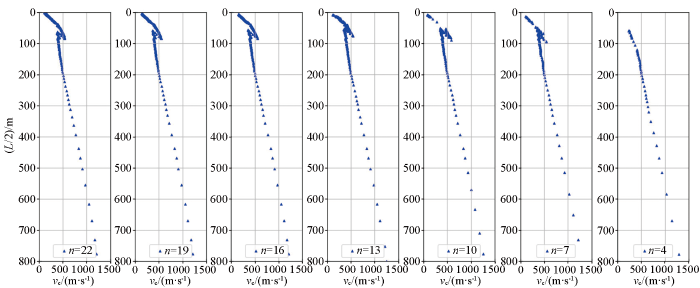
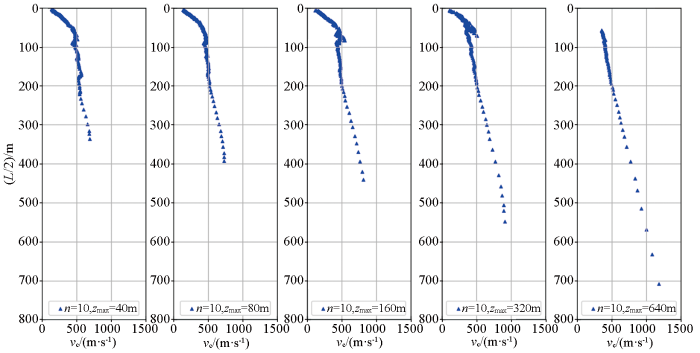
基于嵌套三角形台阵,为探讨采集单元数量对千米深度勘探结果的影响,本节利用7重内嵌三角形台阵进行试验(图3),共22个采集单元,其主频率为0.4 Hz,台阵最大边长为640 m、最小边长10 m,采集时间60 min,采样间隔10 ms。
图3
表1 内嵌三角形台阵规模说明
Table 1
| 台阵说明 | 采集单元 个数n/个 | 最大边长 zmax/m | 最小边长 zmin/m |
|---|---|---|---|
| 7重三角形 | 22 | 640 | 10 |
| 6重三角形 | 19 | 640 | 20 |
| 5重三角形 | 16 | 640 | 40 |
| 4重三角形 | 13 | 640 | 80 |
| 3重三角形 | 10 | 640 | 160 |
| 2重三角形 | 7 | 640 | 320 |
| 1重三角形 | 4 | 640 | - |
图4
图4
不同数量采集单元所得频散曲线
Fig.4
Dispersion curves obtained with different numbers of acquisition units
由图可见:①n=22、19、16时,所得频散曲线基本一致;②相较n=22、19、16,n=13时,所得频散曲线50 m以深基本一致,50 m以浅频散点较为稀疏,但整体趋势一致;③相较n=22、19、16,n=10时,所得频散曲线50 m以深基本一致,50 m以浅几乎无频散点;③相较n=22、19、16,n=7时,所得频散曲线400 m以深频散点较为稀疏分辨力较差,100 m以浅折拐点存在差异结果不可靠;④相较n=22、19、16,n=4时,频散曲线在120 m以浅无分辨能力,在400 m以深分辨能力较差。
通过对比分析,在进行千米深度勘探时,若对浅部资料要求不高最少可选择10个采集单元,即可满足大深度高精度要求。在第3.2节中将讨论,利用10个采集单元如何同时获得深部资料和浅部资料,详见第3.2节。
2.1.2 台阵大小
对于内嵌三角形台阵,其大小主要是指三角形的最大边长。研究表明,采集单元间距离越大,长周期波的相速度精度越高,探测深度越大。
本节介绍了4个千米深度勘探的试验结果,讨论最大边长与勘探深度的关系,均采用3重内嵌三角形台阵(n=10)进行布置。
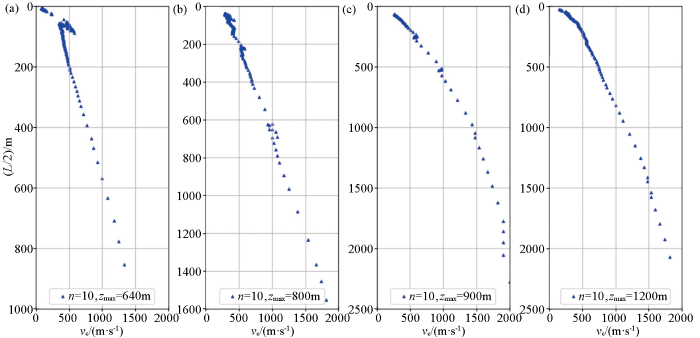
试验点1位于北京顺义某地,地势平坦,且为农耕地,利于台阵布置。如图5a台阵最大边长640 m、最大勘探深度为853 m,勘探深度约为最大边长的1.3倍;
图5
试验点2位于河北燕郊某地,地势平坦,且为农耕地,利于台阵布置。如图5b台阵最大边长800 m、最大勘探深度为1 552 m,勘探深度约为最大边长的1.9倍;
试验点3位于广东广州某地,地处珠江入海口,地势平缓,台阵周围为果园,利于台阵布置。如图5c台阵最大边长900 m、最大勘探深度为2 275 m,勘探深度约为最大边长的2.5倍;
试验点4位于上海某地,地势平坦,为达到2 000 m勘探深度,布设最大边长1 200 m台阵,采集单元分布于农耕地及村庄内。如图5d最大勘探深度为2 068 m,勘探深度约为最大边长的1.7倍。
由以上4个试验,台阵的最大边长越大,各采集单元所能接收到的信号频率越低且信噪比越高,因此增大台阵的最大边长是提高勘探深度的有效手段;同时,经前人研究[14]表明勘探深度约为最大边长的3~7倍,但是根据本节中所介绍的试验案例,对于千米深度勘探最大勘探深度约为台阵最大边长的1~3倍,也就是说,随着台阵最大边长的增大,勘探深度与最大边长的倍率将减小。
2.2 采集单元频率
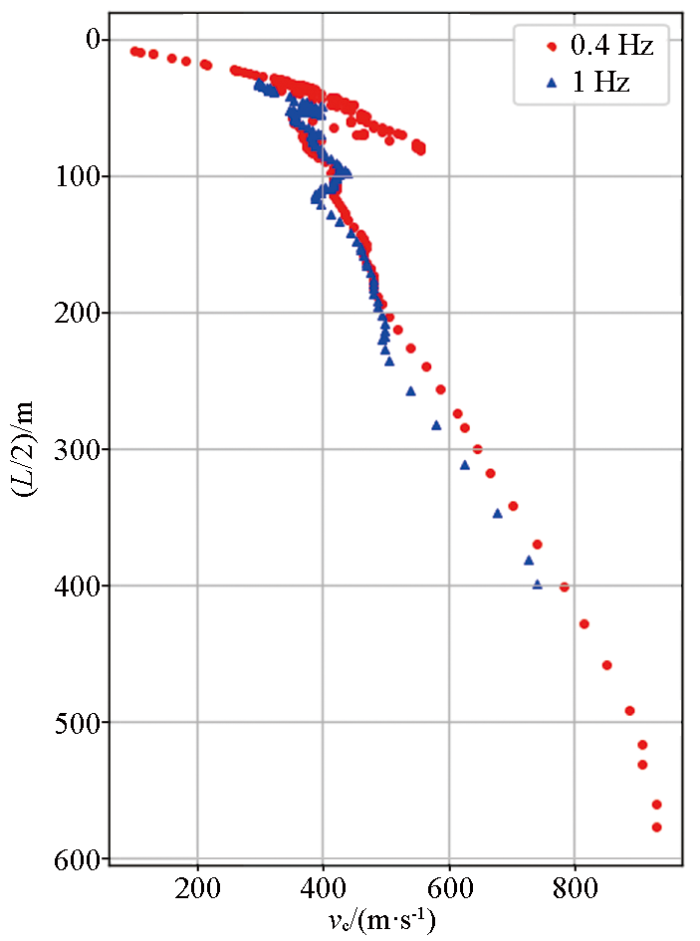
对于微动勘探,采集单元频率也是影响勘探深度的关键因素。通常采集单元频率越低勘探深度越大,本文对比了0.4 Hz和1 Hz采集单元的勘探效果,均采用10个采集单元布置成最大边长为320 m的内嵌三角形台阵。
图6为所获得的两条频散曲线的对比结果,可以看出同等条件下,0.4 Hz采集单元勘探深度大于1 Hz采集单元的勘探深度,并且在200 m以深0.4 Hz采集单元所得频散曲线分辨率更高。因此,在进行千米深度勘探时要选用更低频的采集单元,既能获得更深部的信息又能提高深部探测的精度。
图6
图6
不同频率采集单元所得频散曲线对比
Fig.6
Comparison of dispersion curves obtained by different frequency acquisition units
2.3 采集时长
微动信号在时间和空间上具有随机性,只有当采集到足够长的微动信号才能得到理想的频散曲线,因此采集时长决定着勘探效果以及野外工作效率。对于浅层的千米深度勘探需要布置较大边长的台阵,采集单元间距离较大,布置时费力还需人员看守。这时有根据、有目的的控制采集时长是保证勘探效果、节省成本的有效手段。
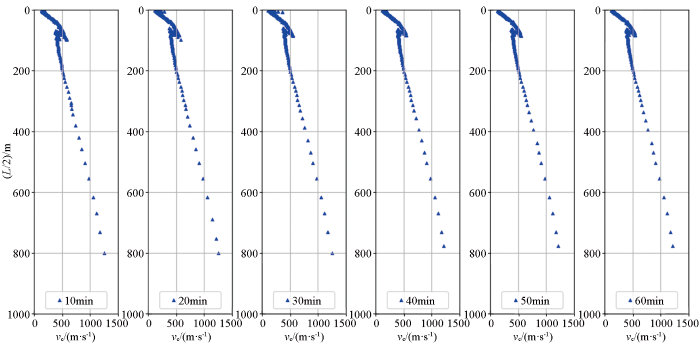
本节中利用采集时长为60 min的数据进行试验分析,将60 min数据分别截取前10 min、前20 min、前30 min、前40 min和前50 min进行处理,得到频散曲线如图7所示,可见随着时间加长,频散曲线逐渐收敛并趋于稳定。
图7
图7
不同采集时长所得频散曲线
Fig.7
Dispersion curves obtained with different acquisition duration
分析不同采集时长和采集效果,采集时间越长勘探结果越精确越稳定,但同时增加了工作时间,因此需要选择合适的采集时间以保证勘探效果及提高工作效率。对于千米深度勘探采集时长最少为30 min,还要结合频散曲线的收敛程度来确定。针对工区附近存在干扰的情况,应适当增大采集时长。
3 讨论
3.1 不同台阵大小对应的频率范围
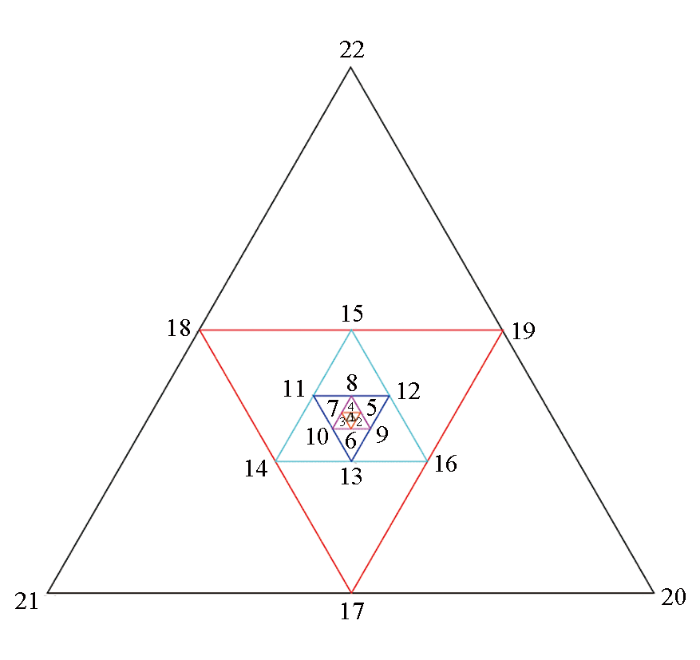
对于三角形台阵,不同台阵大小指三角形边长不同,采集单元间距离不同。研究表明,采集单元间距离越大,长周期波的相速度精度越高,探测深度越大。那么不同采集单元距离所能接收到波的频率范围需要确定,这样若已知工区地下介质岩性,可根据其速度值推断目标探测深度对应布置多大台阵。
图8
表2 不同台阵大小对应频率范围统计
Table 2
| 道数 | 台阵边 长/m | 频率 范围/Hz | 速度/(m·s-1) | 深度范围/m |
|---|---|---|---|---|
| 1,2,3,4 | 10 | 3.71~25.00 | 134.68~481.93 | 2.97~64.93 |
| 1,5,6,7 | 20 | 2.32~16.89 | 137.46~512.82 | 4.55~110.55 |
| 1,8,9,10 | 40 | 1.00~9.47 | 163.27~606.06 | 8.64~302.73 |
| 1,11,12,13 | 80 | 0.95~7.42 | 203.05~769.23 | 13.82~403.94 |
| 1,14,15,16 | 160 | 0.88~2.49 | 310.08~769.23 | 62.26~437.61 |
| 1,17,18,19 | 320 | 0.85~2.44 | 341.88~930.23 | 72.18~544.32 |
| 1,20,21,22 | 640 | 0.78~2.05 | 231.21~1481.4 | 56.7~948.15 |
3.2 千米深度勘探采集单元布置要求
3.2.1 台阵最大边长的选取
如2.1.2所述,对于千米深度勘探,勘探深度约为嵌套三角形台阵最大边长的1~3倍。本节为说明在进行微动勘探时如何根据探测深度要求布置合理大小的台阵做了进一步分析,仍利用7重嵌套三角形台阵测得的数据进行分析(最大边长为640 m、最小边长为10 m),选择3重嵌套三角形台阵(n=10)可得到5个不同台阵大小的数据,最大边长分别为40、80、160、320和640 m。
对所述数据进行处理得到频散曲线如图9所示,所得频散曲线有效勘探深度分别为336、391、439、547、853 m。经计算,勘探深度分别约为嵌套三角形台阵最大边长的8.4倍、4.8倍、2.7倍、1.7倍、1.3倍。由此可知,随着嵌套三角形台阵最大边长的增大,勘探深度与最大边长的倍率逐渐减小。因此,在进行千米深度勘探时要结合探测深度要求适当调整倍率关系布置台阵,避免因预估倍率过大造成勘探深度不足,重新布置采集单元。
图9
图9
不同大小的嵌套三角形台阵所得频散曲线
Fig.9
Dispersion curves obtained with different embedded triangular array sizes
3.2.2 台阵最小边长的选取
对于千米深度勘探,往往需要布置较大边长的台阵,而这会造成浅部资料缺失、盲区过大,这是因为采集单元间距离较大,采集到的信号多为长周期信号,无法获得短周期信号。
经2.1.1节分析,可使用具有10个采集单元的3重嵌套三角形台阵进行工法布置。通常会按照每外层边长是内层边长的2倍,每外层边长的中心是内层三角形顶点来布置。但对于大深度勘探来说,若按照上述来布置会造成浅部大量资料缺失。
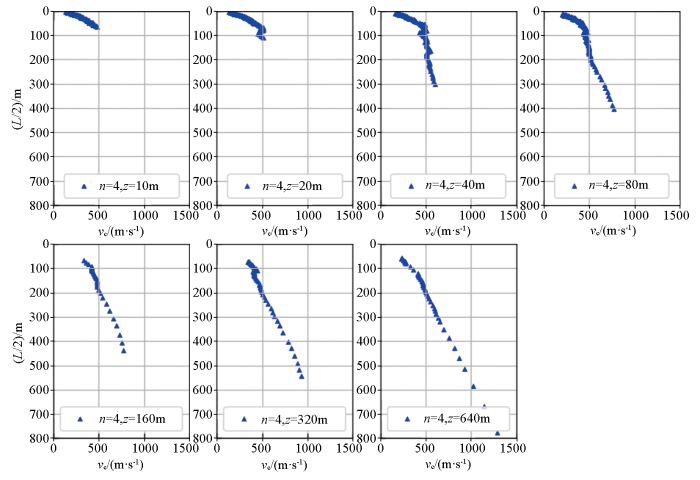
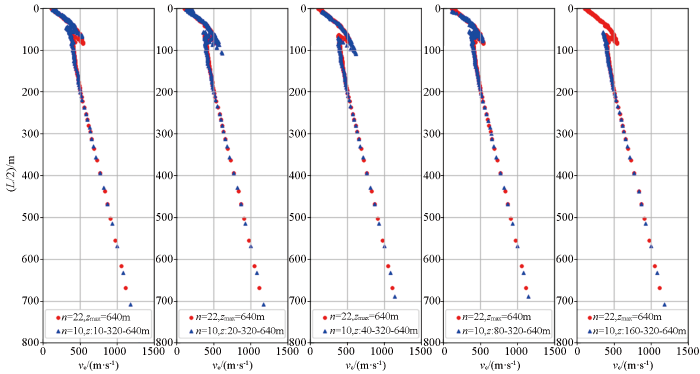
针对上述浅部资料缺失问题,本节利用7重嵌套三角形台阵(n=22)进行分析。首先计算7重嵌套三角形台阵得到的频散曲线(如各图红色圆点所示),再分别提取3个三角形台阵(n=10)(此时台阵最大边长和其相邻边长与7重嵌套三角形台阵一致,改变最小三角形台阵边长),最小边长分别为10、20、40和80 m。计算各台阵频散曲线,最后与7重嵌套三角形台阵进行比较,如图10所示可见:①当最小边长为10 m时,在60~80 m深度与7重嵌套三角形台阵所得频散曲线稍有差异;②当最小边长为20、40和80 m时,与7重嵌套三角形台阵所得频散曲线基本一致;③边长为160 m时,是常规台阵布置工法,可见浅部资料缺失严重。
图10
图10
不同最小边长台阵与7重嵌套三角形台阵所得频散曲线对比
Fig.10
Comparison of dispersion curves obtained by different minimum side length array and 7-embedded triangular array
经上分析,再结合3.1节不同台阵大小对应的频率范围,可根据任务要求,调整台阵布置工法,保证可接收到高频信号,进而获得浅部数据资料。
3.3 迭代样点数对深部探测精度的影响
迭代样点数N直接影响FFT结果进而影响探测精度。做N个点的FFT,表示在时域对原始信号取N个点做频谱分析。比如用10 ms采集即采样频率为100 Hz做256点的FFT之后,频率分辨率为100/256 Hz,对于低频的信号在频谱上无法识别,若使频谱更接近实际,需要提高样点数N做FFT。
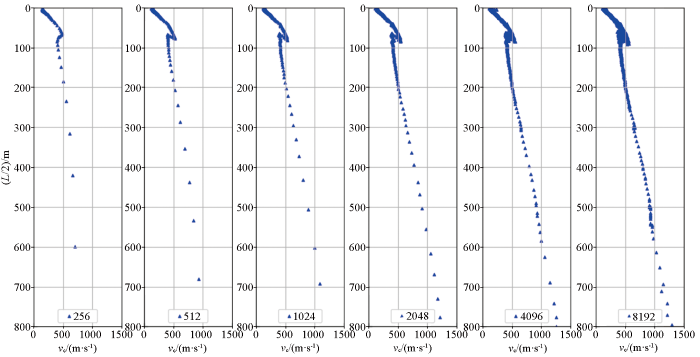
本节中介绍了选择不同迭代样点数N对深部探测精度的影响,分析数据采样间隔为10 ms,分别设置N为256、512、1 024、2 048、4 096、8 192进行处理。随着迭代样点数N增大,根据频点间隔=1/(迭代样点数×采样间隔)可知,频点间隔逐渐减小,即频率分辨能力逐渐提高。由图11可见表现在频散曲线上,分层特征越来越清晰。
图11
图11
不同迭代样点数所得频散曲线
Fig.11
Dispersion curves obtained with different iteration sample number
利用频散曲线进行地质分层,迭代样点数的设置直接决定着频散曲线是否具有清晰的分层能力,即频散曲线的拐点、斜率和频散点疏密变化是否清晰。
但是,随着迭代样点的增加,计算时间会加长。因此,在考虑计算时间的前提下,选择频散曲线具有可分辨的分层能力即可。一般情况,在进行千米深度勘探时迭代样点数取2 048或4 096。
4 结论与展望
4.1 结论
1)在进行千米深度勘探,采用嵌套三角形台阵时,采集单元数量不宜少于10个,采集单元数量越多,频散曲线精度越高;台阵大小直接影响勘探深度,台阵越大勘探深度越大,但是随着台阵的增大,勘探深度与台阵最大边长的倍率逐渐减小,大致为1~3倍。
2)采集单元频率也是影响勘探效果的主要因素,整体上,采集单元频率越低勘探深度越大,对深部的探测精度越高。
3)采集时长影响着勘探效果以及野外工作效率,采集时长越长所得频散曲线越收敛,同时会降低野外工作效率,综合两者,在进行千米深度勘探时,一般采集30~40 min为宜;若工区附近有干扰,应适当增加采集时间。
4)不同台阵大小对应不同的频率范围,台阵越大所采集的信号频率越低,台阵越小采集到的信号频率越高。
5)对于千米深度勘探,先根据最大勘探深度确定台阵的最大边长,一般勘探深度约为最大边长的1~3倍;再根据任务要求是否需要浅部数据,若需要浅部数据则需要调整最小三角形的边长。
6)迭代样点数量影响深部资料的探测精度,随着迭代样点数的增加,频散曲线的分层特征越来越明显;同时会增加计算的速度,一般情况选择2 048或4 096进行数据处理。
4.2 展望
本文中所涉及的试验案例均位于地势平坦、利于布置嵌套三角形台阵的工区。当野外施工条件无法满足布设嵌套三角形台阵时,如城区有建筑遮挡、山区地势起伏较大等,可选择其他类型的二维台阵(如“L”型、“十字”型等);在已知主震源的情况下,也可沿着主震源布设一维台阵。在复杂条件下使用微动技术,有待进一步讨论分析。
参考文献
微动的空间自相关法及其实用技术
[J].
The micromotional spatial autocorrelation methodand its practical technique
[J].
长波微动法及其新进展
[J].
The long-wave microtremors method and its advances
[J].
综合物探在城市地下空间地质调查隐伏断层探测中的应用
[J].
Application of integrated geophysical methods in the detection of hidden faults in urban underground space investigation
[J].
利用微动探测研究城市地下空间结构
[J].
Study on urban underground space structure by micro motion exploration
[J].
利用微动勘察方法探测煤矿陷落柱
[J].
Mapping collapsed columns in coal mines utilizing Microtremor Survey Methods
[J].
微动勘查技术在地热勘探中的应用
[J].
The application of fretting exploration technology in the exploration of middle and deep clean energy
[J].
用微动中的面波信息探测地壳浅部的速度结构
[J].
To determine the velocity structure of shallow crust with surface wave information in microtremors
[J].
覆盖区岩溶溶洞的微动探测试验研究——以福建永安大湖盆地为例
[J].
Application of 2D microtremor section survey method in covered Karst area,taking Yongan Dahu Basin,Fujian Province as example
[J].
利用SPAC法估算地壳S波速度结构
[J].
Application of SPAC method to estimate the crustal S-wave velocity structure
[J].
面波勘探技术要点与最新进展
[J].
Essentials and recent advances of the surface wave exploration technique
[J].
Space and time spectra of stationary stochastic waves,with special reference to microtremors
[J].
High-resolution frequency-wavenumber spectrum analysis
[J].
WD智能天然源面波数据采集处理系统及其应用试验
[J].
Data acquisition and processing system of WD intelligent natural source surface wave and its application test
[J].