Local wavelet packet decomposition of soil hyperspectral for SOM estimation
1
2022
... 土壤有机质(soil organic matter,SOM)是植物和微生物生命活动必不可少的养分和能量来源,是衡量土壤肥力的重要指标,也是陆地土壤碳库的重要组成[1-2],其在调节全球碳循环和土壤理化性质方面有着十分重要的贡献,对于高水平粮食的生产也发挥着重要影响[3].所以,更好地了解SOM空间分布特征可以有效利用土地资源.但是在实际研究中,由于地形要素、社会经济、气候和土壤属性存在差异,使得SOM空间分布不均匀[4⇓⇓⇓⇓⇓-10].另一方面,在对土壤野外调查取样的过程中,由于地形和人为因素,导致取样结果存在误差,所以无法精准指导农业和规划土地利用[11]. ...
Monitoring soil carbon pool in the Hyrcanian coastal plain forest of Iran:Artificial neural network application in comparison with developing traditional models
1
2017
... 土壤有机质(soil organic matter,SOM)是植物和微生物生命活动必不可少的养分和能量来源,是衡量土壤肥力的重要指标,也是陆地土壤碳库的重要组成[1-2],其在调节全球碳循环和土壤理化性质方面有着十分重要的贡献,对于高水平粮食的生产也发挥着重要影响[3].所以,更好地了解SOM空间分布特征可以有效利用土地资源.但是在实际研究中,由于地形要素、社会经济、气候和土壤属性存在差异,使得SOM空间分布不均匀[4⇓⇓⇓⇓⇓-10].另一方面,在对土壤野外调查取样的过程中,由于地形和人为因素,导致取样结果存在误差,所以无法精准指导农业和规划土地利用[11]. ...
Emerging land use practices rapidly increase soil organic matter
1
2015
... 土壤有机质(soil organic matter,SOM)是植物和微生物生命活动必不可少的养分和能量来源,是衡量土壤肥力的重要指标,也是陆地土壤碳库的重要组成[1-2],其在调节全球碳循环和土壤理化性质方面有着十分重要的贡献,对于高水平粮食的生产也发挥着重要影响[3].所以,更好地了解SOM空间分布特征可以有效利用土地资源.但是在实际研究中,由于地形要素、社会经济、气候和土壤属性存在差异,使得SOM空间分布不均匀[4⇓⇓⇓⇓⇓-10].另一方面,在对土壤野外调查取样的过程中,由于地形和人为因素,导致取样结果存在误差,所以无法精准指导农业和规划土地利用[11]. ...
黄土高原县域土壤养分空间变异特征及预测——以陕西省横山县为例
1
2008
... 土壤有机质(soil organic matter,SOM)是植物和微生物生命活动必不可少的养分和能量来源,是衡量土壤肥力的重要指标,也是陆地土壤碳库的重要组成[1-2],其在调节全球碳循环和土壤理化性质方面有着十分重要的贡献,对于高水平粮食的生产也发挥着重要影响[3].所以,更好地了解SOM空间分布特征可以有效利用土地资源.但是在实际研究中,由于地形要素、社会经济、气候和土壤属性存在差异,使得SOM空间分布不均匀[4⇓⇓⇓⇓⇓-10].另一方面,在对土壤野外调查取样的过程中,由于地形和人为因素,导致取样结果存在误差,所以无法精准指导农业和规划土地利用[11]. ...
黄土高原县域土壤养分空间变异特征及预测——以陕西省横山县为例
1
2008
... 土壤有机质(soil organic matter,SOM)是植物和微生物生命活动必不可少的养分和能量来源,是衡量土壤肥力的重要指标,也是陆地土壤碳库的重要组成[1-2],其在调节全球碳循环和土壤理化性质方面有着十分重要的贡献,对于高水平粮食的生产也发挥着重要影响[3].所以,更好地了解SOM空间分布特征可以有效利用土地资源.但是在实际研究中,由于地形要素、社会经济、气候和土壤属性存在差异,使得SOM空间分布不均匀[4⇓⇓⇓⇓⇓-10].另一方面,在对土壤野外调查取样的过程中,由于地形和人为因素,导致取样结果存在误差,所以无法精准指导农业和规划土地利用[11]. ...
利用地形和遥感数据预测土壤养分空间分布
1
2010
... 土壤有机质(soil organic matter,SOM)是植物和微生物生命活动必不可少的养分和能量来源,是衡量土壤肥力的重要指标,也是陆地土壤碳库的重要组成[1-2],其在调节全球碳循环和土壤理化性质方面有着十分重要的贡献,对于高水平粮食的生产也发挥着重要影响[3].所以,更好地了解SOM空间分布特征可以有效利用土地资源.但是在实际研究中,由于地形要素、社会经济、气候和土壤属性存在差异,使得SOM空间分布不均匀[4⇓⇓⇓⇓⇓-10].另一方面,在对土壤野外调查取样的过程中,由于地形和人为因素,导致取样结果存在误差,所以无法精准指导农业和规划土地利用[11]. ...
利用地形和遥感数据预测土壤养分空间分布
1
2010
... 土壤有机质(soil organic matter,SOM)是植物和微生物生命活动必不可少的养分和能量来源,是衡量土壤肥力的重要指标,也是陆地土壤碳库的重要组成[1-2],其在调节全球碳循环和土壤理化性质方面有着十分重要的贡献,对于高水平粮食的生产也发挥着重要影响[3].所以,更好地了解SOM空间分布特征可以有效利用土地资源.但是在实际研究中,由于地形要素、社会经济、气候和土壤属性存在差异,使得SOM空间分布不均匀[4⇓⇓⇓⇓⇓-10].另一方面,在对土壤野外调查取样的过程中,由于地形和人为因素,导致取样结果存在误差,所以无法精准指导农业和规划土地利用[11]. ...
基于定性和定量辅助变量的土壤有机质空间分布预测:以四川三台县为例
1
2014
... 土壤有机质(soil organic matter,SOM)是植物和微生物生命活动必不可少的养分和能量来源,是衡量土壤肥力的重要指标,也是陆地土壤碳库的重要组成[1-2],其在调节全球碳循环和土壤理化性质方面有着十分重要的贡献,对于高水平粮食的生产也发挥着重要影响[3].所以,更好地了解SOM空间分布特征可以有效利用土地资源.但是在实际研究中,由于地形要素、社会经济、气候和土壤属性存在差异,使得SOM空间分布不均匀[4⇓⇓⇓⇓⇓-10].另一方面,在对土壤野外调查取样的过程中,由于地形和人为因素,导致取样结果存在误差,所以无法精准指导农业和规划土地利用[11]. ...
基于定性和定量辅助变量的土壤有机质空间分布预测:以四川三台县为例
1
2014
... 土壤有机质(soil organic matter,SOM)是植物和微生物生命活动必不可少的养分和能量来源,是衡量土壤肥力的重要指标,也是陆地土壤碳库的重要组成[1-2],其在调节全球碳循环和土壤理化性质方面有着十分重要的贡献,对于高水平粮食的生产也发挥着重要影响[3].所以,更好地了解SOM空间分布特征可以有效利用土地资源.但是在实际研究中,由于地形要素、社会经济、气候和土壤属性存在差异,使得SOM空间分布不均匀[4⇓⇓⇓⇓⇓-10].另一方面,在对土壤野外调查取样的过程中,由于地形和人为因素,导致取样结果存在误差,所以无法精准指导农业和规划土地利用[11]. ...
Spatial prediction of soil organic matter content integrating artificial neural network and ordinary kriging in Tibetan Plateau
1
2014
... 土壤有机质(soil organic matter,SOM)是植物和微生物生命活动必不可少的养分和能量来源,是衡量土壤肥力的重要指标,也是陆地土壤碳库的重要组成[1-2],其在调节全球碳循环和土壤理化性质方面有着十分重要的贡献,对于高水平粮食的生产也发挥着重要影响[3].所以,更好地了解SOM空间分布特征可以有效利用土地资源.但是在实际研究中,由于地形要素、社会经济、气候和土壤属性存在差异,使得SOM空间分布不均匀[4⇓⇓⇓⇓⇓-10].另一方面,在对土壤野外调查取样的过程中,由于地形和人为因素,导致取样结果存在误差,所以无法精准指导农业和规划土地利用[11]. ...
Spatial prediction of major soil properties using Random Forest techniques-A case study in semi-arid tropics of South India(Article)
1
2017
... 土壤有机质(soil organic matter,SOM)是植物和微生物生命活动必不可少的养分和能量来源,是衡量土壤肥力的重要指标,也是陆地土壤碳库的重要组成[1-2],其在调节全球碳循环和土壤理化性质方面有着十分重要的贡献,对于高水平粮食的生产也发挥着重要影响[3].所以,更好地了解SOM空间分布特征可以有效利用土地资源.但是在实际研究中,由于地形要素、社会经济、气候和土壤属性存在差异,使得SOM空间分布不均匀[4⇓⇓⇓⇓⇓-10].另一方面,在对土壤野外调查取样的过程中,由于地形和人为因素,导致取样结果存在误差,所以无法精准指导农业和规划土地利用[11]. ...
基于随机森林模型的耕地表层土壤有机质含量空间预测——以河南省辉县市为例
1
2019
... 土壤有机质(soil organic matter,SOM)是植物和微生物生命活动必不可少的养分和能量来源,是衡量土壤肥力的重要指标,也是陆地土壤碳库的重要组成[1-2],其在调节全球碳循环和土壤理化性质方面有着十分重要的贡献,对于高水平粮食的生产也发挥着重要影响[3].所以,更好地了解SOM空间分布特征可以有效利用土地资源.但是在实际研究中,由于地形要素、社会经济、气候和土壤属性存在差异,使得SOM空间分布不均匀[4⇓⇓⇓⇓⇓-10].另一方面,在对土壤野外调查取样的过程中,由于地形和人为因素,导致取样结果存在误差,所以无法精准指导农业和规划土地利用[11]. ...
基于随机森林模型的耕地表层土壤有机质含量空间预测——以河南省辉县市为例
1
2019
... 土壤有机质(soil organic matter,SOM)是植物和微生物生命活动必不可少的养分和能量来源,是衡量土壤肥力的重要指标,也是陆地土壤碳库的重要组成[1-2],其在调节全球碳循环和土壤理化性质方面有着十分重要的贡献,对于高水平粮食的生产也发挥着重要影响[3].所以,更好地了解SOM空间分布特征可以有效利用土地资源.但是在实际研究中,由于地形要素、社会经济、气候和土壤属性存在差异,使得SOM空间分布不均匀[4⇓⇓⇓⇓⇓-10].另一方面,在对土壤野外调查取样的过程中,由于地形和人为因素,导致取样结果存在误差,所以无法精准指导农业和规划土地利用[11]. ...
基于随机森林模型的安徽省土壤属性空间分布预测
1
2019
... 土壤有机质(soil organic matter,SOM)是植物和微生物生命活动必不可少的养分和能量来源,是衡量土壤肥力的重要指标,也是陆地土壤碳库的重要组成[1-2],其在调节全球碳循环和土壤理化性质方面有着十分重要的贡献,对于高水平粮食的生产也发挥着重要影响[3].所以,更好地了解SOM空间分布特征可以有效利用土地资源.但是在实际研究中,由于地形要素、社会经济、气候和土壤属性存在差异,使得SOM空间分布不均匀[4⇓⇓⇓⇓⇓-10].另一方面,在对土壤野外调查取样的过程中,由于地形和人为因素,导致取样结果存在误差,所以无法精准指导农业和规划土地利用[11]. ...
基于随机森林模型的安徽省土壤属性空间分布预测
1
2019
... 土壤有机质(soil organic matter,SOM)是植物和微生物生命活动必不可少的养分和能量来源,是衡量土壤肥力的重要指标,也是陆地土壤碳库的重要组成[1-2],其在调节全球碳循环和土壤理化性质方面有着十分重要的贡献,对于高水平粮食的生产也发挥着重要影响[3].所以,更好地了解SOM空间分布特征可以有效利用土地资源.但是在实际研究中,由于地形要素、社会经济、气候和土壤属性存在差异,使得SOM空间分布不均匀[4⇓⇓⇓⇓⇓-10].另一方面,在对土壤野外调查取样的过程中,由于地形和人为因素,导致取样结果存在误差,所以无法精准指导农业和规划土地利用[11]. ...
Improving estimation of soil organic matter content by combining Landsat 8 OLI images and environmental data:A case study in the river valley of the southern Qinghai-Tibet Plateau
1
2021
... 土壤有机质(soil organic matter,SOM)是植物和微生物生命活动必不可少的养分和能量来源,是衡量土壤肥力的重要指标,也是陆地土壤碳库的重要组成[1-2],其在调节全球碳循环和土壤理化性质方面有着十分重要的贡献,对于高水平粮食的生产也发挥着重要影响[3].所以,更好地了解SOM空间分布特征可以有效利用土地资源.但是在实际研究中,由于地形要素、社会经济、气候和土壤属性存在差异,使得SOM空间分布不均匀[4⇓⇓⇓⇓⇓-10].另一方面,在对土壤野外调查取样的过程中,由于地形和人为因素,导致取样结果存在误差,所以无法精准指导农业和规划土地利用[11]. ...
星地多源数据的区域土壤有机质数字制图
1
2015
... 近年来,随着“3S”技术的发展,数字土壤制图领域中的多种方法和模型被广泛应用于预测土壤养分的空间分布[12-13].其中,普通克里金插值法(ordinary Kriging,OK)因其原理简单被前人广泛使用[14-15].但是OK法仅依赖样本本身的关系,并未考虑其他环境因素的影响,所以预测精度较低,无法满足人们对空间分布图精确性的需求,另外OK法有易造成平滑效应的缺点[16].随着技术的不断深入,很多国内外学者针对OK法存在的问题进行研究,认为可加入辅助变量对土壤养分进行空间分布的预测,并且采用神经网络模型作为预测模型[17-18].国内学者吴俊等[19]将高光谱数据作为辅助变量,采用反向传播神经网络(BPNN)模型与其他模型对比,表明BPNN的预测效果最佳.国外学者Odebiri 等[20]利用光谱数据作为变量输入,采用人工神经网络(ANN)作为预测模型,研究结果表明神经网络模型使得模型精度提高,可以作为预测模型对土壤养分进行空间分布预测.在此研究基础上,很多学者又将神经网络与地统计学方法结合起来,发现该方法对土壤养分的空间分布预测比单独的神经网络预测模型有更高的精度.赖雨晴等[21]选取14个辅助变量,利用RBFNN与 OK相结合的模型(RBFNN-OK)对土壤有机碳(SOC)含量的空间分布进行预测,结果显示RBFNN-OK比单独的模型预测精度要高.张宏帅等[22]选取5个辅助变量,采用BPNN与OK相结合的模型(BPNN-OK)对SOM含量的空间分布进行预测,发现BPNN-OK的模型精度最高.众多研究表明,加入辅助变量并利用神经网络模型与地统计方法相结合的模型,预测精度更高,且此类方法在对土壤养分空间分布预测上也有一定的技术基础.这种混合的地统计模型不仅可对土壤养分进行空间分布预测,也同样适用于土壤重金属的空间分布预测.Song等[23] 研究利用高光谱数据作为辅助变量并混合地质统计学方法(ANN-OK)来预测武清市土壤重金属As、Cd、Cr、Ni和Zn的浓度,研究发现其精度最高,同时也表明混合地统计模型作为一种预测模型是一项首选的技术手段. ...
星地多源数据的区域土壤有机质数字制图
1
2015
... 近年来,随着“3S”技术的发展,数字土壤制图领域中的多种方法和模型被广泛应用于预测土壤养分的空间分布[12-13].其中,普通克里金插值法(ordinary Kriging,OK)因其原理简单被前人广泛使用[14-15].但是OK法仅依赖样本本身的关系,并未考虑其他环境因素的影响,所以预测精度较低,无法满足人们对空间分布图精确性的需求,另外OK法有易造成平滑效应的缺点[16].随着技术的不断深入,很多国内外学者针对OK法存在的问题进行研究,认为可加入辅助变量对土壤养分进行空间分布的预测,并且采用神经网络模型作为预测模型[17-18].国内学者吴俊等[19]将高光谱数据作为辅助变量,采用反向传播神经网络(BPNN)模型与其他模型对比,表明BPNN的预测效果最佳.国外学者Odebiri 等[20]利用光谱数据作为变量输入,采用人工神经网络(ANN)作为预测模型,研究结果表明神经网络模型使得模型精度提高,可以作为预测模型对土壤养分进行空间分布预测.在此研究基础上,很多学者又将神经网络与地统计学方法结合起来,发现该方法对土壤养分的空间分布预测比单独的神经网络预测模型有更高的精度.赖雨晴等[21]选取14个辅助变量,利用RBFNN与 OK相结合的模型(RBFNN-OK)对土壤有机碳(SOC)含量的空间分布进行预测,结果显示RBFNN-OK比单独的模型预测精度要高.张宏帅等[22]选取5个辅助变量,采用BPNN与OK相结合的模型(BPNN-OK)对SOM含量的空间分布进行预测,发现BPNN-OK的模型精度最高.众多研究表明,加入辅助变量并利用神经网络模型与地统计方法相结合的模型,预测精度更高,且此类方法在对土壤养分空间分布预测上也有一定的技术基础.这种混合的地统计模型不仅可对土壤养分进行空间分布预测,也同样适用于土壤重金属的空间分布预测.Song等[23] 研究利用高光谱数据作为辅助变量并混合地质统计学方法(ANN-OK)来预测武清市土壤重金属As、Cd、Cr、Ni和Zn的浓度,研究发现其精度最高,同时也表明混合地统计模型作为一种预测模型是一项首选的技术手段. ...
Digital mapping of soil organic carbon density using newly developed bare soil spectral indices and deep neural network
2
2022
... 近年来,随着“3S”技术的发展,数字土壤制图领域中的多种方法和模型被广泛应用于预测土壤养分的空间分布[12-13].其中,普通克里金插值法(ordinary Kriging,OK)因其原理简单被前人广泛使用[14-15].但是OK法仅依赖样本本身的关系,并未考虑其他环境因素的影响,所以预测精度较低,无法满足人们对空间分布图精确性的需求,另外OK法有易造成平滑效应的缺点[16].随着技术的不断深入,很多国内外学者针对OK法存在的问题进行研究,认为可加入辅助变量对土壤养分进行空间分布的预测,并且采用神经网络模型作为预测模型[17-18].国内学者吴俊等[19]将高光谱数据作为辅助变量,采用反向传播神经网络(BPNN)模型与其他模型对比,表明BPNN的预测效果最佳.国外学者Odebiri 等[20]利用光谱数据作为变量输入,采用人工神经网络(ANN)作为预测模型,研究结果表明神经网络模型使得模型精度提高,可以作为预测模型对土壤养分进行空间分布预测.在此研究基础上,很多学者又将神经网络与地统计学方法结合起来,发现该方法对土壤养分的空间分布预测比单独的神经网络预测模型有更高的精度.赖雨晴等[21]选取14个辅助变量,利用RBFNN与 OK相结合的模型(RBFNN-OK)对土壤有机碳(SOC)含量的空间分布进行预测,结果显示RBFNN-OK比单独的模型预测精度要高.张宏帅等[22]选取5个辅助变量,采用BPNN与OK相结合的模型(BPNN-OK)对SOM含量的空间分布进行预测,发现BPNN-OK的模型精度最高.众多研究表明,加入辅助变量并利用神经网络模型与地统计方法相结合的模型,预测精度更高,且此类方法在对土壤养分空间分布预测上也有一定的技术基础.这种混合的地统计模型不仅可对土壤养分进行空间分布预测,也同样适用于土壤重金属的空间分布预测.Song等[23] 研究利用高光谱数据作为辅助变量并混合地质统计学方法(ANN-OK)来预测武清市土壤重金属As、Cd、Cr、Ni和Zn的浓度,研究发现其精度最高,同时也表明混合地统计模型作为一种预测模型是一项首选的技术手段. ...
... 对于辅助变量的研究,通过Boruta算法计算得知,土壤本身属性对有机质含量的影响最大,全氮含量高的地区加上研究区又是一个降水集中的地区,使得土壤固氮能力强,从而使得SOM含量高,而且土壤有机质是氮素的主要贮存场所,二者相互依存.除了土壤本身因素和自然因素的影响,现在人类活动频繁,人为因素对于SOM含量的空间分布也是一个重要因素,此外大多学者将高光谱数据也作为影响因子对SOM含量空间分布进行预测,并且取得一定的进展.尉芳等[44]将化肥施用量作为一种影响因子进行研究,得出化肥施用量虽然和SOM含量不存在对应关系,但是相关性却达到了0.33,说明人为因素对SOM含量存在影响.Liu等[13]采用近距离光谱、航空高光谱和Sentinel 2多光谱图像预测农业用地的SOCD,得到了很好的预测精度.因此,在之后的预测方法加入人为因素和高光谱数据作为模型输入,对提高模型预测精度有很好的效果,进而可得到更加接近实际的SOM空间分布图. ...
Soil surface salinity prediction using ASTER data:Comparing statistical and geostatistical models
1
2011
... 近年来,随着“3S”技术的发展,数字土壤制图领域中的多种方法和模型被广泛应用于预测土壤养分的空间分布[12-13].其中,普通克里金插值法(ordinary Kriging,OK)因其原理简单被前人广泛使用[14-15].但是OK法仅依赖样本本身的关系,并未考虑其他环境因素的影响,所以预测精度较低,无法满足人们对空间分布图精确性的需求,另外OK法有易造成平滑效应的缺点[16].随着技术的不断深入,很多国内外学者针对OK法存在的问题进行研究,认为可加入辅助变量对土壤养分进行空间分布的预测,并且采用神经网络模型作为预测模型[17-18].国内学者吴俊等[19]将高光谱数据作为辅助变量,采用反向传播神经网络(BPNN)模型与其他模型对比,表明BPNN的预测效果最佳.国外学者Odebiri 等[20]利用光谱数据作为变量输入,采用人工神经网络(ANN)作为预测模型,研究结果表明神经网络模型使得模型精度提高,可以作为预测模型对土壤养分进行空间分布预测.在此研究基础上,很多学者又将神经网络与地统计学方法结合起来,发现该方法对土壤养分的空间分布预测比单独的神经网络预测模型有更高的精度.赖雨晴等[21]选取14个辅助变量,利用RBFNN与 OK相结合的模型(RBFNN-OK)对土壤有机碳(SOC)含量的空间分布进行预测,结果显示RBFNN-OK比单独的模型预测精度要高.张宏帅等[22]选取5个辅助变量,采用BPNN与OK相结合的模型(BPNN-OK)对SOM含量的空间分布进行预测,发现BPNN-OK的模型精度最高.众多研究表明,加入辅助变量并利用神经网络模型与地统计方法相结合的模型,预测精度更高,且此类方法在对土壤养分空间分布预测上也有一定的技术基础.这种混合的地统计模型不仅可对土壤养分进行空间分布预测,也同样适用于土壤重金属的空间分布预测.Song等[23] 研究利用高光谱数据作为辅助变量并混合地质统计学方法(ANN-OK)来预测武清市土壤重金属As、Cd、Cr、Ni和Zn的浓度,研究发现其精度最高,同时也表明混合地统计模型作为一种预测模型是一项首选的技术手段. ...
基于三种空间预测模型的海南岛土壤有机质空间分布研究
1
2018
... 近年来,随着“3S”技术的发展,数字土壤制图领域中的多种方法和模型被广泛应用于预测土壤养分的空间分布[12-13].其中,普通克里金插值法(ordinary Kriging,OK)因其原理简单被前人广泛使用[14-15].但是OK法仅依赖样本本身的关系,并未考虑其他环境因素的影响,所以预测精度较低,无法满足人们对空间分布图精确性的需求,另外OK法有易造成平滑效应的缺点[16].随着技术的不断深入,很多国内外学者针对OK法存在的问题进行研究,认为可加入辅助变量对土壤养分进行空间分布的预测,并且采用神经网络模型作为预测模型[17-18].国内学者吴俊等[19]将高光谱数据作为辅助变量,采用反向传播神经网络(BPNN)模型与其他模型对比,表明BPNN的预测效果最佳.国外学者Odebiri 等[20]利用光谱数据作为变量输入,采用人工神经网络(ANN)作为预测模型,研究结果表明神经网络模型使得模型精度提高,可以作为预测模型对土壤养分进行空间分布预测.在此研究基础上,很多学者又将神经网络与地统计学方法结合起来,发现该方法对土壤养分的空间分布预测比单独的神经网络预测模型有更高的精度.赖雨晴等[21]选取14个辅助变量,利用RBFNN与 OK相结合的模型(RBFNN-OK)对土壤有机碳(SOC)含量的空间分布进行预测,结果显示RBFNN-OK比单独的模型预测精度要高.张宏帅等[22]选取5个辅助变量,采用BPNN与OK相结合的模型(BPNN-OK)对SOM含量的空间分布进行预测,发现BPNN-OK的模型精度最高.众多研究表明,加入辅助变量并利用神经网络模型与地统计方法相结合的模型,预测精度更高,且此类方法在对土壤养分空间分布预测上也有一定的技术基础.这种混合的地统计模型不仅可对土壤养分进行空间分布预测,也同样适用于土壤重金属的空间分布预测.Song等[23] 研究利用高光谱数据作为辅助变量并混合地质统计学方法(ANN-OK)来预测武清市土壤重金属As、Cd、Cr、Ni和Zn的浓度,研究发现其精度最高,同时也表明混合地统计模型作为一种预测模型是一项首选的技术手段. ...
基于三种空间预测模型的海南岛土壤有机质空间分布研究
1
2018
... 近年来,随着“3S”技术的发展,数字土壤制图领域中的多种方法和模型被广泛应用于预测土壤养分的空间分布[12-13].其中,普通克里金插值法(ordinary Kriging,OK)因其原理简单被前人广泛使用[14-15].但是OK法仅依赖样本本身的关系,并未考虑其他环境因素的影响,所以预测精度较低,无法满足人们对空间分布图精确性的需求,另外OK法有易造成平滑效应的缺点[16].随着技术的不断深入,很多国内外学者针对OK法存在的问题进行研究,认为可加入辅助变量对土壤养分进行空间分布的预测,并且采用神经网络模型作为预测模型[17-18].国内学者吴俊等[19]将高光谱数据作为辅助变量,采用反向传播神经网络(BPNN)模型与其他模型对比,表明BPNN的预测效果最佳.国外学者Odebiri 等[20]利用光谱数据作为变量输入,采用人工神经网络(ANN)作为预测模型,研究结果表明神经网络模型使得模型精度提高,可以作为预测模型对土壤养分进行空间分布预测.在此研究基础上,很多学者又将神经网络与地统计学方法结合起来,发现该方法对土壤养分的空间分布预测比单独的神经网络预测模型有更高的精度.赖雨晴等[21]选取14个辅助变量,利用RBFNN与 OK相结合的模型(RBFNN-OK)对土壤有机碳(SOC)含量的空间分布进行预测,结果显示RBFNN-OK比单独的模型预测精度要高.张宏帅等[22]选取5个辅助变量,采用BPNN与OK相结合的模型(BPNN-OK)对SOM含量的空间分布进行预测,发现BPNN-OK的模型精度最高.众多研究表明,加入辅助变量并利用神经网络模型与地统计方法相结合的模型,预测精度更高,且此类方法在对土壤养分空间分布预测上也有一定的技术基础.这种混合的地统计模型不仅可对土壤养分进行空间分布预测,也同样适用于土壤重金属的空间分布预测.Song等[23] 研究利用高光谱数据作为辅助变量并混合地质统计学方法(ANN-OK)来预测武清市土壤重金属As、Cd、Cr、Ni和Zn的浓度,研究发现其精度最高,同时也表明混合地统计模型作为一种预测模型是一项首选的技术手段. ...
应用集成BP神经网络进行田间土壤空间变异研究
1
2004
... 近年来,随着“3S”技术的发展,数字土壤制图领域中的多种方法和模型被广泛应用于预测土壤养分的空间分布[12-13].其中,普通克里金插值法(ordinary Kriging,OK)因其原理简单被前人广泛使用[14-15].但是OK法仅依赖样本本身的关系,并未考虑其他环境因素的影响,所以预测精度较低,无法满足人们对空间分布图精确性的需求,另外OK法有易造成平滑效应的缺点[16].随着技术的不断深入,很多国内外学者针对OK法存在的问题进行研究,认为可加入辅助变量对土壤养分进行空间分布的预测,并且采用神经网络模型作为预测模型[17-18].国内学者吴俊等[19]将高光谱数据作为辅助变量,采用反向传播神经网络(BPNN)模型与其他模型对比,表明BPNN的预测效果最佳.国外学者Odebiri 等[20]利用光谱数据作为变量输入,采用人工神经网络(ANN)作为预测模型,研究结果表明神经网络模型使得模型精度提高,可以作为预测模型对土壤养分进行空间分布预测.在此研究基础上,很多学者又将神经网络与地统计学方法结合起来,发现该方法对土壤养分的空间分布预测比单独的神经网络预测模型有更高的精度.赖雨晴等[21]选取14个辅助变量,利用RBFNN与 OK相结合的模型(RBFNN-OK)对土壤有机碳(SOC)含量的空间分布进行预测,结果显示RBFNN-OK比单独的模型预测精度要高.张宏帅等[22]选取5个辅助变量,采用BPNN与OK相结合的模型(BPNN-OK)对SOM含量的空间分布进行预测,发现BPNN-OK的模型精度最高.众多研究表明,加入辅助变量并利用神经网络模型与地统计方法相结合的模型,预测精度更高,且此类方法在对土壤养分空间分布预测上也有一定的技术基础.这种混合的地统计模型不仅可对土壤养分进行空间分布预测,也同样适用于土壤重金属的空间分布预测.Song等[23] 研究利用高光谱数据作为辅助变量并混合地质统计学方法(ANN-OK)来预测武清市土壤重金属As、Cd、Cr、Ni和Zn的浓度,研究发现其精度最高,同时也表明混合地统计模型作为一种预测模型是一项首选的技术手段. ...
应用集成BP神经网络进行田间土壤空间变异研究
1
2004
... 近年来,随着“3S”技术的发展,数字土壤制图领域中的多种方法和模型被广泛应用于预测土壤养分的空间分布[12-13].其中,普通克里金插值法(ordinary Kriging,OK)因其原理简单被前人广泛使用[14-15].但是OK法仅依赖样本本身的关系,并未考虑其他环境因素的影响,所以预测精度较低,无法满足人们对空间分布图精确性的需求,另外OK法有易造成平滑效应的缺点[16].随着技术的不断深入,很多国内外学者针对OK法存在的问题进行研究,认为可加入辅助变量对土壤养分进行空间分布的预测,并且采用神经网络模型作为预测模型[17-18].国内学者吴俊等[19]将高光谱数据作为辅助变量,采用反向传播神经网络(BPNN)模型与其他模型对比,表明BPNN的预测效果最佳.国外学者Odebiri 等[20]利用光谱数据作为变量输入,采用人工神经网络(ANN)作为预测模型,研究结果表明神经网络模型使得模型精度提高,可以作为预测模型对土壤养分进行空间分布预测.在此研究基础上,很多学者又将神经网络与地统计学方法结合起来,发现该方法对土壤养分的空间分布预测比单独的神经网络预测模型有更高的精度.赖雨晴等[21]选取14个辅助变量,利用RBFNN与 OK相结合的模型(RBFNN-OK)对土壤有机碳(SOC)含量的空间分布进行预测,结果显示RBFNN-OK比单独的模型预测精度要高.张宏帅等[22]选取5个辅助变量,采用BPNN与OK相结合的模型(BPNN-OK)对SOM含量的空间分布进行预测,发现BPNN-OK的模型精度最高.众多研究表明,加入辅助变量并利用神经网络模型与地统计方法相结合的模型,预测精度更高,且此类方法在对土壤养分空间分布预测上也有一定的技术基础.这种混合的地统计模型不仅可对土壤养分进行空间分布预测,也同样适用于土壤重金属的空间分布预测.Song等[23] 研究利用高光谱数据作为辅助变量并混合地质统计学方法(ANN-OK)来预测武清市土壤重金属As、Cd、Cr、Ni和Zn的浓度,研究发现其精度最高,同时也表明混合地统计模型作为一种预测模型是一项首选的技术手段. ...
National soil organic carbon estimates can improve global estimates
1
2019
... 近年来,随着“3S”技术的发展,数字土壤制图领域中的多种方法和模型被广泛应用于预测土壤养分的空间分布[12-13].其中,普通克里金插值法(ordinary Kriging,OK)因其原理简单被前人广泛使用[14-15].但是OK法仅依赖样本本身的关系,并未考虑其他环境因素的影响,所以预测精度较低,无法满足人们对空间分布图精确性的需求,另外OK法有易造成平滑效应的缺点[16].随着技术的不断深入,很多国内外学者针对OK法存在的问题进行研究,认为可加入辅助变量对土壤养分进行空间分布的预测,并且采用神经网络模型作为预测模型[17-18].国内学者吴俊等[19]将高光谱数据作为辅助变量,采用反向传播神经网络(BPNN)模型与其他模型对比,表明BPNN的预测效果最佳.国外学者Odebiri 等[20]利用光谱数据作为变量输入,采用人工神经网络(ANN)作为预测模型,研究结果表明神经网络模型使得模型精度提高,可以作为预测模型对土壤养分进行空间分布预测.在此研究基础上,很多学者又将神经网络与地统计学方法结合起来,发现该方法对土壤养分的空间分布预测比单独的神经网络预测模型有更高的精度.赖雨晴等[21]选取14个辅助变量,利用RBFNN与 OK相结合的模型(RBFNN-OK)对土壤有机碳(SOC)含量的空间分布进行预测,结果显示RBFNN-OK比单独的模型预测精度要高.张宏帅等[22]选取5个辅助变量,采用BPNN与OK相结合的模型(BPNN-OK)对SOM含量的空间分布进行预测,发现BPNN-OK的模型精度最高.众多研究表明,加入辅助变量并利用神经网络模型与地统计方法相结合的模型,预测精度更高,且此类方法在对土壤养分空间分布预测上也有一定的技术基础.这种混合的地统计模型不仅可对土壤养分进行空间分布预测,也同样适用于土壤重金属的空间分布预测.Song等[23] 研究利用高光谱数据作为辅助变量并混合地质统计学方法(ANN-OK)来预测武清市土壤重金属As、Cd、Cr、Ni和Zn的浓度,研究发现其精度最高,同时也表明混合地统计模型作为一种预测模型是一项首选的技术手段. ...
Soil organic carbon prediction using visible-near infrared reflectance spectroscopy employing artificial neural network modelling
1
2020
... 近年来,随着“3S”技术的发展,数字土壤制图领域中的多种方法和模型被广泛应用于预测土壤养分的空间分布[12-13].其中,普通克里金插值法(ordinary Kriging,OK)因其原理简单被前人广泛使用[14-15].但是OK法仅依赖样本本身的关系,并未考虑其他环境因素的影响,所以预测精度较低,无法满足人们对空间分布图精确性的需求,另外OK法有易造成平滑效应的缺点[16].随着技术的不断深入,很多国内外学者针对OK法存在的问题进行研究,认为可加入辅助变量对土壤养分进行空间分布的预测,并且采用神经网络模型作为预测模型[17-18].国内学者吴俊等[19]将高光谱数据作为辅助变量,采用反向传播神经网络(BPNN)模型与其他模型对比,表明BPNN的预测效果最佳.国外学者Odebiri 等[20]利用光谱数据作为变量输入,采用人工神经网络(ANN)作为预测模型,研究结果表明神经网络模型使得模型精度提高,可以作为预测模型对土壤养分进行空间分布预测.在此研究基础上,很多学者又将神经网络与地统计学方法结合起来,发现该方法对土壤养分的空间分布预测比单独的神经网络预测模型有更高的精度.赖雨晴等[21]选取14个辅助变量,利用RBFNN与 OK相结合的模型(RBFNN-OK)对土壤有机碳(SOC)含量的空间分布进行预测,结果显示RBFNN-OK比单独的模型预测精度要高.张宏帅等[22]选取5个辅助变量,采用BPNN与OK相结合的模型(BPNN-OK)对SOM含量的空间分布进行预测,发现BPNN-OK的模型精度最高.众多研究表明,加入辅助变量并利用神经网络模型与地统计方法相结合的模型,预测精度更高,且此类方法在对土壤养分空间分布预测上也有一定的技术基础.这种混合的地统计模型不仅可对土壤养分进行空间分布预测,也同样适用于土壤重金属的空间分布预测.Song等[23] 研究利用高光谱数据作为辅助变量并混合地质统计学方法(ANN-OK)来预测武清市土壤重金属As、Cd、Cr、Ni和Zn的浓度,研究发现其精度最高,同时也表明混合地统计模型作为一种预测模型是一项首选的技术手段. ...
基于CARS-BPNN的江西省土壤有机碳含量高光谱预测
1
2022
... 近年来,随着“3S”技术的发展,数字土壤制图领域中的多种方法和模型被广泛应用于预测土壤养分的空间分布[12-13].其中,普通克里金插值法(ordinary Kriging,OK)因其原理简单被前人广泛使用[14-15].但是OK法仅依赖样本本身的关系,并未考虑其他环境因素的影响,所以预测精度较低,无法满足人们对空间分布图精确性的需求,另外OK法有易造成平滑效应的缺点[16].随着技术的不断深入,很多国内外学者针对OK法存在的问题进行研究,认为可加入辅助变量对土壤养分进行空间分布的预测,并且采用神经网络模型作为预测模型[17-18].国内学者吴俊等[19]将高光谱数据作为辅助变量,采用反向传播神经网络(BPNN)模型与其他模型对比,表明BPNN的预测效果最佳.国外学者Odebiri 等[20]利用光谱数据作为变量输入,采用人工神经网络(ANN)作为预测模型,研究结果表明神经网络模型使得模型精度提高,可以作为预测模型对土壤养分进行空间分布预测.在此研究基础上,很多学者又将神经网络与地统计学方法结合起来,发现该方法对土壤养分的空间分布预测比单独的神经网络预测模型有更高的精度.赖雨晴等[21]选取14个辅助变量,利用RBFNN与 OK相结合的模型(RBFNN-OK)对土壤有机碳(SOC)含量的空间分布进行预测,结果显示RBFNN-OK比单独的模型预测精度要高.张宏帅等[22]选取5个辅助变量,采用BPNN与OK相结合的模型(BPNN-OK)对SOM含量的空间分布进行预测,发现BPNN-OK的模型精度最高.众多研究表明,加入辅助变量并利用神经网络模型与地统计方法相结合的模型,预测精度更高,且此类方法在对土壤养分空间分布预测上也有一定的技术基础.这种混合的地统计模型不仅可对土壤养分进行空间分布预测,也同样适用于土壤重金属的空间分布预测.Song等[23] 研究利用高光谱数据作为辅助变量并混合地质统计学方法(ANN-OK)来预测武清市土壤重金属As、Cd、Cr、Ni和Zn的浓度,研究发现其精度最高,同时也表明混合地统计模型作为一种预测模型是一项首选的技术手段. ...
基于CARS-BPNN的江西省土壤有机碳含量高光谱预测
1
2022
... 近年来,随着“3S”技术的发展,数字土壤制图领域中的多种方法和模型被广泛应用于预测土壤养分的空间分布[12-13].其中,普通克里金插值法(ordinary Kriging,OK)因其原理简单被前人广泛使用[14-15].但是OK法仅依赖样本本身的关系,并未考虑其他环境因素的影响,所以预测精度较低,无法满足人们对空间分布图精确性的需求,另外OK法有易造成平滑效应的缺点[16].随着技术的不断深入,很多国内外学者针对OK法存在的问题进行研究,认为可加入辅助变量对土壤养分进行空间分布的预测,并且采用神经网络模型作为预测模型[17-18].国内学者吴俊等[19]将高光谱数据作为辅助变量,采用反向传播神经网络(BPNN)模型与其他模型对比,表明BPNN的预测效果最佳.国外学者Odebiri 等[20]利用光谱数据作为变量输入,采用人工神经网络(ANN)作为预测模型,研究结果表明神经网络模型使得模型精度提高,可以作为预测模型对土壤养分进行空间分布预测.在此研究基础上,很多学者又将神经网络与地统计学方法结合起来,发现该方法对土壤养分的空间分布预测比单独的神经网络预测模型有更高的精度.赖雨晴等[21]选取14个辅助变量,利用RBFNN与 OK相结合的模型(RBFNN-OK)对土壤有机碳(SOC)含量的空间分布进行预测,结果显示RBFNN-OK比单独的模型预测精度要高.张宏帅等[22]选取5个辅助变量,采用BPNN与OK相结合的模型(BPNN-OK)对SOM含量的空间分布进行预测,发现BPNN-OK的模型精度最高.众多研究表明,加入辅助变量并利用神经网络模型与地统计方法相结合的模型,预测精度更高,且此类方法在对土壤养分空间分布预测上也有一定的技术基础.这种混合的地统计模型不仅可对土壤养分进行空间分布预测,也同样适用于土壤重金属的空间分布预测.Song等[23] 研究利用高光谱数据作为辅助变量并混合地质统计学方法(ANN-OK)来预测武清市土壤重金属As、Cd、Cr、Ni和Zn的浓度,研究发现其精度最高,同时也表明混合地统计模型作为一种预测模型是一项首选的技术手段. ...
Deep learning-based national scale soil organic carbon mapping with Sentinel-3 data
2
2022
... 近年来,随着“3S”技术的发展,数字土壤制图领域中的多种方法和模型被广泛应用于预测土壤养分的空间分布[12-13].其中,普通克里金插值法(ordinary Kriging,OK)因其原理简单被前人广泛使用[14-15].但是OK法仅依赖样本本身的关系,并未考虑其他环境因素的影响,所以预测精度较低,无法满足人们对空间分布图精确性的需求,另外OK法有易造成平滑效应的缺点[16].随着技术的不断深入,很多国内外学者针对OK法存在的问题进行研究,认为可加入辅助变量对土壤养分进行空间分布的预测,并且采用神经网络模型作为预测模型[17-18].国内学者吴俊等[19]将高光谱数据作为辅助变量,采用反向传播神经网络(BPNN)模型与其他模型对比,表明BPNN的预测效果最佳.国外学者Odebiri 等[20]利用光谱数据作为变量输入,采用人工神经网络(ANN)作为预测模型,研究结果表明神经网络模型使得模型精度提高,可以作为预测模型对土壤养分进行空间分布预测.在此研究基础上,很多学者又将神经网络与地统计学方法结合起来,发现该方法对土壤养分的空间分布预测比单独的神经网络预测模型有更高的精度.赖雨晴等[21]选取14个辅助变量,利用RBFNN与 OK相结合的模型(RBFNN-OK)对土壤有机碳(SOC)含量的空间分布进行预测,结果显示RBFNN-OK比单独的模型预测精度要高.张宏帅等[22]选取5个辅助变量,采用BPNN与OK相结合的模型(BPNN-OK)对SOM含量的空间分布进行预测,发现BPNN-OK的模型精度最高.众多研究表明,加入辅助变量并利用神经网络模型与地统计方法相结合的模型,预测精度更高,且此类方法在对土壤养分空间分布预测上也有一定的技术基础.这种混合的地统计模型不仅可对土壤养分进行空间分布预测,也同样适用于土壤重金属的空间分布预测.Song等[23] 研究利用高光谱数据作为辅助变量并混合地质统计学方法(ANN-OK)来预测武清市土壤重金属As、Cd、Cr、Ni和Zn的浓度,研究发现其精度最高,同时也表明混合地统计模型作为一种预测模型是一项首选的技术手段. ...
... 在SOM预测空间分布中,OK法通过邻近相关采样点SOM含量来预测未知点,但是没有考虑环境因素对土壤有机质含量的影响,所以本文采用OK法预测得到的预测精度指标MSE、RMSE、MAE最大,拟合系数最小.4种预测模型中,只有OK法的拟合系数低于0.30,其他3种预测模型的拟合系数都高于0.50,而且GA-BPNN-OK的拟合系数达到了0.78,是3种预测模型中误差最小、精度最高的模型,与前人对SOM预测的研究结果相一致[20].GA-BPNN-OK模型精度高究其原因是其利用Boruta算法从9个变量因子筛选出特征变量为辅助变量用于输入进行建模,能够较好地处理土壤有机质与环境变量的非线性复杂关系,使用Boruta算法也可以剔除冗余特征变量,与全变量模型精度相比有效提高了预测精度.且利用GA优化的BP神经网络计算出残差之后对其进行普通克里金法插值而消除残差空间自相关性,这种方法充分考虑了采样点的结构性和随机性,所以对预测模型的精度有很大的提升,且预测优势十分显著,是研究区SOM含量的最优预测模型. ...
人工神经网络及其与地统计的混合模型在小面积丘陵区土壤有机碳预测制图上的应用研究
1
2017
... 近年来,随着“3S”技术的发展,数字土壤制图领域中的多种方法和模型被广泛应用于预测土壤养分的空间分布[12-13].其中,普通克里金插值法(ordinary Kriging,OK)因其原理简单被前人广泛使用[14-15].但是OK法仅依赖样本本身的关系,并未考虑其他环境因素的影响,所以预测精度较低,无法满足人们对空间分布图精确性的需求,另外OK法有易造成平滑效应的缺点[16].随着技术的不断深入,很多国内外学者针对OK法存在的问题进行研究,认为可加入辅助变量对土壤养分进行空间分布的预测,并且采用神经网络模型作为预测模型[17-18].国内学者吴俊等[19]将高光谱数据作为辅助变量,采用反向传播神经网络(BPNN)模型与其他模型对比,表明BPNN的预测效果最佳.国外学者Odebiri 等[20]利用光谱数据作为变量输入,采用人工神经网络(ANN)作为预测模型,研究结果表明神经网络模型使得模型精度提高,可以作为预测模型对土壤养分进行空间分布预测.在此研究基础上,很多学者又将神经网络与地统计学方法结合起来,发现该方法对土壤养分的空间分布预测比单独的神经网络预测模型有更高的精度.赖雨晴等[21]选取14个辅助变量,利用RBFNN与 OK相结合的模型(RBFNN-OK)对土壤有机碳(SOC)含量的空间分布进行预测,结果显示RBFNN-OK比单独的模型预测精度要高.张宏帅等[22]选取5个辅助变量,采用BPNN与OK相结合的模型(BPNN-OK)对SOM含量的空间分布进行预测,发现BPNN-OK的模型精度最高.众多研究表明,加入辅助变量并利用神经网络模型与地统计方法相结合的模型,预测精度更高,且此类方法在对土壤养分空间分布预测上也有一定的技术基础.这种混合的地统计模型不仅可对土壤养分进行空间分布预测,也同样适用于土壤重金属的空间分布预测.Song等[23] 研究利用高光谱数据作为辅助变量并混合地质统计学方法(ANN-OK)来预测武清市土壤重金属As、Cd、Cr、Ni和Zn的浓度,研究发现其精度最高,同时也表明混合地统计模型作为一种预测模型是一项首选的技术手段. ...
人工神经网络及其与地统计的混合模型在小面积丘陵区土壤有机碳预测制图上的应用研究
1
2017
... 近年来,随着“3S”技术的发展,数字土壤制图领域中的多种方法和模型被广泛应用于预测土壤养分的空间分布[12-13].其中,普通克里金插值法(ordinary Kriging,OK)因其原理简单被前人广泛使用[14-15].但是OK法仅依赖样本本身的关系,并未考虑其他环境因素的影响,所以预测精度较低,无法满足人们对空间分布图精确性的需求,另外OK法有易造成平滑效应的缺点[16].随着技术的不断深入,很多国内外学者针对OK法存在的问题进行研究,认为可加入辅助变量对土壤养分进行空间分布的预测,并且采用神经网络模型作为预测模型[17-18].国内学者吴俊等[19]将高光谱数据作为辅助变量,采用反向传播神经网络(BPNN)模型与其他模型对比,表明BPNN的预测效果最佳.国外学者Odebiri 等[20]利用光谱数据作为变量输入,采用人工神经网络(ANN)作为预测模型,研究结果表明神经网络模型使得模型精度提高,可以作为预测模型对土壤养分进行空间分布预测.在此研究基础上,很多学者又将神经网络与地统计学方法结合起来,发现该方法对土壤养分的空间分布预测比单独的神经网络预测模型有更高的精度.赖雨晴等[21]选取14个辅助变量,利用RBFNN与 OK相结合的模型(RBFNN-OK)对土壤有机碳(SOC)含量的空间分布进行预测,结果显示RBFNN-OK比单独的模型预测精度要高.张宏帅等[22]选取5个辅助变量,采用BPNN与OK相结合的模型(BPNN-OK)对SOM含量的空间分布进行预测,发现BPNN-OK的模型精度最高.众多研究表明,加入辅助变量并利用神经网络模型与地统计方法相结合的模型,预测精度更高,且此类方法在对土壤养分空间分布预测上也有一定的技术基础.这种混合的地统计模型不仅可对土壤养分进行空间分布预测,也同样适用于土壤重金属的空间分布预测.Song等[23] 研究利用高光谱数据作为辅助变量并混合地质统计学方法(ANN-OK)来预测武清市土壤重金属As、Cd、Cr、Ni和Zn的浓度,研究发现其精度最高,同时也表明混合地统计模型作为一种预测模型是一项首选的技术手段. ...
基于BP神经网络与Kriging结合的土壤有机质空间分布模拟——以福建省华安县为例
1
2021
... 近年来,随着“3S”技术的发展,数字土壤制图领域中的多种方法和模型被广泛应用于预测土壤养分的空间分布[12-13].其中,普通克里金插值法(ordinary Kriging,OK)因其原理简单被前人广泛使用[14-15].但是OK法仅依赖样本本身的关系,并未考虑其他环境因素的影响,所以预测精度较低,无法满足人们对空间分布图精确性的需求,另外OK法有易造成平滑效应的缺点[16].随着技术的不断深入,很多国内外学者针对OK法存在的问题进行研究,认为可加入辅助变量对土壤养分进行空间分布的预测,并且采用神经网络模型作为预测模型[17-18].国内学者吴俊等[19]将高光谱数据作为辅助变量,采用反向传播神经网络(BPNN)模型与其他模型对比,表明BPNN的预测效果最佳.国外学者Odebiri 等[20]利用光谱数据作为变量输入,采用人工神经网络(ANN)作为预测模型,研究结果表明神经网络模型使得模型精度提高,可以作为预测模型对土壤养分进行空间分布预测.在此研究基础上,很多学者又将神经网络与地统计学方法结合起来,发现该方法对土壤养分的空间分布预测比单独的神经网络预测模型有更高的精度.赖雨晴等[21]选取14个辅助变量,利用RBFNN与 OK相结合的模型(RBFNN-OK)对土壤有机碳(SOC)含量的空间分布进行预测,结果显示RBFNN-OK比单独的模型预测精度要高.张宏帅等[22]选取5个辅助变量,采用BPNN与OK相结合的模型(BPNN-OK)对SOM含量的空间分布进行预测,发现BPNN-OK的模型精度最高.众多研究表明,加入辅助变量并利用神经网络模型与地统计方法相结合的模型,预测精度更高,且此类方法在对土壤养分空间分布预测上也有一定的技术基础.这种混合的地统计模型不仅可对土壤养分进行空间分布预测,也同样适用于土壤重金属的空间分布预测.Song等[23] 研究利用高光谱数据作为辅助变量并混合地质统计学方法(ANN-OK)来预测武清市土壤重金属As、Cd、Cr、Ni和Zn的浓度,研究发现其精度最高,同时也表明混合地统计模型作为一种预测模型是一项首选的技术手段. ...
基于BP神经网络与Kriging结合的土壤有机质空间分布模拟——以福建省华安县为例
1
2021
... 近年来,随着“3S”技术的发展,数字土壤制图领域中的多种方法和模型被广泛应用于预测土壤养分的空间分布[12-13].其中,普通克里金插值法(ordinary Kriging,OK)因其原理简单被前人广泛使用[14-15].但是OK法仅依赖样本本身的关系,并未考虑其他环境因素的影响,所以预测精度较低,无法满足人们对空间分布图精确性的需求,另外OK法有易造成平滑效应的缺点[16].随着技术的不断深入,很多国内外学者针对OK法存在的问题进行研究,认为可加入辅助变量对土壤养分进行空间分布的预测,并且采用神经网络模型作为预测模型[17-18].国内学者吴俊等[19]将高光谱数据作为辅助变量,采用反向传播神经网络(BPNN)模型与其他模型对比,表明BPNN的预测效果最佳.国外学者Odebiri 等[20]利用光谱数据作为变量输入,采用人工神经网络(ANN)作为预测模型,研究结果表明神经网络模型使得模型精度提高,可以作为预测模型对土壤养分进行空间分布预测.在此研究基础上,很多学者又将神经网络与地统计学方法结合起来,发现该方法对土壤养分的空间分布预测比单独的神经网络预测模型有更高的精度.赖雨晴等[21]选取14个辅助变量,利用RBFNN与 OK相结合的模型(RBFNN-OK)对土壤有机碳(SOC)含量的空间分布进行预测,结果显示RBFNN-OK比单独的模型预测精度要高.张宏帅等[22]选取5个辅助变量,采用BPNN与OK相结合的模型(BPNN-OK)对SOM含量的空间分布进行预测,发现BPNN-OK的模型精度最高.众多研究表明,加入辅助变量并利用神经网络模型与地统计方法相结合的模型,预测精度更高,且此类方法在对土壤养分空间分布预测上也有一定的技术基础.这种混合的地统计模型不仅可对土壤养分进行空间分布预测,也同样适用于土壤重金属的空间分布预测.Song等[23] 研究利用高光谱数据作为辅助变量并混合地质统计学方法(ANN-OK)来预测武清市土壤重金属As、Cd、Cr、Ni和Zn的浓度,研究发现其精度最高,同时也表明混合地统计模型作为一种预测模型是一项首选的技术手段. ...
Using multispectral variables to estimate heavy metals content in agricultural soils:A case of suburban area in Tianjin,China
1
2022
... 近年来,随着“3S”技术的发展,数字土壤制图领域中的多种方法和模型被广泛应用于预测土壤养分的空间分布[12-13].其中,普通克里金插值法(ordinary Kriging,OK)因其原理简单被前人广泛使用[14-15].但是OK法仅依赖样本本身的关系,并未考虑其他环境因素的影响,所以预测精度较低,无法满足人们对空间分布图精确性的需求,另外OK法有易造成平滑效应的缺点[16].随着技术的不断深入,很多国内外学者针对OK法存在的问题进行研究,认为可加入辅助变量对土壤养分进行空间分布的预测,并且采用神经网络模型作为预测模型[17-18].国内学者吴俊等[19]将高光谱数据作为辅助变量,采用反向传播神经网络(BPNN)模型与其他模型对比,表明BPNN的预测效果最佳.国外学者Odebiri 等[20]利用光谱数据作为变量输入,采用人工神经网络(ANN)作为预测模型,研究结果表明神经网络模型使得模型精度提高,可以作为预测模型对土壤养分进行空间分布预测.在此研究基础上,很多学者又将神经网络与地统计学方法结合起来,发现该方法对土壤养分的空间分布预测比单独的神经网络预测模型有更高的精度.赖雨晴等[21]选取14个辅助变量,利用RBFNN与 OK相结合的模型(RBFNN-OK)对土壤有机碳(SOC)含量的空间分布进行预测,结果显示RBFNN-OK比单独的模型预测精度要高.张宏帅等[22]选取5个辅助变量,采用BPNN与OK相结合的模型(BPNN-OK)对SOM含量的空间分布进行预测,发现BPNN-OK的模型精度最高.众多研究表明,加入辅助变量并利用神经网络模型与地统计方法相结合的模型,预测精度更高,且此类方法在对土壤养分空间分布预测上也有一定的技术基础.这种混合的地统计模型不仅可对土壤养分进行空间分布预测,也同样适用于土壤重金属的空间分布预测.Song等[23] 研究利用高光谱数据作为辅助变量并混合地质统计学方法(ANN-OK)来预测武清市土壤重金属As、Cd、Cr、Ni和Zn的浓度,研究发现其精度最高,同时也表明混合地统计模型作为一种预测模型是一项首选的技术手段. ...
MODIS数据植被指数的提取方法研究
1
2006
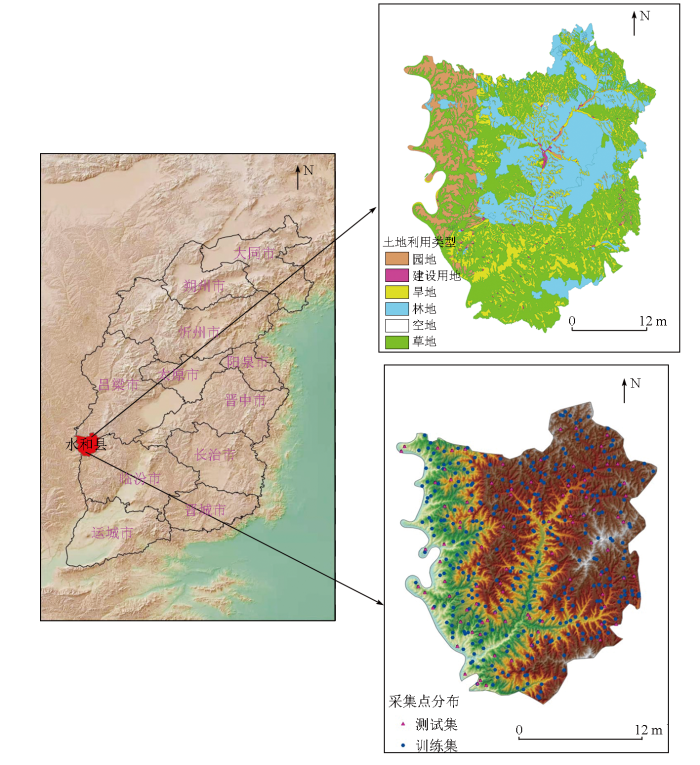
... 本文采用的数字高程模型(DEM)数据和植被数据来源于地理空间数据云(http:// www.gscloud.cn/),在此网站分别下载了分辨率为30 m的DEM数据和分辨率为250 m的陆地合成产品(MODLT1D和MODLT1T).根据ArcGIS 10.7中的最近邻分配方法,对所有环境变量重新采样,空间分辨率为100 m×100 m.利用此数据在 ArcGIS 10.7 软件中提取计算出 6个地形因子和2个植被指数,其中地形因子包括高程(elevation)、坡度(ascent)、坡向(slope)、平面曲率(plan curvature)、剖面曲率(profile curvature)和地形湿度指数(topographicwetness index,TWI),植被指数有归一化植被指数(normalized difference vegetation Index,NDVI)和增强型植被指数(enhanced vegetation index, EVI) [24⇓-26].因为研究区地理位置特殊,土壤类型、成土母质和气候都比较单一,因此,在后续的建模中未考虑如上环境因子,最后选取6个地形因子、2个植被指数和1个代表土壤属性的全氮作为变量因子进行分析. ...
MODIS数据植被指数的提取方法研究
1
2006
... 本文采用的数字高程模型(DEM)数据和植被数据来源于地理空间数据云(http:// www.gscloud.cn/),在此网站分别下载了分辨率为30 m的DEM数据和分辨率为250 m的陆地合成产品(MODLT1D和MODLT1T).根据ArcGIS 10.7中的最近邻分配方法,对所有环境变量重新采样,空间分辨率为100 m×100 m.利用此数据在 ArcGIS 10.7 软件中提取计算出 6个地形因子和2个植被指数,其中地形因子包括高程(elevation)、坡度(ascent)、坡向(slope)、平面曲率(plan curvature)、剖面曲率(profile curvature)和地形湿度指数(topographicwetness index,TWI),植被指数有归一化植被指数(normalized difference vegetation Index,NDVI)和增强型植被指数(enhanced vegetation index, EVI) [24⇓-26].因为研究区地理位置特殊,土壤类型、成土母质和气候都比较单一,因此,在后续的建模中未考虑如上环境因子,最后选取6个地形因子、2个植被指数和1个代表土壤属性的全氮作为变量因子进行分析. ...
ArcGeomorphometry:A toolbox for geomorphometric characterisation of DEMs in the ArcGIS environment
1
2015
... 本文采用的数字高程模型(DEM)数据和植被数据来源于地理空间数据云(http:// www.gscloud.cn/),在此网站分别下载了分辨率为30 m的DEM数据和分辨率为250 m的陆地合成产品(MODLT1D和MODLT1T).根据ArcGIS 10.7中的最近邻分配方法,对所有环境变量重新采样,空间分辨率为100 m×100 m.利用此数据在 ArcGIS 10.7 软件中提取计算出 6个地形因子和2个植被指数,其中地形因子包括高程(elevation)、坡度(ascent)、坡向(slope)、平面曲率(plan curvature)、剖面曲率(profile curvature)和地形湿度指数(topographicwetness index,TWI),植被指数有归一化植被指数(normalized difference vegetation Index,NDVI)和增强型植被指数(enhanced vegetation index, EVI) [24⇓-26].因为研究区地理位置特殊,土壤类型、成土母质和气候都比较单一,因此,在后续的建模中未考虑如上环境因子,最后选取6个地形因子、2个植被指数和1个代表土壤属性的全氮作为变量因子进行分析. ...
Modelling of piping collapses and gully headcut landforms:Evaluating topographic variables from different types of DEM
1
2021
... 本文采用的数字高程模型(DEM)数据和植被数据来源于地理空间数据云(http:// www.gscloud.cn/),在此网站分别下载了分辨率为30 m的DEM数据和分辨率为250 m的陆地合成产品(MODLT1D和MODLT1T).根据ArcGIS 10.7中的最近邻分配方法,对所有环境变量重新采样,空间分辨率为100 m×100 m.利用此数据在 ArcGIS 10.7 软件中提取计算出 6个地形因子和2个植被指数,其中地形因子包括高程(elevation)、坡度(ascent)、坡向(slope)、平面曲率(plan curvature)、剖面曲率(profile curvature)和地形湿度指数(topographicwetness index,TWI),植被指数有归一化植被指数(normalized difference vegetation Index,NDVI)和增强型植被指数(enhanced vegetation index, EVI) [24⇓-26].因为研究区地理位置特殊,土壤类型、成土母质和气候都比较单一,因此,在后续的建模中未考虑如上环境因子,最后选取6个地形因子、2个植被指数和1个代表土壤属性的全氮作为变量因子进行分析. ...
Using the Boruta algorithm and deep learning models for mapping land susceptibility to atmospheric dust emissions in Iran
1
2021
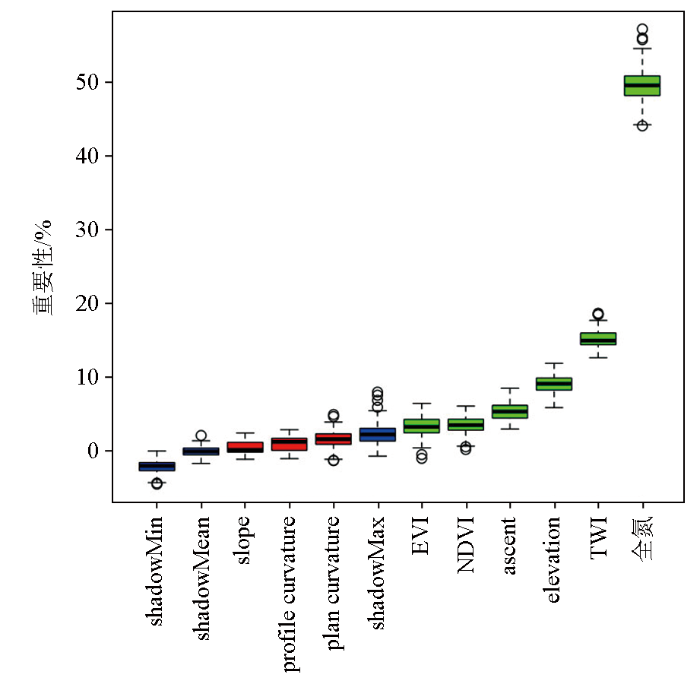
... Boruta算法是一个基于随机森林算法的特征筛选算法,该算法可以在众多特征变量中筛选出与目标变量重要性强的变量,并且可以获取特征变量的重要性排列,为选择的特征变量提供最佳的分类精度[27].本文基于R语言环境,在R 4.0.4软件中使用Boruta软件包对所选取的9个变量因子进行特征筛选,并对适合用于作为模型输入的特征变量进行重要性排列.该算法首先是加载数据集,将所有特征变量以行列矩阵的形式加载进去,总共10个特征变量(有机质为目标变量),随机打乱原始数据集得到所有影响参数的随机阴影特征,为给定数据集提供随机化.然后,运行训练随机森林(RF)分类器,并利用参数重要性来度量评估每个参数的影响.maxRuns(最大迭代次数)和doTrace分别设置成1 000和 2,在每次迭代中度量一个真正的参数是否比其影子参数的最佳值具有更显著的影响,并反复消除被评估为无影响的参数[28].本文最终以迭代749次运行1.50 min,结果以阴影特征重要性的Z分布最大值(shadowMax)为筛选指标,直到所有的特征被指定重要性,既没有暂定特征,最终筛选出6个重要特征变量和3个不重要特征变量 [29-30]. ...
Potential of Vis-NIR to measure heavy metals in different varieties of organic-fertilizers using Boruta and deep belief network
1
2021
... Boruta算法是一个基于随机森林算法的特征筛选算法,该算法可以在众多特征变量中筛选出与目标变量重要性强的变量,并且可以获取特征变量的重要性排列,为选择的特征变量提供最佳的分类精度[27].本文基于R语言环境,在R 4.0.4软件中使用Boruta软件包对所选取的9个变量因子进行特征筛选,并对适合用于作为模型输入的特征变量进行重要性排列.该算法首先是加载数据集,将所有特征变量以行列矩阵的形式加载进去,总共10个特征变量(有机质为目标变量),随机打乱原始数据集得到所有影响参数的随机阴影特征,为给定数据集提供随机化.然后,运行训练随机森林(RF)分类器,并利用参数重要性来度量评估每个参数的影响.maxRuns(最大迭代次数)和doTrace分别设置成1 000和 2,在每次迭代中度量一个真正的参数是否比其影子参数的最佳值具有更显著的影响,并反复消除被评估为无影响的参数[28].本文最终以迭代749次运行1.50 min,结果以阴影特征重要性的Z分布最大值(shadowMax)为筛选指标,直到所有的特征被指定重要性,既没有暂定特征,最终筛选出6个重要特征变量和3个不重要特征变量 [29-30]. ...
基于Boruta-支持向量回归的安徽省土壤pH值预测制图
1
2019
... Boruta算法是一个基于随机森林算法的特征筛选算法,该算法可以在众多特征变量中筛选出与目标变量重要性强的变量,并且可以获取特征变量的重要性排列,为选择的特征变量提供最佳的分类精度[27].本文基于R语言环境,在R 4.0.4软件中使用Boruta软件包对所选取的9个变量因子进行特征筛选,并对适合用于作为模型输入的特征变量进行重要性排列.该算法首先是加载数据集,将所有特征变量以行列矩阵的形式加载进去,总共10个特征变量(有机质为目标变量),随机打乱原始数据集得到所有影响参数的随机阴影特征,为给定数据集提供随机化.然后,运行训练随机森林(RF)分类器,并利用参数重要性来度量评估每个参数的影响.maxRuns(最大迭代次数)和doTrace分别设置成1 000和 2,在每次迭代中度量一个真正的参数是否比其影子参数的最佳值具有更显著的影响,并反复消除被评估为无影响的参数[28].本文最终以迭代749次运行1.50 min,结果以阴影特征重要性的Z分布最大值(shadowMax)为筛选指标,直到所有的特征被指定重要性,既没有暂定特征,最终筛选出6个重要特征变量和3个不重要特征变量 [29-30]. ...
基于Boruta-支持向量回归的安徽省土壤pH值预测制图
1
2019
... Boruta算法是一个基于随机森林算法的特征筛选算法,该算法可以在众多特征变量中筛选出与目标变量重要性强的变量,并且可以获取特征变量的重要性排列,为选择的特征变量提供最佳的分类精度[27].本文基于R语言环境,在R 4.0.4软件中使用Boruta软件包对所选取的9个变量因子进行特征筛选,并对适合用于作为模型输入的特征变量进行重要性排列.该算法首先是加载数据集,将所有特征变量以行列矩阵的形式加载进去,总共10个特征变量(有机质为目标变量),随机打乱原始数据集得到所有影响参数的随机阴影特征,为给定数据集提供随机化.然后,运行训练随机森林(RF)分类器,并利用参数重要性来度量评估每个参数的影响.maxRuns(最大迭代次数)和doTrace分别设置成1 000和 2,在每次迭代中度量一个真正的参数是否比其影子参数的最佳值具有更显著的影响,并反复消除被评估为无影响的参数[28].本文最终以迭代749次运行1.50 min,结果以阴影特征重要性的Z分布最大值(shadowMax)为筛选指标,直到所有的特征被指定重要性,既没有暂定特征,最终筛选出6个重要特征变量和3个不重要特征变量 [29-30]. ...
数字土壤制图及其研究进展
1
2013
... Boruta算法是一个基于随机森林算法的特征筛选算法,该算法可以在众多特征变量中筛选出与目标变量重要性强的变量,并且可以获取特征变量的重要性排列,为选择的特征变量提供最佳的分类精度[27].本文基于R语言环境,在R 4.0.4软件中使用Boruta软件包对所选取的9个变量因子进行特征筛选,并对适合用于作为模型输入的特征变量进行重要性排列.该算法首先是加载数据集,将所有特征变量以行列矩阵的形式加载进去,总共10个特征变量(有机质为目标变量),随机打乱原始数据集得到所有影响参数的随机阴影特征,为给定数据集提供随机化.然后,运行训练随机森林(RF)分类器,并利用参数重要性来度量评估每个参数的影响.maxRuns(最大迭代次数)和doTrace分别设置成1 000和 2,在每次迭代中度量一个真正的参数是否比其影子参数的最佳值具有更显著的影响,并反复消除被评估为无影响的参数[28].本文最终以迭代749次运行1.50 min,结果以阴影特征重要性的Z分布最大值(shadowMax)为筛选指标,直到所有的特征被指定重要性,既没有暂定特征,最终筛选出6个重要特征变量和3个不重要特征变量 [29-30]. ...
数字土壤制图及其研究进展
1
2013
... Boruta算法是一个基于随机森林算法的特征筛选算法,该算法可以在众多特征变量中筛选出与目标变量重要性强的变量,并且可以获取特征变量的重要性排列,为选择的特征变量提供最佳的分类精度[27].本文基于R语言环境,在R 4.0.4软件中使用Boruta软件包对所选取的9个变量因子进行特征筛选,并对适合用于作为模型输入的特征变量进行重要性排列.该算法首先是加载数据集,将所有特征变量以行列矩阵的形式加载进去,总共10个特征变量(有机质为目标变量),随机打乱原始数据集得到所有影响参数的随机阴影特征,为给定数据集提供随机化.然后,运行训练随机森林(RF)分类器,并利用参数重要性来度量评估每个参数的影响.maxRuns(最大迭代次数)和doTrace分别设置成1 000和 2,在每次迭代中度量一个真正的参数是否比其影子参数的最佳值具有更显著的影响,并反复消除被评估为无影响的参数[28].本文最终以迭代749次运行1.50 min,结果以阴影特征重要性的Z分布最大值(shadowMax)为筛选指标,直到所有的特征被指定重要性,既没有暂定特征,最终筛选出6个重要特征变量和3个不重要特征变量 [29-30]. ...
基于环境因子和邻近信息的土壤属性空间分布预测
1
2017
... OK法基于土壤有机质的空间区域化特征,利用邻近相关采样点权重来对未采样点位置的土壤有机质含量进行预测,现已被广大学者应用于土壤有机质的空间插值中,并作为基本参照预测方法[31⇓-33].本文将OK模型作为最基本的对照模型,首先在GS+9.0软件里进行半方差函数分析,然后在ArcGIS里进行OK法空间插值预测. ...
基于环境因子和邻近信息的土壤属性空间分布预测
1
2017
... OK法基于土壤有机质的空间区域化特征,利用邻近相关采样点权重来对未采样点位置的土壤有机质含量进行预测,现已被广大学者应用于土壤有机质的空间插值中,并作为基本参照预测方法[31⇓-33].本文将OK模型作为最基本的对照模型,首先在GS+9.0软件里进行半方差函数分析,然后在ArcGIS里进行OK法空间插值预测. ...
黄土高原不同地貌区农田土壤有机质预测方法研究
1
2021
... OK法基于土壤有机质的空间区域化特征,利用邻近相关采样点权重来对未采样点位置的土壤有机质含量进行预测,现已被广大学者应用于土壤有机质的空间插值中,并作为基本参照预测方法[31⇓-33].本文将OK模型作为最基本的对照模型,首先在GS+9.0软件里进行半方差函数分析,然后在ArcGIS里进行OK法空间插值预测. ...
黄土高原不同地貌区农田土壤有机质预测方法研究
1
2021
... OK法基于土壤有机质的空间区域化特征,利用邻近相关采样点权重来对未采样点位置的土壤有机质含量进行预测,现已被广大学者应用于土壤有机质的空间插值中,并作为基本参照预测方法[31⇓-33].本文将OK模型作为最基本的对照模型,首先在GS+9.0软件里进行半方差函数分析,然后在ArcGIS里进行OK法空间插值预测. ...
基于两点机器学习方法的土壤有机质空间分布预测
1
2022
... OK法基于土壤有机质的空间区域化特征,利用邻近相关采样点权重来对未采样点位置的土壤有机质含量进行预测,现已被广大学者应用于土壤有机质的空间插值中,并作为基本参照预测方法[31⇓-33].本文将OK模型作为最基本的对照模型,首先在GS+9.0软件里进行半方差函数分析,然后在ArcGIS里进行OK法空间插值预测. ...
基于两点机器学习方法的土壤有机质空间分布预测
1
2022
... OK法基于土壤有机质的空间区域化特征,利用邻近相关采样点权重来对未采样点位置的土壤有机质含量进行预测,现已被广大学者应用于土壤有机质的空间插值中,并作为基本参照预测方法[31⇓-33].本文将OK模型作为最基本的对照模型,首先在GS+9.0软件里进行半方差函数分析,然后在ArcGIS里进行OK法空间插值预测. ...
Comparative analysis of BPNN,SVR,LSTM,Random Forest,and LSTM-SVR for conditional simulation of non-Gaussian measured fluctuating wind pressures
1
2022
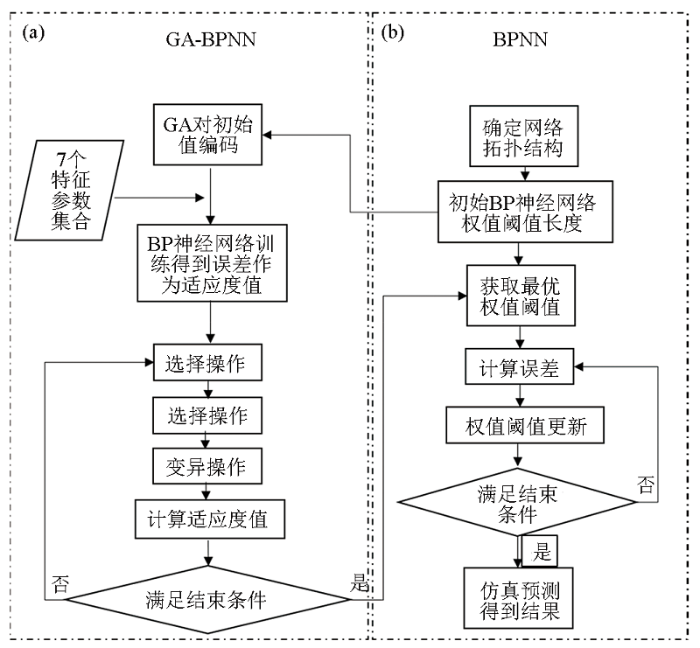
... 反向传播神经网络(BPNN)是在前馈神经网络的基础上加入反向传播实现的[34].BPNN包括输入层、隐含层、输出层3层网络结构,BPNN的流程如图2所示[35].本文用经过Boruta算法筛选出的辅助变量,将其作为特征变量输入到 BPNN 中.为了消除这些因子的量纲不同而带来的影响,在Matlab2018b中利用归一化函数(mapminmax)对输入的变量进行归一化处理.然后创建newff 函数,隐含层和输出层分别用tansing和purelin函数,训练函数使用trainlm函数,步数为1 000,学习率为0.01.在训练的过程中,需设置 BPNN 的隐含层最大节点数.这个参数对模型的精度起着决定性作用,隐含层节点数越大表示神经网络的结构越复杂,输出结果越平滑.但是隐含层最大节点数应介于变量数和样品数之间.为了找到隐含层最佳的节点数,试图将隐含层节点数从7,以间距为1逐渐增加到20,通过对比均方误差最小,选出最佳隐含层节点数(程序运行结果是15).将所有参数设置为最优后进行 BPNN 模型训练,最后将训练结果用于预测整个研究区的SOM含量. ...
基于特征选择和GA-BP神经网络的多源遥感农田土壤水分反演
1
2021
... 反向传播神经网络(BPNN)是在前馈神经网络的基础上加入反向传播实现的[34].BPNN包括输入层、隐含层、输出层3层网络结构,BPNN的流程如图2所示[35].本文用经过Boruta算法筛选出的辅助变量,将其作为特征变量输入到 BPNN 中.为了消除这些因子的量纲不同而带来的影响,在Matlab2018b中利用归一化函数(mapminmax)对输入的变量进行归一化处理.然后创建newff 函数,隐含层和输出层分别用tansing和purelin函数,训练函数使用trainlm函数,步数为1 000,学习率为0.01.在训练的过程中,需设置 BPNN 的隐含层最大节点数.这个参数对模型的精度起着决定性作用,隐含层节点数越大表示神经网络的结构越复杂,输出结果越平滑.但是隐含层最大节点数应介于变量数和样品数之间.为了找到隐含层最佳的节点数,试图将隐含层节点数从7,以间距为1逐渐增加到20,通过对比均方误差最小,选出最佳隐含层节点数(程序运行结果是15).将所有参数设置为最优后进行 BPNN 模型训练,最后将训练结果用于预测整个研究区的SOM含量. ...
基于特征选择和GA-BP神经网络的多源遥感农田土壤水分反演
1
2021
... 反向传播神经网络(BPNN)是在前馈神经网络的基础上加入反向传播实现的[34].BPNN包括输入层、隐含层、输出层3层网络结构,BPNN的流程如图2所示[35].本文用经过Boruta算法筛选出的辅助变量,将其作为特征变量输入到 BPNN 中.为了消除这些因子的量纲不同而带来的影响,在Matlab2018b中利用归一化函数(mapminmax)对输入的变量进行归一化处理.然后创建newff 函数,隐含层和输出层分别用tansing和purelin函数,训练函数使用trainlm函数,步数为1 000,学习率为0.01.在训练的过程中,需设置 BPNN 的隐含层最大节点数.这个参数对模型的精度起着决定性作用,隐含层节点数越大表示神经网络的结构越复杂,输出结果越平滑.但是隐含层最大节点数应介于变量数和样品数之间.为了找到隐含层最佳的节点数,试图将隐含层节点数从7,以间距为1逐渐增加到20,通过对比均方误差最小,选出最佳隐含层节点数(程序运行结果是15).将所有参数设置为最优后进行 BPNN 模型训练,最后将训练结果用于预测整个研究区的SOM含量. ...
基于可见—近红外光谱变量选择的土壤全氮含量估测研究
1
2014
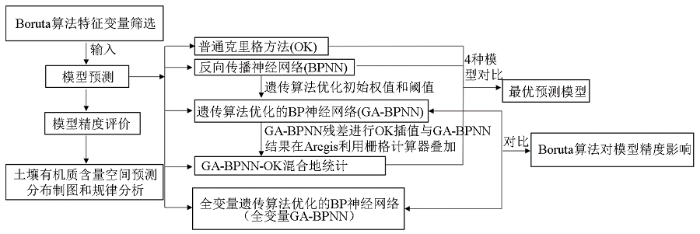
... 由于BPNN初始连接权值和阈值的确定存在一定的随机性,而且存在网络收敛速度慢和容易陷入局部极小的问题,所以利用遗传算法(genetic algorithm,GA)优化BPNN的网络初始权值和阈值,从而构建GA-BPNN预测模型[36-37],GA-BPNN流程如图2所示.在BPNN建立的基础上,在Matlab2018b中首先初始化种群规模,将种群规模设定为10,最大次数设定为 20.使用初始化的BP神经网络的预测误差作为该个体的适应度值,选择操作采取轮盘赌选择;交叉操作采取两点交叉,交叉概率设定为 0.8;变异操作采取高斯变异,变异概率设定为 0.2.通过选择、交叉、变异寻找得到最优的权值和阈值.最后把最优初始阈值权值赋予BPNN进行SOM含量的预测.各预测模型之间的关系如图3所示. ...
基于可见—近红外光谱变量选择的土壤全氮含量估测研究
1
2014
... 由于BPNN初始连接权值和阈值的确定存在一定的随机性,而且存在网络收敛速度慢和容易陷入局部极小的问题,所以利用遗传算法(genetic algorithm,GA)优化BPNN的网络初始权值和阈值,从而构建GA-BPNN预测模型[36-37],GA-BPNN流程如图2所示.在BPNN建立的基础上,在Matlab2018b中首先初始化种群规模,将种群规模设定为10,最大次数设定为 20.使用初始化的BP神经网络的预测误差作为该个体的适应度值,选择操作采取轮盘赌选择;交叉操作采取两点交叉,交叉概率设定为 0.8;变异操作采取高斯变异,变异概率设定为 0.2.通过选择、交叉、变异寻找得到最优的权值和阈值.最后把最优初始阈值权值赋予BPNN进行SOM含量的预测.各预测模型之间的关系如图3所示. ...
Extraction of reflectance spectra features for estimation of surface,subsurface,and profile soil properties
1
2022
... 由于BPNN初始连接权值和阈值的确定存在一定的随机性,而且存在网络收敛速度慢和容易陷入局部极小的问题,所以利用遗传算法(genetic algorithm,GA)优化BPNN的网络初始权值和阈值,从而构建GA-BPNN预测模型[36-37],GA-BPNN流程如图2所示.在BPNN建立的基础上,在Matlab2018b中首先初始化种群规模,将种群规模设定为10,最大次数设定为 20.使用初始化的BP神经网络的预测误差作为该个体的适应度值,选择操作采取轮盘赌选择;交叉操作采取两点交叉,交叉概率设定为 0.8;变异操作采取高斯变异,变异概率设定为 0.2.通过选择、交叉、变异寻找得到最优的权值和阈值.最后把最优初始阈值权值赋予BPNN进行SOM含量的预测.各预测模型之间的关系如图3所示. ...
Spatial variability of selected metals using auxiliary variables in agricultural soils
1
2019
... 利用ArcGIS 10.7划分得到训练集和验证集.因为在非空间方法的预测验证中,独立数据集比普通交叉验证程序更严格,所以采用独立数据集进行验证[38].根据每个样本点的实测值和预测值计算得出均方根误差(RMSE)、平均绝对误差(MAE)、平均相对误差(MRE)和拟合系数(R2).从而可以将4种方法的预测精度对比分析,得出精度评价结果.RMSE、MAE、MRE的值越小,表明预测的精度越佳.拟合系数(R2)越接近1,表明预测值与实测值的拟合程度越高. ...
渝西丘陵区土壤速效钾空间异质性及影响因素
1
2020
... 在GS+9.0里对SOM实测值和GA-BPNN残差进行半变异函数分析,用半变异函数对SOM进行空间变异性分析,以残差接近于0和拟合系数接近于1时作为最佳选择,分析结果见表2.由表2可以得出,SOM实测值和GA-BPNN残差的最优理论模型分别为指数模型和球状模型.SOM实测值的块金值与基台值较低,都小于1,由此表明SOM的空间变异性较低;GA-BPNN残差具有较高的块金值与基台值,得出研究区SOM存在着一定程度的空间变异,而所有模型的块基比均在61.90%~83.1%,说明结构因素和随机因素的影响程度对空间变异的影响基本一致[39-40].从各模型的决定系数可以看出,SOM实测值的模型拟合度较低,为0.23,而GA-BPNN残差的模型拟合度为0.74,相对较高,可见模型拟合度具有较好的合理性.所有数据项的变程都比较大,值在1 110.00~6 985.92 m,表明研究区空间自相关性较强[41]. ...
渝西丘陵区土壤速效钾空间异质性及影响因素
1
2020
... 在GS+9.0里对SOM实测值和GA-BPNN残差进行半变异函数分析,用半变异函数对SOM进行空间变异性分析,以残差接近于0和拟合系数接近于1时作为最佳选择,分析结果见表2.由表2可以得出,SOM实测值和GA-BPNN残差的最优理论模型分别为指数模型和球状模型.SOM实测值的块金值与基台值较低,都小于1,由此表明SOM的空间变异性较低;GA-BPNN残差具有较高的块金值与基台值,得出研究区SOM存在着一定程度的空间变异,而所有模型的块基比均在61.90%~83.1%,说明结构因素和随机因素的影响程度对空间变异的影响基本一致[39-40].从各模型的决定系数可以看出,SOM实测值的模型拟合度较低,为0.23,而GA-BPNN残差的模型拟合度为0.74,相对较高,可见模型拟合度具有较好的合理性.所有数据项的变程都比较大,值在1 110.00~6 985.92 m,表明研究区空间自相关性较强[41]. ...
基于云遗传BP神经网络的黄淮海旱作区土壤有机质预测精度分析
1
2021
... 在GS+9.0里对SOM实测值和GA-BPNN残差进行半变异函数分析,用半变异函数对SOM进行空间变异性分析,以残差接近于0和拟合系数接近于1时作为最佳选择,分析结果见表2.由表2可以得出,SOM实测值和GA-BPNN残差的最优理论模型分别为指数模型和球状模型.SOM实测值的块金值与基台值较低,都小于1,由此表明SOM的空间变异性较低;GA-BPNN残差具有较高的块金值与基台值,得出研究区SOM存在着一定程度的空间变异,而所有模型的块基比均在61.90%~83.1%,说明结构因素和随机因素的影响程度对空间变异的影响基本一致[39-40].从各模型的决定系数可以看出,SOM实测值的模型拟合度较低,为0.23,而GA-BPNN残差的模型拟合度为0.74,相对较高,可见模型拟合度具有较好的合理性.所有数据项的变程都比较大,值在1 110.00~6 985.92 m,表明研究区空间自相关性较强[41]. ...
基于云遗传BP神经网络的黄淮海旱作区土壤有机质预测精度分析
1
2021
... 在GS+9.0里对SOM实测值和GA-BPNN残差进行半变异函数分析,用半变异函数对SOM进行空间变异性分析,以残差接近于0和拟合系数接近于1时作为最佳选择,分析结果见表2.由表2可以得出,SOM实测值和GA-BPNN残差的最优理论模型分别为指数模型和球状模型.SOM实测值的块金值与基台值较低,都小于1,由此表明SOM的空间变异性较低;GA-BPNN残差具有较高的块金值与基台值,得出研究区SOM存在着一定程度的空间变异,而所有模型的块基比均在61.90%~83.1%,说明结构因素和随机因素的影响程度对空间变异的影响基本一致[39-40].从各模型的决定系数可以看出,SOM实测值的模型拟合度较低,为0.23,而GA-BPNN残差的模型拟合度为0.74,相对较高,可见模型拟合度具有较好的合理性.所有数据项的变程都比较大,值在1 110.00~6 985.92 m,表明研究区空间自相关性较强[41]. ...
基于GARBF神经网络的耕地土壤有效磷空间变异分析
2
2012
... 在GS+9.0里对SOM实测值和GA-BPNN残差进行半变异函数分析,用半变异函数对SOM进行空间变异性分析,以残差接近于0和拟合系数接近于1时作为最佳选择,分析结果见表2.由表2可以得出,SOM实测值和GA-BPNN残差的最优理论模型分别为指数模型和球状模型.SOM实测值的块金值与基台值较低,都小于1,由此表明SOM的空间变异性较低;GA-BPNN残差具有较高的块金值与基台值,得出研究区SOM存在着一定程度的空间变异,而所有模型的块基比均在61.90%~83.1%,说明结构因素和随机因素的影响程度对空间变异的影响基本一致[39-40].从各模型的决定系数可以看出,SOM实测值的模型拟合度较低,为0.23,而GA-BPNN残差的模型拟合度为0.74,相对较高,可见模型拟合度具有较好的合理性.所有数据项的变程都比较大,值在1 110.00~6 985.92 m,表明研究区空间自相关性较强[41]. ...
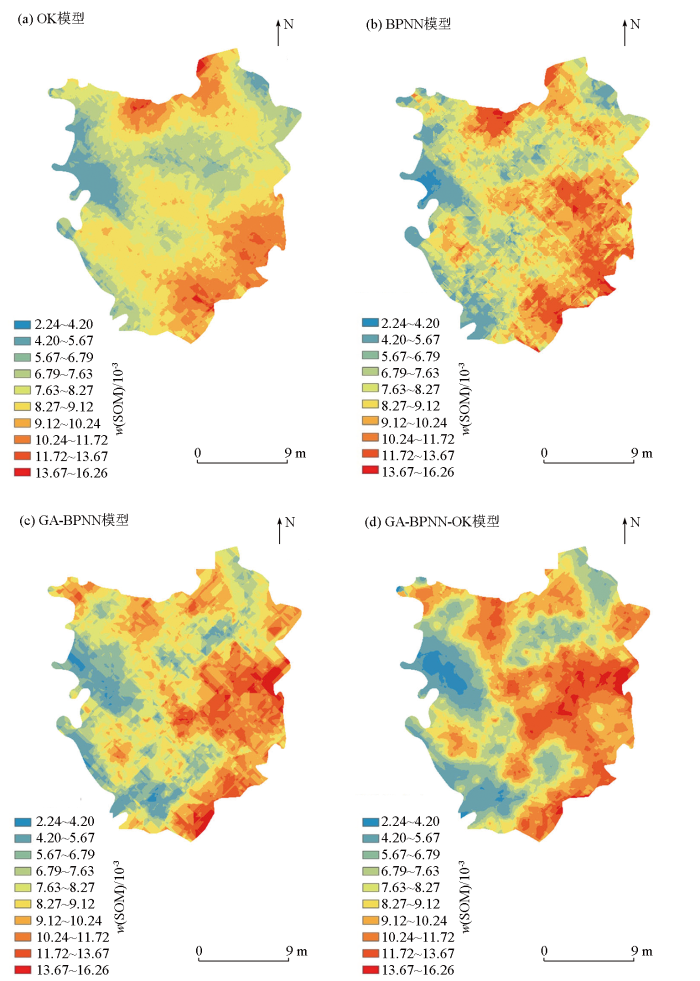
... 基于4种预测模型得到的SOM含量空间预测分布图,SOM含量空间分布的整体趋势是西部和西南部地区低,东部和东南部地区高.东部呈现高值区是因为研究区独特的地理位置,即西部地势低,东部地势高,地势高的地区会影响土壤厚度进而使土壤有机碳得到积累,土壤固碳能力提高导致SOM含量也高.OK法对研究区SOM空间分布的预测结果图的高值区和低值区分布较明显,在东北部和中部地区高值区与低值区分布更为明显,这与徐剑波等[41]、谢梦姣等[42]的研究结果不一致,可能是由于采样点的数量与采样点空间自相关性,说明本研究区样品点的空间自相关性较弱,对预测的结果产生的影响较小.与之相比,基于神经网络模型的SOM空间分布预测图,高值区与低值区的分布更加明显,这是因为神经网络模型具有强的非线性映射能力,可以以任意精度逼近任意连续函数[43],而且也与加入辅助变量有着很大的关系, 所以使得预测分布图更加接近实际.神经网络模型还会有残差项的存在,而残差存在空间自相关,利用GA-BPNN-OK模型预测的SOM的空间分布图充分考虑了样品点的结构性和随机性的空间模拟,与利用GA-BPNN模型预测的SOM分布图相比,GA-BPNN-OK模型预测的SOM分布图对SOM含量的高低界限能够清晰的呈现,但SOM高地区的分布范围基本相同,说明神经网络残差空间自相关很弱,对空间分布预测图的影响较小.总体而言GA-BPNN-OK对SOM含量空间分布预测更加准确和细致,更能精准地指导当地的农业生产. ...
基于GARBF神经网络的耕地土壤有效磷空间变异分析
2
2012
... 在GS+9.0里对SOM实测值和GA-BPNN残差进行半变异函数分析,用半变异函数对SOM进行空间变异性分析,以残差接近于0和拟合系数接近于1时作为最佳选择,分析结果见表2.由表2可以得出,SOM实测值和GA-BPNN残差的最优理论模型分别为指数模型和球状模型.SOM实测值的块金值与基台值较低,都小于1,由此表明SOM的空间变异性较低;GA-BPNN残差具有较高的块金值与基台值,得出研究区SOM存在着一定程度的空间变异,而所有模型的块基比均在61.90%~83.1%,说明结构因素和随机因素的影响程度对空间变异的影响基本一致[39-40].从各模型的决定系数可以看出,SOM实测值的模型拟合度较低,为0.23,而GA-BPNN残差的模型拟合度为0.74,相对较高,可见模型拟合度具有较好的合理性.所有数据项的变程都比较大,值在1 110.00~6 985.92 m,表明研究区空间自相关性较强[41]. ...
... 基于4种预测模型得到的SOM含量空间预测分布图,SOM含量空间分布的整体趋势是西部和西南部地区低,东部和东南部地区高.东部呈现高值区是因为研究区独特的地理位置,即西部地势低,东部地势高,地势高的地区会影响土壤厚度进而使土壤有机碳得到积累,土壤固碳能力提高导致SOM含量也高.OK法对研究区SOM空间分布的预测结果图的高值区和低值区分布较明显,在东北部和中部地区高值区与低值区分布更为明显,这与徐剑波等[41]、谢梦姣等[42]的研究结果不一致,可能是由于采样点的数量与采样点空间自相关性,说明本研究区样品点的空间自相关性较弱,对预测的结果产生的影响较小.与之相比,基于神经网络模型的SOM空间分布预测图,高值区与低值区的分布更加明显,这是因为神经网络模型具有强的非线性映射能力,可以以任意精度逼近任意连续函数[43],而且也与加入辅助变量有着很大的关系, 所以使得预测分布图更加接近实际.神经网络模型还会有残差项的存在,而残差存在空间自相关,利用GA-BPNN-OK模型预测的SOM的空间分布图充分考虑了样品点的结构性和随机性的空间模拟,与利用GA-BPNN模型预测的SOM分布图相比,GA-BPNN-OK模型预测的SOM分布图对SOM含量的高低界限能够清晰的呈现,但SOM高地区的分布范围基本相同,说明神经网络残差空间自相关很弱,对空间分布预测图的影响较小.总体而言GA-BPNN-OK对SOM含量空间分布预测更加准确和细致,更能精准地指导当地的农业生产. ...
人工神经网络与普通克里金插值法对土壤属性空间预测精度影响研究
1
2021
... 基于4种预测模型得到的SOM含量空间预测分布图,SOM含量空间分布的整体趋势是西部和西南部地区低,东部和东南部地区高.东部呈现高值区是因为研究区独特的地理位置,即西部地势低,东部地势高,地势高的地区会影响土壤厚度进而使土壤有机碳得到积累,土壤固碳能力提高导致SOM含量也高.OK法对研究区SOM空间分布的预测结果图的高值区和低值区分布较明显,在东北部和中部地区高值区与低值区分布更为明显,这与徐剑波等[41]、谢梦姣等[42]的研究结果不一致,可能是由于采样点的数量与采样点空间自相关性,说明本研究区样品点的空间自相关性较弱,对预测的结果产生的影响较小.与之相比,基于神经网络模型的SOM空间分布预测图,高值区与低值区的分布更加明显,这是因为神经网络模型具有强的非线性映射能力,可以以任意精度逼近任意连续函数[43],而且也与加入辅助变量有着很大的关系, 所以使得预测分布图更加接近实际.神经网络模型还会有残差项的存在,而残差存在空间自相关,利用GA-BPNN-OK模型预测的SOM的空间分布图充分考虑了样品点的结构性和随机性的空间模拟,与利用GA-BPNN模型预测的SOM分布图相比,GA-BPNN-OK模型预测的SOM分布图对SOM含量的高低界限能够清晰的呈现,但SOM高地区的分布范围基本相同,说明神经网络残差空间自相关很弱,对空间分布预测图的影响较小.总体而言GA-BPNN-OK对SOM含量空间分布预测更加准确和细致,更能精准地指导当地的农业生产. ...
人工神经网络与普通克里金插值法对土壤属性空间预测精度影响研究
1
2021
... 基于4种预测模型得到的SOM含量空间预测分布图,SOM含量空间分布的整体趋势是西部和西南部地区低,东部和东南部地区高.东部呈现高值区是因为研究区独特的地理位置,即西部地势低,东部地势高,地势高的地区会影响土壤厚度进而使土壤有机碳得到积累,土壤固碳能力提高导致SOM含量也高.OK法对研究区SOM空间分布的预测结果图的高值区和低值区分布较明显,在东北部和中部地区高值区与低值区分布更为明显,这与徐剑波等[41]、谢梦姣等[42]的研究结果不一致,可能是由于采样点的数量与采样点空间自相关性,说明本研究区样品点的空间自相关性较弱,对预测的结果产生的影响较小.与之相比,基于神经网络模型的SOM空间分布预测图,高值区与低值区的分布更加明显,这是因为神经网络模型具有强的非线性映射能力,可以以任意精度逼近任意连续函数[43],而且也与加入辅助变量有着很大的关系, 所以使得预测分布图更加接近实际.神经网络模型还会有残差项的存在,而残差存在空间自相关,利用GA-BPNN-OK模型预测的SOM的空间分布图充分考虑了样品点的结构性和随机性的空间模拟,与利用GA-BPNN模型预测的SOM分布图相比,GA-BPNN-OK模型预测的SOM分布图对SOM含量的高低界限能够清晰的呈现,但SOM高地区的分布范围基本相同,说明神经网络残差空间自相关很弱,对空间分布预测图的影响较小.总体而言GA-BPNN-OK对SOM含量空间分布预测更加准确和细致,更能精准地指导当地的农业生产. ...
基于辅助变量和神经网络模型的土壤有机质空间分布模拟
1
2017
... 基于4种预测模型得到的SOM含量空间预测分布图,SOM含量空间分布的整体趋势是西部和西南部地区低,东部和东南部地区高.东部呈现高值区是因为研究区独特的地理位置,即西部地势低,东部地势高,地势高的地区会影响土壤厚度进而使土壤有机碳得到积累,土壤固碳能力提高导致SOM含量也高.OK法对研究区SOM空间分布的预测结果图的高值区和低值区分布较明显,在东北部和中部地区高值区与低值区分布更为明显,这与徐剑波等[41]、谢梦姣等[42]的研究结果不一致,可能是由于采样点的数量与采样点空间自相关性,说明本研究区样品点的空间自相关性较弱,对预测的结果产生的影响较小.与之相比,基于神经网络模型的SOM空间分布预测图,高值区与低值区的分布更加明显,这是因为神经网络模型具有强的非线性映射能力,可以以任意精度逼近任意连续函数[43],而且也与加入辅助变量有着很大的关系, 所以使得预测分布图更加接近实际.神经网络模型还会有残差项的存在,而残差存在空间自相关,利用GA-BPNN-OK模型预测的SOM的空间分布图充分考虑了样品点的结构性和随机性的空间模拟,与利用GA-BPNN模型预测的SOM分布图相比,GA-BPNN-OK模型预测的SOM分布图对SOM含量的高低界限能够清晰的呈现,但SOM高地区的分布范围基本相同,说明神经网络残差空间自相关很弱,对空间分布预测图的影响较小.总体而言GA-BPNN-OK对SOM含量空间分布预测更加准确和细致,更能精准地指导当地的农业生产. ...
基于辅助变量和神经网络模型的土壤有机质空间分布模拟
1
2017
... 基于4种预测模型得到的SOM含量空间预测分布图,SOM含量空间分布的整体趋势是西部和西南部地区低,东部和东南部地区高.东部呈现高值区是因为研究区独特的地理位置,即西部地势低,东部地势高,地势高的地区会影响土壤厚度进而使土壤有机碳得到积累,土壤固碳能力提高导致SOM含量也高.OK法对研究区SOM空间分布的预测结果图的高值区和低值区分布较明显,在东北部和中部地区高值区与低值区分布更为明显,这与徐剑波等[41]、谢梦姣等[42]的研究结果不一致,可能是由于采样点的数量与采样点空间自相关性,说明本研究区样品点的空间自相关性较弱,对预测的结果产生的影响较小.与之相比,基于神经网络模型的SOM空间分布预测图,高值区与低值区的分布更加明显,这是因为神经网络模型具有强的非线性映射能力,可以以任意精度逼近任意连续函数[43],而且也与加入辅助变量有着很大的关系, 所以使得预测分布图更加接近实际.神经网络模型还会有残差项的存在,而残差存在空间自相关,利用GA-BPNN-OK模型预测的SOM的空间分布图充分考虑了样品点的结构性和随机性的空间模拟,与利用GA-BPNN模型预测的SOM分布图相比,GA-BPNN-OK模型预测的SOM分布图对SOM含量的高低界限能够清晰的呈现,但SOM高地区的分布范围基本相同,说明神经网络残差空间自相关很弱,对空间分布预测图的影响较小.总体而言GA-BPNN-OK对SOM含量空间分布预测更加准确和细致,更能精准地指导当地的农业生产. ...
陕西渭北旱塬区农田土壤有机质空间预测方法
1
2022
... 对于辅助变量的研究,通过Boruta算法计算得知,土壤本身属性对有机质含量的影响最大,全氮含量高的地区加上研究区又是一个降水集中的地区,使得土壤固氮能力强,从而使得SOM含量高,而且土壤有机质是氮素的主要贮存场所,二者相互依存.除了土壤本身因素和自然因素的影响,现在人类活动频繁,人为因素对于SOM含量的空间分布也是一个重要因素,此外大多学者将高光谱数据也作为影响因子对SOM含量空间分布进行预测,并且取得一定的进展.尉芳等[44]将化肥施用量作为一种影响因子进行研究,得出化肥施用量虽然和SOM含量不存在对应关系,但是相关性却达到了0.33,说明人为因素对SOM含量存在影响.Liu等[13]采用近距离光谱、航空高光谱和Sentinel 2多光谱图像预测农业用地的SOCD,得到了很好的预测精度.因此,在之后的预测方法加入人为因素和高光谱数据作为模型输入,对提高模型预测精度有很好的效果,进而可得到更加接近实际的SOM空间分布图. ...
陕西渭北旱塬区农田土壤有机质空间预测方法
1
2022
... 对于辅助变量的研究,通过Boruta算法计算得知,土壤本身属性对有机质含量的影响最大,全氮含量高的地区加上研究区又是一个降水集中的地区,使得土壤固氮能力强,从而使得SOM含量高,而且土壤有机质是氮素的主要贮存场所,二者相互依存.除了土壤本身因素和自然因素的影响,现在人类活动频繁,人为因素对于SOM含量的空间分布也是一个重要因素,此外大多学者将高光谱数据也作为影响因子对SOM含量空间分布进行预测,并且取得一定的进展.尉芳等[44]将化肥施用量作为一种影响因子进行研究,得出化肥施用量虽然和SOM含量不存在对应关系,但是相关性却达到了0.33,说明人为因素对SOM含量存在影响.Liu等[13]采用近距离光谱、航空高光谱和Sentinel 2多光谱图像预测农业用地的SOCD,得到了很好的预测精度.因此,在之后的预测方法加入人为因素和高光谱数据作为模型输入,对提高模型预测精度有很好的效果,进而可得到更加接近实际的SOM空间分布图. ...