基于改进蝴蝶优化算法的瑞利波频散曲线反演方法

doi:10.11720/wtyht.2024.1116

基于改进蝴蝶优化算法的瑞利波频散曲线反演方法

彭刘亚^,¹, 冯伟栋¹, 解惠婷¹, 李飞¹, 杨源源¹, 曹均锋¹, 任川²

1.安徽省地震局,安徽合肥 230031

2.安徽惠洲地质安全研究院股份有限公司,安徽合肥 231202

An improved butterfly optimization algorithm in the inversion of Rayleigh wave dispersion curve

PENG Liu-Ya^,¹, FENG Wei-Dong¹, XIE Hui-Ting¹, LI Fei¹, YANG Yuan-Yuan¹, CAO Jun-Feng¹, REN Chuan²

1. Anhui Earthquake Agency,Hefei 230031,China

2. Anhui Huizhou Geology Security Institute Co.,Ltd.,Hefei 231202,China

第一作者: 彭刘亚(1990-),男,工程师,2014年毕业于中国矿业大学(徐州),主要从事工程地球物理勘探方面的研究工作。Email:414147651@qq.com

责任编辑: 叶佩

收稿日期: 2023-04-22 修回日期: 2024-01-2

基金资助:

国家自然科学基金项目(41802224)
2022年安徽省重点研究与开发计划项目(2022m07020005)

Received: 2023-04-22 Revised: 2024-01-2

摘要

瑞利波频散曲线反演问题的多解性和反演目标函数的多极值特点,使得常规非线性优化算法可能会产生收敛不稳定、易陷入局部最优等现象。在基本蝴蝶优化算法的基础上采用动态开关概率,引入非线性自适应权重因子,既增加了算法前期的全局探索能力,也保证了后期的局部开发能力。同时,在迭代过程中对最优解进行逐维柯西变异,利用贪婪算法更新最优位置,引导种群向全局最优靠近,通过对4种常用的Benchmark函数的性能测试,表明改进的蝴蝶优化算法无论是在单峰函数还是多峰函数上的全局寻优能力明显优于遗传算法和粒子群算法。采用不同算法针对3种理论地质模型的频散曲线进行反演,发现改进蝴蝶优化算法在频散曲线含10%随机噪声的情况下仍然能够得到与理论模型更加接近的反演结果。最后将改进蝴蝶优化算法应用于实际瑞利波数据,反演结果与实际钻孔揭露的地层分布情况高度吻合。且与遗传算法和粒子群算法相比,改进蝴蝶优化算法在收敛速度、求解精度和稳定性方面都有显著的提升,具有一定的实用价值和应用前景。

关键词： 频散曲线; 改进蝴蝶优化算法; 反演; 非线性优化

Abstract

Due to the multiplicity of solutions and the multiple extrema of the inversion objection functions,conventional nonlinear optimization algorithms are susceptible to unstable convergence and local optimum in the inversion of Rayleigh wave dispersion curves.This study improved the standard butterfly optimization algorithm by incorporating dynamic switch probability and nonlinear self-adaptive weight factors,yielding an elevated global exploration capacity in the early stage and a high local research ability in the latter stage.Furthermore,the dimension-by-dimension Cauchy mutation,along with a greedy algorithm,was employed to update the current best position during each iteration,ultimately directing the whole swarm population toward the global optimum.Tests of four commonly used benchmark functions demonstrate that the improved butterfly optimization algorithm(IBOA) outperformed other nonlinear algorithms,including the genetic algorithm and particle swarm optimization algorithm,in terms of the global research capacity of both unimodal and multimodal functions.Different algorithms were adopted for the inversion of the dispersion curves of three theoretical geological models.The results show that IBOA yielded inversion results that were closer to the models even when the dispersion curves contained 10% random noise.Finally,the IBOA was applied to actual Rayleigh wave data,and the inversion results were highly consistent with the strata revealed by drilling.Compared with the genetic algorithm and the particle swarm optimization algorithm,the IBOA significantly improved the convergence speed,as well as solution accuracy and stability.Therefore,the IBOA has a certain practical value and application prospects.

Keywords： dispersion curve; improved butterfly optimization algorithm; inversion; nonlinear optimization

PDF (6312KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

彭刘亚, 冯伟栋, 解惠婷, 李飞, 杨源源, 曹均锋, 任川. 基于改进蝴蝶优化算法的瑞利波频散曲线反演方法[J]. 物探与化探, 2024, 48(3): 705-720 doi:10.11720/wtyht.2024.1116

PENG Liu-Ya, FENG Wei-Dong, XIE Hui-Ting, LI Fei, YANG Yuan-Yuan, CAO Jun-Feng, REN Chuan. An improved butterfly optimization algorithm in the inversion of Rayleigh wave dispersion curve[J]. Geophysical and Geochemical Exploration, 2024, 48(3): 705-720 doi:10.11720/wtyht.2024.1116

0 引言

与常规反射地震勘探相比,瑞利波勘探具有效率高、成本低、信噪比高、易采集等特点^[1⇓⇓-4],近年来已成为浅表层结构探测的首选方法之一。通过对瑞利波频散曲线反演,可获得近地表地层的横波速度和厚度等主要物性参数^[5-6],为划分工程场地类别、砂土液化等提供参考依据^[7-8]。

与其他地球物理反演方法类似,瑞利波频散曲线反演也存在多解性或非唯一性的问题,其反演的目标函数具有非线性和多极值的特点。传统线性算法(如最小二乘法等)在高度依赖初始模型的同时,极易陷入局部最优,甚至不收敛,使得反演结果精度较低。当前,采用非线性优化算法反演频散曲线已成为主流手段,主要包括遗传算法^[9-10]、粒子群算法^{[11⇓⇓⇓-15]}、蜂群算法^[16-17]、蚱蜢算法^[18]、蜻蜓算法^[19]等。这类非线性优化算法对初始模型要求低,避免了大量的求导过程,能够在解空间内进行全局搜索,反演结果比传统的线性优化算法更为精确。但单一算法也容易出现早熟、收敛不稳定等问题。近些年来不少学者通过混合算法进一步提升了瑞利波频散曲线反演效果,如崔建文^[20]提出了模拟退火法和遗传算法相结合的策略,提高了全局优化的计算效率;杨博等^[21]提出了自适应混沌遗传粒子群算法,并应用于实际频散曲线反演,结果表明该算法比单独使用粒子群算法和遗传算法时具有更高的寻优能力和收敛速度;蔡伟等^[22]融合了萤火虫和蝙蝠群智能算法,在反演前后期使用不同算法,帮助避免单一算法陷入局部最优,可以有效地对瑞利波频散曲线进行定量解释;王一鸣等^[23]混合了粒子群算法和蚁群算法,对频散曲线反演进行了优化,结果表明相比单独使用粒子群算法或蚁群算法,混合算法更优越、更有效。但混合算法在单一算法的基础上增加了算法的复杂程度,同时参数的不易调整也限制了这类方法在解决多维度、多极值问题优化方面的应用^[17]。此外,鉴于非线性反演优化算法通常没有考虑反演结果的不确定性,近些年不少研究人员将观测数据和模型参数作为随机变量来求解,融合先验信息对模型进行随机采样,并基于贝叶斯理论计算模型频散曲线与实测数据的似然函数,获得模型的后验概率密度,从而反演出较为精确的横波速度和厚度等地层参数^{[24⇓⇓-27]}。贝叶斯理论反演作为一种随机反演方法,虽不依赖于初始模型,但需要更多的先验信息作为约束条件,从而对模型进行采样,而且需要通过大量测试选取合适的参数建立贝叶斯框架。刘昊楠等^[28]通过理论模型的正反演表明该方法反演得到的结果在深层的方差和离散程度较大。也有一些学者将人工神经网络^{[29⇓⇓-32]}和深度学习方法^[33]运用到频散曲线反演中,彻底消除了反演对初始模型的依赖性,通过建立非线性网络映射和特征学习获得最终反演模型。但这类方法在正式反演之前都需要结合钻孔地质资料等相关先验信息建立大量的正演模型获得训练样本,降低计算效率的同时对样本数量的控制程度决定了反演结果的可靠程度。因此在未给定先验地质条件时,对地层的反演受到很大程度的限制和约束。

蝴蝶优化算法(butterfly optimization algorithm,BOA)是Sankalap Arora和Satvir Singh两位学者通过观察蝴蝶觅食行为,提出的一种元启发式的种群优化算法^[34⇓-36]。该算法的核心思想是模拟蝴蝶种群通过分泌、感知和分析“香味”来确定行进方向。基本蝴蝶优化算法与其他种群优化算法相比,不需要通过经验和多次测试设置其他的参数,且易于编程实现。本文在不增加基本蝴蝶优化算法复杂程度的基础上,采用动态开关概率,拓展算法前期的全局搜索空间,提升全局探索能力,加快收敛速度,并在个体位置更新时引入非线性自适应权重因子,保证算法后期的局部开发能力。同时,对当前迭代的最优位置进行逐维柯西变异,利用贪婪算法确定是否保留更新变异后的位置,从而保证种群向全局最优位置靠近,提高求解精度。本文首先通过测试函数的性能表现说明提出的改进蝴蝶优化算法(improved butterfly optimization algorithm,IBOA)改善了遗传算法和粒子群算法收敛慢、易早熟陷入局部最优、稳定性差等不足,同时在基本蝴蝶优化算法的基础上进一步提高了收敛速度和求解精度。为验证算法在瑞利波频散曲线反演方面的可行性,对常见的3种四层地质模型的理论频散曲线分别在无噪声和含10%随机噪声情况下进行反演,试算结果表明改进的蝴蝶优化算法的稳定、可靠程度较高。最后,针对实测瑞利波频散曲线进行反演,结果表明本文提出的改进蝴蝶优化算法与遗传算法和粒子群算法相比,反演结果与真实地层分布情况更为接近,且对地层速度间断面的探测能力更优。

1 基本蝴蝶优化算法

基于大量科学观测和研究表明,蝴蝶在觅食过程中对食物源散发的“香味”具有非常敏锐的嗅觉^[37]。每一只蝴蝶都能产生一定强度且独特的香味,可以被其他蝴蝶感知和接收到,香味的感知强度与外界的物理刺激强度有关,可以通过式(1)表达:

(1)f_i=cI^a,c_t₊₁=c_t+

\frac{0.025}{c_{t} \times M a x I t e r}

,c₀=0.01,

式中:f_i是第i只蝴蝶个体可以产生的香味强度;I是刺激强度,对应寻优过程中的适应度值;a是依赖于模态的幂指数,反应香味吸收的不同程度和变化,通常取a=0.1。c是动态感知因子,随着迭代次数t非线性增大,MaxIter为最大迭代次数。

蝴蝶优化算法在迭代过程中,蝴蝶个体根据香味强度,产生一个0~1之间的随机数,并与开关概率P进行对比,决定是进行全局搜索还是局部搜索,从而更新个体的位置。BOA算法中,蝴蝶个体的更新位置如下:

(2)

x_{i}^{t + 1}

\{\begin{array}{l} x_{i}^{t} + f_{i} (r_{1}^{2} g_{b e s t} - x_{i}^{t}), & r_{3} < P \\ x_{i}^{t} + f_{i} (r_{2}^{2} x_{j}^{t} - x_{k}^{t}), & r_{3} \geq P \end{array}

式中:r₁、r₂、r₃均为0~1之间的随机数; $x_{i}^{t}$ 为第i只蝴蝶个体在第t次迭代时的位置;f_i为第i只蝴蝶的香味大小;g_best为当前全局最优位置; $x_{j}^{t}$ 、 $x_{k}^{t}$ 是从种群内部(解空间)中随机选取的两只蝴蝶个体所在的位置。式(2)表明,当随机数r₃<P时,蝴蝶选择全局探索,向当前全局最优位置移动;否则,则进行局部开发。

不难发现,BOA算法和其他种群优化算法类似,首先在解空间内随机初始化种群的位置,根据式(1)计算各个体感知到的香味强度,通过产生的随机数与开关概率的大小关系来决定进行全局探索或局部开发,按照式(2)来更新个体位置,通过循环迭代直到满足终止条件时输出最优个体位置。

2 蝴蝶优化算法的改进策略

基本BOA算法采用开关概率的方式将蝴蝶种群划分为两种状态,即全局搜索和局部搜索两种方式在解空间中进行移动,并根据香味大小来更新位置,在一定程度上也存在易陷入局部最优、求解精度较低和收敛性不稳定等问题。许多研究人员均针对性地提出了不同的改进策略,本文结合已有的改进策略,首先引入了动态开关概率^[38-39],保证在算法的初期更多可能地进行全局搜索,对全局最优所在的方向进行定位,而在算法的后期增强局部开发的能力,提升算法的求解精度。其次,在全局搜索和局部搜索阶段,均引入了非线性自适应权重因子^[40-41],使得在迭代初期时具有更宽泛的搜索范围,并同时拥有良好的局部寻优能力。最后,利用柯西变异算子增加种群的多样性^[41],有助于算法向全局最优所在位置和方向快速收敛。

2.1 动态开关概率

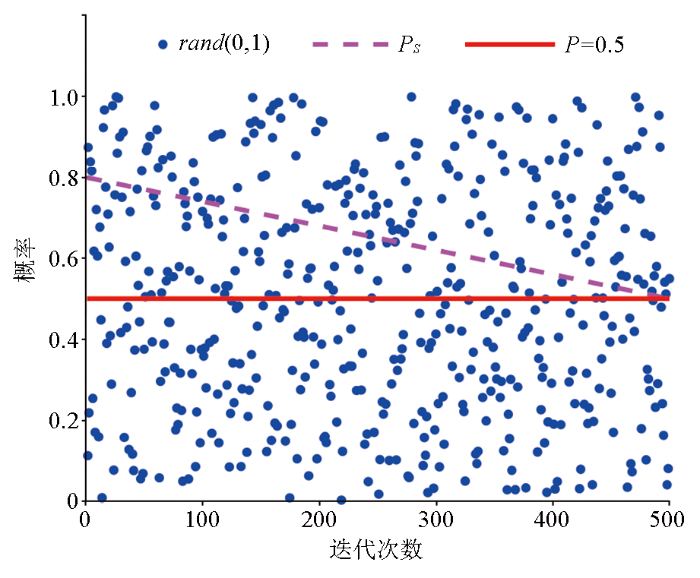
在基本BOA算法中,全局搜索和局部搜索的选择方式是通过比较随机发生数和固定开关概率值(通常取0.5)的大小来决定。为了更好地协调全局探索与局部开发的平衡,保证算法初期进行更强烈的全局搜索而在算法后期更多地进行局部寻优,提高算法的求解精度,引入形如式(3)

(3)P_S=0.5+0.3×

\frac{M a x I t e r - t}{M a x I t e r}

所表示的随迭代发生线性变化的动态开关概率^[38-39]。式中:MaxIter为最大迭代次数,t为当前迭代次数。

图1为500次迭代过程中随机发生数和动态开关概率及固定开关概率取0.5时的分布示意,可以发现使用动态开关概率能够在一定程度上保证算法初期大概率地进行全局搜索,从而确定种群向全局最优方向移动。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 动态开关概率

Fig.1 Dynamic switch probability

2.2 自适应权重因子

根据基本原理可知,BOA算法中蝴蝶个体主要利用了当前位置和当前最优位置以及根据开关概率选择全局搜索或局部搜索来进行位置更新,因此无论在哪个阶段,蝴蝶个体的位置优势可能并没有得到充分利用和发挥。考虑引入自适应权重因子,在全局搜索阶段使用较大的权重因子,增加种群的多样性扩大搜索区域,提升算法的探索能力,保证极大程度地向全局最优解的方向靠近。而在局部搜索阶段,使用较小的权重因子,控制蝴蝶个体移动的方向和距离,保证在最优解附近进行局部开发的能力,从而提升算法的求解精度和收敛能力。本文分别在全局搜索阶段和局部搜索阶段均引入了不同的自适应权重因子w₁和w₂,结合动态开关概率,改进后的算法中蝴蝶个体在全局搜索阶段和局部搜索阶段的位置更新公式分别为式(4)和式(5):

(4)

\begin{array}{l} x_{i}^{t + 1} = w_{1}^{t} x_{i}^{t} + f_{i} (r_{1}^{2} g^{*} - x_{i}^{t}), \\ w_{1}^{t} = 2 e^{- {(\frac{4 t}{M a x I t e r})}^{2}}, r_{3} < P_{S}, \end{array}

(5)

x_{i}^{t + 1}

w_{2}^{t} x_{i}^{t}

+f_i

(r_{2}^{2} x_{j}^{t} - x_{k}^{t})

w_{2}^{t}

=sin(

\frac{π t}{2 M a x I t e r}

+π)+1,r₃≥P_S,

2.3 逐维柯西变异

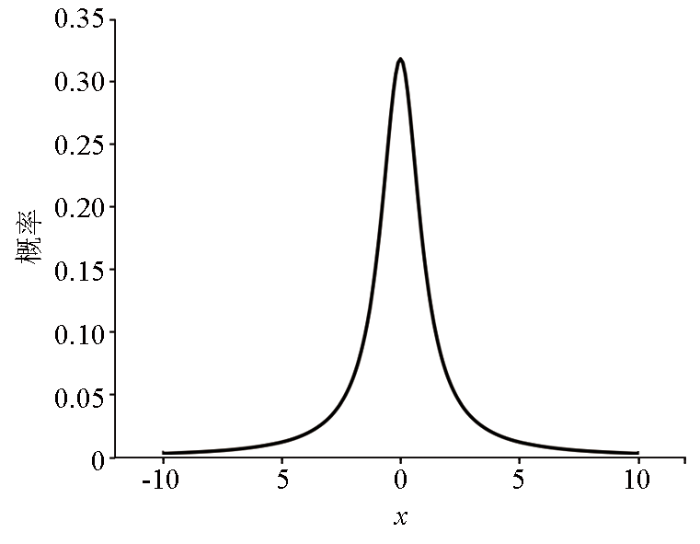
很多研究表明基本蝴蝶优化算法也存在收敛速度慢、易陷入局部最优等缺陷。本文引入柯西变异算子,式(6)

(6)f(x)=

\frac{1}{π (1 + x^{2})}

为标准柯西分布的概率密度分布函数,其示意如图2所示。不难发现,标准柯西分布的概率密度分布函数特征是一个由原点处的峰值缓慢下降到两端的钟形,且两端分布较长,无限接近于x轴但永不相交。因此利用该特征可以产生与原点相距较远的随机数,从而在当前迭代中的最优蝴蝶个体附近产生更大的扰动,拓展蝴蝶种群的全局搜索空间。此外,由于柯西分布的峰值较低,一定程度上能够缩短变异后的个体在邻域附近搜索的时间,有利于变异后的个体逃离局部最优。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 标准柯西分布概率密度函数

Fig.2 Probability density function of standard Cauchy distribution

此外,对于待优化的各目标参数的范围可能不在同一数量级,如瑞利波频散曲线反演的横波速度(通常为几百米每秒)和地层厚度(通常为几米)的取值范围差异较大,因此为了避免不同参数的维度之间可能存在的干扰问题,考虑对最优个体位置采用逐维变异策略。假设搜索空间为d维,当前最优解x_best=[ $x_{_{b e s t}}^{1}$ , $x_{b e s t}^{2}$ ,…, $x_{b e s t}^{d}$ ],利用式(7)

(7)

\{\begin{array}{l} x_{n e w b e s t}^{j} = x_{b e s t}^{j} + x_{b e s t}^{j} \times C a u c h y (0,1), j = 1,2, \dots, d \\ C a u c h y (0,1) = t a n [π \times (r a n d - 0.5)], \end{array}

对当前最优解进行逐维柯西变异处理,其中rand为0~1之间的随机数。

当最优解进行逐维柯西变异后,并无法直观地判断变异后的位置是否更优于变异前的最优解,因此在逐维变异的同时,使用贪婪算法来判断是否接受变异后的新位置。其核心思想是通过迭代,计算各维度变异后的位置对应的适应度函数值,并与当前最优位置对应的适应度函数值比较,若较小,则保留变异后的位置,否则保留原最优位置,不断地以局部最优结果逼近全局最优结果,从而更好地引导种群向最优解靠近,提高收敛速度。

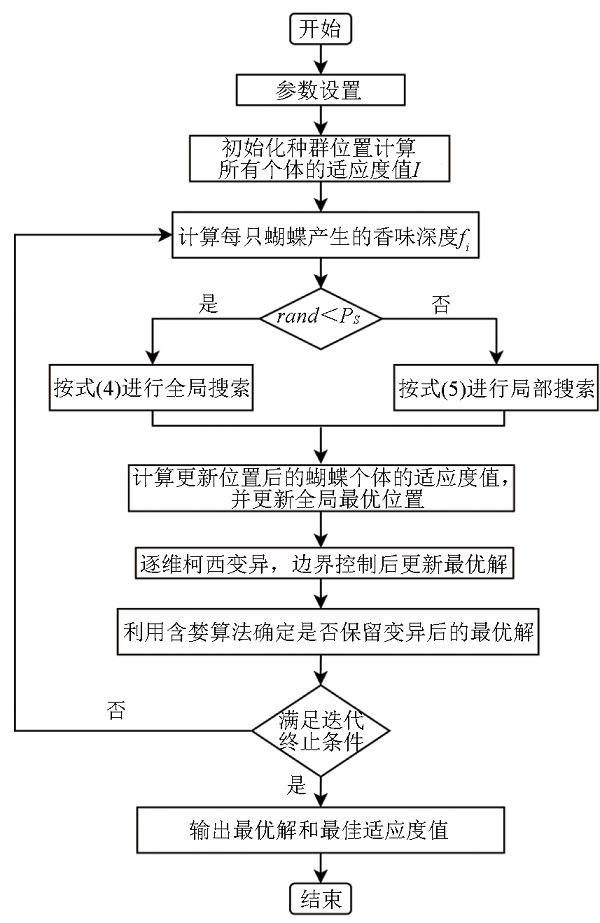
2.4 改进蝴蝶优化算法(IBOA)的流程

图3为IBOA的算法流程,主要包括以下步骤:

1)设置参数,包括种群规模、最大迭代次数、各参数搜索空间的上下边界;

2)在给定搜索空间内随机初始化蝴蝶种群位置,计算所有蝴蝶个体的适应度值,并根据适应度值的大小排序确定初始最优位置;

3)开始迭代,按式(1)计算每只蝴蝶个体产生的香味浓度,并产生0~1之间的随机数rand;按式(3)计算当前迭代时的开关概率P_S,若rand<P_S,则按式(4)进行全局搜索更新位置,否则按式(5)进行局部搜索更新位置;

4)计算更新位置后的蝴蝶个体的适应度值,进行排序后更新全局最优位置;

5)按式(7)对当前全局最优位置进行逐维柯西变异,经边界控制后更新变异得到新的最优解;

6)利用贪婪算法,比较更新变异前后的最优位置对应的适应度值,确定是否保留变异后的最优解;

7)若达到精度要求或最大迭代次数等终止条件,则输出最优解和最佳适应度值,否则返回步骤3)。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 改进蝴蝶优化算法流程

Fig.3 Flowchart of IBOA

3 算法性能测试

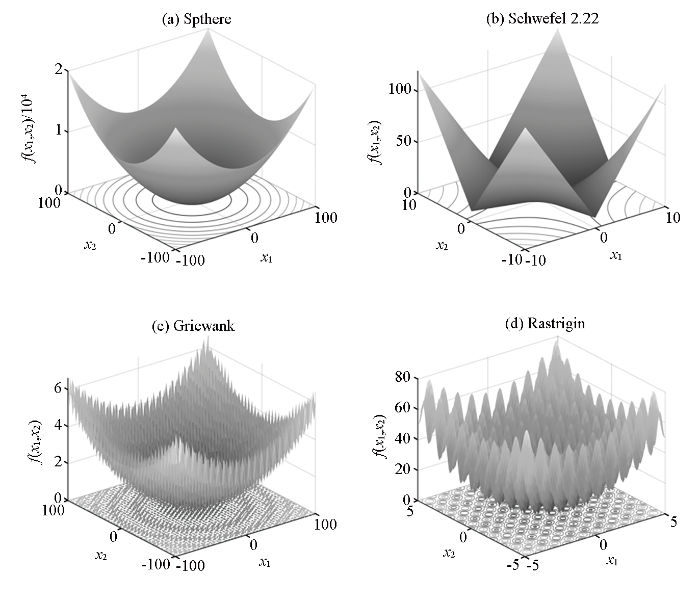
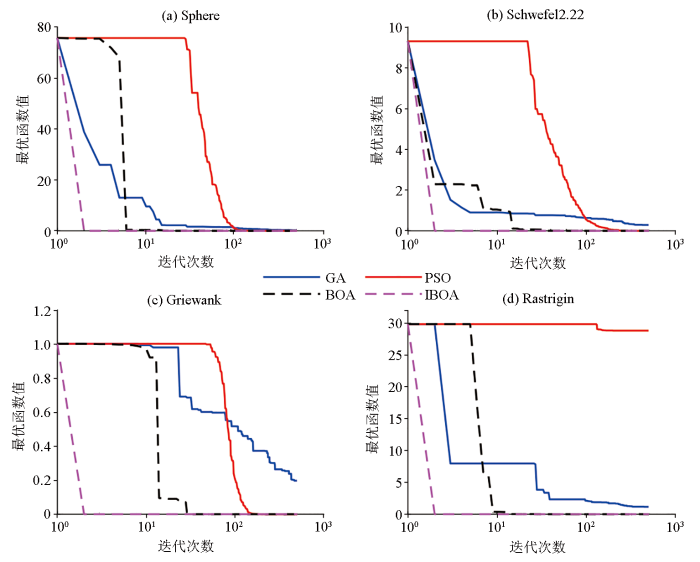
采用4种常用的Benchmark基准测试函数针对包括遗传算法(GA)、粒子群优化算法(PSO)、基本蝴蝶优化算法(BOA)以及本文提出的改进的蝴蝶优化算法(IBOA)的性能进行测试,各测试函数的数学表达式及参数特征见表1。图4为4种测试函数的示意(以二维空间为例)。其中Sphere函数和Schwefel 2.22函数均为典型的单峰函数,即在给定搜索空间内存在唯一极小值,通常可以用于测试算法的收敛性。Griewank函数和Rastrigin函数则为典型的多峰函数,即存在多个局部极小值和一个全局极小值,可以验证算法的全局寻优能力。各算法的参数设置如下:GA算法中,交叉概率为0.9,变异概率为0.1;PSO算法的参数设置参考文献[14]和文献[15],两个学习因子分别取2.8和1.3;BOA算法中采用固定开关概率为0.6,IBOA算法则无需再另外设置参数。测试时各算法的种群规模均为50,最大迭代次数均为500,并保持各算法迭代时种群初始化位置一致,运行50次后统计各算法的误差均值和标准差,计算结果详见表2。

表1 测试函数

Table 1 Test functions

函数名称	数学表达式	变量个数	搜索空间
Sphere	f(x)= $\overset{n}{\sum_{i = 1}} x_{i}^{2}$	30	[-100,100]
Schwefel 2.22	f(x)= $\overset{n}{\sum_{i = 1}} \|x_{i}\|$ + $\overset{n}{\prod_{i = 1}} \|x_{i}\|$	30	[-10,10]
Griewank	f(x)=1+ $\frac{1}{4000} \overset{n}{\sum_{i = 1}} x_{i}^{2}$ - $\overset{n}{\prod_{i = 1}}$ cos( $\frac{x_{i}}{\sqrt{i}}$ )	30	[-600,600]
Rastrigin	f(x)= $\overset{n}{\sum_{i = 1}} [x_{i}^{2} - 10 c o s (2 π x_{i}) + 10]$	30	[-5.12,5.12]

新窗口打开| 下载CSV

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 二维空间测试函数示意

Fig.4 Plots of test functions with two dimensions

表2 各算法优化结果

Table 2 Optimization results of different algorithms

函数特点	函数名称	误差	GA	PSO	BOA
单峰函数	Sphere	平均值	0.1102	8.40×10^-12	1.95×10^-22
		标准差	0.0711	3.18×10^-11	9.53×10^-22
		最优值	0.0004	9.70×10^-15	1.73×10^-28
		最次值	0.2503	2.15×10^-10	6.68×10^-21
	Schwefel 2.22	平均值	0.1465	0.0018	3.69×10^-16
		标准差	0.0648	0.0070	5.10×10^-16
		最优值	0.0030	9.75×10^-8	9.70×10^-19
		最次值	0.2894	0.0458	3.06×10^-15
多峰函数	Griewank	平均值	0.2633	0.0188	0
		标准差	0.1605	0.0238	0
		最优值	0.0040	3.74×10^-14	0
		最次值	0.6071	0.1100	0
	Rastrigin	平均值	0.5285	10.6319	0
		标准差	0.6463	13.7308	0
		最优值	0.0001	1.14×10^-13	0
		最次值	2.6254	29.8488	0

新窗口打开| 下载CSV

表2体现出无论是在单峰函数还是多峰函数的极小值求解过程中,相对于GA和PSO,BOA和IBOA的寻优能力均有显著提升,尤其是本文提出的IBOA算法均能够收敛于全局最小值。其中,在Rastrigin多峰函数的寻优过程中,GA的求解精度较低,而PSO甚至出现500次迭代结束时不收敛现象。50次独立运行的结果的标准差表明IBOA在各测试函数上的稳定性明显强于其他3种算法。图5为各算法的收敛特征曲线,可以看出与PSO相比,由于使用了开关概率,因此避免了由于飞行粒子初始速度和位置的随机性导致的初期收敛较慢问题,BOA在算法的初期收敛速度明显优于PSO,与GA的差异却并不明显。随着迭代的进行,BOA算法由于使用了开关概率,因此有一定概率的可能进行全局搜索,收敛速度迅速上升超过了GA。同时,也可以发现在迭代的中期,BOA也不可避免地陷入短暂的局部搜索。而IBOA使用了动态开关概率,相对于BOA而言,在算法的初期进一步提高了全局搜索的可能性,并在每次迭代结束时对最优位置进行了逐维柯西变异,采用贪婪算法保证种群向全局最优方向搜索,因此在收敛速度上具有非常显著的优势,仅需要很少的迭代次数便可以达到全局最优。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 不同算法在测试函数上的迭代收敛特征

a—Sphere函数迭代收敛曲线;b—Schwefel 2.22函数迭代收敛曲线;c—Griewank函数迭代收敛曲线;d—Rastrigin函数迭代收敛曲线

Fig.5 Convergence Characteristics of test functions by different algorithms

a—convergence curves of Sphere;b—convergence curves of Schwefel 2.22;c—convergence curves of Griewank;d—convergence curves of Rastrigin

表3为不同算法在各测试函数寻优过程中采用并行计算时,50次独立运算所消耗的计算时间。其中,PSO计算效率最高,GA最差,分析造成这种差异的原因在于GA在迭代过程中需要不断的编码和解码,以及父代与子代之间进行交叉变异操作消耗更多的时间。而PSO算法只需要更新粒子的飞行速度和当前位置即可,无需其他操作,因此计算效率相对较高,但极易陷入局部最优,甚至不收敛。BOA需要通过开关概率对全局搜索和局部搜索进行随机性选择,而IBOA由于增加了对当前最优位置进行逐维柯西变异,并采用了贪婪算法比较变异前后的目标函数值,但实际计算耗时并没有显著的增加,却在收敛速度、求解精度及稳定性方面得到了明显的提升,因此可认为本文提出的各项改进策略是有效的。

表3 不同算法50次独立运算计算耗时

Table 3 Consumed seconds of different algorithms under 50 trialss

函数名称	GA	PSO	BOA	IBOA
Sphere	9.4	3.9	4.5	5.0
Schwefel 2.22	9.7	4.2	4.2	5.0
Griewank	10.8	4.0	4.9	6.1
Rastrigin	12.8	3.4	4.8	4.4

新窗口打开| 下载CSV

综上所述,通过测试函数的性能表现,初步认为本文提出的IBOA算法相对于GA和PSO在求解精度和收敛速度上有一定的优势,因此可以尝试将其作为频散曲线反演的优化算法。

4 理论模型反演试算

为了进一步验证IBOA算法在面波频散曲线反演中的可行性,结合实际工程应用中常见的3种地层分布特征,首先建立四层递增型(模型1)、含低速软夹层型(模型2)和含高速硬夹层(模型3)地层模型,模型参数见表4。利用凡友华等的快速标量传递法^[42-43]计算理论频散曲线,结合实际工程应用时面波能量集中的优势范围,将频率设置为4~60 Hz,频率间隔2 Hz,共29个频散点。大量研究表明,纵波速度和密度对面波的相速度影响较小,因此本文在计算理论频散曲线时,不考虑地层的纵波速度和密度对频散曲线的影响,并固定地层的泊松比为0.35, 密度为1.9 g/cm³。再通过构建频散曲线反演的目标函数,采用IBOA算法对频散曲线在无噪声和含10%随机噪声的情况下分别进行反演。

表4 理论模型参数及反演搜索范围

Table 4 Theoretical models and search range

地层序号	模型参数		搜索范围
	横波速度V_s/ (m·s^-1)	厚度H/m	横波速度V_s/ (m·s^-1)	厚度H/m
	模型1(速度递增型地层)
1	150	2	75~225	1~3
2	240	4	120~360	2~6
3	360	6	180~540	3~9
4	500	半空间	250~750	半空间
	模型2(含低速软夹层型地层)
1	200	2	60~300	1~3
2	120	4	60~300	2~6
3	300	6	150~450	3~9
4	500	半空间	250~750	半空间
	模型3(含高速硬夹层型地层)
1	150	2	75~225	1~3
2	300	4	100~500	2~6
3	250	6	100~500	3~9
4	500	半空间	250~750	半空间

新窗口打开| 下载CSV

4.1 反演目标函数

面波频散曲线反演的本质就是在给定搜索空间范围内,寻找最佳的地层参数组合,使得该模型的理论频散曲线与实测频散曲线之间的误差最小^[14],则可以定义待优化的目标函数为:

(8)fitness=

\frac{‖V_{r}^{o b s} - V_{r}^{t h e o}‖}{\sqrt{m}}

式中: $V_{r}^{o b s}$ 为实测频散曲线, $V_{r}^{t h e o}$ 为理论频散曲线,m为频散点个数,‖·‖为L₂范数。由于地球物理反演问题的多解性和非唯一性,目标函数属于典型的多峰函数。

4.2 理论模型反演

4.2.1 无噪声条件下反演测试

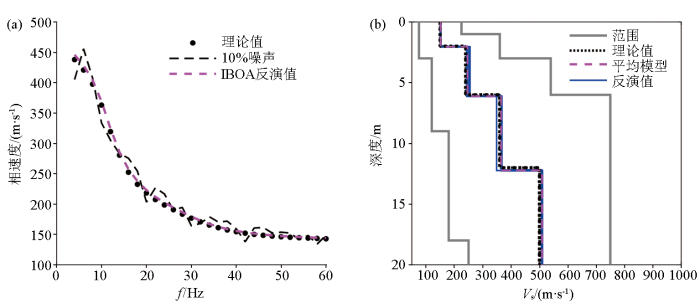
首先,采用本文提出的IBOA算法在频散曲线不含噪声的情况下,对各理论模型进行反演计算。设置算法的种群规模为50,最大迭代次数为100,独立反演10次,各地层参数的搜索范围见表4。

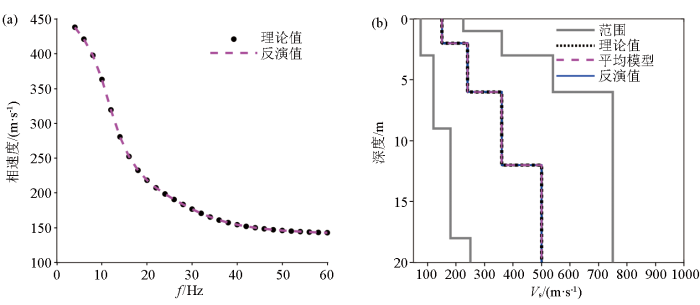
图6、图7、图8分别为模型1、模型2和模型3在频散曲线不含噪声情况下10次独立反演的结果。其中,图6a、图7a、图8a表示对10次反演结果取平均值得到的地层模型所对应的频散曲线(洋红色虚线)和理论频散曲线(黑色实心点)的拟合情况,可以看出吻合程度较高,说明IBOA算法的收敛性较好。图6b、图7b、图8b为10次独立反演得到的单个速度模型(蓝色实线)和模型平均值(洋红色虚线)与理论模型(黑色点线)的对比,可以发现10次独立反演结果均与理论模型高度吻合,说明IBOA算法在保证高精度的同时也具有一定的稳定性。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 无噪声条件下IBOA算法对模型1的反演结果

a—频散曲线拟合情况;b—反演模型速度剖面

Fig.6 Inverted results of model 1 by IBOA without noise

a—dispersion curves of theoretical model and inverted model;b—shear wave structures of theoretical model and inverted model

图7

新窗口打开| 下载原图ZIP| 生成PPT

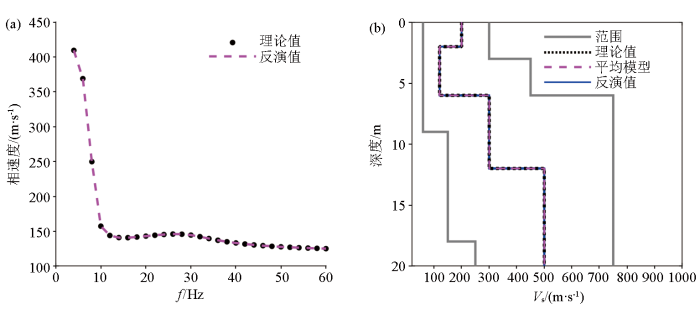
图7 无噪声条件下IBOA算法对模型2的反演结果

a—频散曲线拟合情况;b—反演模型速度剖面

Fig.7 Inverted results of model 2 by IBOA without noise

a—dispersion curves of theoretical model and inverted model;b—shear wave structures of theoretical model and inverted model

图8

新窗口打开| 下载原图ZIP| 生成PPT

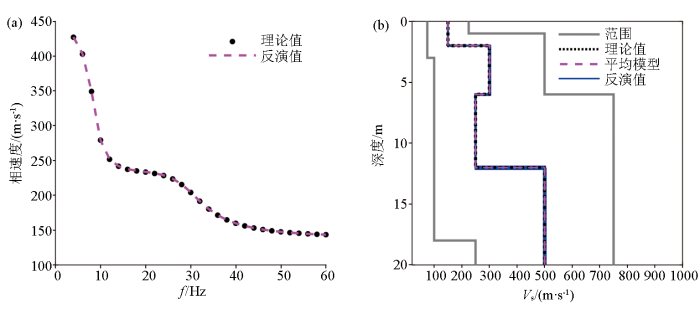
图8 无噪声条件下IBOA算法对模型3的反演结果

a—频散曲线拟合情况;b—反演模型速度剖面

Fig.8 Inverted results of model 3 by IBOA without noise

a—dispersion curves of theoretical model and inverted model;b—shear wave structures of theoretical model and inverted model

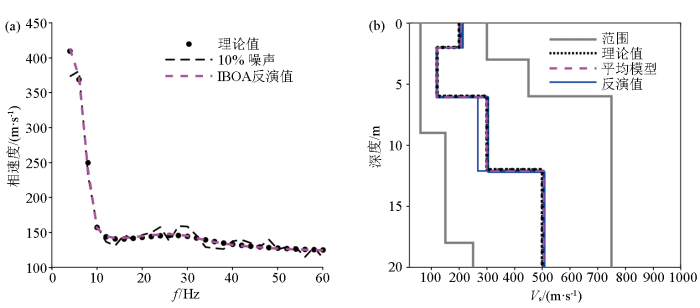
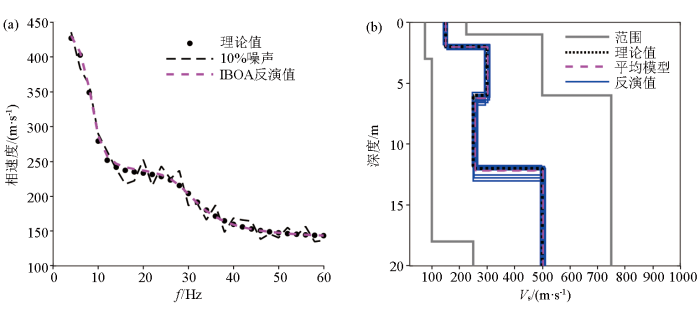
4.2.2 含10%随机噪声条件下反演测试

由于瑞利波实际采集过程不可避免地受到各种噪声的干扰,导致频散曲线的拾取精度受限,从而影响反演结果的可靠性。因此,有必要对反演算法的抗噪性能进行一定的测试。本文在各理论模型的频散曲线中参考式(9)

(9)

V_{r}^{n o i s e}

=V_r[0.9+0.2×rand(0,1)],

加入了10%随机噪声,采用同样的参数进行反演,以此来检验IBOA算法的抗噪能力。

图9、图10、图11分别为模型1、模型2和模型3在频散曲线含10%随机噪声情况下10次独立反演的结果。图9a、图10a、图11a表示对10次独立反演结果取平均值得到的地层模型所对应的频散曲线(洋红色虚线)和理论频散曲线(黑色实心点)以及含噪条件下的频散曲线(黑色虚线)的拟合情况,可以看出在10%噪声条件下,频散曲线的拟合程度依然较高,说明反演结果的收敛性并未受到影响。图9b、图10b、图11b为10次独立反演得到的单个速度模型(蓝色实线)和模型平均值(洋红色虚线)与理论模型(黑色点线)的对比,其中模型1的还原程度最高,几乎没有偏离;当地层中含有速度间断面时,如模型2和模型3,反演结果的精确性虽然在一定程度上受到了随机噪声的干扰,但仍然能够较高程度地还原真实模型,尤其是针对速度间断面的反演较为准确。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 10%随机噪声条件下IBOA算法对模型1的反演结果

a—频散曲线拟合情况;b—反演模型速度剖面

Fig.9 Inverted results of model 1 by IBOA with 10% random noise

a—dispersion curves of theoretical model and inverted model;b—shear wave structures of theoretical model and inverted model

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 10%随机噪声条件下IBOA算法对模型2的反演结果

a—频散曲线拟合情况;b—反演模型速度剖面

Fig.10 Inverted results of model 2 by IBOA with 10% random noise

a—dispersion curves of theoretical model and inverted model;b—shear wave structures of theoretical model and inverted model

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 10%随机噪声条件下IBOA算法对模型3的反演结果

a—频散曲线拟合情况;b—反演模型速度剖面

Fig.11 Inverted results of model 3 by IBOA with 10% random noise

a—dispersion curves of theoretical model and inverted model;b—shear wave structures of theoretical model and inverted model

4.2.3 IBOA算法反演结果分析

表5为模型1、模型2和模型3的理论频散曲线在无噪声和含10%随机噪声情况下IBOA算法反演10次后的各层参数反演结果的平均值及标准差。可以看出,在无噪声情况下,各模型的反演结果与理论值非常接近,相对误差最大不超过0.5%。而在10%随机噪声情况下,虽然反演结果受到一定的影响,最大相对误差也仅有4.88%,说明IBOA算法的抗噪性能较好,且无论频散曲线是否含有噪声,10次独立反演的各模型参数的标准差均比较小,表明算法的稳定性较高。主要原因在于使用动态开关概率有利于IBOA算法在前期更大可能地进行全局搜索,并对每次迭代产生的最优解采用逐维柯西变异,全过程保证了算法的全局优化空间和寻优能力,尽可能地避免陷入局部最优和早熟收敛。

表5 理论模型频散曲线反演结果统计

Table 5 Statistics of inverted results for theoretical models

模型编号	模型参数	理论值	无噪声			含10%随机噪声
模型编号	模型参数	理论值	平均值	相对误差/%	标准差	平均值	相对误差/%	标准差
模型1	V_s1/(m·s^-1)	150	150.01	0.005	0.037	151.36	0.904	0.435
	V_s2/(m·s^-1)	240	239.96	0.017	0.123	246.33	2.637	3.823
	V_s3/(m·s^-1)	360	359.94	0.017	0.185	364.73	1.314	5.600
	V_s4/(m·s^-1)	500	499.91	0.017	0.257	509.11	1.822	1.024
	H₁/m	2	2.00	0.015	0.001	2.04	1.820	0.004
	H₂/m	4	4.00	0.018	0.002	4.07	1.822	0.008
	H₃/m	6	6.00	0.017	0.003	6.11	1.822	0.012
模型2	V_s1/(m·s^-1)	200	200.00	0.002	0.359	206.59	3.293	4.064
	V_s2/(m·s^-1)	120	120.00	0.001	0.086	119.61	0.324	1.246
	V_s3/(m·s^-1)	300	300.00	0.001	0.215	299.56	0.147	11.391
	V_s4/(m·s^-1)	500	500.00	0.001	0.358	505.19	1.038	1.582
	H₁/m	2	2.00	0.000	0.001	2.02	1.040	0.006
	H₂/m	4	4.00	0.000	0.003	4.04	1.038	0.013
	H₃/m	6	6.00	0.000	0.004	6.06	1.038	0.019
模型3	V_s1/(m·s^-1)	150	149.99	0.005	0.599	150.38	0.252	5.109
	V_s2/(m·s^-1)	300	300.98	0.326	1.709	302.61	0.871	7.384
	V_s3/(m·s^-1)	250	249.83	0.067	0.866	257.15	2.860	6.338
	V_s4/(m·s^-1)	500	500.38	0.075	2.591	502.89	0.578	5.939
	H₁/m	2	2.00	0.081	0.012	2.03	1.515	0.130
	H₂/m	4	4.00	0.104	0.032	4.20	4.880	0.234
	H₃/m	6	6.01	0.092	0.054	5.95	0.896	0.172

新窗口打开| 下载CSV

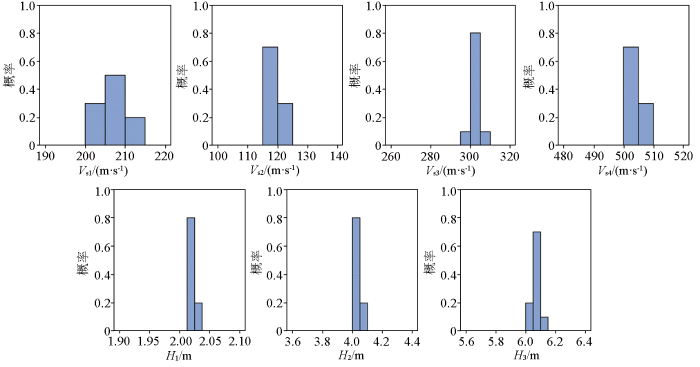
由于频散曲线反演目标函数属于多峰函数,不可避免地面对地球物理问题的多解性和非唯一性,即不同地层参数的组合都可能获得相似的频散曲线拟合,因此在分析评价理论模型反演结果的有效性方面,需要考虑每次独立反演时各参数与理论模型的偏离程度,从而反映出算法的有效和可靠程度。以模型2在频散曲线含10%随机噪声条件下的反演结果为例,图12为10次独立反演中,各层参数在理论值附近的分布概率。该图直观地反映出了各层横波速度的反演结果均落在理论值±10%范围内,最大误差不超过15 m/s;同时,IBOA算法对地层厚度的反演更为精确,最大误差仅为0.1 m,进一步体现出了IBOA算法在反演可靠性和稳定性方面的优势。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 10%随机噪声条件下模型2反演结果分布概率直方图

Fig.12 Histogram of inverted results of model 2 by IBOA with 10% random noise

4.2.4 与GA和PSO算法的对比

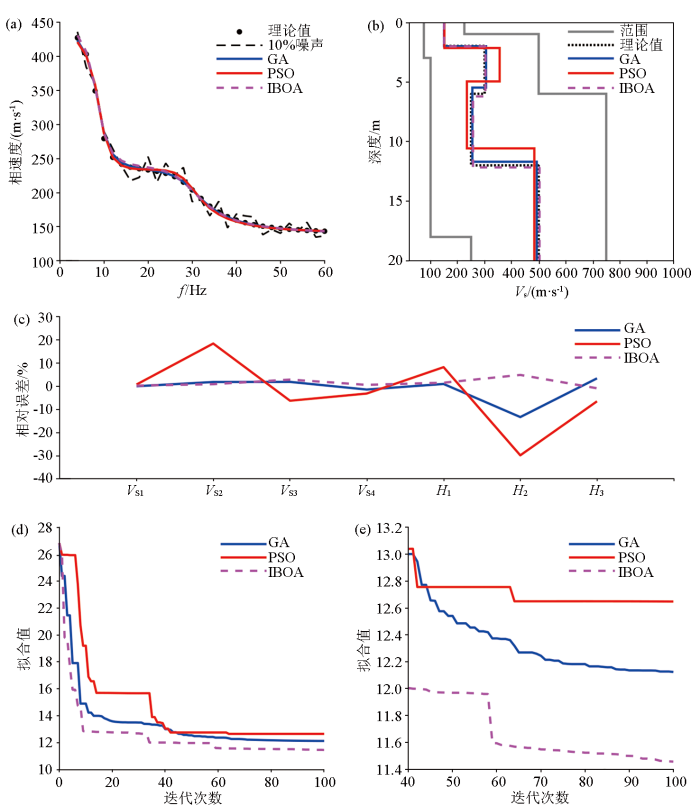
理论模型的反演试算结果初步表明了IBOA算法在面波频散曲线反演中的可行性,且算法具有一定的抗噪性,反演结果的稳定性和可靠程度均较好。为了更好地验证IBOA算法的适用性,将该算法与目前主流且常用的两种频散曲线反演算法,遗传算法(GA)和粒子群算法(PSO)做对比。以含10%随机噪声条件下模型3的频散曲线反演为例,分别采用GA、PSO和IBOA算法进行反演,其中GA算法中,交叉概率为0.9,变异概率为0.1;PSO算法中两个学习因子分别取2.8和1.3。其他参数设置与前文反演测试保持一致,独立反演10次后对反演结果取平均值。

图13a表示对10次独立反演结果取平均值得到的地层模型所对应的频散曲线和理论频散曲线以及含噪条件下的频散曲线的拟合情况,可以看出在10%噪声条件下,各算法反演得到的平均模型对应的频散曲线与理论频散曲线拟合均较好,可认为各算法的收敛性并未受到随机噪声的干扰,均具有一定的抗噪能力;图13b为各算法10次独立反演得到的平均模型与理论模型(黑色点线)的对比,可以直观地发现当频散曲线中含有随机噪声时,在对理论模型的还原程度上,PSO偏离程度最大,其次为GA,IBOA反演结果与理论模型最为接近。图13c为各算法反演结果与理论模型的相对误差曲线,其中,GA和PSO在 ${V_{S}}_{2}$ 、H₂上的相对误差较大,约10%~30%;图13d为各算法的迭代收敛曲线,可以发现IBOA算法在前期的收敛速度最快,明显优于GA和PSO。当迭代到40次左右时(图13e),各算法均收敛到全局最优附近,收敛速度明显有所下降,算法进入局部开发阶段。由于PSO算法通过更新粒子飞行速度来确定更新位置,当频散曲线的拟合程度达到一定时,粒子主要在某个局部最优附近反复飞行和移动,导致后期反演效率较低,极易陷入局部最优;而GA算法通过交叉变异操作,相对PSO而言一定程度上有所改善,但到迭代后期时效果欠佳;IBOA由于在算法前期使用了动态开关概率,保证算法尽可能地进行全局探索,迅速向全局最优的方向靠近,当频散曲线拟合程度较好时,仍然能够通过逐维柯西变异,拓展种群多样性,较大程度地保留全局寻优的机会,从而避免所有个体陷入局部最优。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 10%随机噪声条件下不同算法对模型3的反演结果

a—频散曲线拟合情况;b—反演模型速度剖面;c—反演结果误差曲线;d—迭代收敛曲线;e—后期迭代收敛曲线(40~100次)

Fig.13 Inverted results of model 3 by different algorithms with 10% random noise

a—dispersion curves of theoretical model and inverted model;b—shear wave structures of theoretical model and inverted model;c—relative error between theoretical model and inverted model;d—convergence curves of different algorithms;e—convergence curves of different algorithms during iteration No.40~100

5 应用实例

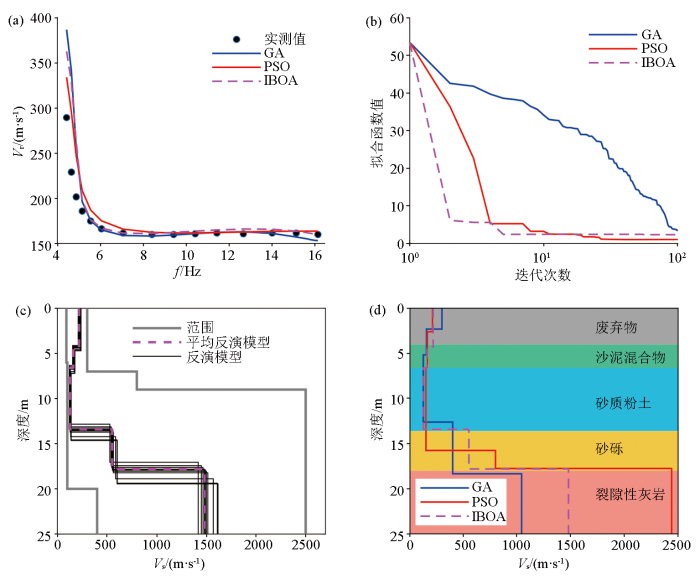
在前面的理论模型的反演试算环节,已经验证了IBOA算法在瑞利波频散曲线反演的目标函数优化过程中,无论是在无噪声还是含10%随机噪声的情况下,均能够得到更加稳定且准确的反演结果。为了测试IBOA算法在实际应用中的表现,以意大利东北部某废物处理厂实际采集的瑞利波数据为例^[44]。根据实际钻孔资料揭露,该地区基岩为裂隙石灰岩,上覆为18 m厚的松散沉积层,并存在低速层。由于近表层存在2 m的废物填埋层,且松散层的物性差异较小,岩土工程特性差,地震记录的信噪比较低,且含有大量的地滚波,频散能量主要集中在4~16 Hz(图14a)。采用GA、PSO和IBOA算法对实测频散曲线分别进行10次独立反演,各算法反演参数与模型试算时保持一致,且每次反演时各算法均使用相同的初始模型。采用5层结构模型和实际钻孔地层分布情况^[45]确定各层参数的搜索空间如表6所示。需要特别说明的是,由于钻孔资料未包含实测波速测井信息,因此本次反演的目标评判准则以地层分界面的埋深为主,横波速度仅反映地层间相对变化趋势。

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 实测资料不同算法反演结果

a—最终反演结果计算得到的理论频散曲线与实测频散数据对比;b—不同算法的迭代收敛曲线;c—IBOA算法10次反演模型结果及平均值;d—最终反演模型与实际钻孔揭露地层对比

Fig.14 Inverted results of actual field data by different algorithms

a—dispersion curves of measured data and inverted models by different algorithms;b—convergence curves of different algorithms;c—shear wave structures of 10 times inversions by IBOA;d—comparison between actual borehole data and inverted models

表6 各层反演参数搜索空间

Table 6 Search range for inversion parameters at each layer

层序号	横波速度V_s/ (m·s^-1)	厚度H/m	密度ρ/ (g·cm^-3)	泊松比
1	90~300	2~6	1.9	0.45
2	100~300	1~4	1.9	0.45
3	100~300	4~10	2.0	0.45
4	400~800	2~6	2.2	0.25
5	1000~2500	-	2.4	0.20

新窗口打开| 下载CSV

对10次独立反演的结果取平均值进行统计,GA、PSO和IBOA算法的目标函数最优值的平均值分别为6.866 5、1.147 9和2.633 3,方差分别为2.304 3、1.364 4和0.205 8。总体上看IBOA算法的目标函数收敛值介于GA算法和PSO算法收敛最优值之间,但稳定性相对最好。对各算法10次独立反演得到的地层模型参数取平均值并计算理论频散曲线,与实测频散曲线(图14a实心黑点)基本吻合,进一步说明了各算法的收敛性。图14b为各算法反演时的迭代收敛情况,其中IBOA算法的收敛速度明显快于GA和PSO算法,仅需要很少的迭代次数就能搜索到全局最优附近,这主要是在每次迭代寻优过程对最优解逐维进行了柯西变异以及贪婪算法,使得种群更快地向全局最优所在的位置和方向搜索。图14c为IBOA算法10次独立反演的各个模型,可以看出反演结果的稳定性较好。虽然3种算法的最终收敛值基本接近,但从最终反演模型结果上看,IBOA算法反演模型与实际钻孔揭露的地层分布最为接近,特别是第三层软夹层的分辨能力相对GA和PSO算法更高,这与前文的理论模型测试结果也一致。这一现象更体现出了面波反演的目标函数是多极值函数且存在多解性的特点,而IBOA算法在整个迭代周期中对寻优策略的选取通过动态开关概率的调节具有一定的随机性,因此在前期快速收敛的基础上,在后期对当前最优解进行了逐维柯西变异依然保持了种群位置的多样性,从而在一定程度上降低了类似GA算法和PSO算法陷入局部最优的可能性。

6 结论

本文研究了改进蝴蝶优化算法在瑞利波频散曲线反演中的应用,通过对地质模型的理论频散曲线在无噪声和含10%随机噪声以及实测频散数据的反演试验,研究结果表明:

1)改进蝴蝶优化算法是一种稳定的非线性优化算法,在频散曲线反演中可以获得有效、精确可靠的反演结果,且抗噪能力较好;

2)与其他非线性优化算法相比,由于使用了动态开关概率,因此极大地保证了算法前期全局搜索能力。同时,在每次迭代时对当前最优解进行逐维柯西变异,并利用贪婪算法不仅可以保证种群多样性,还确保了种群整体向全局最优方向收敛;

3)实测数据反演结果表明,在相同给定搜索空间内,改进的蝴蝶优化算法反演结果与钻孔实际情况更为接近,且对速度间断面的反演探测能力优于遗传算法和粒子群算法;

4)由于采用了逐维柯西变异和贪婪算法,在实际工作中可通过减少种群规模、限制最大迭代次数以及并行计算有效地提高计算效率。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

李庆春, 邵广周, 刘金兰, 等.

瑞雷面波勘探的过去、现在和未来

[J]. 地球科学与环境学报, 2006, 28(3):74-77.