多源频率域地震勘探技术及应用

doi:10.11720/wtyht.2024.1317

多源频率域地震勘探技术及应用

孙红林, 刘铁华^,, 刘铁, 张占荣, 陈支兴

中铁第四勘察设计院集团有限公司, 湖北武汉 430063

Multi-source frequency-domain seismic exploration technique and its application

SUN Hong-Lin, LIU Tie-Hua^,, LIU Tie, ZHANG Zhan-Rong, CHEN Zhi-Xing

China Railway Siyuan Survey and Design Group Co.,Ltd.,Wuhan 430063,China

通讯作者: 刘铁华(1983-),男,高级工程师,长期从事工程地球物理技术与设备研究工作。Email:liutiehua@crfsdi.com

第一作者: 孙红林(1973-),男,教授级高级工程师,注册土木(岩土)工程师

责任编辑: 叶佩

收稿日期: 2023-08-7 修回日期: 2024-03-28

基金资助:

湖北省重点研发计划项目(2021BAA050)
国家重点研发计划项目(2019YFC0605101)

Received: 2023-08-7 Revised: 2024-03-28

摘要

在城市地球物理勘探中,因受到城市中各种强电磁机械干扰和交通建筑阻隔,诸多地球物理勘探技术勘探效果不佳。本文基于瞬态面波、微动台阵和微动谱比,采用多点三分量低频传感器获取的多源频率域地震数据,综合提取两种特征曲线后进行联合反演,实现融合3种技术的多源频率域地震勘探。其中,提出了双源综合频散谱提取技术、双源特征曲线联合反演技术和基于非均匀介质的等效均匀介质正演技术,勘探成果的精度和效率均得到了提高,在工程实践中得到验证。

关键词： 多源频率域地震勘探; 瞬态面波; 微动台阵; 微动谱比

Abstract

Due to various strong electromagnetic mechanical interference and traffic barriers, many geophysical exploration techniques are ineffective in urban geophysical exploration.Based on transient surface waves,microtremor arrays,and microtremor spectral ratios,this study synthetically extracted two kinds of characteristic curves for joint inversion from the multi-source frequency-domain seismic data obtained by multi-point three-component low-frequency sensors.Consequently,this study achieved multi-source frequency-domain seismic exploration that integrated three techniques and developed the two-source synthetic dispersive spectrum extraction technique,the two-source characteristic curve joint inversion technique,and the equivalent homogeneous medium forward modeling technique based on inhomogeneous media.Engineering practice results demonstrate the improvements in the exploration accuracy and efficiency.

Keywords： multi-source frequency-domain seismic exploration; transient surface wave; microtremor array; microtremor spectral ratio

PDF (5836KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

孙红林, 刘铁华, 刘铁, 张占荣, 陈支兴. 多源频率域地震勘探技术及应用[J]. 物探与化探, 2024, 48(3): 618-628 doi:10.11720/wtyht.2024.1317

SUN Hong-Lin, LIU Tie-Hua, LIU Tie, ZHANG Zhan-Rong, CHEN Zhi-Xing. Multi-source frequency-domain seismic exploration technique and its application[J]. Geophysical and Geochemical Exploration, 2024, 48(3): 618-628 doi:10.11720/wtyht.2024.1317

0 引言

21世纪是纵深发展的世纪,现代城市发展环境出现了同质化发展趋势,对城市发展提出新的挑战。城市的平面开发空间渐渐趋于饱和,期待更精细、更大深度的纵向发展,这就需要在既有城市区域的地下开展建设,其最先需要实施的是精细化地下勘查工作,为后期的设计、建设和运维提供基础性数据支撑。

我国城市开发建设与国外先拆迁后勘查的思路不同,是在存在既有建筑、道路等阻碍时开展勘探,常规的钻探工作往往无法有效布置。地球物理勘探因具有对环境影响小、效率高和成本低的特点,成为城市勘探中的重要手段,但由于城市环境中充斥着大量电磁和机械干扰,勘探质量受到影响,勘探的精度和效率均不理想。如何在复杂城市环境中开展有效服务于城市开发的物探工作,成为急需解决的难题。本文基于对3种适应于城市环境的勘探技术的特征分析,提出了一种新的勘探技术——多源频率域地震勘探技术。

1 频率域地震勘探技术

地球物理方法众多,一般基于所采用的不同物理场进行方法命名,如电法、磁法、重力法、地震波法等,在这些方法中,通常根据对当前物理场信号处理的数学域不同进一步细分,如电磁法中有频率域和时间域的区分。相应的,在所有地震波法技术中,地震反射波法、地震折射波法和地震透射波法等都是基于时间域特征进行数据处理的,而瞬态面波法(被动源面波)、微动台阵法(被动源面波)和微动谱比法(单点H/V法)等都是基于震动信号在频率域的特征进行数据处理,地震波法的勘探技术因此也可被分为时间域地震勘探技术和频率域地震勘探技术两类,本文均是在频率域地震勘探技术范围里进行讨论,具体涉及瞬态面波法、微动台阵法、微动谱比法和多源频率域地震波法。

1.1 瞬态面波法

瞬态面波法是利用人工震源激发面波,采用直线型排列方式接收低频地震数据后提取频散曲线,进而反演获取地层横波速度的方法。1953年,Haskell发现层状介质中面波存在频散特性^[1],推导了瑞利面波的频散方程。Aki等^[2]发现瑞利面波与体波相比,具有能量衰减慢、振幅大、质点振动存在椭圆极化等特征。Knopoff、Abozena、Chen、凡友华等提出了计算多层层状介质中瑞利面波频散曲线的Knopoff算法^[3]、Abozena算法^[4]、广义反射—透射系数算法^[5]和快速矢量传递算法^[6]。经过众多国内外学者的研究,瞬态面波法已被成功应用于不同尺度的地层结构勘探中,在浅表层的工程地质调查中得到了广泛应用。

城市工程地质调查中,瞬态面波法通常沿道路布置,通过人工敲击方式获取数据,其数据频散频率主要分布在10~40 Hz之间,有效勘探深度一般不大于30 m,在适当观测参数情况下可实现2~10 m范围的高分辨率勘探。

在复杂城市环境中,尤其是在房屋密集区作业时,因其需要连续的线性作业空间,而实际工程勘探中需要获取连续的线状工程地质信息,导致该方法在城市工程勘探中应用受限。

1.2 微动台阵法

与瞬态面波法不同,微动台阵法不是利用人工震源激发面波,而是利用自然界中本身存在的微弱震动信号作为信号源(微动信号),基于该微动信号提取探测点的频散曲线,进而实现地层属性反演。在获取微动信号时,需要布置多个采集站形成采集台阵^[7],台阵形式可为规则的(“直线型”、 “同心圆型”、“内嵌三角型”等)也可为非规则的。微动台阵法是由Aki^[8]奠定理论基础,从微动信号中提取出面波频散曲线。徐佩芬等^[9]研究了微动多阶瑞雷波系数反演方法,将微动剖面探测法应用于煤矿陷落柱探测^[10],取得了较好的效果。杜亚楠等^[11]研究了噪声源分布特征对台阵的影响。张明辉等^[12]以微动台阵为基础研究短周期密集台阵微动测技术,逐渐成为浅部地层结构探测领域的一项重要手段。

微动台阵法是以平稳随机过程理论为依据的,以其“所采集的数据是来自均匀分布的各方向” 为假设条件,即要求各采集站与目标勘探点的方位角需要尽可能多的均匀分布在各个方向上。考虑到对不同频率信号的敏感性要求,一般认为采用多层内嵌式的台阵最为理想。但在应用中,采用多层内嵌式的台阵采集数据遇到了一些问题:一方面,假设条件不能满足,如在城镇、江河等富有微动信号的区域边界处采集数据时,微动信号往往具有明显的方向性,这需要在数据处理时进行额外处理,没必要进行多方向的信号采集;另一方面,多层内嵌式台阵布置难度较大,效率较低。实际应用中,对于线状工程的勘探一般采用线状台阵,对于面积型工程采用非规则方式,就现场条件自由布置密集型台阵,在后期数据处理时自动抽取不规则台阵进行数据分析。

微动台阵技术利用的是天然的随机扰动信号,布置测点灵活,相较于需要进行主动源激发的方法具有抗干扰能力强、实施便捷和绿色环保等优势。但由于天然微动信号中的高频信号能量较弱,导致浅部信噪比降低,有时会出现局部勘探盲区。

1.3 微动谱比法

微动谱比法与微动台阵法相似,是通过采集微动信号实现地质勘探的一种方法,也被称为微动H/V谱比法、单点H/V谱比法或Nakamura方法。与微动台阵法不同的是,微动谱比法需要采集单点三分量数据,提取的不是基于多点数据的频散曲线,而是单点水平分量和垂直分量的谱比曲线。获取谱比曲线后,可直接基于曲线峰值频率进行地层解释,也可对特征曲线进行地层反演。微动谱比法最早由Nogoshi等^[13]提出,之后经Nakamura^[14]推广应用到场地效应评价方面。Arai^[15]将之应用于求取地表横波速度剖面。张若晗等^[16]、王伟君等^[17]利用微动谱比法探测土石分界面和地表浅层速度结构。刘铁华等^[18]对非均匀介质的微动谱比曲线正演进行研究,提高了非均匀地层的探测精度。

微动谱比法因其基于单点三分量微动信号,具有天然抗干扰能力和极强场地适应性,这方面刚好是城市地球物理勘探的痛点。但在对谱比曲线反演时高度依赖初始模型,要求掌握较为准确的表层速度,而实际地层速度是不确定的。同时,在基岩波速大于1 500 m/s时微动谱比与地震动谱比的峰值频率才满足一致性,而谱比曲线峰值小于3、覆盖层与基岩波阻抗比很小或基岩埋藏较浅时需格外小心。所以,微动谱比法可用于城市复杂环境的地质勘探中,用于解决其他方法无法实施或效果欠佳的难题,但应在满足应用条件下进行。

2 多源频率域地震波法

频率域地震波法中,早在1998年王振东^[19]提出了基于瞬态面波法和微动台阵法的双源面波法,指出可利用主动源面波数据和被动源面波数据进行联合处理;2005年起,堪萨斯地质调查局(KGS)的Park等^[20]利用双源面波数据进行了联合勘察的研究,指出联合成像能够拓展探测的深度和提高多阶模式频散曲线提取精度并编制了数据处理软件;刘铁华^[21]进行了双源面波技术在地铁勘探中适用性的量化研究,并将之运用到城市钻探盲区的地质勘探中^[22],取得了较好的效果。

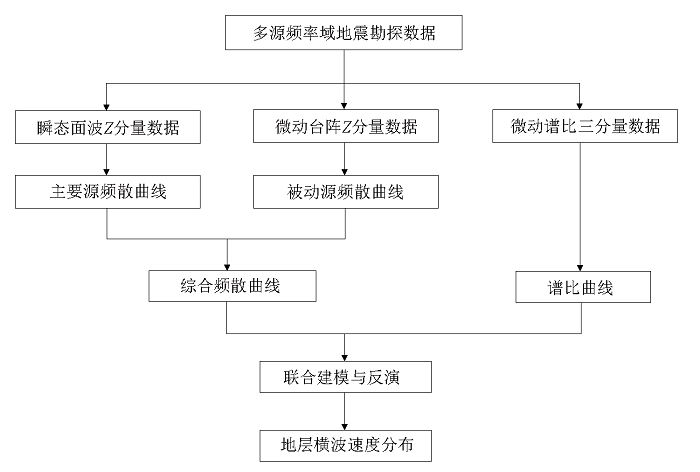
双源面波法取长补短,在勘探效率和质量上有所提升,其在数据采集时要求在同一测线上布置低频检波器,分别采集多道主、被动源面波数据,然后提取人工源和天然源的综合频散曲线,反演生成测线下方的横波速度剖面。轨道交通勘探中,测线往往呈线性分布,不可避免地穿越房屋密集区,时有勘探盲区出现。基于双源面波法在数据采集和处理方面的相似性和微动谱比法较强的场地适应能力,本文提出融合了主动源面波法(瞬态面波法)、被动源面波法(微动台阵法)和微动谱比法的多源频率域地震波法,利用人工源和天然源的振动信号,基于多点低频三分量传感器获取的主被动源面波,综合获取每个测点的频散和谱比特征曲线,在联合反演的基础上提取高分辨率的地层速度信息,实现复杂城市环境下的地质勘探,整个技术流程如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 多源频率域地震勘探技术流程

Fig.1 Technical flow of multi-source frequency domain seismic wave exploration

2.1 数据采集

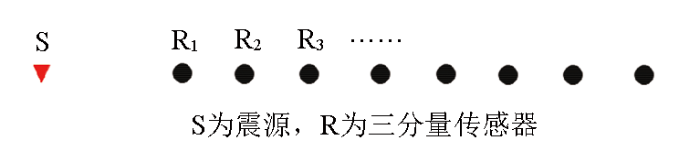
实际工作中,多源频率域地震波法的数据观测一般采用特定的观测装置,通常采用线性台阵进行,如图2所示,各采集站为分布式低频三分量传感器,可非等间距布置传感器。在线性台阵的沿线方向人工激发信号,记录三分量瞬态地震数据和长周期微动数据,其瞬态数据的记录长度不低于1 s,长周期微动数据一般不低于20 min。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 线性观测装置数据采集示意

Fig.2 Schematic of data acquisition for linear observation device

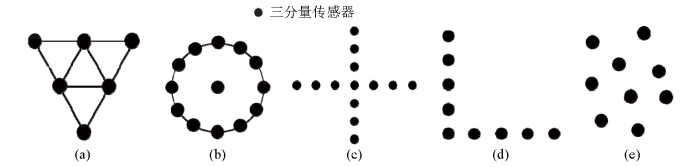
在无法进行线性布置时,也可采用“内嵌三角型”、“同心圆型”、“十字型”、“L型”和“不规则型”进行数据采集,如图3所示,各采集站为分布式低频三分量传感器,无人工激发点,记录三分量长周期微动数据,记录时长一般不低于20 min。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 非线性观测装置数据采集示意

a—内嵌三角形型;b—同心圆型;c—十字型;d—L型;e—不规则型

Fig.3 Schematic of data acquisition for nonlinear observation device

a—embedded triangle type;b—concentric type;c—cross-bonding type;d—L-type;e—irregular type

数据采集时,应尽量减少装置半径范围内的近场干扰,存在不可避免的随机干扰时应增加数据采集时长以获取足够的平稳信号。

2.2 特征曲线提取

多源频率域地震勘探中,单一台阵数据可获取传统方法中同一采集点位置范围的瞬态面波、微动台阵法和微动谱比法数据,如图1所示,基于瞬态面波数据和多点垂直微动数据计算频散特征曲线,基于单点三分量微动数据分析每个采集站的谱比特征曲线。

在线性台阵观测装置下,基于同一台阵瞬态面波数据和微动台阵数据提取的面波速度在不进行方向校正时是存在固定比例的速度差。同时,由于瞬态面波的震源在台阵沿线方向,其提取的频散曲线可视为真速度且在高频段具有更高的收敛性,可靠性更高。所以,两种数据的综合频散曲线可以在低频段通过采用固定比例校正的方式将两种数据源的频散曲线整合。为提高数据处理效率,一般可先计算校正后的综合频散谱,后拾取双源频散特征曲线。瞬态面波和微动台阵的频散谱可被视为一个矩阵,其综合频散谱可用式(1)计算获得。为确保频散谱合成的协调性,主动源合成系数矩阵 $K_{a}$ 和被动源合成系数矩阵 $K_{p}$ 均为大于0的数,且满足式(3)要求。一般地,主动源面波在10 Hz以上频段的数据收敛性较好,可靠性更高,而被动源面波在15 Hz以下频段优势更明显,可靠性更高,主、被动源面波的分界频率可在10~15 Hz之间取值,其系数矩阵内各项数值也将根据分界频率值对应取0或1,工作中可根据实际频散曲线情况选择。

(1)

\begin{array}{l} [\begin{array}{l} D a_{0,0} & \dots & D a_{n F - f, 0} \\ ︙ & ⋱ & ︙ \\ D a_{0, n V e l - 1} & \dots & D a_{n F - f, n V e l - 1} \end{array}] \times [\begin{array}{l} K a_{0} & \dots & K a_{0} \\ ︙ & ⋱ & ︙ \\ K a_{n f - 1} & \dots & K a_{n f - 1} \end{array}] \\ + [\begin{array}{l} D p_{0,0} & \dots & D p_{n F - f, 0} \\ ︙ & ⋱ & ︙ \\ D p_{0, n V e l - 1} & \dots & D p_{n F - f, n V e l - 1} \end{array}] \times [\begin{array}{l} K p_{0} & \dots & K p_{0} \\ ︙ & ⋱ & ︙ \\ K p_{n f - 1} & \dots & K p_{n f - 1} \end{array}] = [\begin{array}{l} D_{0,0} & \dots & D_{n F - f, 0} \\ ︙ & ⋱ & ︙ \\ D_{0, n V e l - 1} & \dots & D_{n F - f, n V e l - 1} \end{array}] \end{array}

式(1)简化后如式(2)所示:

(2)

D_{a} \times K_{a} + D_{p} \times K_{p} = D

式中: $D_{a} = [\begin{array}{l} D a_{0,0} & \dots & D a_{n F - f, 0} \\ ︙ & ⋱ & ︙ \\ D a_{0, n V e l - 1} & \dots & D a_{n F - f, n V e l - 1} \end{array}]$ 表示瞬态面波频散谱;

$D_{p} = [\begin{array}{l} D p_{0,0} & \dots & D p_{n F - f, 0} \\ ︙ & ⋱ & ︙ \\ D p_{0, n V e l - 1} & \dots & D p_{n F - f, n V e l - 1} \end{array}]$ 表示速度校正后的微动台阵频散谱;

$D = [\begin{array}{l} D_{0,0} & \dots & D_{n F - f, 0} \\ ︙ & ⋱ & ︙ \\ D_{0, n V e l - 1} & \dots & D_{n F - f, n V e l - 1} \end{array}]$ 表示综合频散谱;

$K_{a} = [\begin{array}{l} K a_{0} & \dots & K a_{0} \\ ︙ & ⋱ & ︙ \\ K a_{n f - 1} & \dots & K a_{n f - 1} \end{array}]$ 为瞬态面波系数矩阵;

$K_{p} = [\begin{array}{l} K p_{0} & \dots & K p_{0} \\ ︙ & ⋱ & ︙ \\ K p_{n f - 1} & \dots & K p_{n f - 1} \end{array}]$ 为微动台阵系数矩阵;

(3)

K_{a} + K_{p} = [\begin{array}{l} 1 & \dots & 1 \\ ︙ & ⋱ & ︙ \\ 1 & \dots & 1 \end{array}]

。

在非线性台阵观测装置下,因缺乏瞬态面波信息,可基于微动台阵数据直接计算频散谱后再拾取双源频散特征曲线,也可直接计算频散曲线。

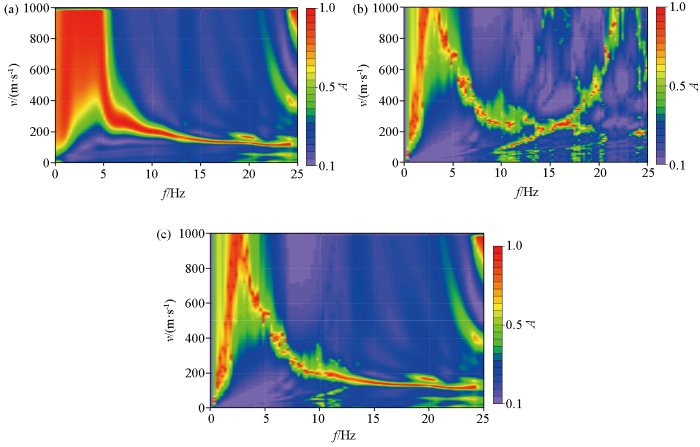
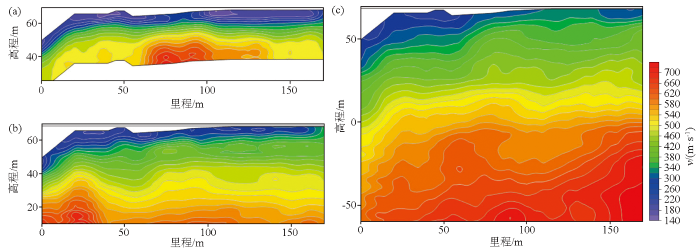
图4为某一线性装置情况下的多源频率域地震数据的瞬态面波频散谱、微动台阵数据频散谱和综合频散谱,对比可以看出瞬态面波频散谱在10 Hz以上具有较为良好的收敛性,主要反应了10 m以内的浅表层速度分布信息,而微动台阵数据频散谱在4~10 Hz频段具有较好的收敛性,其主要体现75 m以内的表层速度分布信息。相比而言,综合频散谱保留了两种数据的有效信息,同时也去除了收敛性不佳频段,结合面波速度一致性的校正,综合频散谱收敛性更高、更有利于技术人员对频散曲线的拾取。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 多源数据的频散谱合并前后对比

a—瞬态面波源频散谱;b—微动台阵源频散谱;c—混合源频散谱

Fig.4 Comparison of dispersion spectrum of multi-source data before and after merging

a—transient surface wave source dispersion spectrum;b—frequency dispersion spectrum of micro motion array source;c—mixed source dispersion spectrum

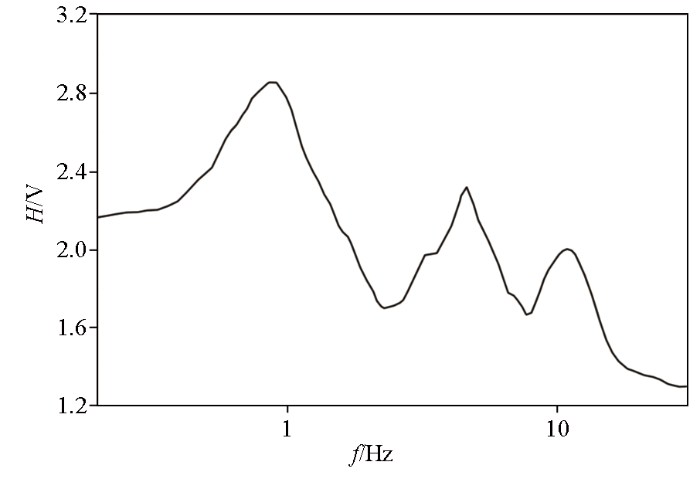
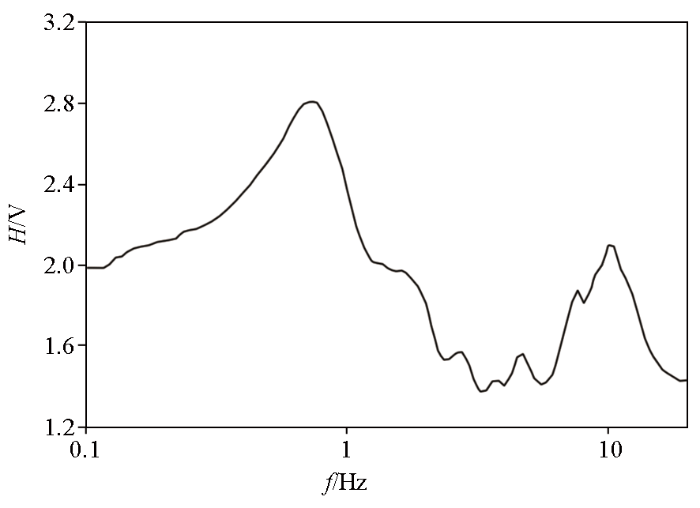
谱比特征曲线是在剔除随机振动干扰信号后计算获得的,其为不同频率信号在水平与垂直两个方向能量的比值,表现为一个具有单个或多个峰的曲线。图5为某处的谱比特征曲线,存在3处明显的峰值间还有多个局部峰值,说明存在3个典型速度分界面。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 微动谱比曲线

Fig.5 Image of microtremor spectral ratio curve

2.3 地层反演

提取特征曲线后,通过经验公式获得地层视横波速度分布情况,或通过地层反演的方式获得地层横波速度分布情况,两种方法均能获取完整的地层结构分布,仅在数值上存在差别,两者数值较为相近。

采用经验公式法时,通过频散特征曲线和谱比特征曲线对地层结构直接给出划分分层,速度值主要依据频散特征曲线的面波速度计算获得,可依据式(4)对剖面上各点的视横波速度进行内插得到视横波速度剖面。其中,地层分层是由式(5)控制,计算深度往往是个迭代过程,因平均速度的计算与地层深度关联,需要不停的尝试,在深度误差允许范围内时确定最终模型深度。特别需要注意的是,基于频散曲线深度转换系数通常取2,而基于谱比曲线峰值深度转换系数通常取4,也可根据勘探范围内的已知信息进行调整。

(4)

V_{s, i} = {(\frac{t_{i} \cdot V_{R, i}^{4} - t_{i - 1} \cdot V_{R, i - 1}^{4}}{t_{i} - t_{i - 1}})}^{1 / 4}

式中: $V_{s, i}$ 为第i频点对应的视横波速度,m/s; $V_{R, i}$ 为第i频点对应的面波相速度,m/s; $t_{i}$ 为第i频点对应的周期,s。

(5)

h_{i} = \frac{V'_{s}}{k \cdot f_{i}}

式中: $f_{i}$ 为第i频点的频率值,Hz; $h_{i} 为第 i$ 频点对应的深度,m; $V'_{s} 为第 i$ 频点对应深度以上地层的平均速度,m/s; $k$ 为深度转换系数,无量纲。

采用地层反演法时,首先需要确定反演的目标函数。本文提出了一种基于两种特征曲线的联合反演,其目标函数如式(6)所示。理想情况下, $S [r_{c} (x), r_{b}]$ 和 $S [H V_{c} (x), H V_{p}]$ 趋于0,目标函数 $F (x)$ 整体趋于0,其 $r_{c}$ 、 $r_{b}$ 、 $H V_{c}$ 、 $H V_{p}$ 均是关于频率 $f$ 的函数。

(6)

F (x)

S [r_{c} (x), r_{b}] \times w_{r b}

S [H V_{c} (x), H V_{p}] \times w_{h v}

(7)

S [r_{c} (x), r_{b}] = \sqrt[]{\frac{\overset{N - 1}{\sum_{j = 0}} {(\frac{r_{c} (f_{i}) - r_{b} (f_{i})}{r_{c} (f_{i})})}^{2}}{N}}

(8)

S [H V_{c} (x), H V_{p}] = \sqrt[]{\frac{\overset{N - 1}{\sum_{j = 0}} {(\frac{H V_{c} (f_{i}) - H V_{p} (f_{i})}{H V_{c} (f_{i})})}^{2}}{N}}

式中: $x$ 为当前测点的一系列模型参数; $r_{c} (x)$ 为理论频散曲线; $r_{b}$ 为实际混合源频散曲线; $H V_{c} (x)$ 为理论谱比曲线; $H V_{p}$ 为实测谱比曲线; $S [r_{c} (x), r_{b}]$ 为 $r_{c} (x)$ 与 $r_{b}$ 的均方差; $S [H V_{c} (x), H V_{p}]$ 为 $H V_{c} (x)$ 与 $H V_{p}$ 的均方差; $w_{r b}$ 、 $w_{h v}$ 为频散曲线和谱比曲线的权重,且满足 $w_{r b} + w_{h v} = 1$ ,一般情况下,可分别取0.7、0.3(频散曲线的正演拟合度较高,谱比曲线相对频散曲线的拟合度稍低),可根据实际数据情况取值(频散曲线与谱比曲线较差者,权重值可适当小一些)。

采用地层反演法时,通常需要基于模型计算特征曲线(频散和谱比),然后结合实测特征计算目标函数,在目标函数与期望误差满足要求后说明模型即为实测地层结构,若不是则对模型进行修正进入下一个迭代过程。反演过程中,如何计算模型的理论特征曲线最为关键,目前采用解析解直接计算频散特征曲线和谱比特征曲线的理论均是基于水平层状介质假设,实际地层尤其是浅表地层应该被看作为非均匀介质,存在横向变化较大时理论特征曲线与实测曲线拟合度有限,勘探精度低。由面波传播理论可知,面波的能量和探测深度主要集中于一个波长范围内,不同波长具有不同的穿透深度。即可认为,非均匀介质中地表某点的特征曲线是由来自不同深度范围的介质在不同频率按椎体形态按一定比例组成的。笔者给出了基于非均匀介质的特征曲线等效水平介质正演方法——动态优选法^[18],如式(9)所示。其特征曲线是关于频率和空间坐标的函数;孔径系数为小于90的角度,45时表示影响区域为以测点为圆心的向下45°角的圆锥体; $λ$ 为优选系数,小于1且趋于1,通常取0.9~1.0之间。该方法在谱比曲线计算时能直观观测出其明显差异,因其地层均是基于面波理论,该方法也适用于频散曲线的计算。

(9)

C (x_{0}, f) = \underset{x_{b} \leq x \leq x_{e}}{m a x} A (x, f) \cdot [1 - λ \frac{2 (x - x_{0})}{x_{e} - x_{b}}]

(10)

x_{b} = x_{0} - 0.25 t a n (θ) V e l (x, z) / f

(11)

x_{e} = x_{0} + 0.25 t a n (θ) V e l (x, z) / f

式中: $A (x, f)$ 为特征曲线; $V e l (x, z)$ 为模型给出的横波速度; $f$ 为频率; $x$ 为当前测点的空间坐标值; $z$ 为当前测点的深度值; $x_{0}$ 为当前测点的横向坐标值; $θ$ 为孔径系数。

以非均匀条件下微动谱比曲线的正演为例,说明动态优选法实施的具体思路:首先,计算测点附近一定影响范围内不同位置的等效水平层状模型的谱比曲线;其次,计算随频率变化的孔径范围和加权系数,通过动态优选法的方式计算测点处的综合谱比曲线,计算流程如下:

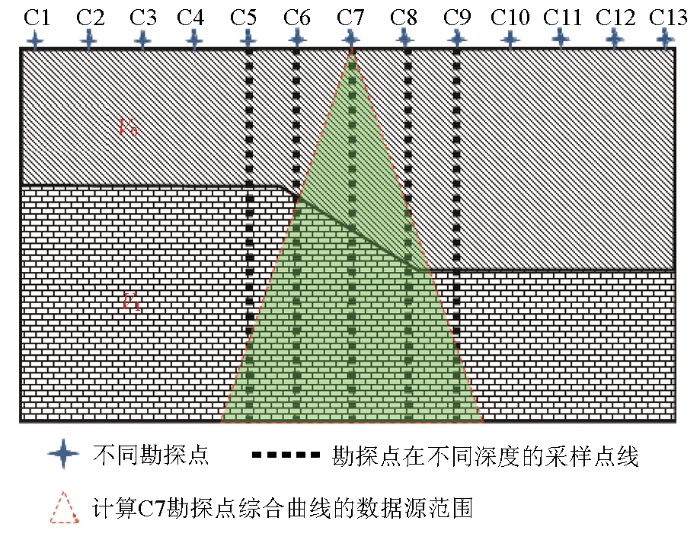
1)建立等效水平层状模型。将非均匀介质按一定距离dx分割成多个独立模型,再将每个独立模型等效为水平层状模型。如图6,可建立两层模型,上层覆盖层速度设为V₀,下层基岩速度设为V₁;

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 动态优选法原始示意

Fig.6 Schematic of equivalent dynamic weighting method

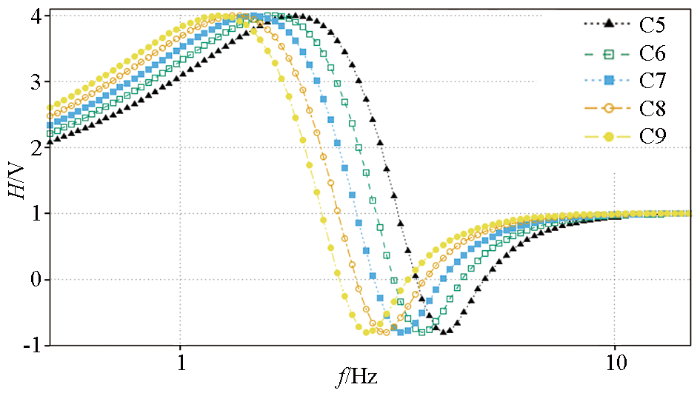
2)计算各等效水平层状模型的谱比曲线。计算步骤1)中按固定间隔dx分割的等效水平层状模型的理论谱比曲线;图6中 C5、C6、C7、C8、C9等5个的等效水平层状模型点对应的理论谱比曲线如图7所示;

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 不同测点谱比曲线

Fig.7 Spectral ratio curves of different measuring points

3)计算模拟点频率f的影响孔径。以当前模拟点为中心,计算不同频率 $f 的影响孔径, 计算公式为 R = 0.25 \times k \times V_{0} / f, 其中 R 为孔径的半径; V_{0} 为覆盖层速度; k$ 为空间转换系数,为一常数,通常可取1;对于C7测点的影响孔径,通过计算可能为C5、C6、C7、C8、C9五处等效水平层状模型点;

4)搜索频率f对应孔径内模拟点数。对孔径内各模拟点的对应频点f,以步骤3)中计算得到的空间R为半径,搜索该范围内符合条件的模拟点的模拟谱比曲线,取频率f对应的谱比值Q_i,1≤i≤n,n为孔径内的模拟点个数。

5)计算f对应孔径内各点权系数。对步骤4)中各点,按各点到所计算模拟点的距离计算权值W_i=1-λr/R,其中r为各点到模拟点的距离,i为孔径内点编号,i≤n,λ为优选系数;

6)各模拟点频率f对应的综合特征值计算。对步骤4)中搜索得到孔径范围内的特征值Q_i,按步骤5)中计算得到的系数W_i,依据大值优选原则,选取孔径范围内的极大值 $C (x_{0}, f) = \underset{x_{b} \leq x \leq x_{e}}{m a x} (Q_{i} \times W_{i})$ ;

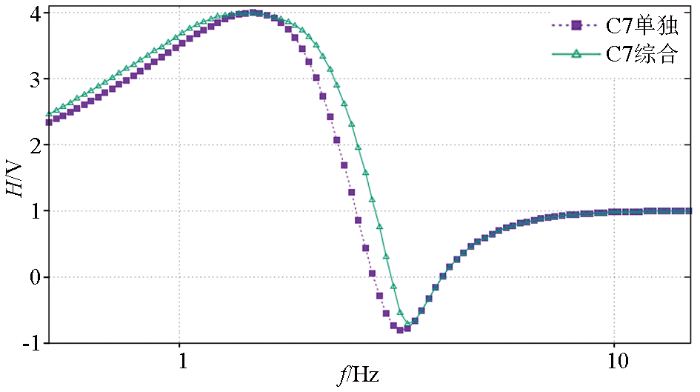
7)综合特征曲线计算。重复步骤3)~6)的过程,计算所有频率f对应的综合特征值,得到综合特征曲线,如图8所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 C7测点综合谱比曲线

Fig.8 C7 comprehensive spectral ratio curve

以上步骤为双层非均匀介质条件下的特征曲线计算简化流程,在实际正演计算中通常更为复杂,不能简单地按照频率进行优选,需先根据模型的层速度信息将频率域的特征曲线转化到深度域,再在深度域进行优选,最终将优选的特征曲线转换到频率域。

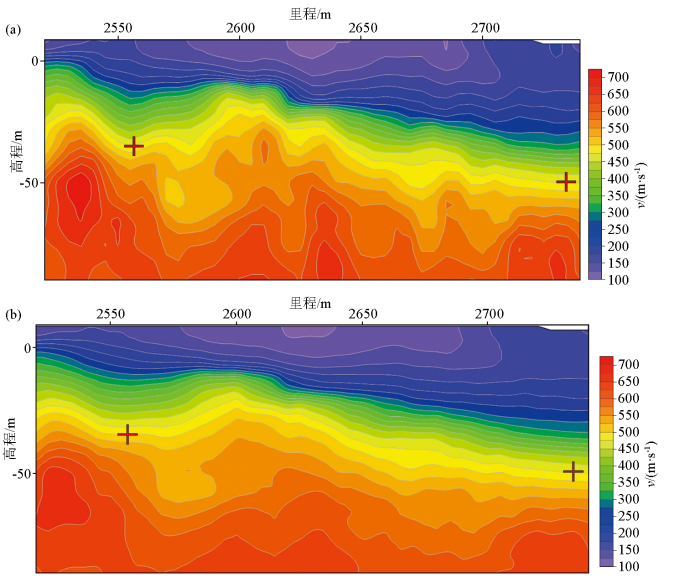
图9为某典型单斜—水平地层探测的结果,测线长200 m,自左向右基岩逐渐变深。该测线的单斜—水平地层结构在测线不同位置的谱比曲线形态上也有所体现,在基岩埋深渐变段谱比曲线为较窄的单峰结构,而末端近似水平段的谱比曲线表现为较宽单峰形态。在进行反演时,分别采用常规方法和前文所述的等效水平介质法进行了联合反演。在里程2 565 m和2 760 m处布置了两个钻孔,钻孔揭示该测段的土石界面(W2与W3风化界线)处的横波速度约为475 m/s,如图中“十”字标所示。在右侧近水平段两种方法反演结果基本一致,而左侧基岩起伏段采用了等效水平介质法进行联合反演的成果所解释的土石界限更准确。成果对比表明非均匀介质模型的反演横波速度剖面对横向的不均匀性灵敏度更高,对基岩探测具有更高的探测精度。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 反演后的横波速度剖面成果

a—基于非均匀介质反演的横波速度剖面;b—基于水平水层层状介质反演的横波速度剖面

Fig.9 The section plan of shear wave velocity after inversion

a—shear wave velocity profile based on inhomogeneous medium inversion;b—shear wave velocity profile based on horizontal water layered medium inversion

3 应用

3.1 地层分层勘察

某铁路大桥段,位于汉江南侧,地表为第四系覆盖,下覆为较厚的圆砾土层,基岩为砂岩,需查明圆砾土层和覆盖层厚度的分布情况。采用了多源频率域地震勘探技术进行勘察,外业采用5 m点距7道接收的采集装置,采集间隔4 ms,采集过程干扰少,数据质量良好,主动源面波数据频散特征典型,被动源三分量微动数据无强随机干扰。

数据处理过程中,为体现不同数据源情况的差异,分别基于“瞬态面波”、“瞬态面波+微动台阵”和“瞬态面波+微动台阵+微动谱比”的数据形式进行了数据处理,如图10所示。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 不同数据源情况下的成果图对比

a—瞬态面波;b—瞬态面波+微动台阵;c—瞬态面波+微动台阵+微动谱比

Fig.10 Comparison of the results of different data sources

a—transient surface wave;b—transient surface wave + micro motion array;c—transient surface wave + micro motion array + micro motion spectral ratio

对比瞬态面波与双源面波(瞬态面波+微动台阵)的成果可见,线内里程60~100 m、高程40~50 m范围存在一局部高速区,在结合微动台阵后,该高速区的精度得到进一步提高,深度方向延伸更深。虽然双源面波形式取得相比瞬态面波更深的效果,但勘探深度约为60 m,没能在整个勘探范围获得基岩的分布情况。从后期的钻孔资料(钻孔入岩10 m左右终孔)可以看出,该区域的从上到下地层有“粉质黏土层—细砂层—细圆砾土层—全风化砂岩层”,这一点可以从谱比特征曲线的峰值规律分辨出,如图11所示。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 勘探测线内的典型谱比特征曲线

Fig.11 Typical spectral ratio characteristic curve in exploration line

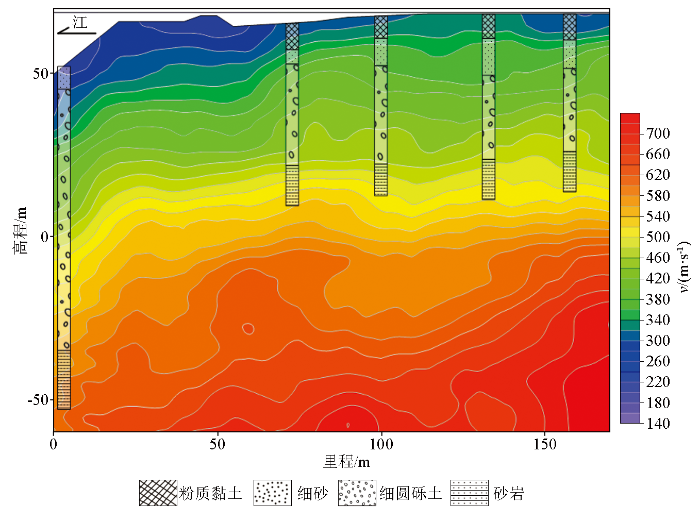
从图11可以发现,存在10.52、7.63、4.71、2.76、1.71、0.73 Hz等6个局部优势峰值频率,根据反演横波速度可按式(5)计算出对应的钻孔揭示的“粉质黏土—细砂层”、“细砂层—细圆砾土层”、“细圆砾土层内部分层”、“细圆砾土层—全风化砂岩”和两个钻孔未揭示的地层界线,1.71 Hz对应着“全风化砂岩—砂岩”界面,0.73 Hz可能对应砂岩与下覆岩层的界线。图12为完整测线的横波速度剖面图,结合钻孔示意图,具有出以下特征:

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 多源频率域地震勘探反演成果与钻孔对比示意

Fig.12 Schematic of comparison between inversion results of multi-source frequency domain seismic wave exploration and boreholes

1)多源频率域地震波法能识别出场地的“粉质黏土层—细砂层—细圆砾土层—全风化砂岩层”地层结构,各地层界线在反演横波速度和谱比曲线的优势频率两个方面具有反应。“粉质黏土—细砂层”界线对应340 m/s速度,“细砂层—细圆砾土层”界线对应380 m/s速度, “细圆砾土层—全风化砂岩”界线对应460 m/s速度;

2)相较于常规单一方法或双源面波法,结合了瞬态面波、微动台阵和微动谱比数据源的多源频率域地震波法的勘探深度更深;

3)勘探精度受起伏地形条件影响,水平地形条件下勘探精度更高。

3.2 隧道洞室探测

武汉市某单位位于繁华市区,旁房屋密集,开展房屋建筑前需对建筑范围内的某洞室进行勘查处理,因为场地有限且周边电磁、机械振动干扰大,常规方法实施困难。洞室位于下覆泥岩内,洞室内部部分充水,经现场探勘后,采用多源频率域地震波法进行探测洞室埋深。

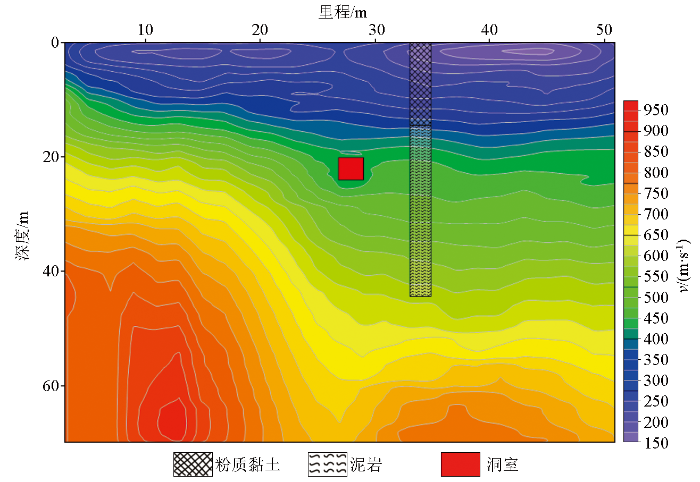
实施过程中,采用线性观测装置,采集站点距2 m,主动源记录长度1 s,采集间隔1 ms,被动源记录长度25 min,采集间隔4 ms,测线长度48 m(里程为3~51 m)。数据采集完成后,基于多点低频三分量传感器获取的主动源和被动源面波信息,综合获取每个测点的频散和谱比特征曲线,在联合建模和反演的基础上提取高分辨率的地层速度信息,反演得到的横波速度剖面如图13所示。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 反演与解释成果

Fig.13 Inversion and interpretation results

从横波速度剖面分析,测线左侧靠近附近小山,基岩埋深总体呈现左浅右深的特点,测线里程27~29 m段埋深20~22 m处存在一相对低速异常,在测线34 m附近有一已知工程钻孔揭示覆盖层14.5 m厚。推测洞室异常规模符合常规洞室特征,埋深与前期调查信息(位于下覆泥岩内)一致。结合成果剖面的整体速度分布特点,基本可以确定目标洞室的具体位置为上述异常位置。

4 结论

多源频率域地震波法是解决复杂城市环境勘探难题的一种有效勘探手段,也适用于常规勘探环境。相比其他方法,其具有天然的抗干扰能力和较强的场地适应性,也存在信噪比越高勘探精度越高的规律。该方法的有效实施,首先要基于场地发育面波等有效波场,其次应避免规律性的近场干扰,成果解释时应结合测线周边构筑物的分布特点进行综合解释。

多源频率域地震波法是建立在瞬态面波、微动台阵和微动谱比的融合利用的基础上的,也不可避免地存在这些方法自身固有的缺点,如存在基岩出露或覆盖层较浅时效果不佳等问题。瞬态面波信息的利用还需建立在直线观测装置下,如何进一步突破装置的限制,实现任意观测装置的3种信号源的多源频率域地震勘探,是今后进一步研究的方向。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Haskell

N A

The dispersion of surface waves on multilayered media

[J]. Bulletin of the Seismological Society of America, 1953, 43(1):17-34.