E-mail Alert Rss
 

物探与化探, 2024, 48(1): 98-104 doi: 10.11720/wtyht.2024.2567

方法研究·信息处理·仪器研制

考虑软矿物纵横比的页岩岩石物理建模及其应用

杨骐羽,1,2, 李景叶1,2, 吴凡1,2, 李文瑾1,2, 崔津铭1,2

1.油气资源与探测国家重点实验室,北京 102249

2.中国石油大学(北京) 地球物理学院,北京 102249

A petrophysical model of shales considering soft-mineral aspect ratios and its application

YANG Qi-Yu,1,2, LI Jing-Ye1,2, WU Fan1,2, LI Wen-Jin1,2, CUI Jin-Ming1,2

1. State Key Laboratory of Petroleum Resource and Prospecting,Beijing 102249,China

2. College of Geophysics,China University of Petroleum(Beijing),Beijing 102249,China

责任编辑: 叶佩

收稿日期: 2022-11-25   修回日期: 2023-09-8  

基金资助: 国家自然科学基金项目(41774131)
国家自然科学基金项目(41774129)
国家重点研发计划项目(2019YFC0312000)

Received: 2022-11-25   Revised: 2023-09-8  

作者简介 About authors

杨骐羽(1999-),博士在读,专业为地质资源与地质工程,研究重点为地震反演与储层预测、页岩气“甜点”预测。Email:2021310418@student.cup.edu.cn

摘要

以往针对页岩储层的岩石物理建模常忽略孔隙类型与软矿物纵横比对弹性模量的影响。本文同时考虑孔隙类型、孔隙形状与软矿物纵横比,建立横向各向同性页岩岩石物理模型:将固体矿物分为硬矿物与软矿物两类,考虑软矿物的各向异性特征与形状变化;基于储层实际情况将孔隙分为粒内孔、有机孔与粒间孔三类,孔隙形状分为硬孔隙与软孔隙两种;最后,利用粒子群法反演输入参数,进一步计算纵横波速度、各向异性参数与岩石力学参数。结合实际资料应用,用已知测井横波速度与各向同性岩石力学计算结果进行对比,结果表明该模型的应用效果较好。

关键词： 软矿物纵横比; 孔隙纵横比; 横向各向同性; 岩石物理模型; 页岩; 横波速度预测

Abstract

Previous petrophysical modeling of shale reservoirs often ignored the influence of pore types and soft-mineral aspect ratios on the elastic modulus.This study built a petrophysical model for transversely isotropic shales considering pore types and shapes,and soft-mineral aspect ratios.In this study,solid minerals were divided into hard and soft minerals,and soft minerals'anisotropic characteristics and shape changes were considered.According to the actual conditions of reservoirs, pores were categorized into intragranular,organic,and intergranular pores,and they were classified into stiff and soft pores based on their shapes.Finally,the input parameters were inverted using the particle swarm optimization algorithm to further calculate compressional and shear wave velocities,anisotropy parameters,and rock mechanical parameters.Combined with the actual data application,the results of this study were compared with the known results of shear wave velocity and isotropic rock mechanical calculation,suggesting that the model in this study is effective.

Keywords： soft-mineral aspect ratio; pore aspect ratio; transverse isotropy; petrophysical model; shale; shear-wave velocity prediction

PDF (3776KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

杨骐羽, 李景叶, 吴凡, 李文瑾, 崔津铭. 考虑软矿物纵横比的页岩岩石物理建模及其应用[J]. 物探与化探, 2024, 48(1): 98-104 doi:10.11720/wtyht.2024.2567

YANG Qi-Yu, LI Jing-Ye, WU Fan, LI Wen-Jin, CUI Jin-Ming. A petrophysical model of shales considering soft-mineral aspect ratios and its application[J]. Geophysical and Geochemical Exploration, 2024, 48(1): 98-104 doi:10.11720/wtyht.2024.2567

0 引言

建立更精确的页岩岩石物理模型,将有助于分析储层物性参数与弹性参数的关系,寻找敏感性参数,开展“甜点”预测等工作。1981年,Jones和Wang[1]提出页岩内部垂直定向排列的裂缝所引起的HTI(horizontal transverse isotropy)各向异性程度远小于由颗粒定向排列导致的VTI(vetical transverse isotropy)各向异性。对于垂向裂缝不发育的页岩储层,通常建立横向各向同性页岩岩石物理模型。

1994年,Hornby等[2]将自相容模型(self compatible model,SCA)和微分等效介质模型(differential equivalent medium model,DEM)推广至各向异性,为各向异性储层岩石物理建模提供理论基础。2007年,原宏壮[3]对Xu-White模型进行改进,将孔隙分为黏土孔隙与砂岩孔隙,建立了各向同性双重孔隙泥质砂岩有效介质模型。Bandyopadhyay[4]、Wu等[5] 与胡起等[6-7]分别考虑到页岩储层中有机质的各向异性与孔隙形状对弹性模量的影响,建立页岩岩石物理模型,但均忽略了黏土的各向异性及其形状的变化。2015年,王璞等[8]认为孔隙形状与矿物形状共同影响着岩石的纵横波速度,建立适用于各向同性介质的S-S模型。2019年,张琦斌等[9]基于各向同性假设,将孔隙分为干酪根中存在的有机孔与混合物中的粒间孔,建立了一种考虑含混合流体干酪根的页岩岩石物理模型,该模型的前提假设限制了模型精度。Ruiz等[10-11]通过实验室测量,证明了岩石基质中存在软孔隙(低孔隙纵横比),分别讨论了软孔隙与单一孔隙纵横比对岩石物理建模的影响,研究说明考虑页岩储层中的孔隙变化是有必要的。此后,桂俊川等[12]、张益明等[13]、刘致水等[14]以不同方法精细描述孔隙形状,建立了不同的岩石物理模型。

考虑到页岩储层的各向异性的特征,“甜点”区的孔隙度一般在0.01附近,且矿物形状与孔隙形状共同影响着储层的弹性模量[3]。本文基于页岩储层的实际地质情况,建立了同时考虑孔隙类型、孔隙形状与软矿物形状的横向各向同性的页岩岩石物理模型,基于粒子群法反演输入参数,开展纵横波速度、各向异性参数与岩石力学参数计算的工作,并结合实际资料进行验证。

1 页岩岩石物理建模及参数反演

1.1 储层特征分析

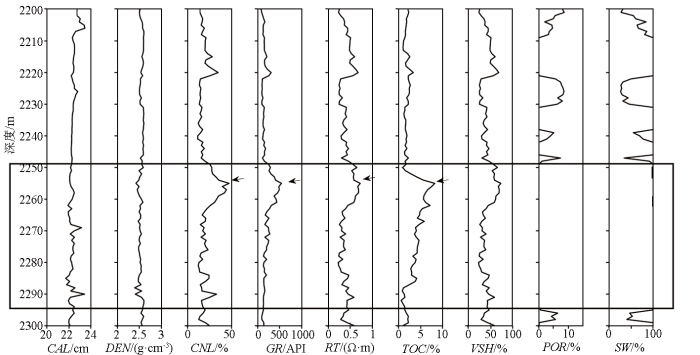
我们针对鄂尔多斯盆地某页岩储层建立岩石物理模型。梁晓伟等[15]对鄂尔多斯盆地页岩储层展开系统研究,其研究区内岩石中存在的主要陆源碎屑矿物成分为石英、长石和黏土矿物,其中石英含量在16.9%~80.4% 之间,斜长石与钾长石的总量一般为 9%~43%,黏土矿物含量在 8%~62% 之间,孔隙度主要介于0.85%~9.57%之间。曹尚等[16]对鄂尔多斯盆地孔隙发育特征展开对比分析,认为页岩储层主要发育着粒间孔、粒内孔和有机孔三类孔隙,其中粒间孔主要发育在黏土矿物与石英、长石等刚性颗粒间,粒内孔主要发育在脆性矿物内,有机孔多发于有机质与黏土矿物的分界面上。

图1为研究工区储层测井曲线,其中,CAL为井径曲线、DEN为密度曲线、CNL为中子孔隙度曲线、GR为自然伽马曲线、RT为电阻率曲线;TOC为干酪根含量曲线;VSH为泥质含量曲线、POR为孔隙度曲线、SW为含水饱和度曲线;图中箭头所指区域为测井曲线指示的“甜点”区。本文选取黑色线框(2 250~2 290 m)区域为研究区进行岩石物理建模。在深度为2 269 m和2 290 m处有明显的扩径现象,可能导致预测精度的降低。目标层内干酪根含量基本高于0.02,具有工业开发价值;孔隙度整体较小,大致在1%附近,含水饱和度较高,大致在99%附近,且变化趋势不大。页岩在微观尺度下黏土、干酪根以及不为球形孔隙的定向排列,使得页岩具有较强的各向异性特征,且页岩储层内部矿物成分和孔隙类型较为复杂。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   测井曲线

Fig.1   Well logging curve


1.2 岩石物理建模框架及其原理

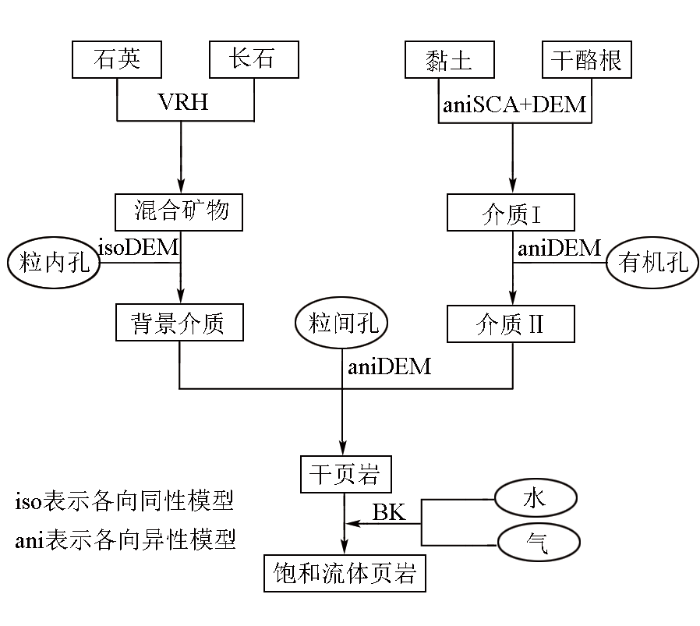
研究区具有孔隙度低、干酪根含量高、泥质含量高的特征,扁平状孔隙、黏土与干酪根的定向排列均使得页岩具有较强的各向异性特征。若考虑过多因素进行岩石物理建模,必将使得模型的输入参数增加,给正演模拟带来一定困难。

页岩储层矿物成分复杂,本文将固体矿物分为脆性矿物(石英与长石)与软矿物(黏土、干酪根)两类。认为脆性矿物表现为各向同性特征,基于VRH平均模量(式1)计算脆性矿物混合物的弹性模量:

MVRH=MV+MR2

式中:MVRH为Voigt上限与Reuss下限的算术平均;MV与MR分别为Voigt基于等应变平均提出的Voigt上限模量[17]和Reuss基于等应力平均提出的Reuss下限模量[18],具体形式如下:

MV=∑i=1NfiMi
1MR=∑i=1NfiMi

式中:fi为各组分的体积含量,Mi为各组分弹性模量。VRH模型将不同组分的矿物均匀混合,通常被用于估算混合物的弹性模量。

考虑黏土与干酪根相互嵌合的实际情况,计算各向异性两相介质混合的弹性模量。对于多相介质混合物, Berryman[19]给出了各向同性多相介质的SCA模型。两相介质混合时,不少学者均发现SCA模型的第二相介质含量需要为40%~60%时,才能保证介质双相流通[3]。因此,SCA模型通常与DEM模型共同使用,建立双相介质;即,先以第二相介质含量为50%利用SCA模型混合,再利用DEM模型调节包含物的含量。参考桂俊川等[12] 计算多相介质等效模量的方法,结合各向异性SCA与DEM模型建立黏土与干酪根混合物(介质I),如式(4)和(5)。

CSCA=∑n=1NvnCn[I+G^(Cn-CSCA)]-1×∑P=1NvP[I+G^ijkl(CP-CSCA)]-1-1
ddv[CDEM(v)]=11-v[Ci-CDEM(v)]×{I+G^ijkl[Ci-CDEM(v)]}-1

式中:vn与Cn分别为第n相的体积含量和刚度矩阵;I为等效的刚度张量;G^ijkl=18π(G-ijkl+G-jkil),G-为与包含物形状相关的刚度张量。对于背景介质为横向各向同性时,可通过线积分表示;CDEM(v)和Ci分别为替换了体积为v后的等效介质的刚度张量和第i相的刚度张量;CSCA与CDEM分别为SCA模型与DEM模型最终输出结果。

建立矿物混合物后,将储层孔隙按其类型分为脆性矿物中存在的粒内孔、介质I中存在的有机孔以及所有矿物混合物中的粒间孔,并利用各向异性DEM模型添加不同种类的孔隙。最后,基于Brown和Korringa[20]提出的各向异性流体替换模型(式6),得到饱和流体页岩岩石物理模型:

Sijkl(dry)-Sijkl(sat)=(Sijαα(dry)-Sijαα0)(Sklαα(dry)-Sklαα0)(Sααββ(dry)-Sααββ0)+(βfl-β0)φ

式中:Sijkl(dry)为岩石骨架的柔度矩阵;Sijkl0为各组分矿物的柔度矩阵;βfl为孔隙流体的可压缩性;β0为矿物的可压缩性;φ为孔隙度;Sijkl(sat)为输出的饱和流体的岩石有效弹性柔度矩阵。基于上述分析及实际储层特征,考虑黏土与干酪根的各向异性特征,储层内孔隙分布的3种类型(粒内孔、有机孔、粒间孔),建立饱和流体页岩岩石物理模型,流程如图2所示,具体步骤如下。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   岩石物理建模流程

Fig.2   Flow chart of petrophysical modeling


1)选取长石的体积模量为37.5 GPa,剪切模量为15 GPa;石英的体积模量为37 GPa,剪切模量为4 GPa。工区内缺少脆性矿物含量,考虑到石英与长石模型差异不大,基于工区地质背景认为工区内4脆性矿物占比为常数(石英在混合矿物中占比为75%)。利用VRH模型计算得到混合矿物的等效模量,并基于各向同性DEM模型在混合矿物中添加粒内孔将其作为背景介质。

2)选取黏土的体积模量为21 GPa,剪切模量为7 GPa;干酪根的体积模量为2.9 GPa,剪切模量为2.7 GPa。干酪根的弹性模量较小,且实际储层中黏土与干酪根是相互嵌合的。考虑软矿物的各向异性特征,基于各向异性SCA+DEM模型建立介质I,并基于各向异性DEM模型中加入有机孔建立介质II。

3)基于各向异性DEM模型,先后将介质II与粒间孔逐步加入到步骤1)所建立的背景介质中,建立干页岩。

4)考虑工区内含水饱和度较高,基于地质背景认为孔隙内的混合流体为水和天然气。基于Reuss等应力平均模型计算混合流体的弹性模量。最后,利用各向异性流体替换模型(BK)进行流体替换,建立饱和流体页岩岩石物理模型。

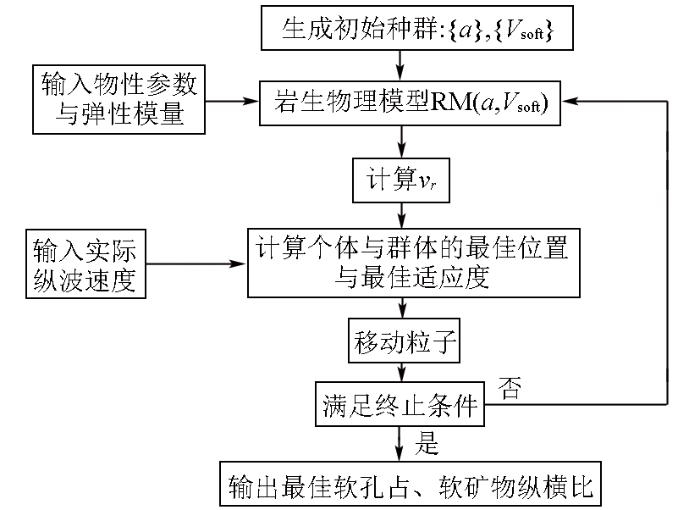
1.3 模型参数的确定及其反演

岩石物理模型的输入参数可以分为各组分含量、各组分模量及描述孔隙与矿物几何形状的三类参数,其中各组分含量(干酪根含量、黏土含量、孔隙度等)可由工区测井曲线获得,各组分模量可通过查阅获得(如表1)。因此,本文所建立的岩石物理模型仅剩下3个参数:软矿物纵横比、孔隙纵横比和不同种类孔隙占比,其中,软矿物纵横比与孔隙纵横比均为地层压力、地应力等共同作用的结果,不易通过选取某一常数等效模拟。

表1   各组分弹性模量[21-22]

Table 1  Elastic modulus of each component[21-22]

组分体积模量/GPa剪切模量/GPa
矿物石英3744
长石37.515
黏土2.92.7
干酪根217
流体天然气0.010
水2.20

新窗口打开| 下载CSV


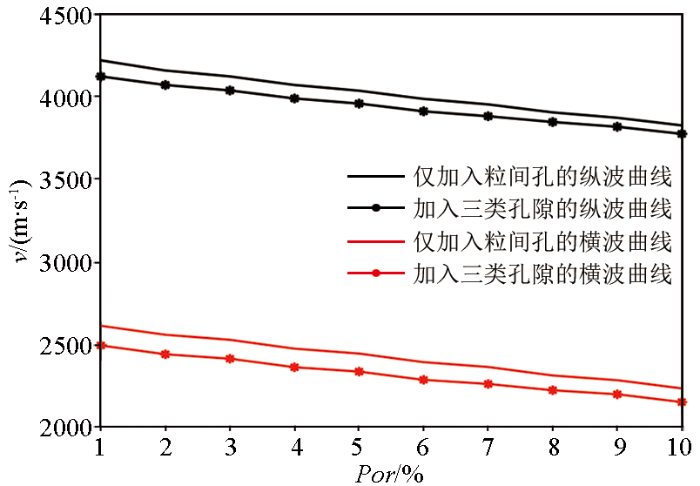
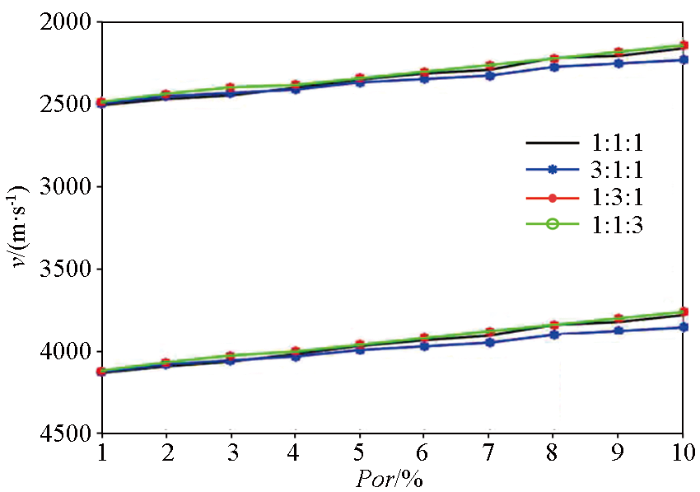
本文将孔隙细分为粒内孔、粒间孔和有机孔三类。将泥质含量设定为0.4,干酪根含量设定位0.05,含水饱和度设定为0.9,密度设定为2.2 g/cm3,分析仅加入粒间孔与加入三类孔隙对速度的影响,如图3所示。图3中黑线和红线分别为仅加入粒间孔得到的纵波速度曲线与横波速度曲线;带星号的黑线和红线分别为本文所提出的将孔隙细分为粒内孔、有机孔与粒间孔得到的纵波速度与横波速度,且三类孔隙占比为1∶1∶1。将孔隙细分后的速度明显降低;因此,有必要将孔隙按照储层实际情况进行细分。三类孔隙占比对速度的影响如图4所示,其中黑线表示粒内孔、有机孔、粒间孔的占比为1∶1∶1,蓝色星线表示占比为3∶1∶1,红色点线表示占比为1∶3∶1,绿色圈线表示占比为1∶1∶3。当孔隙度小于0.05时,纵波速度与横波速度并未受到孔隙占比的变化,其值基本没有变化;当孔隙度大于0.05时,纵波速度与横波速度随着孔隙占比的变化略微波动,但并不明显。基于上述分析,本文参考Xu-White模型,将各类孔隙按矿物在总矿物中的占比进行分配。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   单一孔与三类孔对速度的影响

Fig.3   Effect of single hole and three kinds of hole on velocity


图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   不同孔隙占比对速度的影响

Fig.4   Influence of different pore ratio on velocity


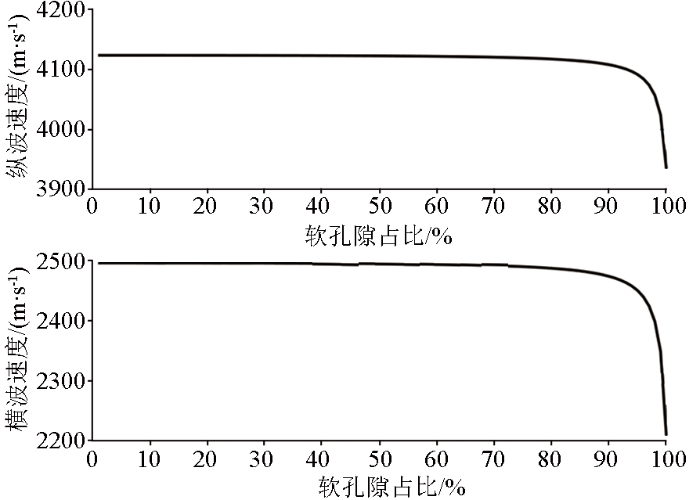
设定与上文相同参数,分析与形状相关的参数对速度和各向异性参数的影响。三类孔隙的孔隙纵横比均由硬孔隙(孔隙纵横比为1)与软孔隙(孔隙纵横比为0.01)加权得到:

α=Vsoft×0.01+(1-Vsoft)×1

式中:α为孔隙纵横比;Vsoft为软孔隙占比。

软孔隙占比越大孔隙越扁平,各向异性越明显。设定软矿物纵横比为0.5,分析软孔隙占比对纵横波速度与Thomsen各向异性参数ε、δ、γ的影响,如图5与图6所示。软孔隙占比小于0.9时,纵横波速度与各向异性参数均对其不敏感;软孔隙占比大于0.9时,纵横波速度与各向异性参数明显降低,即孔隙越扁平,速度变化就越剧烈且各向异性程度越高。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   软孔隙占比对速度的影响

Fig.5   Influence of soft pore ratio on velocity


图6

新窗口打开| 下载原图ZIP| 生成PPT

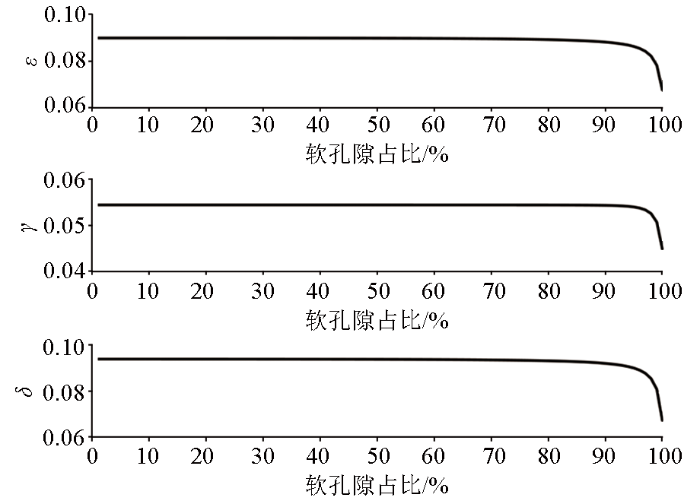
图6   软孔隙占比对Thomsen各向异性参数的影响

Fig.6   Influence of soft pore ratio on Thomsen anisotropy parameters


设定软孔隙纵横比为0.5,分析软矿物纵横比对纵横波速度与各向异性参数的影响,如图7与图8所示。软矿物纵横比与速度呈正相关,随着软矿物的增加,横波速度的变化逐渐缓慢;相比于软孔隙占比,速度对软矿物纵横比更敏感。软矿物纵横比与各向异性参数ε、δ呈负相关,与各向异性参数γ呈正相关,随着软矿物的增加各向异性参数的变化逐渐缓慢;相比于软孔隙占比,各向异性参数也对软矿物纵横比更敏感。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   软矿物纵横比对速度的影响

Fig.7   Influence of soft mineral aspect ratio on velocity


图8

新窗口打开| 下载原图ZIP| 生成PPT

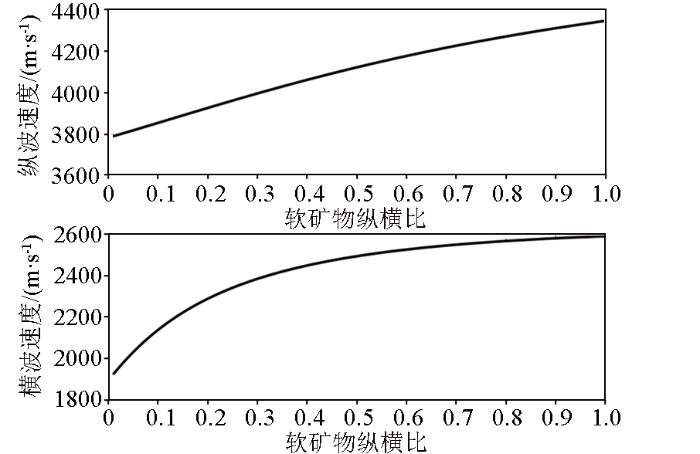
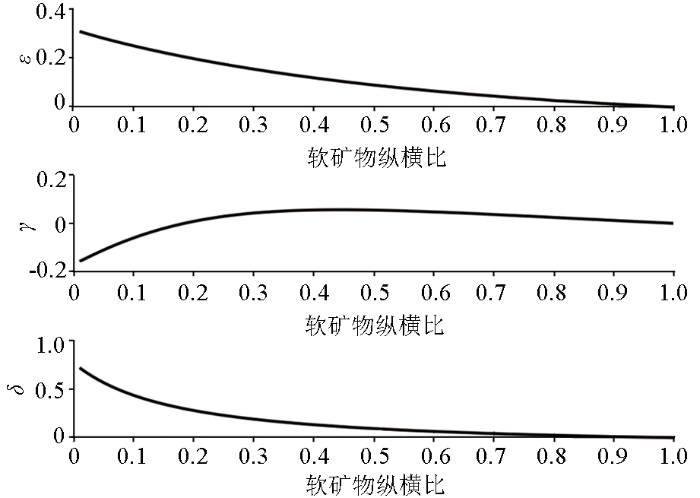
图8   软矿物纵横比对Thomsen各向异性参数的影响

Fig.8   Influence of soft mineral aspect ratio on Thomsen anisotropy parameters


软孔隙占比与软矿物纵横比均对弹性参数较为敏感,在岩石物理建模中不易选取某一常数模拟。本文利用粒子群法反演软矿物纵横比与软孔隙含量,具体流程如图9所示。图9中,a、Vsoft分别为软矿物纵横比与软孔隙占比。首先生成模型输入参数的初始种群,构造的个体最佳适应度与群体最佳适应度更新种群粒子位置,进行粒子群迭代直至满足终止条件,最终输出最佳模型参数软矿物纵横比与软孔隙占比。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   岩石物理参数反演流程

Fig.9   Inversion flow of petrophysical parameters


2 模型测试与应用

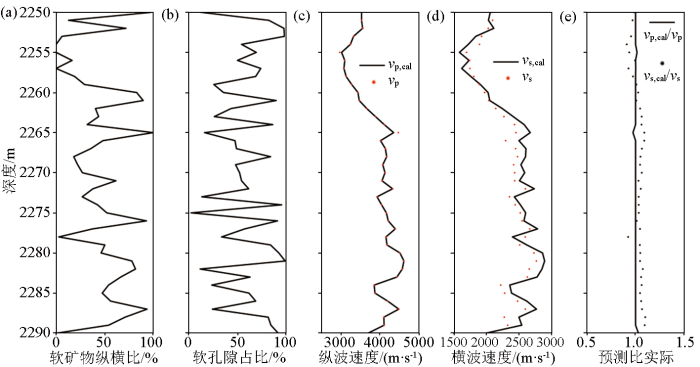
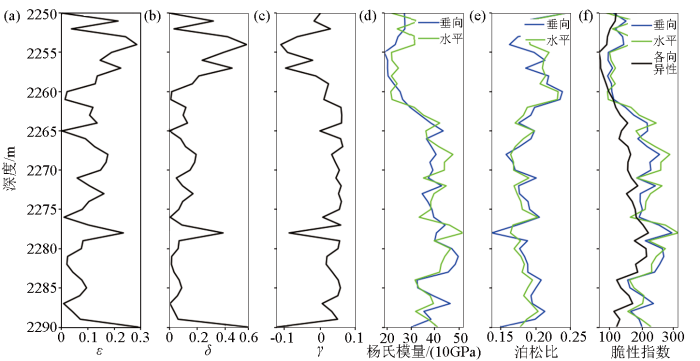
选取工区长7的井资料用于验证岩石物理模型的准确性与适用性。基于粒子群法的模型参数反演结果如图10a、b所示。参考Thomsen 给出的横向各向同性介质弹性参数的表达式(式 8)[23]计算纵横比速度,其结果如图10c~e所示,其中黑色实线与红色点线分别为模型得到的速度曲线和测井得到的速度曲线,图10e中黑色实线与黑色点线分别为模型得到的纵波速度与实际纵波速度的比值和模型得到的横波速度与实际横波速度的比值。由于纵波速度参与构造最佳适应度,模型得到的纵波速度与测井得到的纵波速度基本吻合,其相对误差介于[-0.03,0.03]之间,模型得到的横波速度与测井得到的横波速度吻合度低于纵波速度,但仍具有一定的精度,其相对误差介于[-0.09,0.09]之间。基于Thomsen给出的各向异性参数与等效刚度系数的关系式[20],其结果如图11a~c所示;在测井指示的“甜点”各向异性参数ε、δ明显增加,γ明显降低。基于桂俊川等[24]给出的VTI介质垂直方向与水平方向杨氏模量和泊松比与等效刚度系数的关系式,计算各向异性杨氏模量、泊松比,其结果如图11d、e所示,其中蓝色实线与绿色实线分别为垂直方向与水平方向的岩石力学参数。参考Guo等[25]建立的脆性指数,计算常规基于各向同性假设计算的脆性指数与模型输出的各向异性脆性指数,图11f中黑色实线为各向同性理论计算得到的脆性指数。基于本模型计算得到的各向异性脆性指数与各向同性计算得到的结果具有相同变化趋势,各向异性脆性指数分别从水平方向与垂直方向刻画脆性变化,考虑到储层的各向异性特征使得其具有更多细节变化。

vP0=c33ρ,vS0=c44ρ,ε=c11-c332c33,γ=c66-c442c44,δ=(c13+c44)2-(c33-c44)22c33(c33-c44)

式中:c*为岩石物理模型输出的等效刚度系数;vP0、vS0为沿对称轴方向传播的纵波速度与横波速度;ε、γ、δ为各向异性参数,ε描述了纵波速度在垂直与水平方向的差异,γ描述了水平方向SH波与SV波速度的差异。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   反演曲线与模型得到的速度曲线

Fig.10   Inversion curve and velocity curve obtained by the model


图11

新窗口打开| 下载原图ZIP| 生成PPT

图11   各向异性参数与岩石力学参数计算结果

Fig.11   Anisotropy parameter and rock mechanics parameter calculation results


3 结论

本文同时考虑页岩储层孔隙类型、孔隙形状与软矿物形状,利用粒子群法反演主要参数,建立了一种更精确描述页岩储层的横向各向同性岩石物理模型,开展了基于该模型的横波速度预测、各向异性参数与岩石力学参数计算的工作。结合研究区实际测井资料和常规各向同性岩石力学参数计算结果对比验证,模型输出的波速度具有较高精度,各向异性参数与岩石力学参数具有一定的参考价值,本文所提出的模型对页岩储层具有一定的应用性。

参考文献

Jones L E A, Wang H F.

Ultrasonic velocities in Cretaceous shales from the Williston Basin

[J]. Geophysics, 1981, 46(3):288-297.

DOI:10.1190/1.1441199      URL     [本文引用: 1]

Compressional and shear‐wave velocities were measured in the laboratory from 1 bar to 4 kbar confining pressure for wet, undrained samples of Cretaceous shales from depths of 3200 and 5000 ft in the Williston basin, North Dakota. These shales behave as transversely isotropic elastic media, the plane of circular symmetry coinciding with the bedding plane. For compressional waves, the velocity is higher for propagation in the bedding plane than at right angles to it, and the anisotropy is greater for the 5000-ft shale. For shear waves, the SH‐wave perpendicular to bedding and the SV‐wave parallel to bedding propagate with the same speed, which is about 25 percent lower than that for the SH‐wave parallel to bedding. In general, compressional and shear velocities are higher for the indurated 5000-ft shale than for the friable 3200-ft shale. All velocities increase with in‐increasing confining pressure to 4 kbar. The 3200-ft shale exhibits velocity hysteresis as a function of pressure, whereas this effect is almost nonexistent for the 5000-ft shale. Many features of the dependence of velocity on pressure can be explained by consideration of effective pressure and the degree of water saturation. For both shales, laboratory compressional wave velocities are on average 10 percent higher than log‐derived velocities. The discrepancy cannot be explained completely, but likely contributing factors are sampling bias, velocity dispersion, and formation damage in situ.

Hornby B E, Schwartz L M, Hudson J A.

Anisotropic effective-medium modeling of the elastic properties of shales

[J]. Geophysics, 1994, 59(10):1570-1583.

DOI:10.1190/1.1443546      URL     [本文引用: 1]

Shales are complex porous materials, normally consisting of percolating and interpenetrating fluid and solid phases. The solid phase is generally comprised of several mineral components and forms an intricate and anisotropic microstructure. The shape, orientation, and connection of the two phases control the anisotropic elastic properties of the composite solid. We develop a theoretical framework that allows us to predict the effective elastic properties of shales. Its usefulness is demonstrated with numerical modeling and by comparison with established ultrasonic laboratory experiments. The theory is based on a combination of anisotropic formulations of the self‐consistent (SCA) and differential effective‐medium (DEM) approximations. This combination guarantees that both the fluid and solid phases percolate at all porosities. Our modeling of the elastic properties of shales proceeds in four steps. First, we consider the case of an aligned biconnected clay‐fluid composite composed of ellipsoidal inclusions. Anisotropic elastic constants are estimated for a clay‐fluid composite as a function of the fluid‐filled porosity and the aspect ratio of the inclusions. Second, a new processing technique is developed to estimate the distribution of clay platelet orientations from digitized scanning electron microphotographs (SEM). Third, the derived clay platelet distribution is employed to estimate the effective elastic parameters of a solid comprising clay‐fluid composites oriented at different angles. Finally, silt minerals are included in the calculations as isolated spherical inclusions.

原宏壮. 各向异性介质岩石物理模型及应用研究[D]. 北京: 中国石油大学(北京), 2007.

[本文引用: 3]

Yuan H Z. Study of anisotropic rock physics model and application[D]. Beijing: China University of Petroleum, 2007.

[本文引用: 3]

Bandyopadhyay K. Seismic anisotropy-geological causes and its implications to reservior geophysics[D]. Stanford University, 2009.

[本文引用: 1]

Wu X, Chapman M, Li X Y, et al.

Anisotropic elastic modeling for organic shales

[C]// 74th Conference and Exhibition,EAGE,Extended Abstracts, 2012.

[本文引用: 1]

胡起, 陈小宏, 李景叶.

基于单孔隙纵横比模型的有机页岩横波速度预测方法

[J]. 地球物理学进展, 2014, 29(5):2388-2394.

[本文引用: 1]

Hu Q, Chen X H, Li J Y.

Shear velocity prediction for organic shales based on the single aspect ratio model

[J]. Progress in Geophysics, 2014, 29(5):2388-2394.

[本文引用: 1]

胡起. 页岩气储层岩石物理模型的构建及其应用[D]. 北京: 中国石油大学(北京), 2014.

[本文引用: 1]

Hu Q. Construction and application of the rock physics model for shale gas reservoirs[D]. Beijing: China University of Petroleum, 2014.

[本文引用: 1]

王璞, 吴国忱.

基于自相容近似的致密储层岩石物理建模

[J]. 地球物理学进展, 2015, 30(5):2233-2238.

[本文引用: 1]

Wang P, Wu G C.

The rock physics modeling for tight reservoir based on the self-consistent approximation

[J]. Progress in Geophysics, 2015, 30(5):2233-2238.

[本文引用: 1]

张琦斌, 郭智奇, 刘财, 等.

针对有机质微观特性的页岩储层岩石物理建模及应用

[J]. 地球物理学进展, 2018, 33(5):2083-2091.

[本文引用: 1]

Zhang Q B, Guo Z Q, Liu C, et al.

Rock physics model and its applications in the Longmaxi shale based on the quantification of microstructural properties of organic matter

[J]. Progress in Geophysics, 2018, 33(5):2083-2091.

[本文引用: 1]

Ruiz F, Azizov I.

Tight shale elastic properties using the soft-porosity and single aspect ratio models

[C]// SEG Technical Program Expanded Abstracts 2011,Society of Exploration Geophysicists, 2011:2241-2245.

[本文引用: 1]

Ruiz F, Cheng A.

A rock physics model for tight gas sand

[J]. The Leading Edge, 2010, 29(12):1484-1489.

DOI:10.1190/1.3525364      URL     [本文引用: 1]

Tight gas reservoirs are often defined as gas-bearing sandstones or carbonates having in-situ permeabilities to gas less than 0.1 mD (Holditch, 2006; Smith et al., 2009). Tight gas reservoir rocks can be at different in-situ physical conditions: deep or shallow; over- or underpressured; high temperature or low temperature; and under different stress states. The reservoir-forming rock can have different textures such as shaley and silty unconsolidated sandstones or clean-cemented sandstones. These different rocks produce gas at low rates. Tight reservoir rocks can be blanket or lenticular, homogeneous or heterogeneous, and can contain a single layer or multiple layers, be fractured or unfractured, and mainly produce dry natural gas.

桂俊川, 马天寿, 陈平.

横观各向同性页岩岩石物理模型建立——以龙马溪组页岩为例

[J]. 地球物理学报, 2020, 63(11):4188-4204.

DOI:10.6038/cjg2020N0294      [本文引用: 2]

在龙马溪页岩微观物性特征分析的基础上，综合利用测井解释、微观测试分析资料，建立了一种适用于龙马溪页岩的横观各向同性岩石物理模型，该模型建模过程：将各向异性SCA和DEM模型联合模拟得到的黏土和干酪根混合物作为背景介质；采用SCA模型对脆性矿物混合物进行模拟，利用各向异性DEM将脆性矿物混合物添加到背景介质；进一步将空孔隙添加到页岩基质，并利用Brown-Korringa模型进行各向异性条件下的流体替换，从而得到横观各向同性页岩岩石物理模型.通过对四川盆地A井龙马溪页岩进行岩石物理建模分析，计算了孔隙纵横比、纵横波速、各向异性系数和弹性参数，检验了模型的准确性.研究结果表明：矿物颗粒和孔隙纵横比是影响模型精度的关键参数，黏土和干酪根颗粒纵横比为0.05，图像识别获得的脆性矿物颗粒纵横比主要分布于0.45~1.0（集中分布于0.5~0.85），横波波速反演获得的孔隙纵横比主要分布于0.1~0.3（平均值约为0.22）；模型预测和实测纵波波速之间误差为-2.40%~2.21%（平均绝对误差仅1.20%），预测和实测横波波速之间误差为-1.93%~1.42%（平均绝对误差仅0.64%），证实了本文模型的准确性和精度.本文模型能够准确计算页岩5个独立的刚度系数，为页岩弹性参数、声波波速、各向异性和脆性分析提供了有效手段，也为后续地球物理和工程地质参数分析提供了重要依据.

Gui J C, Ma T S, Chen P.

Rock physics modeling of transversely isotropic shale:an example of the Longmaxi formation in the Sichuan basin Chinese

[J]. Chinese Journal of Geophysics, 2020, 63(11):4188-4204.

[本文引用: 2]

张益明, 秦小英, 郭智奇, 等.

针对致密砂岩气储层复杂孔隙结构的岩石物理模型及其应用

[J]. 吉林大学学报:地球科学版, 2021, 51(3):927-939.

[本文引用: 1]

Zhang Y M, Qin X Y, Guo Z Q, et al.

Petrophysical model for complex pore structure and its applications in tight sand gas reservoirs

[J]. Journal of Jilin University:Earth Science Edition, 2021, 51(3):927-939.

[本文引用: 1]

刘致水, 包乾宗, 刘俊州, 等.

一种简化的二维规则多边形孔隙岩石物理模型

[J]. 石油地球物理勘探, 2022, 57(1):140-148.

[本文引用: 1]

Liu Z S, Bao Q Z, Liu J Z, et al.

A simplified 2D petrophysical model for regular polygon pores

[J]. Oil Geophysical Prospecting, 2022, 57(1):140-148.

[本文引用: 1]

梁晓伟, 关梓轩, 牛小兵, 等.

鄂尔多斯盆地延长组7段页岩油储层储集性特征

[J]. 天然气地球科学, 2020, 31(10):1489-1500.

[本文引用: 1]

Liang X W, Guan Z X, Niu X B, et al.

Reservoir characteristics of shale oil in Chang 7 Member of Yanchang Formation,Ordos Basin

[J]. Natural Gas Geoscience, 2020, 31(10):1489-1500.

[本文引用: 1]

曹尚, 李树同, 党海龙, 等.

鄂尔多斯盆地东南部长7段页岩孔隙特征及其控制因素

[J]. 新疆石油地质, 2022, 43(1):11-17.

[本文引用: 1]

Cao S, Li S T, Dang H L, et al.

Pore characteristics and controlling factors of Chang 7 shale in Southeastern Ordos Basin

[J]. Xinjiang Petroleum Geology, 2022, 43(1):11-17.

[本文引用: 1]

Voigt W.

Lehrbuch der Kristallphysik:Teubner

[M]. Leipzig, 1928:1-20.

[本文引用: 1]

Reuss A.

Berechnung der flieβgrenze von mischkristallen auf grund der plastizitätsbedingung für einkristalle

[J]. ZAMM-Journal of Applied Mathematics and Mechanics, 1929, 9(1):49-58.

DOI:10.1002/zamm.v9:1      URL     [本文引用: 1]

Berryman J G.

Single-scattering approximations for coefficients in Biot's equations of poroelasticity

[J]. The Journal of the Acoustical Society of America, 1992, 91(2):551-571.

DOI:10.1121/1.402518      URL     [本文引用: 1]

Three single-scattering approximations for coefficients in Biot’s equations of poroelasticity are considered: the average T-matrix approximation (ATA), the coherent potential approximation (CPA), and the differential effective medium (DEM). The scattering coefficients used here are exact results obtained previously for scattering from a spherical inclusion of one Biot material imbedded in another otherwise homogeneous Biot material. The CPA has been shown previously to guarantee that, if the coefficients for the scattering materials satisfy Gassmann’s equation, then the effective coefficients for the composite medium satisfy Brown and Korringa’s generalization of Gassmann’s equation. A collection of similar results is obtained here showing that the coefficients derived from ATA, CPA, or DEM all satisfy the required conditions for consistency. It is also shown that Gassmann’s equation will result from any of these single-scattering approximations if the collection of scatterers includes only spheres of fluid and of a single type of elastic solid.

Brown R J S, Korringa J.

On the dependence of the elastic properties of a porous rock on the compressibility of the pore fluid

[J]. Geophysics, 1975, 40(4):608-616.

DOI:10.1190/1.1440551      URL     [本文引用: 2]

An equation is derived for the dependence of the elastic properties of a porous material on the compressibility of the pore fluid. More generally, the elastic properties of a container of arbitrary shape are related to the compressibility of the fluid filling a cavity in the container. If the pore system or cavity under consideration is filled with a fluid of compressibility [Formula: see text], the compressibility κ* of the closed container is given by [Formula: see text] Here [Formula: see text] is the compressibility of the container with the fluid pressure held constant in the interconnected pore system or cavity. Fluids in other pores or cavities not connected with the one in question contribute to the value of [Formula: see text]. ϕ is the porosity, i.e., the volume fraction corresponding to the pore system or cavity in question. The equation contains two distinct effective compressibilities, [Formula: see text] and [Formula: see text], of the material exclusive of the pore fluid. When this material is homogeneous, one has [Formula: see text], and the equation reduces to a well‐known relation by Gassmann. For the other elastic properties, we also obtain expressions which generalize Gassmann’s work and which also differ from it only in the appearance of [Formula: see text] instead of [Formula: see text] in one term. Our result is intimately related to the reciprocity theorem of elasticity. Special cases are discussed.

Blangy,Jean-Pierre Dominique. Integrated seismic lithologic interpretation:The petrophysical basis.(Volumes I and II)[D]. Stanford University,1992.

[本文引用: 2]

Carmichael R S. Practical handbook of physical properties of rocks and minerals(1988)[M]. CRC Press, 2017.

[本文引用: 2]

Thomsen L.

Weak elastic anisotropy

[J]. Geophyscis, 1986, 51(10):1954-1966.

[本文引用: 1]

桂俊川, 陈平, 马天寿.

正交各向异性岩石弹性参数的空间展布

[J]. 西南石油大学学报:自然科学版, 2019, 41(3):13-28.

[本文引用: 1]

Gui J C, Chen P, Ma T S.

The spatial distribution of elastic parameters of Orthotropic Rocks

[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2019, 41(3):13-28.

[本文引用: 1]

Guo Z Q, Chapman M, Li X Y.

A shale rock physics model and its application in the prediction of brittleness index,mineralogy,and porosity of the Barnet Shale

[C]// SEG Technical Program Expanded Abstracts 2012,Society of Exploration Geophysicists, 2012:1-5.

[本文引用: 1]

/

〈 〉

京ICP备05055290号-3
版权所有 © 2021《物探与化探》编辑部
通讯地址：北京市学院路29号航遥中心 邮编：100083
电话：010-62060192；62060193 E-mail：whtbjb@sina.com , whtbjb@163.com