E-mail Alert Rss
 

物探与化探, 2023, 47(5): 1236-1249 doi: 10.11720/wtyht.2023.1489

方法研究·信息处理·仪器研制

山峰对电性源地面瞬变电磁响应的影响及校正方法

周钟航,, 张莹莹,

新疆大学 地质与矿业工程学院,新疆 乌鲁木齐 830047

Correction of the influence of mountains on grounded-source transient electromagnetic responses

ZHOU Zhong-Hang,, ZHANG Ying-Ying,

School of Geology and Mining Engineering, Xinjiang University, Urumqi 830047, China

通讯作者: 张莹莹(1989-),女,副教授,博士,主要从事瞬变电磁场的理论与应用研究工作。Email:zhangyy19890423@163.com

责任编辑: 叶佩

收稿日期: 2022-09-29   修回日期: 2022-10-30  

基金资助: 新疆维吾尔自治区天池博士计划项目

Received: 2022-09-29   Revised: 2022-10-30  

作者简介 About authors

周钟航(1998-),男,在读硕士,研究方向为瞬变电磁数值建模与应用。Email:zhou1229hang@163.com

摘要

在山区进行应用电性源瞬变电磁法勘探易受复杂地形影响,瞬变电磁响应会产生畸变,给数据解释造成困难。为此,基于三维非结构时间域有限元算法,开展了地形效应影响规律和校正方法的研究。首先,利用非结构四面体网格对山峰地形进行精细刻画,计算多种带地形模型响应,分析地形效应的影响规律;然后,基于电磁场线性叠加原理提出地形效应校正方法,根据实际高程数据建立山峰地电模型,通过三维正演计算出山峰模型响应,将山峰模型响应减去平坦大地模型响应得到地形响应,再从总响应中剔除地形响应,获得地形校正后的瞬变电磁响应。研究表明:山峰地形对瞬变电磁响应的影响主要集中在早期,随着时间推移,影响逐渐减弱;地形效应主要集中于山体附近,影响强度取决于测点距山顶的距离;影响范围与响应幅值与山体规模成正比;相对高阻山体的地形影响强度更大。通过设计多种带地形简单规则异常体模型进行仿真,发现经过校正的瞬变电磁响应与直接正演的响应吻合较好,在一定程度上能够有效消除地形效应。对地形效应影响和校正方法的研究,可为复杂地形地区瞬变电磁数据处理解释提供参考。

关键词： 电性源瞬变电磁法; 山峰; 地形效应; 地形校正方法; 三维正演

Abstract

The grounded-source transient electromagnetic (TEM) method, which enjoys the advantages of high topographic adaptability and large exploration depths, is suitable for deep resource exploration in mountainous areas. However, the TEM responses can be distorted due to topographic effects, causing great difficulties in data interpretation. This study investigated the influence patterns and correction method of topographic effects based on the three-dimensional unstructured time-domain finite element method. First, this study conducted the fine-scale description of mountains using unstructured tetrahedral grids, calculated the response of various topographic models, and analyzed the influence patterns of topographic effects. Then, it proposed a correction method for topographic effects based on the principle of the linear superposition principle of electromagnetic fields, established a geoelectric model of mountains according to the actual elevation data, and calculated the model responses through three-dimensional forward modeling. Subsequently, this study determined the topographic responses by subtracting the flat Earth model responses from the mountain model responses and then obtained the corrected TEM responses by removing the topographic responses from the total responses. The results are as follows: (1) The influence of mountains on the TEM responses is concentrated in the early stage and weakens gradually with time; (2) The topographic effects are concentrated near mountains, and their intensity depends on the distance of survey points from mountain peaks; (3) The influencing range and response amplitude of mountains are proportional to the mountain scale. In other words, a larger mountain scale corresponds to a larger influencing range and higher response amplitude; (4) Mountains with relatively high resistivity show more intense topographic influence. As shown by multiple models with simple and regular topographic anomalies, the corrected TEM responses, which match well with the responses from direct forward modeling, can effectively eliminate topographic effects to a certain extent. The research on the influence and correction method of topographic effects can be used as a reference for the processing and interpretation of TEM data of areas with complex terrain.

Keywords： grounded-source transient electromagnetic method; hill; topographic effect; terrain correction; three-dimensional forward modeling

PDF (5591KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

周钟航, 张莹莹. 山峰对电性源地面瞬变电磁响应的影响及校正方法[J]. 物探与化探, 2023, 47(5): 1236-1249 doi:10.11720/wtyht.2023.1489

ZHOU Zhong-Hang, ZHANG Ying-Ying. Correction of the influence of mountains on grounded-source transient electromagnetic responses[J]. Geophysical and Geochemical Exploration, 2023, 47(5): 1236-1249 doi:10.11720/wtyht.2023.1489

0 引言

瞬变电磁法(TEM)是一种建立在电磁感应原理基础上的人工源电磁探测方法,该法首先发射大功率一次电磁信号,然后在断电间歇观测导电大地中感应涡流产生的二次电磁场,通过分析二次场的空间和时间分布特征获得地下电性结构信息[1]。目前,瞬变电磁法以其探测效率高、收发装置灵活、勘探成本低、分辨率相对较高等优点,广泛应用于矿产资源勘查、煤矿水文地质调查、油气资源探查、采空区探测、隧道勘察等领域[2⇓⇓⇓⇓⇓-8]。

近年来,随着我国经济的快速发展,对矿产资源的需求量不断增加,找矿工作正从地形相对平坦的地区逐渐转移至地形切割剧烈的山区。但是,在山区开展瞬变电磁工作时,复杂地形会造成瞬变电磁响应畸变,这种畸变通常称为地形效应,若直接对采集到的数据进行处理与解释,会给解释结果带来较大误差[9⇓⇓-12]。因此,消减地形效应影响,有助于提高复杂地形地区瞬变电磁勘探精度,获得更好的地质效果。国内外学者很早就注意到地形会给瞬变电磁数据带来很大影响,并开展了消除地形效应的相关研究工作[13⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-29]。

目前的地形效应校正方式主要可分为两类,一类是比值校正法,另一类是带地形反演方法。总的来说,比值校正法是基于经验校正系数,对视电阻率参数进行归位的一种校正手段,该类方法的主要特点是校正速度快,但校正效果依赖于校正经验系数的选取,且校正精度一般不高。近些年,随着瞬变电磁法正反演技术和计算机软硬件的发展,带地形反演方法得以实现,这类方法在选取合适的初始模型以及参数的情况下可以很好地恢复复杂地形情况下地下异常体的真实信息,但计算时长普遍较长,不能满足实际工作中快速解译的需求。为了兼顾地形影响校正的效率与精度,便于在生产中推广使用,本文在电磁场线性叠加理论的基础上,从瞬变电磁响应本身出发,提出一种以瞬变响应为校正参量的地形效应校正方法,以期在复杂地形条件下快速恢复地下异常的真实响应。

1 三维正演理论

本文采用非结构时间域有限元算法进行三维正演模拟。首先从时间域麦克斯韦方程出发,考虑到位移电流远小于传导电流时,可以忽略位移电流[30],得到时间域电场扩散方程:

$\frac{1}{\mu} \nabla \times \nabla \times \boldsymbol{e}(\boldsymbol{r}, t)+\sigma \frac{\partial \boldsymbol{e}(\boldsymbol{r}, t)}{\partial t}+\frac{\partial \boldsymbol{j}_{\mathrm{s}}(\boldsymbol{r}, t)}{\partial t}=0,$

式中:μ为介质磁导率;∇为矢量微分算子;e(r,t)为r处t时刻的电磁场;σ为介质电导率;js(r,t)为源电流密度。采用非结构四面体网格对整个地电模型进行剖分,并对发射源、测点、地形和异常体位置进行局部网格加密处理,然后利用矢量插值基函数对时间域电磁扩散方程进行空间离散。四面体单元任意位置的电场为[31]

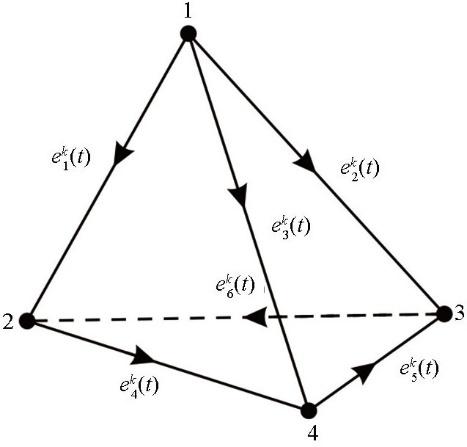
$\boldsymbol{e}^{k}(\boldsymbol{r}, t)=\sum_{i=1}^{6} e_{i}^{k}(t) \boldsymbol{n}_{i}^{k}(\boldsymbol{r}),$

式中:eik(t)为第k个单元的第i条棱边上的切向电场值(图1);nik(r)为第k个单元的第i条棱边的矢量插值基函数。式(2)可以自动满足电场散度为零的条件,即可以自动满足单元面上电场切向分量保持连续。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   四面体单元棱边电场分布

Fig.1   Edged electrical fields in a tetrahedral element


利用Galerkin方法离散式(1),建立有限元控制方程

$\boldsymbol{A} \frac{\mathrm{d} \boldsymbol{e}(\boldsymbol{r}, t)}{\mathrm{d} t}+\boldsymbol{B} \boldsymbol{e}(\boldsymbol{r}, t)+S=0,$

式中:A为单元质量矩阵;B为单元刚度矩阵;S为电流源项。对于每一个矢量四面体单元,可分别表示为

$\boldsymbol{A}_{i, j}^{k}=\iiint_{V^{k}} \sigma^{k} \boldsymbol{n}_{i}^{k}(\boldsymbol{r}) \boldsymbol{n}_{j}^{k}(\boldsymbol{r}) \mathrm{d} V,$
$\boldsymbol{B}_{i, j}^{k}=\frac{1}{\mu} \iiint_{V^{k}}\left(\nabla \times \boldsymbol{n}_{i}^{k}(\boldsymbol{r})\right) \cdot\left(\nabla \times \boldsymbol{n}_{j}^{k}(\boldsymbol{r})\right) \mathrm{d} V,$
$S_{i}^{k}=\iiint_{V^{k}} \boldsymbol{n}_{i}^{k}(\boldsymbol{r}) \cdot \frac{\partial \boldsymbol{j}_{\mathrm{s}}(\boldsymbol{r}, t)}{\partial t} \mathrm{~d} V,$

式中:Vk为第k个单元的体积。利用非结构四面体网格可以灵活离散的特点,本文将接地导线分解成若干段导线,每段导线可以近似视为电偶极子,每个电偶极子可以表示为

$\boldsymbol{j}_{\mathrm{s}}(\boldsymbol{r}, t)=I(t) \delta\left(\boldsymbol{r}-\boldsymbol{r}_{\mathrm{s}}\right) \boldsymbol{u} \mathrm{d} l,$

式中:I(t)为t时刻电流强度;δ为脉冲函数;r为发射源位置;rs为电偶极子的空间位置坐标;u为电流方向;dl是电偶极子穿过四面体单元长度。采用二阶后退欧拉离散格式对式(3)进行时间离散,可得无条件稳定的隐式差分方程:

$(3 \boldsymbol{A}+2 \Delta t \boldsymbol{B}) \boldsymbol{e}^{m+2}=\boldsymbol{A}\left(4 \boldsymbol{e}^{m+1}-\boldsymbol{e}^{m}\right)-2 \Delta t \boldsymbol{S}^{m+2}, $

式中:Δt为时间步长;em为m时刻的电场;Sm为m时刻的源项。

为了满足电磁波在空间中传播的衰减规律,需要在足够远的网格边界上设置切向电场为零。本文采用齐次狄利克雷边界条件来保证无穷远处切向电场为零:

$e|\Gamma =0,$

式中:Γ表示计算区域的外边界。设置初始条件为直流电场eDC,求解直流电场方程得到各节点上的电位;通过求取棱边方向上的电位梯度获得棱边上的eDC后,利用直接求解器Pardiso求解式(8),获得不同时刻的空间电场分布;最后,根据法拉第电磁感应定律计算测点处的磁场响应。

2 山峰影响分析

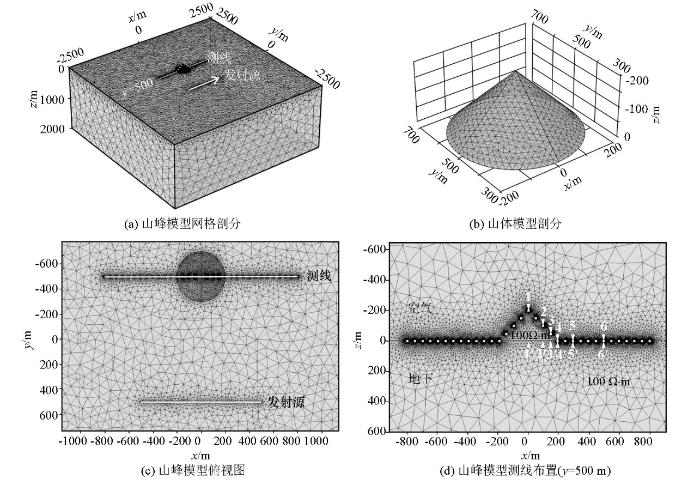
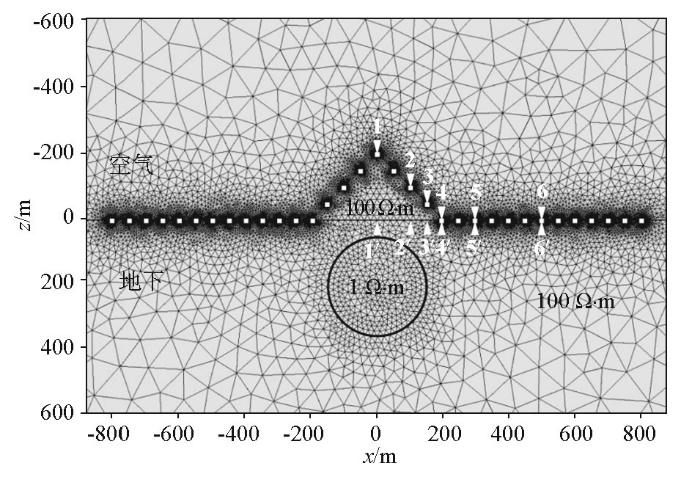
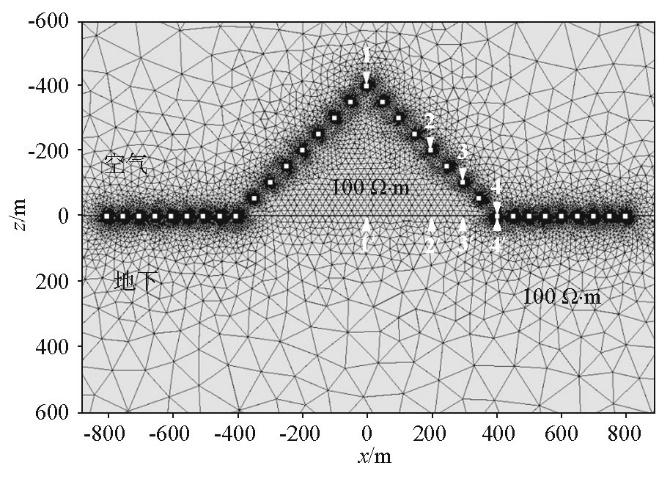
为分析山峰地形对瞬变电磁响应的影响,设计了如图2所示的带地形均匀大地模型:x轴沿发射源铺设方向,y轴垂直于发射源铺设方向,z轴向下,整体坐标系满足右手坐标系准则;空气电阻率为108 Ω·m,山体与地下半空间电阻率均为100 Ω·m,山体为圆锥体,底面半径200 m,最高起伏200 m,坡角为45°,山顶位于(0 m,500 m,-200 m) (图2b);发射源长度为1 000 m,中心点坐标为(0 m,-500 m,0 m),发射电流10 A,发射电流方向如图2a箭头所示;测线长度为1 600 m,位于y=500 m处,测点间距为50 m,共33个测点,采样时间为10-5~10-1 s,共离散为600个时间步长;模型的核心计算区域为5 km×5 km×2 km,为避免狄利克雷边界条件对正演精度的影响,对每个方向分别设置40 km的扩边,为提高计算速度,在保证测点处的计算精度的前提下,利用非结构四面体网格灵活离散的特点,对核心计算区域采用体积较小的四面体单元,在扩边区域采用体积较大的四面体单元。为了提高三维有限元正演数值模拟的精度,对发射源、测点及山体进行局部加密,利用非结构四面体网格对整个计算区域进行剖分,共计402 207个四面体单元。

为方便讨论山峰地形对瞬变电磁响应的影响,选取6个距山顶不同距离(x=0、100、150、200、300、500 m)的测点1~6,并给出平坦大地模型同一水平位置处测点1'~6'作为参考,分析山峰地形对瞬变电磁响应的影响。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   山峰模型示意

Fig.2   Sketch map of the hill model


2.1 距离的影响

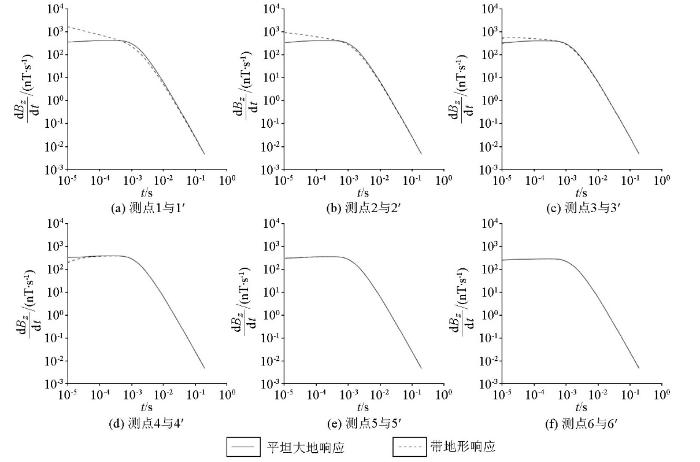
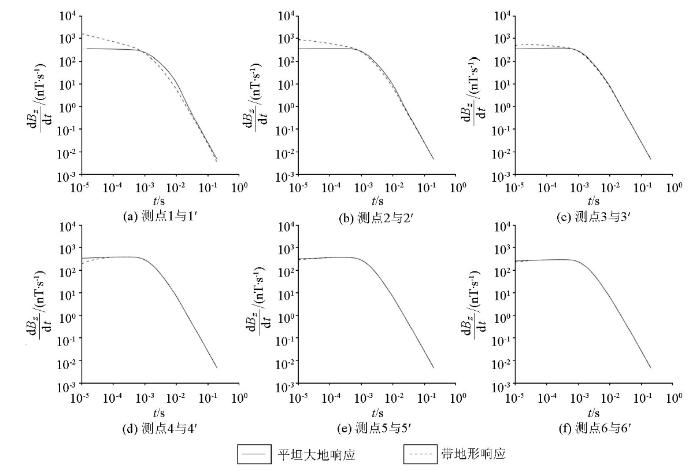
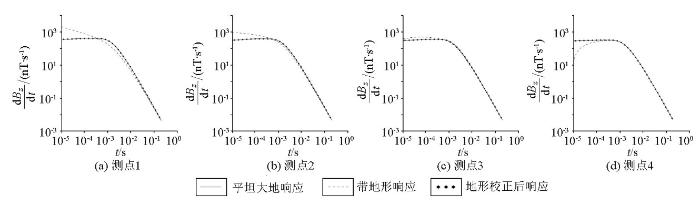
图3为1 000 m偏移距平坦大地模型和带地形均匀大地模型的瞬变电磁响应。测点1~3位于山峰地形上,与平坦大地响应相比,3个测点的早期响应幅值增强,且随测点位置的降低,响应幅值逐渐减小,但仍强于平坦大地响应;中期响应差距逐渐缩小,晚期响应与平坦大地响应逐渐趋于吻合,说明在晚期地形影响逐渐消失(图3a-c)。测点4位于山脚位置,早期响应幅值弱于平坦大地响应,中期至晚期响应趋于重合(图3d)。测点5~6位于距山体一定距离处,此处观测到的响应无论在早期道或是晚期道都与平坦大地响应吻合良好,说明在远离山峰的平坦位置处地形影响逐步消失,地形效应对瞬变电磁响应的干扰可以忽略(图3e、f)。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   1 000 m偏移距山峰模型瞬变电磁响应

Fig.3   Comparison of TEM responses for the hill model with 1 000 m offset


综上,山峰地形对瞬变电磁响应影响强烈,主要集中在早期道,随着时间的推移,地形影响逐渐减弱;地形效应对瞬变电磁响应的影响程度主要取决于测点到山顶的水平距离,测点距离山顶越远,地形的影响越小。

2.2 偏移距的影响

为研究山体在不同偏移距条件下对瞬变电磁响应的影响,以图2所示山峰模型为例,调整发射源至y=-2 500 m处,其余参数均保持不变。图4为3 000 m偏移距平坦大地模型和带地形均匀大地模型的瞬变电磁响应,对比图3可见,随着偏移距的增大,瞬变电磁响应出现幅值减弱的现象,整体来看,不同偏移距带地形均匀大地模型响应皆保留了地形影响特征。为不失一般性,本文后续研究中的偏移距均设置为1 000 m。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   3 000 m偏移距山峰模型瞬变电磁响应

Fig.4   Comparison of TEM responses for the hill model with 3 000 m offset


2.3 对地下异常体的影响

基于前述分析,本节进一步讨论山峰地形对地下异常体响应的影响。设计山峰下赋存良导球体模型(图5),山峰最高起伏为200 m,坡角为45°,山体与地下半空间电阻率均为100 Ω·m,球体半径150 m,电阻率为1 Ω·m,埋深200 m,测点布置保持与图2模型一致。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   山峰带异常体模型示意

Fig.5   Sketch map of the hill model with an abnormal body


图6为平坦大地带异常体模型与山峰带异常体模型的瞬变电磁响应。对比图3的带地形均匀大地响应可见,图6保留了山峰地形效应影响特征,如山峰地形对响应的影响集中于早期;影响程度取决于测点距山顶的距离。当地下存在异常体时,带地形响应(图3a-c)与直接正演得到的平坦大地响应(图6a-c)之间的差异愈加明显。由此可见,地形效应引起的响应畸变十分强烈,无论地下是否存在异常体,地形影响皆不容忽视。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   山峰带异常体模型瞬变电磁响应

Fig.6   Comparison of TEM responses for the hill model with an abnormal body


2.4 电阻率的影响

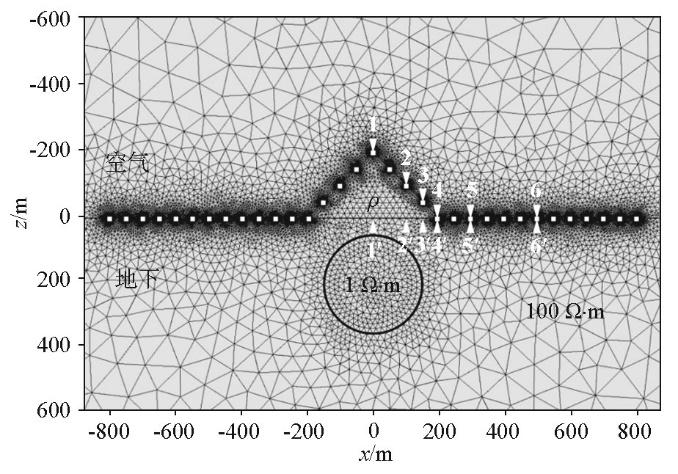
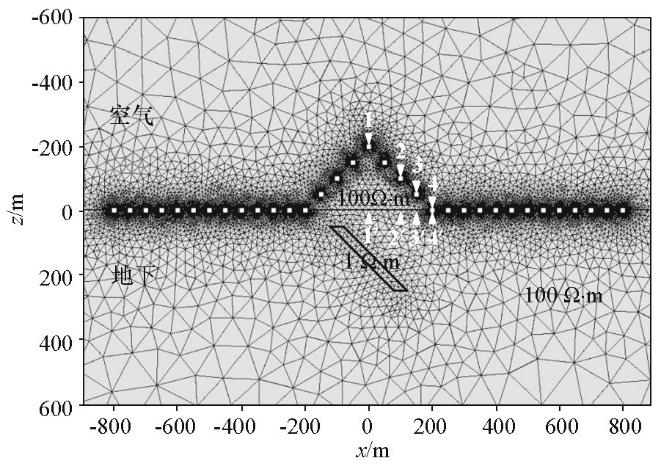
为研究不同电阻率的山体对瞬变电磁响应的影响,以山峰带异常体模型为例(图7),保持山峰最高起伏为200 m,坡角为45°,地下半空间电阻率100 Ω·m,球体半径150 m,电阻率为1 Ω·m,埋深200 m,测点布置不变,参考前人的研究,设置山体电阻率(ρ)分别为10、100、1 000 Ω·m[19]。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   不同电阻率山峰带异常体模型示意

Fig.7   Sketch map of the hill model with different resistivities


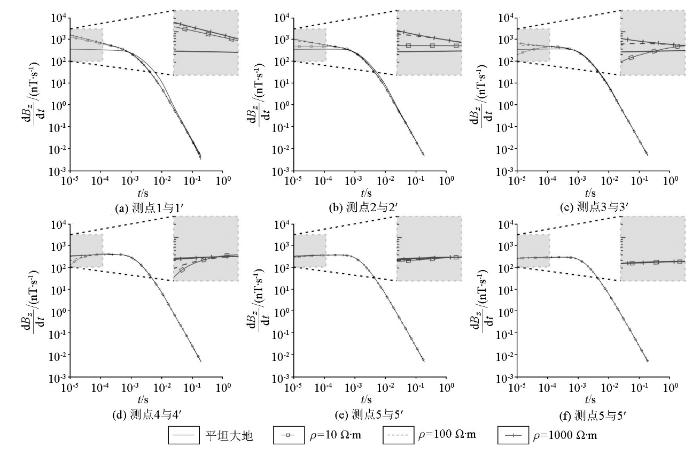
图8为不同电阻率山峰模型的瞬变电磁响应。以ρ=100 Ω·m的瞬变电磁响应为参考,可以看出:当ρ=10 Ω·m时,早期响应均低于100 Ω·m山体的早期响应,说明当山体呈现为低阻时会导致响应幅值整体减弱;当ρ=1 000 Ω·m时,早期响应均高于100 Ω·m的山体响应,说明当山体为高阻时会导致整体响应幅值增强。由此可见,无论山体电阻率整体呈现为低阻还是高阻,地形效应引起的响应畸变不可忽略,相对高阻山体的地形影响强度更大;若不考虑地形影响,直接利用畸变的观测数据进行解释会导致结果远离真实模型,严重影响着瞬变电磁法的应用效果。因此,进行瞬变电磁观测数据的地形效应校正很有必要。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   不同电阻率山峰模型瞬变电磁响应

Fig.8   Comparison of TEM responses for the hill model with different resistivities


3 地形校正

3.1 地形校正方法

瞬变电磁法作为一种低频电磁勘探方法,其Maxwell方程组可以忽略位移电流项,满足准静态近似条件[32],故Maxwell方程组满足线性叠加原理,即总场等于每个场源在采集位置产生电磁场的线性叠加[33]。当位于地表的发射装置停止供电后,异常体感应出涡流,不同的异常体(山体、异常体)产生涡流,涡流产生的瞬变电磁响应在地面观测位置线性叠加。在复杂地形条件下,地下存在异常体时,地表测得的瞬变电磁响应可视为山体响应、异常体响应以及平坦大地响应的叠加。因此,山体在整个模型中造成的地形效应影响可认为不随模型的变化而变化,只与山体规模和背景电阻率有关。

基于瞬变电磁场线性叠加原理,本文利用三维正演在总响应(含有山体、异常体)中直接剔除山体的响应,获得校正后的瞬变电磁响应,消除地形效应影响。具体实施过程如下。

1)对校正区域进行小极距直流电法测试,获取地表电阻率并取作大地的背景电阻率。

2)利用该地表电阻率对平坦大地模型进行三维正演计算,得到平坦大地模型的三维瞬变响应dBz/dthill-off。

3)依据测地工作获取的高程信息建立带地形的三维模型,得到带地形模型三维瞬变响应dBz/dthill-in。

4)将带地形模型响应与平坦大地模型响应做差,得到该区域地形自身产生的纯异常场响应:

$\frac{\mathrm{d} B_{z}}{\mathrm{~d} t_{\text {topography }}}=\frac{\mathrm{d} B_{z}}{\mathrm{~d} t_{\text {hill-in }}}-\frac{\mathrm{d} B_{z}}{\mathrm{~d} t_{\text {hill-off }}},$

式中:dBz/dttopography为地形效应产生的纯异常场响应;dBz/dthill-in和dBz/dthill-off分别代表带地形模型与平坦大地模型瞬变电磁响应。

5)在实测数据中减去地形效应产生的纯地形响应,即可得到经过地形校正后的瞬变响应:

$\frac{\mathrm{d} B_{z}}{\mathrm{~d} t_{\text {corrected }}}=\frac{\mathrm{d} B_{z}}{\mathrm{~d} t_{\text {measured }}}-\frac{\mathrm{d} B_{z}}{\mathrm{~d} t_{\text {topography }}},$

式中:dBz/dtcorrected和dBz/dtmeasured分别表示校正后的和实测的瞬变电磁响应。

3.2 均匀大地模型

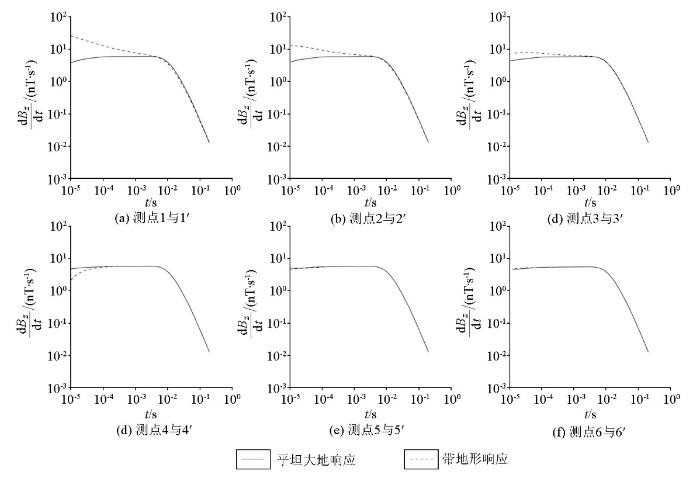
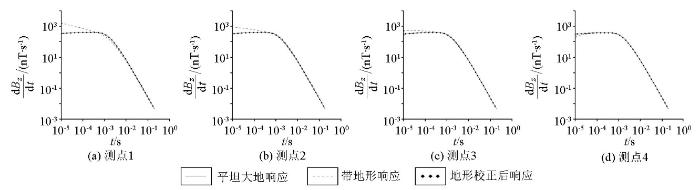
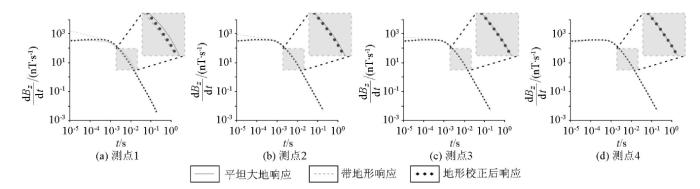
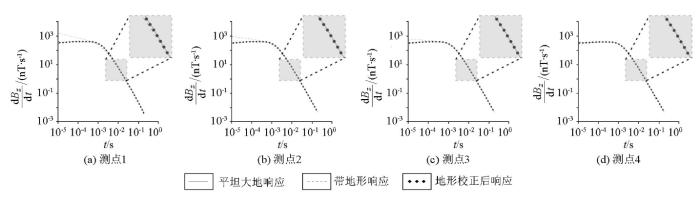
基于以上方法开展地形校正,图9为图2模型中测点1~4地形校正前后的瞬变电磁响应。可以看出:当测点位于山峰地形上时(图9a-c),对早期与中期存在响应幅值增强的现象进行校正,校正后的瞬变电磁响应与平坦大地响应吻合良好;当测点位于山脚位置时(图9d),对早期存在响应幅值减弱的现象进行校正,校正后响应与平坦大地响应吻合良好。可见,无论测点位于山峰地形的任何位置,本文提出的地形校正方法皆可以有效消除早期与中期可能出现的异常响应。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   山峰模型地形校正前后瞬变电磁响应

Fig.9   Comparison of TEM correction response for the hill model


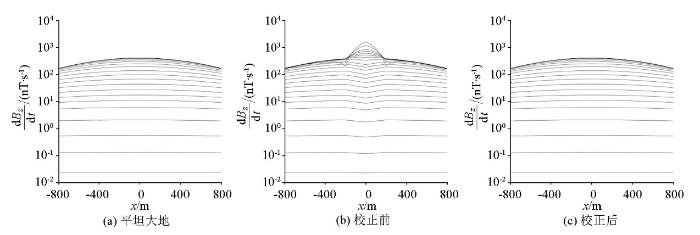
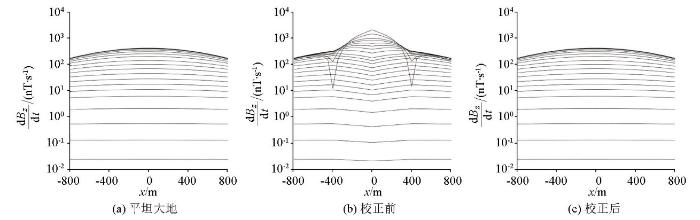
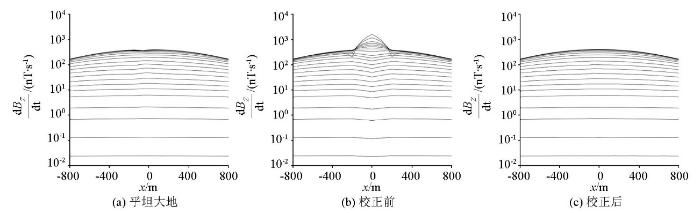
图10为将图2模型各测点校正前后的瞬变电磁响应绘制成多测道图。对比平坦大地响应(图10a)和带地形均匀大地响应(图10b)可见,图10b中响应畸变主要集中于山体附近,早期明显出现响应幅值增强的特征,异常形态类似“山峰”,并且两侧山脚处出现幅值异常减小的虚假异常;随着时间的推进,出现响应幅值减弱的特征,异常形态类似“反山峰”,无法进行有效的解释。与图10b相比可见,校正后的响应(图10c)很好地恢复了地下均匀半空间的特征,与图9a的响应特征对应较好。可见本文的校正方法针对不同测点存在的地形影响进行校正,保留了地下真实结构特征,基本消除了山体作为处于地表附近的异常体所带来的影响,说明本文采用的地形效应校正方法是可行的。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   山峰模型瞬变电磁校正响应多测道曲线

Fig.10   Multi-channels curve of TEM correction response for the hill model


在实际工作中,会遇到存在不同山体规模的情况,为了验证这种情况下的校正效果,给出了如图11所示的山峰模型。山峰最高起伏为400 m,坡角为45°,山顶位于(0 m,500 m,-400 m)处,其余参数同图2模型。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11   不同规模山峰模型示意

Fig.11   Sketch map of the hill model with different sizes


图12为图11模型中测点1~4地形校正前后的瞬变电磁响应。与带地形均匀大地校正响应(图9)进行对比,可见山体规模越大,山峰模型响应与平坦大地响应的响应差异越大,表明地形影响越强;经过校正处理后的响应与直接正演得到的平坦大地响应基本吻合。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12   不同规模山峰模型地形校正前后瞬变电磁响应

Fig.12   Comparison of TEM correction response for the hill model with different sizes


将图11模型中各测点校正前后的瞬变电磁响应绘制成多测道图(图13),与带地形均匀大地响应(图10b)对比,可见山峰规模越大,地形影响造成的水平范围与响应幅值越大。对比图13b和图13c,校正后的响应较好消除了由地形效应引起的响应畸变,说明该校正方法不受山体规模影响,能够有效削弱地形影响。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13   不同规模山峰模型瞬变电磁校正响应多测道曲线

Fig.13   Multi-channels curve of TEM correction response for the hill model with different sizes


3.3 球体模型

为考察山峰地形赋存球体异常情况下的校正效果,对图5所示模型进行地形校正。结果(图14)显示:校正后响应与直接正演得到的平坦大地带球体模型响应吻合良好,可以有效消除地形影响造成的早期响应异常。相较于图9,图14中测点1、2校正后的个别时间道响应与平坦大地带球体模型响应之间存在一定校正差异,表现为校正后响应略弱于平坦大地响应(图14a、b),测点3、4校正效果较好(图14c、d)。

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14   山峰带球体异常模型地形校正前后瞬变电磁响应

Fig.14   Comparison of TEM correction response for the hill model with a conductive sphere


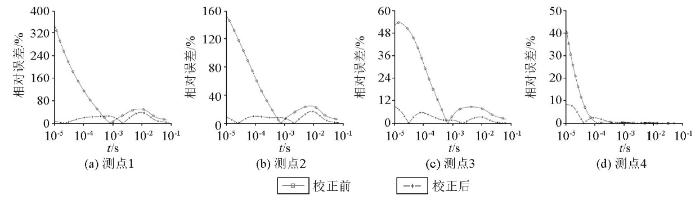
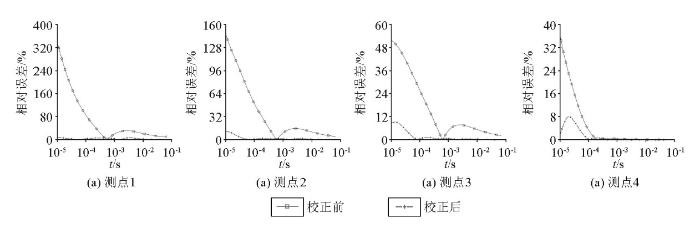
图15为山峰带球体异常模型地形校正前后瞬变电磁响应相对误差,可以看出,山体对瞬变电磁响应的影响主要集中在早期且跟测点位置相关,山顶位置的1号测点受山体影响相对误差较大;山腰及以下位置的相对误差有减小的趋势,说明山体的影响在逐渐减弱,但相对误差值仍较大,校正后相对误差降至校正前相对误差的10%左右,说明本文所述地形校正方法可较好地压制山体的影响。通过前述地形影响规律可知,距离山顶较近的测点,如1号测点,由于位于地下异常体的正上方,受山体与地下目标体的耦合作用影响最强,故相对误差最大,随着测点逐渐远离山顶和地下异常体,受耦合作用影响减弱,相对误差逐渐减小。

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15   山峰带球体异常模型地形校正前后瞬变电磁响应相对误差

Fig.15   Comparison of relative errors in TEM response for the hill model with a conductive sphere


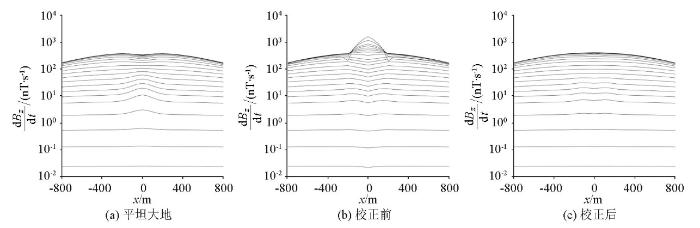
将图5模型中各测点校正前后的瞬变电磁响应绘制成多测道图(图16),可见:校正前的异常体响应始终被地形影响压制(图16b),无法给出有效解释,而经地形校正后能够很好消除早期“山峰”形态的响应畸变(图16c)。相较于图16a,图16c保留了球体异常响应,但存在一定的校正差异,其校正后的异常体响应弱于平坦大地异常体响应。通过前述校正响应分析可知,这种现象可能是由山体与地下异常体之间的耦合造成的。

图16

新窗口打开| 下载原图ZIP| 生成PPT

图16   山峰带球体异常模型瞬变电磁校正响应多测道曲线

Fig.16   Multi-channels curve of TEM correction response for the hill model with a conductive sphere


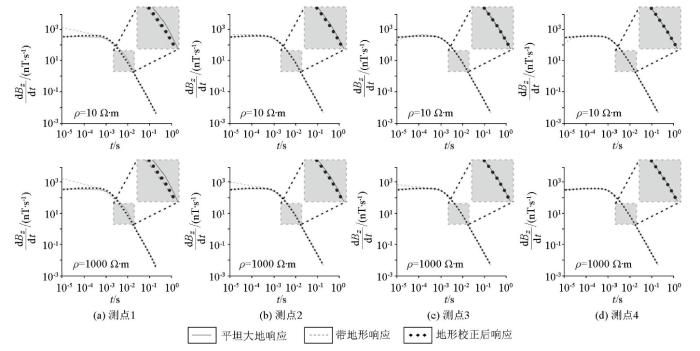
为考察不同电阻率山峰地形情况下的校正效果,对图7所示模型进行地形校正(图17),可以看出:不同电阻率山峰模型校正后的响应与直接正演得到的平坦大地带球体模型响应皆吻合良好,能够消除地形影响造成的早期响应异常。其中测点1、2校正后的个别时间道响应存在一定校正差异,与上述校正差异特征相同,主要表现为校正后的响应略弱于平坦大地响应(图17a、b)。

图17

新窗口打开| 下载原图ZIP| 生成PPT

图17   不同电阻率山峰模型地形校正前后瞬变电磁响应

Fig.17   Comparison of TEM correction response for the hill model with different resistivities


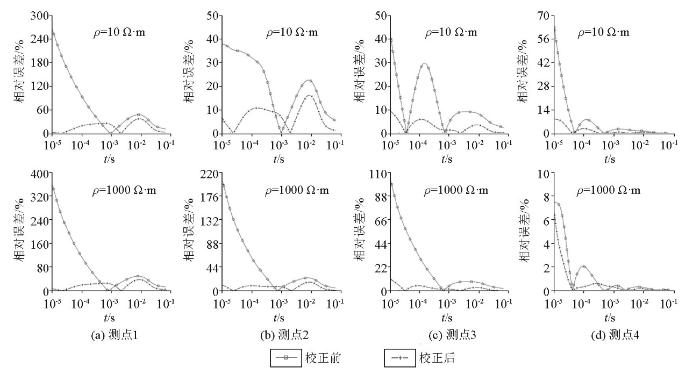
图18为不同电阻率山峰模型地形校正前后瞬变电磁响应相对误差,可见经过地形校正后,各时间道的相对误差均有所减小,特别是反映山峰影响的早期响应,误差下降幅度最大。对比图15可知,本文提出的山峰地形校正方法不受山峰电阻率的影响,能够有效消除不同电阻率山体带来的早期响应畸变。

图18

新窗口打开| 下载原图ZIP| 生成PPT

图18   不同电阻率山峰模型地形校正前后瞬变电磁响应相对误差

Fig.18   Comparison of relative errors in TEM response for the hill model with different resistivities


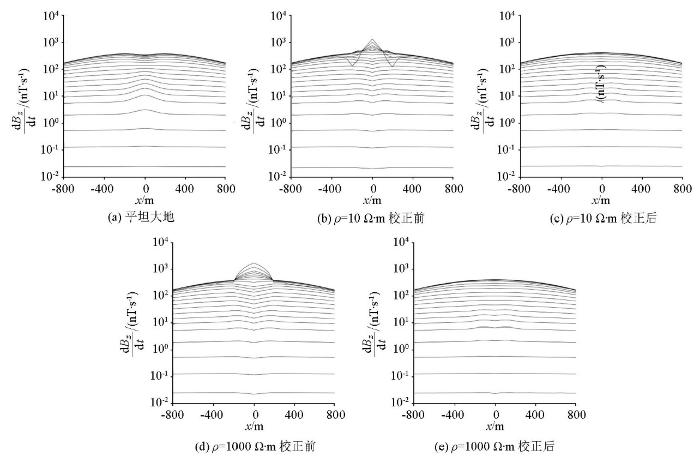
将图7模型中各测点校正前后的瞬变电磁响应绘制成多测道图(图19)。对比山峰电阻率为100 Ω·m的模型响应(图16b),从图19b、d可以看出,当ρ=10 Ω·m时,早期山顶处类似“山峰”的“假异常”范围与强度被削弱,两侧山脚处的“假异常”强度和范围进一步增强;当山体电阻率为1 000 Ω·m时,早期的山顶“假异常”范围与强度被增强,而两侧山脚处的“假异常”强度和范围进一步被削弱,皆无法对异常体进行有效解释。图19c、e显示,地形校正很好地消除了不同电阻率山峰所造成的不同形态的早期响应畸变并保留了球体异常响应,说明该校正方法不受山体电阻率的影响,能够有效削弱地形影响。

图19

新窗口打开| 下载原图ZIP| 生成PPT

图19   不同电阻率山峰模型瞬变电磁校正响应多测道曲线

Fig.19   Multi-channels curve of TEM correction response for the hill model with different resistivities


3.4 倾斜板状体模型

以倾斜板状体为研究对象,设计了如图20所示的山峰地形带倾斜板状体模型。倾斜板状体电阻率为1 Ω·m,厚度为40 m,倾角为45°,中心埋深为(0 m,500 m,150 m),顶板中心位置为(-100 m,500 m,50 m),底板中心位置为(100m,500 m,250 m),其余参数同图2模型。

图20

新窗口打开| 下载原图ZIP| 生成PPT

图20   山峰带倾斜板状体模型示意

Fig.20   Sketch map of the hill model with an inclined sheet


图21为图20模型中测点1~4地形校正前后的瞬变电磁响应,可以看出,校正后响应与直接正演得到的平坦大地响应吻合较好,能够有效消除地形效应。

图21

新窗口打开| 下载原图ZIP| 生成PPT

图21   山峰带倾斜板状体模型地形校正前后瞬变电磁响应

Fig.21   Comparison of TEM correction response for the hill model with an inclined sheet


图22为山峰带倾斜板状体模型地形校正前后瞬变电磁响应相对误差。对比图15可见,针对不同的规则形体模型,如球体和倾斜板状体,该法均能得到较好的校正效果;对于倾斜板状体模型,校正后的相对误差下降更多,山峰地形校正效果优于球体模型,这可能是由于倾斜板状体规模较小,与山体的耦合作用减弱造成的。

图22

新窗口打开| 下载原图ZIP| 生成PPT

图22   山峰带倾斜板状体模型地形校正前后瞬变电磁响应相对误差

Fig.22   Comparison of relative errors in TEM response for the hill model with an inclined sheet


将图20模型中各测点校正前后的瞬变电磁响应绘制成多测道图(图23)。图23b显示山峰模型响应出现明显畸变,尤其是早期响应的影响格外剧烈,异常体响应始终被地形影响压制,而校正后在一定程度上消除了地形产生的响应畸变(图23c)。与图16c相比,图23c的校正差异相对较小,该模型的校正效果优于球体模型。可见当地下存在异常体时,异常体规模越小,该校正方法的效果越好。

图23

新窗口打开| 下载原图ZIP| 生成PPT

图23   山峰带倾斜板状体模型瞬变电磁校正响应多测道曲线

Fig.23   Multi-channels curve of TEM correction response for the hill model with an inclined sheet


4 结论

文中提出一种以电磁场线性叠加原理为基础的地形校正方法,通过对不同电性参数的带地形简单规则异常体模型校正试算可见,该校正方法能够去除大部分地形效应的影响,可为复杂地形地区的瞬变电磁数据处理解释提供参考。

在本文的校正算例中,由于测点随地形起伏,产生的高程变化会在一定程度上影响校正结果的精度,故开展复杂地形区域测点高度校正将是下一步的工作目标。

致谢

衷心感谢李貅教授团队在非结构时间域有限元算法方面所提供的帮助。

参考文献

Nabighian M N.

Electromagnetic methods in applied geophysics:Volume 1,theory

[M]. Society of Exploration Geophysicists, 1988.

[本文引用: 1]

薛国强, 宋建平, 武军杰, 等.

瞬变电磁法探测公路隧道工程中的不良地质构造

[J]. 长安大学学报:地球科学版, 2003, 25(4):73-75.

[本文引用: 1]

Xue G Q, Song J P, Wu J J, et al.

Application of TEM to detect the harmful geological structures in highway tunnel engineering

[J]. Journal of Chang`an University:Earth Science Edition, 2003, 25(4):73-75.

[本文引用: 1]

张建智, 胡富杭, 刘海啸, 等.

煤矿老窑采空区地-井TEM响应特征

[J]. 物探与化探, 2022, 46(1):191-197.

[本文引用: 1]

Zhang J Z, Hu F H, Liu H X, et al.

TEM response characteristics of borehole in goaves of old coal mines

[J]. Geophysical and Geochemical Exploration, 2022, 46(1):191-197.

[本文引用: 1]

于景邨, 刘志新, 刘树才, 等.

深部采场突水构造矿井瞬变电磁法探查理论及应用

[J]. 煤炭学报, 2007, 32(8):818-821.

[本文引用: 1]

Yu J C, Liu Z X, Liu S C, et al.

Theoretical analysis of mine transient electromagnetic method and its application in detecting water burst structures in deep coal stope

[J]. Journal of China Coal Society, 2007, 32(8):818-821.

[本文引用: 1]

侯彦威, 徐亚飞.

低阻覆盖层下深部富水区的TEM探测效果

[J]. 物探与化探, 2013, 37(4):715-719.

[本文引用: 1]

Hou Y W, Xu Y F.

The effect of the transient electromagnetic method in detecting deep water-rich area under low resistivity layer

[J]. Geophysical and Geochemical Exploration, 2013, 37(4):715-719.

[本文引用: 1]

柳建新, 赵然, 郭振威.

电磁法在金属矿勘查中的研究进展

[J]. 地球物理学进展, 2019, 34(1):151-160.

[本文引用: 1]

Liu J X, Zhao R, Guo Z W.

Research progress of electromagnetic methods in the exploration of metal deposits

[J]. Progress in Geophysics, 2019, 34(1):151-160.

[本文引用: 1]

Hördt A, Andrieux P, Neubauer F M, et al.

A first attempt at monitoring underground gas storage by means of time-lapse multichannel transient electromagnetics

[J]. Geophysical Prospecting, 2000, 48:489-509.

DOI:10.1046/j.1365-2478.2000.00192.x      URL     [本文引用: 1]

李贺. 特殊探测环境下的瞬变电磁探测方法研究[D]. 西安: 长安大学, 2021.

[本文引用: 1]

Li H. Research on transient electromagnetic detection method under special detection environment[D]. Xi’an: Chang’an University, 2021.

[本文引用: 1]

Ku C C, Hsieh M S, Lim S H.

The topographic effect in electromagnetic fields

[J]. Canadian Journal of Earth Sciences, 1973, 10(5):645-656.

DOI:10.1139/e73-065      URL     [本文引用: 1]

By making use of the analogy between the network quantities and the electromagnetic fields, a numerical method is employed to investigate the possible topographic effect in the earth's EM fields for several simple models in two dimensional problems. It is found that various topographies may give rise to distortions in the earth's EM fields, and some EM anomalies observed on the ground surface may be simply due to such a topographic effect.

Hördt A, Müeller M D.

Understanding LOTEM data from mountainous terrain

[J]. Geophysics, 2000, 65(4):1113-1123.

DOI:10.1190/1.1444804      URL     [本文引用: 1]

Long‐offset transient electromagnetic (LOTEM) data from the Vesuvius volcano, in Italy, show that the EM response of the topography is a potential cause of data distortions. A modeling study was carried out to simulate the effect of mountainous terrain on vertical magnetic‐field time derivatives using a 3-D finite‐difference code. The objectives were to assess the importance of topographic effects and to help identify them in existing field data. The total effect of topography on the LOTEM response can be considered as a combination of four distortions of the corresponding responses for a flat terrain. First, the receiver is at some height above the flat surface. Second, the mountain acts as a conductive body displacing air. Third, large loop receivers are nonhorizontal and sense a combination of horizontal and vertical magnetic fields. Finally, the electromagnetic coupling between the mountain and deeper‐lying structure modifies the structure response. Each of the effects can be identified in field data recorded at Mount Vesuvius. The topographic induced distortions for the model used in this study are moderate in the sense that 1-D inversions of the theoretical data still recover the gross conductivity structure, albeit with small deviations from the true parameters. Although this result might imply that topography might be ignored during the first stage of an interpretation, no simple correction method is evident, so topography will have to be included in any 2-D or 3-D inversion attempt.

Yin C C, Qi Y F, Liu Y H, et al.

3D time-domain airborne EM forward modeling with topography

[J]. Journal of Applied Geophysics, 2016, 134:11-22.

DOI:10.1016/j.jappgeo.2016.08.002      URL     [本文引用: 1]

Li J H, Lu X S, Farquharson C G, et al.

A finite-element time-domain forward solver for electromagnetic methods with complex-shaped loop sources

[J]. Geophysics, 2018, 83(3):E117-E132.

DOI:10.1190/geo2017-0216.1      URL     [本文引用: 1]

A finite-element time-domain (FETD) electromagnetic forward solver for a complex-shaped transmitting loop is presented. Any complex-shaped source can be viewed as a combination of electric dipoles (EDs), each of which can be further decomposed into two horizontal EDs along the [Formula: see text]- and [Formula: see text]-directions and one vertical ED along the [Formula: see text]-direction. Using this method, a complex-shaped loop can be easily handled when implementing an FE method based on the total-field algorithm and an unstructured tetrahedral mesh. The FETD solver that we developed used a vector FE method and the first-order backward Euler method to discretize in space and time, respectively. Unstructured tetrahedral girds combined with a local refinement technique was used to exactly delineate topography and a deformed loop. This FETD solver was tested by the five following scenarios: a rectangular loop on a flat-surface half-space, a circular loop on a stratified medium, a rectangular loop laid on a slope-surface half-space, a rectangular loop laid on a slope with a conductive cubic body, and a complex-shaped loop on a real-life topography. The results of this FETD solver agreed well with the ones evaluated by the analytic methods for the first three examples, and with a frequency-domain FE solver combined with a cosine transform for the last two examples.

Jiracek G R.

Near-surface and topographic distortions in electromagnetic induction

[J]. Surveys in Geophysics, 1990, 11(2):163-203.

DOI:10.1007/BF01901659      URL     [本文引用: 1]

肖怀宇. 带地形的瞬变电磁法三维数值模拟[D]. 北京: 中国地质大学(北京), 2006.

[本文引用: 1]

Xiao H Y. Three-dimensional numerical modeling considering the topography of TEM[D]. Beijing: China University of geosciences(Beijing), 2006.

[本文引用: 1]

Tang X G, Hu W B, Yan L J.

Topographic effects on long offset transient electromagnetic response

[J]. Applied Geophysics, 2011, 8(4):277-284.

DOI:10.1007/s11770-011-0297-x      URL     [本文引用: 1]

邱卫忠.

回线源TEM山地勘探中的地形影响和校正方法

[J]. 煤田地质与勘探, 2012, 40(5):78-81.

[本文引用: 1]

Qiu W Z.

Topographic effects and correction methods of loop source TEM in mountainous exploration

[J]. Coal Geology & Exploration, 2012, 40(5):78-81.

[本文引用: 1]

张博, 殷长春, 刘云鹤, 等.

起伏地表频域/时域航空电磁系统三维正演模拟研究

[J]. 地球物理学报, 2016, 59(4):1506-1520.

[本文引用: 1]

Zhang B, Yin C C, Liu Y H, et al.

3D modeling on topographic effect for frequency/time-domain airborne EM systems

[J]. Chinese Journal of Geophysics, 2016, 59(4):1506-1520.

[本文引用: 1]

陈明生.

对瞬变电磁测深几个问题的思考(五)——地形对TEM资料的影响

[J]. 煤田地质与勘探, 2017, 45(6):139-142.

[本文引用: 1]

Chen M S.

Reflections on several lssues of transient electromagnetie sounding (5):The influence of topography on TEM data

[J]. Coal Geology & Exploration, 2017, 45(6):139-142.

[本文引用: 1]

赵越, 李貅, 王祎鹏, 等.

三维起伏地形条件下航空瞬变电磁响应特征研究

[J]. 地球物理学报, 2017, 60(1):383-402.

[本文引用: 2]

Zhao Y, Li X, Wang Y P, et al.

Characteristics of terrain effect of 3-D ATEM

[J]. Chinese Journal of Geophysics, 2017, 60(1):383-402.

[本文引用: 2]

马炳镇.

起伏地形下地面瞬变电磁法三维正演数值模拟研究

[J]. 物探与化探, 2018, 42(4):777-784.

[本文引用: 1]

Ma B Z.

Three dimensional numerical simulation of transient electromagnetic method in undulating terrain

[J]. Geophysical and Geochemical Exploration, 2018, 42(4):777-784.

[本文引用: 1]

齐彦福, 李貅, 孙乃泉, 等.

短偏移距电性源瞬变电磁地形影响特征分析

[J]. 吉林大学学报:地球科学版, 2021, 52(1):247-260.

[本文引用: 1]

Qi Y F, Li X, Sun N Q, et al.

Analysis of influence characteristics of topography on short-offset grounded-source transient electromagnetic responses

[J]. Journal of Jilin University:Earth Science Edition, 2021, 52(1):247-260.

[本文引用: 1]

Sternberg B K, Washburne J C, Pellerin L.

Correction for the static shift in magnetotellurics using transient electromagnetic soundings

[J]. Geophysics, 1988, 53(11):1459-1468.

DOI:10.1190/1.1442426      URL     [本文引用: 1]

Shallow inhomogeneities can lead to severe problems in the interpretation of magnetotelluric (MT) data by shifting the MT apparent resistivity sounding curve by a scale factor, which is independent of frequency on the standard log‐apparent‐resistivity versus log‐frequency display. The amount of parallel shift, commonly referred to as the MT static shift, can not be determined directly from conventionally recorded MT data at a single site. One method for measuring the static shift is a controlled‐source measurement of the magnetic field. Unlike the electric field, the magnetic field is relatively unaffected by surface inhomogeneities. The controlled‐source sounding (which may be a relatively shallow sounding made with lightweight equipment) can be combined with a deep MT sounding to obtain a complete, undistorted model of the earth. Inversions of the static shift‐corrected MT data provide a much closer match to well‐log resistivities than do inversions of the uncorrected data. The particular controlled‐source magnetic‐field sounding which we used was a central‐induction Transient ElectroMagnetic (TEM) sounding. Correction for the static shift in the MT data was made by jointly inverting the MT data and the TEM data. A parameter which allowed vertical shifts in the MT apparent resistivity curves was included in the computer inversion to account for static shifts. A simple graphical comparison between the MT apparent resistivities and the TEM apparent resistivities produced essentially the same estimate of the static shift (within 0.1 decade) as the joint computer inversion. Central‐induction TEM measurements were made adjacent to over 100 MT sites in central Oregon. The complete data base of over 100 sites showed an average static shift between 0 and 0.2 decade. However, in the rougher topography and more complex structure of the Cascade Mountain Range, the majority of the sites had static shifts of the order of 0.3 to 0.4 decade. The static shifts in this area are probably due to a combination of topography and surficial inhomogeneities. The TEM apparent resistivity (which is used to estimate the unshifted MT apparent resistivity) does not necessarily agree with either the transverse electric (TE) or the transverse magnetic (TM) MT polarization. TEM apparent resistivity may occur between the two, or may agree with one of the two polarizations, or may lie outside the MT polarizations.

李金铭. 地电场与电法勘探[M]. 北京: 地质出版社, 2005.

[本文引用: 1]

Li J M. Geoelectric fields and electrical exploration[M]. Beijing: Geological Press, 2005.

[本文引用: 1]

严良俊, 王正茂, 谢兴兵.

表层结构调查中的TEM地形校正

[J]. 勘探地球物理进展, 2007, 30(5):396-398.

[本文引用: 1]

Yan L J, Wang Z M, Xie X B.

TEM terrain correction in surface structure surveys

[J]. Progress in Exploration Geophysics, 2007, 30(5):396-398.

[本文引用: 1]

王信文, 冯宏, 高志宏, 等.

TEM技术地形校正初探

[C]// 陕西省地球物理文集, 2008:127-131.

[本文引用: 1]

Wang X W, Feng H, Gao Z H, et al.

TEM technology terrain correction

[C]// Geophysics Collection of Shanxi province, 2008:127-131.

[本文引用: 1]

范涛.

煤田电法勘探中的TEM地形校正方法

[J]. 物探与化探, 2012, 36(2):246-249.

[本文引用: 1]

Fan T.

TEM topographic correction in coal field electrical exploration

[J]. Geophysical & Geochemical Exploration, 2012, 36(2):246-249.

[本文引用: 1]

薛国强, 闫述, 陈卫营.

电磁测深数据地形影响的快速校正

[J]. 地球物理学报, 2016, 59(12):4408-4413.

[本文引用: 1]

Xue G Q, Yan S, Chen W Y.

A fast topographic correction method for electromagnetic data

[J]. Chinese Journal of Geophysics, 2016, 59(12):4408-4413.

[本文引用: 1]

Liu Y H, Yin C C, Qiu C K, et al.

3-D inversion of transient EM data with topography using unstructured tetrahedral grids

[J]. Geophysical Journal International, 2019, 217(1):301-318.

DOI:10.1093/gji/ggz014      URL     [本文引用: 1]

齐彦福, 智庆全, 李貅, 等.

考虑关断时间的地面瞬变电磁三维带地形反演

[J]. 地球物理学报, 2021, 64(7):2566-2577.

[本文引用: 1]

Qi Y F, Zhi Q Q, Li X, et al.

Three-dimensional ground TEM inversion over a topographic earth considering ramp time

[J]. Chinese Journal of Geophysics, 2021, 64(7):2566-2577.

[本文引用: 1]

Yin C C, Hodges G S.

Influence of displacement currents on the response of helicopter electromagnetic systems

[J]. Geophysics, 2005, 70(4):G95-G100.

DOI:10.1190/1.1993710      URL     [本文引用: 1]

For the purpose of shallow-earth geophysical mapping, progressively higher frequencies have been developed for helicopter electromagnetic (HEM) systems. However, concern has been expressed about the vulnerability of high-frequency EM signals to the influence of the displacement current, especially the phase shift of the HEM signal resulting from the finite speed of light that describes the propagation of the EM wave in free space. In this paper we investigate the influence of the displacement current and the finite speed of light on HEM responses, based on a full solution of the EM field for a conductive, magnetically, and dielectrically polarizable earth half-space and an overlying half-space of air with free-space dielectric permittivity. We calculate the amplitude change and the phase shift of the HEM signal and the change in the apparent resistivity. We find that the displacement current, when both the air and the earth half-space assume the free-space dielectric permittivity, has a small influence on the HEM signal, while substantial influence may occur when the earth is dielectrically polarizable. The finite speed of the EM propagation in free space does not result in significant phase changes in the HEM signal.

齐彦福. 复杂介质中时间域航空电磁数据仿真技术研究[D]. 长春: 吉林大学, 2017.

[本文引用: 1]

Qi Y F. Time-domain airborne electromagnetic simulation for complex medium[D]. Changchun: Jilin University, 2017.

[本文引用: 1]

Zhdanov M S, Keller G V. The Geoelectrical Methods in Geophysical Exploration[M]. Amsterdam:Elsevier, 1994.

[本文引用: 1]

孙怀凤, 李貅, 卢绪山, 等.

隧道强干扰环境瞬变电磁响应规律与校正方法:以TBM为例

[J]. 地球物理学报, 2016, 59(12):4720-4732.

[本文引用: 1]

Sun H F, Li X, Lu X S, et al.

Transient electromagnetic responses in tunnels with strong interferences and the correcting method:A TBM example

[J]. Chinese Journal of Geophysics, 2016, 59(12):4720-4732.

[本文引用: 1]

/

〈 〉

京ICP备05055290号-3
版权所有 © 2021《物探与化探》编辑部
通讯地址：北京市学院路29号航遥中心 邮编：100083
电话：010-62060192；62060193 E-mail：whtbjb@sina.com , whtbjb@163.com