地表起伏对地下管线GPR探测的影响

doi:10.11720/wtyht.2023.1516

地表起伏对地下管线GPR探测的影响

曾波^,¹, 刘硕², 杨军³, 冯德山^,², 袁忠明³, 柳杰³, 王珣²

1.广州市城市规划勘测设计研究院,广东广州 510060

2.中南大学地球科学与信息物理学院,湖南长沙 410083

3.广州市市政工程设计研究总院有限公司,广东广州 510060

Influence of surface undulations on GPR-based underground pipeline detection

ZENG Bo^,¹, LIU Shuo², YANG Jun³, FENG De-Shan^,², YUAN Zhong-Ming³, LIU Jie³, WANG Xun²

1. Guangzhou Urban Planning and Design Survey Research Institute,Guangzhou 510060,China

2. School of Geosciences and Info-Physics,Central South University,Changsha 410083,China

3. Guangzhou Municipal Engineering Design & Research Institute Co. Ltd.,Guangzhou 510060,China

通讯作者: 冯德山(1978-),男,博士,教授,博导,从事地球物理正反演与数据处理研究工作。Email:fengdeshan@126.com

第一作者: 曾波(1977-),男,高级工程师,主要从事地下管线探测和地下空间测绘工作。Email:75813052@qq.com

责任编辑: 叶佩

收稿日期: 2022-10-24 修回日期: 2023-06-9

基金资助:

国家自然科学基金项目(42074161)
国家自然科学基金项目(42104143)
湖南省自然科学基金项目(2021JJ30806)
湖南省自然科学基金项目(2022JJ40584)
湖南省研究生科研创新项目(CX20220188)

Received: 2022-10-24 Revised: 2023-06-9

摘要

地下管线是城市的重要设施,承担着能源输送、信息传递等功能,为城市生活提供了便利和保障。探地雷达(ground penetrating radar,GPR)作为一种高分辨率、高精度、非开挖、非破坏性的探测技术,在管线测量中具有巨大的优势。然而地表地形复杂,多有起伏,对于GPR探测地下管线有很大的影响。因此,本文采用有限单元法对地下管线探测进行了数值模拟,该方法可以与非结构网格结合,更好地拟合地表起伏地形;此外,介绍了如何进行高度校正,将所得剖面数据与地形相吻合,更容易分析异常体特征。最后开展了两个数值实验,分析了起伏地表对于不同埋深、不同间距、不同材质及不同填充物管线探测的影响,为GPR数据解释提供理论基础。实验结果表明,因地表起伏原因,波形和反射波能量将发生畸变,并不能作为判断管线信息的唯一依据。因此,需进行高度校正,利用双曲线的顶点来判断管线的埋深、材质等信息。

关键词： 探地雷达; 管线探测; 地表起伏; 有限单元法; 高度校正

Abstract

As important urban facilities,underground pipelines perform the functions of energy transfer and information transmission,providing convenience and guarantee for urban life.Ground-penetrating radar (GPR),as a high-resolution,high-precision,trenchless,and non-destructive detection technique,has great advantages in pipeline surveys.However,undulating surfaces with complex terrain greatly influence GPR-based detection of underground pipelines.Therefore,this study conducted numerical simulations of the underground pipeline detection using the finite element method,which can be combined with an unstructured grid to fit the undulating surfaces effectively.Furthermore,this study introduced the height correction method to match the obtained geologic sections with terrain,making it easier to analyze the anomaly characteristics.Finally,through numerical experiments,this study analyzed the influence of undulating surfaces on the detection of pipelines with different burial depths,spacings,materials,and fillers,providing a theoretical basis for GPR data interpretation.The experimental results show that waveforms and reflected wave energy,subjected to distortion due to surface undulations,cannot be used as the sloebasis for judging pipeline information.Therefore,height correction is required,and the vertexes of hyperbolas can be used to judge the burial depths and materials of pipelines.

Keywords： ground penetrating radar; pipeline detection; surface undulating; finite element method; height correction

PDF (3759KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

曾波, 刘硕, 杨军, 冯德山, 袁忠明, 柳杰, 王珣. 地表起伏对地下管线GPR探测的影响[J]. 物探与化探, 2023, 47(4): 1064-1070 doi:10.11720/wtyht.2023.1516

ZENG Bo, LIU Shuo, YANG Jun, FENG De-Shan, YUAN Zhong-Ming, LIU Jie, WANG Xun. Influence of surface undulations on GPR-based underground pipeline detection[J]. Geophysical and Geochemical Exploration, 2023, 47(4): 1064-1070 doi:10.11720/wtyht.2023.1516

0 引言

随着城市的发展和进步,地下管线发挥着越来越重要的作用。城市地下管线种类繁多,有电线电缆、用于水和油气运输的管道以及复杂的地下排水系统^[1]。然而,由于城市建设初期地下空间信息的不完善,在城市的持续建设过程中,地下管线往往会面临老化、改道等问题。这些问题不仅会影响到正常的城市生活,而且还会造成火灾、断水、停电等事故^[2]。为了避免此类事故的发生,需要对地下管线进行全面的调查、记录和系统管理。管线探测仪是目前城市地下管道检测中较为常用的设备,但此类设备只能检测金属管道^[3]。而探地雷达(ground penetrating radar,GPR)不仅能探测金属和非金属管道,还具有高效、显示实时、使用灵活、非破坏性等特点,是管线检测的首选设备^[4-5]。

利用探地雷达进行地下管线探测时,因地下介质的非均匀性、管线错综复杂以及人为干扰等因素,会导致电磁波传播过程十分复杂,雷达数据难以解释^[6]。因此,需要开展探地雷达正演模拟,了解地下GPR波的传播特征,为数据的解释奠定理论基础。梁小强等^[7]应用时域有限差分算法(finite difference time domain,FDTD)^[8-9]开展了不同情况下探地雷达探测效果的分析,了解并掌握了管线探测与各种影响参数之间的关系;王书等^[10]将FDTD算法应用到了地下水污染调查中,说明GPR可划分地下水的含水层界面;Gao等^[11]采用FDTD算法对探地雷达非平稳信号进行了分析,讨论了不同特征的地下管线的雷达信号及泄漏油的变化情况,提高了地下管线和污染土壤的雷达解释精度。但FDTD算法通常用于直交网格,不能与非结构化网格结合,对于边界几何不规则的地质体,易产生虚假反射^[12-13]。雷建伟等^[14]采用共形辛Euler算法高效、精细地识别了地下非金属管道,有效降低了由于阶梯近似造成的虚假绕射波,但是该算法还是基于结构化网格,对于拟合非规则边界有一定的缺陷。时域有限单元法( finite element time domain,FETD)^[15-16]能够与非结构化网格结合,较好地拟合地质体的边界,在地球物理领域数值模拟得到了广泛应用^[17-18]。因此,文中将采用有限单元法对不同情况下的管线进行正演模拟,分析雷达剖面的图像特征。

此外,近地表地形复杂,有一定起伏。实际探测管线时,各种反射波、绕射波、干扰波混淆在一起,无法区分与解释^[19-20]。侯爵等^[21]开展了起伏地表下的地震偏移成像数值实验,表明其方法的灵活性。刘四新等^[22]利用FDTD算法对典型的起伏地形模型进行数值模拟,并重点介绍了机载探地雷达的发展应用。但将FETD算法应用到起伏地形下管线的GPR探测中,目前还未见到相关报道。因此,文中对比了水平地表和起伏地表对于管线探测的影响,分析了不同间距、不同深度、不同材质、不同填充物管线的雷达剖面特征,对实际探测GPR数据的解释工作提供了理论依据。

1 方法原理

方法原理分两部分来阐述,第一部分为有限单元法推导Maxwell方程组,得到其离散格式,用来模拟GPR模型;第二部分为高度校正,实际工作时,一般会在地表进行探测,因此要做高度校正,将雷达剖面向实际地形契合,方便GPR数据的处理和解释。

1.1 有限单元法求解GPR波动方程

由电磁波传播理论可知^[23],雷达波在有耗媒介中的传播遵循Maxwell方程组。时间域二维TM模式下电场标量波动方程可以表示为

(1)-

\frac{1}{μ} \frac{\partial^{2} E_{z}}{\partial x^{2}}

\frac{1}{μ} \frac{\partial^{2} E_{z}}{\partial y^{2}}

+σ

\frac{\partial E_{z}}{\partial t}

+ε

\frac{\partial^{2} E_{z}}{\partial t^{2}}

\frac{\partial J_{z}}{\partial t}

=0,

其中,μ为磁导率(H/m);x,y为电磁波传播方向;E_z为z方向上的电场分量(V/m);σ为电导率(S/m);t为时间(s);J_z为z方向上的外加电流密度(A/m²)。

采用FETD算法求解上式。将整个模拟区域Ω采用三角单元进行离散,假设每个单元内部的电性参数相同,则单元内部线性插值函数为^[16]

(2)E_e

(x, y)

\overset{3}{\sum_{j = 1}} N_{j}^{e}

E_j,

其中, $N_{j}^{e}$ 为形函数,只与该三角单元的顶点坐标、面积和x、y有关;E_j为3个顶点上的电场数值。将式(2)代入到式(1),乘以形函数,并在单元内部积分,则可以写为

(3)Μ^eË_e+K^eE_e+C^e

{\overset{\cdot}{E}}_{e}

+F^e=0,

式中:M^e为质量矩阵;K^e为刚度矩阵;C^e为阻尼矩阵; ${\overset{\cdot}{E}}_{e}$ 为时间的一次导数;Ë_e为时间的二次导数;F^e为源项。它们具体的表达式为

(4)Μ^e=ε_e∬_eN^TNdxdy,

(5)K_e=K_e_x+K_e_y=

\frac{1}{μ}

∬_e

(\frac{\partial N^{T}}{\partial x} \frac{\partial N}{\partial x} + \frac{\partial N^{T}}{\partial y} \frac{\partial N}{\partial y})

dxdy,

(6)C^e=σ_e∬_eN^TNdxdy,

(7)F^e=ε_e∬_eN^T

\frac{\partial J_{z}}{\partial t}

dxdy。

将式(3)扩展到全局,并进行单元合成,可以得到整个求解域的GPR有限元微分方程组:

(8)ΜË+KE+

\overset{\cdot}{C E}

+F=0,

式中的一阶及二阶时间导数采用中心差分近似:

(9)

{\overset{\cdot}{E}}^{n}

\frac{1}{2 Δ t} [E^{n + 1} - E^{n - 1}]

(10)Ëⁿ=

\frac{1}{{(Δ t)}^{2}} [E^{n + 1} - 2 E^{n} + E^{n - 1}]

其中,Eⁿ为n时刻的电场值;Eⁿ^-1为n-1时刻的电场值;Eⁿ⁺¹为n+1时刻的电场值。通过这种时间离散方案,即可得到FETD算法求解Maxwell方程组的递推公式,模拟GPR电磁场在时域上的进程,其迭代公式为

(11)

(\frac{M}{{(Δ t)}^{2}} + \frac{C}{2 Δ t})

Eⁿ⁺¹=

(\frac{2 M}{{(Δ t)}^{2}} - K)

Eⁿ+

(\frac{C}{2 Δ t} - \frac{M}{{(Δ t)}^{2}})

Eⁿ^-1-fⁿ,

因上式方程左边每一个时间步的求解不包括刚度矩阵K,因此是显式算法。其数值稳定性条件为

(12)Δt≤

\frac{2}{\sqrt{ρ (M^{- 1} K)}}

式中: $\sqrt{ρ (M^{- 1} K)}$ 表示矩阵M^-¹K的谱半径,也为其最大特征值。

1.2 高度校正

在起伏地表做管线探测时,得到的雷达剖面中异常体位置与实际情况有一定的差距,因此需要做高度校正,将数据与实际地形相契合,这样有利于GPR数据的处理与解释。所得到的雷达剖面,横向为水平距离,纵向为时间,因此需要得到高度差所引起的“滞后时间”值,具体公式为

(13)t=

\frac{2 H}{v}

式中: t为时间;H为高度差,即某一标准水平线与地表测点之间的垂直距离;v为电磁波传播速度,与背景介质有关:

(14)v=

\frac{c}{\sqrt{ε_{r} μ_{r}}}

其中,c为真空中的光速,为3×10⁸m/s;ε_r为背景介质的相对介电常数;μ_r为背景介质的相对磁导率,一般为1。

2 数值案例

以下数值案例中的模型均用Comsol软件进行Delaunay三角剖分,在异常变化较大的区域会对网格进行加密,更加贴合其边界,提高计算精度。

2.1 地形对不同埋深、不同间距管线探测的影响

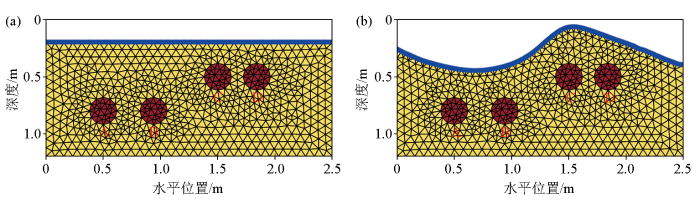
设计一个不同埋深、不同间距的金属管线模型,如图1所示。模拟区域大小为2.5 m×1.2 m。其背景相对介电常数为6,电导率为0.01 S/m,相对磁导率为1。模拟区域中有4个金属管(从左到右分别为A,B,C,D管),如图中红色圆形所示,其相对介电常数为1,电导率为10⁷ S/m,半径为0.12 m,从左到右圆心依次为(0.5 m,1 m)、(0.94 m,1 m)、(1.5 m,0.5 m)和(1.84 m,0.5 m),间距分别为0.2 m和0.1 m。图1a为水平地表模型的网格示意,总共70 424个单元,35 563个节点,0~0.2 m为空气层;图1b为起伏地表模型的网格示意,整个模拟区域的单元数为66 414,节点数为33 566,与水平地表模型的网格数大约相同。地表平均高度为0.2 m,上下起伏约为0.2 m。两者均在地表采用自激自收方式采集数据,激励源为中心频率600 MHz的Ricker子波,蓝色三角表示激发点(接收点)。采样间隔为0.01 m,总共接收250道数据;时间采样间隔为0.008 ns,总记录时长为30 ns。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 不同埋深、不同间距的模型网格示意

a—水平地表;b—起伏地表

Fig.1 Grid diagram of the model with different burial depths and different spacings

a—flat surface;b—ragged surface

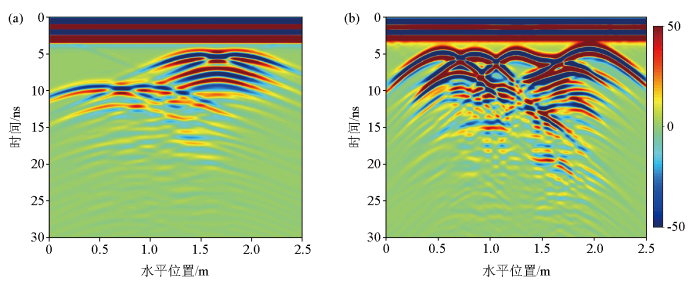
图2a、b为水平地表和起伏地表的正演剖面。从中可以看到,金属管线作为导体,将高频电磁波全反射,反射系数为-1,因此其相位与直达波相反。在图2a中,因为是水平地表,其双曲线的位置对应管线的埋深,左边两个金属管线(A和B)的反射波振幅明显小于右边两个管线(C和D)。此外,因为C管线和D管线的间距较近,所以在其剖面下方,会有一道很明显的反射曲线,这是电磁波在两个管线之间来回传播的反射波;在A管和B管的剖面下侧也可以看到,只不过因其间距偏大一些,与金属管的反射双曲线离得较远。在图2b中,可以明显看到4个金属管的强反射波,由于起伏地表的原因,不能对应管线的埋深,C管的反射波也因起伏地表而变形,非对称的双曲线。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 正演剖面

a—水平地表;b—起伏地表

Fig.2 Forward profiles

a—flat surface;b—ragged surface

图3为高度校正后的剖面。为了与起伏地表对比,同样将水平地表的剖面图做了统一的高度校正,即图1模型中0 m处的位置。由图可见,做完高度校正的两个剖面,金属管的双曲线位置大约在同一高度,但振幅却不相同。而且,B金属管的双曲线并不完整,因起伏地表和另外金属管的作用下,其反射波被其他杂波所湮没。因此,起伏地表所得到的剖面,并不能根据其振幅和双曲线的位置判断其埋深,需要做高度校正,且剖面较水平地表的剖面较为混乱。

图3

新窗口打开| 下载原图ZIP| 生成PPT

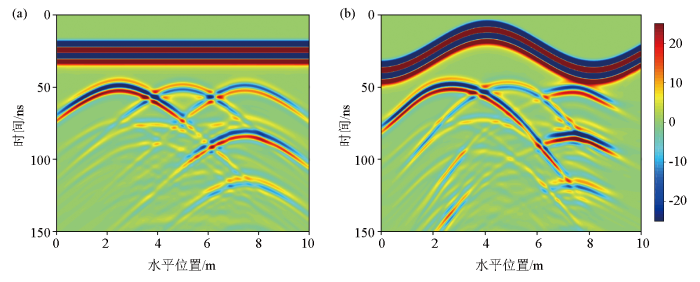
图3 高度校正后的正演剖面

a—水平地表;b—起伏地表

Fig.3 Forward profiles with height correction

a—flat surface;b—ragged surface

2.2 地形起伏对不同材质、不同填充物管线探测的影响

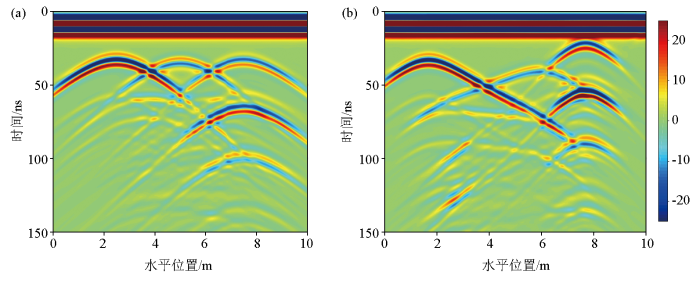
图4为不同材质、不同填充物的模型示意。模拟区域大小为10 m×4 m。其背景相对介电常数为9,电导率为0.001 S/m,相对磁导率为1。模拟区域中有3个管线,最左边的红色管线为金属管(A管),其相对介电常数为1,电导率为10⁷ S/m,半径为0.3 m,圆心为(2.5 m,2.5 m);中间的白色管线为充满空气的PVC管(B管),其相对介电常数为1,电导率为0,半径为0.3 m,圆心为(5 m,2.5 m);最右边的蓝色管线为充满水的PVC管(C管),其相对介电常数为80,电导率为0.002 S/m,半径为0.3 m,圆心为(7.5 m,2.5 m)。图4a为水平地表模型的网格示意,总共65 378个单元,33 048个节点,0~0.8 m为空气层;图4b为起伏地表模型的网格示意,整个模拟区域的单元数为66 003,节点数为33 364,与水平地表模型的网格数大约相同。地表平均高度为0.8 m,上下起伏约0.8 m。两者均在地表采用自激自收方式采集数据,激励源为中心频率100 MHz的Ricker子波,蓝色三角表示激发点(接收点)。采样间隔为0.037 m,总共接收270道数据;时间采样间隔为0.03 ns,总记录时长为150 ns。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 不同材质、不同填充物的模型网格示意

a—水平地表;b—起伏地表

Fig.4 Grid diagram of the model with different materials and fillers

a—flat surface;b—ragged surface

图5a、b为水平地表和起伏地表的正演剖面。由图可见,A金属管的反射波最强,且相位与直达波相反;B空气管的反射波较弱,相位与直达波相同;C水管由于与背景介质的相对介电常数相差较大,因此形成了多次反射波,其相位与直达波相反。图5a中,3个管线的反射曲线大约在同一时刻,因此在水平地表探测管线时,可以根据反射曲线顶点的位置判断其埋深,根据其相位和反射振幅、是否有多次波来判断管线材质、填充物等信息。在图5b中,因为在起伏地表上探测,3个管线的反射曲线已不在同一高度,但是同样看到,A金属管的反射能量最强,相位与直达波相反;B空气管的反射能量最弱,相位与直达波相同。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 正演剖面

a—水平地表;b—起伏地表

Fig.5 Forward profiles

a—flat surface;b—ragged surface

图6为高度校正后的剖面。为了与起伏地表对比,同样将水平地表的剖面图做了统一的高度校正,即图4模型中0 m处的位置。由图可见,直达波的形态与起伏地表相契合,管线的双曲线大约校正在了同一高度。对比图6a、b,起伏地表下的水管反射波能量要强于水平地表下的反射能量,且两翼并不完整,这是由于地表在水管正上方凹陷,垂直距离近,且在上坡地段探测时,能量被下凹界面反射,到达水管的能量较弱,因此双曲线两翼能量较弱。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 高度校正后的正演剖面

a—水平地表;b—起伏地表

Fig.6 Forward profiles with height correction

a—flat surface;b—ragged surface

3 结论

1)采用有限单元法对GPR管线探测进行了正演模拟,该算法可以与非结构网格结合,能更好地贴合实际地表。推导了FETD算法求解GPR波动方程的公式,并介绍了高度校正的具体实现过程,有利于雷达数据的处理与解释。

2)通过两个数值案例,对不同间距、不同埋深、不同材质、不同填充物的管线进行正演模拟,分析了起伏地表对探测的影响。实验结果表明:起伏的地表会导致探测到的反射波变得畸形,电磁波能量不均匀,并不是对称的双曲线;此外,不能简单地通过管线在探测结果中的上下位置来判断埋深,需要进一步进行高度校正。高度校正过后,可以根据双曲线顶点来推断管线的埋深,也可根据振幅、相位、是否有多次波来大致推断管线的材质和填充物。需要注意的是,因为地表起伏的原因,波形较为复杂、混乱,其反射波的能量不能作为唯一的判断依据,因此应结合其他信息来进行GPR数据解释。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

赵欣, 王希良, 刘珍岩, 等.

复杂条件下的地下管线探测模拟

[J]. 物探与化探, 2014, 38(6):1307-1312.