E-mail Alert Rss
 

物探与化探, 2023, 47(1): 110-119 doi: 10.11720/wtyht.2023.2606

方法研究·信息处理·仪器研制

联合核磁共振测井与Thomeer模型评价碳酸盐岩储层饱和度

陈星河,1,2, 张超谟,1,2, 朱林奇1,3, 张冲1,2, 张占松1,2, 郭建宏1,2

1.长江大学 地球物理与石油资源学院,湖北 武汉 430100

2.油气资源与勘探技术教育部重点实验室(长江大学),湖北 武汉 430100

3.中国科学院 深海科学与工程研究所,海南 三亚 572000

Evaluation of the saturation of carbonate reservoirs by combining the nuclear magnetic resonance logging and the Thomeer model

CHEN Xing-He,1,2, ZHANG Chao-Mo,1,2, ZHU Lin-Qi1,3, ZHANG Chong1,2, ZHANG Zhan-Song1,2, GUO Jian-Hong1,2

1. College of Geophysics and Petroleum Resources,Yangtze University,Wuhan 430100,China

2. Key Laboratory of Exploration Technologies for Oil and Gas Resources,Ministry of Education,Yangtze University,Wuhan 430100,China

3. Institute of Deep-sea Science and Engineering,Chinese Academy of Science,Sanya 572000,China

通讯作者: 张超谟(1962-),男,教授,主要从事测井地层评价、油藏描述等方向的工作。Email:zhangcm@yangtzeu.edu.cn

责任编辑: 叶佩

收稿日期: 2021-11-19   修回日期: 2022-02-28  

基金资助: 国家自然科学基金青年基金项目(42106213)
国家重大专项(2017ZX05032-003)
长江大学教育部实验室开放基金项目(K2021-03)
长江大学教育部实验室开放基金项目(K2021-08)

Received: 2021-11-19   Revised: 2022-02-28  

作者简介 About authors

陈星河(1997-),男,硕士研究生,主要从事测井数据处理与综合解释研究工作。Email:1637715221@qq.com

摘要

碳酸盐岩储层孔隙类型多样、孔隙结构复杂,传统的饱和度评价模型无法表征岩石的微观结构,给饱和度评价工作带来了极大的困难。针对该问题,本文以毛管压力曲线资料与核磁共振测井资料为基础,提出了结合核磁共振测井的Thomeer饱和度模型。分析压汞资料的孔隙系统结构信息,利用Thomeer函数拟合得到多孔隙类型的毛管压力曲线分布,将复杂的孔隙结构表征为多条Thomeer曲线的共同作用。核磁共振测井是唯一能够连续定量表征储层孔隙结构特征的测井方法,利用核磁共振横向弛豫时间谱参数T2算术平均值(T2LM)与核磁孔隙度(MPHS),结合R35岩石物理分类计算Thomeer参数Bv、Pd、G和最大孔喉直径模态元素Porositon,构建复杂孔隙结构碳酸盐岩的饱和度评价模型,该模型解决了实验手段无法开展连续地层孔隙结构评价研究的问题。将该模型应用到中东X油田复杂孔隙结构碳酸盐岩储层进行饱和度评价,与J函数模型、阿尔奇公式进行对比。结果表明该联合模型方法相比于J函数模型与阿尔奇公式,相对误差分别从0.496、0.442降低到0.272,且能较好地表征变化趋势,无论是在高饱和度储层还是低饱和度储层,都取得了较好的应用效果。该模型可以最大程度上避免复杂孔隙碳酸盐岩储层带来的影响,提高饱和度评价精度。

关键词： 碳酸盐岩; 饱和度; 核磁共振测井; Thomeer函数; 毛管压力曲线

Abstract

Carbonate reservoirs have various pores and complex pore structures.However,the microstructure of rocks cannot be characterized using conventional saturation evaluation models,making it extremely difficult to perform the saturation evaluation of carbonate reservoirs.Given this,this study proposed a Thomeer saturation model combined with the nuclear magnetic resonance (NMR) logging based on the data of capillary pressure curves and NMR logging.Specifically,information about the structure of the pore system in the mercury injection data was analyzed,and then the capillary pressure curves of multiple pore types were obtained through fitting using the Thomeer function.Finally,the complex pore structure was characterized using multiple Thomeer curves.The NMR logging is the only logging method that can continuously and quantitatively characterize the pore structure of reservoirs.The Thomeer parameters Bv,Pd,and G and the modal element Porositon of the maximum pore throat diameter were calculated using the logarithmic mean of T2 transverse relaxation time for NMR (T2LM) and the NMR total porosity (MPHS),as well as the classification of pore throat R35.Accordingly,the saturation evaluation model for carbonates reservoirs with complex pore structures was constructed.This model allows for the continuous evaluation of formation pore structure that cannot be achieved using experimental methods.This model was applied to the saturation evaluation of the carbonate reservoirs with complex pore structures in oilfield X in the Middle East.By comparison with the J function model and Archie's formula,this model decreased the relative error from 0.496 and 0.442,respectively to 0.272,better characterized the variation trend,and achieved encouraging application effects regardless of the saturation of reservoirs.Therefore,this model can minimize the impacts of carbonate reservoirs with complex pore structures and improve the precision of the reservoir saturation evaluation.

Keywords： Carbonate; saturation; nuclear magnetic resonance logging; Thomeer function; capillary pressure curve

PDF (4400KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

陈星河, 张超谟, 朱林奇, 张冲, 张占松, 郭建宏. 联合核磁共振测井与Thomeer模型评价碳酸盐岩储层饱和度[J]. 物探与化探, 2023, 47(1): 110-119 doi:10.11720/wtyht.2023.2606

CHEN Xing-He, ZHANG Chao-Mo, ZHU Lin-Qi, ZHANG Chong, ZHANG Zhan-Song, GUO Jian-Hong. Evaluation of the saturation of carbonate reservoirs by combining the nuclear magnetic resonance logging and the Thomeer model[J]. Geophysical and Geochemical Exploration, 2023, 47(1): 110-119 doi:10.11720/wtyht.2023.2606

0 引言

目前世界范围内剩余油气资源60%以上位于碳酸盐岩储层中,中东地区油气产量约占全世界产量的70%以上,且其中80%产量来自碳酸盐岩油气田[1⇓-3],巨大的储量使碳酸盐岩储层勘探开发一直备受关注。近几年,中国各大石油公司加大了中东地区碳酸盐岩油气藏的勘探开发力度。中东地区碳酸盐岩油气藏多为厚层块状,油气储量巨大,其储层多以孔隙为主,不同于国内碳酸盐岩储层主要以溶洞、裂缝为主。但中东碳酸盐岩储层孔隙结构复杂、孔隙类型多样,非均质性强,造成该区块储层参数评价困难[4⇓-6]。

含水饱和度一直是油田勘探开发中的重要储层参数,准确评价该参数对储层水淹级别评价、油田开发方案调整等后续动态评价开发都具有重要意义[7-8]。以往确定储层含水饱和度大多是采用阿尔奇公式及其衍生公式,但是当储层非均质性强时,会导致胶结指数m及饱和度指数n的变化范围加大,m值可在1.1~7.3变化[9⇓-11],n值可在1.2~3.5变化,因此在利用其公式计算含水饱和度会存在较大的误差。为此近几年来,国内外专家学者试图从导电机理、孔隙结构、孔隙类型变化等不同方面来寻求合理的饱和度计算模型。按孔隙发育类型划分,Serra提出基于基质孔隙与次生孔隙的双孔隙模型[12],Aguilera等[13]改进了基质孔隙、裂缝和非联通孔隙的三孔隙模型,但如何获得基质系统电阻率是极为困难的。按孔隙尺寸大小划分,该类模型的初衷是突出微小孔隙对碳酸盐岩系统导电性的贡献[14],但该类模型对大、中、小孔隙仅靠岩心核磁测量形态划分,缺少严格的数值上的界定,限制了其思想的推广;基于有效介质理论的饱和度模型[15],以麦克斯韦理论为基础,认为孔隙之间没有明显的串并联关系。但有效介质理论参数确定困难,导致该模型仍停留在实验室数值模拟阶段,在实际应用中实例较少。通过以上研究发现,油藏含水饱和度分布除一定程度上服从地质统计学规律,受岩相、岩性、孔隙度的影响外,更与岩石的微观结构有关,它主要是岩石毛管压力的函数[7]。因此利用毛管压力曲线确定碳酸盐岩储层含水饱和度已经是一种重要手段,常见方法有含油柱高度法[16]、J函数法[17]、Purcell法[18]等。含油柱高度法偏向理论,脱离实际地层情况;J函数法和Purcell法考虑了孔隙度、渗透率等因素,但无法考虑岩石微观结构的影响[19-20],不适合这类复杂的储层。

通过岩石物理分类研究发现Thomeer函数能够很好的表征孔隙系统复杂的碳酸盐岩储层,可以将复杂的孔隙系统表征为多条Thomeer曲线的共同作用结果,对评价复杂孔隙结构的碳酸盐岩储层具有一定的优势。但毛管压力实验只能测量孤立的、数量有限的岩心样品,无法开展连续的孔隙结构评价研究,且存在一定的危险性,而核磁共振测井T2谱能够反映储层孔隙结构特征与渗流能力,同时核磁测井数据具有连续性[21-22]。为此本文以中东区块X油田N层组为研究对象,在Thomeer函数的基础上,结合核磁数据与毛管压力数据明确基于核磁共振测井的Thomeer参数计算方法,建立基于核磁共振测井的碳酸盐岩储层饱和度评价模型,以提高A区块X油田碳酸盐岩储层饱和度计算精度。

1 研究区块储层基本特征

中东地区X油田主要岩石类型为生屑颗粒灰岩、生屑泥粒灰岩、生屑粒泥灰岩、孔虫泥粒灰岩、粒泥灰岩,属于比较纯净的石灰岩储层。储层储集空间以孔隙为主,发育有溶蚀孔、粒间孔、原生基质微孔、体腔孔。不同的孔隙类型对储层的渗流能力影响程度不同[23⇓-25],对研究区块的岩心物性资料进行分析,见图1。可以明显发现岩心孔渗相关性并不明显,岩心孔隙度(Cpor)在0.04~0.3,岩心渗透率(Cperm)在0.03~10 mD,属于低渗—超低渗储层。这种复杂孔隙结构的低渗—超低渗储层使得含水饱和度评价困难。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   岩心孔渗关系

Fig.1   Porosity-permeability relationship of rock core


2 表征碳酸盐岩孔隙结构的Thomeer方法

2.1 Thomeer函数

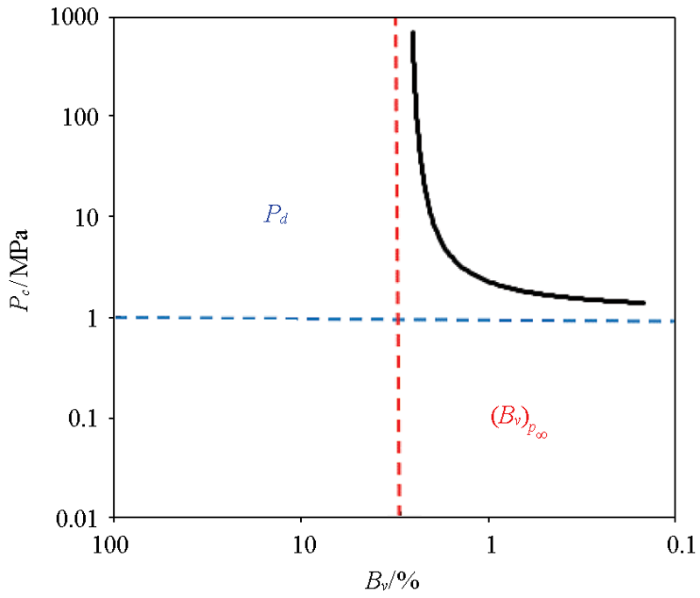
岩石的孔隙结构是指岩石孔隙与喉道的大小、分布、几何形状及相互连通性之间的关系,可用毛管压力曲线或孔喉分布曲线来表征。毛管压力曲线反映了在一定驱替压力下水银可以进入的孔隙喉道大小及这种喉道的孔隙体积,孔喉分布曲线是通过压汞资料计算得到的孔隙和喉道分布规律,更能直观反映孔隙结构特征。理论上确定孔喉分布曲线的大小、位置、曲线形态这3个特征参数就能确定孔喉分布曲线,进而表征孔隙结构。但传统的孔隙结构表征方法往往只考虑孔喉半径的影响,Swanson参数、R35、Katz和Thompson确定的最大孔喉半径等都只能表征一种特定的孔喉半径,只适合孔喉分布均匀、连通性好的岩石,对复杂孔隙结构的碳酸盐岩适用性有限。Thomeer发现在双对数坐标下,毛管压力曲线呈现双曲线形态,见图2,综合考虑3个特征参数,提出一种拟合曲线模型[26]:

(Bv)Pc(Bv)P∞=e-Glg(Pc/Pd)

式中:(Bv)Pc,注汞压力为Pc时对应的汞的体积,%;(Bv)P∞,注汞压力为无穷大时对应的汞的体积,%;Pc,注汞压力,MPa;Pd,排驱压力,MPa;G,几何因子,描述曲线弯曲程度,无量纲。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   Thomeer原理

Fig.2   Thomeer schematic diagram


在双对数坐标下,毛管压力曲线拟合为近似双曲线的形态。曲线距离水平轴和垂直轴的大小是由两条渐近线决定的。在无穷大的压力下,曲线无穷接近垂直渐近线,表示(Bv)P∞。当注汞体积趋近于0时,曲线无穷接近水平渐近线,表示排驱压力Pd。曲线形状则由几何因子确定。

孔喉分布曲线大小,曲线包络面积即进汞体积(Bv)P∞;曲线的位置可由排驱压力Pd确定,排驱压力可以表示最大孔隙半径处的端点,进而确定曲线位置;曲线形态则由几何因子G表征。Thomeer参数相比于传统孔隙结构参数更能表示孔隙分布曲线,进而表征孔隙结构。

对于多模态分布的复杂孔隙结构碳酸盐岩储层,不同孔隙类型都可以由不同毛管压力曲线表征,即等价为多条Thomeer双曲线集合。每条Thomeer曲线都可以表征不同的孔隙结构,单独研究,互不影响[27]。

2.2 Thomeer参数提取

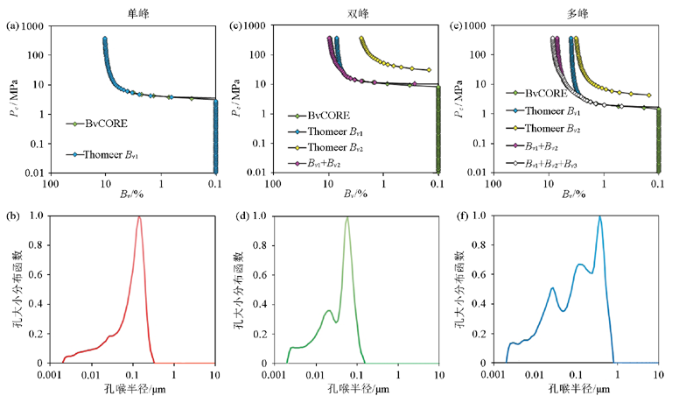
通过整理X油田N层组共计488块压汞样品,发现其孔喉半径分布曲线有单峰、双峰和多峰3种形态,见图3b、d、f,分布曲线峰的形态越复杂,其对应的孔隙结构越复杂,孔喉连通性越差。对于单峰、双峰、多峰的分布形态,即可用1条Thomeer曲线、2条Thomeer曲线、3条Thomeer曲线进行拟合,以表征其复杂的孔隙结构。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   Thomeer雅克比行列式法参数提取

Fig.3   Parameter extraction diagram of Thomeer jacobian determinant method


为了准确提取参数,采用雅克比行列式最优线性逼近法和牛顿阻尼迭代法(可提高迭代的收敛性)提取参数[28]。提取效果见图3a、c、e。图中BvCORE是岩心毛管压力曲线;Thomeer Bv1是第1个峰经过Thomeer函数拟合的曲线,其下标2、3分别为第2个峰、第3个峰的拟合结果;Bv1+Bv2是由2条Thomeer曲线构建的双峰分布的总毛管压力曲线;Bv1+Bv2+Bv3是由3条Thomeer曲线构建的多峰分布的总毛管压力曲线。提取的具体步骤为:先对毛管压力曲线进行麻皮校正[29],校正掉岩样制作过程中可能形成的汞蒸气空腔;然后通过牛顿阻尼迭代,将3个参数往误差最小的方向迭代,直到满足误差要求(3个参数的误差均小于0.00001),提取参数Bv、Pd和G。

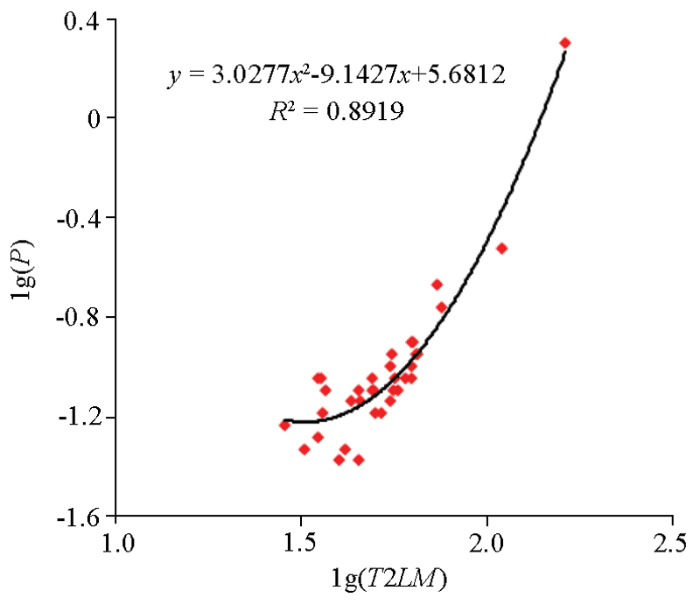
Clerke基于Thomeer参数提出了一种新的元素Porositon(简称P),最大孔喉直径模态元素[30,31],他将这些元素命名为“多孔体”。在碳酸盐岩孔隙系统的Thomeer最大孔喉直径的统计中,这类孔洞稳定、本征且重复出现,对表征储层孔隙系统模态具有重大作用。Porositon理论值为多模态孔隙体系中较大部分孔喉半径分布的峰值。对累计进汞量进行归一化处理,求取其第一个极大值,即Porositon值。Jan Buiting[32-33]利用Thomeer参数中的G和Pd开发了计算Porositon的方法。根据压汞样品,将提取的Porositon值与Pd、G进行多项式拟合,得到拟合关系:

P=e3.626/(G10.6353×Pd1)

式中:P,多孔体,最大孔喉直径模态元素,μm;G1、Pd1,下标1为压汞曲线第1个峰对应的Thomeer曲线1参数,下标2、3即为第2个峰、第3个峰对应的Thomeer曲线2、3参数。

Thomeer参数Bv、Pd、G和P 都可以很好的表征碳酸盐岩储层的复杂孔隙结构,其中Bv更是和孔隙进油体积具有关联。建立Bv、Pd、G、P和饱和度Sw的关系,就可以克服仅用孔渗或单一毛管压力数据的缺点,进而提高碳酸盐岩储层饱和度评价的准确性。

3 含水饱和度的计算

根据Thomeer函数和Porositon的定义,在出现多个模态的孔隙系统后,对整个孔隙结构起主要贡献的是孔喉半径区间最大的孔喉体系单元[30-31]。即当毛管压力曲线出现多峰形态时,前两个峰形之后峰的贡献可以忽略不计。所以本文重点通过Thomeer曲线1参数与Thomeer曲线2参数建立饱和度模型。

3.1 利用核磁共振测井计算Thomeer参数

3.1.1 Porositon值计算

Porositon作为最大孔喉直径模态,其值越大,对应的最大孔喉半径越大,相应的孔隙结构越好。T2LM是核磁共振测井T2分布谱的一种宏观形式,与孔隙结构密切相关,而且能反映储层的微观孔隙结构[34]。建立T2LM与Porositon关系,见图4。可以发现,T2LM与Porositon具有极佳的相关性,其R2可以达到0.89。这说明T2LM能够反映Porositon参数的变化。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   T2LM与Porositon关系

Fig.4   Relationship between T2LM and Porositon


3.1.2 Thomeer曲线1参数计算

1)Pd1值计算

毛束管力计算公式:

Pc=2σcosθ/r

式中:Pc,毛管压力,MPa;σ,油水界面张力,mN/m;θ,润湿接触角,°;r,毛细管半径,μm。

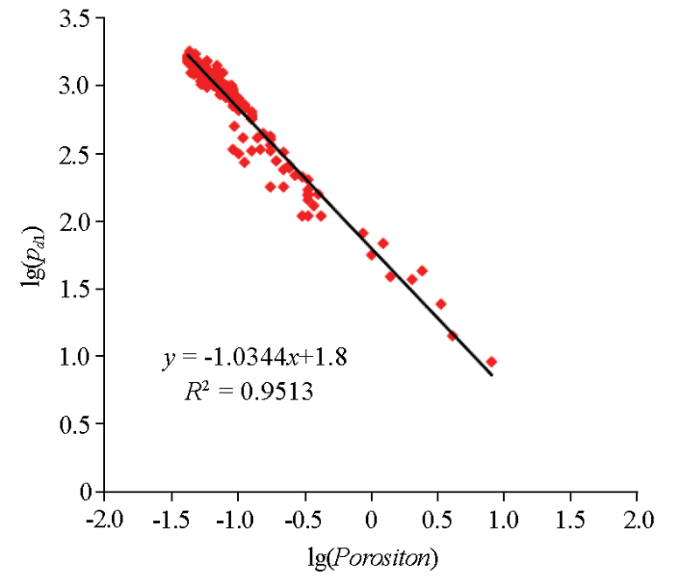
根据毛束管力计算公式毛管压力Pc与毛细管半径r是负相关,而排驱压力Pd与最大孔喉直径模态Porositon与Pc、r是存在对应关系,即Pd是可以和Porositon进行转换的。建立Pd1与Porositon关系,见图5,其呈现出极强的负相关性,R2可达到0.95,因此可以用Porositon来计算Pd1。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   Porositon和Pd1关系

Fig.5   Relationship between Porositon and Pd1


2)Bv1值计算

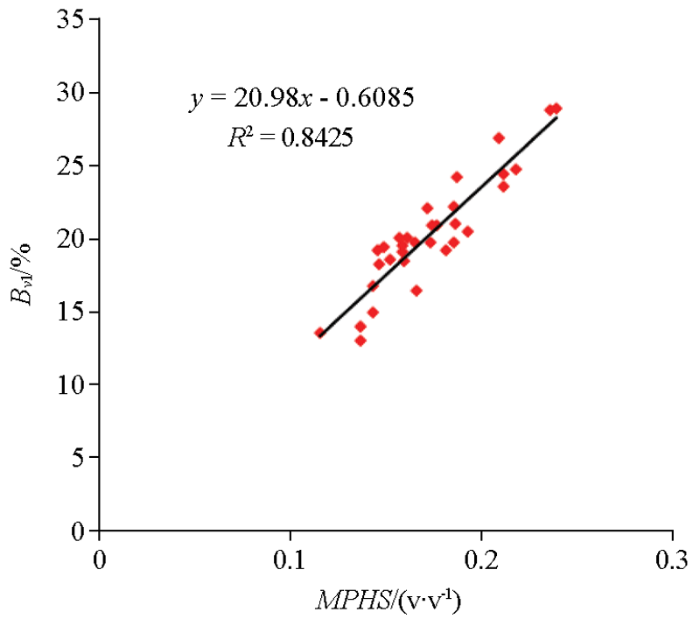
根据Bv的定义,在多孔隙类型发育的碳酸盐岩中,Bv1指的是大孔进油所占的体积,可以将其等效为岩样的有限流动孔隙度,有效流动孔隙度与孔隙度应存在正相关性。核磁孔隙度测井响应相较于常规孔隙度测井响应,反映的是孔隙中流体的信号,能够较准确地得到地层孔隙。建立Bv1与核磁孔隙度MPHS关系,见图6,发现两者有着极好的相关性,R2可达到0.84。于是用MPHS来表征Bv1参数。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   MPHS和Bv1关系

Fig.6   Relationship between MPHS and Bv1


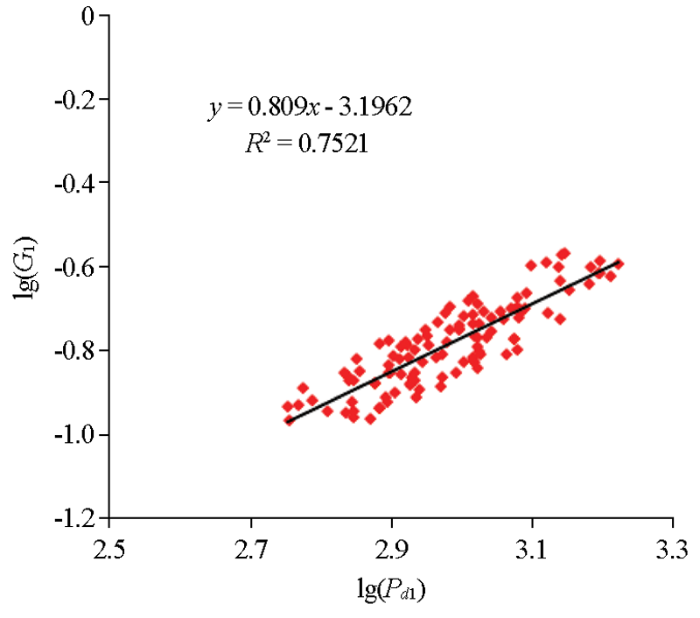
3)G1值计算

由Buiting等[33]研究可知,几何因子G1值越大,Thomeer曲线弯曲度越小,曲线越往上偏移。即其对应的毛管压力越大,物性更差,孔隙结构越复杂。几何因子G1和排驱压力Pd1建立关系,见图7。可以发现两者相关性明显,R2可达到0.84。这说明可以用Pd1来表征G1。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   Pd1和G1关系

Fig.7   Relationship between Pd1 and G1


综上,Thomeer曲线1参数响应关系见表1。

表1   Thomeer曲线1参数计算公式

Table 1  Thomeer curve 1 parameter calculation formula

参数计算公式
PorositonP=103.0277×(logT2LM)2-9.1427×logT2LM+5.6812
Bv1Bv1=120.98×MPHS-0.6085
Pd1Pd1=P-1.0344×101.8
G1G1=Pd10.809×10-3.1962

新窗口打开| 下载CSV


3.1.3 Thomeer曲线2参数

Thomeer曲线2参数Pd2、Bv2、G2,即多孔隙结构类型第二个峰对应的参数。因为Bv1和Bv2共同组成有效孔隙度,因此:Bv2=MPHS-Bv1。而Pd2和G2因为第二峰对应孔隙系统的物性差,其与测井响应的规律太弱[33]。

为了解决该地区碳酸盐岩储层的复杂性,利用毛管压力资料计算饱和度通常在储层岩石物理分类的基础上。本文参考FZI/RQI[35]分类和Winland R35[36]分类,将R35(压汞曲线在累计饱和度为35%时对应的孔喉半径)按照升序排列,在横坐标为对数坐标下的R35值、纵坐标为序号值的坐标图上,绘制R35与序列号半对数交会图,根据R35斜率的变化,寻找拐点,进行储层分类(PRT),见图8。将研究层段分成4类。分类标准见表2。

图8

新窗口打开| 下载原图ZIP| 生成PPT

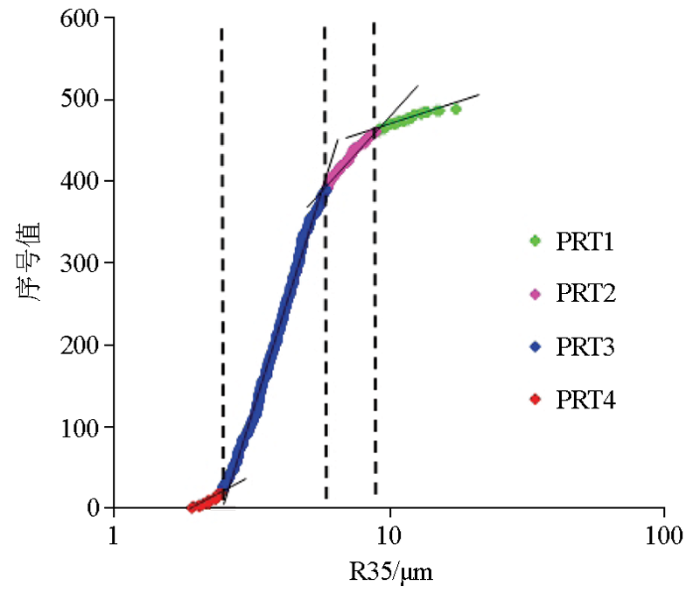
图8   以R35为基础的岩石物理分类

Fig.8   Petrophysical rock typing result based on R35 parameter slope method


表2   岩石物理分类标准

Table 2  Boundaries of petrophysical rock typing

岩石物理分类R35/μm
1>8.94
25.91~8.94
32.45~5.91
4<2.45

新窗口打开| 下载CSV


根据储层分类类型取平均值的方法,各层位Pd2和G2取值见表3。

表3   不同岩石物理分类的Thomeer曲线2参数取值

Table 3  Thomeer curve 2 parameters values of different petrophysical rock typing

岩石物理分类Pd2 /MPaG2
11.0450.296
224.1870.329
319.5630.418
426.3710.233

新窗口打开| 下载CSV


3.2 地层毛管压力与实验室毛管压力转换

根据研究区块油水样分析结果,N层组的油与水平均密度ρo=0.75g/cm3,ρw=1.1 679 g/cm3。查阅研究区块的地质资料,自由水界面FWL取-2 915 m。根据油藏的毛管压力与油水的重力差平衡原理[37],油藏条件下的毛管压力:

Pc,res=(ρw-ρo)×g×h/1000

式中:Pc,res,储层的毛管压力,MPa;ρw,水的密度,g/cm3;ρo,油的密度,g/cm3;g,重力加速度,取9.8 m/s2;h,油柱的高度(FWL与目的层的深度差值),m。

然后将油藏条件下的毛管压力转换为实验条件下的毛管压力:

Pc,hg=Pc,res×(σlcosθl)(σrcosθr)

式中:Pc,hg为实验室条件下的毛管压力,MPa;σl、σr分别为实验室和地层条件下的表面张力,mN/m;θl、θr分别为实验室和地层条件下的润湿角,°。根据研究区块资料及不同润湿系统的润湿性数据[37],见表4。可知:σrcosθr=16,σlcosθl=367。

表4   常见界面张力和润湿角

Table 4  Common interfacial tension and wetting angle

条件体系接触角θ/
(°)		界面张力σ/
(mN·m-1)		σcosθ/
(mN·m-1)
实验室空气—水07272
油—水304842
空气—汞140480367
油藏水—油303026
油—气05050
气—水044.644.6

新窗口打开| 下载CSV


3.3 Thomeer饱和度模型

由Thomeer函数可知,当Pc大于排驱压力Pd时,油克服毛管压力进入岩石孔隙中,此时的进油体积可以计算:

Bvocc=Bv×e-Glg(Pc/Pd)

式中:Bvocc,进油体积,小数。即当Pd1<Pc<Pd2时,此时的孔隙结构为单峰,油克服毛管压力开始进入岩石孔隙中,进油体积为:

Bvocc=Bv1×e-G1lg(Pc/Pd1)

当Pc>Pd2时,此时的孔隙结构为双峰,油克服毛管压力进入岩石孔隙中,进油体积为:

Bvocc=Bv1×e-G1lg(Pc/Pd1)+Bv2×e-G2lg(Pc/Pd2)

于是,根据含水饱和度的定义,计算公式为:

Sw=1-Bvocc/MPHS

式中:Sw,含水饱和度,小数。

4 应用效果对比分析

针对复杂孔隙结构的碳酸盐岩储层,通常采用J函数法计算含水饱和度,但在研究区块实际应用效果较差。为验证结合核磁共振测井的Thomeer模型计算效果,对研究区块近50口井的实际资料处理,以实际岩心资料为依据,与该区已有的J函数法及阿尔奇公式计算效果进行对比分析。其中阿尔奇参数依据本区岩电实验,取a=1,b=0.8,m=2.15,n=2.15,Rw=0.025 Ω·m。

4.1 J函数

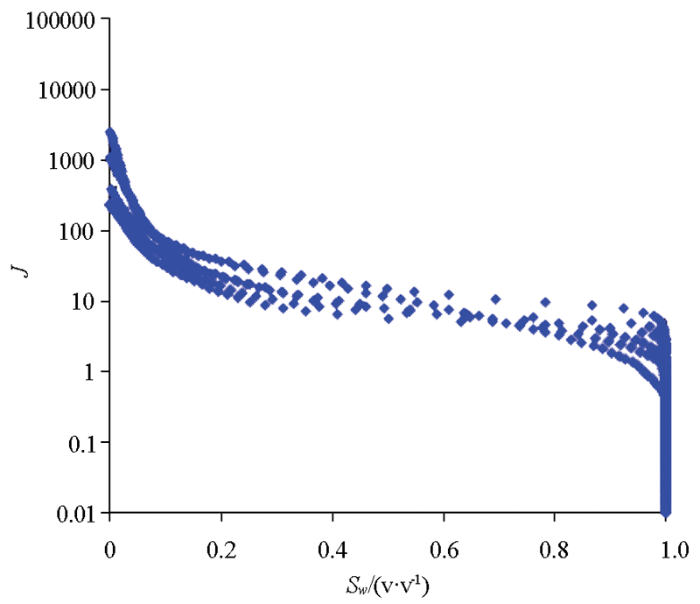
Leverett通过J函数建立毛管压力曲线与储层岩石物理性质之间的关系,来反映油藏的整体特征:

J=PcσcosθKφ

式中:K,渗透率,mD;ψ,孔隙度,v/v。

函数饱和度Sw与J函数的拟合关系见图9,计算模型如下:

Sw=[ln(J/205.68)]/(-7.023)

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   平均毛管压力曲线的J函数

Fig.9   J-function of average capillary pressure curve


4.2 应用效果分析

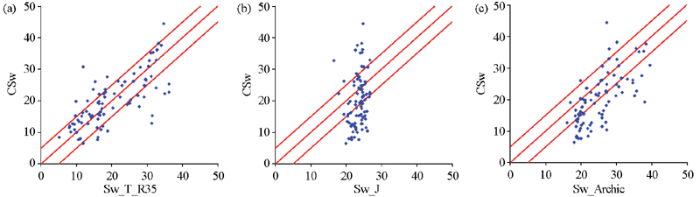
从上述岩心井中随机选择进行饱和度模型精度分析,见图10。其中第7道SW_T_R35为为本文提出的方法饱和度计算结果,第8道SW_ J是J函数方法饱和度计算结果,第9道SW_Archie是阿尔奇公式饱和度计算结果。可以看出Thomeer模型计算结果没有剧烈的震荡变换,与岩心饱和度变化趋势整体一致,与岩心饱和度更加接近。但J函数模型计算结果却难以反映岩心饱和度变化趋势,与岩心饱和度数值差距较大,明显存在低含水饱和度时计算结果偏高,高含水饱和度时计算结果偏低的情况;而阿尔奇公式计算结果也存在低含水饱和度时计算结果偏高的情况。统计3种方法计算饱和度与岩心饱和度的误差,见图11(CSw为岩心含水饱和度),其中J函数模型相对误差为0.496,均方根误差为8.66;阿尔奇公式相对误差为0.442,均方根误差为7.88,而Thomeer模型相对误差为0.272,均方根误差为6.11。尤其在高含油层段(Sw<20%),Thomeer模型相对于J函数模型、阿尔奇公式,将饱和度计算相对误差分别从0.764、0.661降低到0.331,均方根误差从9.66、8.92降低至5.64,具有良好的应用效果。联合核磁共振测井的Thomeer模型计算精度明显高于J函数模型与阿尔奇公式。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   MXX井部分层段测井解释成果(第7道为本文提出方法饱和度计算结果,第8道为J函数方法饱和度计算结果,第9道为阿尔奇公式饱和度计算结果)

Fig.10   Log interpretation results of some intervals in well MXX(track 7 is the saturation calculation result of the method proposed in this paper, and track 8 is the saturation calculation result of the J function method, track 9 is the saturation calculation result of the Archie’s formulas)


图11

新窗口打开| 下载原图ZIP| 生成PPT

图11   在±5%精度下的效果对比分析

a—联合核磁共振测井的Thomeer饱和度模型;b—J函数饱和度模型;c—阿尔奇公式饱和度模型

Fig.11   Comparative analysis of effects undert the accuracy of ±5%

a—Thomeer saturation model for combined nuclear magnetic resonance logging;b—J function saturation model;c—Archie formula saturation model


这是因为J函数模型仅仅只是考虑宏观上渗透率与孔隙度的影响,其模型是对已有的压汞岩样数据进行拟合,难以代表地层整体的孔隙结构,并不能考虑到地层复杂孔隙结构带来的影响。且研究区块属于低渗—超低渗储层,而J函数作为孔渗指数的函数,面对这种复杂碳酸盐岩储层,储层含水饱和度计算效果较差。阿尔奇公式因为没有考虑微观孔隙结构对饱和度的影响,在复杂孔隙结构的低含水饱和度储层计算结果较差。因此结合了核磁共振测井的Thomeer模型,综合考虑了全井段复杂孔隙结构与渗流能力的影响,面对中东区块X油田复杂孔隙结构、低渗—超低渗的碳酸盐岩储层,Thomeer饱和度模型优势更加明显。

5 结论

1)在多模态的复杂孔隙结构下,成功提取Thomeer参数Pd、Bv、G及Porositon。综合分析核磁T2谱和Thomeer参数之间的关系,解决毛管压力样品深度不连续问题,实现了Thomeer函数饱和度模型的连续计算。

2)在低渗—超低渗的复杂孔隙结构碳酸盐岩中,J函数、阿尔奇公式受其影响,导致计算结果较差,且难以表征饱和度变化趋势,Thomeer饱和度计算结果与岩心饱和度更加吻合,能够更好表征变化趋势,相比于J函数模型与阿尔奇公式,相对误差分别从0.496、0.442降低到0.272,均方根误差分别从8.66、7.88降低到6.11,在高含油层段,相对误差分别从0.764、0.661降低至0.331,均方根误差分别从9.66、8.92降低至5.64,更是具有良好的应用效果,其整体效果明显优于J函数模型与阿尔奇公式,能够较为准确地确定该地区复杂碳酸盐岩储层的原始含水饱和度。

3)结合核磁共振测井的Thomeer模型在确定含水饱和度的过程中,Thomeer曲线2的参数确定需要进行储层岩石物理分类,储层岩石物理分类效果的差异为模型计算精度奠定了基础,但也使得该模型确定含水饱和度具有一定的局限性。

参考文献

童晓光, 张光亚, 王兆明, 等.

全球油气资源潜力与分布

[J]. 石油勘探与开发, 2018, 45(4):727-736.

[本文引用: 1]

Thong X G, Zhang G Y, Wang Z M, et al.

Distribution and potential of global oil and gas resources

[J]. Petroleum Exploration and Development, 2018, 45(4):727-736.

[本文引用: 1]

康玉柱.

世界油气资源潜力及中国海外油气发展战略思考

[J]. 天然气工业, 2013, 33(3):1-4.

[本文引用: 1]

Kang Y Z.

Status of world hydrocarbon resource potential and strategic thinking of overseas oil and gas projects for China

[J]. Natural Gas Industry, 2013, 33(3):1-4.

[本文引用: 1]

张宁宁, 何登发, 孙衍鹏, 等.

全球碳酸盐岩大油气田分布特征及其控制因素

[J]. 中国石油勘探, 2014, 19(6):54-65.

[本文引用: 1]

Zhang N N, He D F, Sun Y P, et al.

Distribution patterns and controlling factors of giant carbonate rock oil and gas fields worldwide

[J]. China Petroleum Exploration, 2014, 19(6):54-65.

[本文引用: 1]

高利君, 李宗杰, 李海英, 等.

塔里木盆地深层岩溶缝洞型储层三维雕刻“五步法”定量描述技术研究与应用

[J]. 物探与化探, 2020, 44(3):691-697.

[本文引用: 1]

Gao L J, Li Z J, Li H Y, et al.

The deep karst fissure and cavern reservoir in Tarimbasin carved in three dimensions: Research and application of “five-step method” quantitative description technology

[J]. Geophysical and Geochemical Exploration, 2020, 44(3):691-697.

[本文引用: 1]

屈雪峰, 赵中平, 雷启鸿, 等.

鄂尔多斯盆地合水地区延长组裂缝发育特征及控制因素

[J]. 物探与化探, 2020, 44(2):262-270.

[本文引用: 1]

Qu X F, Zhao Z P, Lei Q H, et al.

Fracture development characteristics and controlling factors of Yanchang formation in Heshui area,Ordos Basin

[J]. Geophysical and Geochemical Exploration, 2020, 44(2):262-270.

[本文引用: 1]

Zhang X, Pang X, Jin Z, et al.

Depositional model for mixed carbonate-clastic sediments in the Middle Cambrian Lower Zhangxia Formation,Xiaweidian,North China

[J]. Advances in Geo-Energy Research, 2020, 4(1):29-42.

DOI:10.26804/ager.2020.01.04      URL     [本文引用: 1]

胡勇, 于兴河, 陈恭洋, 等.

平均毛管压力函数分类及其在流体饱和度计算中的应用

[J]. 石油勘探与开发, 2012, 39(6):733-738.

[本文引用: 2]

Hu Y, Yu X H, Chen G Y, et al.

Classification of the average capillary pressure function and its application in calculating fluid saturation

[J]. Petroleum Exploration and Development, 2012, 39(6):733-738.

[本文引用: 2]

Zhu L, Zhang C, Zhang Z, et al.

High-precision calculation of gas saturation in organic shale pores using an intelligent fusion algorithm and a multi-mineral model

[J]. Advances in Geo-Energy Research, 2020, 4(2):135-151.

DOI:10.26804/ager.2020.02.03      URL     [本文引用: 1]

Aguilera R.

Analysis of naturally fractured reservoirs from sonic and resistivity logs

[J]. Journal of Petroleum Technology, 1974, 26(11):1233-1238.

DOI:10.2118/4398-PA      URL     [本文引用: 1]

Honarpour M M, Sprunt E S, Hensel W M, et al.

Compilation of electrical resistivity measurements performed by twenty-five laboratories

[J]. Log Analysts, 1988, 29(1):13-29.

[本文引用: 1]

Degraaf J D, Schipper B A, Smits R M M, et al.

Measurements and evaluation of resistivity index curves

[J]. Log Analysts, 1991, 32(5):583-595.

[本文引用: 1]

Serra O.

Formation microscanner image interpretation

[C]// SMP 7028 Schlumberger Educational Service, 1989.

[本文引用: 1]

Aguilera R F, Aguilera R.

A triple porosity model for petrophysical analysis of naturally reservoirs

[J]. Petrophysics, 2004, 45(2):157-166.

[本文引用: 1]

Fleury M, Efnik M, Kalam M Z.

Evaluation of water saturation from resistivity in a carbonate field from laboratory to logs

[C]// CA 2004-22 the International Symposium of the Society of Core Analysts,2004.

[本文引用: 1]

Kazatchenko E, Markov M, Mousatov A, et al.

Simulation of the electrical resistivity of double porosity carbonate formations saturated with fluid mixtures

[C]// SPWLA 46th Annual Logging Symposium, 2005.

[本文引用: 1]

潘和平, 王兴, 樊政军, 等.

储层原始含油饱和度计算方法研究

[J]. 现代地质, 2000, 14(4):451-453.

[本文引用: 1]

Pan H P, Wang X, Fan Z J, et al.

Computing method of reservoir originality oil saturation

[J]. Geoscience, 2000, 14(4):451-453.

[本文引用: 1]

Leverett M C.

Capillary behaviors in porous solids

[J]. Transactions of the AIME, 1941, 142(1):152-169.

DOI:10.2118/941152-G      URL     [本文引用: 1]

Purcell W R.

Capillary pressures—Their measurement using mercury and the calculation of permeability therefrom

[J]. Journal of Petroleum Technology, 1949, 1(2):39-48.

DOI:10.2118/949039-G      URL     [本文引用: 1]

司马立强, 李清, 杨毅, 等.

用J函数法求取碳酸盐岩储层饱和度方法探讨

[J]. 岩性油气藏, 2014, 26(6):106-110.

[本文引用: 1]

Sima L Q, Li Q, Yang Y, et al.

Using J-function method to calculate saturation of carbonate reservoirs

[J]. Lithologic Reservoirs, 2014, 26(6):106-110.

[本文引用: 1]

郭晓博.

采用孔隙体积法计算平均毛管压力曲线

[J]. 中南大学学报:自然科学版, 2012, 43(11):4514-4521.

[本文引用: 1]

Guo X B.

Calculation of average capillary pressure curve using hole volume

[J]. Journal of Central South University:Science and Technology, 2012, 43(11):4514-4521.

[本文引用: 1]

Rafiei Y, Motie M.

Improved reservoir characterization by employing hydraulic flow unit classification in one of Iranian carbonate reservoirs

[J]. Advances in Geo-Energy Research, 2019, 3(3):277-286.

DOI:10.26804/ager.2019.03.06      URL     [本文引用: 1]

Zhang F, Zhang C.

Evaluating the potential of carbonate sub-facies classification using NMR longitudinal over transverse relaxation time ratio

[J]. Advances in Geo-Energy Research, 2021, 5(1):87-103.

DOI:10.46690/ager.2021.01.09      URL     [本文引用: 1]

刘航宇, 田中元, 郭睿, 等.

复杂碳酸盐岩储层岩石分类方法研究现状与展望

[J]. 地球物理学进展, 2017, 32(5):2057-2064.

[本文引用: 1]

Liu H Y, Tian Z Y, Guo R, et al.

Review and prospective of rock-typing for complex carbonate reservoirs

[J]. Progress in Geophysics, 2017, 32(5):2057-2064.

[本文引用: 1]

张萌, 乔占峰, 高计县, 等.

伊拉克哈法亚油田Mishrif组MB1-2亚段局限台地碳酸盐岩储层特征及评价

[J]. 东北石油大学学报, 2020, 44(5):35-45.

[本文引用: 1]

Zhang M, Qiao Z F, Gao J X, et al.

Characteristics and evaluation of carbonate reservoirs in restricted platform in the MB1-2 Sub-Member of Mishrif formation,Halfaya oilfield,Iraq

[J]. Journal of Northeast Petroleum University, 2020, 44(5):35-45.

[本文引用: 1]

Lucia F J.

Petrophysical parameters estimated from visual descriptions of carbonate rocks:A field classification of carbonate pore space

[J]. Journal of Petroleum Technology, 1983, 35(3):629-637.

DOI:10.2118/10073-PA      URL     [本文引用: 1]

Thomeer J H M.

Introduction of a pore geometrical factor defined by the capillary pressure curve

[J]. Journal of Petroleum Technology, 1960, 12(3):73-77.

[本文引用: 1]

Buiting J J.

Upscaling saturation-height technology for Arab carbonates for improved transition-zone characterization

[J]. SPE Reservoir Evaluation and Engineering, 2011, 14(1):11-24.

DOI:10.2118/125492-PA      URL     [本文引用: 1]

曹建胜, 武周.

牛顿法及带阻尼牛顿法的收敛域定理

[J]. 南京师大学报:自然科学版, 1989, 12(2):24-27.

[本文引用: 1]

Cao J S, Wu Z.

Theorems of convergence region of Newton and Damped Newton methods

[J]. Journal of Nanjing Normal University:Natural Science Edition, 1989, 12(2):24-27.

[本文引用: 1]

张关根, 赖翔友.

麻皮效应对压汞资料的影响

[J]. 石油勘探与开发, 1988, 17(6):84-86.

[本文引用: 1]

Zhang G G, Lai X Y.

The effect of pockmarks effect on mercury injection data

[J]. Petroleum Exploration and Development, 1988, 17(6):84-86.

[本文引用: 1]

Clerke E A, Mueller H W, Phillips E C, et al.

Application of Thomeer Hyperbolas to decode the pore systems,facies and reservoir properties of the Upper Jurassic Arab D limestone,Ghawar filed,Saudi Arabia:A “Rosetta Stone” approach

[J]. GeoArabia, 2008, 13(4):113-160.

DOI:10.2113/geoarabia1304113      URL     [本文引用: 2]

Clerke E A.

Permeability,relative permeability,microscopic displacement efficiency and pore geometry of M_1 bimodal pore systems in Arab-D limestone

[J]. Society of Petroleum Engineers, 2009, 14(3):524-531.

[本文引用: 2]

Buiting J J.

Fully Upscaled saturation-height functions for reservoir modeling based on Thomeer's method for analyzing capillary pressure measurements

[C]// SPE 105139 Middle East Oil and Gas Show and Conference,2007.

[本文引用: 1]

Buiting J J, Clerke E A.

Permeability from porosimetry measurements: derivation for a tortuous and fractal tubular bundle

[J]. Journal of Petroleum Science and Engineers, 2013, 108:267-278.

[本文引用: 3]

高敏, 安秀华, 祗淑华, 等.

用核磁共振测井资料评价储层的孔隙结构

[J]. 测井技术, 2000, 24(3):188-193.

[本文引用: 1]

Gao M, An X H, Zhi S H, et al.

Evaluating porous structure of reservoir with MRIL data

[J]. Well Logging Technology, 2000, 24(3):188-193.

[本文引用: 1]

Amaefule J O, Altunbay M.

Enhanced reservoir description:Using core and log data to identify hydraulic (flow) units and predict permeability in uncored intervals/wells

[C]// SPE 26436 Annual Technical Conference and Exhibition of the society,1993.

[本文引用: 1]

Al-Qenae K J, Al-Thaqafi S H.

New approach for the classification of rock typing using a new technique for iso-pore throat lines in Winland's plot

[C]// SPE 177327 Annual Caspian Technical Conference and Exhibition,2015.

[本文引用: 1]

欧阳健. 石油测井解释与储层描述[M]. 北京: 石油工业出版社,1994.

[本文引用: 2]

Ouyang J. Well log interpretations and reservoir descriptions[M]. Beijing: Petroleum Industry Press,1994.

[本文引用: 2]

/

〈 〉

京ICP备05055290号-3
版权所有 © 2021《物探与化探》编辑部
通讯地址：北京市学院路29号航遥中心 邮编：100083
电话：010-62060192；62060193 E-mail：whtbjb@sina.com , whtbjb@163.com