基于地磁坐标的多地磁台站日变改正方法

doi:10.11720/wtyht.2022.1649

基于地磁坐标的多地磁台站日变改正方法

高姗^,¹, 王文博^,², 崔志伟³^,⁴, 张琦洁¹, 闫红雨¹, 高维¹

1.中国自然资源航空物探遥感中心,北京 100083

2.61365部队,天津 300100

3.北京大学地球与空间科学学院,北京 100091

4.32011部队,北京 100094

Diurnal variation correction method for multiple geomagnetic stations based on geomagnetic coordinates

GAO Shan^,¹, WANG Wen-Bo^,², CUI Zhi-Wei³^,⁴, ZHANG Qi-Jie¹, YAN Hong-Yu¹, GAO Wei¹

1. China Aero Geophysical Survey and Remote Sensing Center for Natural Resources, Beijing 100083, China

2.61365 Troops,Tianjin 300100, China

3. School of Earth and Space Sciences, Peking University,Beijing 100091,China

4.32011 Troops,Beijing 100094,China

通讯作者: 王文博(1997-),男,毕业于解放军信息工程大学,主要从事大地测量数据处理方法研究工作。Email:2677393237@qq.com

责任编辑: 王萌

收稿日期: 2021-12-5 修回日期: 2022-06-3

基金资助:

海丝路工程“××××重点海域航空重磁精密测量”(DD20191001)
自然资源部航空地球物理遥感地质重点实验室课题(20202YEL10)

Received: 2021-12-5 Revised: 2022-06-3

作者简介 About authors

高姗(1988-),女,工程师,主要从事航空物探数据处理与制图研究工作。Email:shannely@163.com

摘要

传统多地磁台站日变改正都基于地理坐标,通过改进计算方法的方式来提高日变改正精度,本文通过比较分析传统日变改正的方法,并根据地磁坐标与地磁场强度具有更强相关性的特征,提出基于地磁坐标进行拟合的日变改正方法——地磁坐标拟合法。实验结果表明,基于地磁坐标的多站日变改正方法普遍提高了日变改正的精度,为多站日变改正提供了新的研究思路。

关键词： 多站日变改正; 地磁坐标拟合法; 日变改正精度

Abstract

The conventional diurnal variation correction of multiple geomagnetic stations based on geographic coordinates is to increase the precision of diurnal variation correction by improving the calculation methods. Based on the comparative analysis of conventional diurnal variation correction methods, this study proposed the geomagnetic coordinate fitting method for diurnal variation correction based on the high correlation between geomagnetic coordinates and geomagnetic field strength. The experimental results show that the diurnal variation correction of multiple geomagnetic stations based on geomagnetic coordinates generally improves the precision of diurnal variation correction and, thus, serves as a new study approach for diurnal variation correction of multiple geomagnetic stations.

Keywords： diurnal variation correction of multiple geomagnetic station; geomagnetic coordinate fitting method; precison of diurnal variation correction

PDF (683KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

高姗, 王文博, 崔志伟, 张琦洁, 闫红雨, 高维. 基于地磁坐标的多地磁台站日变改正方法[J]. 物探与化探, 2022, 46(6): 1518-1522 doi:10.11720/wtyht.2022.1649

GAO Shan, WANG Wen-Bo, CUI Zhi-Wei, ZHANG Qi-Jie, YAN Hong-Yu, GAO Wei. Diurnal variation correction method for multiple geomagnetic stations based on geomagnetic coordinates[J]. Geophysical and Geochemical Exploration, 2022, 46(6): 1518-1522 doi:10.11720/wtyht.2022.1649

0 引言

地磁场是由地球内部不同构造部分的磁性物质和动力学过程中地球内部和外部的电流体系所产生的各种磁场组合叠加的结果^[1]。在高精度的地磁测量中,变化磁场和感应磁场所引起的地磁日变值决定了地磁测量结果的精度。为了尽量减小地磁日变的影响,消除磁测数据时变信息,地磁数据的通化是高精度地磁测量中必不可少的一个重要步骤,磁测数据的精度在很大程度上取决于地磁日变改正的精度^[2]。

地磁日变在相同(相近)纬度上的地磁场日变化依赖于地方时,从形态到幅值均很相似,经度变化对此影响很小,在同一经度上的不同纬度的日变化之间的差异较大^[3],日变场总强度的大小由电流中心向南北两侧递增,即在电流中心以南日变场为北向,数值随磁纬度降低而增大;在电流中心以北日变场为南向,数值随磁纬度的增加而增大^[4]。通常,在进行区域地磁测量时,需在测区附近架设地磁日变观测站,或者使用测区周围同纬度附近现有的地磁台站作为日变观测站来对测区进行地磁日变改正。然而,在实际工作中存在测区同纬度附近难以架设地磁日变观测站、测区同纬度附近没有地磁台站和测区范围过大以至于单个地磁日变观测站不能对整个测区进行控制等情况。在这种情况下,应选择利用测区周围已有的多个地磁台站进行日变改正,这称为多站日变改正。近年来国内外学者较多的研究了多站日变改正计算方法在航空磁力测量和海洋磁力测量中的应用。在研究多站日变改正计算方法方面,单汝俭等^[5]提出了二维多项式最小二乘拟合法、时空拟合法和线性内插法这3种小范围地磁日变改正的拟合方法;边刚等^[6]分析了加权平均法和函数拟合法在海洋磁力测量中的应用,并提出了纬距加权法和纬度坐标拟合方法;卞光浪等^[7-8]提出基于纬差加权法的海洋磁力测量多站地磁日变改正值计算方法;顾春雷等^[9]利用反距离加权插值法对地磁矢量数据进行通化取得较好的地磁日变改正精度。国内外学者关于多站日变改正方法多是基于地理坐标系框架,对地磁场分布规律考虑较少,相比地理坐标,地磁坐标与地磁场强度具有更强的相关性。本文引入了地磁坐标来表征站点的空间经纬度,提出基于地磁坐标的函数拟合法,并在实验中对比验证了基于地磁坐标函数拟合法进行日变改正的有效性。

1 方法理论

1.1 加权平均法

测区任一点的地磁日变改正值由局部邻域内的 $m$ 个同步地磁日变观测站的日变改正值通过距离加权平均得到,这是加权平均法。设测点 $P$ 的日变改正值为 $T$ ,第i个地磁日变观测站的日变改正值为 $T_{i}$ ,测点 $P$ 与第i个地磁日变观测站的距离为d_i,记各地磁日变观测站距离权函数为 $f (d_{i})$ ,则测点 $P$ 的地磁日变改正值 $T$ 可通过式(1)计算:

(1)

T = \frac{(\overset{m}{\sum_{i = 1}} f (d_{i}) T_{i})}{\overset{m}{\sum_{i = 1}} f (d_{i})}

设权函数 $f (d_{i})$ 与距离 $μ (μ \geq 0)$ 次方的倒数成正比,距离权函数根据 $μ$ 的不同可选择如下形式:

(2)

\{\begin{array}{l} I_{O P} = 1, f (d_{i}) = \frac{1}{(d_{i} {+ ε)}^{0.5}} \\ I_{O P} = 2, f (d_{i}) = \frac{1}{(d_{i} {+ ε)}^{1}} \\ I_{O P} = 3, f (d_{i}) = \frac{1}{(d_{i} {+ ε)}^{2}} \\ I_{O P} = 4, f (d_{i}) = \frac{1}{(d_{i} {+ ε)}^{3}} \\ I_{O P} = 5, f (d_{i}) = \frac{1}{(d_{i} {+ ε)}^{4}} \end{array}

式中: $ε$ 为不为零的小数,当 $d_{i}$ 的值较大时可以忽略; $I_{O P}$ 为指标参数,指标参数不同的加权平均法可以得到不同的日变改正值。

1.2 函数拟合法

任一点 $P$ 的地磁日变改正值由其周围的 $m$ 个同步地磁日变观测站的日变改正值通过函数拟合得到,即为函数拟合法。建立如下某一点日变改正值 $T$ 与该点地理坐标 $(x, y)$ 之间的数学模型:

(3)

T (x, y) = a_{1} + a_{2} f (x) + a_{3} f (y)

式中: $a_{1}$ , $a_{2}$ , $a_{3}$ 为待定系数; $f (x)$ , $f (y)$ 分别为地理纬度函数和地理经度的函数;选择不同的指标参数 $I_{O P}$ ,模型形式存在如下差异:

(4)

\{\begin{array}{l} I_{O P} = 1, f (x) = x, f (y) = y \\ I_{O P} = 2, f (x) = x, f (y) = 1 n y \\ I_{O P} = 3, f (x) = x, f (y) = \sqrt{y} \\ I_{O P} = 4, f (x) = 1 n x, f (y) = y \\ I_{O P} = 5, f (x) = \sqrt{x}, f (y) = y \end{array}

设测点 $P$ 的日变改正值为 $T (x, y)$ ,地理经纬度为 $(x, y)$ ,第i个地磁日变观测站的日变改正值为 $T_{i} (x_{i}, y_{i})$ ,地理经纬度为 $(x_{i}, y_{i})$ 。在某一时刻,将 $m$ 个日变观测站的日变改正值和地理经纬度代入数学模型(3),可以得到 $m$ 个方程,每个方程有3个未知数 $a_{1}$ , $a_{2}$ , $a_{3}$ 。假设m=4,则可以得到如下具有3个未知数4个方程的方程组:

(5)

\{\begin{array}{l} T_{1} (x_{1}, y_{1}) = a_{1} + a_{2} f (x_{1}) + a_{3} f (y_{1}) \\ T_{2} (x_{2}, y_{2}) = a_{1} + a_{2} f (x_{2}) + a_{3} f (y_{2}) \\ T_{3} (x_{3}, y_{3}) = a_{1} + a_{2} f (x_{3}) + a_{3} f (y_{3}) \\ T_{4} (x_{4}, y_{4}) = a_{1} + a_{2} f (x_{4}) + a_{3} f (y_{4}) \end{array}

设 $Y = (a_{1}, a_{2}, a_{3})^{T}$ , $B = (T_{1}, T_{2}^{}, T_{3}, T_{4})^{T}$ ,则方程组即为:

(6)

A Y = B

(7)

A = |\begin{array}{l} 1 f (x_{1}) f (y_{1}) \\ 1 f (x_{2}) f (y_{2}) \\ 1 f (x_{3}) f (y_{3}) \\ 1 f (x_{4}) f (y_{4}) \end{array}|

其中:A、B分别为已知系数矩阵和已知日变改正数向量。Y为未知向量,由最小二乘法计算得到方程组的最小二乘解:

(8)

Y = (A^{T} {A)}^{- 1} A^{T} B

。

2 地磁坐标拟合法

地理坐标系和地磁坐标系属于不同的坐标参考系,地理坐标系的参考椭球体是一个近似于地球表面的扁圆椭球体,以地球的旋转轴作为参考椭球体的轴。地磁坐标系是一个球形极坐标系,极轴与地球的北分偶极(地磁)轴重合,与地理轴有大约 $11 °$ 夹角^[10]。同一日变观测站在这两种坐标系下经纬度是不同的。因此地球参考系的选择将会对日变改正精度产生影响。目前所使用的参考坐标系都是基于地理坐标系得到的经纬度坐标,本文基于地磁场的分布引入地磁坐标来表征站点的空间经纬度。

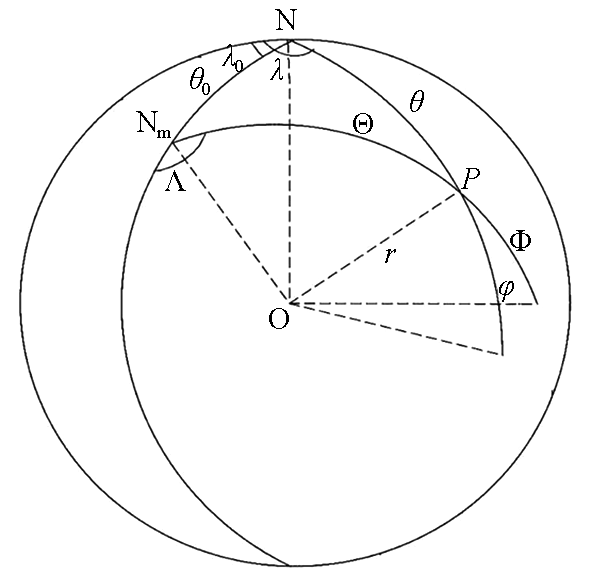
对地球主磁场做近似的描述通常采用地心倾斜偶极子模型。按照与地理坐标相同的定义方式定义的地心倾斜偶极子坐标系,又叫作地磁坐标系^[11]。地磁轴与地面的交点叫作地磁极,经过地理南极的地磁经线(即过地理南极、地磁北极、地磁南极3点的地磁经线)为 $0 °$ 地磁经线,地磁经度以此向东为 $0 °$ ~ $360 °$ 。地磁纬度在地磁赤道处为 $0 °$ ,向地磁北极逐渐变为 $90 °$ ,向地磁南极逐渐变为 $- 90 °$ 。由此可知,地面上某一点的地磁余纬即为地心与该点的连线与地磁轴的夹角,地面上某一点的地磁经度即为过该点的地磁子午面与零度地磁经线的夹角。

图1表示地磁坐标与地理坐标之间的关系。N_m和N分别表示地磁北极和地理北极。用 $Λ$ 和 $Φ$ 表示地面点 $P$ 的地磁经纬度, $λ$ 和 $φ$ 表示地面点 $P$ 的地理经纬度, $Θ$ 和 $θ$ 分别表示地磁余纬和地理余纬,地磁北极 $N_{m}$ 的地理余纬和经度分别为 $θ_{0}$ 和 $λ_{0}$ 。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 地磁坐标与地理坐标的关系

Fig.1 The relationship between geomagnetic corrdinates and geographic coordinates

根据球面三角公式,可以得到地磁坐标与地理坐标之间的转换公式:

(9)

\begin{matrix} \{\begin{array}{l} c o s Θ = c o s θ c o s θ_{0} + s i n θ s i n θ_{0} c o s (λ - λ_{0}), \\ s i n Λ = s i n θ s i n (λ - λ_{0}) / s i n Θ 。 \end{array} \end{matrix}

在函数拟合法中的变量采用地磁纬度和地磁经度为x,y变量,则为地磁坐标拟合法。

3 实验分析

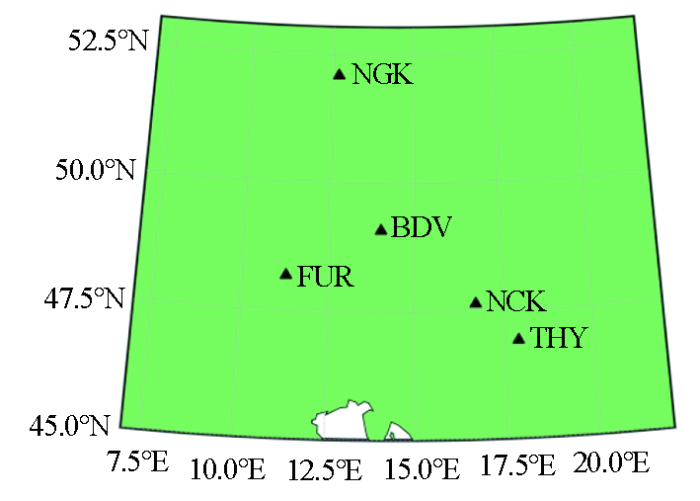
为了对地磁坐标拟合法在多站日变改正计算中的应用效果进行分析,本文选择了国际地磁台站网中位于欧洲的BDV、NGK、FUR、NCK和THY共5个地磁台站观测数据进行实验,其地理坐标及换算的地磁坐标如表1,分布情况如图2所示。台站间距离较近,以BDV台站为例,它到NGK、FUR、NCK和THY的距离分别为347、224、255、376 km。同步观测时间为2014年1月1日00:00~24:00,属于地磁非磁扰日,磁场变化相对平稳,选取日均值作为日变基值,则各站的地磁日变曲线如图3所示。

表1 各台站地理坐标与地磁坐标

Table 1 Geographic and geomagnetic coordinates of Geomagnetic stations

站点	地理纬度	地理经度	地磁纬度	地磁经度
BDV	49.07°	14.02°	48.71°	97.68°
FUR	48.17°	11.28°	48.30°	94.69°
NCK	47.63°	16.72°	46.87°	99.73°
NGK	52.07°	12.68°	51.83°	97.63°
THY	46.90°	17.90°	45.96°	100.60°

新窗口打开| 下载CSV

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 台站分布

Fig.2 Geomagnetic station distribution

图3

新窗口打开| 下载原图ZIP| 生成PPT

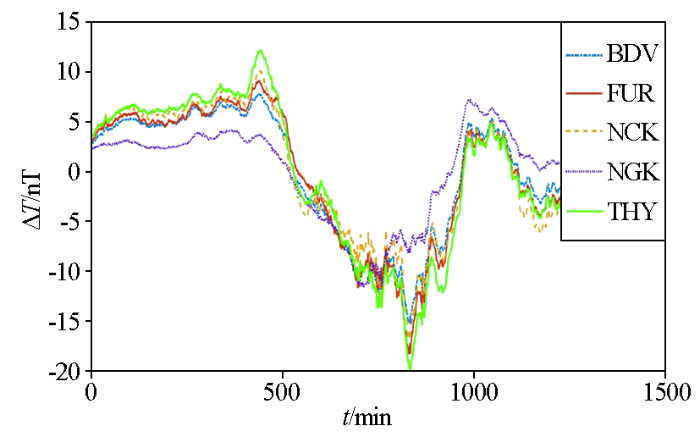
图3 同步日变曲线

Fig.3 Synchronous daily curve

由图3可以看出,5个地磁台站的数据日变幅度最大不超过40 nT,且夜间的日变曲线变化较为平稳,其中,台站FUR、NCK、BDV和THY的同步日变曲线相似,相关程度较强,台站NGK与其他4个台站距离较远,纬度差别大,其日变曲线与其他4个台站的日变曲线相关程度较低。由此可以看出不同台站的日变曲线变化趋势相同,但日变数据的幅值随纬度变化有所差别,且具有一定的相关性,日变曲线的相关程度随站间距离增大而降低。

为了充分说明地磁坐标拟合改进方法的优势,本文分别选取BDV、FUR作为验证站,利用其他4个台站的地磁日变数据,分别利用加权平均法、函数拟合法和地磁坐标拟合法对验证站进行地磁日变改正并进行精度评估。加权平均法仅与距离相关,与坐标系无关,坐标系变化不影响加权平均法精度结果。函数拟合法中的变量分别采用地理纬度和地理经度、地磁纬度和地磁经度为x,y变量,即分别为地理坐标拟合法和地磁坐标拟合法。

本次实验通过统计不同方法计算得到的日变改正值与验证站实测日变值的均方根误差 $σ$ 来评价不同日变改正计算方法的精度式(10), $σ$ 越小表示计算得到的日变改正数据精度越高,反之越低。

(10)

σ = \sqrt{\frac{\overset{n}{\sum_{i = 1}} λ_{i}^{2}}{n}}

式中: $n$ 为参加统计数据的个数, $λ_{i}$ 为第 $i$ 个多站日变计算值与实测值之差。

表2和表3分别统计了以BDV和FUR为验证站,加权平均法、函数拟合法、地磁坐标拟合法及利用单站日变改正的精度情况。

表2 BDV验证台站各方法内插精度统计

Table 2 BDV verification station method interpolation accuracy statisticsnT

$I_{O P}$	加权平均法	函数拟合法		单站日变改正
$I_{O P}$	加权平均法	地理坐标	地磁坐标	单站日变改正
1	0.425	0.355	0.351	THY	1.800
2	0.480	0.378	0.355	NGK	2.626
3	0.550	0.366	0.353	FUR	0.936
4	0.624	0.370	0.366	NCK	1.443
5	0.691	0.373	0.368

新窗口打开| 下载CSV

表3 FUR验证台站各方法外推精度统计

Table 3 FUR verification station method extrapolation accuracy statisticsnT

$I_{O P}$	加权平均法	函数拟合法		单站日变改正
$I_{O P}$	加权平均法	地理坐标	地磁坐标	单站日变改正
1	1.085	0.943	0.921	BDV	0.936
2	1.077	1.187	0.941	NCK	1.385
3	1.046	1.043	0.931	NGK	3.467
4	1.000	1.004	0.969	THY	1.211
5	0.980	1.132	0.955

新窗口打开| 下载CSV

当BDV作为验证站时这种网型结构称之为内插网型,当FUR作为验证站时网型称之为外推网型。由实验结果可以看出,加权平均法的精度与指标参数 $I_{O P}$ 的选择有关,与坐标系无关。地理坐标函数拟合法和地磁坐标函数拟合法当 $I_{O P}$ 为1时精度最高,而加权平均法对不同网型而言精度随 $I_{O P}$ 的变化规律不同。综合分析实验结果可知,对于内插网型来说加权平均法 $I_{O P}$ 越小精度越高,即幂指数 $μ$ 越小拟合效果越好,日变改正精度越高,而对于外推网型则相反。无论是内插还是外推,不管指标参数如何选择,本文基于地磁场的分布而提出的地磁坐标函数拟合方法相对于传统的函数拟合法,在精度上有所提升。为避免偶然性,本文还选用了多组不同台站进行实验,实验结果均表明地磁坐标拟合法精度有普遍提升。

4 结论

本文基于地磁坐标与地磁场强度具有更强的相关性,提出了地磁坐标函数拟合方法,通过实验验证了地磁坐标拟合法在多站日变改正中的适用性,相对于传统的基于地理坐标的函数拟合法提高了多站日变改的精度,为多站日变改正提供了一种精度更高的方法。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

徐文耀.

地磁学[M]. 北京: 地震出版社, 2003.