基于深度加权的三维地震斜率层析成像

doi:10.11720/wtyht.2022.1586

基于深度加权的三维地震斜率层析成像

田坤^,¹, 王常波¹, 刘立彬¹, 张建中²

1.中国石化胜利油田分公司物探研究院, 山东东营 257022

2.中国海洋大学海洋地球科学学院,山东青岛 266000

3D seismic slope tomography based on depth weighting

TIAN Kun^,¹, WANG Chang-Bo¹, LIU Li-Bin¹, ZHANG Jian-Zhong²

1. Geophysical Research Institute,Shengli Oilfield Branch Company of Sinopec,Dongying 257022,China

2. College of Marine Geosciences,Ocean University of China,Qingdao 266000,China

责任编辑: 叶佩

收稿日期: 2021-11-1 修回日期: 2022-08-11

基金资助:

中国石化股份公司科技攻关项目(P19015-3)
胜利油田科技攻关项目(YKW2002)
胜利油田科技攻关项目(YKB2009)

Received: 2021-11-1 Revised: 2022-08-11

作者简介 About authors

田坤(1986-),男,高级工程师,主要从事地震资料处理方法技术的研究与应用工作。Email:tiankunwudi@163.com

摘要

地震斜率层析成像是一种联合使用反射波局部相干同相轴的走时和斜率来建立宏观速度模型的有效方法。对于低信噪比资料,往往能够拾取的深层有效反射波数据远远少于浅层反射波数据,使深部地层速度的层析反演效果差。因此,提出了一种基于深度加权的三维地震斜率层析成像方法。在每次迭代的线性层析反演方程中,对观测数据关于离散模型节点速度的核函数进行深度加权,权系数根据离散模型节点深度和当前迭代的各个炮—检对的反射点深度来确定,实现了加大深部反射波数据对深层速度的约束作用、浅层速度主要由浅部反射波数据约束的目的,在保持浅层速度反演精度的同时,改善对深层速度的反演效果。对理论模型数据和实际资料应用测试的良好效果,表明了该方法的有效性。

关键词： 速度建模; 地震反射波; 斜率层析成像; 深度加权

Abstract

The seismic slope tomography is an effective method for building macro-velocity models using the travel time and slopes of locally coherent events of reflected waves.For data with low signal-to-noise ratios,the deep effective reflection wave data that can be picked are often far fewer than the shallow reflection wave data,resulting in a poor tomographic inversion effect of the velocity of the deep strata.Therefore,this study proposed a 3D seismic slope tomography method based on depth weighting.In the linear tomographic inversion equation of each iteration,the depth weighting was performed for the kernel function of the observed data on the node velocity of the discrete model.The weighting coefficient was determined according to the node depth of the discrete model and the reflection point depth of each shot-detection pair of the current iteration,increasing the constraining effect of deep reflection wave data on the deep velocity.Meanwhile,the shallow velocity was mainly constrained by the shallow reflection wave data.As a result,the inversion effect of deep velocity could be improved while maintaining the inversion precision of shallow velocity.The application and tests of both theoretical model data and actual data yielded satisfactory results,verifying the effectiveness of the method.

Keywords： velocity model; seismic reflection wave; slope tomography; depth weighting

PDF (3463KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

田坤, 王常波, 刘立彬, 张建中. 基于深度加权的三维地震斜率层析成像[J]. 物探与化探, 2022, 46(6): 1485-1491 doi:10.11720/wtyht.2022.1586

TIAN Kun, WANG Chang-Bo, LIU Li-Bin, ZHANG Jian-Zhong. 3D seismic slope tomography based on depth weighting[J]. Geophysical and Geochemical Exploration, 2022, 46(6): 1485-1491 doi:10.11720/wtyht.2022.1586

0 引言

斜率层析成像是一种联合使用反射波局部相关同相轴的走时和斜率数据,同时反演地层速度和反射点位置的有效方法^[1]。该方法在共炮道集和共检波点道集拾取反射波走时和斜率数据时,在层析反演中引入地震斜率信息,能够克服反射波射线的多路径问题,特别是在层析反演中不需要建立反射同相轴与地层界面的对应关系,对低信噪比资料有更强的适应性。斜率层析成像方法由Billette等^[1]于1998年提出后的几年内,成功应用于海上实际资料处理,并将二维斜率层析成像发展至三维情形^[2⇓⇓-5]。斜率层析成像方法不断得到完善和发展,提出了适于OBN资料反演的斜率层析成像^[6]、各向异性斜率层析成像^[7-8]、基于程函方程的伴随状态法斜率层析成像^[9]、适用于起伏地表的斜率层析成像^[10]、慢度平方三角网格斜率层析成像^[11]等。在斜率层析成像的正则化方面,发展了基于反射角的结构性平滑约束^[12]、地层格架正则化约束^[13]等方法。走时和斜率数据的拾取技术得到较大发展,一是在不同的数据域进行拾取,如叠前时间域^[14-15]、叠后时间域^[16]以及深度偏移域^[17⇓-19]等数据域;二是对拾取的方法原理进行改进,如基于直线和双曲线叠加的斜率自动拾取^[20]、基于曲波变换的地震反射波同相轴斜率的拾取^[21]、应用运动学反偏移提取斜率数据^[22]等方法,提高了斜率数据的拾取精度。

对于实际地震资料,由于地震波的球面扩散和介质吸收衰减作用,使来自深部地层的地震波能量较弱^[23-24]。在构造复杂多样、地层速度变化较大的地区,深部反射波变化复杂,地震资料信噪比往往较低。济阳坳陷中—古生界潜山构造复杂,叠前反射地震同相轴能量弱,十分杂乱,能够拾取的深部反射波走时和斜率数据往往较少,导致深部地层射线覆盖不足,层析反演速度的效果较差。为了解决该问题,本文在层析反演方程中,对数据关于地层速度的核函数进行深度加权处理,增强深部反射波数据对深层速度的约束作用,从而提出一种基于深度加权的三维地震斜率层析成像方法,并通过理论模型合成的地震数据和济阳坳陷古潜山实测地震资料的测试,验证了提出方法的有效性。

1 方法原理

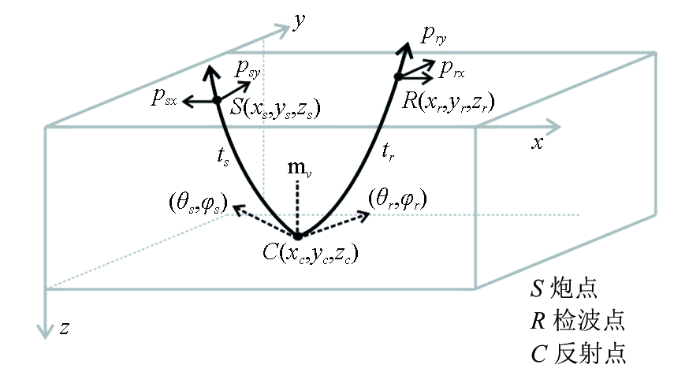
地震斜率是反射波走时关于水平距离的导数,即慢度矢量的水平分量,可用之确定射线从炮点出发和到达检波点的角度。地震立体层析成像^[1]把一个炮—检对的反射射线看成是从反射点分别到炮点和检波点的两段射线(如图1所示),通过不断修改速度模型和反射点位置,使计算的两段射线与地面的交点及对应的斜率和走时与观测数据达到一致,从而形成了一种有效的斜率层析成像方法^[25]。为了提高对深部地层速度的层析反演效果,在地震立体层析成像方法基础上,我们提出了一种基于深度加权的三维斜率层析成像方法。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 模型参数与观测数据几何关系

Fig. 1 Geometric relationship between model parameters and observation data

1.1 模型离散化及走时和斜率计算

采用规则网格对速度模型进行离散化,已知网格节点上的速度值,模型空间中任意位置的速度值由网格节点速度值的三次B样条函数表示。当给定射线的出发位置和出射角度时,采用二阶Runge-Kutta法求解下列程函方程^[2],获得从反射点到地表位置的射线路径及其走时和斜率数据:

(1)

\{\begin{array}{l} \frac{d x}{d t} = \nabla_{p} H = v^{2} (x) p (x) \\ \frac{d p (x)}{d t} = - \nabla_{x} H = - \frac{\nabla v (x)}{v (x)} \\ p^{2} (x) = \frac{1}{v^{2} (x)}, (t = 0) \end{array}

式中:x=(x,y,z)表示位置矢量,p=(p_x, p_y, p_z)表示慢度矢量,t是沿射线波传播时间,v为传播速度,Ñ代表梯度算子。

1.2 数据空间和模型空间

三维斜率层析的数据空间d可表示为:

(2)

\begin{array}{l} d = \\ [(x_{s}, y_{s}, z_{s}, p_{s x}, p_{s y}, x_{r}, y_{r}, z_{r}, p_{r x}, p_{r y}, t_{s r})_{n}]_{n = 1}^{N} \end{array}

其中,(x_s, y_s, z_s)为炮点S的坐标,p_sx和p_sy分别为炮点处沿x方向和y方向的斜率,(x_r, y_r, z_r)为检波点R的坐标,p_rx和p_ry分别为检波点处沿x方向和y方向的斜率,t_sr为炮点S和检波点R之间的反射走时,N表示射线对的个数,下标n表示第n个射线对。炮点、检波点的位置和高程从野外观测系统文件中获得,炮点、检波点的斜率和双程走时数据,用倾斜叠加等方法^[14,20,21]在叠前地震道集上拾取。

模型空间m由离散速度参数m_v和射线段参数m_ray组成,可表示为:

(3)m=(m_v,m_ray)^T,

(4)m_v=[v_m

]_{m}^{M}

(5)m_ray=[(x_c,y_c,z_c,θ_s,φ_s,θ_r,φ_r, t_s,t_r)_n

]_{n}^{N}

=1,

其中,(x_c, y_c, z_c) 为反射点C的坐标,θ_s, φ_s,θ_r和φ_r分别表示从反射点到炮点S和检波点R的射线出射角,t_s和t_r分别表示从反射点到炮点和检波点的走时,N是炮-检对或反射点的总数,v_m是离散速度模型第m个节点的速度值,M表示整个离散速度模型的节点数。

1.3 反演方程及求解

斜率层析反演的目标函数为:

(6)

\begin{array}{l} O (m) = \frac{1}{2} {[d_{c a l} (m) - d_{o b s}]}^{T} C_{d}^{- 1} [d_{c a l} (m) - d_{o b s}] + \\ \frac{1}{2} λ (m - m_{0})^{T} C_{m}^{- 1} L^{T} L (m - m_{0}) \end{array}

其中,第一项是数据残差项,第二项是模型约束项,l是阻尼系数,调节这两项作用的相对大小。d_obs和d_cal分别是观测数据和计算数据,m是模型,m₀是先验模型,L表示拉普拉斯算子,对模型进行光滑约束,上标T表示矩阵转置。C_d和C_m分别是数据和模型的协方差矩阵,分别对数据项和模型参数项进行加权处理,并分别对走时、斜率等不同量级的观测数据以及速度、反射点位置等不同量级的模型参数进行归一化处理。

d_cal(m)是一个非线性函数,在初始模型m₀处,对该函数进行泰勒级数展开,取至线性项得

(7)

d_{c a l} (m) = d_{c a l} (m_{0}) + G (m - m_{0})

其中,G=(G_v,G_ray)^T,G_v为数据关于离散模型节点速度的核函数矩阵,G_ray为数据关于射线参数(反射点坐标、射线出射角、射线走时)的核函数矩阵^[24]。

为了求取目标函数 (6)的极小解,把式 (7)代入式 (6)后,令目标函数对模型空间参数的导数等于0,则得到下列线性反演方程:

(8)

(\begin{array}{l} G_{v}^{T} C_{d}^{- 1} G_{v} & G_{r a y}^{T} C_{d}^{- 1} G_{r a y} \\ λ C_{m}^{- 1} L & 0 \end{array}) (\begin{array}{l} Δ m_{v} \\ Δ m_{r a y} \end{array}) = (\begin{array}{l} G_{v}^{T} C_{d}^{- 1} Δ d \\ 0 \end{array})

其中,Dd表示数据残差向量,其元素是观测数据与当前反演模型计算的数据之差,Dm_v和Dm_ray分别是射线段参数和离散速度值的修正量。

一般地,地震资料中的深层反射波能量低于浅层反射波能量。对于低信噪比地震资料,能够拾取并利用的深层反射波走时和斜率数据,远远少于浅层反射波走时和斜率数据。在反演过程中,这样的观测数据对浅层模型参数的约束较充分,而对深层模型参数的约束不足。同时,由于一个反射数据对其射线通过的不同深度的各个模型参数的约束权重是一样的,所以浅层反射数据只约束浅层模型参数,深层反射数据同时约束浅层与深层模型参数,且对浅层与深层模型参数的约束作用相当。这些因素往往导致对深层模型参数的反演效果欠佳。反演方程(8)中的数据协方差矩阵 $G_{d}^{- 1}$ 调整各个数据的相对作用,但不能调节同一个数据对不同深度模型参数的约束作用。为此,我们通过对上述反演方程的深度加权处理来克服这种缺陷。通过深度加权,使每个反射波数据对模型参数的约束作用随深度逐渐增强,从而达到增大深层反射波数据对深层速度参数约束作用的目的。

反演方程(8)中包含各个反射波数据对其射线穿过的不同深度速度参数的核函数,我们对速度参数对应的核函数进行深度加权处理,建立下列含有深度加权的反演方程:

(9)

\begin{array}{l} (\begin{array}{l} G_{v}^{T} w_{v} C_{d}^{- 1} G_{v} & G_{r a y}^{T} C_{d}^{- 1} G_{r a y} \\ λ C_{m}^{- 1} L & 0 \end{array}) (\begin{array}{l} Δ n_{v} \\ Δ n_{r a y} \end{array}) = \\ (\begin{array}{l} G_{v}^{T} C_{d}^{- 1} Δ d \\ 0 \end{array}) \end{array}

其中,w_v是对速度参数对应的核函数矩阵的深度加权矩阵,计算式见下面的式(11),D ${n_{}}_{r a y}$ 和Dn_v分别是与射线段参数和速度参数对应的待反演的未知向量。应用LSQR算法^[26]求解该反演方程,得到D ${n_{}}_{r a y}$ 和Dn_v。该解是引入深度加权后的解,再利用下式把该解换算成模型参数的修正量:

(10)

Δ m = (\begin{array}{l} Δ m_{v} \\ Δ m_{r a y} \end{array}) = (\begin{array}{l} {\bar{w}}_{v} C_{m}^{- 1} Δ n_{v} \\ C_{m}^{- 1} Δ n_{r a y} \end{array})

其中, ${\bar{w}}_{v}$ 为由每一个速度参数的换算因子组成的矩阵,计算式见下面的式(12)。用求得的模型修正量Dm更新当前模型,就得到新模型。这样,不断迭代地进行,直到反演模型计算数据与观测数据之间的均方误差满足给定的误差限为止。

1.4 深度加权系数

斜率层析反演的模型空间包含反射点深度,每次迭代后获得了各个炮—检对的反射波数据对应的反射点深度。用各个反射波数据对应的反射点深度,建立式(9)中的深度加权系数矩阵w_v。该矩阵是对角矩阵,其元素应随着离散速度节点深度的增大而增大。经研究试验,构造的深度加权系数表达式为:

(11)

w_{i k} = \frac{\frac{h_{k}}{z_{i}}}{\overset{N_{i}}{\sum_{k = 1}} \frac{h_{k}}{z_{i}}}

式中,w_ik表示第i个反射波数据关于第k个节点速度的核函数的深度加权系数,z_i是第i个反射点深度,h_k是第i个反射波射线路径穿过的第k个单元节点的深度,N_i是第i个反射波射线穿过的单元节点总数。

我们用每个节点速度对应的所有深度加权系数的均值,构造式(10)中速度修正量的换算因子矩阵 ${\bar{w}}_{v}$ 。该矩阵为对角矩阵,各元素的计算式为:

(12)

{\bar{w}}_{m} = \frac{\overset{N_{m}}{\sum_{i = 1}} w_{i m}}{N_{m}}

式中, ${\bar{w}}_{m}$ 为第m个节点速度的换算因子,w_im为第i个炮—检对数据对应第m个节点速度的深度加权系数,N_m为第m个单元节点对应的射线条数或炮-检对总数。

2 理论模型试验

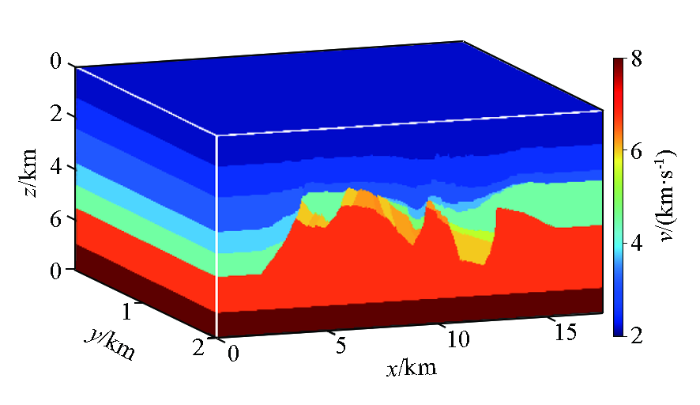
根据济阳坳陷埕岛地区古潜山构造特征和有关地震、钻井资料,建立一个三维古潜山理论速度模型,用于测试本文方法的效果。如图2所示,模型长17.5 km,宽2 km,深7.8 km,速度变化范围为2.2~8.0 km/s。浅部速度界面几乎水平,且速度差异小;潜山顶位于4 km深度以下,潜山速度界面起伏较大,且与上覆地层存在较大的速度差异;潜山内部地层无反射界面信息。将反射点均匀分布于各个速度界面,在各个反射点以θ为15°、30°、45°和55°,φ为10°、20°、30°和35°的角度向地表方向发射地震射线,追踪射线至地表为止,获得51 216组观测数据。其中,来自潜山顶面以下的深部反射波数据较少。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 古潜山理论速度模型

Fig. 2 Theoretical velocity model of buried hill

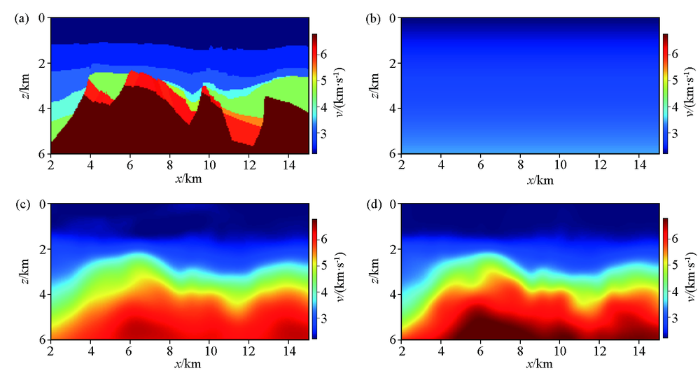
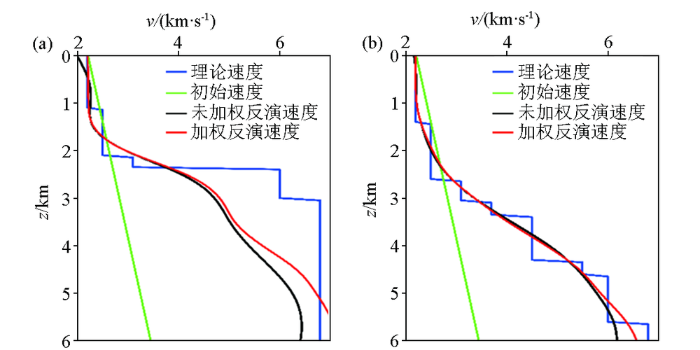
取y=1 km的速度模型切片(图3a),初始速度v₀=(2.2+0.25z)km/s(图3b)。分别用无深度加权和有深度加权(α=1)的三维斜率层析成像方法对上述模拟数据进行反演。模型离散网格在x、y和z这3个方向上的尺寸皆为250 m,反演速度模型在y=1km处的速度切片如图3c和3d所示,反演速度沿深度的变化曲线与理论模型速度曲线的对比见图4。可以看出,浅部地层反演模型与理论模型吻合较好,且有无深度加权,对潜山顶面上部地层的反演结果影响不大。但是,当无深度加权时,对深层潜山的反演速度比理论模型速度整体偏小,且误差较大;当用了深度加权后,对深部潜山速度的反演效果得到了明显提高,与理论速度变化趋势吻合得更好。说明了层析反演中深度加权的作用及其有效性。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 y=1km的速度模型切片

a—理论模型;b—初始模型;c—无深度加权的反演模型;d—有深度加权的反演模型

Fig. 3 Speed model slice with y=1 km

a—theoretical model;b—initial model;c—inversion model without depth weighting;d—inversion model with depth weighting

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 理论速度与反演速度随深度变化曲线的对比

a—x=6 km处速度曲线;b—x=12 km处速度曲线

Fig. 4 Comparison between theoretical velocity and inversion velocity curves with depth

a—velocity curve with x=6 km;b—velocity curve with x=12 km

3 实际资料应用

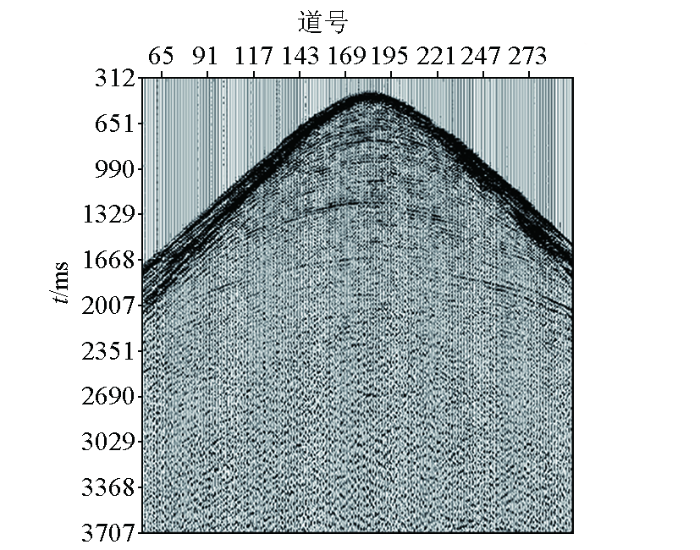
本文方法应用于胜利油田孤岛地区的三维地震资料。炮线和检波点线分别呈EW向和SN向布设,炮间距50 m,检波点间距25 m。对地震数据进行噪声压制、振幅补偿、初至切除等预处理。预处理后的单炮地震记录,如图5所示,其中1.5 s以上的浅部反射同相轴密集分布,而深部反射同相轴稀少,能拾取到的有效走时和斜率数据较少。基于倾斜叠加原理^[14],分别在共炮域和共检波点域拾取了局部相干同相轴的走时和斜率,一共获得150 047组观测数据,用该组数据反演研究区的三维速度模型。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 预处理后单炮地震记录

Fig. 5 Single shot seismic record after preprocessing

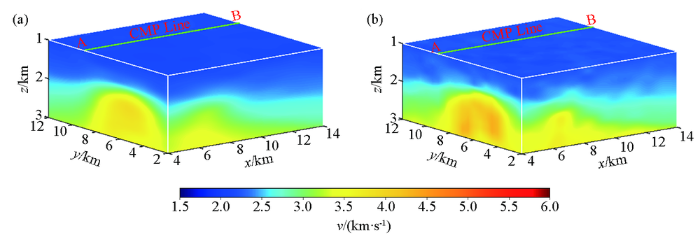
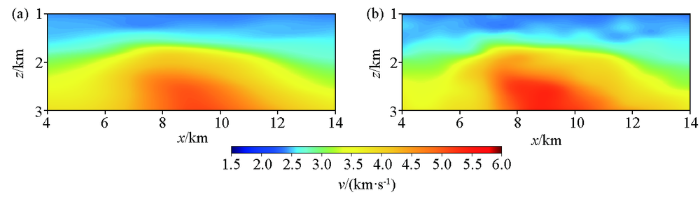
根据研究区地表速度及有关速度等先验信息,建立了一个速度随深度线性递增的初始速度模型v₀=(2.2+0.6z)km/s。模型在x方向长度为15 km,在y方向宽度为4 km,z方向厚度为5 km。模型离散网格在x、y和z方向的大小分别为250 m、250 m和200 m,分别使用无深度加权斜率层析成像方法和有深度加权斜率层析成像方法进行了反演,深度加权系数中的α取值为0.5,迭代20次后反演的三维速度模型如图6所示,沿y=9 km测线的反演速度模型切片如图7所示。可以看出,两个模型的浅层速度相差较小,而中深部速度相差较大,有深度加权斜率层析成像方法反演的潜山速度值明显增大,且整个反演模型的变化细节更明显。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 斜率层析成像反演的速度模型

a—无深度加权;b—有深度加权

Fig. 6 Velocity model of slope tomography inversion

a—no depth weighting;b—with depth weighting

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 斜率层析成像反演速度模型沿y=9 km测线(图6AB线段位置)切片

a—无深度加权;b—有深度加权

Fig. 7 Slope tomography inversion velocity model slice along the measuring line y=9 km (figure 6AB line position)

a—no depth weighting;b—with depth weighting

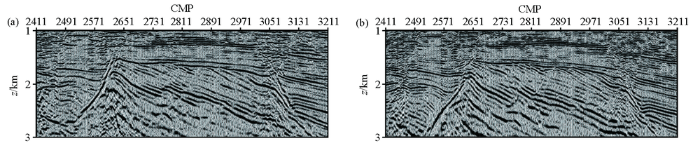
分别使用无深度加权和有深度加权的斜率层析成像反演的速度模型进行叠前深度偏移处理,沿y=9 km测线的叠前深度偏移剖面如图8所示。比较两个剖面可以看出,在浅部两个模型的偏移效果相差较小,但在中深部,特别在潜山顶面及其以下,使用深度加权斜率层析成像速度模型的偏移成像效果更好。可见,有深度加权的斜率层析成像提高了反演速度模型的效果。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 使用不同速度模型的叠前深度偏移剖面

a—无深度加权斜率层析反演模型;b—有深度加权斜率层析反演模型

Fig. 8 Prestack depth migration profiles using different velocity models

a—non depth weighted slope tomography of inversion model;b—depth weighted slope tomography inversion model

4 结论

当地震勘探资料信噪比较低时,能够获取的深层反射波走时和斜率数据往往较少,常规斜率层析成像对深层速度的反演效果较差。为此,本文利用离散模型节点深度和反演过程获得的各个炮-检对的反射点深度,构造了一种针对斜率层析反演核函数矩阵的深度加权方程,通过对斜率层析反演方程进行自适应深度加权处理,使各个反射波数据对地下速度模型的约束作用随着深度逐渐增强,从而提出一种基于深度加权的三维地震斜率层析成像方法。理论模型和实际资料测试结果表明,该方法能够在保持浅层速度反演精度的同时,提高对深层速度的反演效果,改善整体反演速度模型的质量,为低信噪比地震资料速度建模提供一种有效技术。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Billette

, Lambaré

Velocity macro-model estimation from seismic reflection data by stereotomography

[J]. Geophysical Journal International, 1998, 135(2):671-690.

DOI:10.1046/j.1365-246X.1998.00632.x URL [本文引用: 3]

[2]

Billette

, Le

B S

, Podvin

, et al.

Practical aspects and applications of 2D stereotomography

[J]. Geophysics, 2003, 68:1008-1021.

DOI:10.1190/1.1581072 URL [本文引用: 2]

[3]

Begat

S L

Application of 2D stereotomography to marine seismic reflection data

[C]// SEG Technical Program Expanded Abstracts, 2000, 19(1):2484.