E-mail Alert Rss
 

物探与化探, 2022, 46(6): 1431-1443 doi: 10.11720/wtyht.2022.0181

方法研究·信息处理·仪器研制

基于非结构化有限元的三维井地电阻率法约束反演

王智,1, 王程2, 方思南3

1.长江大学 电子信息学院,湖北 荆州 434023

2.中煤科工集团 西安研究院有限公司,陕西 西安 710077

3.长江大学 地球物理与石油资源学院,湖北 武汉 430100

Constraint inversion of three-dimensional borehole-to-surface resistivity based on unstructured finite element

WANG Zhi,1, WANG Cheng2, FANG Si-Nan3

1. Electronics and Information School, Yangtze University, Jingzhou 434023,China

2. Xi’an Research Institute Co. Ltd., China Coal Technology and Engineering Group Corp., Xi’an 710077, China

3. College of Geophysics and Petroleum Resources,Yangtze University,Wuhan 430100,China

责任编辑: 王萌

收稿日期: 2022-04-13   修回日期: 2022-07-9  

基金资助: 国家自然科学基金项目“起伏地形下的井中激电井—地方式并行反演研究”(41604093)
天地科技股份有限公司科技创新创业资金专项(2020-TD-QN11)
中国博士后科学基金(2017M622382)

Received: 2022-04-13   Revised: 2022-07-9  

作者简介 About authors

王智(1985-),男,湖北省武汉市人,博士,副教授,主要研究方向为电磁法数值模拟。Email:1324385898@qq.com

摘要

电磁探测反演是典型的不适定问题,易造成反演结果的多解性,不适定性是反演自身固有的特征,没有求解的附加信息这一本质困难是很难克服的,解决该问题的有效方法是研究约束反演。本文采用目前较为主流的高斯牛顿—共轭梯度法(GN-CG),在反演目标函数中直接施加约束条件,将介质电阻率的取值范围作为先验信息和约束条件以外点罚函数法的方式引入到反演目标函数中,与常规三维电阻率反演目标函数相比,增加了不等式约束项的目标函数,理论上可以压制反演的多解性。通过多种理论模型的测试结果表明,本文基于不等式约束的三维井地电阻率反演算法有效地改善了反演结果的精度,以惩罚函数法施加不等式约束条件的方式是现实可行及有效的。

关键词： 井地电阻率法; 反演; 高斯牛顿—共轭梯度法; 不等式约束; 惩罚函数法

Abstract

The inversion of electromagnetic detection data is a typical ill-posed problem and is prone to cause a multiplicity of solutions of the inversion results. The ill-posedness is an inherent characteristic of inversion and is difficult to overcome without additional information. An effective way to solve this problem is constrained inversion. In this study, the Gauss-Newton - conjugate gradient (GN-CG) method was used to directly impose constraints on the inversion objective function. Specifically, the dielectric resistivity range was introduced into the inversion objective function as the prior information and constraints using the exterior penalty function method. Compared with the conventional three-dimensional resistivity inversion objective function, the objective function with inequality constraints can suppress the multiplicity of solutions in theory. As revealed by the testing results of various theoretical models, the three-dimensional borehole-to-surface resistivity inversion algorithm based on inequality constraints effectively improves the precision of inversion results, and the way of imposing inequality constraints using the penalty function method is feasible and effective.

Keywords： borehole-to-surface resistivity method; inversion; GN-CG; inequality constraint; penalty function method

PDF (5887KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

王智, 王程, 方思南. 基于非结构化有限元的三维井地电阻率法约束反演[J]. 物探与化探, 2022, 46(6): 1431-1443 doi:10.11720/wtyht.2022.0181

WANG Zhi, WANG Cheng, FANG Si-Nan. Constraint inversion of three-dimensional borehole-to-surface resistivity based on unstructured finite element[J]. Geophysical and Geochemical Exploration, 2022, 46(6): 1431-1443 doi:10.11720/wtyht.2022.0181

0 引言

电磁法勘探是以地壳中不同岩石之间的电性差异为物理基础(如导电性、导磁性、介电性以及电化学性质的差异),通过观测研究人工或天然形成电磁场的时间和空间分布规律,从而达到寻找地下有用矿产资源、查明地下地质构造以及解决地质问题的目的[1]。电磁法勘探方法主要分为基于几何测深原理的直流电法、基于频率域测深原理的大地电磁法(MT/AMT/CSAMT)与基于时间域测深原理的瞬变电磁法(TEM)[2]等。直流电阻率法是电法勘探的最经典方法之一,在金属矿产、非金属矿产、煤田、油气及地下水等资源勘探中获得广泛而有效的应用,并已拓展到水文、工程、环境、考古等与国民经济建设、人类社会生活密切相关的探测领域[3]。直流电阻率法有多种灵活的观测方式,如单极、偶极及多极装置的电剖面法、电测深法等,井地电阻率法是在井中供电,在地面接收电磁场的一类电法,供电装置总是放入钻孔深部使其接近于被探测的对象,从而增大电流强度或被接收的异常响应[4-5],井地电阻率法主要用于金属矿矿山的二次资源勘查及油藏边界的预测[6]等,通常采集装置沿着具有不同电极阵列的平行线在网格上进行数据采集,并使用3D反演算法进行解释。随着计算机及数值计算技术的发展,电阻率三维正反演算法分别在网格的剖分(结构化[7⇓⇓⇓⇓-12]、非结构化[13⇓⇓⇓⇓⇓⇓⇓-21]),数值方法(有限差分法[22⇓⇓⇓⇓-27]、有限元法[28-29]),目标函数的求解(高斯—牛顿法(GN)[3,19,30⇓⇓⇓⇓⇓⇓ -37]、拟牛顿法(QN)[38⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-54]、非线性共轭梯度法(NLCG)[45,51,55⇓⇓⇓⇓⇓⇓⇓ -63]等)等方面取得很大进展。

由于结构化单元的网格不能适应复杂地形下的电阻率三维反演,因此非结构有限元方法在复杂地形电阻率三维数值模拟中取得极大成功,非结构化网格具有单元质量可控、允许局部加密、能够模拟复杂几何模型等优点,使得三维非结构有限单元求解效率大幅提高。同等计算精度情况下,非结构化网格相对于结构化规则网格,计算时间和存储量均可下降约一个数量级[3]。在电阻率三维反演中,由于反演参数多且数据量大,雅可比矩阵(偏导数矩阵)对巨大的计算量和存储需求难于克服,许多学者研究可避开计算雅可比矩阵的反演算法,Zhang等[26]、吴小平等[36]引入共轭梯度方法,解决了电阻率三维正演效率及三维反演中雅可比矩阵求取、存储两方面问题,实现比较快速有效地电阻率三维反演。在三维数据反演中采用的最优化方法主要有非线性共轭梯度法(NLCG)、高斯—牛顿法(GN)和拟牛顿法(QN)。NLCG和QN只需要目标函数的梯度信息,无需显式计算灵敏度矩阵,由于仅仅使用了目标函数的一阶导数(梯度)信息,只有线性收敛性,模型需要反复更新很多次才能收敛到理想的值,而GN法同时使用了目标函数的一阶导数(Gradient)和二阶导数(Hessian)的信息,表现出近似二次收敛性,所需的模型更新次数远远少于NLCG和QN法,每次高斯牛顿迭代的法方程使用预条件共轭梯度法(PCG)求解,不仅可以避免显示求解和存储灵敏度矩阵,还能减少PCG的迭代次数来减小反演的计算时间。由于反演的非线性特征,这种非精确求解对于线性化迭代反演不仅减小了计算量,而且还避免了每次GN迭代中对法方程的过度求解,因此在反演搜索过程中有机会跳出局部极小值[33]。

压制电阻率三维反演多解性的有效方法是发展约束反演,将已有的先验信息通过数学手段加入到反演过程中,提高反演精度。Sasaki Y[21]提出了光滑约束,使得相邻网格之间的电阻率差异极小,光滑过渡,这种约束具有天然的合理性,已经成为电阻率反演中常用的一种约束形式;Kim等[64]按照光滑约束的施加形式,定义了一个新的参数向量来表征模型参数,将不等式约束施加到反演方程中,获得了不错的效果;Li等[65]利用约束最优化里的内点罚函数法将不等式约束条件加入到目标函数里,提高了反演成像的精度;黄俊革等[66]和宛新林等[67]分别对粗糙度矩阵进行改进,提高了三维反演的效果;刘斌等[68]在反演目标函数中引入自适应加权光滑约束,控制深部分辨率并在其文献中[69-70]讨论了不等式和先验结构约束条件的加入方法,去除了反演成像中的假异常和多余构造,明显地压制了电阻率探测反演的多解性问题。

电磁探测反演是典型的不适定问题,易造成反演结果的多解性,不适定性是反演自身固有的特征, 没有求解的附加信息这一本质困难是很难克服的[71],如何利用相关技术引入先验信息实现地下结构的高精度成像是未来电磁法重要的发展方向之一[72]。电阻率的变化范围是一个很重要的先验信息,如何将不等式约束施加到反演方程中是一个关键性的难题。Kim等[64]采取的方法是一种经验式施加方式,在反演过程中该约束项繁琐、不容易理解;Li等[65]采用内点罚函数法,在目标函数中加入对数形式的障碍函数,这种施加形式简单,但是内点法要求初始值的选取必须在可行域内,并且初始点应选择一个离约束边界较远的可行点,太靠近某一约束边界会造成求解的困难。如果约束条件较为复杂时,选择初始点有一定难度,并且内点法只能解决约束为不等式情形,外点法可以解决约束为等式和不等式混合的情形,外点法对初始点也没有要求。结合前人研究与上述反演存在的问题,本文将表征模型参数变化范围的不等式约束作为先验信息以外点罚函数的方式引入到目标函数中[73],选择井地观测方式、非结构化四面体的有限单元法与高斯牛顿法(GN)相结合方式实现了井地电阻率法的三维约束反演算法,通过典型三维理论模型合成观测数据来验证所开发的算法的稳定性及有效性。

1 三维正演理论

1.1 控制方程

三维直流电阻率法点电流源场总电位满足的偏微分方程及其边界条件为[9,16,74]:

∇·(σ(x,y,z)∇u(x,y,z))=-4πωAIδ(rA),inΩ∂u∂n=0,onΓs∂u∂n+cosθru=0,onΓ∞

其中:σ是岩石电导率;u是电位;I是电流强度;δ是狄拉克函数;rA是源点位置;ω是源点对地下区域Ω的张开角,若源点在地面,则ωA=2π;若源点在地下,ωA=4π,n是边界Γ∞边界上的外法向向量;r是点电源到边界点的距离;Γs是自然边界条件;Γ∞是无穷远边界;θ是无穷远边界上点的外法向向量n与场源到边界点距离r之间的夹角。采用加权余量法可导出式(1)对应的变分问题的积分方程:

F(u)=∫Ω[12σ(∇u)2-4πωAδ(A)u]dΩ+∫Γ∞12σu2cos(r,n)rdΓδF(u)=0

计算区域采用四面体剖分与线性差值,最终形成的大型稀疏对称线性方程组,矩阵表达形式如下:

Ku=P

其中:K是一个n×n的对称矩阵;u为n×1列向量,表示三维网格节点上的电位向量;P是含有场源信息的列向量;P=(0,…,I,…,0),为了节约内存采用行压缩存储(compressed sparse row or compressed row storage)处理系数矩阵K,使用对称超松弛预条件共轭梯度算法[11,20](SSORPCG)求解方程组(3)。

1.2 算法验证

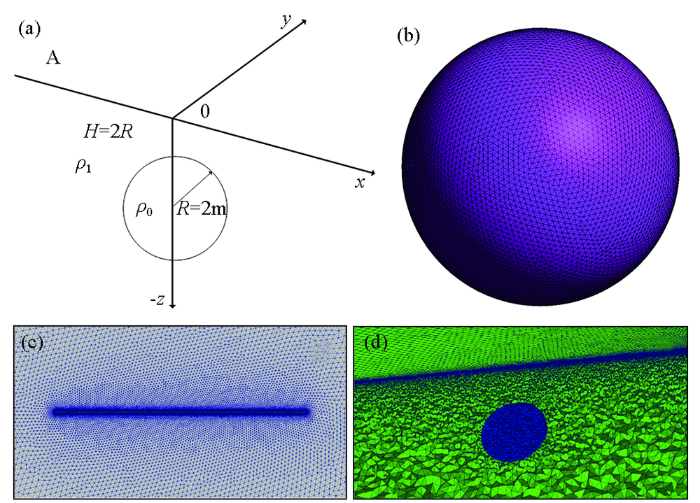
为了验证本文正演程序的正确性,本文设计了一个均匀半空间中埋藏球体的模型,如图1a所示,该模型为均匀半空间中嵌入一个球形异常体[16],球体的半径为R=2.25 m,球体中心坐标为(0,0,-4.5),球体电阻率值ρ0=1Ω·m,地层围岩电阻率值为ρ1=10Ω·m,点电流源A坐标在(-5,0,0)处,电流大小为1 A,测量电极M沿x方向,间距为0.25 m。整个计算区域大小为500 m×500 m×300 m,目标区域大小为100 m×100 m×100 m,网格节点总数为273 582,网格单元总数为1 625 838,网格剖分效果见图1b~1d,分别在源点、测点与球体处进行了加密处理。采用pole-pole装置,由本文的有限元正演程序计算得到测点处电位值,并与解析解进行了比较,如图2所示,本文的计算结果与解析解有很好的一致性,最大误差小于0.34%(见图3)。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   球体模型结构及网格剖分示意

a—球体模型示意;b—球体模型网格剖分放大效果;c—点与测点网格加密效果;d—网格剖分示意

Fig.1   Sphere model structure and mesh division

a—diagram of the sphere model structure;b—diagram of spherical model meshing;c—diagram of source point and measuring point mesh refinement;d—diagram of mesh generation


图2

新窗口打开| 下载原图ZIP| 生成PPT

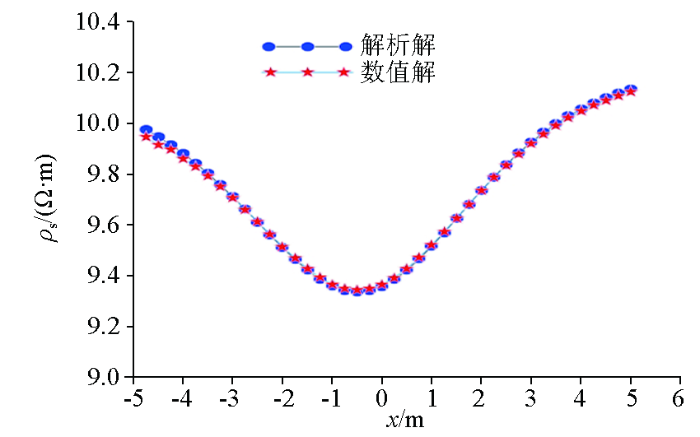
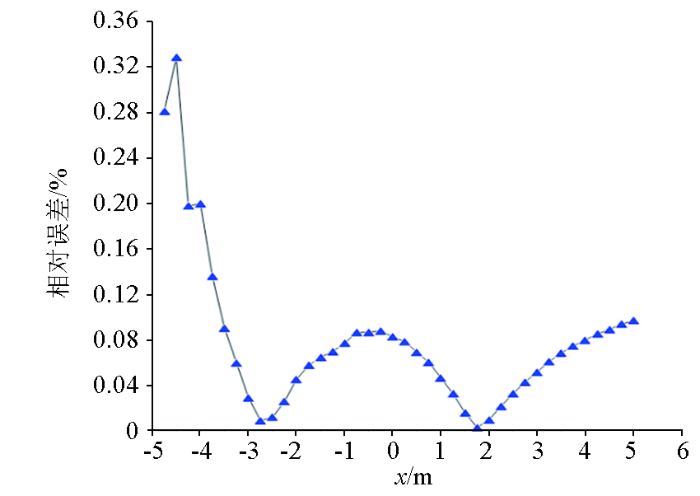
图2   地下球体的解析解与数值解对比

Fig.2   Comparison of analytical and numerical solutions of underground sphere


图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   解析解与数值解的相对误差

Fig.3   Relative error of analytical and numerical solutions


2 三维反演理论

2.1 目标函数

依据Tikhonov正则化理论,最小二乘意义下的反演目标函数为[3,19,31]:

Φ(m)=Φd(m)+λΦm(m)=Wd(dobs-F(m))22+λWm(m-mref)22

其中:F(m)为正演响应函数;m为模型参数(mi,i=1,2,…,M),dobs(dj,j=1,2,…,N)为观测数据,Wd为N×N阶观测数据误差加权矩阵,Wd=diag(1/σ1,1/σ2,…,1/σn),σi为第i个观测数据的标准差;Wm为M×M阶模型加权矩阵,通常用模型单元的离散差分算子来定义,一般取一阶正则化约束。λ为正则化因子,用来平衡数据拟合和模型光滑度的权重;mref为含有模型参数先验信息的参考模型。反演的观测参数dobs为pole-pole的电位值,模型参数为单元的电导率值σ,由于变化范围很大,为了反演的稳定性,通常采用对数来标定观测数据及模型参数,即d=lnφobs,m=lnσ。光滑约束的施加请参考文献[62],不等式约束施加的原理详见文献[62-63],常规电阻率反演目标函数中构造出带有不等式约束的反演目标函数见式(5):

Φ(m)=Φd(m)+λΦm(m)+μP(m)=‖Wd(dobs-F(m))‖22+λ‖Wm(m-mref)‖22+μ[(min(m-mmin),0)2+μ(min(mmax-m),0)2]

式中:mmin,mmax为每个单元网格电阻率的上下限。式(5)即为本文带不等式约束条件的三维电阻率反演的目标函数,与常规三维电阻率反演目标函数相比,该方法增加了不等式约束项,该表达式简单、容易理解、易于实现。目前常用于三维电阻率反演的最优化方法有拟牛顿法(QN),高斯牛顿法(GN)、非线性共轭梯度法(NLCG)以及这些方法的变种[33,75]。对目标函数(5)进行二阶Taylor展开,忽略高阶项得到高斯—牛顿法(Gauss-Newton,GN)的法方程(normal equation)为:

H(m)△(m)=-g(m)

其中:g(m)为目标函数的一阶导数(梯度矩阵,Gradient),H(m)为目标函数的二阶近似导数(海森矩阵,Hessian),分别表示如下:

g(m)=∇Φ(m)=-2JT(m)WdTWd[dobs-F(m)]+2λWmTWm(m-mref)+　　　2μ[min(m-mmin,0)-min(mmax-m,0)]H(m)=JT(m)WdTWdJ(m)+λWmTWm+μWc

其中:J(m)为灵敏度矩阵(正演响应函数F(m)的一阶导数),Wc为不等式约束矩阵:其元素Wc(i,j)取值如下:

Wc(i,j)=0,　mmin≤m≤mmax1,　m<mmin1,　m>mmax

在GN法中,为获得模型的修改量,每次迭代都需要求解法方程式(6),由式(7)可知,梯度矩阵g与海森矩阵H的计算关键在于灵敏度矩阵J的计算,直接求解式(6)需要显式的计算和存储灵敏度矩阵以及海森矩阵,而且涉及到大量正演计算,需要消耗大量的计算内存以及运算时间,现有计算资源难以满足要求,为避开雅克比矩阵的直接计算,通常采用共轭梯度法来迭代求解式(6),形成GN-CG法。在CG算法中,只需要计算和存储雅克比矩阵或者其转置与任意一维向量的乘积Jx与JyT,因此无需考虑雅克比矩阵的存储问题,并且Jx与JyT的计算相当于求解一次正演问题,从而大大地加快了反演的计算速度。Zhang等[26]在其论文中对计算Jx与JyT进行了详细的分析。

2.2 模型更新

利用CG法求得法方程(6)的解Δm后,需要进行线性搜索来获得每次GN迭代的模型更新量,更新公式为:

mk+1=mk+αΔm

其中:α为模型的更新步长,步长α的精确线搜索往往需要大量的计算,一般采用非精确一维线性搜索方法得到步长,常用的策略是采用Wofe-Powell准则来进行非精确线性搜索得到更新步长α,Wofe-Powell准则包括充分下降条件与曲率条件,公式为:

Φ(mk+αkpk)≤Φ(mk)+c1αk∇Φ(mk)Tpk∇Φ(mk+αkpk)Tpk≥c2∇Φ(mk)Tpk

其中:Φ为正演算子,mk为第k次反演迭代的模型参数;αk为迭代步长;pk为搜索方向;c1与c2为常数,满足0<c1<c2<1,具体的搜索方式请参考文献[73]。一般情况下,c2越小线性搜索越精确,c2=0.1就得到一个相当精确的线性搜索,取c2=0.9得到一个相当弱的线性搜索,c2越小,搜索的时间就越长,根据前人的研究[45],通常GN法和L_BFGS法中一般取c1=10-4,c2=0.9。

2.5 反演流程

GN-CG法反演流程如下[73,76]:

  

GN-CG反演算法
1) 给定初始模型m0与参考模型mref,设置收敛系数ε,正则化因子λ和惩罚因子μ,给定光滑度矩阵Wm;
2) 开始GN-CG 迭代, 设k=1,2,…,NmaxGN;
3) 计算Δdk=dobs-F(mk),并计算r0=-gk;
gk=-JkTWdTWdΔdk+λWmTWm(m-mref)+μ[min(m-mmin,0)-min(mmax-m,0)];
4) 开始CG 迭代, 令Δm=0,p0=r0,设i=1,2,…,Nmaxcg;
4-1)计算Hk=JkTWdTWdJk+λWmTWm+μWc, 得到Hkpi;
4-2)计算ti=riTripiTHpi;
4-3)计算Δmi+1=Δmi+tipi;
4-4)计算ri+1=ri-tiHkpi;
4-5)计算βiFR=ri+1Tri+1riTri;
4-6)计算pi+1=ri+1+βipi;
5) CG迭代结束, 求得Δm,根据Wofe-Powell条件(式12)进行一维搜索得到最优步长αk,更新模型:mk+1=mk+αkΔmk;
6) 如果RMS<ε 则停止GN-CG迭代,输出mk,否则令k=k+1 转到步骤3);

新窗口打开| 下载CSV


3 合成数据反演

为了验证开发的基于不等式约束井地电阻率三维反演算法的正确性与有效性,本文设计了2个三维模型来分别模拟井地电阻率法的测量情况,并对这2个三维模型的合成数据进行三维反演测试。本文的所有计算均在小型计算机上完成,其配置CPU为Intel I7-4712MQ,主频为2.3 GHz,内存16 G,正反演程序均采用Inter Fortran编译运行,非结构化四面体网格剖分采用Gmsh-4.8.4[77],非结构化四面体网格的显示采用Paraview-5.6.0[78]。

3.1 平坦地形下单个异常体

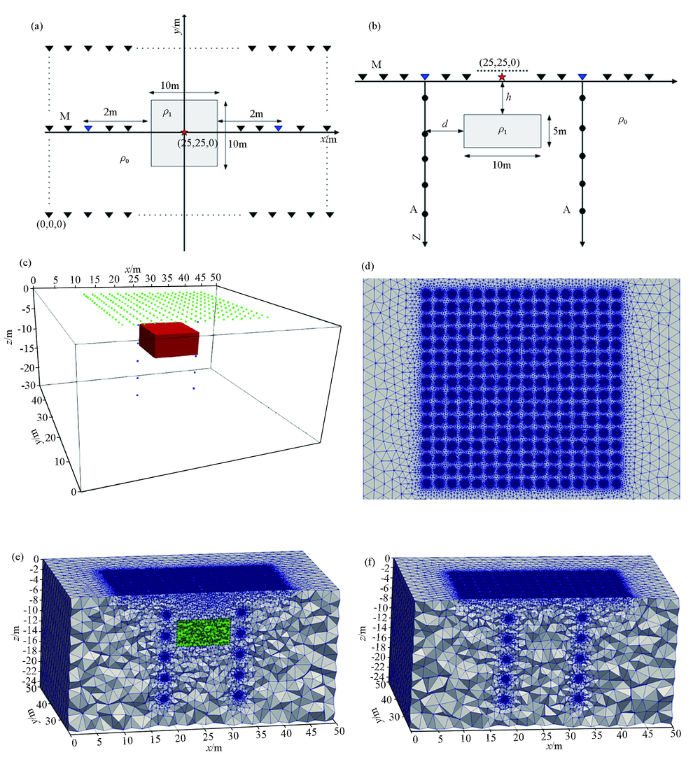
长方体模型如图4a、4b所示,围岩电阻率ρ0=100Ω·m,低阻体电阻率ρ1=10Ω·m,低阻长方体大小为10 m×10 m×5 m,顶面埋深h=5 m,底面埋深为10 m。蓝色三角形代表钻井井口位置(18,25,0)与(32,25,0),异常体离两边钻井的水平距离d=2 m。本次反演采用的测线范围为10~40 m,测线之间的间距为2 m,每条测线上16个测点,测点M(测量电极)沿x方向的位置坐标为x=10~40 m,y=10~40 m,间距为2 m;源点A(供电电极)移动范围在井下-4~-20 m,间隔为4 m,一共设置10个点源;地表测量装置位置见图4c。为了测试反演算法的稳定性,避免反演偏差,反演网格采用不同于合成数据所用的正演网格:正演网格分别在测点、源点与异常体附近进行网格加密;反演网格在源点与测点处进行加密,不仅提高了正演的精度,还减少了源点附近的数值模拟误差,测点局部加密示意图见图4d。图4e、图4f分别为正演与反演所使用的非结构化四面体网格,正演网格单元总数为1 288 357。反演网格中网格单元总数为1 090 207,通过三维有限元正演程序共得到2 560个一次场的”电位实测数据”,正演一次约130 s,反演一次约14 400 s。反演参数选择如下:正则化参数λ=0.05,惩罚因子μ=1.0,在反演过程中始终保持不变,反演终止的收敛系数ε=1.0×10-5,反演的迭代次数10次,反演过程中RMS变化如图5所示。从图6可以看出,数据拟合差稳定下降,说明本文的带约束的GN法对于三维井地电阻率法的数据收敛性较好,图5分别给出了传统正则化反演与施加不等式约束反演结果的xoy与xoz剖面,两种反演方法得到的模型与真实模型吻合较好,地下低阻异常体的位置与电阻率值基本一致,验证了本文反演方法的有效性。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   平坦地形下长方体模型

a—xoy水平截面; b—xoz垂直断面;c—三维异常体模型;d—测点加密示意;e—正演网格;f——反演网格

Fig.4   Cuboid model under flat terrain

a—xoy plane view of the model;b—xoz cross section view of the model;c—3D abnormal body model diagram;d—diagram of mesh refinement at measuring point;e—forward mesh;f—inversion mesh


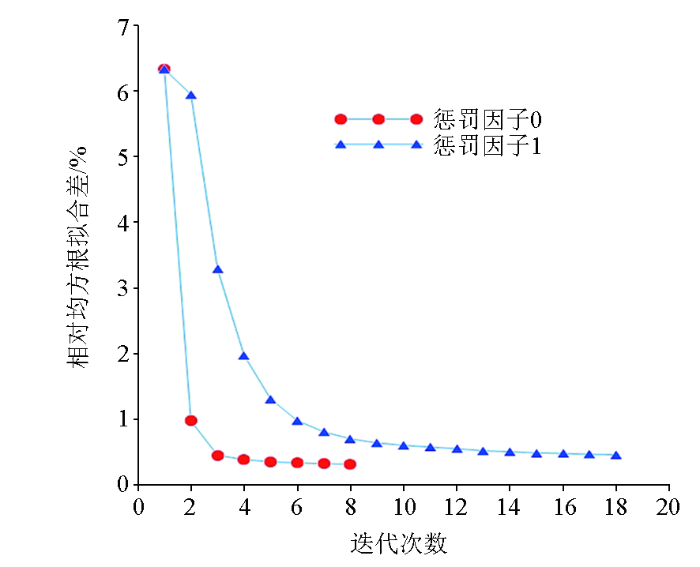
图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   迭代次数与RMS的关系

Fig.5   The relationship between the number of iterations and RMS


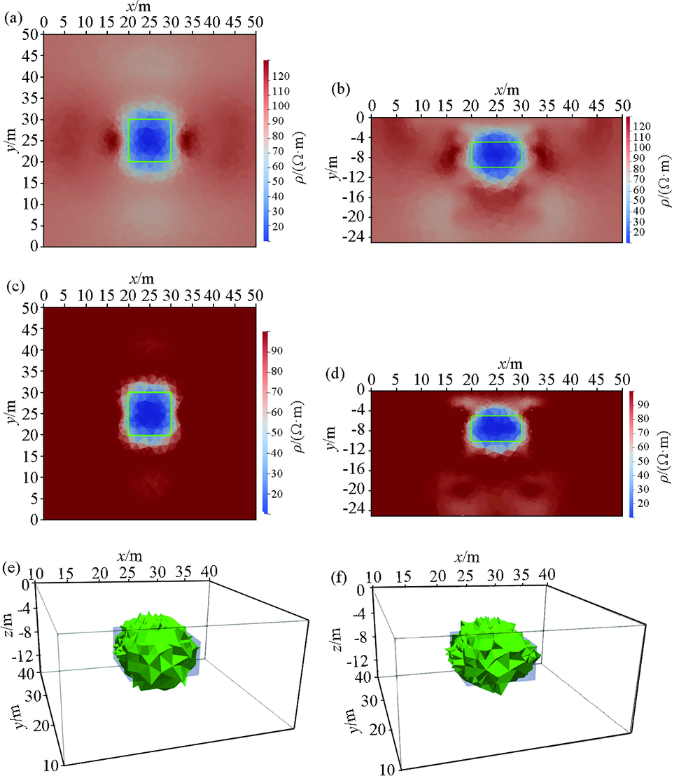
图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   三维反演结果

a—传统电阻率反演结果z=-7 m处xoy切片;b—传统电阻率反演结果y=25 m处xoz切片;c—施加不等式约束的反演结果z=-7 m处xoy切片;d—施加不等式约束的反演结果y=25 m处xoz切片;e—传统电阻率反演结果的三维剖面(电阻率小于50Ω·m);f—施加不等式约束反演结果的三维剖面(电阻率小于50 Ω·m)

Fig.6   3D inversion results

a—traditional resistivity inversion results:horizontal slice xoy at z=-7 m; b—traditional resistivity inversion results:cross-section slice xoz at y=25 m; c—inversion results with inequality constraints:horizontal slice xoy at =-7 m; d—inversion results with inequality constraints:cross-section slice xoz at y=25 m; e—3D view of traditional resistivity inversion results(resistivity is less than 50 Ω·m); f—3D view of inversion results with inequality constraints(resistivity is less than 50 Ω·m)


3.2 五个异常体模型

为了测试所开发的反演算法对于复杂模型的有效性,考虑浅地表存在的电阻率异常干扰,在背景为1 000 Ω·m的均匀半空间中放置5个电阻率异常体[79-80],其中3个长方体顶界面位于浅地表以下10 m(S1,S2,S3),用于模拟浅地表的电阻率异常干扰,另外两个顶界面埋深分别为60 m和95 m的长方体(B1,B2)模拟探测目标体,各项参数见表1,三维模型见图7a。整个模型的研究区域(目标区域与边界区域)x、y、z这3个方向的剖分范围分别是(-1 000,2 000)、(-1 000,2 000)和(-1 500,0),目标区域x、y、z这3个方向的剖分范围分别是(0,1 000)、(0,1 000)和(-500,0)。采用的测线范围为50~950 m,测线之间的间距为50 m,每条测线上19个测点,测点M(测量电极)沿x方向的位置坐标为x=50~950 m,y=50~950 m,间距为50 m;井口坐标分别为(500,200,0)与(500,800,0),源点A(供电电极)移动范围在井下-40~-360 m,间隔为80 m,一共设置10个点源。地表测量装置与点源位置分别见图7b与7c。正演网格单元总数为2 511 215,反演网格中网格单元总数为1 037 303,通过三维有限元正演程序共得到3 610个一次场的”电位实测数据”,正演一次约275 s,反演一次约17 039 s。

表1   长方体参数

Table 1  Cuboid parameter

长方体编号电阻率/(Ω·m)尺寸/(m×m×m)
S1200100×100×40
S2100100×100×40
S32000350×50×40
B12000350×100×200
B2100100×150×180

新窗口打开| 下载CSV


图7

新窗口打开| 下载原图ZIP| 生成PPT

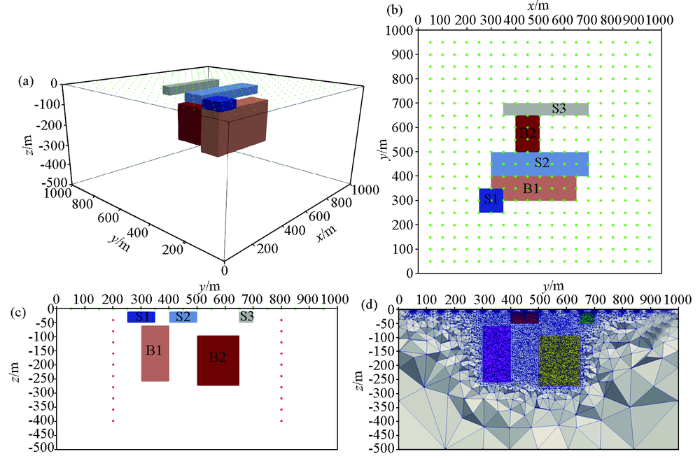
图7   异常体模型位置与网格剖分

a—三维异常体模型位置; b—地表数据观测系统;c—垂直剖面yoz; d—非结构化网格加密示意

Fig.7   Diagram of abnormal body model location and mesh generation

a—location of 3D abnormal model;b—observation system of surface data;c—cross-section profile yoz; d—diagram of unstructured refinement mesh


浅层地震勘探、地质雷达探测法对异常体界面识别和定位方面具有较好的效果,在电阻率探测时利用这些方法获得的异常体位置与形态信息是一种极为重要的先验构造信息[62,63,69],因此在三维井地电阻率反演中将构造位置的先验信息作为局部约束加入。由其他地球物理探测方法假设可知异常体的构造位置与形态信息,由探区矿石标本物性参数可得:分别在①250 m≤x≤350 m,250 m≤y≤350 m,-50 m≤z≤-10m处异常体的电阻率值在220Ω·m以内,将此处网格单元的电阻率上限设为220 Ω·m,下限设为0;②300 m≤x≤700 m、400 m≤y≤500 m、-50 m≤z≤-10 m处异常体的电阻率值在120Ω·m以内,将此处网格单元的电阻率上限设为120 Ω·m,下限设为0 Ω·m;③350 m≤x≤700 m、650 m≤y≤700 m、-50 m≤z≤-10 m处异常体的电阻率值在2200Ω·m以内,将此处网格单元的电阻率上限设为2 200 Ω·m,下限设为1 800 Ω·m;④300 m≤x≤650 m、300 m≤y≤400 m、-260 m≤z≤-60 m处异常体的电阻率值在2200Ω·m以内,将此处网格单元的电阻率上限设为2 200 Ω·m,下限设为1 800 Ω·m;⑤400 m≤x≤500 m、500 m≤y≤650 m、-275 m≤z≤-95 m处异常体的电阻率值在120Ω·m以内,下限设为0 Ω·m。各项反演参数的设置与模型1的反演参数设置一样。图8c与图8d为施加不等式约束后的电阻率反演结果,由反演结果可以看出,5个异常体水平和横向的分辨率较传统反演结果(图8a,图8b)有了明显提高,与原模型在电阻率值、规模、位置、形状等特征方面均基本一致,带不等式约束的正则化反演能够得到更为精确的三维反演成像结果。

图8

新窗口打开| 下载原图ZIP| 生成PPT

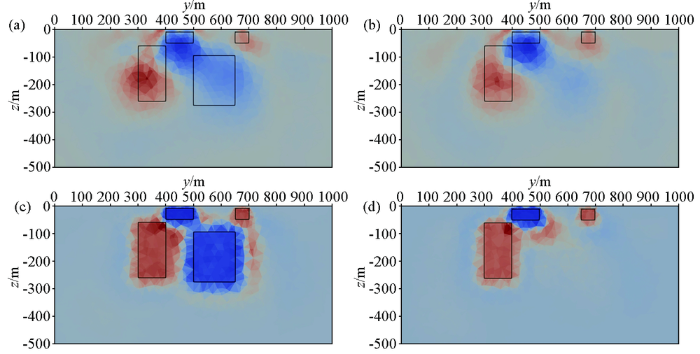
图8   井—地二极装置传统正则化反演与约束反演结果

a—传统正则化反演x=400 m处yoz剖面; b—传统正则化反演x=600 m处yoz剖面;c—约束反演x=400 m处yoz剖面; d—约束反演x=600 m处yoz剖面

Fig.8   Traditional regularized inversion and constrained inversion results of well-surface with pole-pole device

a—traditional resistivity inversion results:cross-section profile yoz at x=400 m; b—traditional resistivity inversion results:cross-section profile yoz at x=600 m;c—constrained inversion: cross-section profile yoz at x=400 m;d—constrained inversion:cross-section profile yoz at x=600 m


4 结论

本文实现了一种以外点惩罚函数法的方式将带有电阻率取值范围的不等式约束施加到井地电阻率三维反演方程中的GN-CG反演算法,正演采用有限元法与非结构化网格对控制方程离散化并使用SSORPCG法求解离散所得的大型线性方程;反演中采用高斯牛顿最优化算法,在目标函数中加入不等式与构造约束来降低反演的多解性。以上这些技术的综合使用,使得本文带约束的GN-CG算法稳定且准确,适用于陆地与井中的电阻率法勘探情况。通过对理论模型的反演试算,验证了本文反演算法的可靠性与有效性,带约束的三维井地电阻率反演方法能得到更精确的反演结果;惩罚因子的取值与不等式约束的范围给定是两个难点,本文惩罚因子的取值采用的是实验法,过大或者过小的惩罚因子都会影响反演的效果,有时甚至会出现不收敛的情况,可以通过结合其他物探方法给出异常体较为准确的边界范围以及电阻率值的上下限,给出的范围越精确,反演结果就越准确。

参考文献

柳建新, 赵然, 郭振威.

电磁法在金属矿勘查中的研究进展

[J]. 地球物理学进展, 2019, 34(1):151-160.

[本文引用: 1]

Liu J X, Zhao R, Guo Z W.

Research progress of electromagnetic methods in the exploration of metal deposits

[J]. Progress in Geophysics, 2019, 34(1):151-160.

[本文引用: 1]

吕庆田, 张晓培, 汤井田, 等.

金属矿地球物理勘探技术与设备:回顾与进展

[J]. 地球物理学报, 2019, 62(10):3629-3664.

[本文引用: 1]

Lyu Q T, Zhang X P, Tang J T, et al.

Review on advancement in technology and equipment of geophysical exploration for metallic deposits in China

[J]. Chinese Journal of Geophysics, 2019, 62(10):3629-3664.

[本文引用: 1]

吴小平, 刘洋, 王威.

基于非结构网格的电阻率三维带地形反演

[J]. 地球物理学报, 2015, 58(8):2706-2717.

[本文引用: 4]

Wu X P, Liu Y, Wang W.

3D resistivity inversion incorporating topography based on unstructured meshes

[J]. Chinese Journal of Geophysics, 2015, 58(8):2706-2717.

[本文引用: 4]

王智, 吴爱平, 李刚.

起伏地表条件下的井中激电井地观测正演模拟研究

[J]. 石油物探, 2018, 57(6):927-935, 951.

[本文引用: 1]

Wang Z, Wu A P, Li G.

Forward modeling of borehole-ground induced polarization method under undulating topography

[J]. Geophyscial Prospecting for Petroleum, 2018, 57(6):927-935,951.

[本文引用: 1]

潘和平.

井中激发极化法在矿产资源勘探中的作用

[J]. 物探与化探, 2013, 37(4):620-626.

[本文引用: 1]

Pan H P.

The Role of Borehole induced polarization/resistivity method in the exploration of mineral resoueces

[J]. Geophysics and Geochemical Exploration, 2013, 37(4):620-626.

[本文引用: 1]

汤井田, 张继锋, 冯兵, 等.

井地电阻率法歧离率确定高阻油气藏边界

[J]. 地球物理学报, 2007, 50(3):926-931.

[本文引用: 1]

Tang J T, Zhang J F, Feng B, et al.

Detemination of borders for resistive oil and gas reservoirs by deviation rate using the hole-to-surface resistivity method

[J]. Chinese Journal of Geophysics, 2007, 50(3):926-931.

[本文引用: 1]

黄俊革, 王家林, 阮百尧.

三维高密度电阻率E-SCAN法有限元模拟异常特征研究

[J]. 地球物理学报, 2006, 49(4):1206-1214.

[本文引用: 1]

Huang J G, Wang J L, Ruan B Y.

A study on FEM modeling of anomalies of 3-D high-density E-SCAN resistivity survey

[J]. Chinese Journal of Geophysics, 2006, 49(4):1206-1214.

[本文引用: 1]

Li Y, Spitzer K.

Finite element resistivity modelling for three-dimensional structures with arbitrary anisotropy

[J]. Physics of the Earth & Planetary Interiors, 2005, 150(1-3):15-27.

[本文引用: 1]

Wu X.

A 3-D finite-element algorithm for DC resistivity modelling using the shifted incomplete Cholesky conjugate gradient method

[J]. Geophysical Journal International, 2003, 154(3):947-956.

[本文引用: 2]

吴小平, 汪彤彤.

利用共轭梯度算法的电阻率三维有限元正演

[J]. 地球物理学报, 2003, 46(3):428-432.

[本文引用: 1]

Wu X P, Wang T T.

A 3-D finite-element resistivity forward modeling using conjugate gradient algorithm

[J]. Chinese Journal of Geophysics, 2003, 46(3):428-432.

[本文引用: 1]

Li Y, Klaus S.

Three-dimensional DC resistivity forward modelling using finite elements in comparison with finite-difference solutions

[J]. Geophysical Journal International, 2002, 51(3):924-934.

[本文引用: 2]

黄俊革, 阮百尧, 鲍光淑.

齐次边界条件下三维地电断面电阻率有限元数值模拟法

[J]. 桂林工学院学报, 2002, 22(1):11-14.

[本文引用: 1]

Huang J G, Ruan B Y, Bao G S.

Fem under quantic-boundary condition for modeling resistivity on 3-D geoelectric section

[J]. Journal of Guilin Institute of Technology, 2002, 22(1):11-14.

[本文引用: 1]

Ren Z, Qiu L, Tang J, et al.

3-D direct current resistivity anisotropic modelling by goal-oriented adaptive finite element methods

[J]. Geophysical Journal International, 2018, 212(1):76-87.

[本文引用: 1]

Ren Z, Tang J.

A goal-oriented adaptive finite-element approach for multi-electrode resistivity system

[J]. Geophysical Journal International, 2014, 199(1):136-145.

[本文引用: 1]

Wei W, Xiaoping W, Spitzer K.

Three-dimensional DC anisotropic resistivity modelling using finite elements on unstructured grids

[J]. Geophysical Journal International, 2013, 193(2):734-746.

[本文引用: 1]

Ren Z, Jingtian T.

3D direct current resistivity modeling with unstructured mesh by adaptive finite-element method

[J]. Geophysics, 2010, 75(1):H7-H17.

[本文引用: 3]

Blome M, Maurer H R, Schmidt K.

Advances in three-dimensional geoelectric forward solver techniques

[J]. Geophysical Journal International, 2009, 176(3):740-752.

[本文引用: 1]

Rücker C, Günther T, Spitzer K.

Three-dimensional modelling and inversion of dc resistivity data incorporating topography-I. Modelling

[J]. Geophysical Journal International, 2006, 166(2):495-505.

[本文引用: 1]

Günther T, Rücker C, Spitzer K.

Three-dimensional modelling and inversion of DC resistivity data incorporating topography-II. Inversion

[J]. Geophysical Journal of the Royal Astronomical Society, 2006, 166(2):506-517.

[本文引用: 3]

Zhou B, Greenhalgh S A.

Finite element three-dimensional direct current resistivity modelling; accuracy and efficiency considerations

[J]. Geophysical Journal International, 2001, 145(3):679-688.

[本文引用: 2]

Sasaki Y.

3-D resistivity inversion using finite-element method

[J]. Geophysics, 1994, 59(12):1839.

[本文引用: 2]

Wu X, Xiao Y, Qi C, et al.

Computations of secondary potential for 3-D DC resistivity modelling using an incomplete Choleski conjugate-gradient method

[J]. Geophysical Prospecting, 2003, 51(6):567-577.

[本文引用: 1]

吴小平, 徐果明.

利用ICCG迭代技术加快电阻率三维正演计算

[J]. 煤田地质与勘探, 1999, 27(3):63-67.

[本文引用: 1]

Wu X P, Xu G M.

3-D resistivity forward calculation accelerated by ICCG iteration technique

[J]. Coal Geology and Exploration, 1999, 27(3):63-67.

[本文引用: 1]

吴小平, 徐果明, 李时灿.

利用不完全Cholesky共轭梯度法求解点源三维地电场

[J]. 地球物理学报, 1998, 41(6):848-855.

[本文引用: 1]

Wu X P, Xu G M, Li S C.

The calculation of three-dimensional geoelectric field of point source by incomplete cholesky conjugate gradient method

[J]. Chinese Journal of Geophysics, 1998, 41(6):848-855.

[本文引用: 1]

Zhao S, Yedlin M J.

Some refinements on the finite-difference method for 3-D dc resistivity modeling

[J]. Geophysics, 1996, 61(5):1301-1307.

[本文引用: 1]

Zhang J, Mackie R L, Madden T R.

3-D resistivity forward modeling and inversion using conjugate gradients

[J]. Geophysics, 1995, 60(5):1313-1325.

[本文引用: 3]

Spitzer K.

A 3-D finite-difference algorithm for DC resistivity modelling using conjugate gradient methods

[J]. Geophysical Journal International, 1995, 123(3):903-914.

[本文引用: 1]

汤井田, 王飞燕, 任政勇.

基于非结构化网格的2.5-D直流电阻率自适应有限元数值模拟

[J]. 地球物理学报, 2010, 53(3):708-716.

[本文引用: 1]

Tang J T, Wang F Y, Ren Z Y.

2.5-D DC resistivity modeling by adaptive finite-element method with unstructured triangulation

[J]. Chinese Journal of Geophysics, 2010, 53(3):708-716.

[本文引用: 1]

任政勇, 汤井田.

基于局部加密非结构化网格的三维电阻率法有限元数值模拟

[J]. 地球物理学报, 2009, 52(10):2627-2634.

[本文引用: 1]

Ren Z Y, Tang J T.

Finite element modeling of 3-D DC resistivity using locally refined unstructured meshes

[J]. Chinese Journal of Geophysics, 2009, 52(10):2627-2634.

[本文引用: 1]

彭荣华, 胡祥云, 李建慧, 等.

频率域海洋可控源电磁垂直各向异性三维反演

[J]. 地球物理学报, 2019, 62(6):2165-2175.

[本文引用: 1]

Peng R H, Hu X Y, Li J H, et al.

3D inversion of frequency-domain marine CSEM data in VTI media

[J]. Chinese Journal of Geophysics, 2019, 62(6):2165-2175.

[本文引用: 1]

Gundogdu N Y, Candansayar M E.

Three-dimensional regularized inversion of DC resistivity data with different stabilizing functionals

[J]. Geophysics, 2018, 83(6):E399-E407.

[本文引用: 2]

郭来功, 戴广龙, 杨本才, 等.

多先验信息约束的三维电阻率反演方法

[J]. 石油地球物理勘探, 2018, 53(6):1333-1340.

[本文引用: 1]

Guo L G, Dai G L, Yang B C. et al.

3D resistivity inversion with multiple priori-information constraint

[J]. Oil Geophysical Prospecting, 2018, 53(6):1333-1340.

[本文引用: 1]

彭荣华, 胡祥云, 韩波.

基于高斯牛顿法的频率域可控源电磁三维反演研究

[J]. 地球物理学报, 2016, 59(9):3470-3481.

[本文引用: 3]

Peng R H, Hu X Y, Han B.

3D inversion of frequency-domain CSEM data based on Gauss-Newton optimization

[J]. Chinese Journal of Geophysics, 2016, 59(9):3470-3481.

[本文引用: 3]

Oldenburg D W, Haber E, Shekhtman R.

Three dimensional inversion of multisource time domain electromagnetic data

[J]. Geophysics, 2013, 78(1):E47-E57.

[本文引用: 1]

Pidlisecky A, Haber E, Knight R J.

RESINVM3D: A 3D resistivity inversion package

[J]. Geophysics, 2007, 72(2):H1-H10.

[本文引用: 1]

吴小平, 徐果明.

利用共轭梯度法的电阻率三维反演研究

[J]. 地球物理学报, 2000, 43(3):420-427.

[本文引用: 2]

Wu X P, Xu G M.

Study on 3-D resistivity inversion using conjugate gradient method

[J]. Chinese Journal of Geophysics, 2000, 43(3):420-427.

[本文引用: 2]

徐凯军, 李桐林, 张辉, 等.

基于共轭梯度法的垂直有限线源三维电阻率反演

[J]. 煤田地质与勘探, 2006, 34(3):68-71.

[本文引用: 1]

Xu K J, Li T L, Zhang H, et al.

3D resistivity inversion of vertical finite line source using conjugate gradients

[J]. Coal Geology and Exploration, 2006, 34(3):68-71.

[本文引用: 1]

Cao X Y, Huang X, Yin C C, et al.

3D MT anisotropic inversion based on unstructured finite-element method

[J]. Journal of Environmental & Engineering Geophysics, 2021, 26(1):49-60.

[本文引用: 1]

惠哲剑, 殷长春, 刘云鹤, 等.

基于非结构有限元的时间域海洋电磁三维反演

[J]. 地球物理学报, 2020, 63(8):3167-3179.

[本文引用: 1]

Hui Z J, Yin C C, Liu Y H, et al.

3D inversion of time-domain marine EM data based on unstructured finite-element method

[J]. Chinese Journal of Geophysics, 2020, 63(8):3167-3179.

[本文引用: 1]

余辉, 邓居智, 陈辉, 等.

起伏地形下大地电磁L-BFGS三维反演方法

[J]. 地球物理学报, 2019, 62(8):3175-3188.

[本文引用: 1]

Yu H, Deng J Z, Chen H, et al.

Three-dimensional magnetotelluric inversion under topographic relief based on the limited-memory quasi-Newton algorithm(L_BFGS)

[J]. Chinese Journal of Geophysics, 2019, 62(8):3175-3188.

[本文引用: 1]

邓琰, 汤吉, 阮帅.

三维大地电磁自适应正则化有限内存拟牛顿反演

[J]. 地球物理学报, 2019, 62(9):3601-3614.

[本文引用: 1]

Deng Y, Tang J, Ruan S.

Adaptive regularized three-dimensional magnetotelluric inversion based on the LBFGS quasi-Newton method

[J]. Chinese Journal of Geophysics, 2019, 62(9):3601-3614.

[本文引用: 1]

殷长春, 朱姣, 邱长凯, 等.

航空电磁拟三维模型空间约束反演

[J]. 地球物理学报, 2018, 61(6):2537-2547.

[本文引用: 1]

Yin C C, Zhu J, Qiu C K, et al.

Spatially constrained inversion for airborne EM data using quasi-3D models

[J]. Chinese Journal of Geophysics, 2018, 61(6):2537-2547.

[本文引用: 1]

秦策, 王绪本, 赵宁.

基于二次场方法的并行三维大地电磁正反演研究

[J]. 地球物理学报, 2017, 60(6):2456-2468.

[本文引用: 1]

Qin C, Wang X B, Zhao N.

Parallel three-dimensional forward modeling and inversion of magnetotelluric based on a secondary field approach

[J]. Chinese Journal of Geophysics, 2017, 60(6):2456-2468.

[本文引用: 1]

赵宁, 王绪本, 秦策, 等.

三维频率域可控源电磁反演研究

[J]. 地球物理学报, 2016, 59(1):330-341.

[本文引用: 1]

Zhao N, Wang X B, Qin C, et al.

3D frequency-domain CSEM inversion

[J]. Chinese Journal of Geophysics, 2016, 59(1):330-341.

[本文引用: 1]

刘云鹤, 殷长春.

三维频率域航空电磁反演研究

[J]. 地球物理学报, 2013, 56(12):4278-4287.

[本文引用: 3]

Liu Y H, Yin C C.

3D inversion for frequency-domain HEM data

[J]. Chinese Journal of Geophysics, 2013, 56(12):4278-4287.

[本文引用: 3]

Avdeev D, Avdeeva A.

3D Magnetotelluric inversion using a limited-memory quasi-Newton optimization

[J]. Geophysics, 2009, 74(3):F45.

[本文引用: 1]

Xiao Y, Wei Z, Wang Z.

A limited memory BFGS-type method for large-scale unconstrained optimization

[J]. Computers & Mathematics with Applications, 2008, 56(4):1001-1009.

[本文引用: 1]

Eldad, Haber, Douglas, et al.

Inversion of time domain three-dimensional electromagnetic data

[J]. Geophysical Journal International, 2007, 171(2):B23-B34.

[本文引用: 1]

Avdeeva A, Avdeev D B.

A limited memory quasi-Newton inversion for 1D magnetotellurics

[J]. Geophysics, 2006, 71(5):G191-G196.

[本文引用: 1]

Haber E.

Quasi-Newton methods for large-scale electromagnetic inverse problems

[J]. Inverse Problems, 2005, 21(1):305-323.

[本文引用: 1]

Newman G A, Boggs P T.

Solution accelerators for large-scale 3D electromagnetic inverse problems

[J]. Inverse Problems, 2004, 20(6):S151-S170.

[本文引用: 2]

Nash S G, Nocedal J.

A numerical study of the limited memory BFGS method and the truncated-Newton method for large scale optimization

[J]. SIAM Journal on Optimization, 1991, 1(3):358-372.

[本文引用: 1]

Nocedal J.

Updating quasi-Newton matrices with limited storage

[J]. Mathematics of Computation, 1980, 35(151):773-782.

[本文引用: 1]

唐传章, 程见中, 严良俊, 等.

基于边界约束有限内存的拟牛顿CSAMT一维反演及应用

[J]. 煤田地质与勘探, 2019, 47(5):193-200.

[本文引用: 1]

Tang C Z, Cheng J Z, Yan L J, et al.

LBFGS CSAMT 1D inversion of limited memory based on boundary constraint and its application

[J]. Coal Geology and Exploration, 2019, 47(5):193-200.

[本文引用: 1]

马欢, 郭越, 吴萍萍, 等.

基于MPI并行算法的电阻率法多种装置数据的三维联合反演

[J]. 地球物理学报, 2018, 61(12):5052-5065.

[本文引用: 1]

Ma H, Guo Y, Wu P P, et al.

3-D joint inversion of multi-array data set in the resistivity method based on MPI parallel algorithm

[J]. Chinese Journal of Geophysics, 2018, 61(12):5052-5065.

[本文引用: 1]

董浩, 魏文博, 叶高峰, 等.

基于有限差分正演的带地形三维大地电磁反演方法

[J]. 地球物理学报, 2014, 57(3):939-952.

[本文引用: 1]

Dong H, Wei W B, Ye G F, et al.

Study of Three-dimensional magnetotelluric inversion including surface topography based on Finite-difference method

[J]. Chinese Journal of Geophysics, 2014, 57(3):939-952.

[本文引用: 1]

张昆, 董浩, 严加永, 等.

一种并行的大地电磁场非线性共轭梯度三维反演方法

[J]. 地球物理学报, 2013, 56(11):3922-3931.

[本文引用: 1]

Zhang K, Dong H, Yan J Y, et al.

A NLCG inversion method of magnetotellurics with parallel structure

[J]. Chinese Journal of Geophysics, 2013, 56(11):3922-3931.

[本文引用: 1]

林昌洪, 谭捍东, 舒晴, 等.

可控源音频大地电磁三维共轭梯度反演研究

[J]. 地球物理学报, 2012, 55(11):3829-3838.

[本文引用: 1]

Lin C H, Tan H D, Shu Q, et al.

Three-dimensional conjugate gradient inversion of CSAMT data

[J]. Chinese Journal of Geophysics, 2012, 55(11):3829-3838.

[本文引用: 1]

胡祖志, 胡祥云, 何展翔.

大地电磁非线性共轭梯度拟三维反演

[J]. 地球物理学报, 2006, 49(4):1226-1234.

[本文引用: 1]

Hu Z Z, Hu X Y, He Z X.

Pseudo-three-dimensional magnetotelluric using nonlinear conjugate gradients

[J]. Chinese Journal of Geophysics, 2006, 49(4):1226-1234.

[本文引用: 1]

Rodi W L, Mackie R L.

Nonlinear conjugate gradients algorithm for 2-D magnetotelluric inversion

[J]. Geophysics, 2001, 66(1):174-187.

[本文引用: 1]

Newman G A, Alumbaugh D L.

Three-dimensional magnetotelluric inversion using non-linear conjugate gradients

[J]. Geophysical Journal International, 2000, 140(2):410-424.

[本文引用: 1]

王智, 潘和平, 骆玉虎, 等.

基于不等式约束的井地电阻率法三维非线性共轭梯度反演研究

[J]. 地球物理学进展, 2016, 31(1):360-370.

[本文引用: 4]

Wang Z, Pan H P, Luo Y H, et al.

3-D hole-to-surface resistivity inversion with nonlinear conjugate gradients method under the constraint of inequality

[J]. Progress in Geophysics, 2016, 31(1):360-370.

[本文引用: 4]

王智, 潘和平, 吴爱平, 等.

基于不等式约束的井中激电三维反演研究

[J]. 石油物探, 2016, 55(3):455-466.

[本文引用: 3]

Wang Z, Pan H P, Wu A P, et al.

3D inversion of borehole induced polarization under the inequality constraint

[J]. Geophysical Prospecting for Petroleum, 2016, 55(3):455-466.

[本文引用: 3]

Kim H J, Song Y, Lee K H.

Inequality constraint in least-squares inversion of geophysical data

[J]. Earth, Planets and Space, 1999, 51(4):255-259.

[本文引用: 2]

Li Y, Oldenburg D W.

3-D Inversion of induced polarization data

[J]. Geophysics, 2000, 65(6):1931-1945.

[本文引用: 2]

黄俊革, 阮百尧, 鲍光淑.

基于有限单元法的三维地电断面电阻率反演

[J]. 中南大学学报:自然科学版, 2004, 35(2):295-299.

[本文引用: 1]

Huang J G, Ruan B Y, Bao G S.

Resistivity inversion on 3-D section based on FEM

[J]. Journal of Central South University:Science and Technology, 2004, 35(2):295-299.

[本文引用: 1]

宛新林, 席道瑛, 高尔根, 等.

用改进的光滑约束最小二乘正交分解法实现电阻率三维反演

[J]. 地球物理学报, 2005, 48(2):439-444.

[本文引用: 1]

Wan X L, Xi D Y, Gao E G, et al.

3-D resistivity inversion by the least-squares QR factorization method under improved smoothness constraint condition

[J]. Chinese Journal of Geophysics, 2005, 48(2):439-444.

[本文引用: 1]

刘斌, 李术才, 聂利超, 等.

基于自适应加权光滑约束与PCG算法的三维电阻率探测反演成像

[J]. 岩土工程学报, 2012, 34(9):1646-1653.

[本文引用: 1]

Liu B, Li S C, Nie L C, et al.

Inversion imaging of 3D resistivity detection using adaptive-weighted smooth constraint and PCG algorithm

[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(9):1646-1653.

[本文引用: 1]

刘斌, 李术才, 李树忱, 等.

基于不等式约束的最小二乘法三维电阻率反演及其算法优化

[J]. 地球物理学报, 2012, 55(1):260-268.

[本文引用: 2]

Liu B, Li S C, Li S C, et al.

3D electrical resistivity inversion with least-squares method based on inequality constraint and its computation effciency optimization

[J]. Chinese Journal of Geophysics, 2012, 55(1):260-268.

[本文引用: 2]

刘斌, 聂利超, 李术才, 等.

三维电阻率空间结构约束反演成像方法

[J]. 岩石力学与工程学报, 2012, 31(11):2258-2268.

[本文引用: 1]

Liu B, Nie L C, Li S C, et al.

3D electrical resistivity inversion tomography with spatial structural constraint

[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(11):2258-2268.

[本文引用: 1]

底青云, 薛国强, 殷长春, 等.

中国人工源电磁探测新方法

[J]. 中国科学:地球科学, 2020, 50(9):1219-1227.

[本文引用: 1]

Di Q Y, Xue G Q, Yin C C, et al.

New methods of controlled-source electromagnetic detection in China

[J]. Science China Earth Sciences, 2020, 50(9):1219-1227.

[本文引用: 1]

殷长春, 刘云鹤, 熊彬.

地球物理三维电磁反演方法研究动态

[J]. 中国科学:地球科学, 2020, 50(3):432-435.

[本文引用: 1]

Yin C C, Liu Y H, Xiong B.

Status and prospect of 3D inversions in EM geophysic

[J]. Science China Earth Sciences, 2020, 50(3):432-435.

[本文引用: 1]

Nocedal J, Wright S J, Mikosch T V, et al.

Numerical Optimization

[M]. Berlin:Springer, 1999.

[本文引用: 3]

徐世浙. 地球物理中的有限单元法[M]. 北京: 科学出版社, 1994.

[本文引用: 1]

Xu S Z. FEM in geophysics[M]. Beijing: Science Press, 1994.

[本文引用: 1]

韩波, 胡祥云, 何展翔, 等.

大地电磁反演方法的数学分类

[J]. 石油地球物理勘探, 2012, 47(1):177-188.

[本文引用: 1]

Han B, Hu X Y, He Z X, et al.

Mathematical classification of magnetotelluric inversion methods

[J]. Oil Geophysical Prospecting, 2012, 47(1):177-188.

[本文引用: 1]

Siripunvaraporn W.

Three-dimensional magnetotelluric inversion: An introductory guide for developers and users

[J]. Surveys in Geophysics, 2012, 33(1):5-27.

[本文引用: 1]

Geuzaine C, Remacle J F.

Gmsh: A three-dimensional finite element mesh generator with built-in pre-and post-processing facilities

[J]. International Journal for Numerical Methods in Engineering, 2009, 79(1):1309-1331.

[本文引用: 1]

Ahrens J, Geveci B, Law C. ParaView: An end-user tool for large data visualization[M]. New York: Academic Press, 2005.

[本文引用: 1]

Ellis R G, Oldenburg D W.

The pole-pole 3-D Dc-resistivity inverse problem:A conjugategradient approach

[J]. Geophysical Journal of the Royal Astronomical Society, 1994, 119(1):187-194.

[本文引用: 1]

Li Y, Oldenburg D W.

Inversion of 3-D DC resisitivity data using an approximate inverse mapping

[J]. Geophysical Journal International, 1994, 116(4):527-537.

[本文引用: 1]

/

〈 〉

京ICP备05055290号-3
版权所有 © 2021《物探与化探》编辑部
通讯地址：北京市学院路29号航遥中心 邮编：100083
电话：010-62060192；62060193 E-mail：whtbjb@sina.com , whtbjb@163.com