希尔伯特—黄变换(HHT)在EH-4数据去噪处理中的应用

doi:10.11720/wtyht.2022.1437

希尔伯特—黄变换(HHT)在EH-4数据去噪处理中的应用

黄泽佼^,¹^,², 徐子东^,¹^,², 罗晗², 黄远生²

1.海南省海洋地质资源与环境重点实验室,海南海口 570206

2.海南水文地质工程地质勘察院,海南海口 571100

Application of Hilbert-Huang transform in EH-4 data processing

HUANG Ze-Jiao^,¹^,², XU Zi-Dong^,¹^,², LUO Han², HUANG Yuan-Sheng²

1. The key Laboratory of Marine Geological Resources and Environment of Hainan Province,Haikou 570206,China

2. Hainan Investigation Institute of Hydrogeology and Engineering Geology, Haikou 571100, China

通讯作者: 徐子东(1985-),男,硕士研究生,2009年毕业于中国地质大学(武汉),长期从事水文地质调查及物探资料解释方面的研究工作。Email:70199117@qq.com

责任编辑: 王萌

收稿日期: 2021-08-12 修回日期: 2021-12-6

Received: 2021-08-12 Revised: 2021-12-6

作者简介 About authors

黄泽佼(1989-),男,硕士研究生,2015年毕业于中国地质大学(武汉),主要从事电磁数据处理,正、反演与解释方面的研究工作。Email:1020236730@qq.com

摘要

工频噪声源于社会生产活动中产生的电磁噪声,常会造成视电阻率曲线病态或发散。为了提高数据处理与解释的精度,本文针对EH-4数据中常见的工频噪声,采用希尔伯特—黄变换进行去噪处理,通过对实际数据的时间序列处理分析可知,该方法利用数据自身的时间尺度特征自适应地分解信号,能够很好地去除工频噪声,为大地电磁信号的去噪提供了一条有效的路径。另外,本文还针对经验模态分解过程中产生严重的模态混叠及“端点效应”进行分析,运用聚合经验模态(EEMD)对仿真信号及实测数据的时间序列进行分解,有效地解决了模态混叠等问题。

关键词： EH-4去噪; 经验模态法(EMD); 希尔伯特—黄变换(HHT); 聚合经验模态(EEMD)

Abstract

Industrial frequency noise comes from the electromagnetic noise produced in social activities, and it causes apparent resistivity curves to become pathological or divergent. To improve the accuracy of data processing and interpretation, this study used the Hilbert-Huang transform (HHT) to remove the common power frequency noise in EH-4 data. According to the time series processing and analysis results of measured data, this method can self-adaptively decompose signals according to the time-scale characteristics of the data and successfully remove the industrial frequency noise in the data, thus providing an effective way to remove the noise in magnetotelluric signals. In addition, this study also analyzed the serious modal aliasing and "end effect" occurring in the process of the empirical mode decomposition and decomposed simulation signals and the time series of measured data using the ensemble empirical mode decomposition (EEMD), effectively solving problems such as modal aliasing.

Keywords： EH-4 data denoising; empirical mode decomposition(EMD); Hilbert-Huang transform; ensemble empirical mode decomposition (EEMD)

PDF (5973KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

黄泽佼, 徐子东, 罗晗, 黄远生. 希尔伯特—黄变换(HHT)在EH-4数据去噪处理中的应用[J]. 物探与化探, 2022, 46(5): 1232-1240 doi:10.11720/wtyht.2022.1437

HUANG Ze-Jiao, XU Zi-Dong, LUO Han, HUANG Yuan-Sheng. Application of Hilbert-Huang transform in EH-4 data processing[J]. Geophysical and Geochemical Exploration, 2022, 46(5): 1232-1240 doi:10.11720/wtyht.2022.1437

0 引言

大地电磁测深法是一种以天然交变电磁场为场源的电磁勘探方法,其特点为:信噪比弱、频带分布较宽、极易受到各种噪声的干扰,是典型非线性、非平稳信号^[1-2],加之人文干扰噪声日益加剧,严重影响了电磁勘探的处理和解释精度。自大地电磁法提出以来,随着解释需求的提高,去噪方法一直都是学者们所关心的话题。

傅里叶变换、小波变换等方法常用来分析复杂的信号,但其具有较大的局限性^[3]:傅里叶变换只适合分析频率固定的平稳信号,并不适合分析非平稳、非线性的大地电磁信号;而小波变换本质上是一种窗口可调的傅里叶变换,其窗口内的信号必须是平稳的,并没有摆脱傅里叶变换的束缚,分解效果很大程度上依赖于小波基函数的选取。另外,小波变换是非适应性的,小波基一经选定,在整个信号分析过程中是固定不变的。

1998年,美国国家航空航天局(NASA)首席专家Norden E.Huang(黄锷)院士在Proceeding of the Royal Society of London(英国皇家学会会刊)发表了一篇经典文章,一个全新的时频分析方法——希尔伯特—黄变换(Hilbert-Huang transformation, HHT)由此产生^[4-5]。通过HHT对信号进行一维经验模态分解(empirical mode decomposition, EMD),将信号分解为各阶本征模态函数(intrinsic mode function,IMF)和一个剩余分量(residue, res),各阶的IMF频率由高到低变化,且每一阶的IMF分量有其自身的物理意义。再对IMF进行Hilbert变换,可得到包含时间—能量—频率三维离散时频谱的分布特征。希尔伯特—黄变换不仅具有多分辨率的特性,而且具有自适应性,该方法的提出很好地解决了非线性、非平稳信号的时频分析问题^[6-7]。化希瑞、汤井田等^[8-9]引入HHT方法对EH-4原始时间序列进行时频分析,根据EMD将复杂信号分解为随频率变换的各阶本征模态函数,对受干扰的原始时间序列进行处理,得到了很好的效果。但是其文章没有对EMD分解存在的一些问题,如“模态混叠”、“端点效应”等进行讨论及处理。

本文主要针对EH-4数据中常见的干扰噪声——工频噪声,采用希尔伯特—黄变换(HHT)进行去噪处理。对于工频噪声,由于我国工业电流的基频并不是稳定的50 Hz,而是在其左右波动,应用其他的去噪方法效果不佳,尤其是陷波法。本文采用希尔伯特—黄变换(HHT)对实测的时间序列进行EMD分解,结合各阶本征模态分量(IMF)的希尔伯特谱,在一定程度上能将工频噪声的影响去除,但从重构后的信号上看,EMD分解过程中会产生严重的“模态混叠”^[10]及“端点效应”。针对此问题,本文引入聚合经验模态(EEMD)法,很好地抑制了“模态混叠”及“端点效应”。通过实测数据表明,基于聚合经验模态(EEMD)的希尔伯特—黄变换(HHT)是一种有效的去噪手段,为大地电磁信号的去噪提供了一条有效的路径。

1 大地电磁信号噪声干扰分类及工频噪声的特点

严家斌^[11]将噪声归类分为:人文噪声、随机噪声、场源噪声和地质噪声。有些干扰信号在时间序列上具有明显特征,如工频噪声等;有的干扰信号在频率域上有很强的特征,如地磁噪声等;而有的干扰信号在时间域上和频率域上均无任何明显特征,如地质噪声等。所以,噪声类型不同,其表现出的电磁特征也是不一样,因此,在物探工作过程中,研究噪声的形成机制、分布特征及规律以及压制与消除噪声的方法是至关重要的。

本文主要考虑的是人文噪声中尤为常见的工频噪声。人文噪声源于社会生产活动中产生的电磁噪声,主要有高压电线、无线电通讯、铁路公路等。人文噪声的信号强度比天然电磁信号强几十甚至几百倍,常会造成视电阻率曲线病态或发散,严重影响电磁勘探的效果,因此在采集数据时尽可能要偏离供电线,最好是能协调当地供电部门停电。但是有时不可避免的会在有供电环境的干扰下进行信号的观测采集,当外在环境影响无法剔除时,这就迫切需要数据处理技术的提高,所以,如何在强工频干扰的环境下提取弱的有效信号就显得尤为重要了。

2 HHT在工频噪声去除中的应用

2.1 经验模态分解(EMD)分解过程

经验模态分解就是将信号 $x (t)$ 分解成一系列满足条件的IMF的过程,具体实现步骤^[3,12⇓-14](图1)为:

图1

新窗口打开| 下载原图ZIP| 生成PPT

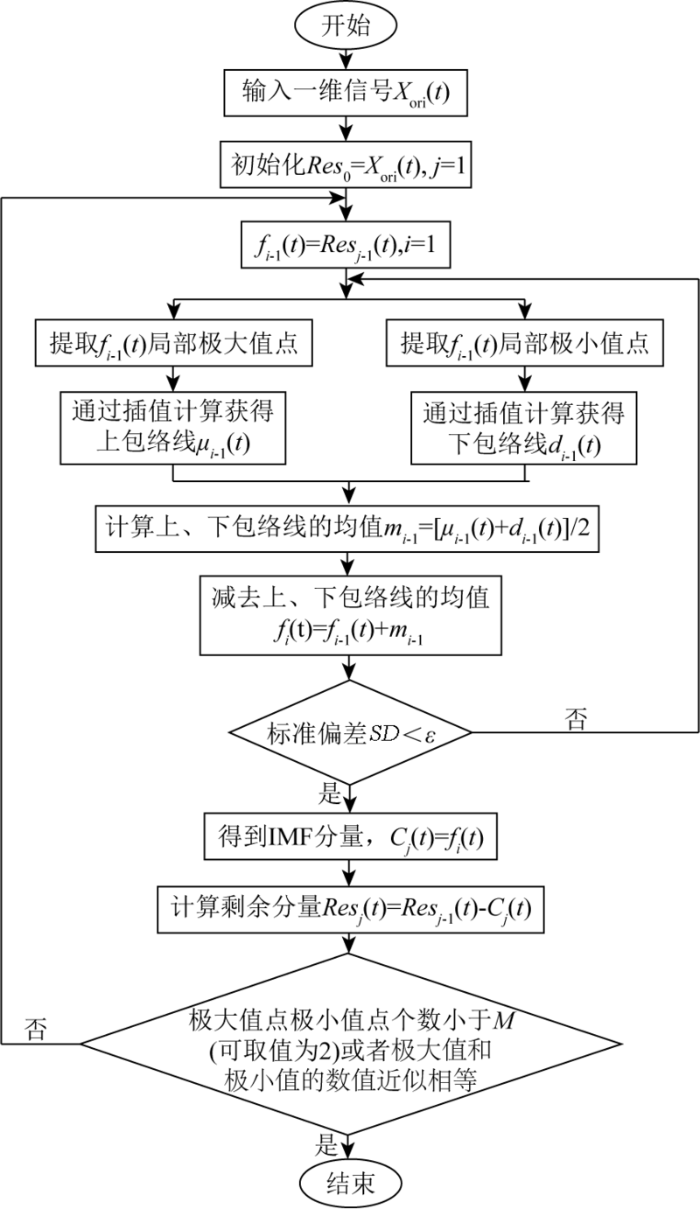
图1 一维经验模态分解的筛分流程

Fig.1 Sieve graph divided by empirical mode decomposition(EMD)

1)获得信号 $x (t)$ 全部极值点,并通过插值方法构建上下包络线的线性方程 $μ_{0} (t)$ 、 $d_{0} (t)$ ,一般常用的插值方法为三次样条插值。

2)通过上下包络线曲线方程计算得到平均值曲线,得到 $m_{0} (t) = [μ_{0} (t) + d_{0} (t)] / 2$ ;记 $h_{1} (t) = x (t) - m_{0} (t)$ 。

3)判断 $h_{1} (t)$ 是否满足上面的IMF条件,若不满足,令 $x (t) = h_{1} (t)$ ,重复步骤1)、2),直到 $h_{n} (t)$ 满足IMF条件,记 $c_{1} = h_{n} (t)$ ,即得到第一个IMF。

4)将原始信号减去 $c_{1} (t)$ ,得到分解剩余项,即 $R e s_{1} (t) = x (t)$ ,对 $R e s_{1} (t)$ 重复前4个步骤的分解,即可获得一系列的单分量信号 $c_{i} (t) (i = 1,2, \dots, n) 。$

5)事先给定特定的值,当剩余项小于该值时,则分解结束,可得:

$x (t) = \overset{n}{\sum_{i = 1}} c_{i} (t) + R e s_{n} (t)$ 。

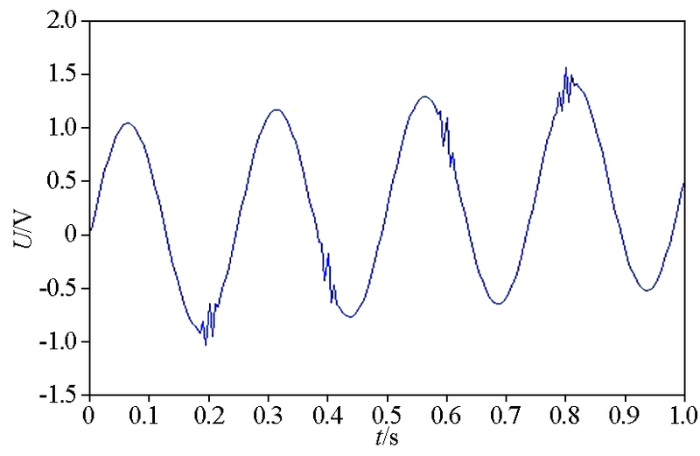
2.2 经验模态分解(EMD)的模态混叠问题

当信号存在跳跃性变化或是间断时,分解过程中一些时间尺度就会丢失,信号本身存在的极值点分布不均匀,这时就会造成分解的混乱,出现模态混叠的情况,这时候所分解得到的各阶IMF分量就不存在所谓的物理意义。模态混叠包括两个方面:①一个本征模态函数IMF中同时包含了不属于同一频率内的两个频率;②同一个本征模态函数包含了尺度差异较大的信号分量^[15⇓-17]。

建立如图2待分解的仿真信号,其中图3为模拟信号的分量。由图3可知,待分解的仿真信号由3个信号分量组成,其中有1个信号分量为间断跳跃性信号、1个正弦信号及1个线性信号。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 待分解的仿真电压信号

Fig.2 The simulation voltage signal to be decomposed

图3

新窗口打开| 下载原图ZIP| 生成PPT

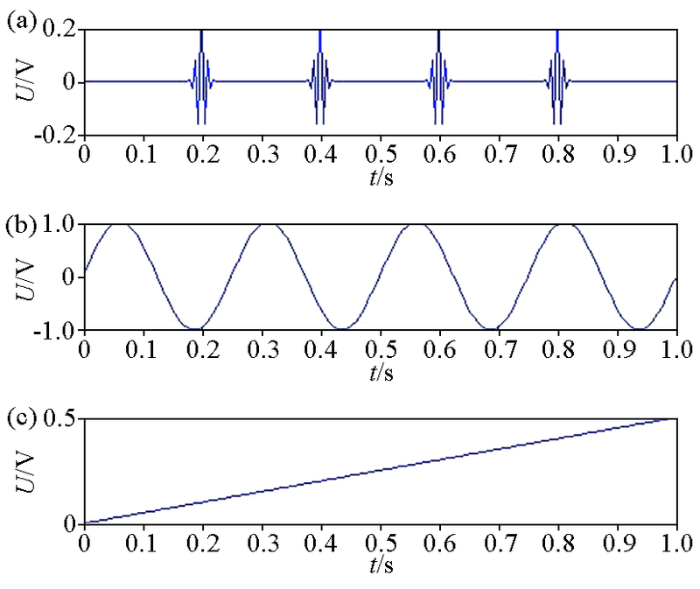
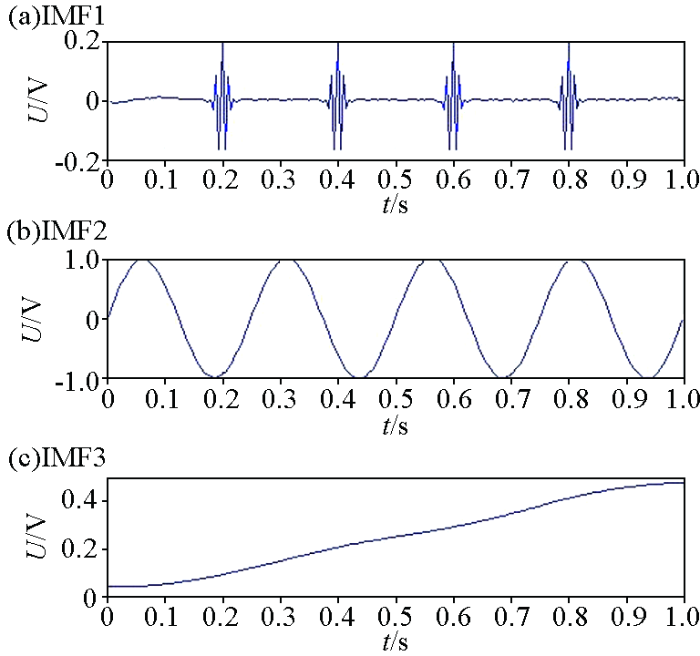
图3 模拟信号的分量

a—间断性跳跃信号;b—正弦信号;c—线性信号

Fig.3 The components of simulation signal

a—intermittent skip signal; b—sinusoidal signal; c—linear signal

运用EMD方法对待分解的仿真信号进行经验模态分解,得到如图4。从原理上分析,由于待分解的信号中存在间断性跳跃信号,会造成包络线的突变,EMD分解时会出现模态混叠现象。事实上,从图4中可知,各阶的IMF分量,即不同的频率之间互相干扰严重,EMD并不能够将待分解的3个信号分量完全分解出来。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 EMD分解结果

Fig.4 The result of EMD decomposition

图5为某工区的实测数据,由图5原始信号可以明显地看到,数据受到了很强的工频干扰,完全无法观察到天然电磁场的特性。将实际信号通过EMD自适应地分解得到18阶固有本征模态函数(IMF),如图5(b)~(s)所示。通过分析可知,IMF5~IMF10分量包含了不属于同一频率段的信息,每一阶的IMF分量并没有表现出某一尺度范围的模态,即同一阶的IMF分量表现出两个甚至多个频率的信息,各阶IMF分量彼此间出现了严重的模态混叠现象。

图5

新窗口打开| 下载原图ZIP| 生成PPT

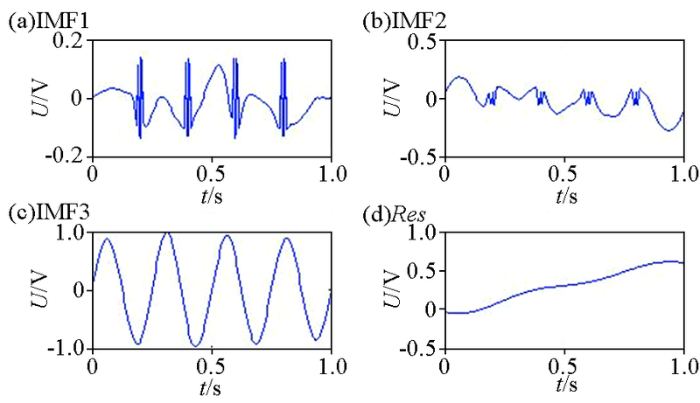
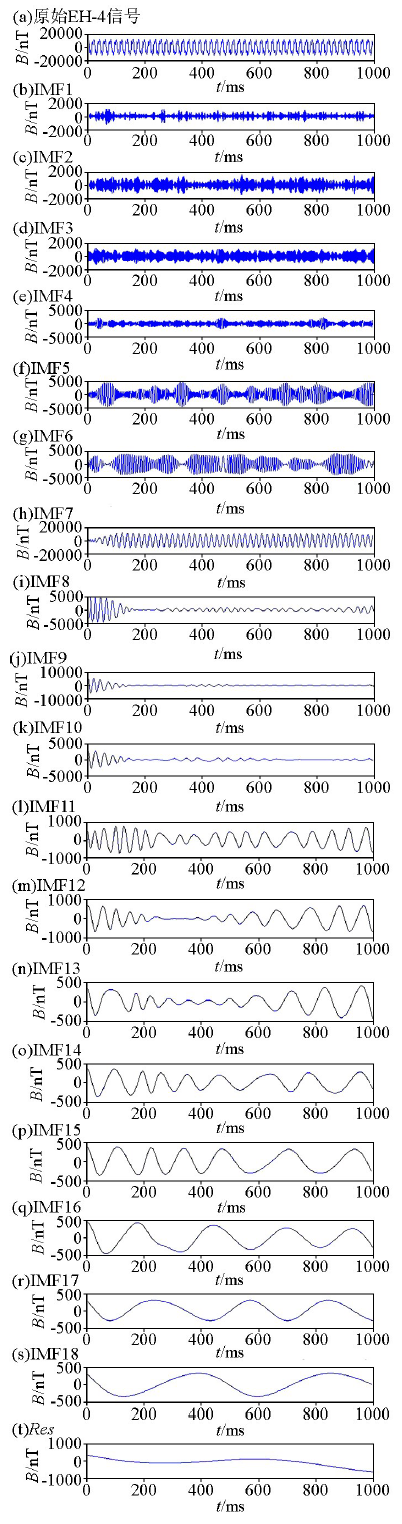
图5 实测EH-4信号EMD分解及各阶本征模态函数

Fig.5 EMD decomposition and levels of intrinsic mode function based on measured EH-4 signal

2.3 聚合经验模态分解(EEMD)抑制模态混叠

EEMD的目的在于使白噪声相互抵消,其原理^[18]为:高斯白噪声的频率分布很均匀,当信号混入高斯白噪声之后,信号的极值点就会发生改变,使极值点分布更为均匀,包络线不存在畸变的现象,从而抑制了模态混叠现象。另外,高斯白噪声具有随机性,每次加入的噪声信号都是独立的,所以,只有加入了足够的噪声组,利用噪声的不相关性使其均值为零,才能消除高斯白噪声对真实信号的影响。EEMD的分解步骤^{[15⇓⇓-18]}为:

1)在原始信号x(t)的N次分解时(N>1)加入均值为零的高斯白噪声;

2)对加有高斯白噪声的信号进行EMD分解,得到K个IMF和一个剩余分量Res;

3)由于高斯白噪声属于随机噪声,具有不相关的特性,其均值为零。将各阶相对应的IMF分量进行求和取总平均,以消除多次加入高斯白噪声对真实IMF和Res的影响,得到最终EEMD分解结果。

对上一节提到的仿真信号采用EEMD进行分解:由图6可知,通过加入的白噪声,EEMD分解很好地分离了3个模拟信号分量,模态混叠现象得到了很好地抑制,使得到的各阶IMF分量有实质的物理意义。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 EEMD分解结果

Fig.6 The result of EEMD decomposition

上小节提到,对实测数据的原始时间序列进行EMD分解,由于模态混叠现象,在信号重构的过程中就有可能导致有效信号也被剔除,各阶IMF分量也失去了分解的意义。对此,本文采用EEMD方法对原始数据进行分解处理。本次EEMD分解采用的噪声方差为0.01,组数为400的白噪声,经分解得到各阶本征模态函数,见图7。由图7可知,各阶的IMF分量只包含其自身频率相近的信号成分,EMD分解中的模态混叠现象已经被EEMD完全抑制。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 实测信号EEMD分解及各阶本征模态函数

Fig.7 EEMD decomposition and each intrinsic mode function based on measured EH-4 signal

2.4 HHT去噪过程分析

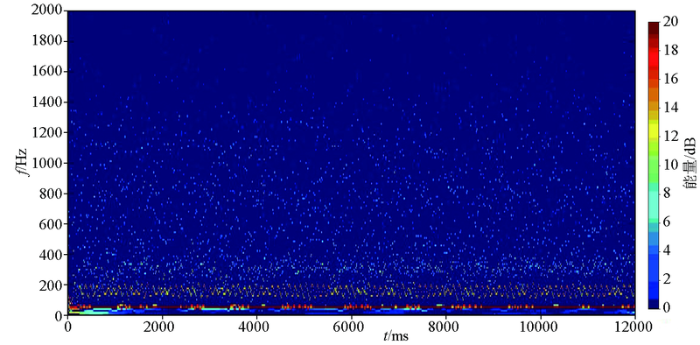
图8为信号通过HHT变换后得到的时间—能量—频率三维离散时频谱。EH-4低频段的频率为10~1 000 Hz,从希尔伯特谱上可以看出,这个区域内的能量很强,且分布不均匀。在0~200 Hz内可以看到,50 Hz左右有一红色的、能量很强且频率固定的水平条带;另外在150 Hz左右也存在类似的高能量水平条带。可以判断这2个能量高的条带是由50 Hz及其谐波所引起的工频噪声。另外,从希尔伯特谱也可以看到,图中的能量点越多就表示被分解的信号的能量就越强,越有利于数据的处理与解释。所以,在实际数据处理中,可以通过时间序列的希尔伯特谱,将能量弱的叠加去除,保留能量强的叠加,这样在一定程度上可以增加信号的信噪比。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 EH-4实测信号时间—频率—能量希尔伯特谱

Fig.8 Time-frequency-energy spectrum of EH-4 signal

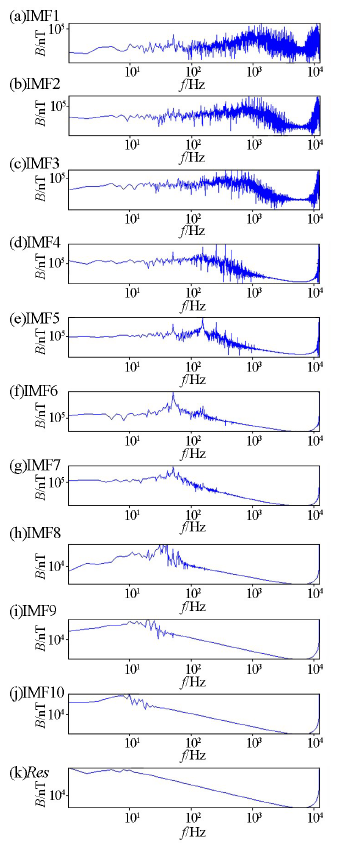
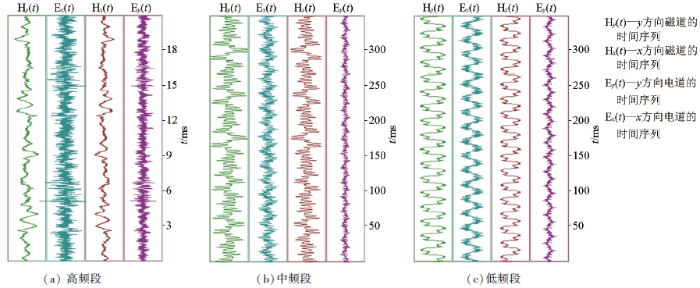
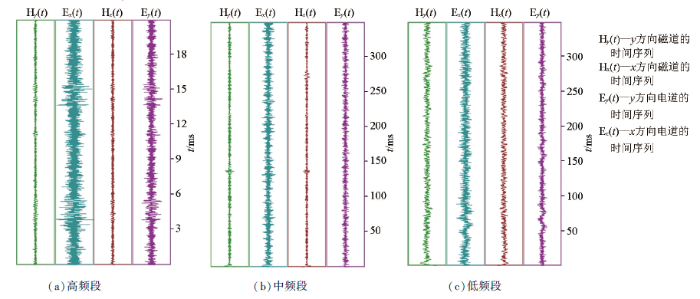
将EEMD分解的各阶本征模函数做希尔伯特变换,进行频谱谱分析,得到图9。分析找出哪阶IMF是由于工频电引起的,将该阶IMF置零,然后将信号进行重构,重构信号在一定程度上就能消除工频电的干扰。从图9可知,在频率域中,EEMD分解过程表现为从高频到低频的滤波过程。具体表现为:IMF1~IMF4分量能够很好地体现原始电磁信号的高频细节信息;IMF5分量在150 Hz左右幅值表现为突然性的“尖窄”跳跃且变化较大,同样IMF6分量及IMF7分量在50 Hz左右幅值也存在同一规律的异常跳跃;IMF8~IMF10能够很好地体现原始电磁信号的低频细节信息。综上所述,从各阶本征模态分量的频谱中可以看出IMF5~IMF7分量中包含了异常信息且与工频噪声的特征吻合较好,应作为噪声源去掉。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 EEMD分解的各阶IMF分量的频谱

Fig.9 The frequency spectrum of IMF decomposed by EEMD

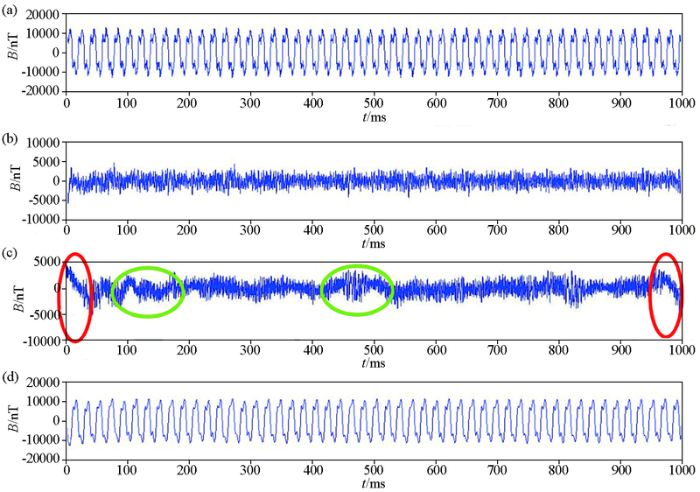
分别将EMD与EEMD分析处理后的信号进行重构,可得图10。由EMD 分解重构后的信号可知,在重构后信号的首部和尾部出现了信号的变形(如图中红框内所示),这种现象称之为“端点效应”^[5]。这种现象引起的原因为,当信号的边界端点不是极值点时,这就导致构成上下包络线的三次样条曲线在数据序列的两端出现发散。解决的方式有两种:其一,对于短数据序列,可以将原始信号进行扩边,即对原始数据的首尾各加一定量的数值,在运算结束后进行裁边,恢复序列的原始长度。另一种方法为“掐头去尾”^[19-20]。另外,其重构后的信号局部有非正常的起跳(如图中绿框内所示),预测其引起的原因为由于模态混叠的原因将过多的IMF分量删除,使相应的有效信号丢失所造成。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 去噪后信号重构结果

a—原始信号;b—EEMD分解重构后的信号;c—EMD分解重构后的信号;d—信号重构后的误差

Fig.10 The result of signal reconfiguration after denoising

a—original signal ;b—signal reconfiguration decomposed by EEMD;c—signal reconfiguration decomposed by EMD; d—the error of signal reconstruction

由EEMD 分解重构后的信号可知,EEMD在一定的程度上解决了边界问题所引起的“端点效应”,且重构的信号其间没有不正常的波动,可见模态混叠现象得到明显的抑制,信号恢复了天然信号所具备的特点,信号分解重构后的误差正是所去除的工频噪声,信号整体上平稳变化且频率是固定的。

3 EH-4去工频噪声实例分析

图11为某勘查区某测点的EH-4时间序列,该点旁有输电线,采集受到严重的干扰。由图11可知,测点高频段的电道未见明显的工频干扰,高频段的磁道、中频段的电道磁道及低频段的电道磁道均受到工频干扰较为明显。本文采用的噪声组数为200组,均方差0.001,根据上述EEMD分析方法,去除工频噪声并将信号进行重构,将重构后的时间序列写成二进制Y文件,导入EH-4自带的处理系统IMAGEM。去噪后的时间序列如图12所示,各频段的噪声得到了很好地压制。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 某测点的原始时间序列示意

Fig.11 The original time series of measuring point

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 去工频噪声后的时间序列示意

Fig.12 The time series after de-noising power frequency

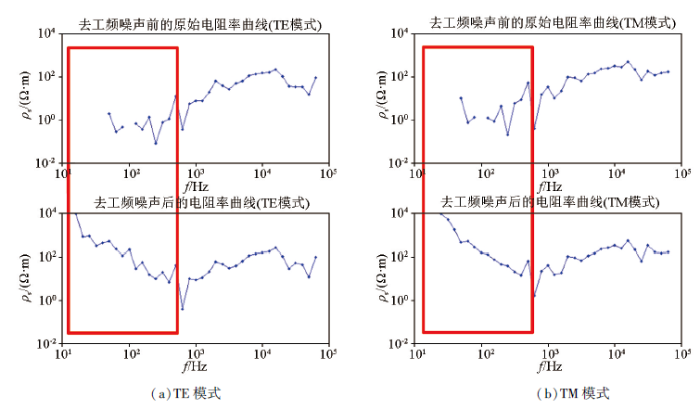
通过IMAGEM软件处理所得到的阻抗视电阻率曲线如图13所示,图中红色框线显示:无论是TE还是TM模式,中、低频信号在未去除工频噪声之前,有效信号被严重压制,视电阻率曲线出现了病态或发散的现象,曲线在中、低频段存在大量的缺点、间断,走势形态完全无法判断。而在中、低频信号去除工频噪声之后,视电阻率曲线的中低频段曲线缺点及间断现象得到较好地改善,曲线的走势形态趋于明显,尤其是TM模式,中、低频的电阻率曲线更加的平滑。可见,去噪的效果很明显。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 TE模式(a)和TM模式(b)去工频噪声前后视电阻率曲线对比

Fig.13 Contrast of apparent resistivity curve of TE mode(a) and TM mode(b) before and after de-noising power frequency

4 结论

本文研究了EH-4数据处理的方法,以工频噪声作为主要研究对象,通过分析得出以下结论:

1) 通过对野外实测大地电磁信号进行希尔伯特—黄(HHT)变换、二维Hilbert时频分析,结果显示HHT变换能充分体现大地电磁信号的特征,该方法在一定程度能去除工频干扰噪声。本文应用聚合经验模态分解(EEMD)法,通过实际数据的处理,较好地抑制了EMD分解所引起的模态混叠现象,在去除信号的同时保留了更多有效信号,在一定程度上也很好地解决了“端点效应”的问题。

2) 采用基于EEMD的HHT变换对实际数据进行去噪,在中、低频信号去除工频噪声之后,视电阻率曲线的中、低频段曲线间断的现象得到明显的改善,曲线的走势形态趋于明显,充分说明基于EEMD的HHT变换在去工频噪声中的可行性。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

王书明, 王家映.

大地电磁信号统计特征分析

[J]. 地震学报, 2004, 26(6): 669-674.